滚动轴承作为机械设备的重要传动部件,其工作状况对设备产生极大的影响。滚动轴承的故障往往会降低设备的可靠性和精度,不仅影响生产,减少设备寿命,甚至会造成事故。目前,滚动轴承的故障诊断研究集中在故障特征提取和故障模式识别,这是实现滚动轴承智能状态检测与诊断的核心技术,其主要研究对象为滚动轴承的振动信号。当滚动轴承存在局部损坏时会产生周期性冲击,轴承的故障信息则隐含在冲击信号的频率特征中。然而,滚动轴承的工作环境一般较为复杂,受工作环境影响,实际采集到的振动信号通常会被淹没在噪声中; 因此如何从强背景噪声中提取故障特征是进行轴承故障诊断的重点。在损伤故障发生的初期,强噪声淹没下的微弱故障特征的提取和识别是防止故障恶化和加强故障诊断及时性的关键。
文献[1]提出变分模态分解(VMD)与最大相关峭度解卷积(MCKD)相结合的方法;文献[2]提出了基于最优参数MCKD与总体局部均值分解方法相结合的轴承复合故障诊断方法,皆证明了MCKD算法在提取噪声中的周期成分时具有显著的优势。但MCKD的降噪能力有限,尤其在故障产生早期,且信噪比较低的情况下效果并不理想,需要增强故障的瞬态特征。文献[3-4]通过计算重构信号的Teager能量谱来突出故障冲击特征,基于Teager能量算子对瞬态特征的有效分析实现了良好的去噪效果。因此,本文提出了MCKD算法与Teager能量算子相结合的故障特征提取方法。首先,采用MCKD算法对原始信号降噪,检测信号中的周期成分;然后,利用Teager能量算子增强重构信号中的周期冲击特征,实现弱周期冲击特征的有效提取。
在实现对强烈背景噪声中周期冲击特征提取的同时,需要用模式识别的方法对提取的特征参数进行诊断。随着人工智能技术的不断发展,基于深度学习的轴承故障智能诊断已成为现阶段的研究热点。文献[5-9]利用卷积神经网络对数据特征的自适应性,实现了故障模式的智能识别。虽然卷积神经网络在诊断结果上可以得到较高的精度,但是存在一个主要问题,即卷积神经网络及一般的机器学习模型对以时间序列作为输入的数据,其前后关联性不强。
滚动轴承的振动数据是一种具有时间连续性的一维信号数据,充分利用数据的时间相关性是实现滚动轴承故障识别的关键。因此,本文提出以长短期神经网络(LSTM)对Teager能量时间序列进行端到端故障诊断的方法。LSTM是时间序列模型,其特点是通过“门”结构控制神经网络中每个时刻的信息状态,能持续记忆多时刻信息,挖掘数据在时间上的相关性。本文中,MCKD与Teager能量算子过滤后的信号具有强时序特征的性质,因此LSTM在对滚动轴承振动信号的时序特征识别上更具有优势。
1 滚动轴承故障特征的提取 1.1 MCKD算法MCKD算法由McDonald[10]在2012年提出,因其对信号中周期成分优异的提取效果被成功运用于齿轮、轴承等机械零件的故障诊断中[11]。滚动轴承的振动信号一般为时间序列下的振动幅值,其发生故障时因出现局部碰撞会产生周期性冲击信号y=[y1 y2 ⋯ yn]。冲击信号y传递到传感器上时不仅会因传输路径的影响被衰减,而且会参杂大量的噪声。若采样点数为n,则由传感器采集到的信号可以表示为
| $ \mathit{\boldsymbol{x}} = \mathit{\boldsymbol{h}} \cdot \mathit{\boldsymbol{y}} + \mathit{\boldsymbol{e}} $ | (1) |
式中:x为传感器实际采集到的信号,h为原始信号在传输时经过的系统传递函数,e为轴承工作环境下的噪声。MCKD算法是寻找一个长度为L的滤波器f=[f1 f2 ⋯ fL],使得信号y的相关峭度最大,可以将采集信号x还原为冲击信号y,即
| $ \boldsymbol{y}=\boldsymbol{f} \cdot \boldsymbol{x}=\sum\limits_{k=1}^{L} f_{k} x_{n-k+1} $ | (2) |
MCKD以相关峭度作为评定恢复信号y性能的指标。当y的相关峭度达到最大时,则认为此时的f即为期望的目标。对于信号yn,其相关峭度定义为
| $ C{K_M}(t) = \frac{{\sum\limits_{n = 1}^N {{{\left( {\prod\limits_{m = 0}^M {{y_{n - mT}}} } \right)}^2}} }}{{{{\left( {\sum\limits_{n = 1}^N {y_n^2} } \right)}^{M + 1}}}} $ | (3) |
式中:T为解卷积的周期,一般为故障振动信号周期;M为解卷积的位移数,位移数增加则会增加周期脉冲的数量。
MCKD算法以相关峭度最大化作为目标,即
| $ \mathop {\max }\limits_T C{K_M}(T) = \mathop {\max }\limits_f \left( {C{K_M}(T)} \right) $ | (4) |
为了求解式(4),并且要得到最优滤波器f,则综合式(2)和式(3)对式(4)的等价方程进行求解:
| $ \frac{\mathrm{d} C K_{M}(T)}{\mathrm{d} f_{k}}=0 \quad(k=1, \cdots, L) $ | (5) |
将式(5)整理后得到式(6),为最优滤波器的矩阵形式[12],将得到的最优滤波器代入式(2)即可得到周期性冲击信号。
| $ \boldsymbol{f}=\frac{\left\|\boldsymbol{y}^{2}\right\|}{2\|\boldsymbol{\beta}\|^{2}}\left(\boldsymbol{X}_{0} \boldsymbol{X}_{0}^{\mathrm{T}}\right)^{-1} \sum\limits_{m=0}^{M} \boldsymbol{X}_{m T} \boldsymbol{\alpha}_{m} $ | (6) |
式中:
| $ \boldsymbol{\beta}=\left[\begin{array}{c} y_{1} y_{1-T} \cdots y_{1-m T} \\ y_{2} y_{2-T} \cdots y_{2-m T} \\ \vdots \\ y_{n} y_{n-T} \cdots y_{n-m T} \end{array}\right] $ |
| $ \boldsymbol{X}_{m T}=\left[\begin{array}{ccccc} x_{1-m T} & x_{2-m T} & x_{3-m T} & \cdots & x_{n-m T} \\ 0 & x_{1-m T} & x_{2-m T} & \cdots & x_{n-1-m T} \\ 0 & 0 & x_{1-m T} & \cdots & x_{n-2-m T} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & x_{n-l-m T+1} \end{array}\right]_{L \times n} $ |
| $ \boldsymbol{\alpha}_{m}=\left[\begin{array}{c} y_{1-m T}^{-1}\left[y_{1}^{2} y_{1-T}^{2} \cdots y_{1-m T}^{2}\right] \\ y_{2-m T}^{-1}\left[y_{2}^{2} y_{2-T}^{2} \cdots y_{2-m T}^{2}\right] \\ \ \ \ \ \ \ \ \ \ \ \ \vdots \\ y_{n-m T}^{-1}\left[y_{n}^{2} y_{n-T}^{2} \cdots y_{n-m T}^{2}\right] \end{array}\right] $ |
根据轴承的参数和转动频率求解滚动轴承的故障频率, 得到解卷积周期T=1/f,而故障频率指的是滚动体滚过内圈或外圈某固定点的频率:
| $ \left\{\begin{array}{l} f_{\text {ic }}=\frac{1}{2} Z\left(1+\frac{d}{D} \cos \alpha\right) f_{\mathrm{r}} \\ f_{\text {oc }}=\frac{1}{2} Z\left(1-\frac{d}{D} \cos \alpha\right) f_{\mathrm{r}} \\ f_{\mathrm{b}}=\frac{1}{2} \frac{D}{d}\left(1-\left(\frac{d}{D}\right)^{2} \cos ^{2} \alpha\right) f_{\mathrm{r}} \end{array}\right. $ | (7) |
式中:fic为滚动轴承内圈故障频率,foc为外圈故障频率,fb为滚动体的故障频率,fr为转频,d和D分别为滚动体和节圆的直径,Z为滚动体数目,α为轴承接触角。
1.2 Teager能量算子Teager能量算子是一种非线性算子[13],可以理解为信号的能量,可通过对振动信号的瞬时值及其微分进行非线性组合来放大信号的瞬态能量成分,从而增强冲击特征。对于连续时间信号x(t),Teager能量算子的定义为
| $ \varphi[x(t)]=[\dot{x}(t)]^{2}-x(t) \ddot{x}(t) $ | (8) |
式中:ẋ(t)和ẍ(t)分别为连续时间信号x(t)的一阶和二阶导数,φ[x(t)]为连续时间信号的瞬时能量值。
若x(t)为离散信号,则用差分代替微分,Teager能量算子被近似定义为
| $ \varphi[x(n)]=[x(n)]^{2}-x(n+1) x(n-1) $ | (9) |
由式(9)可以看出,对于离散时间信号,只要已知当前时刻和前、后时刻的样本,即可计算出当前时刻的Teager能量。Teager能量算子中包含了信号的微分项,考虑了信号的瞬时频率,对信号中的瞬态成分十分敏感。相比于主要考虑信号幅值的传统信号能量算子,Teager能量算子可以增强背景噪声信号中的高频冲击特征,适合处理经过MCKD重构后的信号。
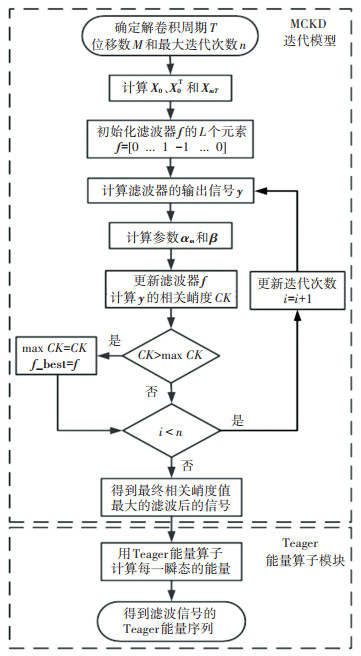
1.3 基于MCKD和Teager能量算子的滚动轴承故障特征提取方法滚动轴承的故障信号为非平稳信号,往往被淹没在强背景噪声中,其故障特征提取难度较大。为了从采集到的受噪声严重污染的信号中还原出原始信号的周期冲击故障特征,采用MCKD算法对信号降噪,但MCKD算法在故障产生初期且信噪比较低的情况下效果并不理想。因此,本文结合MCKD算法与Teager能量算子的优势,用Teager能量算子对MCKD算法重构后的信号进行计算,增强重构信号中的周期冲击特征。图 1为提取滚动轴承故障特征的流程图。
|
图 1 MCKD-Teager能量算子故障特征提取过程 Fig. 1 Fault feature extraction process of MCKD-Teager energy operator |
其具体步骤如下:
Step 1 确定解卷积周期T,位移数M和最大迭代次数n;
Step 2 计算信号x(n)的X0, X0T和XmT;
Step 3 用L个样本初始化滤波器f,为了防止MCKD算法收敛到局部解,通常将滤波器f初始化为[0 ⋯ 1 -1 ⋯ 0];
Step 4 根据式(2)计算输出信号y;
Step 5 基于信号y计算αm和β;
Step 6 根据式(6)更新滤波器f,并计算信号y的相关峭度CK;
Step 7 若CK大于当前迭代步的最大相关峭度max CK,则max CK=CK,且最优滤波器f_best等于f。
Step 8 判断迭代次数是否大于给定阈值n,如果满足此条件或者迭代次数等于n,则终止迭代过程,否则迭代次数加1并返回Step4。
Step 9 一旦获得最优滤波器f_best,用式(2)可计算出MCKD算法的输出信号。
Step 10 根据式(9)计算MCKD输出信号中每一瞬时的能量,得到Teager能量序列。
2 基于LSTM的故障诊断方法 2.1 LSTM单元结构LSTM模型是由Hochreater等[14]提出的一种网络结构,是一种特殊的循环神经网络(RNN),通过在隐藏层的细胞单元中引入了更为复杂的门结构激活方式,有效地解决了RNN中梯度消失或梯度爆炸的问题,使模型具有学习长期依赖信息的能力[14]。
LSTM在神经元中加入输入门i、输出门o和遗忘门f。LSTM神经元结构如图 2所示。

|
图 2 LSTM单元结构 Fig. 2 LSTM cell structure |
遗忘门ft用来决定信息的遗忘和更新,其通过输入当前状态的输入信息和上一状态隐藏层的输出信息到Sigmoid函数σ中,产生0(完全舍弃)到1(完全保留)之间的值后再与上一时刻的记忆单元值相乘来确定信息的取舍。
输入门it用来选择存储到信息传送带中的信息,计算方法与遗忘门类似;临时记忆状态ct′需要在更新记忆单元ct之前计算,通过tanh函数来计算当前时刻的候选记忆单元值。
细胞状态ct为当前时刻的记忆单元值,由遗忘门、上一时刻的记忆单元值、输入门和临时记忆状态值共同作用。
输出门ot用来确定当前单元输出的信息;由Sigmoid函数产生的数值来决定。当前细胞状态值ct通过tanh函数激活后再与ot相乘,即可得到当前细胞单元的输出信息ht。
各个门的计算方法为
| $ \left\{\begin{array}{l} \boldsymbol{f}_{t}=\sigma\left(\boldsymbol{w}_{\mathrm{xf}} \boldsymbol{x}_{t}+\boldsymbol{w}_{\mathrm{hf}} \boldsymbol{h}_{t-1}+\boldsymbol{b}_{\mathrm{f}}\right) \\ \boldsymbol{i}_{t}=\sigma\left(\boldsymbol{w}_{\mathrm{xi}} \boldsymbol{x}_{t}+\boldsymbol{w}_{\mathrm{hi}} \boldsymbol{h}_{t-1}+\boldsymbol{b}_{\mathrm{i}}\right) \\ {\boldsymbol{c}^{\prime}}_{t}=\tanh \left(\boldsymbol{w}_{\mathrm{xc}} \boldsymbol{x}_{t}+\boldsymbol{w}_{\mathrm{hc}} \boldsymbol{h}_{t-1}+\boldsymbol{b}_{\mathrm{c}}\right) \\ \boldsymbol{c}_{t}=\boldsymbol{f}_{t} \boldsymbol{c}_{t-1}+\boldsymbol{i}_{t} {\boldsymbol{c}^{\prime}}_{t} \\ \boldsymbol{o}_{t}=\sigma\left(\boldsymbol{w}_{\mathrm{xo}} \boldsymbol{x}_{t}+\boldsymbol{w}_{\mathrm{ho}} \boldsymbol{h}_{t-1}+\boldsymbol{b}_{\mathrm{o}}\right) \\ \boldsymbol{h}_{t}=\boldsymbol{o}_{t} \tanh \left(\boldsymbol{c}_{t}\right) \end{array}\right. $ | (10) |
式中:wxf、wxi、wxc、wxo分别为输入层与隐藏层各个门之间的连接权值,whf、whi、whc、who分别为上一时刻的隐藏层输出与当前时刻隐藏层各个门之间的连接权值,bf、bi、bc、bo分别为隐藏层各个门的偏置向量。
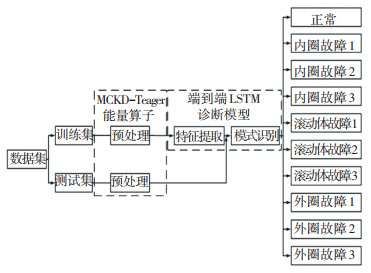
2.2 LSTM故障诊断模型滚动轴承故障诊断的目的是从众多振动信号中准确地对其中任何一种数据进行分类识别,包括学习训练、测试诊断两个过程。首先,将预处理后的训练集输入到LSTM中进行参数学习,并用ADAM算法不断更新权重w和偏置b,使得损失函数值减小。最后将训练好的参数应用于测试集,从而得到故障诊断结果,故障状态识别过程如图 3所示。
|
图 3 故障状态识别过程 Fig. 3 Fault status identification process |
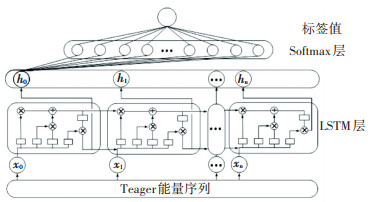
学习训练与测试诊断均包括数据预处理过程,即前文所述基于MCKD-Teager能量算子的故障特征提取方法,处理后的数据已降低了背景噪声的影响,在时间序列上有很强的故障特征信息,将会大大减少LSTM的训练成本。本文提出的端到端LSTM故障诊断模型如图 4所示。
|
图 4 端到端LSTM故障诊断模型 Fig. 4 End-to-end LSTM fault diagnosis model |
LSTM故障诊断模型包含1个LSTM单元模型层和一个Softmax逻辑层,其输入为Teager能量序列。LSTM层各单元构成的网络结构仅能通过训练集训练来获得权重,虽然具有自主学习和聚类的能力,但是不能对信号进行分类。因此在模型的顶层加入具有判别能力的Softmax回归逻辑层,以此来对不同类型的信号进行分类,其损失代价函数为
| $ J_{\theta}=-\frac{1}{m}\left[\sum\limits_{i=1}^{m} \sum\limits_{j=1}^{k}\left\{y^{(i)}=j\right\} \lg \frac{\exp \left(\boldsymbol{\theta}_{j}^{\mathrm{T}} \boldsymbol{x}^{(i)}\right)}{\sum\limits_{l=1}^{k} \exp \left(\boldsymbol{\theta}_{l}^{\mathrm{T}} \boldsymbol{x}^{(i)}\right)}\right] $ | (11) |
式中:[x(i) y(i)]为训练样本,m为样本数;y(i)为每种数据的分类标签,可以取2个及2个以上的值;x(i)为输入的信号特征;θ为使代价函数最小化的训练模型参数。
3 实验验证 3.1 CWRU数据集实验数据为美国凯斯西储大学公开的滚动轴承振动信号数据集[15]。实验用电动机转速为1 797 r/min,采样频率为12 kHz。本文选取驱动端轴承座振动信号的10种故障模式,分别为正常状态以及内圈、外圈、滚动体分别在直径0.18、0.36、0.54 mm的损伤斑点下的故障模式。每个轴承故障诊断样本序列取1 024个采样点,每类故障信号取1 000个样本,500个样本为训练集,500个样本为测试集,共建立了一个大小为10 000×1 024的数据集。
表 1为实验所用型号为SKF6205的滚动轴承参数。由式(7)可计算出故障特征频率,如表 2所示。
| 表 1 滚动轴承SKF6205参数 Tab. 1 Parameters of rolling bearing SKF6205 |
| 表 2 SKF6205故障特征参数 Tab. 2 Fault characteristic parameters of SKF 6205 |
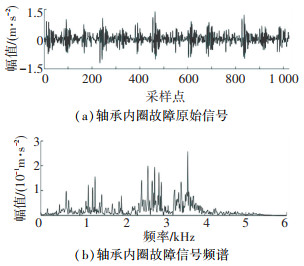
图 5为采样点数1 024、采样时长约为0.085 s、损伤直径0.18 mm的滚动轴承内圈故障原始信号和频谱图。内圈故障特征周期为74个采样间隔,其至少包含13次故障冲击。由图 5(a)可见,其周期冲击成分被噪声严重干扰,故障特征难以识别;由图 5(b)可见,中、高频处的能量较大,而内、外圈和滚动体的故障特征频率皆处于低频段,依旧难以识别。原始信号中的故障特征辨识度极差,在进行故障诊断之前需要对信号进行特征提取,充分挖掘信号中存在的故障信息。
|
图 5 轴承内圈故障原始信号及其频谱图 Fig. 5 Original signal of bearing inner ring failure and its spectrum |
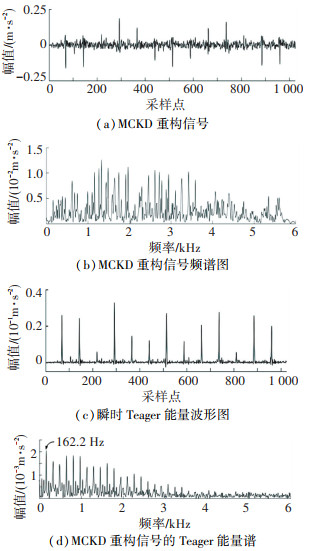
对轴承内圈故障振动信号的1 024个采样点进行MCKD-Teager能量算子特征提取。图 6(a)为以74为故障特征周期对图 5(a)信号做MCKD特征提取。与图 5(a)相比,信号中的噪声得到抑制,冲击成分得到凸显,但在图 6(b)MCKD重构信号的频谱图中信号的高频能量仍然占据较大比重。利用Teager能量算子对图 6(a)信号进行计算后得到图 6(c)所示的瞬时能量波形图,其在6(a)的基础上强烈抑制了背景噪声、冲击特征更加明显,且从其Teager能量谱图 6(d)可知,与图 5(b)、图 6(b)相比,162.2 Hz的故障特征频率处的能量值达到最高,峰值谱线突出,其倍频成分也直观可见。
|
图 6 轴承内圈故障特征提取过程 Fig. 6 Fault feature extraction process of bearing inner ring |
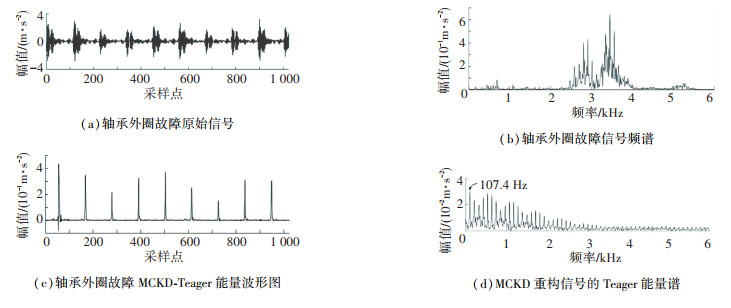
图 7(a)为滚动轴承外圈故障信号,取1 024个采样点,外圈的故障特征周期为112个采样点,则至少包含9次故障冲击。图 7为损伤直径为0.18 mm轴承外圈故障特征提取过程,由图 7(b)可知,原始信号图 7(a)中低频周期冲击能量相比于中高频成分十分微弱。原始信号经过MCKD-Teager能量算子重构后得到图 7(c),由其频谱7(d)可知107.4 Hz的故障频率能量达到最大,特征提取效果较好。
|
图 7 轴承外圈故障特征提取过程 Fig. 7 Fault feature extraction process of bearing outer ring |
将经过MCKD-Teager能量算子处理后的10种故障模式数据集输入到2.2节提出的LSTM故障诊断模型中进行训练。在不同输入作用下,分别进行了LSTM与随机森林(RF)、支持向量机(SVM)、前馈神经网络和卷积神经网络(CNN)这4种诊断模型的对比实验,结果如表 3所示,实验平台为windows10+Python,CPU采用英特尔Corei5-6300。
| 表 3 CWRU数据集在5种模型下的故障识别正确率 Tab. 3 Fault identification accuracy of CWRU data set under five models |
由表 3可知,以原始信号、MCKD重构信号和MCKD-Teager能量序列作为输入的识别正确率依次提高;5种诊断模型对原始信号的识别结果均较低;而对MCKD-Teager能量序列LSTM模型的诊断效果达到最好。
前馈神经网络的结构采用与LSTM模型结构类似的1个全连接层和1个Softmax层,CNN模型的结构为一个卷积层和一个池化层。图 8为3种网络模型(LSTM、前馈神经网络和CNN)的故障识别过程。

|
图 8 故障识别训练过程对比 Fig. 8 Comparison of fault identification training process |
图 8中,(a)、(d)、(g)为前馈神经网络诊断模型的识别结果,(b)、(e)、(h)为CNN模型的识别结果,(c)、(f)、(i)为LSTM诊断模型的识别结果。图 8(a)、(b)、(c)的输入为原始信号,可见无论是LSTM、CNN还是前馈神经网络,在测试集上的故障识别正确率均不高,30轮训练后正确率分别为77.8%、80.5%和79.5%。图 8(d)、(e)、(f)的输入为经过MCKD算法重构后的信号,可见3种模型的识别正确率有所提高,LSTM模型的正确率93.4%要高于前两种网络模型。虽然三者在训练集上的正确率都达到了100%,但训练集与测试集的差距较大。图 8(g)、(h)、(i)的输入为MCKD-Teager能量序列,LSTM诊断模型在训练集和测试集上的差距明显减小,正确率达到99.6%,显著高于前两者。
表 4、5分别为不同诊断模型在滚动轴承内圈损伤直径0.18 mm(IR018)和外圈损伤直径0.18 mm(OR018)两种故障模式下经过MCKD-Teager能量算子滤波后识别结果的混淆矩阵。由表 4、5可知,混淆矩阵得到5种诊断模型RF、SVM、前馈神经网络、CNN和LSTM在IR018、OR018两种故障模式下的识别错误率分别为10.1%、7.5%、10.5%、7.0%、0.3%和10.5%、8.6%、10.2%、6.8%、0.4%。可以看出LSTM诊断模型的错误率要低于前4种模型,识别效果较好。
| 表 4 IR018故障模式下的识别结果 Tab. 4 Confusion matrix of identification results under fault mode IR018 |
| 表 5 OR018故障模式下的识别结果 Tab. 5 Confusion matrix of identification results under fault mode OR018 |
搭建旋转机械故障实验平台,平台主要由驱动电机、测试轴承、同步带等装置组成,并使用东华测试的便携式数据采集分析系统(DH5901)来采集轴承座处的振动信号,采样频率为12.8 kHz。实验所用的轴承型号为外圈可拆卸式N205E和内圈可拆卸式NU205E,滚子数目为13个,其他参数与表 1的SKF6025参数相同。用线切割加工的方式分别在内、外圈和滚动体上加工出不同程度的损伤。转速为900 r/min时轴承的故障特征参数如表 6所示。
| 表 6 N205E/NU205E故障特征参数 Tab. 6 Fault characteristic parameters of N205E/NU205E |
实验有9种故障模式,分别是正常、滚动体轻-重两种程度的故障、内圈和外圈轻-中-重3种程度的故障。每类故障信号选取1 000个有1 024个采样点的样本,500个样本为训练集,500个样本为测试集,建立大小为9 000×1 024的数据集。
图 9为轻度故障下,滚动轴承内、外圈和滚动体故障信号经过MCKD-Teager能量算子处理后的波形图。设计了与3.1节相同的故障诊断对比实验,结果如图 10所示。通过对图 10中9张图的横向比较可以看出,前馈神经网络和CNN相比于LSTM诊断模型,因对时序特征提取效果不强,导致其在测试集和训练集上的差距较大,容易产生过拟合;而纵向比较可以看出MCKD-Teager能量算子序列处理后的信号, 识别正确率优于前两种输入,是一种挖掘信号时间相关性的特征提取方法。

|
图 9 轻度故障下MCKD-Teager能量算子特征提取图 Fig. 9 Feature extraction diagram of MCKD-Teager energy operator under mild failure |

|
图 10 实验数据集故障识别对比实验结果 Fig. 10 Comparison of fault identification results of test datasets |
表 7、8分别为不同诊断模型在滚动轴承内圈轻度故障和外圈轻度故障两种故障模式下经过MCKD-Teager能量算子滤波后识别结果的混淆矩阵。由表 7、8可知,混淆矩阵得到5种诊断模型RF、SVM、前馈神经网络、CNN和LSTM在内圈轻度故障和外圈轻度故障两种故障模式下的识别错误率分别为16.1%、15.4%、11.5%、11.3%、1.1%和15.6%、16.0%、12.0%、9.9%、1.2%,与3.1节的识别结果类似,LSTM诊断模型的错误率要低于前4种模型,具有较好的识别效果。
| 表 7 内圈轻度故障下的识别结果 Tab. 7 Confusion matrix of identification results under mild inner ring faults |
| 表 8 外圈轻度故障下的识别结果 Tab. 8 Confusion matrix of identification results under mild outer ring faults |
本文提出一种基于MCKD-Teager能量算子和LSTM的故障诊断方法。将故障信号的特征提取和识别分类结合在一起,是一种端到端的轴承故障诊断模式。首先计算滚动轴承的故障特征周期,通过MCKD-Teager能量算子提取出相应的故障特征,再进行故障识别实验,得出如下结论:
1) MCKD算法和Teager能量算子相结合的方式可以在时间序列上很好的提取出不同的故障特征,所得到的Teager能量波形序列能够在测试集上取得非常好的效果。
2) 一般的分类模型对时序特征不敏感,而本文提出的LSTM故障诊断模型能够有效地提取输入信号的时间相关性,充分利用经过MCKD-Teager能量算子处理后信号的强时序特征,显著提高故障识别正确率。
| [1] |
王建国, 陈帅, 张超. VMD与MCKD在轴承故障诊断中的应用与研究[J]. 组合机床与自动化加工技术, 2017(5): 69. WANG Jianguo, CHEN Shuai, ZHANG Chao. Application and research of VMD and MCKD in bearing fault diagnosis[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2017(5): 69. DOI:10.13462/j.cnki.mmtamt.2017.05.018 |
| [2] |
杨斌, 张家玮, 樊改荣, 等. 最优参数MCKD与ELMD在轴承复合故障诊断中的应用研究[J]. 振动与冲击, 2019, 38(11): 59. YANG Bin, ZHANG Jiawei, FAN Gairong, et al. Application of OPMCKD and ELMD in bearing compound fault diagnosis[J]. Journal of Vibration and Shock, 2019, 38(11): 59. DOI:10.13465/j.cnki.jvs.2019.11.010 |
| [3] |
张小龙, 张氢, 秦仙蓉, 等. 基于ITD-形态滤波和Teager能量谱的轴承故障诊断[J]. 仪器仪表学报, 2016, 37(4): 788. ZHANG Xiaolong, ZHANG Qing, QIN Xianrong, et al. Fault diagnosis method for rolling bearing based on ITD-morphological filter and Teager energy spectrum[J]. Chinese Journal of Scientific Instrument, 2016, 37(4): 788. DOI:10.19650/j.cnki.cjsi.2016.04.010 |
| [4] |
周洋, 向阳, 黄陈哲, 等. 基于VMD-SVD能量标准谱-Teager能量算子的轴承故障诊断方法[J]. 噪声与振动控制, 2019, 39(4): 212. ZHOU Yang, XIANG Yang, HUANG Chenzhe, et al. Bearing fault diagnosis method based on VMD-SVD energy standard spectrum and Teager energy operator[J]. Noise and Vibration Control, 2019, 39(4): 212. DOI:10.3969/j.issn.1006-1355.2019.04.039 |
| [5] |
李恒, 张氢, 秦仙蓉, 等. 基于短时傅里叶变换和卷积神经网络的轴承故障诊断方法[J]. 振动与冲击, 2018, 37(19): 124. LI Heng, ZHANG Qing, QIN Xianrong, et al. Fault diagnosis method for rolling bearings based on short-time Fourier transform and convolutional neural network[J]. Journal of Vibration and Shock, 2018, 37(19): 124. DOI:10.13465/j.cnki.jvs.2018.19.020 |
| [6] |
朱丹宸, 张永祥, 潘洋洋, 等. 基于多传感器信号和卷积神经网络的滚动轴承故障诊断[J]. 振动与冲击, 2020, 39(4): 172. ZHU Danchen, ZHANG Yongxiang, PAN Yangyang, et al. Fault diagnosis for rolling element bearings based on multi-sensor signals and CNN[J]. Journal of Vibration and Shock, 2020, 39(4): 172. DOI:10.13465/j.cnki.jvs.2020.04.022 |
| [7] |
宫文峰, 陈辉, 张美玲, 等. 基于深度学习的电机轴承微小故障智能诊断方法[J]. 仪器仪表学报, 2020, 41(1): 195. GONG Wenfeng, CHEN Hui, ZHANG Meiling, et al. Intelligent diagnosis method for incipient fault of motor bearing based on deep learning[J]. Chinese Journal of Scientific Instrument, 2020, 41(1): 195. DOI:10.19650/j.cnki.cjsi.J1905073 |
| [8] |
蒙志强, 董绍江, 潘雪娇, 等. 基于改进卷积神经网络的滚动轴承故障诊断[J]. 组合机床与自动化加工技术, 2020(2): 79. MENG Zhiqiang, DONG Shaojiang, PAN Xuejiao, et al. Fault diagnosis of rolling bearing based on improved convolutional neural network[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2020(2): 79. DOI:10.13462/j.cnki.mmtamt.2020.02.019 |
| [9] |
唐波, 陈慎慎. 基于深度卷积神经网络的轴承故障诊断方法[J]. 电子测量与仪器学报, 2020, 34(3): 88. TANG Bo, CHEN Shenshen. Method of bearing fault diagnosis based on deep convolutional neural network[J]. Journal of Electronic Measurement and Instrument, 2020, 34(3): 88. DOI:10.13382/j.jemi.B1902628 |
| [10] |
MCDONALD G L, ZHAO Q, ZUO M J. Maximum correlated kurtosis deconvolution and application on gear tooth chip fault detection[J]. Mechanical Systems and Signal Processing, 2012, 33: 237. DOI:10.1016/j.ymssp.2012.06.010 |
| [11] |
LYU Xuan, HU Zhanqi, ZHOU Haili, et al. Application of improved MCKD method based on QGA in planetary gear compound fault diagnosis[J]. Measurement, 2019, 139: 236. DOI:10.1016/j.measurement.2019.02.071 |
| [12] |
LI Zheng, MING Anbo, ZHANG Wei, et al. Fault feature extraction and enhancement of rolling element bearings based on maximum correlated kurtosis deconvolution and improved empirical wavelet transform[J]. Applied Sciences, 2019, 9(9): 1876. DOI:10.3390/app9091876 |
| [13] |
MARAGOS P, KAISER J F, QUATIERI T F. Energy separation in signal modulations with application to speech analysis[J]. IEEE Transactions on Signal Processing, 1993, 41(10): 3024. DOI:10.1109/78.277799 |
| [14] |
HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735. DOI:10.1162/neco.1997.9.8.1735 |
| [15] |
The Case Western Reserve University. Bearing data center seeded fault test data[EB/OL]. [2020-05-30]. https://csegroups.case.edu/bearingdatacenter/home
|
 2021, Vol. 53
2021, Vol. 53


