燃料电池的排放物是水,不污染环境,其能量密度约为锂离子电池的2~3倍,可使整车拥有较长的续航里程。鉴于上述优点,燃料电池汽车已成为当下研究热点。虽然燃料电池因没有卡诺循环的限制而能够获得较高的能量转换效率,使整车获得较好的经济性,但如何进一步提升整车经济性仍然是研发过程中急需解决的问题。当前针对燃料电池汽车经济性的研究多集中于参数匹配优化[1-2]和控制策略研发[3-5]。在参数匹配优化的研究方面,Feroldi等[6]提出3种动力性测试方法来确定燃料电池和超级电容参数,使整车有较好的动力性、经济性和较低的成本;Kwan等[7]采用NSGA-Ⅱ优化算法进行控制参数和部件参数的优化,不仅提高了燃料电池动力系统动态稳定性和经济性,而且延长了电池的使用寿命;Xu等[8]对动力系统参数进行经济性和燃料电池耐久性的多目标优化。在控制策略研究方面,Ettihir等[9]使用自适应递归最小二乘法进行燃料电池模型在线辨识,并基于辨识模型来寻求燃料电池系统的最佳工作点。Zhou等[10]提出基于PSVM-DS的在线控制器,可以在实际驾驶循环中实现相对稳定的运行和更高的燃料电池系统效率。Song等[11]提出基于学习矢量量化神经网络算法的燃料电池汽车多模式能量管理策略并获得较好的经济性。Fletcher等[12]提出基于随机动态规划方法进行经济性和燃料电池寿命的同时优化,在经济性几乎不降低的前提下获得显著延长燃料电池使用寿命的效果。
目前,对整车构型的研究多关注于直接燃料电池系统和间接燃料电池系统之间特性的区别[13-14],较少关注超级电容存在与否对整车经济性的影响。上述研究对提高整车经济性具有重要意义,但尚缺少从部件层面上对能耗影响因素的量化分析,以及控制策略、超级电容存在与否对整车经济性影响机理的细致分析。
本文从部件、控制和构型3个方面进行燃料电池汽车深度节能分析,意在为燃料电池汽车设计阶段遇到的构型选择、部件选取和能量管理策略的制定等一系列问题提供理论指导。
1 构型对比分析 1.1 整车基本参数在整车设计初期,根据市场调研和法规要求,给定整车基本参数、动力性和经济性指标分别为:整车总质量1 787 kg,迎风面积2.65 m2,轮胎滚动半径353 mm,空气阻力系数0.37,滚动阻力系数0.007,最高车速180 km/h,最大爬坡度为>30%(速度为30 km/h时),百公里加速时间指标为 < 11.2 s,百公里氢耗指标为0.77 kg(根据丰田Mirai标称5 kg氢气可以行使650 km得到)。根据初始条件对两种动力系统(见图 1和图 2)进行参数匹配。参数匹配不是本文研究重点,所以直接给出匹配得到的结果:主减速比6.6732,燃料电池峰值功率80 kW,FC+B构型蓄电池容量44 A·h,FC+B+C构型蓄电池容量12 A·h,超级电容单体容量2 500 F,超级电容串/并联数为154/1。
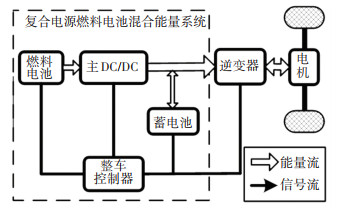
|
图 1 FC+B构型结构形式 Fig. 1 Configuration of FC+B |
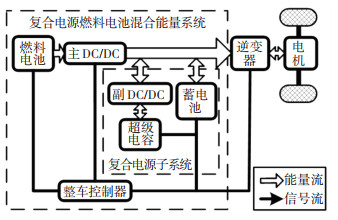
|
图 2 FC+B+C构型结构形式 Fig. 2 Configuration of FC+B+C |
针对有无超级电容两种构型,分别在advisor中建立整车仿真模型[15],燃料电池和辅助动力源之间使用功率跟随控制策略。功率跟随控制策略不仅可有效解决燃料电池频繁启停问题,而且可以修正电池SOC,能够有效防止电池的过充和过放[16]。
两种构型经济性仿真结果见表 1,可以看出,有无超级电容对整车经济性影响不大,加超级电容后百公里氢耗减少3.5 g。但是,此时并没有考虑实际中超级电容的端电压随其SOC变化较大,超级电容应串联DC/DC后再与蓄电池并联,若考虑该双向DC/DC的效率(当前技术较好的约93%),整车经济性将变差。超级电容可以对蓄电池需求功率进行较好的滤波,滤波效果如图 3所示。
| 表 1 FC+B和FC+B+C两构型仿真结果 Tab. 1 Simulation results of FC+B and FC+B+C configurations |
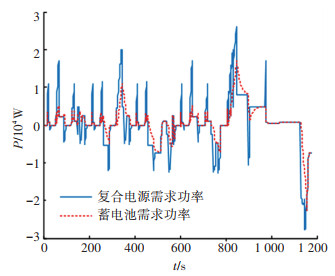
|
图 3 超级电容滤波效果 Fig. 3 Filter effect of super capacitor |
由图 3可知,超级电容可以对蓄电池需求功率进行滤波,而蓄电池又可对燃料电池需求功率进行滤波,因此在保证蓄电池使用寿命不减少的前提下,加入超级电容可适当增强蓄电池对燃料电池的滤波作用,即FC+B+C构型可延长燃料电池和蓄电池的使用寿命。本文关注点为燃料电池汽车的经济性,因此下文选取FC+B构型进行深度节能分析。
2 影响因素量化分析 2.1 理论氢耗模型图 4为FC+B构型燃料电池汽车动力系统的能量传递模型[17],动力系统分为动力源模块、传动系统模块和车体模块。
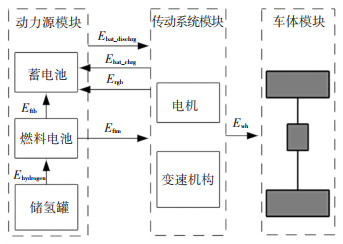
|
图 4 燃料电池汽车动力系统能量传递 Fig. 4 Energy transfer of fuel cell vehicle power system |
定义平均综合传动效率为有效益的能量与供给传动系总能量的比值。在不考虑各种效率时,平均综合传动效率也就变成了整车总效率,其计算公式为
| $ \eta_{\mathrm{tr}}=\frac{E_{\mathrm{wh}}+\left(E_{\mathrm{bat}\_{\mathrm{chrg}}}\right)}{E_{\mathrm{hydrogen}}+E_{\mathrm{rgb}}+\left(E_{\text {bat_dischrg }}\right)} $ | (1) |
| $ E_{\mathrm{wh}}=\sum\limits_{t=0}^{n}\left[\left\{\begin{array}{ll} \left.F_{t}(t) * v(t) / 1000\right) & \left(F_{t}(t)>0\right) \\ 0 & \left(F_{t}(t)<0\right) \end{array}\right]\right. $ | (2) |
式中:Ewh为循环工况总驱动能量的理论值,Ebat_chrg为循环工况结束后蓄电池中增多的能量,Ehydrogen为消耗的氢气所包含的能量,Ergb为再生制动充入蓄电池的能量,Ebat_dischrg为循环工况结束后蓄电池中减少的能量。
实际情况中效率不能忽略,当考虑部件及传动系统效率影响时,文中定义的平均综合传动效率为
| $ \begin{aligned} &\eta_{\mathrm{tr}}=\\ &\frac{E_{\text {wh }}+E_{\text {bat_chrg }} \times \eta_{\text {bat_dischrg }} \times \eta_{\text {tr }}}{E_{\text {hydrogen }} \times \eta_{\text {fc }}+E_{\text {rgb }} \times \eta_{\text {bat_dischrg }}+E_{\text {bat_dischrg }} \times \eta_{\text {bat_dischrg }}} \end{aligned} $ | (3) |
式中:ηbat_dischrg为蓄电池平均放电效率,ηfc为燃料电池效率,Ehydrogen×ηfc为燃料电池实际输出的能量,最终得到整车理论综合氢耗计算模型为
| $ f_{\text {e_unify }}=E_{\mathrm{wh}}\left[1-\frac{E_{\mathrm{rgb}}}{E_{\mathrm{wh}}} \eta_{\mathrm{tr}} \eta_{\mathrm{bat}_{-} \mathrm{dischrg}}\right] / \eta_{\mathrm{tr}} \cdot b_{\mathrm{e}\_{\mathrm{avg}}} \cdot C $ | (4) |
式中:fe_unify为理论综合百公里氢耗量,C为氢电转换系数,be_avg为燃料电池的平均氢气消耗率。
根据式(4)得到理论氢耗模型的影响因素(见表 2)。再生制动回收的能量与多个参数有关,包括滚动阻力系数、整车质量、机械传动效率、电机效率等,本文分析上述参数一定时再生制动策略的影响。此外,因机械效率受当前技术限制难以提高,电池的充放电效率也已经非常高(约0.98),进行量化分析意义不大。
| 表 2 理论氢耗模型影响因素 Tab. 2 Influencing factors of theoretical hydrogen consumption model |
综上,本文定量分析燃料电池效率、电机效率、滚动阻力系数、整车质量及再生制动策略对整车经济性的影响。
2.2 仿真分析通过自建模型与advisor对标,验证自建模型的准确性,对标结果见表 3。由表 3可知,理论值与仿真值之间误差较小,进一步了说明理论模型和自建模型的准确性。
| 表 3 自建模型与advisor对标结果 Tab. 3 Comparison results of self-built model and advisor |
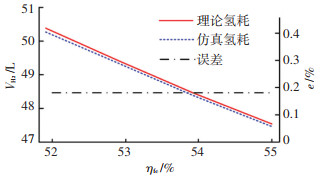
以仿真的燃料电池平均效率为基础,通过自建模型和理论模型双重计算,量化燃料电池效率对整车经济性的影响,结果如图 5,燃料电池平均工作效率每提升1%,整车百公里氢耗减少约0.95 L(17.1 g)。
|
图 5 燃料电池效率与氢耗的关系 Fig. 5 Relation between hydrogen consumption and each fuel cell efficiency |
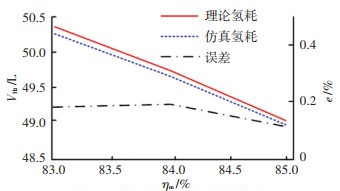
前述仿真所用电机的平均工作效率为83%,若电机得到技术改进,满足2018“新能源汽车”重点专项中提出的超过85%的高效率区不低于85%的指标,电机的平均工作效率将可达到85%。分析电机的平均工作效率从83%每次提升1%,直到85%时对经济性的影响,结果如图 6,电机平均工作效率每提升1%,整车氢耗降低0.63 L(11.3 g)。
|
图 6 电机效率与氢耗的关系 Fig. 6 Relation between hydrogen consumption and each motor efficiency |
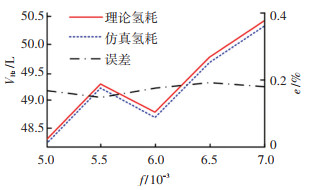
当前,最先进的技术水平的滚动阻力系数可达到0.005,下面分析滚动阻力系数从0.007 0降低到0.005 0的过程中每降低0.000 5,对整车经济性的影响,量化分析结果如图 7所示。
|
图 7 滚动阻力系数与氢耗的关系 Fig. 7 Relation between hydrogen consumption and each rolling resistance coefficient |
由图 7可知,滚动阻力系数每降低0.000 5,百公里氢耗减少约0.78 L(14.0 g)。但是滚动阻力系数从0.006 0下降到0.005 5时,百公里氢耗不减反增,这是由于滚阻系数的减小劣化了电机的工作点分布,使电机平均驱动效率降低,最终导致整车氢耗有所增大。这也从侧面说明电机高效区的匹配应随滚动阻力系数的改变而改变,但不限于滚动阻力系数,一切影响滚动阻力的因素都将改变电机的工作点,进而影响电机的平均工作效率和整车经济性。
2.2.4 整备质量的微观经济性分析轻量化设计主要包括有限元机构优化设计、碳纤维等轻质材料和高强度钢等新工艺的使用,若进行较好的轻量化设计,整备质量将有效减少。整备质量微观经济性分析结果见图 8,整备质量每降低50 kg,百公里氢耗减少约0.67 L(12.1 g)。

|
图 8 整备质量与氢耗的关系 Fig. 8 Relation between hydrogen consumption and each curb weight |
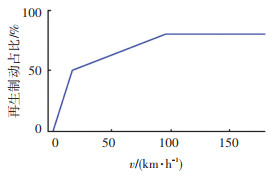
仿真所使用的控制策略为部分再生制动策略,如图 9所示。其中再生制动占比是电机提供个制动转矩与总需求制动转矩的比值。
|
图 9 再生制动策略 Fig. 9 Strategy of regenerative braking |
使用不同再生制动策略时整车的经济性见表 4。其中制动能量回收率为回收的能量占总制动能量的比值,再生制动占比为回收的能量占理论驱动总能量的比值。当前最先进的再生制动策略的制动能量回收率约为90%,从表 4可以看出,再生制动策略对整车的经济性产生显著影响,同时,当前的再生制动策略有较大的提升空间。
| 表 4 不同再生制动策略下经济性对比 Tab. 4 Economic comparison under different regenerative braking strategies |
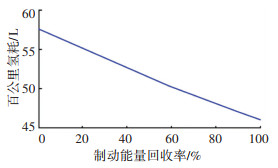
分析再生制动能量回收率每提升10%,对整车氢耗的影响,结果见图 10。由图 10可知,再生制动的能量回收率每提升10%,百公里氢耗减少约1.17 L (21.06 g)。
|
图 10 制动能量回收率与氢耗的关系 Fig. 10 Relation between hydrogen consumption and each braking energy recovery rate |
采用一种终止状态受约束的动态规划方法,分析所研究车型在控制策略改进后的氢耗极限,并以此作为衡量控制策略可优化程度的标准[18-19]。
3.1 终端约束动态规划简介在DP逆向寻优过程中选取蓄电池SOC为状态量,燃料电池的输出功率为控制量,其成本函数为
| $ L_{k}(x(k), u(k))=L_{\mathrm{H}_{2}}(k)+\alpha L_{\mathrm{ele}}(k) $ | (5) |
式中:α为氢电权重系数,LH2(k)为k时刻消耗的氢气的能量,L(elek)为k时刻蓄电池放出的能量。
将NEDC工况分为0-N时刻,从k时刻到k+1时刻,对于同一状态变量SOC,不同的控制变量会导致不同的成本和k+1时刻的不同状态变量。当k逆向寻优到0时刻时,即可得到0时刻不同状态对应的最优总成本函数:
| $ J=\sum\limits_{k=0}^{N} L_{k}(x(k), u(k)) $ | (6) |
| $ x(k+1)=f(x(k), u(k)), k=0, 1, \cdots N-1 $ | (7) |
终态约束的实现方法如下:
1) 根据离散的燃料电池功率和当前时刻电机的需求功率确定离散的蓄电池功率。
2) 根据电池模型
| $ I_{\mathrm{bat}}=\frac{-E+\sqrt{E^{2}+4 r_{\mathrm{int}} P_{\mathrm{bat}}}}{2 r_{\mathrm{int}}} $ | (8) |
确定当前时刻离散的电流,进而可确定离散电流的最大最小值。式中,Ibat为蓄电池的电流,E为蓄电池端电压,rint为蓄电池内阻,Pbat为蓄电池功率。
3) 根据k+1时刻SOC的边界和k时刻电流的边界可确定k时刻SOC的上下边界,当逆向寻优时给定N时刻SOC值,即可确定之前各时刻SOC的边界值。设定蓄电池SOC的上下限分别为0.8和0.4。
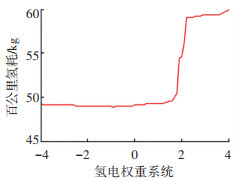
3.2 氢电权重系数动态规划算法最核心的问题为成本函数中氢电权重系数的确定。氢电权重系数受燃料电池效率、电池充电效率和电池放电效率等多因素耦合影响,其数值难以直接确定[20]。考虑到动态规划逆向寻优的本质思想为遍历寻找全局最优解,对氢电权重系数的确定也采用该思想,通过遍历寻找对应的最低氢耗的氢电权重系数。对氢电权重系数进行从-4到4的遍历,遍历间隔为0.1,遍历结果见图 11。
|
图 11 氢电权重系数与氢耗的关系 Fig. 11 Relation between hydrogen consumption and each hydrogen-electric weight coefficient |
由图 11可知,氢电权重系数在1.87时,DP结果有明显变动;当权重系数 < 1.87时,燃料电池的能耗比重放大;当权重系数>1.87时,蓄电池的能耗比重放大。不同权重系数下SOC变化曲线如图 12所示。当权重系数分别为1.5和2.5时,SOC在不同时刻差别较大。

|
图 12 SOC变化曲线 Fig. 12 Variation curves of SOC |
当权重系数为0时,此时蓄电池的唯一作用是调整燃料电池的工作点,使其尽可能多的工作于高效区。但此时蓄电池仍存在充放电现象,充放电带来的损失没有考虑在内。当权重系数为负时,较多的充放电会增大总成本函数,需要将蓄电池的充放电带来的损失考虑在内。
上述对权重系数的遍历结果显示,权重系数为-0.9时,动态规划的百公里氢耗最小。当权重系数继续减少,蓄电池充放电会使总成本函数增大较多,这会降低蓄电池对燃料电池工作点的调节作用,因此,百公里氢耗会再次增大。由于蓄电池的充放电效率较高,约0.98,因此当权重系数从0继续减少,其对百公里氢耗的影响不大。
综上所述,简便起见,对于终态约束的动态规划,氢电权重系数可以取0。权重系数为0时的DP结果见表 5。由表 5可知,动态规划策略下的整车经济性比功率跟随控制策略的提升2.4%。采用动态规划后只有燃料电池的效率得到提升,电机效率和再生制动回收的能量都不变。这是由于工况确定,电机的工作点即确定,再生制动策略也确定,则再生制动回收的能量也被确定。从动态规划的结果可知,能量管理策略优化的直接作用只能是提高燃料电池的平均工作效率,即从提高经济性角度考虑进行控制策略优化的本质为提高燃料电池的平均工作效率。此外,从上述动态规划结果可知,能实时应用的功率跟随控制策略可使整车获得较好的经济性。
| 表 5 动态规划结果 Tab. 5 Results of dynamic planning |
为满足百公里氢耗0.77 kg/100 km的经济性设计要求(见表 1),根据现有技术水平对各影响因素提出合理的改进方案,得到的经济性变化见表 6。将实际仿真中百公里氢耗变化量与根据前述分析得到的理论变化量进行对比,误差均小于10%。
| 表 6 量化分析结果汇总 Tab. 6 Summary of quantitative analysis results |
将各影响因素依次进行改善后,整车经济性可满足设计要求。同时得到以下结论:1)有无超级电容对整车经济性的影响最小;2)滚动阻力系数和再生制动策略的改进可对整车经济性有显著影响;3)驱动控制优化可在成本提升较小的前提下,较大的提升整车经济性。
5 结论1) 宏观经济性分析表明:在构型选择时,若为获得较好的经济性,应选择FC+B构型;若为获得较长的燃料电池使用寿命,应选择FC+B+C构型。
2) 微观经济性分析表明:理论氢耗模型的提出不仅从理论层面上揭示了能耗影响因素,而且可与仿真进行相互验证,提高量化分析结果的准确性与可靠性。理论和仿真相结合的量化分析不仅揭示了不同氢耗影响因素对整车经济性影响的重要程度,而且可为整车设计阶段的部件优选指明了方向。
3) 用动态规划方法分析整车控制策略表明:功率跟随控制策略能较好发挥整车经济性,同时揭示了从节能方面优化控制策略的本质为改善燃料电池的工作点进而提升燃料电池的平均工作效率。
| [1] |
李奇, 孟翔, 陈维荣, 等. 燃料电池混合动力系统参数匹配与多目标优化[J]. 西南交通大学学报, 2019, 54(5): 1079. LI Qi, MENG Xiang, CHEN Weirong, et al. Parameter matching and multi-objective optimization of fuel cell hybrid system for trams[J]. Journal of Southwest Jiaotong University, 2019, 54(5): 1079. |
| [2] |
贠海涛, 徐煜超, 曹爱霞, 等. 燃料电池叉车动力系统结构设计与参数匹配[J]. 济南大学学报(自然科学版), 2018, 32(1): 1. YUN Haitao, XU Yuchao, CAO Aixia, et al. Design of power system configuration and matching parameter for fuel cell forklift[J]. Journal of University of Jinan (Science and Technology), 2018, 32(1): 1. DOI:10.13349/j.cnki.jdxbn.2018.01.001 |
| [3] |
赵治国, 沈沛鸿, 郏怡颖, 等. 燃料电池轿车模型预测实时优化控制[J]. 同济大学学报(自然科学版), 2018, 46(5): 648. ZHAO Zhiguo, SHEN Peihong, JIA Yiying, et al. Model predictive real-time optimal control of fuel cell car[J]. Journal of Tongji University (Natural Science), 2018, 46(5): 648. DOI:10.11908/j.issn.0253-374x.2018.05.012 |
| [4] |
何洪文, 林逸, 魏跃远. 燃料电池混合动力汽车控制策略研究[J]. 北京理工大学学报, 2007, 27(3): 223. HE Hongwen, LIN Yi, WEI Yueyuan. Study on the control strategy for a fuel cell hybrid vehicle[J]. Transactions of Beijing Institute of Technology, 2007, 27(3): 223. DOI:10.3969/j.issn.1001-0645.2007.03.009 |
| [5] |
金振华, 欧阳明高, 卢青春, 等. 燃料电池混合动力系统优化控制策略[J]. 清华大学学报(自然科学版), 2009, 49(2): 273. JIN Zhenhua, OUYANG Minggao, LU Qingchun, et al. Optimal control strategy for a fuel cell hybrid powertrain[J]. Journal of Tsinghua University (Science and Technology), 2009, 49(2): 273. |
| [6] |
FEROLDI D, CARIGNANO M. Sizing for fuel cell/supercapacitor hybrid vehicles based on stochastic driving cycles[J]. Applied Energy, 2016, 183: 645. DOI:10.1016/j.apenergy.2016.09.008 |
| [7] |
KWAN T H, WU Xiaofeng, YAO Qinghe. Parameter sizing and stability analysis of a highway fuel cell electric bus power system using a multi-objective optimization approach[J]. International Journal of Hydrogen Energy, 2018, 43(45): 20976. DOI:10.1016/j.ijhydene.2018.09.113 |
| [8] |
XU Liangfei, MUELLER C D, LI Jianqiu, et al. Multi-objective component sizing based on optimal energy management strategy of fuel cell electric vehicles[J]. Applied Energy, 2015, 157: 664. DOI:10.1016/j.apenergy.2015.02.017 |
| [9] |
ETTIHIR K, BOULON L, AGBOSSOU K. Optimization-based energy management strategy for a fuel cell/battery hybrid power system[J]. Applied Energy, 2016, 163: 142. DOI:10.1016/j.apenergy.2015.10.176 |
| [10] |
ZHOU Daming, AL-DURRA A, GAO F, et al. Online energy management strategy of fuel cell hybrid electric vehicles based on data fusion approach[J]. Journal of Power Sources, 2017, 366: 278. DOI:10.1016/j.jpowsour.2017.08.107 |
| [11] |
SONG Ke, LI Feiqiang, HU Xiao, et al. Multi-mode energy management strategy for fuel cell electric vehicles based on driving pattern identification using learning vector quantization neural network algorithm[J]. Journal of Power Sources, 2018, 389: 230. DOI:10.1016/j.jpowsour.2018.04.024 |
| [12] |
FLETCHER T, THRING R, WATKINSON M. An energy management strategy to concurrently optimise fuel consumption & PEM fuel cell lifetime in a hybrid vehicle[J]. International Journal of Hydrogen Energy, 2016, 41(46): 21503. DOI:10.1016/j.ijhydene.2016.08.157 |
| [13] |
BERNARD J, HOFER M, HANNESEN U, et al. Fuel cell/battery passive hybrid power source for electric powertrains[J]. Journal of Power Sources, 2011, 196(14): 5867. DOI:10.1016/j.jpowsour.2011.03.015 |
| [14] |
SAMSUN R C, KRUPP C, BALTZER S, et al. A battery-fuel cell hybrid auxiliary power unit for trucks: analysis of direct and indirect hybrid configurations[J]. Energy Conversion and Management, 2016, 127: 312. DOI:10.1016/j.enconman.2016.09.025 |
| [15] |
TURKMEN A C, SOLMAZ S, CELIK C. Analysis of fuel cell vehicles with advisor software[J]. Renewable and Sustainable Energy Reviews, 2017, 70: 1066. DOI:10.1016/j.rser.2016.12.011 |
| [16] |
GENG Cong, JIN Xiaofei, ZHANG Xin. Simulation research on a novel control strategy for fuel cell extended-range vehicles[J]. International Journal of Hydrogen Energy, 2019, 44(1): 408. DOI:10.1016/j.ijhydene.2018.04.038 |
| [17] |
曾小华, 纪人桓, 宋大凤, 等. 燃料电池汽车的氢耗分析模型与应用[J]. 湖南大学学报(自然科学版), 2019, 46(2): 36. ZENG Xiaohua, JI Renhuan, SONG Dafeng, et al. Hydrogen-consumption analysis model of fuel cell vehicles and its application[J]. Journal of Hunan University (Natural Sciences), 2019, 46(2): 36. |
| [18] |
ZHOU Wei, YANG Lin, CAI Yishan, et al. Dynamic programming for new energy vehicles based on their work modes, part Ⅰ: electric vehicles and hybrid electric vehicles[J]. Journal of Power Sources, 2018, 406: 151. DOI:10.1016/j.jpowsour.2018.10.047 |
| [19] |
ZHOU Wei, YANG Lin, CAI Yishan, et al. Dynamic programming for new energy vehicles based on their work modes, Part Ⅱ: fuel cell electric vehicles[J]. Journal of Power Sources, 2018, 407: 92. DOI:10.1016/j.jpowsour.2018.10.048 |
| [20] |
纪人桓. 全功率燃料电池汽车动力系统优化设计与能量管理[D]. 长春: 吉林大学, 2020 JI Renhuan. Power system optimization design and energy management of full power fuel cell vehicle[D]. Changchun: Jilin University, 2020 |
 2021, Vol. 53
2021, Vol. 53


