2. 哈尔滨工业大学(威海) 汽车工程学院, 山东 威海 264209
2. School of Automobile Engineering, Harbin Institute of Technology, Weihai, Weihai 264209, Shandong, China
近年来,电动汽车以优越的环保和节能特性,已然成为21世纪汽车发展的主要趋势[1]。IGBT模块在电动汽车上的应用越来越普遍,但是,由于逆变器本身的温升、散热条件以及周围环境的限制,功率损耗导致的热循环与恶劣的工作环境相结合会导致大范围以及不可预测的结温波动与过热[2],致使器件乃至于整个系统崩溃。研究表明,超过半数的逆变器失效都是由于过温引起的,因此实时监测IGBT温度尤为必要。
各国学者在结温估计方面进行了大量的试验,提出多种测量方法,总体可归结为物理接触测量法、光学法、电热耦合模型法以及热敏参数法[3-5]4类。文献[6-9]利用有限元仿真软件搭建IGBT的三维模型,提取了器件的瞬态阻抗曲线与热网络参数,并搭建IGBT的热网络结构模拟芯片散热过程,结合IGBT的损耗与热阻网络建立了热-电耦合模型, 对结温进行估算。该模型考虑了大多数仿真软件在计算IGBT损耗时忽略的温度影响因素,所得损耗模型更加准确,提高了结温估计的准确性。文献[10]利用热敏参数关断延迟时间以及栅极-发射极电压、集电极电流和集电极-发射极电压,根据材料参数随温度的变化而变化建立对应关系来测量结温,实现了结温较为精确的估计。文献[11]对多种热敏电参数测量结温分别进行测量对比,得出门极阈值电压是较适合进行在线估计结温的参数。文献[12]介绍了各种热敏电参数,并归类总结为经典热敏电参数、静态和动态特性参数。
IGBT结温预测的4种方法各有优劣。物理接触测量法与光学法属于直接测量方法,需要破坏IGBT的封装,附加昂贵的测试设备,不适合在线实时估算结温。电热耦合模型法虽然是非破坏性的,但是无法避免器件老化带来的估计误差,该方法属于开环估计,无法对结温起到一定的反馈调节。热敏参数法能够快速且准确的估计结温,但是需要附加额外的电路,难以实现在实际运行工况下的在线实时估算,为工程实现带来一定的困难,但该方法可用于对其他结温估计算法的验证。
针对现有方法的不足,本文在热电耦合模型的基础上设计全阶状态观测器,并进行反馈调节,提高结温估计的准确性与鲁棒性,最后通过搭建仿真和实验平台对模型进行了准确性验证。
1 IGBT损耗建模IGBT损耗问题与工作温度直接相关,损耗都将转化为热量导致功率模块的温度上升,所以损耗在结温的估计方面有着至关重要的作用。IGBT的损耗主要由导通损耗与开关损耗组成[13-14]。
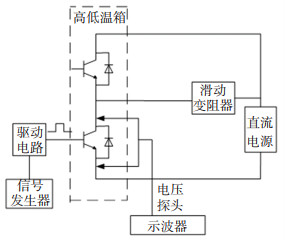
1.1 导通损耗IGBT导通状态下的功率损耗,通常由流过器件的电流和电压的乘积来确定。而饱和压降(Vce-sat)主要受到导通电流与结温两个因素影响。因此只需标定出IGBT在不同导通电流、不同温度下的压降曲线即可计算导通损耗。饱和压降的测试方法主要有脉冲法和直流法。由于直流法会使器件长时间导通,导致温度升高,影响测量结果,本文基于单脉冲法测试原理搭建测试平台,如图 1所示。
|
图 1 IGBT饱和压降测量平台示意图 Fig. 1 Schematic diagram of IGBT saturation voltage drop measurement platform |
测试时,将待测IGBT放入高低温箱控制其环境温度为设定值,调节直流电源与滑动变阻器使得电路导通时流过规定的测试电流,采用示波器获取该电流下的器件饱和压降。单个IGBT控制周期内的平均导通损耗为
| $ P_{\text {cond }}=V_{\text {ce_sat }} \cdot I_{\mathrm{c}} \cdot \varepsilon $ | (1) |
式中ε为PWM波的占空比,饱和压降(Vc-sat)主要受到导通电流与结温两个因素影响。表 1给出了不同导通电流和工作温度下的饱和压降,由于IGBT饱和压降由导通压降(uce0)和通态电阻(rc)上的压降两部分组成,所以可以将饱和压降曲线进行线性拟合,其导通损耗描述为[15]
| 表 1 不同IGBT状态下测得的饱和压降 Tab. 1 Saturation voltage drop measured under different IGBT states |
| $ P_{\text {cond }}=\left(u_{\mathrm{ce} 0}+r_{\mathrm{c}} \cdot I_{\mathrm{c}}\right) I_{\mathrm{c}} \cdot \varepsilon $ | (2) |
考虑温度因素的影响,测量两个温度下的导通损耗,通过线性拟合的方式推导任意温度下的IGBT导通损耗[15]为
| $ P_{\text {cond }_{-} T}=P_{\text {cond_ } T 1}+\left(P_{\text {cond_ } T 2}-P{_{{\text {cond_ }}T1}}\right) \frac{T-T_{1}}{T_{2}-T_{1}} $ | (3) |
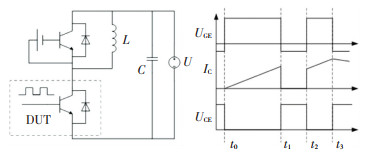
由于数据手册上参数获得工况与实际工况有所不同,直接利用数据手册来计算功率损耗会带入比较大的误差,所以需要通过双脉冲实验获取数据,建立开关损耗模型。图 2给出了IGBT双脉冲实验的测试电路与时序。其中,DUT是被测IGBT,UGE、UCE、IC分别表示被测IGBT的驱动电压、集射极两端电压、集电极电流。双脉冲测试的第一个脉冲的作用是为了建立测试电路的电流,第二个脉冲主要是用于观测被测IGBT的开通过程,其具体实现方式见文献[16]。
|
图 2 双脉冲实验电路与测试时序 Fig. 2 Double pulse experimental circuit and test sequence |
IGBT双脉冲离线测试平台框架如图 3,测试平台主要由以下几部分组成:驱动控制、待测IGBT、感性负载测试电路、温度控制。

|
图 3 双脉冲实验电路与测试时序 Fig. 3 IGBT double pulse test platform |
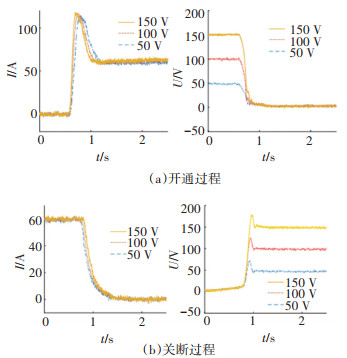
本文针对三菱模块PM600CLA060进行测试,研究IGBT开关特性在不同温度、电压以及电流下的变化趋势,为后续开关损耗的计算提供数据基础。不同测试电压(50、100、150 V)下的IGBT测试开关波形如图 4所示。
|
图 4 不同电压下的开关波形 Fig. 4 Switching waveforms at different voltages |
从图 4可以看出,随着测试电压的增大,在开通与关断过程中IGBT的电压与电流重合面积越大,开通损耗增加。
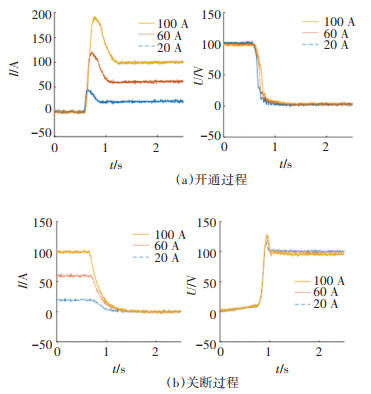
图 5给出了不同测试电流(20、60、100 A)下的开关波形。由图 5可知,随着测试电流的增大,开通时间越长,开通损耗增加,而关断过程电压过冲和更加明显的拖尾效应,使得测试电流的增加导致的关断损耗也增加。
|
图 5 不同电流下的开关波形 Fig. 5 Switching waveforms at different currents |
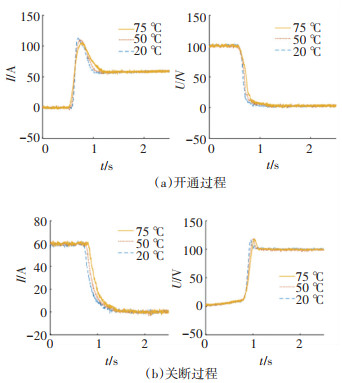
图 6给出不同的环境温度(20、50、75 ℃)下的IGBT测试结果,高温条件下,基极载流子的移动速度会变缓慢,导致电流的上升速率下降,同时载流子复合过程的时间变长,因此随着工作温度的增加损耗变大。
|
图 6 不同温度下的开关波形 Fig. 6 Switching waveforms at different temperatures |
传统的热阻计算公式是建立在稳态传热工况下,需要测得传热稳定阶段的结温与壳温,计算得到稳态热阻。但是在实际应用中,IGBT需要经历瞬态过程,器件往往不处于热平衡状态,所以仅仅依靠稳态热阻无法实时估算结温。因此,需要使用瞬态热阻公式[17]
| $ R_{\mathrm{je}}=\frac{T_{\mathrm{j} 0}-T_{\mathrm{j}}(t)}{P} $ | (4) |
式中Tj0为IGBT结温的初始值,Tj(t)为IGBT结温的随时间变化值。基于热敏参数法测量瞬态热阻的测试方法,首先标定饱和压降在恒定小电流导通下与结温的线性关系曲线[18]。接着对IGBT模块施加已知的加热功率直到IGBT的结温不再发生变化,切断加热功率,改为恒定小电流导通状态,记录饱和压降的变化过程,利用线性关系曲线计算结温,带入式(4)计算相应的热阻。
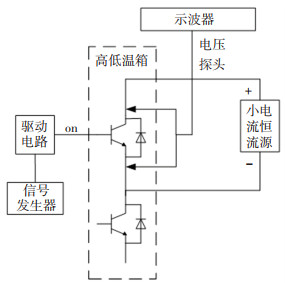
IGBT在恒定小电流导通条件下,饱和压降随结温的变化呈线性关系,设计图 7平台将IGBT模块放置在不同环境温度下,施加10 mA的测试电流,研究饱和压降与结温的关系。
|
图 7 饱和压降-结温标定平台 Fig. 7 Saturation voltage drop-junction temperature calibration platform |
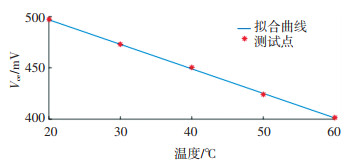
获取测量数据后,通过曲线拟合可以得到在10 mA电流导通下IGBT结温与饱和压降的变化曲线如图 8所示,从图 8中可以看出,10 mA小电流下,IGBT的饱和压降与结温是线性关系,随着结温的升高,饱和压降不断降低。
|
图 8 10 mA电流下饱和压降和结温的关系 Fig. 8 Relation between saturation voltage drop and junction temperature at current of 10 mA |
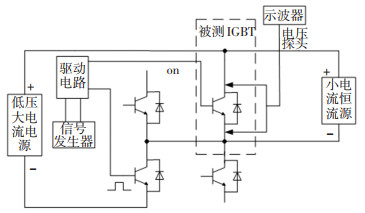
瞬态热阻测试平台如图 9所示,将IGBT模块固定在散热器上,控制两个IGBT同时导通,施加75 A的加载电流。当在示波器中观察到器件饱和压降曲线不再变化,说明器件已经达到稳态,然后控制左侧下桥臂IGBT断开,切断加热电流,这时仅仅由小电流源供10 mA电流流过被测IGBT,记录Vce与外壳热敏电阻的温度变化,将换算得到的结温带入式(4),得到了瞬态过程的热阻曲线。
|
图 9 IGBT瞬态热阻测试平台 Fig. 9 IGBT transient thermal resistance test platform |
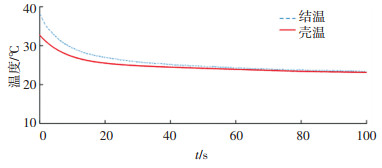
基于IGBT模块瞬态热阻测试平台测得饱和压降曲线,通过图 8换算成结温随时间的变化曲线如图 10所示。将图 10获得的升温曲线带入式(4)可以计算出IGBT芯片到环境的总热阻与散热器到环境的热阻,它们之间的差值就是结壳之间的热阻。
|
图 10 结温与壳温的升温曲线 Fig. 10 Temperature rise curves of junction temperature and shell temperature |
IGBT模块瞬态热阻曲线如图 11,瞬态热阻由小到大,最后趋于稳定值,热流从最顶层的IGBT芯片经过模块外壳、散热器、最后传到环境,形成整个热传导回路。结壳间的稳态热阻最终趋于0.068 5 ℃/W,与器件数据手册给出的结壳热阻最大值不超过0.07 ℃/W相符。

|
图 11 IGBT模块各部分瞬态热阻曲线 Fig. 11 Transient thermal resistance curves of each part of IGBT module |
热网络模型是把研究对象沿主要的热流路径细分成不同的单元节点,每个热节点内部温度在同一瞬间看做同一温度。热阻网络也被称为热电模拟,热网络和电路网络有很多类似的地方,根据热-电比拟理论将热阻网络的温度、热流、热阻、热容分别与电路中电压、电流、电阻、电容进行等效,可用类似电路的基尔霍夫定律来求解热网络内的温差和热流。
Foster网络和Cauer网络是热分析中较常见的热网络模型,网络中的热阻热容只是等效参数,不与IGBT内部传热路径上各层的热阻和热容一一对应,但该模型简单,计算方便,可用于搭建结温仿真模型的被控对象,网络中的参数可以通过瞬态热阻曲线进行拟合求解,拟合公式为
| $ Z_{\mathrm{th}}=\sum\limits_{i=1}^{n} R_{i}\left[1-\exp \left(-\frac{t}{R_{i} C_{i}}\right)\right]. $ | (5) |
考虑算法的实现、计算能力和精度要求,将式(5)采用二阶拟合,将IGBT芯片到模块外壳和散热器到环境这两部分热阻分别进行二阶拟合,得到Foster网络的热阻与热容。
Cauer网络能够真实地反映IGBT模块的热传递过程,见图 12,物理意义明显,但是Cauer网络的参数难以直接获取,可以通过Foster网络转换法构建。

|
图 12 Cauer网络 Fig. 12 Cauer network |
根据Cauer网络模型,在IGBT的垂直传热路径建立个温度节点,它们分别为IGBT芯片的温度、IGBT芯片与壳之间一点的温度、模块外壳的温度、散热器内部一点的温度。根据热阻网络选择好热节点后,由传热路径,可根据基尔霍夫定理,写出每个节点的控制方程:
| $ \left\{\begin{array}{l} i_{P_{\text {diss }}}=i_{R_{1}}+i_{C_{1}}=\frac{V_{C_{1}}-V_{C_{2}}}{R_{1}}+C_{1} \cdot \dot{V}_{C_{1}} \\ i_{R_{1}}=i_{R_{2}}+i_{C_{2}}=\frac{V_{C_{2}}-V_{C_{3}}}{R_{2}}+C_{2} \cdot \dot{V}_{C_{2}} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\vdots \\ i_{R_{n-1}}=i_{R_{n}}+i_{C_{n}}=\frac{V_{C_{n}}-V_{T_{\text {amb }}}}{R_{n}}+C_{n} \cdot \dot{V}_{C_{n}} \end{array}\right. $ | (6) |
选择每个热节点的温度作为系统状态:
| $ \boldsymbol{x}=\left[\begin{array}{llll} V_{C_{1}} & V_{C_{2}} & \cdots & V_{C_{n}} \end{array}\right]^{\mathrm{T}} $ |
系统的输入为IGBT功率损耗与环境温度:
| $ \boldsymbol{u}=\left[\begin{array}{ll} i_{P_{\text {diss }}} & T_{\text {amb }} \end{array}\right]^{\mathrm{T}} $ |
系统的输出为各节点的温度:
| $ \boldsymbol{y}=\boldsymbol{x} $ |
由式(6)节点控制方程推导得:
| $ \boldsymbol{A}=\left[\begin{array}{ccccc} -\frac{1}{C_{1} R_{1}} & \frac{1}{C_{1} R_{1}} & \cdots & 0 & 0 \\ \frac{1}{C_{2} R_{1}} & -\frac{1}{C_{2} R_{1}}-\frac{1}{C_{2} R_{2}} & \cdots & 0 & 0 \\ \vdots & \vdots & & \vdots & \vdots \\ 0 & 0 & \cdots & -\frac{1}{C_{n-1} R_{n-2}}-\frac{1}{C_{n-1} R_{n-1}} & \frac{1}{C_{n-1} R_{n-1}} \\ 0 & 0 & \cdots & \frac{1}{C_{n} R_{n-1}} & -\frac{1}{C_{n} R_{n-1}}-\frac{1}{C_{n} R_{n}} \end{array}\right],\\ \boldsymbol{B}=\left[\begin{array}{ccc} \frac{1}{C_{1}} & 0 \\ 0 & 0 \\ \vdots & \vdots \\ 0 & \frac{1}{C_{n} R_{n}} \end{array}\right], \boldsymbol{C}=I, \boldsymbol{D}=0 $ | (7) |
利用热阻网络的状态空间表达式,可以实现对IGBT结温的开环估计。但是在实际运行中,受模型精度以及各种随机干扰等的影响,估计精度将受到影响。因此,采用状态观测器实现温度的闭环估计,利用模型输出和实际的NTC热敏电阻温度之间的误差对结温估计值进行实时修正,从而保证估计值的准确性。
系统的状态观测器模型为
| $ \left\{\begin{array}{l} \dot{\hat{\boldsymbol{x}}}=\boldsymbol{A} \hat{\boldsymbol{x}}+\boldsymbol{B} \boldsymbol{u} \\ \hat{\boldsymbol{y}}=\boldsymbol{C} \hat{\boldsymbol{x}}+\boldsymbol{D} \boldsymbol{u} \end{array}\right. $ | (8) |
由于在实际工程应用中很难保证状态观测器的初始条件与原系统完全一样。状态观测器与原系统之间存在的初始误差势必会导致随后的估计存在误差。这个误差无法随着时间收敛于零,因此,在状态观测器中引入原系统和观测器系统输出的差值进行反馈,基于反馈控制,在输出误差基础上加入反馈环节,控制输出误差趋于零。得到如图 13所示的结温状态观测器结构图。

|
图 13 结温状态观测器 Fig. 13 Junction temperature observer |
由图 13可知,当观测器的状态变量与原系统状态变量不一致时,就会产生一误差信号,再通过反馈环节输送到观测器输入端,参与观测器状态变量的调节,使得观测器状态变量能够快速、稳定且准确的逼近于原系统的实际状态。状态观测器的状态空间表达为
| $ \dot{\hat{\boldsymbol{x}}}=\boldsymbol{A} \hat{\boldsymbol{x}}+\boldsymbol{Bu}+\boldsymbol{G}(\boldsymbol{y}-\hat{\boldsymbol{y}}) $ | (9) |
| $ \hat{\boldsymbol{y}}=\boldsymbol{C} \hat{\boldsymbol{x}}+\boldsymbol{D} \boldsymbol{u} $ | (10) |
状态观测器与原系统的估计误差为
| $ \dot{\boldsymbol{x}}_{e}=\dot{\boldsymbol{x}}-\dot{\hat{\boldsymbol{x}}}=(\boldsymbol{A}-\boldsymbol{G} \boldsymbol{C})(\boldsymbol{x}-\hat{\boldsymbol{x}}) $ | (11) |
式中,A-GC是观测器的系统矩阵,G是结温观测器的反馈矩阵。反馈矩阵G的设计最主要的是保证观测器能够快速稳定的收敛,即使得特征矩阵A-GC的特征值都处于实轴的负半部,保证观测器的收敛性。收敛速度则可根据离虚轴的距离来确定,特征值离虚轴越远则观测器的状态逼近原系统状态的速度就越快; 但是并非越快越好,一般观测器极点取原系统极点的2~5倍即可。
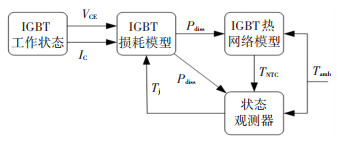
基于状态观测器的IGBT结温估计模型分为3个部分:电学模型、热学模型以及观测器模型,实现结温估计原理框架如图 14所示。
|
图 14 IGBT结温估计原理框图 Fig. 14 Block diagram of IGBT junction temperature estimation |
图 15为基于全阶状态观测器的IGBT模块结温预测仿真模型,模型包括IGBT工作电路、损耗模型、等效热网络模型以及结温状态观测器,基于真实的壳温与观测器观测到的壳温之间的误差进行输出反馈调节,从而实现对结温估计值的实时修正。

|
图 15 Simulink仿真模型 Fig. 15 Simulink simulation model |
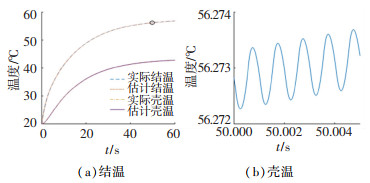
IGBT在如图 15所示的工作电路下运行,工作状态为:导通电流为300 A、母线电压为300 V、开关频率为1 kHz、驱动信号方波的占空比为0.3、环境温度为20 ℃,仿真得到了如图 16所示的IGBT结温与壳温升高曲线。仿真结果表明,器件在正常运行过程中,导通损耗与开关损耗使得结温升高,当功率损耗产生的热量与外界散热达到平衡时,进入稳定状态,平均结温不再升高。而且从图中可以看出无论是估计的结温还是壳温都能够很好地跟随实际的温度曲线。
|
图 16 IGBT结温与壳温观测仿真波形 Fig. 16 Observed simulated waveforms of IGBT junction temperature and shell temperature |
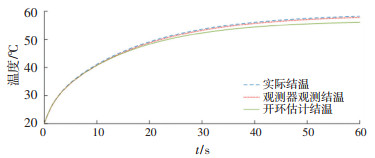
图 17为两种方法估计结温的对比结果,当建立的IGBT热网络模型与实际的IGBT传热过程存在误差时,本文所设计得状态观测器能够在很大程度上消除估计误差,实现准确的预测结温,而传统的热电耦合模型属于开环估计,太过依赖模型的准确性,一旦模型存在误差或者受到随机干扰则无法准确估计结温。
|
图 17 不同方法预测结温对比仿真波形 Fig. 17 Comparison of different methods for predicting junction temperature |
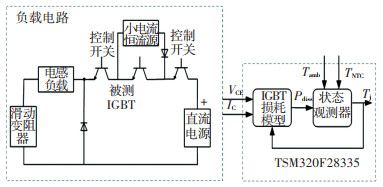
实验平台的原理图见图 18,实验平台主要由感性负载电路与TMS320F28335系统构成。负载电路包含两个IGBT,被测IGBT是结温估计对象,由正常PWM波驱动,在开关和导通过程产生功率损耗使结温上升。而控制开关是用来选择导通电流的,对结温状态观测器准确性进行验证。当控制开关一直处于导通状态时,被测IGBT处于正常回路运行,每隔5 s关断控制开关并且使被测IGBT恒打开,此时被测IGBT流过的则是通过小电流恒流源提供的10 mA电流,短暂测量后两个IGBT又恢复正常运行。
|
图 18 结温估计实验平台原理图 Fig. 18 Schematic diagram of junction temperature estimation experimental platform |
电感负载为240 μH的SDK-60 A的输出电抗器,滑动变阻器是RX20-T大功率可调电阻,其功率为5 kW、最大阻值1 Ω。直流电源为爱德克斯大功率IT6523D电源,额定功率为3 kW。恒定小电流源采用艾德克斯IT6720直流源,可提供10 mA电流。被测IGBT采用三菱模块PM600CLA060,该模块采用新的第5代IGBT芯片,额定电压为600 V,额定电流为600 A,结温范围为-20~150。搭建如图 19所示的实验平台实物图。实验时,28335控制器的A/D模块对IGBT的运行状态进行实时采集,结合初始设定的占空比与开关频率输入损耗模型计算当前IGBT的功率损耗。NTC热敏电阻的温度通过变送器转换成电压信号被采集,输入给状态观测器,利用观测器估算的壳温和实际的热敏电阻温度的误差对结温估计值进行实时修正。

|
图 19 结温估计实验平台实物图 Fig. 19 Photo of junction temperature estimation experimental platform |
实验条件:母线电压为100 V, 开关频率为10 kHz, 驱动信号的PWM波占空比为0.2,导通电流为40 A,得到的实验验证结果如图 20。从图 20中可以看出,器件在正常运行过程中,导通损耗与频繁开关带来的开关损耗使得结温不断升高,当功率损耗产生的热量与外界散热达到平衡时,结温进入稳定状态。观测器估算的壳温很好跟随实际NTC热敏电阻测量得到的壳温,同时由热敏参数法采集的实际结温与状态观测器估算的结温间的误差也很小,说明了本文设计的状态观测器的准确性。

|
图 20 结温估计实验验证结果 Fig. 20 Verification results of junction temperature estimation experiment |
1) IGBT总损耗随着导通电流、母线电压、结温的增大而增加,搭建了IGBT的损耗模型,综合考虑了电流、母线电压和结温的影响,计算结果更精确。
2) 根据IGBT饱和压降在恒定小电流下与器件结温呈线性相关的性质,拟合了温度与瞬态热阻变化曲线,建立了具备物理意义的热网络模型。
3) 针对基于状态方程对结温开环估计无法进行反馈调节的不足,设计了全阶状态观测器,利用观测器输出壳温和实测的壳温之间的误差对结温估计值进行实时修正;在Matlab/Simulink中验证了状态观测器结温估计方法的准确性与鲁棒性;基于热敏参数法的实验结果表明状态观测器能够很好实时在线估算结温。
| [1] |
黄莹. 电动汽车用电机控制器电力电子技术研究[D]. 长春: 吉林大学, 2012 HUANG Ying. The research of power electronic devices used in electric vehicle controller[D]. Changchun: Jilin University, 2012 |
| [2] |
XU Dewei, LU Haiwei, HUANG Lipei, et al. Power loss and junction temperature analysis of power semiconductor devices[J]. IEEE Transactions on Industry Applications, 2002, 38(5): 1426. DOI:10.1109/TIA.2002.802995 |
| [3] |
罗皓泽. 基于动态热敏电参数法的大容量IGBT模块结温在线提取原理和方法研究[D]. 杭州: 浙江大学, 2017 LUO Haoze. Research on the principle and method of on-line extraction of large-capacity IGBT module junction temperature based on dynamic thermistor parameter method[D]. Hangzhou: Zhejiang University, 2017 |
| [4] |
汪绪彬. 电动汽车变流器的器件损耗与结温研究[D]. 广州: 华南理工大学, 2017 WANG Xubin. Research onpower losses and junction temperature of power devices for EV converters[D]. Guangzhou: South China University of Technology, 2017 |
| [5] |
王祥. 基于组合式动态热敏电参数的功率IGBT模块结温提取研究与应用[D]. 杭州: 浙江大学, 2017 WANG Xiang. Research and application of junction temperature extraction of power IGBT module based on combined dynamic thermistor parameters[D]. Hangzhou: Zhejiang University, 2017 |
| [6] |
侯月. 高温环境下IGBT建模与结温预测方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2017 HOU Yue. Research onmodeling and junction temperature predicting of IGBT under high temperature[D]. Harbin: Harbin Institute of Technology, 2017 |
| [7] |
吴岩松. 基于IGBT开关动态特性离线测试系统的大功率逆变器热-电耦合研究[D]. 杭州: 浙江大学, 2013 WU Yansong. Electro-thermal coupling researches on high power inverters based on the IGBT switching dynamic performance offline test system[D]. Hangzhou: Zhejiang University, 2013 |
| [8] |
陈明, 胡安. IGBT结温模拟和探测方法比对研究[J]. 电机与控制学报, 2011, 15(12): 44. CHEN Ming, HU An. Study on the junction temperature simulation and detection method of IGBT power electronic devices[J]. Electric Machines and Control, 2011, 15(12): 44. DOI:10.15938/j.emc.2011.12.003 |
| [9] |
XU Yang, CHEN Hao, LV Sen, et al. Thermal model for power converters based on thermal impedance[J]. Journal of Power Electronics, 2013, 13(6): 1080. DOI:10.6113/JPE.2013.13.6.1080 |
| [10] |
ZHANG Zheyu, WANG F, COSTINETT D J, et al. Online junction temperature monitoring using turn-off delay time for silicon carbide power devices[C]// Proceedings of 2016 IEEE Energy Conversion Congress and Exposition. Milwaukee: IEEE, 2016. DOI: 10.1109/ECCE.2016.7855308
|
| [11] |
AVEBAS Y, DUPONT L, KHATIR Z. Temperature measurement of power semiconductor devices by thermo-sensitive electrical parameters review[J]. IEEE Transactions on Power Electronics, 2012, 27(6): 3081. DOI:10.1109/TPEL.2011.2178433 |
| [12] |
BAKER N, LISERRE M, DUPONT L, et al. Improved reliability of power modules: A review of online junction temperature measurement methods[J]. IEEE Industrial Electronics Magazine, 2014, 8(3): 17. DOI:10.1109/MIE.2014.2312427 |
| [13] |
熊妍, 沈燕群, 江剑, 等. IGBT损耗计算和损耗模型研究[J]. 电源技术应用, 2006, 9(5): 55. XIONG Yan, SHEN Yanqun, JIANG Jian, et al. Study on loss calculation and model for IGBT[J]. Power Supply Technologies and Applications, 2006, 9(5): 55. |
| [14] |
杨洪波, 王征宇, 黄宜山. IGBT损耗和结温计算研究[J]. 大功率变流技术, 2016(1): 30. YANG Hongbo, WANG Zhengyu, HUANG Yishan. Study of calculation for IGBT loss and junction temperature[J]. High Power Converter Technology, 2016(1): 30. DOI:10.13889/j.issn.2095-3631.2016.01.007 |
| [15] |
吴锐, 温家良, 于坤山, 等. 电压源换流器开关器件损耗建模[J]. 中国电机工程学报, 2012, 32(21): 1. WU Rui, WEN Jialiang, YU Kunshan, et al. Power loss modeling of switching devices in voltage source converters[J]. Proceedings of the CSEE, 2012, 32(21): 1. DOI:10.13334/j.0258-8013.pcsee.2012.21.003 |
| [16] |
陈娜, 何湘宁, 邓焰, 等. IGBT开关特性离线测试系统[J]. 中国电机工程学报, 2010, 30(12): 50. CHEN Na, HE Xiangning, DENG Yan, et al. An off-line IGBT switching characteristics measurement system[J]. Proceedings of the CSEE, 2010, 30(12): 50. |
| [17] |
丁现朋. IGBT热阻热谱和热瞬态过程的研究[D]. 济南: 山东大学, 2014 DING Xianpeng. The research on the thermal resistance and thermal spectrum and the process of thermal transient of IGBT[D]. Jinan: Shandong University, 2014 |
| [18] |
李志刚, 张亚玲, 曹博, 等. IGBT热阻测量方法的综述[J]. 电子元件与材料, 2015, 34(9): 25. LI Zhigang, ZHANG Yaling, CAO Bo, et al. Review of IGBT thermal resistance measurement method[J]. Electronic Components and Materials, 2015, 34(9): 25. DOI:10.14106/j.cnki.1001-2028.2015.09.005 |
 2021, Vol. 53
2021, Vol. 53


