2. 哈尔滨工业大学(威海) 汽车工程学院,山东 威海 264209
2. School of Automotive Engineering, Harbin Institute of Technology, Weihai, Weihai 264209, Shandong, China
在汽车行业中,锂电池作为当今世界应用最广泛和最有发展前景的电池之一,具有比能量高、工作寿命长、安全操作性能高和成本较低的优点[1],在储能领域逐渐取得优势。随着电动车的普及,车用电池的性能、成本、寿命、安全隐患也逐渐成为人们关注的重点。着重一体化电动底盘,加大新体系的动力电池的研发力度,有望解决电动汽车(EV)目前的发展瓶颈[2]。电池生产厂家除了加强研发便于更换的单体电池、模块组配方式之外,电池管理系统(Battery management system,BMS)的研发也逐渐成为热点[3]。BMS具备检测电池包、电池模组和单体电池的电压、温度、电流的能力,也具备准确估算电池剩余电量(State of Charge,SOC)、电池健康状态(State of Health,SOH)和电池剩余寿命的能力。决定电量使用范围的是容量最小的电池单元,精确的SOC可以提供可靠的电池信息,避免产生过充、过放等缩短电池循环寿命的情况。
国内外学者对电池的SOC估算展开了相关研究。电池SOC估算的输入参数有离线参数辨识和在线参数辨识两种获取方式。马群[4]基于二阶RC等效电路模型,采用离线辨识的方法获取电池内部参数的定值并利用中心差分卡尔曼滤波算法估算SOC;He等[5]基于改进的戴维南模型,采用扩展卡尔曼滤波算法(Extended Kalman Filter,EKF)算法在线辨识模型参数,然后采用自适应扩展卡尔曼滤波算法(Adaptive Extended Kalman Filter,AEKF)算法估算SOC。也有学者选择从数学描述方面进行优化,电池的SOC与开路电压之间存在着非线性关系,可以通过提高开路电压的描述精度来提高模型的精度。常用的开路电压拟合方式有分段线性拟合[6]、多项式拟合[7]、晶格气体模型拟合[8]、电化学极化模型拟合[9]等。在SOC算法方面,Xing等[10]结合开路电压法和卡尔曼滤波算法研究SOC估算,在Rint模型的基础上考虑温度的影响,加入SOC-OCV-T查表,利用最小二乘法辨识模型参数并且采用UKF估算SOC。聂文亮等[11]采用自回归各态历经(Autoregressive exogenous,AEX)模型建立锂离子电池等效电路模型,模型的阶数由基于赤池信息准则的遗传算法决定,AEX模型系数的求解由递推最小二乘法实现。Sahinoglu等[12]提出了一种使用高斯回归(GPR)框架的机器学习方法估算SOC。Chemali等[13]提出了一种利用具有长期记忆的周期神经网络(RNN)的方法,能够对锂离子电池进行精确地估算。Ahmed等[14]基于降阶的电化学模型采用滑膜观测器估算SOC。Sbarufatti等[15]提出了一种基于粒子滤波与径向函数神经网络结合的锂离子电池放电结束的方法,主要创新在于径向基函数模型是在网上得到自适应训练。
在参数辨识方面,固定电池参数的离线辨识的端电压拟合精度低于基于数据驱动的在线辨识,但计算量远小于后者。为此本文采用离线辨识,加入SOC以及充放电状态对电池内部参数的影响,研究聚合物锂电池的SOC估算。在SOC估算算法方面,相较于学习算法,使用自适应滤波法不需要大量的实验数据。自适应滤波算法是基于模型的,影响算法精度的因素除了算法自身的精度之外,还与电池模型的精度有关,所以可以采用改进的模型来提高算法的精度。综合以上考虑,本文将基于优化的电池模型,采用离线辨识结合自适应卡尔曼滤波算法展开对聚合物锂电池的参数辨识和SOC估算。
1 建立锂电池模型 1.1 电池外特性曲线获取本文使用三元聚合物锂离子电池,正极是三元材料。可用容量实验参考QC/T897—2011《电动汽车用电池管理系统技术条件》,得到电池的实际可用容量为8.2 A·h。为了得到电池的开路电压和SOC的关系曲线,对容量未衰减的电池进行实验,进行了两组充放电脉冲实验, 实验过程如表 1所示,实验步骤参考QC/T897—2011。
| 表 1 脉冲充放电实验 Tab. 1 Pulse charge and discharge experiment |
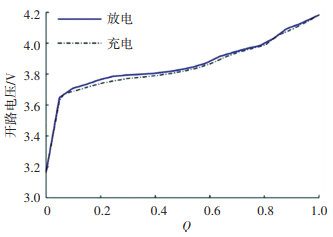
脉冲实验包括充电脉冲实验和放电脉冲实验。根据实验获取的参数,处理脉冲电压数据,建立参考SOC和开路电压的对应关系,如图 1所示。本文中的SOC用变量Q来表示。
|
图 1 开路电压和SOC的关系曲线 Fig. 1 Curve of open circuit voltage and SOC |
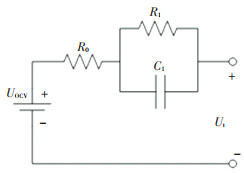
现阶段常用的电池模型包括电化学模型[16]、神经网络模型[17]、PNGV模型[18]、戴维南模型[19]、Rint模型[20]、GNL模型[20]、可变阶次等效电路模型[21]等。PNGV模型、戴维南模型、GNL模型等都属于等效电路RC模型。戴维南模型结构如图 2所示。等效电路模型是指用一系列的电气元件描述电池的电压响应特性。Rint模型只考虑了电池的欧姆内阻,通过加入并联的电阻电容增加了极化内阻和极化电容构成RC模型,其中大部份元件的数值和权值都是通过经验获取,故此一般的RC模型只能满足充电、放电单一方向的精度,通过改进RC模型来使其在充电、放电双向上都有较高的精度,从而提高模型的适用性。戴维南模型通过一个RC环节,可以很好地模拟电池的动态特性,但是其中的开路电压、内阻等值并未考虑到温度、充放电状态的影响。PNGV模型则考虑电池开路电压随SOC变化的因素,增加了一个电容来表示。GNL模型增加了自放电内阻,精度较前几个模型有一定提高,参数辨识简单,计算量小,对处理器的要求不高,而且模型的精度可以通过优化算法来提高。
|
图 2 戴维南模型 Fig. 2 Thevenin model |
戴维南模型的端电压:
| $ U_{\mathrm{t}}=U_{\mathrm{ocv}}-U_{1}-R_{0} I $ | (1) |
式中:Uocv为开路电压,U1为极化环节的电压,第3项为欧姆内阻上的压降,R0为欧姆内阻,I为流过电池的电流。
极化环节计算公式为
| $ \dot{U}_{1}=-\frac{1}{R_{1} C_{1}} U_{1}+\frac{1}{C_{1}} I $ | (2) |
式中:R1为极化内阻,C1为极化电容。
将式(2)看作是线性定常系统,可求解出
| $ U_{1, k+1}=\mathrm{e}^{-\frac{\Delta t}{\tau}} U_{1, k}-\left(1-\mathrm{e}^{-\frac{\Delta t}{\tau}}\right) R_{1} I_{k} $ | (3) |
式中:τ为时间常数,为极化电阻和极化电容的乘积;e为指数常数;Δt为采样时间间隔。
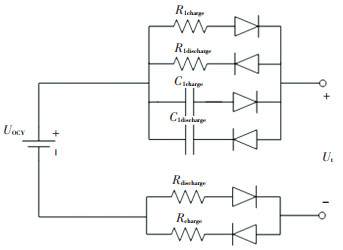
结合RC模型适用性差的缺点,在戴维南模型的基础上,将充放电过程的欧姆内阻、极化电阻和极化电容分开讨论,借此来提高模型的精度和适用性,同时并未增加模型的计算量。优化的模型如图 3所示。
|
图 3 优化的模型 Fig. 3 Optimized model |
图 3中用充电内阻Rcharge和放电内阻Rdischarge代替图 2中的欧姆内阻,表示为R0=f1(Q, s),充电极化电阻R1charge和放电极化电阻R1discharge代替图 2中的极化内阻,充电极化电容C1和放电极化电容C1discharge代替图 2中的极化电容。其中s表示充放电状态,Q为荷电状态。与戴维南模型相比,优化的戴维南模型的开路电压Uocv也随充放电状态而变化,可以表示为Uocv=f2(Q, s),即开路电压是与SOC和充放电状态相关的函数。
结合优化的模型,将图 3优化模型中的参数R0、Uocv带入式(1)中得
| $ U_{t, k}=f_{2}(Q, s)-U_{1, k}-f_{1}(Q, s) I_{k} $ | (4) |
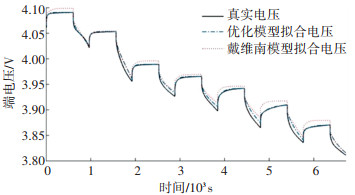
图 4是放电脉冲工况下电池模型电压拟合结果与真实电压对比图,图 5是电池模型的端电压拟合误差。为了得到优化模型的端电压拟合效果图,运行脉冲放电工况与混合工况,同时将该优化模型的端电压拟合误差图与戴维南模型拟合的端电压误差图进行对比。可以看出,两个模型都能跟随真实电压的变化情况,其中优化模型的跟随效果优于戴维南模型,戴维南模型在端电压回弹阶段拟合出的电压基本上一直大于优化的模型的拟合电压。优化模型的端电压拟合的平均误差为3 mV,最大误差为15 mV,而戴维南模型端电压拟合的平均误差为9 mV,最大误差为19 mV。
|
图 4 放电脉冲工况模型的端电压拟合 Fig. 4 Terminal voltage fitting curve of model under discharge pulse working condition |

|
图 5 放电脉冲工况端电压拟合误差 Fig. 5 Terminal voltage fitting error curve of model under discharge pulse working condition |
离线参数获取需要对每一段脉冲的静置阶段进行数学拟合。电池处于充电结束阶段时,电压响应达到的最大值,随后电流发生瞬时变化,由最大值变为0,电压也由最大值降至某一点,该阶段可以理解为欧姆内阻上的压降;此后的静置阶段,电流都为0,电压则逐渐下降接近开路电压值,至此,电压保持不变,这一阶段可以看作是等效电路模型中的RC环节的零输入响应。放电阶段亦是如此。
不同电池的内阻等内部参数不同,为了使电池模型能够精确反映出所研究电池的端电压,需要对模型的充放电内阻(Rcharge、Rdischarge)、充放电极化电阻(R1charge、R1discharge)和充放电极化电容(C1charge、C1discharge)进行参数辨识。对电池外特性进行拟合可以获取电池内阻、极化内阻和极化电容等参数。采用式(5)进行拟合:
| $ U_{t}=U_{\mathrm{ocv}}-R_{1} I \mathrm{e}^{-\frac{\Delta t}{\tau}}-R_{0} I $ | (5) |
在电流变为0时的单位采样时间内,采用式(6)获取欧姆内阻。
| $ R_{0}=\frac{U_{t+\Delta t}-U_{t}}{I} $ | (6) |
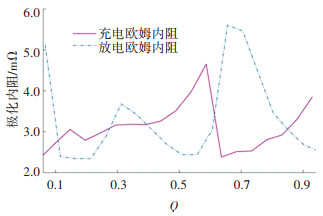
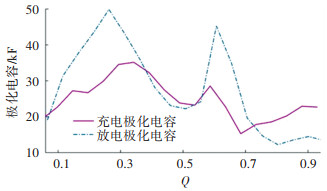
式中:Δt是单位采样间隔,Ut+Δt、Ut是端电压的采样数据。拟合出的充放电周期的欧姆内阻、极化内阻和极化电容如图 6~8所示。

|
图 6 充电欧姆内阻与放电欧姆内阻 Fig. 6 Charged ohmic internal resistance and discharged ohmic internal resistance |
|
图 7 充电极化内阻与放电极化内阻 Fig. 7 Charged polarization internal resistance and discharged polarization internal resistance |
|
图 8 充电极化电容与放电极化电容 Fig. 8 Charged polarization capacitor and discharged polarization capacitor |
将上述实验获取的数据应用于搭建的优化模型中,得到充电脉冲工况下的端电压拟合效果图和拟合电压误差图。如图 9~10。
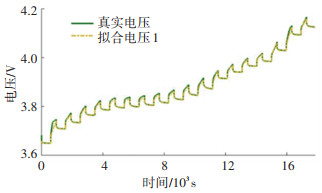
|
图 9 真实电压与离线辨识拟合电压 Fig. 9 True voltage and offline identification fitting voltage |

|
图 10 真实电压与离线辨识拟合电压误差 Fig. 10 True voltage and offline identification fitting voltage error |
由图 9可以看出,采用离线辨识的优化模型的电压跟随效果良好。图 10为脉冲充电工况下的真实电压与离线辨识拟合电压误差。在脉冲充电工况下,采用离线辨识方法的模型端电压最大误差为31 mV,平均绝对误差为3 mV,标准差为0.005 22 V,误差较小。
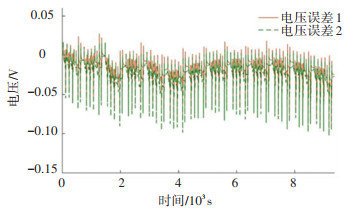
2.2 离线参数辨识与在线参数辨识对比采用的自定义工况包含充电和放电脉冲。这里只选取离线辨识和在线辨识进行对比实验。在自定义工况下,上述两种方案的端电压拟合效果如图 11所示,拟合误差如图 12所示。图 11中拟合电压1和拟合电压2分别是离线辨识和在线辨识电池模型计算出的端电压,最大绝对误差、平均绝对误差和标准差如表 2所示。由表 2可看出,离线参数辨识的3项评价指标均为最优,其最大绝对误差为0.093 V,平均绝对误差为0.017 V,标准差为0020 V。
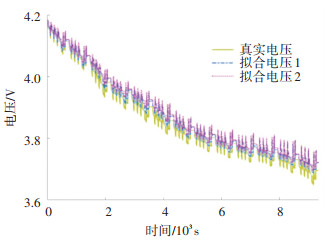
|
图 11 真实电压与两种方案拟合电压 Fig. 11 True voltage and two fitting voltages |
|
图 12 真实电压与2种方案拟合电压的误差 Fig. 12 True voltage and two fitting voltage error |
| 表 2 在线辨识与离线辨识在混合脉冲工况下的估算误差 Tab. 2 Estimation error indicators for online identification and offline identification under mixed pulse conditions |
由此可知,基于优化模型的离线参数辨识的精度高于在线辨识的精度。所以本文后续工作基于离线辨识开展。
3 基于AEKF估算SOC 3.1 AEKF算法仿真EKF是建立在线性卡尔曼滤波的基础上,为解决非线性问题而提出的。其核心思想是将非线性函数保留一阶Taylor展开项。非线性离散方程状态方程式为
| $ \boldsymbol{X}_{k+1}=f\left(k, \boldsymbol{X}_{k}, \boldsymbol{u}_{k}\right)+\boldsymbol{G}_{k} \boldsymbol{w}_{k} $ | (7) |
观测方程为
| $ \boldsymbol{Y}_{k}=h\left(k, \boldsymbol{X}_{k}, \boldsymbol{u}_{k}\right)+\boldsymbol{\nu}_{k} $ | (8) |
式中:wk为过程噪声,νk为观测噪声,Gk是噪声驱动矩阵。
本文采用自适应扩展卡尔曼滤波(Adaptive Extended Kalman Filter,AEKF)算法估算电池的SOC。
对函数f(k, Xk|k-1, uk)在滤波值xk|k-1处进行一阶泰勒展开,得到状态转移矩阵:
| $ \boldsymbol{A}_{k}=\frac{\partial f\left(k, \boldsymbol{X}_{k \mid k-1}, \boldsymbol{u}_{k}\right)}{\partial x_{k \mid k-1}} $ | (9) |
同理,对式(8)的函数h(k, Xk|k-1, uk)在xk|k-1处进行一阶泰勒展开,得到观测矩阵:
| $ \boldsymbol{C}_{k}=\frac{\partial h\left(k, \boldsymbol{X}_{k \mid k-1}, \boldsymbol{u}_{k}\right)}{\partial x_{k \mid k-1}} $ | (10) |
启动AEKF算法,输入向量初值X0和协方差矩阵P0,通过迭代计算公式,得到SOC的估算值。
车用电池的SOC定义为电池当前剩余电量与最大可用容量的百分比:
| $ Q=Q_{0}+\int \frac{\eta \Delta t}{C_{\mathrm{a}}} i \mathrm{~d} t $ | (11) |
式中,Q0为初始SOC,η为充放电效率,这里视作1;Ca为最大可用容量(A·h),实验得到Ca实际容量为8.2 A·h。
离散化后应用AEKF算法计算电池SOC时,定义状态方程的状态量为Xk=[Qk U1, k]T,状态方程为
| $ \begin{aligned} \left[\begin{array}{c} Q_{k} \\ U_{1, k} \end{array}\right]=&\left[\begin{array}{lc} 1 & 0 \\ 0 & \mathrm{e}^{\frac{-\Delta t}{\tau}} \end{array}\right]\left[\begin{array}{c} Q_{k-1} \\ U_{1, k-1} \end{array}\right]+\\ &\left[\begin{array}{c} \frac{\eta \Delta t}{C_{\mathrm{a}}} \\ \left(1-\mathrm{e}^{-\frac{\Delta t}{\tau}}\right) R_{0} \end{array}\right] i_{k}+w_{k} \end{aligned} $ | (12) |
测量方程为
| $ U_{k}=\left[\frac{\mathrm{d} U_{\mathrm{ocv}, k}}{\mathrm{~d} Q_{k}}-1\right]\left[\begin{array}{c} Q_{k} \\ U_{1, k} \end{array}\right]+\left(-R_{0}\right) i_{k}+v_{k} $ | (13) |
结合式(12)和(13)可得
| $ \boldsymbol{A}_{k}=\left[\begin{array}{cc} 1 & 0 \\ 0 & \mathrm{e}^{-\Delta t / \tau} \end{array}\right] \quad \boldsymbol{C}_{k}=\left[\frac{\mathrm{d} U_{\mathrm{ocv}, k}}{\mathrm{~d} Q_{k}}-1\right] $ | (14) |
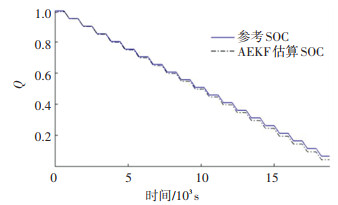
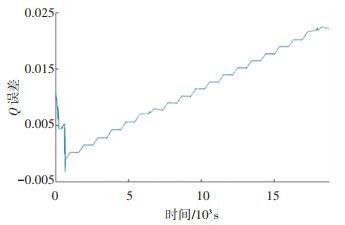
AEKF算法模型输入为工况电池电流、电压以及离线辨识获取的电池参数,输出为状态量中的SOC。SOC的初始值设置为1,仿真结果如图 13所示,误差如图 14所示。
|
图 13 AEKF估算SOC仿真结果 Fig. 13 Estimation of SOC by AEKF |
|
图 14 AEKF估算SOC仿真结果误差 Fig. 14 Estimation error of SOC by AEKF |
由图 13可知,AEKF算法估算的SOC能跟随真实SOC变化。由图 14可以看出,算法先开始收敛,误差减小达到最小值,之后开始呈现一直上升的趋势,这个误差的积累过程源于开路电压多项式-SOC拟合曲线的误差积累。
3.2 DST工况验证电动汽车的电池包实际面临的工况非常恶劣,为了更加合理地对比这几种算法的精度,采用动态压力测试(Dynamic Stress Test,DST)工况进行实验验证。DST工况是《USABC电动汽车电池测试程序手册中》一种试验方法,现已被广泛使用。
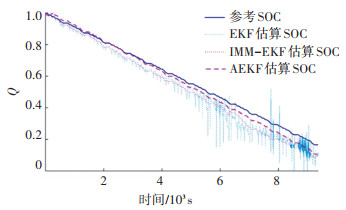
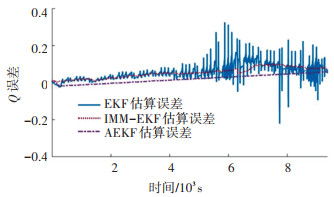
为了对比AEKF的算法性能,加入EKF和交互多模型(Interacting Multiple Model,IMM)-EKF与AEKF的估算结果进行对比。图 15是在DST工况下3种算法EKF[22]、IMM-EKF[22]和AEKF的SOC估算结果。图 16是这3种算法的估算误差。
|
图 15 DST工况下3种算法估算SOC Fig. 15 Estimation of SOC by three algorithms under DST condition |
|
图 16 3种算法估算SOC仿真结果误差 Fig. 16 Estimation error of SOC by three algorithms under DST condition |
由图 15、16可以看出,两类自适应算法的估算SOC曲线能更好地贴合真实曲线的变化,而且AEKF明显优于IMM-EKF。
为对比EKF、IMM-EKF和AEKF的精度,将DST工况下这3个算法的误差评价指标列入表 3中。
| 表 3 DST工况下3种算法的估算误差评价指标 Tab. 3 Estimation error evaluation indicators for three algorithms under DST condition |
根据QC/T897—2011《电动汽车用电池管理系统技术条件》的4.2.4,要求SOC估算精度不大于10%,IMM-EKF与AEKF符合要求。从表 3可以看出,AEKF的最大绝对误差为0.058,远小于另外两种算法的指标。其平均绝对误差为0.020,与EKF的0.057和IMM-EKF的0.052相比,也具有明显优势。AEKF的标准差为0.031,也是这3种算法中最小的。
4 结论1) 在戴维南模型的基础上,将开路电压和模型参数加入充放电状态和SOC对模型参数的影响,该优化模型精度在脉冲工况下的端电压拟合精度高于原始模型;
2) 基于优化的戴维南模型,考虑了充放电状态和SOC变化后,与在线辨识相比,在变电流工况下,其离线辨识的精度高于在线辨识的精度;
3) 在DST工况下,AEKF SOC估算精度高于IMM-EKF和EKF的估算精度。
| [1] |
王福鸾, 杜军, 裴金海. 全球锂电池市场状况和应用发展综述[J]. 电源技术, 2014, 38(3): 564. WANG Fuluan, DU Jun, PEI Jinhai. Overview on global lithium battery market and application[J]. Chinese Journal of Power Sources, 2014, 38(3): 564. DOI:10.3969/j.issn.1002-087X.2014.03.051 |
| [2] |
马建, 刘晓东, 陈轶嵩. 中国新能源汽车产业与技术发展现状及对策[J]. 中国公路学报, 2018, 31(8): 1. MA Jian, LIU Xiaodong, CHEN Yisong. Current status and countermeasures for China's new energy automobile industry and technology development[J]. China Journal of Highway and Transport, 2018, 31(8): 1. DOI:10.3969/j.issn.1001-7372.2018.08.001 |
| [3] |
张剑波, 卢兰光, 李哲. 车用动力电池系统的关键技术与学科前沿[J]. 汽车安全与节能学报, 2012, 3(2): 87. ZHANG Jianbo, LU Languang, LI Zhe. Key technologies and fundamental academic issues for traction battery systesms[J]. Journal of Automotive Safety and Energy, 2012, 3(2): 87. |
| [4] |
马群. 基于中心差分卡尔曼滤波的动力电池SOC估算研究[D]. 长春: 吉林大学, 2014 MA Qun. Research on SOC estimation of power battery based on central differential Kalman filter[D]. Changchun: Jilin University, 2014. |
| [5] |
HE Hongwen, XIONG Rui, ZHANG Xiaowei, et al. State-of-charge estimation of the lithium-ion battery using an adaptive extended Kalman filter based on an improved Thevenin model[J]. IEEE Transactions on Vehicular Technology, 2011, 60(2): 1461. DOI:10.1109/-TVT.2011.2132812 |
| [6] |
孙豪豪, 潘庭龙, 吴定会. 基于自适应电池模型的SOC加权在线估计[J]. 系统仿真学报, 2017, 29(8): 1677. SUN Haohao, PAN Tinglong, WU Dinghui. Weighted online estimation of SOC based on adaptive battery model[J]. Journal of System Simulation, 2017, 29(8): 1677. DOI:10.16182/j.issn1004731x.joss.201708008 |
| [7] |
DAOWD M, OMAR N, VAN DEN BOSSCHE P, et al. An extended PNGV battery model for electric and hybrid vehicles[J]. IEEE International Review of Electrical Engineering, 2011, 6(4): 1264. DOI:10.1109/MIAS.2010.939621 |
| [8] |
KALIKMANOV V I, KOUDRIACHOVA M V, de LEEUW S W. Lattice-gas model for intercalation compounds[J]. Solid State Ionics, 2000, 136(11): 1373. DOI:10.1016/S0167-2738(00)00579-8 |
| [9] |
黄泽波. 基于电化学模型估算锂电池SOC的方法研究[J]. 电源世界, 2016(7): 26. HUANG Zebo. Lithium battery SOC estimation method study based on electrochemical model[J]. The World of Power Supply, 2016(7): 26. |
| [10] |
XING Yinjiao, HE Wei, PECHT M, et al. State of charge estimation of lithium-ion batteries using the open-circuit voltage at various ambient temperatures[J]. Applied Energy, 2014, 113: 106. DOI:10.1016/j.apenergy.2013.07.008 |
| [11] |
聂文亮, 谭伟杰, 邱刚, 等. 基于ARX模型的锂离子电池荷电状态在线估算[J]. 中国电机工程学报, 2018, 38(18): 5415. NIE Wenliang, TAN Weijie, QIU Gang, et al. Online state-of-charge estimation for lithium-ion batteries based on the ARX model[J]. Proceedings of the CSEE, 2018, 38(18): 5415. DOI:10.13334/j.0258-8013.pcsee.172196 |
| [12] |
SAHINOGLU G O, PAJOVIC M, SAHINOGLU Z, et al. Battery state-of-charge estimation based on regular/recurrent Gaussian process regression[J]. IEEE Transactions on Industrial Electronics, 2018, 65(5): 4311. DOI:10.1109/TIE.2017.2764869 |
| [13] |
CHEMALI E, KOLLMEYER P J, PREINDL M A, et al. Long short-term memory networks for accurate state-of-charge estimation of Li-ion batteries[J]. IEEE Transactions on Industrial Electronics, 2018, 65(8): 6730. DOI:10.1109/TIE.2017.2787586 |
| [14] |
AHMED R, El SAYED M, ARASARATNAM I, et al. Reduced-order electrochemical model parameters identification and state of charge estimation for healthy and aged Li-ion batteries, part Ⅱ: aged battery model and state of charge estimation[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2014, 2(3): 678. DOI:10.1109/JESTPE.2014.2331062 |
| [15] |
SBARUFATTI C, CORBETTA M, GIGLIO M, et al. Adaptive prognosis of lithium-ion batteries based on the combination of particle filters and radial basis function neural networks[J]. Journal of Power Sources, 2017, 344: 128. DOI:10.1016/j.jpowsour.2017.01.105 |
| [16] |
赵侃, 朱聪, 曾诚, 等. 基于电化学模型的电动公交车续驶里程预测及分析[J]. 公路交通科技, 2013, 30(8): 153. ZHAO Kan, ZHU Cong, ZENG Cheng, et al. Prediction and analysis of driving range of electric bus based on electrochemical model[J]. Journal of Highway and Transportation Research and Development, 2013, 30(8): 153. |
| [17] |
黄贵鸿, 雷霞, 芦杨, 等. 考虑用户满意度的电动汽车用户侧最优智能充放电策略[J]. 电力系统保护与控制, 2015, 43(24): 40. HUANG Guihong, LEI Xia, LU Yang, et al. Optimus smart charge-discharge tactics in electric vehicle user profile considering user's satisfaction[J]. Power System Protection and Control, 2015, 43(24): 40. |
| [18] |
CHARKHGARD M, FARROKHI M. State-of-charge estimation for lithium-ion batteries using neural networks and EKF[J]. IEEE Transactions on Industrial Electronics, 2010, 57(12): 4178. DOI:10.1109/-TIE.2010.2043035 |
| [19] |
欧少端, 杨晓力, 周乃君. 基于PNGV电容模型的LiFePO4电池性能仿真与实验[J]. 电源技术, 2013, 37(7): 1133. OU Shaoduan, YANG Xiaoli, ZHOU Naijun. Simulation and experiment study on PNGV capacitance model of LiFePO4 power battery for vehicle[J]. Chinese Journal of Power Sources, 2013, 37(7): 1133. DOI:10.3969/j.issn.1002-087X.2013.07.015 |
| [20] |
张东华, 马燕, 陈思琪, 等. 锂电池模型参数估计与荷电状态估算研究[J]. 武汉理工大学学报(信息与管理工程版), 2015, 37(2): 179. ZHANG Donghua, MA Yan, CHEN Siqi, et al. Parameter analysis method for lithium-ion battery circuit model and state of charge estimation[J]. Journal of Wuhan University of Technology (Information & Management Engineering), 2015, 37(2): 179. DOI:10.3963/j.issn.2095-3852.2015.02.012 |
| [21] |
LIN Cheng, YU Quanqing, XIONG Rui, et al. A study on the impact of open circuit voltage tests on state of charge estimation for lithium-aion batteries[J]. Applied Energy, 2017, 205: 892. DOI:10.1016/j.apenergy.2017.-08.124 |
| [22] |
黄小平, 王岩. 卡尔曼滤波原理及应用: MATLAB仿真[M]. 北京: 电子工业出版社, 2015: 77. HUANG Xiaoping, WANG Yan. Kalman filter principle and application: MATLAB simulation[M]. Beijing: Publishing House of Electronics Industry, 2015: 77. |
 2021, Vol. 53
2021, Vol. 53


