随着中国经济的高速发展,国内的货物运输尤其是能源矿产运输也在飞速增长。相关研究表明,运输车辆质量每减轻100 kg,燃油消耗可降低0.3~0.5L/100 km,同时还能有效减少车辆的尾气排放总量[1]。货箱作为矿用卡车(简称矿车)的主要承载部件,自重较大,约占整车质量的30%,对矿车燃油经济性影响显著[2-3]。因此,矿车货箱的轻量化设计成为亟需解决的问题。
矿区的道路环境条件复杂,在不同工作条件下矿车货箱受到的载荷并不相同,即工作状况复杂多变,货箱的设计和优化过程中需要同时考虑多种工况条件下的设计参数协调化。目前国内外学者对货箱轻量化设计进行了一些研究,例如,王晓楠等[4]使用高强度钢板代替普通钢板对自卸车货箱进行轻量化设计,并在在静载工况条件对优化后的货箱强度进行验证。董志明等[5]对矿用自卸车货箱满载匀速行驶、举升卸货等4种工况进行力学性能分析,为轻量化设计提供了理论依据;Li等[6]基于模态理论对空载工况下货箱的动态性能进行分析研究;王金刚等[7]对展开工况下翼开启式车厢骨架进行静力学分析,根据分析结果进行尺寸优化设计;刘钊等[8]基于克里格(Kriging)近似模型技术,依次对货箱在举升卸货和装载工况条件下单独进行优化。
在汽车结构轻量化设计方法方面,Trivers等[9]对静态工况条件下的汽车座椅进行无参数的拓扑优化,提高了座椅安全性能并实现轻量化设计;谢然等[10]建立白车身碰撞模型,对扭转工况下的白车身进行满足可靠性的轻量化设计;王禹琪等[11]对汽车轮毂进行多工况疲劳分析,以转弯行驶工况进行了单一工况的轮毂多目标轻量化设计;Mi等[12]对矿车车架进行疲劳寿命分析,采用试验设计方法和近似模型技术对车架质量和疲劳寿命进行了协同优化。
目前国内外对货箱轻量化设计存在的问题在于:1)缺乏系统的优化设计方法,企业一般直接使用高强度钢板等效替换,然后在不同工况条件下验证轻量化设计的货箱是否满足要求,导致设计周期较长且缺少后续结构优化设计分析[4-5]。2)轻量化设计过程中未能将多个工况下的性能参数同时进行优化,往往只是选择某一典型工况下的参数进行优化分析,然后采用不同工况验证设计的正确性[7-8, 10-11]。因此,本文以某工程机械装备公司所制造的矿用卡车货箱为研究对象,提出一种货箱二工况综合轻量化设计方法,对货箱的结构设计参数进行系统优化设计,设计流程如图 1所示。即首先建立货箱有限元模型,选择两种典型工况对货箱进行强度分析;通过试验设计选取变量参数生成样本点,搭建两种工况综合分析模型并计算样本点得到对应响应;然后采用近似模型技术,建立响应面进行多目标优化求解,得到不同的优化设计方案。进而根据设计要求开展方案对比分析,选择合适设计方案并进行有限元仿真验证,实现货箱的轻量化设计。

|
图 1 矿车货箱轻量化设计流程 Fig. 1 Lightweight design process of mining truck cargo box |
矿用卡车货箱的结构件主要由高强度钢板焊接而成,由以下几部分即底板总成、左右侧板总成、前板总成和后板总成组成。该货箱尺寸为6 000 mm× 4 000 mm×2 000 mm,额定载货重量60 t;货箱材料均为Q690高强度钢板,密度为7 850 kg/m3,泊松比为0.3,弹性模量为210 GPa,屈服强度σ为690 MPa。
对货箱进有限元分析时,为了减少计算量,提升计算效率,需要将货箱模型进行简化,略去挡泥板、吊耳等对货箱性能影响较小的零部件。使用SolidWorks三维建模软件建立货箱参数化模型,无缝导入AnsysWorkbench进行有限元分析。货箱为相同材料的钢板焊接而成,因此使用Bonded接触形式代替焊缝进行分析;货箱整体为薄壁件,使用壳单元进行网格划分;液压缸支座和货箱与车架铰接处为实体零件,采用实体单元进行网格划分。有限元模型共包括737 429节点,364 652个单元,如图 2所示。

|
图 2 矿车货箱有限元模型 Fig. 2 Finite element model of mining truck cargo box |
矿用卡车的工作环境恶劣,货箱是矿卡的主要承重部件,在使用过程中不允许出现结构断裂或者有较大的应力集中。货箱损坏主要因素有过载导致超出静态强度设计要求,以及疲劳破坏等。疲劳破坏多发生在局部,改进方法为改进局部结构和进行工艺处理。静态强度分析是为了满足货箱设计要求进行的重要分析,在静态强度分析的基础上可以进行疲劳强度验证。本文选取以下两种典型工况进行分析:1)满载匀速行驶工况是货箱工作时间最长的工况,因此要求平稳的力学性能,保证长时间的平稳运行。2)举升卸货工况是一个连续的动态过程,在货箱升起过程中,货箱前板处受到举升力,尾部只有与车架铰接处受支撑力,其应力值是动态变化的。根据文献[5, 8, 13]可知起升角度为0°的瞬间,此时的状态货箱整体受力最为严峻。因此,选取满载匀速行驶和起升角度为0°时刻举升卸货两种典型工况进行分析。
针对这两种典型工况,首先处理工作过程中的载荷,在Workbench中采用方向竖直向下的重力加速度来模拟货箱自重;举升力根据货物重量和车身自重施加;采用静水压来模拟货物对底板和各侧板的载荷[8],货箱所受载荷自下而上呈线性分布如图 3所示。货箱底板所受压力为货物的正压力P,其计算方法为
| $ P = F/S = \rho gH $ | (1) |

|
图 3 货箱载荷分布图 Fig. 3 Distribution diagram of container load |
式中:F为货物总重;S为底板面积;ρ为货物密度取1.43 t/m3;g为重力加速度,取9.8 m/s2;H为货箱高度。采用库伦土力学理论计算侧板压力P(h)与物料装载高度到底板的距离h的关系[14]。
| $ P\left( h \right) = {K_a}\rho gh $ | (2) |
式中Ka为主动土压力系数,根据所载货物有效摩擦角(煤的有效摩擦角为26.6°),通过查《主动土压力系数Ka值表》得到Ka=0.66。则可以得到货箱侧板的真实压力为相同高度下静水压的0.66倍。且考虑到实际工作中受力复杂,仿真分析时载荷按理论计算载荷的1.2倍施加。
按照上述的方法施加载荷,然后添加各工况下的约束条件。满载匀速行驶工况下,两根主纵梁采用远端位移约束,货箱铰接孔与车架铰接孔处只释放X方向旋转自由度。举升工况下,两根主纵梁约束X方向平动自由度和Y、Z方向的旋转自由度,货箱铰接孔与车架铰接孔只释放X方向旋转自由度,液压缸与支撑座销轴处仅释放X方向旋转自由度。对上述工况进行计算分别得到两种典型工况的应力云图如图 4所示。
|
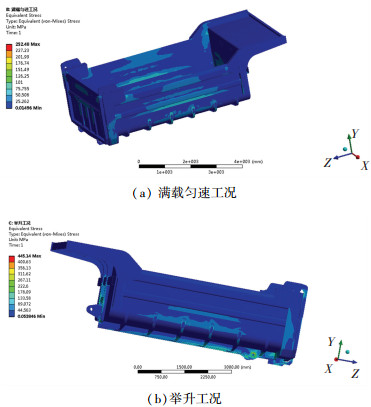
图 4 原始货箱典型工况应力云图 Fig. 4 Stress nephogram of original mining truck cargo box under typical working conditions |
由图 4(a)可知:满载匀速工况下货箱最大应力为252.48 MPa,出现在侧板与后板的连接处,高应力区域主要分布在货箱侧板与底板的连接处以及加强筋交叉位置。由图 4(b)可知:举升工况下货箱的最大应力为445.14 MPa,应力最大位置在货箱与车架的铰接处,这是因为货箱举升时,此处为整个货箱唯一支撑点,因此受力比较严峻;货箱前板处应力也比较大,此处承受较大的举升力。
货箱的强度设计要求安全系数为1.5,可以得到其许用应力为460 MPa。对于应力较大部位,可以通过局部的结构改进,降低最大应力。例如,满载工况下最大应力处,增加局部板厚和增加横梁内部筋板个数进行结构改进;对于底板与侧板连接处,添加肋板辅助焊接,增加焊接处强度;举升工况下,货箱与车架铰接处增加局部板厚,并进行工艺强化处理,降低局部应力。
2 货箱二工况轻量化设计多数研究在优化货箱的过程中未能将多个典型工况分析结果同时进行优化[7-8, 11],仅考虑某一个工况进行优化设计。因此本文提出一种货箱二工况轻量化设计方法,利用AnsysWorkbench软件建立二工况综合分析流程,如图 5所示。首先利用SolidWorks生成货箱参数模型无缝导入AnsysWorkbench中实现网格划分、两种工况加载以及求解计算,然后将两种工况分析结果导入多学科优化软件ISIGHT.2016中进行多目标优化求解[15],实现货箱两种工况同时进行结构优化设计。

|
图 5 两个典型工况的综合轻量化设计流程 Fig. 5 Integrated lightweight design process of two typical working conditions |
由图 2的有限元模型可知,该货箱主要由不同厚度的钢板焊接而成,其中底板、侧板、前板、后板和主纵梁是货箱的主要组成部分和受力关键部位。因此选取如表 1所示的5个参数作为设计变量,在Workbench中生成样本,并以质量和不同工况下最大应力为响应,进行参数相关性计算,以验证变量选取的合理性[12, 15]。
| 表 1 选取设计变量 Tab. 1 Selected design variables |
首先定义相关系数r为
| $ {r_i} = \frac{{\sum {\left( {{X_i} - \overline {{X_i}} } \right)} \left( {{Y_i} - {{\bar Y}_i}} \right)}}{{\sqrt {\sum {{{\left( {{X_i} - \overline {{X_i}} } \right)}^2}} \sqrt {{{\left( {{Y_i} - {{\bar Y}_i}} \right)}^2}} } }} $ | (3) |
式中:i为变量个数,Xi为输入变量,Xi为输入变量均值,Yi为对应的输出变量,Yi为对应输出变量均值。将ri归一化处理
| $ {C_i} = {r_i}/\sum\limits_{i = 1}^k {{r_i}} $ | (4) |
Ci为归一化处理后各变量对响应的影响值,k为相关性分析样本个数。
归一化处理后,按照相关性数值的绝对值大小进行排序,绘制敏感性Pareto图如图 6所示,其中蓝色条形带表示正效应,红色表示负效应。然后影响程度根据Pareto图的二八定律,累计百分数在70%~80%范围内的因素,是主要的影响因素[16]。

|
图 6 变量对不同响应目标的灵敏度图 Fig. 6 Sensitivity chart of variables to different response targets |
分析图 6发现同一个设计变量对不同响应的影响存在差异,例如变量T1对货箱质量影响为正效应,对满载匀速工况最大应力为负效应,对举升工况最大应力为正效应。因此需要对货箱进行综合多个工况的多目标优化设计,以综合评判设计变量对货箱轻量化和可用性的影响。
确定设计变量之后,采用最优拉丁超立方抽样(Optimal Latin hypercube sampling,OLHS)选取样本点。与拉丁超立方抽样(Latin hypercube sampling,LHS)相比最优拉丁超立方抽样改进了拉丁超立方设计的均匀性,使用φp准则对样本空间距离进行约束,使抽样结果更加具有代表性[17]。
| $ {\varphi _p} = {\left[ {\sum\limits_{i = 1}^s {{J_i}} d_i^{ - p}} \right]^{1/p}} $ | (5) |
式中:di是样本间距离d(xi, xj)的测度值,Ji不同距离的测度值的个数,s是di的个数。如果样本能使得φp准则最小,则LHS满足优化。
两种抽样方法的均匀性可以通过响应面的拟合精度R2验证,分别使用OLHS和LHS抽样选取20组初始样本点,使用RBF近似模型进行质量响应拟合,并计算抽样方法拟合精度。然后依次增加样本点进行拟合,经过5次拟合,两种抽样方法的抽样精度都达到了0.95以上,其拟合精度对比如图 7所示。

|
图 7 OLHS抽样与LHS抽样质量响应拟合精度对比 Fig. 7 Comparison between fitting accuracy of OLHS and LHS |
通过对比图 7发现:在样本点数量相同的情况下,使用OLHS抽样近似模型精度更高,使用32个样本点便能达到近似模型精度要求。因此采用最优拉丁超立方抽样,生成50个样本点,并在图 5搭建的AnsysWorkbench二工况综合分析模型中进行求解得到货箱质量和不同工况下的最大应力。计算结果如表 2所示,其中T1~T5为设计变量,S1和S2分别为满载匀速工况和举升工况的最大应力,M为货箱质量。
| 表 2 最优拉丁超立方样本点及其对应的响应 Tab. 2 OLHS and corresponding responses |
为了降低工程问题的计算成本,近似模型技术得到了广泛的应用[8, 11, 18]。常见的近似模型技术有克里格模型(Kriging)、响应面法(Response Surface Methodology,RSM)和径向基近似模型(Radial Basis Function,RBF)等,其中RBF径向基模型是一种采用径向单元隐层和线性单元输出层的神经网络,其特点是训练速度较快,网络结构紧凑,适用于处理非线性问题,并在许多工程优化设计中得到了广泛的应用[19]。
RBF近似模型是一个三层前馈网络。响应面对应的网络ŷi(x)输出[20]为
| $ {\hat y_i}(x) = \sum\limits_{i = 1}^m {{w_i}} \varphi \left( {\left\| {x - {x_i}} \right\|} \right) = {\mathit{\boldsymbol{\beta }}^{\rm{T}}}\mathit{\boldsymbol{\varphi }} $ | (6) |
式中,权向系数β=(w1, …, wm)T,基函数φ=φ(‖x-xi‖), …, φ(‖x-xm‖T,m为样本点数量,xi为输入变量。式(6)表示为矩阵形式如下:
| $ \mathit{\boldsymbol{A\beta }} = \mathit{\boldsymbol{y}} \Rightarrow \mathit{\boldsymbol{\beta }} = {\mathit{\boldsymbol{A}}^{ - 1}}\mathit{\boldsymbol{y}} $ | (7) |
其中
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {\varphi \left( {\left\| {x - {x_i}} \right\|} \right.}& \cdots &{\varphi \left( {\left\| {x - {x_i}} \right\|} \right)}\\ \vdots &{}& \vdots \\ {\varphi \left( {\left\| {x - {x_i}} \right\|} \right.}& \cdots &{\varphi \left( {\left\| {x - {x_i}} \right\|} \right)} \end{array}} \right] $ | (8) |
通过式(8)计算得出每个基函数的权重大小。基函数使用高斯函数作为径向基函数
| $ \varphi (r) = {e^{\left( {\frac{{ - {r^2}}}{{{c^2}}}} \right)}} $ | (9) |
其中,r为预测点与任意样本点间的距离,c为形状参数,调节径向基函数形状,通常取c=0.2~0.3。
建立响应面后,通过确定性系数R2检验模型拟合的准确性,R2∈[0, 1],当R2值越接近1代表响应面的拟合精度越高,可信度越高[21]。
| $ {R^2} = 1 - \frac{{\sum\limits_{i = 1}^n {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} }}{{\sum\limits_{i = 1}^n {{{\left( {{y_i} - {{\bar y}_i}} \right)}^2}} }} $ | (10) |
式中:n为验证点个数,yi为真实的响应值,ŷi为预测值,y为yi的平均值。
通过最优拉丁超立方抽样和有限元仿真得到样本点以及对应响应值,使用RBF近似模型进行拟合计算,建立响应面,该模型具有5个输入变量和3输出响应。为了验证RBF近似模型的精确性,分别建立Kriging和RSM近似模型[12, 18]与其进行对比。首先从抽样点中随机选取10个样本点如表 3所示,然后代入不同近似模型进行交叉验证,得到预测值如图 8所示。
| 表 3 随机选取交叉验证样本点 Tab. 3 Randomly selected cross-validation sample points |

|
图 8 模拟值与各响应面预测值对比 Fig. 8 Comparison between simulated values and predicted values of each response surface |
通过对比分析图 8发现:RBF与RSM近似模型对满载匀速工况下应力的预测精度大致相同,Kriging模型预测结果较差;对举升工况下应力的预测,对于点3、4、5三种近似模型精度都稍有偏差,但RBF模型在样本点8、9、10处预测最为接近,总体拟合度仍然满足要求;对于质量响应三种模型预测效果整体良好,但Kriging模型个别点偏差较大。因此选择RBF近似模型建立响应面。根据式(10)计算不同类型响应面所对应响应的R2值,验证拟合精度,如表 4所示。根据文献[19]可知,当R2大于0.95就能满足拟合精度要求,从表 4可以看出RBF模型各响应值的R2都在0.95以上,与其他模型相比有较高的精度。
| 表 4 响应面确定性系数R2对比 Tab. 4 Response surface deterministic coefficient R2 comparison |
根据轻量化设计要求以及货箱性能分析结果,定义货箱质量最小、满载匀速工况应力最小化和举升工况应力最小化为目标,其多目标优化数学模型如下:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathop{\rm Min}\nolimits} \left\{ {M(x), {S_1}(x), {S_2}(x)} \right\}}\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}\left\{ {\begin{array}{*{20}{l}} {{S_1}(x) \le 300{\rm{MPa}}}\\ {{S_2}(x) \le 460{\rm{MPa}}}\\ {x_i^{\min } \le {x_i} \le x_i^{\max }} \end{array}} \right.} \end{array}} \right. $ |
式中:x为设计变量集合;M(x)为货箱质量;S1(x)为货箱在满载匀速工况下应力;S2(x)为货箱在举升工况下应力;ximin、ximax为各设计变量取值的下限和上限。
基于RBF近似模型,在多学科优化软件ISIGHT.2016中,使用NSGA-Ⅱ多目标遗传算法进行优化求解[22-23]。设置算法种群个数为60,进化100代,交叉概率为0.9,变异概率为软件内置参数,交叉分布指数为15,变异分布指数为20,经过6 000次运算,得到Pareto解集如图 9(a)所示。

|
图 9 多目标优化的Pareto解集及Pareto前沿 Fig. 9 Pareto solution set of multi-objective optimization and pairwise Pareto frontier |
为了清晰表达各个目标之间的变化关系,图 9(b)、(c)为两种工况下应力与质量的Pareto前沿,从中可以看出货箱的质量和应力是矛盾的,货箱质量减小,应力会增大。因此多目标优化问题的解决方案是根据Pareto最优解找到尽可能多的代表性解集,然后根据分析对象的要求和工程案例的实际经验,从中选择综合满意度最高的优化结果。
2.4 轻量化优化设计方案选取与验证 2.4.1 多目标优化结果分析从Pareto解集中选取以下优化设计方案进行分析如表 5所示。根据企业的设计需求和矿区的工作环境,选择不同的优化设计方案。如果要求设计倾向于降低货箱质量,可以采用1号和2号方案;如果倾向于降低货箱满载匀速行驶工况应力,可以采用3号和4号方案;如果偏好于降低举升工况应力,可以选择5号和6号方案。通过1.2节的强度分析,满载匀速工况下货箱安全系数较高,而举升工况下应力较大。因此货箱的优化设计要求为:在货箱质量减轻的同时,提高货箱在举升工况下的力学性能。因此选择方案2作为最终优化结果。
| 表 5 轻量化设计方案分析 Tab. 5 Analysis of lightweight design schemess |
在2.2节中对近似模型的选取做了相关的对比分析,为了进一步验证RBF模型在本案例的优势,分别建立以Kriging和RSM近似模型为基础的优化模型,其他参数保持不变,使用NSGA-Ⅱ进行优化分别得到各自Pareto解集,根据2.4.1小节中货箱设计要求,分别得到Kriging和RSM近似模型最优设计方案,并进行对比分析如表 6所示。
| 表 6 三种近似模型最优方案对比 Tab. 6 Comparison of optimal schemes of three approximate models |
通过分析发现,基于RSM模型的优化方案与基于RBF模型优化方案相比,侧板厚度T2增加1.02 mm,其余变量差别较小,各工况应力S1和S2分别减小2.65 MPa和10.91 MPa,但质量却增加了75.63 kg,从轻量化角度分析,基于RBF模型的优化效果更好。基于Kriging模型的优化结果与RBF和RSM模型相比,各变量的优化值与RSM和RBF模型相差较大,应力S1差异较小,举升工况最大应力S2优于其他两种模型,但是质量与RBF模型相比增加了178.75 kg。从最优方案的对比分析得出,响应面的拟合精度能够影响优化设结果,不同的优化问题需要选用合适的建模方法,才能保证优化的准确性。
2.4.3 优化后货箱强度分析与验证该货箱的强度设计标准要求:货箱的安全系数为1.5,由1.1节可知货箱材料为Q690高强度钢,其屈服强度为σ为690 Mpa,则货箱最大应力不应该超过其许用应力[σ]为460 MPa。根据国家标准GB/T 1591-2018低合金高强度结构钢生产标准,对优化后的变量进行圆整,提高其可制造性[24]。然后重新建立货箱参数化模型,分别进行两种工况下的静态强度验证,优化后货箱的应力云图如图 10所示。结果发现:优化后的货箱与原货箱相比,静态工况下最大应力为281.92 MPa,与原始货箱相比增加了29.44 MPa,但仍远小于钢板的小于材料的许用应力;举升工况下的最大应力由445.14 MPa减小到418.23 MPa,没有超过材料许用应力值460 MPa,且货箱与车架的铰接处应力集中明显减小;货箱总质量减小了733.1 kg,下降幅度为7.47%。货箱轻量化设计前后对比结果如表 7所示。(注:变化量为货箱圆整后参数与优化前参数对比结果)

|
图 10 优化后货箱典型工况应力云图 Fig. 10 Stress nephogram of the optimized container under typical working conditions |
| 表 7 轻量化设计前后优化结果对比 Tab. 7 Comparison of optimization results before and after lightweight design |
通过分析发现,举升工况下,货箱所受应力最大,容易发生疲劳破坏。因此在AnsysWorkbench中使用疲劳分析模块(Fatigue Tool)进行举升工况下应力疲劳分析,验证优化后货箱的疲劳寿命是否达到设计要求。举升工况下,货箱的载荷谱如图 11所示。

|
图 11 举升工况下载荷谱 Fig. 11 Load spectrum under lifting condition |
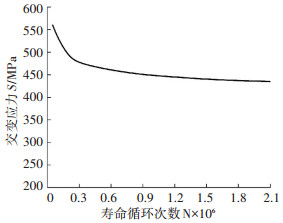
采用名义应力法(S-N曲线法)描述货箱最大应力与疲劳寿命之间的关系,进行货箱疲劳寿命的预估[11]。Q690的疲劳寿命曲线通过实验获得,如图 12所示。
|
图 12 Q690高强度钢的S-N曲线 Fig. 12 S-N curve of Q690 high strength steel |
在Fatigue Tool中进行载荷谱的加载,并计算货箱疲劳寿命,得到货箱在举升工况下疲劳寿命云图如图 13所示。通过疲劳寿命分析得出,货箱的最低疲劳循环为67 125次,发生在货箱与底盘铰接处。根据设计要求:货箱使用寿命需要满足18 000 h。假设每小时装卸3次,则设计要求的循环次数为54 000次。因此轻量化后的货箱满足疲劳强度要求。

|
图 13 货箱疲劳寿命云图 Fig. 13 Life nephogram of mining truck cargo box |
1) 采用RBF近似模型建立货箱钢板厚度与不同工况下应力和质量的响应的关系,并与Kriging模型和RSM模型进行对比分析,发现对于货箱轻量化设计问题,RBF模型具有更好的建模精度,能够保证后续优化设计的准确性。
2) 综合考虑了满载匀速和举升卸货两种典型工况下的性能参数,通过最优拉丁超立方试验和RBF近似模型技术建立了货箱二工况综合分析模型。采用ISIGHT软件平台进行数据点响应面建模和多目标优化,最终在满足货箱静态强度的同时,货箱质量减轻733.1 kg,下降幅度为7.47%。
3) 通过对矿用卡车货箱进行有限元模型建立、载荷计算、二工况下性能分析建立近似模型和多目标优化计算,提出了一种基于两种工况下货箱综合轻量化设计流程和实现方法,为之后箱体类机械产品在两种或者更多工况下的轻量化设计提供了理论依据和技术指导。
| [1] |
范子杰, 桂良进, 苏瑞意. 汽车轻量化技术的研究与进展[J]. 汽车安全与节能学报, 2014, 5(1): 2. FAN Zijie, GUI Liangjin, SU Ruiyi. Research and progress of automobile lightweight technology[J]. Journal of Automotive Safety and Energy, 2014, 5(1): 2. |
| [2] |
王振兴. 矿用自卸车车厢优化设计[D]. 长沙: 湖南大学, 2014 WANG Zhenxing. Optimization design of mining dump truck compartment[D]. Changsha: Hunan University, 2014 |
| [3] |
SAHOO L K, BANDYOPADHYAY S, BANERJEE R. Benchmarking energy consumption for dump trucks in mines[J]. Applied Energy, 2014, 113: 1384. |
| [4] |
王晓南, 邸洪双, 梁冰洁, 等. 轻量化设计的重型卡车车厢应力有限元数值模拟[J]. 东北大学学报(自然科学版), 2010, 31(1): 63. WANG Xiaonan, DI Hongshuang, LIANG Bingjie, et al. Finite element numerical simulation of stress in heavy-duty truck compartment with lightweight design[J]. Journal of Northeastern University (Natural Science Edition), 2010, 31(1): 63. |
| [5] |
董志明, 郭海全, 潘艳君, 等. 矿用自卸车车厢力学性能研究[J]. 中国矿业, 2017, 26(7): 161. DONG Zhiming, GUO Haiquan, PAN Yanjun, et al. Study on the mechanical properties of the mining dump truck compartment[J]. China Mining Industry, 2017, 26(7): 161. |
| [6] |
LI X, CAO J, LIU S, et al. Study on modal analysis and dynamic performance of electric wheel self-dumping truck carriage[J]. Manufacturing Technology and Machinery Automation, 2012, 127: 398. |
| [7] |
王金刚, 李春玉, 李海涛, 等. 翼开启厢式车车厢主体骨架的轻量化设计[J]. 河北工业大学学报, 2019, 48(1): 25. WANG Jingang, LI Chunyu, LI Haitao, et al. Lightweight design of the main frame of the wing-opening van[J]. Journal of Hebei University of Technology, 2019, 48(1): 25. |
| [8] |
刘钊, 朱平, 籍庆辉. 静动态工况下的自卸车车厢轻量化设计[J]. 机械科学与技术, 2016, 35(05): 763. LIU Zhao, ZHU Ping, JI Qinghui. Lightweight design of dump truck compartment under static and dynamic conditions[J]. Mechanical Science and Technology, 2016, 35(05): 763. |
| [9] |
TRIVERS N C, CARRICK C A, KIM I Y. Design optimization of a business aircraft seat considering static and dynamic certification loading and manufacturability[J]. Structural and Multidisciplinary Optimization, 2020, 62: 3457. DOI:10.1007/s00158-020-02650-z |
| [10] |
谢然, 兰凤崇, 陈吉清, 等. 满足可靠性要求的轻量化车身结构多目标优化方法[J]. 机械工程学报, 2011, 47(4): 122. XIE Ran, LAN Fengchong, CHEN Jiqing, et al. Multi-objective optimization method of lightweight body structure to meet reliability requirements[J]. Chinese Journal of Mechanical Engineering, 2011, 47(4): 122. |
| [11] |
王禹琪, 刘昕晖, 陈晋市, 等. 钢制组装式车轮的轻量化设计及多目标优化[J]. 哈尔滨工业大学学报, 2020, 52(7): 176. WANG Yuqi, LIU Xinhui, CHEN Jinshi, et al. Lightweight design and multi-objective optimization of steel assembled wheels[J]. Journal of Harbin Institute of Technology, 2020, 52(7): 176. |
| [12] |
MI C, GU Z, ZHANG Y, et al. Frame weight and anti-fatigue co-optimization of a mining dump truck based on Kriging approximation model[J]. Engineering Failure Analysis, 2016, 66: 106. |
| [13] |
陈柳. 6×4自卸车U型上装研究与开发[D]. 西安: 长安大学, 2017 CHEN Liu. Research and development of U-type trolley for 6×4dump truck[D]. Xi'an: Chang'an University, 2017 |
| [14] |
马洪锋, 董栓牢, 孟庆勇, 等. 某型矿用自卸车车厢结构设计与分析[J]. 工程机械, 2012, 43(8): 34. MA Hongfeng, DONG Shuanlao, MENG Qingyong, et al. Structure design and analysis of a certain type of mining dump truck[J]. Construction Machinery, 2012, 43(8): 34. |
| [15] |
赖宇阳, 姜欣. Isight参数优化理论与实例详解[M]. 北京: 北京航空航天大学出版社, 2012. LAI Yuyang, JIANG Xin. Isight parameter optimization theory and detailed examples[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2012. |
| [16] |
CHINCHULUUN A, PARDALOS P M, MIGDALAS A, et al. Pareto optimality, game theory and equilibria[M]. New York: Springer, 2008.
|
| [17] |
MORRIS M D, MITCHELL T J. Exploratory designs for computational experiments[J]. Journal of Statistical Planning and Inference, 1995, 43(3): 384. |
| [18] |
童水光, 何顺, 童哲铭, 等. 基于组合近似模型的轻量化设计方法[J]. 中国机械工程, 2020, 31(11): 1338. TONG Shuiguang, HE Shun, TONG Zheming, et al. Lightweight design method based on combined approximate model[J]. China Mechanical Engineering, 2020, 31(11): 1338. |
| [19] |
LI Z, DUAN L B, CHENG A G, et al. Lightweight and crashworthiness design of an electric vehicle using a six-sigma robust design optimization method[J]. Engineering Optimization, 2018, 51(8): 1402. |
| [20] |
KITAYAMA S, ARAKAWA M, YAMAZAKI K. Sequential approximate optimization using radial basis function network for engineering optimization[J]. Optimization and Engineering, 2010, 12(4): 540. DOI:10.1007/s11081-010-9118-y/email/correspondent/c1/new |
| [21] |
高云凯, 王婧人, 方剑光, 等. 基于双层规划的白车身结构优化[J]. 机械工程学报, 2012, 48(22): 101. GAO Yunkai, WANG Jingren, FANG Jianguang, et al. Body-in-white structure optimization based on bi-level programming[J]. Chinese Journal of Mechanical Engineering, 2012, 48(22): 101. |
| [22] |
DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 184. |
| [23] |
张帅, 郭志军, 王传青. 基于分析驱动设计的参数化白车身前端结构轻量化多目标优化[J]. 汽车工程, 2019, 41(9): 1105. ZHANG Shuai, GUO Zhijun, WANG Chuanqing. Multi-objective optimization of parametric body-in-white front end structure lightweight based on analysis-driven design[J]. Automotive Engineering, 2019, 41(9): 1105. |
| [24] |
低合金高强度结构钢: GB/T 38146.2—2018[S]. 北京: 中国标准出版社, 2018 Low-alloy high-strength structural steel: GB/T 38146.2—2018[S]. Beijing: Standards Press of China, 2018 |
 2021, Vol. 53
2021, Vol. 53


