2. 新能源汽车动力总成技术北京市重点实验室(北京交通大学),北京 100044
2. Beijing Key Laboratory of Powertrain Technology for New Energy Vehicles (Beijing Jiaotong University), Beijing 100044, China
作为最有发展前景的新能源汽车之一,燃料电池汽车的相关研究是目前的一大热点。为了提高系统效率和寿命,燃料电池汽车能量管理策略研究具有重要的价值和迫切的需求[1-2]。
在燃料电池车的能量管理策略的开发过程中,需要在保证整车经济性的基础上,兼顾车用燃料电池的耐久性,避免其性能衰退,延长其使用寿命[3]。在汽车行驶过程中,当车用燃料电池处于功率波动状态、启停变化状态、怠速运行状态(输出功率低于怠速功率的状态)和大功率运行状态(输出功率高于额定功率的状态)这4种工作状态时,其性能会发生显著的衰退。其中,剧烈的功率波动和频繁的启停变化是燃料电池性能衰退的关键影响因素[4-6]。
针对燃料电池的功率波动,文献[7-8]设置了燃料电池输出功率变化率的约束条件,文献[9-10]设置了低通滤波器对需求功率进行过滤;针对燃料电池的启停变化,文献[8]设置了燃料电池最低输出功率约束条件从而禁止燃料电池关闭,文献[11]建立了燃料电池启停变化衰退量目标函数,间接减少启停次数,文献[12]设定了固定的燃料电池启停间隔约束防止燃料电池频繁启停。目前针对燃料电池频繁启停问题的能量管理策略研究中,少有将启停过程的优化对经济性和耐久性的影响考虑在内的研究,缺乏综合考虑多目标的燃料电池启停控制方法。
基于此,本文针对增程式燃料电池汽车,建立基于改进动态规划(DP)算法的经济性与耐久性联合优化能量管理策略。该策略将燃料电池的启停状态增设为状态变量,并在燃料电池的启动和关闭状态之间增加了怠速过渡阶段,实现了燃料电池的自适应启停间隔控制,避免了燃料电池的频繁启停。并使用燃料电池性能衰退指数为耐久性代价,整车能耗为经济性代价,构建经济性与耐久性多目标联合代价函数,实现了两者的联合优化控制。
1 增程式燃料电池汽车模型增程式燃料电池汽车(ER-FCV)以燃料电池为增程器,负责延长车辆的续驶里程,并能够辅助输出动力[13]。ER-FCV动力系统结构如图 1所示,图中燃料电池和动力电池输出的直流电经过DC/AC逆变器转换为交流电,流向驱动电机,输出动力驱动车辆行驶。建模中所需的整车关键参数由北汽某款燃料电池原型车预研项目提供,如表 1所示。
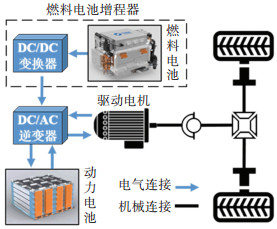
|
图 1 ER-FCV动力系统 Fig. 1 ER-FCV power system |
| 表 1 ER-FCV主要参数 Tab. 1 Main parameters of ER-FCV |
燃料电池的等效电路模型包括电化学模块、热平衡模块和等效电路模块[14]。本文基于该数学模型在Matlab/Simulink中搭建了燃料电池仿真模型。
1.1.1 燃料电池电化学模块燃料电池由于在反应过程中会产生多种不可逆损失,以反应过电压形式表示如式(1)、(2)所示:
| $ V_{\text {cell }}=E_{\text {nernst }}-v_{\text {act }}-v_{\Omega}-v_{\text {con }} $ | (1) |
| $ V_{\text {stack }}=N \cdot V_{\text {cell }} $ | (2) |
式中:Vcell为燃料电池单电池的输出电压, Enernst是热力学电动势, vact是活化过电压, vΩ是欧姆过电压, vcon是浓差过电压。将N个燃料电池单电池串联即可得到燃料电池电堆的总输出电压Vstack。
式(1)中的各项的数学模型如下:
| $ \left\{ {\begin{array}{*{20}{l}} {{E_{{\rm{nernst }}}} = \frac{{\varDelta G}}{{2F}} + \frac{{\varDelta S}}{{2F}}\left( {T - {T_{{\rm{ref }}}}} \right) + }\\ {\quad \frac{{RT}}{{2F}}\left[ {\ln \left( {{p_{{{\rm{H}}_2}}}} \right) + \frac{1}{2}\ln \left( {{p_{{{\rm{O}}_{\rm{2}}}}}} \right)} \right]}\\ {{v_{{\rm{act }}}} = {\xi _1} + {\xi _2}T + {\xi _3}T\ln \left( {{C_{{{\rm{O}}_{\rm{2}}}}}} \right) + {\xi _4}T\ln i}\\ {{v_\Omega } = i{R_\Omega }}\\ {{v_{{\rm{con }}}} = - B\ln \left( {1 - \frac{J}{{{J_{\max }}}}} \right)} \end{array}} \right. $ | (3) |
式中:ΔG是吉布斯自由能的变化值;F是法拉第常量;ΔS是熵的变化值;R为气体常数;pH2是氢气在阳极催化剂/气体界面的分压;pO2是氧气在阴极催化剂/气体界面的分压;T为电池温度;i为电池电流;ξ为经验参数;CO2是阴极气液界面氧气浓度;RΩ为燃料电池欧姆电阻;J为实际电流密度;Jmax为最大电流密度;B是取决于燃料电池工作情况的经验系数,取值为0.016。
1.1.2 燃料电池热平衡模块基于能量守恒方程搭建热平衡模块
| $ C_{\mathrm{t}} \frac{\mathrm{d} T^{\prime}}{\mathrm{d} t}=P_{\mathrm{tot}}-P_{\text {elec }}-\dot{Q}_{\mathrm{cool}}-\dot{Q}_{\mathrm{loss}} $ | (4) |
式中:Ct为热容,T′为电堆温度,Ptot为进入电堆总功率,Pelec为输出电功率,
式(4)中的各项的数学模型如下:
| $ \left\{\begin{array}{l} P_{\mathrm{tot}}=\dot{m}_{\mathrm{H}_{2}} \cdot \varDelta H \\ P_{\text {elec }}=V_{\text {stack }} i \\ \dot{Q_{\mathrm{cool}}}= \\ U A_{\mathrm{HX}} \frac{\left(T^{\prime}-T_{\mathrm{w}, \mathrm{in}}\right)-\left(T^{\prime}-T_{\mathrm{w}, \mathrm{out}}\right)}{\ln \left[\left(T^{\prime}-T_{\mathrm{w}, \mathrm{in}}\right) /\left(T^{\prime}-T_{\mathrm{w}, \text { out }}\right)\right]} \\ \dot{Q}_{\mathrm{loss}}=\frac{T^{\prime}-T_{\mathrm{amb}}}{R_{\mathrm{t}}} \end{array}\right. $ | (5) |
式中:
| $ U A_{\mathrm{HX}}=h_{\text {cond }}+h_{\text {conv }} \cdot i $ | (6) |
式中hcond、hconv是2个热交换器的参数,分别描述其导热和对流特性。
1.1.3 燃料电池等效电路模块利用等效电容表示燃料电池"双层电荷层"的影响,利用等效电阻表示燃料电池活化损失和浓差损失的影响,搭建燃料电池的等效电路,如图 2所示。
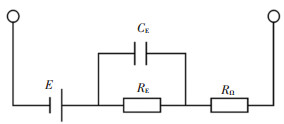
|
图 2 燃料电池等效电路 Fig. 2 Equivalent circuit of fuel cell |
图中:E表示燃料电池的电动势,RE表示等效电阻,CE表示等效电容,RΩ为燃料电池内的欧姆电阻。等效电阻RE等效电容CE上的动态电压体现了燃料电池的动态特性,用微分方程描述为
| $ \frac{\mathrm{d} v_{\mathrm{E}}}{\mathrm{d} t}=\frac{i}{C_{\mathrm{E}}}-\frac{v_{\mathrm{E}}}{\tau} $ | (7) |
| $ v_{\mathrm{E}}=v_{\mathrm{act}}+v_{\mathrm{con}}=i \cdot R_{\mathrm{E}}-C_{\mathrm{E}} \mathrm{e}^{-\frac{t}{R_{\mathrm{E}} \cdot C}} $ | (8) |
式中vE为等效电阻上的总极化过电压,时间常数τ可表示为
| $ \tau=C_{\mathrm{E}} R_{\mathrm{E}}=C_{\mathrm{E}}\left(\frac{v_{\mathrm{act}}+v_{\mathrm{con}}}{i}\right) $ | (9) |
稳态时的电堆电压为
| $ V_{\text {stack }}=N \cdot\left[E-i\left(R_{\mathrm{E}}+R_{\Omega}\right)\right]=V_{\mathrm{OC}}-i R_{\mathrm{E}, \text { total }} $ | (10) |
式中VOC为开路电压,RE, total为电堆的总等效电阻。
1.2 动力电池模型动力电池模型基于内阻模型搭建,将动力电池系统等效为电源与内阻的串联电路[12]。根据电路原理可将模型表示为
| $ V_{\mathrm{B}}=V_{\mathrm{OC}}-i_{\mathrm{B}} \cdot R_{\mathrm{B}} $ | (11) |
| $ i_{\mathrm{B}}=\frac{V_{\mathrm{OC}}-\sqrt{V_{\mathrm{OC}}^{2}-4 R_{\mathrm{B}} P_{\mathrm{B}}}}{2 R_{\mathrm{B}}} $ | (12) |
式中:VB为电池两端电压,VOC为电池的开路电压,iB为电池的电流,RB为电池内阻,PB为电池的功率。
电池SOC是电池的荷电状态,可以表征电池的剩余电量情况,由式(13)计算得出:
| $ \mathrm{SOC}=\frac{Q}{Q_{\mathrm{C}}} $ | (13) |
式中: Q代表电池剩余容量,QC表示电池充满电时的容量。在内阻模型中,SOC的求取选择安时法,如式(14)所示:
| $ \mathrm{SOC}_{t}=\mathrm{SOC}_{\text {initial }}-\frac{1}{3\ 600 Q_{\mathrm{C}}} \int_{0}^{t} i_{\mathrm{B}} \mathrm{d} t $ | (14) |
式中SOCt代表t时刻的SOC值,SOCinitial表示动力电池的初始SOC。
1.3 整车模型基于汽车行驶的动力学方程搭建车辆纵向动力学模型,通过式(15)得到车辆在行驶过程中所受的力:
| $ F_{\mathrm{t}}=F_{\mathrm{r}}+F_{\mathrm{a}}+F_{\mathrm{g}}+F_{\mathrm{j}} $ | (15) |
式中:Ft为车辆的驱动力,Fr为车辆所受的滚动阻力,Fa为空气阻力,Fg为坡度阻力,Fj为加速阻力。
| $ \left\{\begin{array}{l} F_{\mathrm{r}}=f m \mathrm{g} \cos \theta, F_{\mathrm{a}}=\frac{\mathrm{C}_{\mathrm{d}} A u_{a}^{2}}{21.15} \\ F_{\mathrm{g}}=m \mathrm{g} \sin \theta, F_{\mathrm{j}}=\delta m \frac{\mathrm{d} u_{\mathrm{a}}}{\mathrm{d} t} \end{array}\right. $ | (16) |
式中:m为车辆质量,f为车轮滚阻系数,θ为行驶路面的坡度,A为迎风面积,Cd为空气阻力系数,ua为行驶车速,δ为旋转质量转换系数。
由式(17)得到车辆行驶功率平衡方程(18):
| $ P_{\mathrm{t}}=\frac{u_{\mathrm{a}} F_{\mathrm{t}}}{\eta_{\mathrm{t}}} $ | (17) |
| $ P_{\mathrm{t}}=\frac{u_{\mathrm{a}}}{\eta_{\mathrm{t}}}\left(\frac{f m \mathrm{g}}{3\ 600}+\frac{\mathrm{C}_{\mathrm{d}} A u_{\mathrm{a}}^{2}}{76140}+\frac{m \mathrm{g} i_{\mathrm{s}}}{3\ 600}+\frac{\delta m}{3\ 600} \cdot \frac{\mathrm{d} u_{\mathrm{a}}}{\mathrm{d} t}\right) $ | (18) |
式中:Pt是驱动车辆行驶所需的功率,即需求功率;is是当前道路的坡度。
2 基于改进DP的联合优化策略针对燃料电池的性能衰退问题,基于改进DP算法建立了ER-FCV经济性与耐久性优化能量管理控制策略(后文简称FC-DP策略),在满足动力性的前提下尽量提高整车经济性和燃料电池耐久性。其中经济性的目标是降低动力电池的电耗和燃料电池的氢耗;燃料电池耐久性的目标则是减少导致燃料电池性能衰退的启停变化、功率波动等状态。
2.1 改进DP优化变量设置算法中的控制变量u为燃料电池输出功率,通过下式来控制两个动力源之间的功率分配:
| $ P_{\mathrm{fc}}^{(\mathrm{u})}=P_{\mathrm{t}}-P_{\mathrm{B}} $ | (19) |
式中:Pfc(u)是作为控制变量的燃料电池输出功率,PB是动力电池输出功率。
对以下变量设定约束条件,限定其取值范围:
| $ \left\{\begin{array}{l} P_{\mathrm{fc}, \min } \leqslant P_{\mathrm{fc}}<P_{\mathrm{fc}, \max } \\ P_{\mathrm{B}, \min } \leqslant P_{\mathrm{B}}<P_{\mathrm{B}, \max } \\ \mathrm{SOC}_{\min } \leqslant \mathrm{SOC}<\mathrm{SOC}_{\max } \\ C_{\mathrm{H}_{2}, \min } \leqslant C_{\mathrm{H}_{2}}<C_{\mathrm{H}_{2}, \max } \end{array}\right. $ | (20) |
状态变量x分别为动力电池SOC、燃料电池输出功率、燃料电池启停状态。其中将SOC作为第一状态变量,将燃料电池输出功率作为第二状态变量,此时燃料电池输出功率既是控制变量,也是状态变量,通过限制其状态转移范围,限制燃料电池的功率波动,剔除不可达状态的无效计算。如图 3所示,每一时刻内的坐标系横轴为燃料电池输出功率,纵轴为动力电池SOC。以t1时刻的燃料电池输出功率为基准,在t2时刻其降低或升高的变化幅度被限定于中间的绿色范围内。
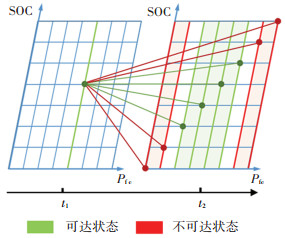
|
图 3 状态转移过程中的不可达状态 Fig. 3 Unreachable state in the process of state transition |
将燃料电池启停状态作为第三状态变量,减少燃料电池的启停变化。3个状态变量的转移方程如式(21)所示:
| $ \left\{\begin{array}{l} \mathrm{SOC}_{k+1}=F\left(\mathrm{SOC}_{k}, P_{\mathrm{fc}, k}^{(u)}\right) \\ P_{\mathrm{fc}, k+1}^{(x)}=G\left(P_{\mathrm{fc}, k}^{(x)}, P_{\mathrm{fc}, k}^{(u)}\right) \\ \operatorname{state}_{k+1}=H\left(\operatorname{state}_{k}, P_{\mathrm{fc}, k}^{(u)}\right) \end{array}\right. $ | (21) |
式中:Pfc(x)是作为状态变量的燃料电池输出功率,state是燃料电池的启停状态。
F函数由式(12)、(14)和式(19)得到;G函数如式(22)所示,即当前时刻作为控制变量的燃料电池输出功率,等于下一时刻作为状态变量的燃料电池输出功率。
| $ P_{\mathrm{fc}, k+1}^{(x)}=P_{\mathrm{fc}, k}^{(u)} $ | (22) |
式(21)中的H函数是一个逻辑计算过程,代表燃料电池启停状态的切换逻辑,将在2.2节中说明。
2.2 燃料电池自适应启停间隔控制为了避免频繁启停导致的性能衰退,并且能够结合燃料电池状态、动力电池状态和行驶工况,自适应控制启停间隔,将燃料电池的启停状态设为了状态变量,并在燃料电池的启动与关闭状态之间增加了一个怠速过渡阶段。
表 2中定义了燃料电池启停状态之间的切换逻辑,以及不同状态对应的输出功率变化情况。燃料电池的完全启动状态和完全关闭状态之间禁止直接切换,必须经过一个怠速过渡阶段的缓冲。在完全关闭状态时,燃料电池停止工作,输出功率为零。在完全启动状态时,燃料电池输出功率大于其怠速功率。在怠速过渡状态时,燃料电池的输出功率大于零且低于怠速功率。由于燃料电池处于怠速以下功率工作会导致其性能衰退,处于这一状态的时间要求尽量短,所以控制燃料电池处于怠速过渡状态时,其输出功率保持与前一状态相同的方向(升高或降低)进行变化,变化幅度则保持最大变载率(最大升载率或最大降载率),令燃料电池尽快离开怠速运行。
| 表 2 燃料电池启停状态切换逻辑 Tab. 2 Switching logic of fuel cell start-stop switch |
上述切换逻辑令燃料电池一个完整的启停变化必须依次经历完全关闭——怠速过渡——完全启动——怠速过渡——完全关闭的过程。
如图 4所示,红色代表完全关闭状态,绿色代表完全启动状态,黄色代表怠速过渡状态,连接2个状态的箭头代表不同的燃料电池输出功率决策,该决策可以导致"维持原状态"或"进入新状态"2种结果。
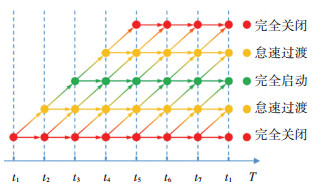
|
图 4 燃料电池启停状态转移原理 Fig. 4 Principle of fuel cell start-stop state transfer |
由于怠速过渡状态的存在,当完全启动的燃料电池可以选择关闭时,会进行一次状态转移的计算。在满足当前工况动力性要求的前提下,比较关闭燃料电池与保持开启这两个决策导致的代价函数值。只有当进入怠速过渡状态并关闭燃料电池造成的性能衰退代价,低于保持燃料电池开启造成的能耗代价时,才会令其关闭,从而实现了燃料电池的自适应启停间隔控制。
2.3 经济性与耐久性联合代价函数以整车经济性和燃料电池耐久性为目标,建立联合代价函数。
2.3.1 经济性代价经济性代价包含动力电池电耗和燃料电池等效电耗两部分,如式(23)所示:
| $ J_{\mathrm{eco}}=S(k) \cdot \dot{m}_{\mathrm{batt}}+\dot{m}_{\mathrm{fc}} $ | (23) |
式中,Jeco为经济性代价,
惩罚函数S主要由动力电池SOC计算得出[15]。对SOC标准化处理,得到标准化系数α:
| $ \alpha=\left\{\begin{array}{l} 1, \quad \mathrm{SOC} \geqslant \mathrm{SOC}_{\text {high }} \\ \frac{\mathrm{SOC}-\frac{\mathrm{SOC}_{\text {high }}+\mathrm{SOC}_{\mathrm{low}}}{2}}{\frac{\mathrm{SOC}_{\text {high }}-\mathrm{SOC}_{\mathrm{low}}}{2}},\qquad \mathrm{SOC}_{\mathrm{low}}>\mathrm{SOC} \geqslant \mathrm{SOC}_{\text {high }} \\ -1, \quad \mathrm{SOC}<\mathrm{SOC}_{\mathrm{low}} \end{array}\right. $ | (24) |
式中α是一个正负1之间的值,代表当前SOC偏离SOC变化区间中点的程度。得到动力电池电耗的惩罚函数S:
| $ S(x)=1-a \alpha^{3}+b \alpha^{4} $ | (25) |
该函数随SOC偏离变化区间中点的程度不同而输出不同的值。取式(25)中(a, b)值为(3, 2),函数图像如图 5所示。
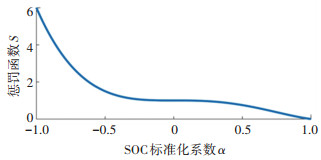
|
图 5 动力电池电耗惩罚函数 Fig. 5 Penalty function of battery power consumption |
为了量化燃料电池的性能衰退情况,设立燃料电池耐久性代价函数。通过统计燃料电池在行驶过程中处于不同工作状态的次数与时间,将其换算为行驶结束后燃料电池四个主要部件的衰退率,得到燃料电池的性能衰退评价指数,以此作为燃料电池的耐久性代价函数,同时也作为最终评价燃料电池耐久性的量化指标[16]。
| $ {J_{{\rm{du}}}} = \sum\nolimits_{i = 1}^4 {{r_i} \times {\omega _{1i}}} $ | (26) |
式中:Jdu表示燃料电池的耐久性代价;r代表燃料电池主要部件的性能衰退率,包括催化剂及碳载体、质子交换膜、气体扩散层和双极板;ω1代表上述主要部件对应的性能衰退权重系数,由式(27)计算得到。
| $ \boldsymbol{\omega}_{1}=\boldsymbol{\omega}_{2} \times \boldsymbol{M} $ | (27) |
式中ω2代表燃料电池4种工作状态对应的性能衰退权重系数,由文献[4]中的加速老化实验得到,其取值如式(28)所示:
| $ \boldsymbol{\omega}_{2}=\left[\begin{array}{llll} 0.4145 & 0.2447 & 0.1573 & 0.1835 \end{array}\right] $ | (28) |
式中依次是功率波动状态、启停变化状态、怠速运行状态和大功率运行状态的性能衰退权重。
式(27)中的M是一个单因素评价矩阵,由燃料电池工作状态对不同部件性能衰退影响的的半量化分析表进行处理得到[16],如表 3所示。
| 表 3 燃料电池工作状态对不同部件性能衰退的影响程度 Tab. 3 Influence of fuel cell working states on performance degradation of different components |
对表 3基于相关研究和工程经验将"较大: 中等: 较小"量化为3:1:0,然后将不同状态的影响程度归一化,得到单因素评价矩阵M[16]。
| $ \boldsymbol{M}=\left[\begin{array}{cccc} 0.375 & 0.375 & 0.125 & 0.125 \\ 0.600 & 0.200 & 0.200 & 0 \\ 0.200 & 0.600 & 0.200 & 0 \\ 0.500 & 0.500 & 0 & 0 \end{array}\right] $ | (29) |
式(26)中燃料电池主要部件的衰退率r,可由式(30)及式(31)得到:
| $ r=\left[\begin{array}{llll} r_{1} & r_{2} & r_{3} & r_{4} \end{array}\right] $ | (30) |
| $ {\left[\begin{array}{llll} r_{1} & r_{2} & r_{3} & r_{4} \end{array}\right]=\boldsymbol{k} \times \boldsymbol{M}} $ | (31) |
式中:k代表燃料电池工作状态在行驶中的占比。
| $ \boldsymbol{k}=\left[\begin{array}{llll} k_{1} & k_{2} & k_{3} & k_{4} \end{array}\right] $ | (32) |
式(32)中依次是功率波动状态、启停变化状态、怠速运行状态和大功率运行状态在行驶过程中的占比。
| $ k_{1}=\frac{d}{q t}, k_{2}=\frac{n}{t}, k_{3}=\frac{t_{\mathrm{low}}}{t}, k_{4}=\frac{t_{\mathrm{high}}}{t} $ | (33) |
式中:d是大幅功率波动的次数;q是燃料电池加速老化实验过程中每小时加载大幅功率波动的次数,取值56;t是行驶时间;n是启停次数;tlow是燃料电池处于怠速运行状态的时间;thigh是燃料电池处于大功率运行状态的时间[4]。
将经济性代价和耐久性代价转化为联合代价函数:
| $ J=\omega_{\mathrm{eco}} \cdot J_{\mathrm{eco}}+\omega_{\mathrm{du}} \cdot J_{\mathrm{du}} $ | (34) |
式中:J代表综合代价函数;ωeco和ωdu分别代表经济性代价和耐久性代价的权重系数,主要取决于燃料电池的性能衰退情况,当燃料电池性能衰退较少时,ωdu的取值也较小,当燃料电池性能衰退严重时,ωdu的取值将变大。将ωdu取值为0.25,ωdu取值为0.75.
2.4 改进DP算法结构DP算法流程可分为4个步骤,分别是数据输入、正向寻优、逆向求解和数据输出,其中正向寻优和逆向求解是关键[17]。
正向寻优的目的是计算从起始时刻到终止时刻,整个可行状态空间内的所有决策序列,得到包含最优决策解集的决策序列矩阵。
在寻优过程中,对每一个状态的代价进行比较,得到当前最优状态对应的代价与决策。最优代价函数J*如式(35)所示:
| $ J^{*}=\min J=\min \left(\omega_{\mathrm{eco}} \cdot J_{\mathrm{eco}}+\omega_{\mathrm{du}} \cdot J_{\mathrm{du}}\right) $ | (35) |
第三步是逆向求解,即从终止时刻开始逆推,筛选取出上述矩阵中的一条符合末状态要求的最优决策序列。图 6为改进DP算法正向寻优流程。

|
图 6 ER-FCV多目标优化DP算法正向寻优流程图 Fig. 6 Flow chart of forward optimization of DP algorithm for ER-FCV multi-objective optimization |
以全局经济性最优经典的DP策略作为对比。使用两种策略进行仿真,设定SOC初状态为0.8,末状态为0.5,分别进行行驶工况为10次NEDC循环工况和10次UDDS循环工况的仿真,2种循环工况的速度曲线如图 7、图 8所示[18-19]。

|
图 7 NEDC循环工况速度曲线 Fig. 7 NEDC cycle speed curve |
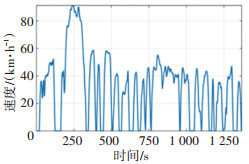
|
图 8 UDDS循环工况速度曲线 Fig. 8 UDDS cycle speed curve |
2种策略的性能对比数据如表 4所示。以NEDC工况为例,2种策略比较如图 9、图 10所示。
| 表 4 FC-DP策略和CDP策略性能对比 Tab. 4 Performance comparison between FC-DP and CDP |
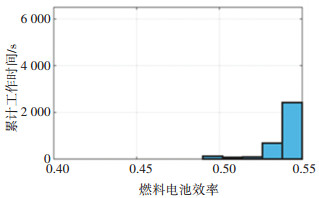
|
图 9 CDP策略下燃料电池输出效率分布 Fig. 9 Fuel cell efficiency distribution under CDP strategy |
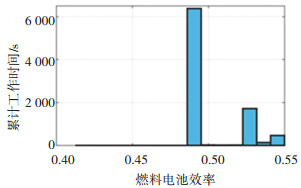
|
图 10 FC-DP策略下燃料电池输出效率分布 Fig. 10 Fuel cell efficiency distribution under FC-DP strategy |
在经济性方面,分析表 4数据,NEDC工况下的FC-DP策略的燃料电池等效电耗比CDP策略升高6.9%,动力电池电耗降低5.9%,整车能耗升高了5.3%,燃料电池的输出效率降低了3.9%;UDDS工况下FC-DP策略的燃料电池等效电耗比CDP策略升高了8.4%,动力电池电耗降低了2.3%,整车能耗升高了7.2%,燃料电池的输出效率降低了4.3%.
图 9和图 10是2种策略在NEDC循环仿真中的燃料电池输出效率分布情况,CDP策略下燃料电池处于高效工作区域的时间更多,FC-DP策略较少。
可见所提出的FC-DP策略有效控制了整车的能耗水平,在经济性方面能够接近CDP策略。但FC-DP策略无法达到全局经济性最优,这是由于FC-DP策略对燃料电池进行了限制,牺牲部分效率以保护燃料电池的健康运行。
在燃料电池耐久性方面,主要通过耐久性代价函数中的燃料电池性能衰退评价指数来量化分析,该指数代表了燃料电池衰退程度,其值越小代表燃料电池的衰退程度越小,即耐久性表现越好,越利于延长燃料电池的使用寿命。
由表 4中的数据可见,在NEDC工况下,FC-DP策略下的燃料电池衰退程度比CDP策略降低了65.5%;在UDDS工况下,FC-DP策略下的燃料电池衰退程度比CDP策略降低了70.2%.
图 11是2种策略在NEDC工况下的燃料电池输出功率曲线。可见FC-DP策略下的燃料电池输出功率波动较少,变化平缓。燃料电池在启动后的大部分时间内,能够保持在怠速功率和额定功率之间运行,且在需求功率较低的工况下,燃料电池能够以略高于怠速功率的状态稳定工作。
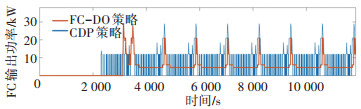
|
图 11 FC-DP策略与CDP策略的燃料电池输出功率曲线 Fig. 11 Fuel cell output power curve under FC-DP strategy and CDP strategy |
图 12和图 13是2种策略在不对末状态进行约束的条件下,各自的全部最优决策解集对应的SOC曲线集,图中曲线上不同的颜色代表燃料电池不同的启停状态。由图可见CDP策略下的燃料电池的启停分布分散,黄色区域所代表的完全启动状态无法长时间保持。而FC-DP策略下的燃料电池在启动后能够长时间保持开启状态,避免了燃料电池的频繁启停。同时由图 13中不同起止点的黄色线条可见,对于不同的末状态约束,燃料电池的启停间隔也各不相同,体现了FC-DP策略的燃料电池自适应启停间隔控制。

|
图 12 CDP策略的燃料电池启停状态分布 Fig. 12 Start-stop state distribution of fuel cell based on CDP strategy |

|
图 13 FC-DP策略的燃料电池启停状态分布 Fig. 13 Start-stop state distribution of fuel cell based on FC-DP strategy |
可见FC-DP策略有效地减少了燃料电池的频繁启停、功率波动等状态,减轻了燃料电池的性能衰退,在燃料电池耐久性方面得到了优于CDP策略的效果。
4 结论1) 在经典DP策略的基础上,将燃料电池的启停状态设为了状态变量,在燃料电池的启动与关闭状态之间增加了一个怠速过渡阶段,实现了燃料电池的自适应启停间隔控制。
2) 将燃料电池性能衰退评价指数作为耐久性代价,将动力电池电耗和燃料电池等效电耗的整车能耗作为经济性代价,建立了经济性与耐久性联合代价函数。
3) 仿真结果表明,增程式燃料电池车经济性与耐久性联合优化控制策略,能达到接近经典DP策略的经济性效果,并减轻了燃料电池的性能衰退,得到优于经典DP策略的耐久性。
| [1] |
YUE M, SAMIR J, RAFAEL G, et al. Review on health-conscious energy management strategies for fuel cell hybrid electric vehicles: Degradation models and strategies[J]. International Journal of Hydrogen Energy, 2019, 44(13): 6844. DOI:10.1016/j.ijhydene.2019.01.190 |
| [2] |
张峻恺. 复合电源燃料电池客车能量管理策略研究[D]. 长春: 吉林大学, 2018 ZHANG Junkai. Study on energy management strategy of fuel cell-battery-supercapacitor hybrid bus[D]. Changchun, Jilin University, 2018 |
| [3] |
林林, 吴睿, 张欣欣. 商业尺寸质子交换膜燃料电池性能实验研究[J]. 哈尔滨工业大学学报, 2011, 43(3): 117. LIN Lin, WU Rui, ZHANG Xinxin. Experimental investigation of membrane thickness and operating conditions on PEM fuel cell performance[J]. Journal of Harbin Institute of Technology, 2011, 43(3): 117. DOI:10.3969/j.issn.1009-1971.2011.03.024 |
| [4] |
PEI Pucheng, CHANG Qianfei, TANG Tian. A quick evaluating method for automotive fuel cell lifetime[J]. International Journal of Hydrogen Energy, 2008, 33(14): 3829. DOI:10.1016/j.ijhydene.2008.04.048 |
| [5] |
CHEN Hhuicui, PEI Pucheng, SONG Mancui. Lifetime prediction and the economic lifetime of proton exchange membrane fuel cells[J]. Applied Energy, 2015, 142: 154. DOI:10.1016/j.apenergy.2014.12.062 |
| [6] |
ZHANG Tong, WANG Peiqi, CHEN Huicui, et al. A review of automotive proton exchange membrane fuel cell degradation under start-stop operating condition[J]. Applied Energy, 2018, 223: 249. DOI:10.1016/j.apenergy.2018.04.049 |
| [7] |
LIU Yonggang, LIU Junjun, ZHANG Yuanjian, et al. Rule learning based energy management strategy of fuel cell hybrid vehicles considering multi-objective optimization[J]. Energy, 2020, 207: 118212. DOI:10.1016/j.energy.2020.118212 |
| [8] |
王哲, 谢怡, 臧鹏飞, 等. 基于极小值原理的燃料电池客车能量管理策略[J]. 吉林大学学报(工学版), 2020, 50(1): 37. WANG Zhe, XIE Yi, ZANG Pengfei, et al. Energy management strategy of fuel cell bus based on Pontryagin' s minimum principle[J]. Journal of Jilin University (Engineering and Technology Edition), 2020, 50(1): 3. |
| [9] |
SUN Haochen, FU Zhumu, TAO Fazhan, et al. Data-driven reinforcement-learning based hierarchical energy management strategy for fuel cell/battery/ultracapacitor hybrid electric vehicles[J]. Journal of Power Sources, 2020, 455: 227964. DOI:10.1016/j.jpowsour.2020.227964 |
| [10] |
LI Qi, CHEN Weirong, LIU Zhixiang, et al. Development of energy management system based on a power sharing strategy for a fuel cell-battery-supercapacitor hybrid tramway[J]. Journal of Power Sources, 2015, 279: 267. DOI:10.1016/j.jpowsour.2014.12.042 |
| [11] |
张晗, 杨继斌, 张继业, 等. 燃料电池有轨电车能量管理Pareto多目标优化[J]. 自动化学报, 2019, 45(12): 2379. ZHANG Han, YANG Jibin, ZHANG Jiye, et al. Pareto-based multi-objective optimization of energy management for fuel cell tramway[J]. Acta Automatica Sinica, 2019, 45(12): 2379. |
| [12] |
蒋永琛. 增程式电动客车能量管理控制策略研究[D]. 北京: 北京理工大学, 2016 JIANG Yongchen. Study on energy management control strategy for extended-range electric bus[D]. Beijing: Beijing Institute of Technology, 2016 |
| [13] |
周雅夫, 麻笑艺, 胡晓炜, 等. 微型燃气涡轮机增程式电动汽车设计[J]. 哈尔滨工业大学学报, 2017, 49(7): 100. ZHOU Yafu, MA Xiaoyi, HU Xiaowei, et al. Design of range extended electric vehicle with micro gas turbine[J]. Journal of Harbin Institute of Technology, 2017, 49(7): 100. |
| [14] |
孙术发, 杨洁, 唐华林, 等. PEMFC输出特性建模与多因素仿真分析[J]. 哈尔滨工业大学学报, 2019, 51(10): 144. SUN Shufa, YANG Jie, TANG Hualin, et al. PEMFC output characteristics modeling and multi-factor simulation analysis[J]. Journal of Harbin Institute of Technology, 2019, 51(10): 144. DOI:10.11918/j.issn.0367-6234.201807059 |
| [15] |
胡红斐, 黄向东, 罗玉涛, 等. HEV实时等效能量消耗最小控制策略[J]. 汽车工程, 2006, 28(6): 516. HU Hongfei, HUANG Xiangdong, LUO Yutao, et al. Real-time equivalent energy consumption minimization strategy for HEV[J]. Automotive Engineering, 2006, 28(6): 516. DOI:10.3321/j.issn:1000-680X.2006.06.002 |
| [16] |
SONG Ke, CHEN Huan, WEN Peimin, et al. A comprehensive evaluation framework to evaluate energy management strategies of fuel cell electric vehicles[J]. Electrochimica Acta, 2018, 292: 960. DOI:10.1016/j.electacta.2018.09.166 |
| [17] |
李卫民. 混合动力汽车控制系统与能量管理策略研究[D]. 上海: 上海交通大学, 2008 LI Weimin. Research of hybrid electric vehicle control system and energy management strategy[D]. Shanghai: Shanghai Jiao Tong University, 2008 |
| [18] |
林歆悠, 夏玉田, 李雪凡, 等. 燃料电池汽车行驶里程自适应ECMS策略[J]. 汽车工程, 2019, 41(7): 750. LIN Xinyou, XIA Yutian, LI Xuefan, et al. Equivalent consumption minimization strategy adaptive to various driving ranges for fuel cell vehicles[J]. Automotive Engineering, 2019, 41(7): 750. |
| [19] |
李宏才, 闫正军, 王伟达, 等. 并联混合动力汽车改进双参数换挡规律设计[J]. 哈尔滨工业大学学报, 2018, 51(1): 102. LI Hongcai, YAN Zhengjun, WANG Weida, et al. Design method of improved two-parameter gearshift schedule for parallel HEV[J]. Journal of Harbin Institute of Technology, 2018, 51(1): 102. |
 2021, Vol. 53
2021, Vol. 53


