2. 重庆大学 机械工程学院,重庆 400044
2. College of Mechanical Engineering, Chongqing University, Chongqing 400044, China
外骨骼助力机器人[1-9]作为一种高度集成化的人机交互装备,系统的设计需要满足柔顺性好、可靠性强、清洁和精度高等要求。为解决上述关键问题,气动肌肉驱动的外骨骼助力机器人[5-9]成为研究热点。气动肌肉是一种仿人体肌肉提供收缩力的执行元件,且与液压驱动与电机驱动相比,气动肌肉所具有的功率-质量比大、柔顺性好、清洁等优点使其广泛应用于外骨骼机器人的关节设计。其中以拮抗对拉关节[5-8]与气动肌肉-复位弹簧关节[9]为基础的外骨骼机器人应用最广。采用上述两种关节结构,每增加一个自由度,整机会增加一根气动肌肉或复位弹簧,不但增加了经济成本,也减少了机器人内部可用空间。因此,本文从缩小整机体积、降低经济成本出发,设计一种简单经济的上肢外骨骼助力机器人。其每个关节仅使用一根气动肌肉,通过钢丝绳带动滑轮,实现关节旋转,气动肌肉安装位置相对灵活,从而释放了整机内部空间。
由于气动肌肉具有复杂的输出力特性且难以精确建模,再加上气动系统固有的模型不确定性及强非线性,造成传统比例-积分-微分(PID)控制器轨迹跟踪控制效果较差,难以满足外骨骼助力机器人控制要求。
为解决气动肌肉伺服系统高精度轨迹跟踪控制问题,国内外学者设计了许多相关非线性控制器,如非线性PID控制[10]、滑模控制[8, 11-15]、H∞鲁棒控制[16]、动态滑模面控制、模糊控制、自适应控制[17-18]、自抗扰控制和自适应鲁棒控制[19]等。其中王斌锐[14]等设计了一种拮抗式气动肌肉关节驱动的四足机器人,并成功地将滑模控制应用于其髋、膝关节轨迹的跟踪控制;Aschemann H[15]等为一种气动肌肉驱动的直线运动装置设计了滑模控制律,实现了其在高速状态下的轨迹跟踪控制;杨钢[8]等提出了基于CMAC(cerebellar model articulation controller)的气动肌肉两层滑模变结构控制方法,CMAC神经网络估计系统的不确定性通过前馈进行补偿,余下的不确定性估计误差由滑模控制律抑制;朱笑丛[19]等采用自适应鲁棒控制策略实现了三自由度并联平台位姿跟踪控制,其采用梯度自适应率对参数进行在线估计并进行前馈补偿,从而抑制了系统的参数不确定性。现阶段,虽然针对气动肌肉关节的轨迹跟踪控制研究很多,但实际应用中存在换向误差较大、抗干扰能力差及输出颤振等现象,气动肌肉关节的高精度轨迹跟踪控制依然是一个难点。
本文在传统鲁棒控制器基础上,采用递归最小二乘法设计参数自适应率,采用梯度法设计快速动态补偿项,构建一种自适应鲁棒控制器。搭建实验样机,对比所设计自适应鲁棒控制器与鲁棒控制器的性能差别,分别验证参数不确定性补偿和进一步的参数估计误差及未建模误差补偿的作用;进行干扰测试实验,验证所设计的自适应鲁棒控制器的抗干扰能力。
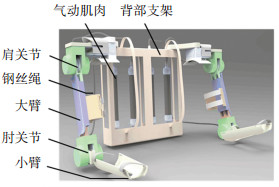
1 上肢外骨骼助力机器人的结构图 1展示了设计的上肢外骨骼助力机器人的整体结构,其主要由5个组成部分:小臂、肘关节、大臂、肩关节和背部气动肌肉支架。由于轻量化是外骨骼机器人设计的重要指标,除肩、轴关节部分零件采用45钢以外,其余机械主体均采用7075-T6轻质铝合金。
|
图 1 上肢外骨骼助力机器人整体结构 Fig. 1 Structure of upper-limb exoskeleton robot |
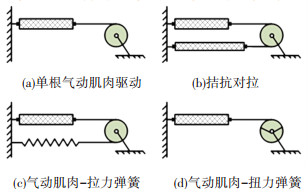
图 2(a)给出了肩、肘关节采用的单根气动肌肉驱动关节结构,与拮抗对拉关节(图 2(b))、气动肌肉-拉力弹簧关节(图 2(c))、气动肌肉-扭力弹簧关节(图 2(d))不同,其不需要复位元件,通过单根肌肉的充放气控制气动肌肉的收缩,进而实现关节的旋转。此关节结构设计使得气动肌肉安装位置灵活,避免了传感器的装配干涉,降低了经济成本,释放了机器人内部空间,但同时造成关节的角度跟踪控制完全依赖于单根气动肌肉的控制,需要考虑或克服更加完整的气动肌肉关节系统的非线性动态。
|
图 2 几种典型的气动肌肉驱动关节 Fig. 2 Structures of typical pneumatic muscle actuated joints |
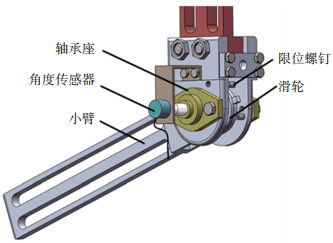
图 3展示了肘关节部位设计图,助力过程中,关节处承受主要载荷,宜采用简单、经济的轴承座支撑,角度传感器通过键与滑轮进行连接。为防止肘关节旋转角度超过人体肘关节运动范围而造成的穿戴者损伤,必须在关节处安装限位螺钉。
|
图 3 肘关节结构设计图 Fig. 3 Elbow joint mechanisms |
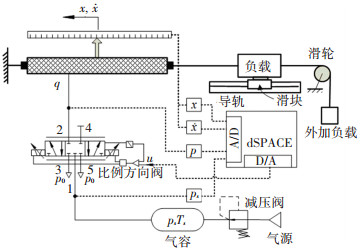
上述单根气动肌肉的关节角度跟踪控制本质上为气动肌肉长度的控制,因此,为进一步体现所设计的控制器对单根气动肌肉关节伺服系统的适用性,本文搭建了如图 4所示的单根气动肌肉关节伺服系统。单根气动肌肉由一个三位五通的比例方向阀控制, 系统的动力学方程为
| $ m \ddot{x}=F_{\mathrm{M}}-B \dot{x}-A S_{\mathrm{f}}(\dot{x})-F_{\mathrm{L}}+f_{\mathrm{n}}+\tilde{f}_{0} $ | (1) |
|
图 4 单关节气动肌肉伺服系统 Fig. 4 Single pneumatic muscle actuated servo system |
式中:x、
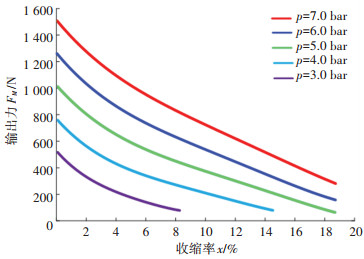
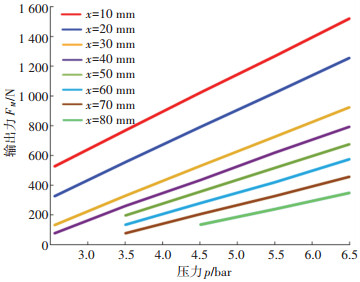
图 5展示了不同压力下气动肌肉输出力曲线,实验测得曲线与Festo公司DMSP型气动肌肉产品手册给出的曲线基本一致。实验也证明了在收缩量一定情况下,气动肌肉输出力FM与气动肌肉内部绝对压力p呈线性关系,其关系曲线如图 6所示。因此,气动肌肉输出力模型可表示为
| $ \left\{\begin{array}{l} F_{\mathrm{M}}(x, p)=a(x) p+b(x) \\ a(x)=\sum\limits_{m=0}^{3} a_{m} x^{m}, b(x)=\sum\limits_{n=0}^{4} b_{n} x^{n} \end{array}\right. $ | (2) |
|
图 5 不同压力下气动肌肉输出力 Fig. 5 Contraction force of pneumatic muscle under different pressure |
|
图 6 输出力与压力的线性关系(一定收缩量) Fig. 6 Relation between contraction force and pressuer at certain contraction |
式中am(m=0, 1, 2, 3)和bn(n=0, 1, 2, 3, 4)为多项式系数。
气动肌肉内部压力的动态可认为是一个理想气体多变过程[20],其动态方程如下:
| $ \left\{\begin{array}{l} \dot{p}=G_{\mathrm{p}}(x, \dot{x}, p)+D_{\mathrm{p}}(x) q+d_{\mathrm{n}}+\tilde{d}_{0} \\ G_{\mathrm{p}}(x, \dot{x}, p)=-\frac{\lambda p \bar{V}(x, \dot{x})}{V(x)} \\ D_{\mathrm{p}}(x)=\frac{\lambda R T}{V(x)} \end{array}\right. $ | (3) |
式中:λ为多变系数;R为气体常量;T为气动肌肉内部气体绝对温度;dn为压力动态建模误差及外界干扰的标称量;
| $ \left\{ {\begin{array}{*{20}{l}} {V = \frac{{{\rm{ \mathsf{ π} }}{D_0}^2}}{{4{{\sin }^2}{\alpha _0}}}\left( {{L_0} - x} \right)\left( {1 - \frac{{{{\left( {{L_0} - x} \right)}^2}{{\cos }^2}{\alpha _0}}}{{L_0^2}}} \right)}\\ {\dot V = \frac{{{\rm{ \mathsf{ π} }}{D_0}^2}}{{4{{\sin }^2}{\alpha _0}}}\left( {\frac{{3{{\left( {{L_0} - x} \right)}^2}{{\cos }^2}{\alpha _0}}}{{L_0^2}} - 1} \right)\dot x} \end{array}} \right. $ | (4) |
式中:α0、L0、D0分别为气动肌肉初始编织角、初始长度、初始直径。
比例方向阀气体质量流量模型参考文献[21]。定义未知参数向量θa=[θa1, θa2, θa3, θa4, θa5, θa6, θa7]T和θb=[θb]T分别定义为θa1=b0-FL+fn,θa2=b1,θa3=b2,θa4=b3,θa5=b4,θa6=-B,θa7=-A,θb=dn,同时定义状态变量向量x=[x1, x2, x3]T=[x,
| $ \left\{\begin{array}{l} \dot{x}_{1}=x_{2} \\ m \dot{x}_{2}=a\left(x_{1}\right) x_{3}+\theta_{\mathrm{a} 1}+\theta_{\mathrm{a} 2} x_{1}+\theta_{\mathrm{a} 3} x_{1}^{2}+\theta_{\mathrm{a} 4} x_{1}^{3}+ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \theta_{\mathrm{a} 5} x_{1}^{4}+\theta_{\mathrm{a} 6} x_{2}+\theta_{\mathrm{a} 7} S_{\mathrm{f}}\left(x_{2}\right)+\tilde{f}_{0} \\ \dot{x}_{3}=D_{\mathrm{p}}\left(x_{1}\right) q+G_{\mathrm{p}}\left(x_{1}, x_{2}, x_{3}\right)+\theta_{\mathrm{b}}+\tilde{d}_{0} \end{array}\right. $ | (5) |
虽然参数向量θa和θb无法完全准确获得,但其可在参数离线辨识实验中获得各分量的上界和下界,并且在实际应用中,系统的建模误差及外界干扰的范围也是可以预测的。因此,可对系统的不确定性做出如下假设[22]:
| $ \mathrm{A} 1:\boldsymbol{\theta}_{\mathrm{a}} \in \boldsymbol{\varOmega}_{\boldsymbol{\theta}_{\mathrm{a}}} \triangleq\left\{\boldsymbol{\theta}_{\mathrm{a}}: \boldsymbol{\theta}_{\mathrm{amin}} \leqslant \boldsymbol{\theta} \leqslant \boldsymbol{\theta}_{\mathrm{amax}}\right\} $ |
| $ \mathrm{A} 2:\boldsymbol{\theta}_{\mathrm{b}} \in \boldsymbol{\varOmega}_{\theta \mathrm{b}} \triangleq\left\{\boldsymbol{\theta}_{\mathrm{b}}: \boldsymbol{\theta}_{\mathrm{bmin}} \leqslant \boldsymbol{\theta} \leqslant \boldsymbol{\theta}_{\mathrm{bmax}}\right\} $ |
| $ \mathrm{A} 3: \tilde{f}_{0} \in \boldsymbol{\varOmega}_{\mathrm{f}} \triangleq\left\{\tilde{f}_{0}:\left|\tilde{f}_{0}\right| \leqslant f_{\max }\right\} $ |
| $ \mathrm{A} 4: \tilde{d}_{0} \in \boldsymbol{\varOmega}_{\mathrm{d}} \triangleq\left\{\tilde{d}_{0}:\left|\tilde{d}_{0}\right| \leqslant d_{\max }\right\} $ |
式中:θamax和θamin分别为参数向量θa的上界、下界向量,θbmax和θbmin分别为参数θb的上界和下界,fmax和dmax为已知正值,Ωθa、Ωθb、Ωf和Ωd分别为已知凸集。
3 控制器设计为了下文描述方便,作出如下说明:·i为向量·的第i个元素,两个向量之间的符号"≤"是对向量中每个分量定义,
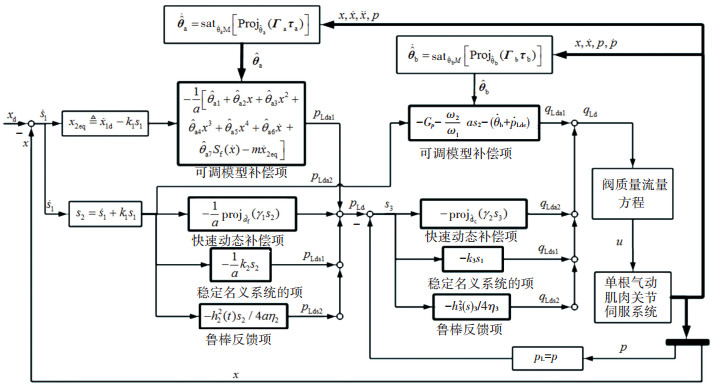
Yao Bin等[22]针对一类半严格反馈(semi-strict feedback form)非线性系统提出了自适应鲁棒控制器设计方法,其性能已在直线电机、液压缸及气缸的非线性控制中得到了验证。注意到系统动态式(5)相对阶为3阶,因此基于反步法结合自适应鲁棒方法设计适用于单根肌肉关节伺服系统控制器。图 7展示了算法结构图,整个算法为两层级联结构,每层各包含一个确定性鲁棒控制律(包含调模型补偿项、稳定名义系统项及鲁棒反馈项)、参数自适应和快速动态补偿项,且参数自适应律与鲁棒控制律的设计完全独立进行。
|
图 7 单根气动肌肉关节伺服系统的自适应鲁棒控制算法 Fig. 7 Framework of the DIARC algorithm |
在系统参数离线辨识过程中,注意到各参数之间数量级差距较大,若不统一数量级,在参数更新时,会造成因数值计算误差过大导致的参数自适应失效。因此,做出如下处理:θa1=θa1/10,θa2=θa2/103,θa3=θa3/104,θa4=θa4/105,θa5=θa5/105。假设系统式(5)仅存在参数不确定性,即
| $ \left\{\begin{array}{l} y_{\mathrm{a}}=a\left(x_{1}\right) x_{3}-m \dot{x}_{2}=-\boldsymbol{\varphi}_{\mathrm{a}}\left(x_{1}, x_{2}\right)^{\mathrm{T}} \overline{\boldsymbol{\theta}}_{\mathrm{a}} \\ y_{\mathrm{b}}=D_{\mathrm{p}}\left(x_{1}\right) q+G_{\mathrm{p}}\left(x_{1}, x_{2}, p\right)-\dot{x}_{3}=-\boldsymbol{\varphi}_{\mathrm{b}}^{\mathrm{T}} \overline{\boldsymbol{\theta}}_{\mathrm{b}} \end{array}\right. $ | (6) |
式中:θa=[θa1, θa2, θa3, θa4, θa5, θa6, θa7]T, φa(x1, x2)=([1×10, x1×103, x12×104, x13×105, x14×105, x2, Sf(x2)]Tθb=θb,φbf=[-1f]T。为避免参数辨识时加速度、速度信号的测量噪声干扰量的影响,选用相对阶大于等于3的线性时不变(LTI)低通滤波器(例如
| $ \left\{\begin{array}{l} y_{\mathrm{af}}=H_{\mathrm{f}}\left[a x_{3}-m \dot{x}_{2}\right]=\boldsymbol{\varphi}_{\mathrm{af}}\left(x_{1}, x_{2}\right)^{\mathrm{T}} \overline{\boldsymbol{\theta}}_{\mathrm{a}} \\ y_{\mathrm{bf}}=H_{\mathrm{f}}\left[D_{\mathrm{p}}\left(x_{1}\right) q+G_{\mathrm{p}}\left(x_{1}, x_{2}, p\right)-\dot{x}_{3}\right]=\boldsymbol{\varphi}_{\mathrm{bf}}^{\mathrm{T}} \overline{\boldsymbol{\theta}}_{\mathrm{b}} \end{array}\right. $ | (7) |
式中:φaf(x1, x2)=[-1f×10, -x1f×103, -x1f2×104, -x1f3×105, -x1f4×105, -x2, -Sff(x2)]T和φbf=[-1f]T分别为φa(x1, x2)和φb通过滤波器Hf(s)的输出。式(7)进一步表示为
| $ {y_{i{\rm{f}}}} = \mathit{\boldsymbol{\varphi }}_{i{\rm{f}}}^{\rm{T}}{\mathit{\boldsymbol{\bar \theta }}_i},i = {\rm{a}},{\rm{b}} $ | (8) |
同时定义
| $ \varepsilon_{i}=\hat{y}_{i{\mathrm{f}}}-y_{i{\mathrm{f}}}=\boldsymbol{\varphi}_{i{\mathrm{f}}}^{\mathrm{T}} \tilde{\bar{\boldsymbol{\theta}}}_{i}, i=\mathrm{a}, \mathrm{b} $ | (9) |
Yao Bin[23]等为实现参数自适应律与鲁棒控制律设计的完全独立,引入标准投影映射Proj(·)和饱和函数sat(·),并利用递归最小二乘估计算法设计参数更新率。类似地,参数更新率选择为
| $ \dot{\hat{\bar{\boldsymbol{\theta}}}}_{i}=\operatorname{sat}_{\dot{\theta}_{i \mathrm{M}}}\left[\operatorname{Proj}_{\hat{\theta}_{i}}\left(\boldsymbol{\varGamma}_{i} \boldsymbol{\sigma}_{i}\right)\right], i=\mathrm{a}, \mathrm{b} $ | (10) |
自适应率矩阵Γi为
| $ \dot{\boldsymbol{\varGamma}}_{i}=\left\{\begin{array}{l} \alpha_{i} \boldsymbol{\varGamma}_{i}-\frac{\boldsymbol{\varGamma}_{i} \boldsymbol{\varphi}_{i \mathrm{f}} \boldsymbol{\varphi}_{i \mathrm{f}}^{\mathrm{T}} \boldsymbol{\varGamma}_{i}}{1+\nu_{i} \boldsymbol{\varphi}_{i \mathrm{f}}^{\mathrm{T}} \boldsymbol{\Gamma}_{i} \boldsymbol{\varphi}_{i \mathrm{f}}}, \\ \text { if } \lambda_{\max }\left(\boldsymbol{\varGamma}_{i}(t)\right) \leqslant \rho_{i \mathrm{M}} \text { and }\left\|\operatorname{Proj}_{\hat{\theta} i}\left(\boldsymbol{\varGamma}_{i} \boldsymbol{\tau}_{i}\right)\right\| \leqslant \dot{\bar{\boldsymbol{\theta}}}_{i \mathrm{M}} \\ 0, \text { otherwise } \end{array}\right. $ | (11) |
式中:αi≥0为遗忘因子,νi≥0为归一化因子,ρiM为自适应率矩阵预设上界,保证Γi(t)≤ρiMI, ∀t。
自适应函数τi为
| $ \boldsymbol{\tau}_{i}=\frac{1}{1+\nu_{i} \boldsymbol{\varphi}_{i f}^{\mathrm{T}} \boldsymbol{\varGamma}_{i} \boldsymbol{\varphi}_{i f}} \boldsymbol{\varphi}_{i f} \boldsymbol{\varepsilon}_{i} $ | (12) |
对于任意θi(i=a, b),设计的参数自适应率有下列性质:
| $ \mathrm{P} 1: \hat{\boldsymbol{\theta}}_{i}(t) \in \overline{\boldsymbol{\varOmega}}_{\theta i}, \forall t $ |
| $ \mathrm{P} 2: \widetilde{\boldsymbol{\theta}}_{i}^{\mathrm{T}}\left[\boldsymbol{\varGamma}_{i}^{-1} \operatorname{Proj}\left(\boldsymbol{\varGamma}_{i} \tau_{i}\right)-\tau_{i}\right] \leqslant 0, \forall \tau_{i} $ |
| $ \mathrm{P} 3:\left|\dot{\hat{\boldsymbol{\theta}}}_{i}(t)\right| \leqslant \dot{\boldsymbol{\theta}}_{i M}, \forall t $ |
式中Ωθi为已知凸集Ωθi的开集。
3.2 鲁棒控制律设计尽管参数的自适应可有效补偿系统参数不确定性,但剩余的参数不确定性估计误差、建模误差及外界干扰高频分量仍影响控制器稳定性和性能,因而进一步利用梯度法设计快速动态补偿项补偿其部分信息,最后利用鲁棒反馈来抑制其不可补偿部分的影响。
步骤一:定义一个类似滑模面的变量为
| $ s_{2}=\dot{s}_{1}+k_{1} s_{1}=x_{2}-x_{2 \mathrm{eq}}, x_{2 \mathrm{eq}} \triangleq \dot{x}_{1 \mathrm{~d}}-k_{1} s_{1} $ | (13) |
式中s1=x1-x1d表示跟踪误差,k1为正的反馈增益。明显地,传递函数Gs1s2(s)=1/(s+k1)是稳定的,使得当s2收敛到0时,s1将以指数收敛率k1收敛到0。微分式(13)并将式(5)第二个等式带入可得
| $ \begin{array}{l} m \dot{s}_{2}=a x_{3}+\theta_{\mathrm{a} 1}+\theta_{\mathrm{a} 2} x_{1}+\theta_{\mathrm{a} 3} x_{1}^{2}+\theta_{\mathrm{a} 4} x_{1}^{3}+\theta_{\mathrm{a} 5} x_{1}^{4}+ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \theta_{\mathrm{a} 6} x_{2}+\theta_{\mathrm{a} 7} S_{\mathrm{f}}\left(x_{2}\right)+\tilde{f}_{0}-m \dot{x}_{2 \mathrm{eq}} \end{array} $ | (14) |
定义一个Lyapunov函数为
| $ V_{2}=\frac{1}{2} \omega_{2} m s_{2}^{2} $ | (15) |
式中ω2为权重因子。微分式(15)可得
| $ \begin{aligned} \dot{V}_{2}=& \omega_{2} s_{2}\left[a p_{\mathrm{L}}+\theta_{\mathrm{a} 1}+\theta_{\mathrm{a} 2} x_{1}+\theta_{\mathrm{a} 3} x_{1}^{2}+\theta_{\mathrm{a} 4} x_{1}^{3}+\right.\\ &\left.\theta_{\mathrm{a} 5} x_{1}^{4}+\theta_{\mathrm{a} 6} x_{2}+\theta_{\mathrm{a} 7} S_{\mathrm{f}}\left(x_{2}\right)+\tilde{f}_{0}-m \dot{x}_{2 \mathrm{eq}}\right] \end{aligned} $ | (16) |
式中pL=x3为步骤一的虚拟控制输入。然后设计如下期望虚拟控制输入pLd,即步骤一的控制律:
| $ \left\{\begin{array}{l} p_{\mathrm{Ld}}= p_{\mathrm{Lda} 1}+p_{\mathrm{Lda} 2}+p_{\mathrm{Lds} 1}+p_{\mathrm{Lds} 2} \\ p_{\mathrm{Lda} 1}=-\frac{1}{a}\left[\hat{\theta}_{\mathrm{a} 1}+\hat{\theta}_{\mathrm{a} 2} x_{1}+\hat{\theta}_{\mathrm{a} 3} x_{1}^{2}+\hat{\theta}_{\mathrm{a} 4} x_{1}^{3}+\hat{\theta}_{\mathrm{a} 5} x_{1}^{4}+\right.\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left.\hat{\theta}_{\mathrm{a} 6} x_{2}+\hat{\theta}_{\mathrm{a} 7} S_{\mathrm{f}}\left(x_{2}\right)-m \dot{x}_{2 \mathrm{q}}\right] \\ p_{\mathrm{Lds} 1}=-\frac{1}{a} k_{2} s_{2} \end{array}\right. $ | (17) |
式中:k2>0是正的反馈增益,pLda1为关于参数估计
定义s3=pL-pLd表示实际和期望虚拟控制输入之间的误差,式(16)可写成
| $ \begin{aligned} \dot{V}_{2}=&-\omega_{2} k_{2} s_{2}^{2}+\omega_{2} s_{2} a s_{3}+\omega_{2} s_{2} a p_{\mathrm{Lda} 2}+\omega_{2} s_{2} a p_{\mathrm{Lds} 2}-\\ & \omega_{2} s_{2}\left[\tilde{\theta}_{\mathrm{a} 1}+\tilde{\theta}_{\mathrm{a} 2} x_{1}+\tilde{\theta}_{\mathrm{a} 3} x_{1}^{2}+\tilde{\theta}_{\mathrm{a} 4} x_{1}^{3}+\tilde{\theta}_{\mathrm{a} 5} x_{1}^{4}+\right.\\ &\left.\tilde{\theta}_{\mathrm{a} 6} x_{2}+\tilde{\theta}_{\mathrm{a} 7} S_{\mathrm{f}}\left(x_{2}\right)-\tilde{f}_{0}\right] \end{aligned} $ | (18) |
明显地,式(18)中括号中集中了所有参数的不确定性估计误差、建模误差及外界干扰高频分量,进一步将其分为低频分量df和高频分量Δ1(t),即
| $ \begin{aligned} d_{\mathrm{f}}+\varDelta_{1}=&-\left[\tilde{\theta}_{\mathrm{a} 1}+\tilde{\theta}_{\mathrm{a} 2} x_{1}+\tilde{\theta}_{\mathrm{a} 3} x_{1}^{2}+\tilde{\theta}_{\mathrm{a} 4} x_{1}^{3}+\tilde{\theta}_{\mathrm{a} 5} x_{1}^{4}+\right.\\ &\left.\tilde{\theta}_{\mathrm{a} 6} x_{2}+\tilde{\theta}_{\mathrm{a} 7} S_{\mathrm{f}}\left(x_{2}\right)-\tilde{f}_{0}\right] \end{aligned} $ | (19) |
更进一步,利用快速动态补偿项pLda2补偿低频分量df,pLda2选择为
| $ p_{\text {Lda} 2}=-\frac{1}{a} \hat{d}_{\mathrm{f}} $ | (20) |
更新率
| $ \dot{\hat{d}}_{\mathrm{f}}=\operatorname{proj}_{\hat{d}_{\mathrm{f}}}\left(\gamma_{1} s_{2}\right)=\left\{\begin{array}{l} 0,\left|\hat{d}_{\mathrm{f}}(t)\right|=d_{\mathrm{fM}} \text { and } \hat{d}_{\mathrm{f}}(t) s_{2}>0 \\ \gamma_{1} s_{2}, \text { otherwise } \end{array}\right. $ | (21) |
式中:γ1>0为自适应率,dfM>0为
结合式(19)和式(20),式(18)有
| $ \begin{aligned} \dot{V}_{2}=&-\omega_{2} k_{2} s_{2}{}^{2}+\omega_{2} s_{2} a s_{3}+\omega_{2} s_{2}\left\{a p_{\mathrm{Lds} 2}+\right.\\ &\left.\left[\varDelta_{1}(t)-\tilde{d}_{\mathrm{f}}\right]\right\} \end{aligned} $ | (22) |
利用鲁棒反馈项pLds2抑制式(22)中括号内系统剩余不确定性的影响,保证控制器的稳定性。pLds2选择为
| $ p_{\mathrm{Lds} 2}=-\frac{h_{2}^{2}(t)}{4 a \eta_{2}} s_{2} $ | (23) |
式中η2>0为边界层厚度,h2(t)为系统剩余不确定性的边界函数,且选择为
| $ \begin{aligned} h_{2}(t)=&\left\|\left[1, x_{1}, x_{1}^{2}, x_{1}^{3}, x_{1}^{4}, x_{2}, S_{\mathrm{f}}\left(x_{2}\right)\right]\right\| \times \| \theta_{\operatorname{amax}}-\\ &\theta_{\mathrm{amin}} \|+d_{\mathrm{fM}}+f_{\max } \end{aligned} $ | (24) |
注 1 结合A1,A3,P1~P 3及式(21)的有界投影映射性质,当跟踪轨迹足够光滑时,总能找到一个满足上述2个条件的边界函数h2(t)。
鲁棒反馈项pLds2满足下列2个条件:
| $ \left\{\begin{array}{l} s_{2} a \mathrm{p}_{\mathrm{Lds} 2} \leqslant 0 \\ s_{2}\left\{a \mathrm{p}_{\mathrm{Lds} 2}+\left[\varDelta_{1}(t)-\tilde{d}_{\mathrm{f}}\right]\right\} \leqslant \eta_{2} \end{array}\right. $ | (25) |
将式(25)带入式(22)可得
| $ \dot{V}_{2} \leqslant-\omega_{2} k_{2} s_{2}{}^{2}+\omega_{2} s_{2} a s_{3}+\omega_{2} \eta_{2} $ | (26) |
由此可得,当不存在实际和期望虚拟控制输入之间的误差,即s3=0时,s2始终以被一个确定函数界定,具体描述为
| $ \left|s_{2}(t)\right|^{2} \leqslant\left|s_{2}(0)\right|^{2} \mathrm{e}^{-\beta t}+\frac{2 \omega_{2} \eta_{2}}{\beta m}\left(1-\mathrm{e}^{-\beta t}\right) $ | (27) |
式中β=2k2/m。在上述条件下,当跟踪轨迹足够光滑时,相关的系统信号都是有界的,输出跟踪有确定的暂态响应,且跟踪误差s2最终指数收敛于确定的球域。因此,下一步控制器设计目标是使s3收敛于0或足够小的值。
步骤二:微分s3并将式(5)第三个等式带入可得
| $ \begin{array}{l} \dot{s}_{3}=\dot{p}_{\mathrm{L}}-\dot{p}_{\mathrm{Ld}}=D_{\mathrm{p}}\left(x_{1}\right) q+G_{\mathrm{p}}\left(x_{1}, x_{2}, x_{3}\right)+\theta_{\mathrm{b}}+ \\ \ \ \ \ \ \ \ \ \ \tilde{d}_{0}-\left(\dot{p}_{\mathrm{Ldc}}+\dot{p}_{\mathrm{Ldu}}\right) \end{array} $ | (28) |
式中:
| $ \dot{p}_{\mathrm{Ldc}}=\frac{\partial p_{\mathrm{Ld}}}{\partial x_{1}} x_{2}+\frac{\partial p_{\mathrm{Ld}}}{\partial x_{2}} \hat{\dot{x}}_{2}+\left[\frac{\partial p_{\mathrm{Ld}}}{\partial \hat{\theta}_{\mathrm{a}}}\right]^{\mathrm{T}} \dot{\hat{\theta}}_{\mathrm{a}}+\frac{\partial p_{\mathrm{Ld}}}{\partial \hat{d}_{\mathrm{f}}} \dot{\hat{d}}_{\mathrm{f}}+\frac{\partial p_{\mathrm{Ld}}}{\partial t} $ | (29) |
式中:
| $ \begin{array}{l} \frac{{\partial {p_{{\rm{Ld}}}}}}{{\partial {{\hat d}_{\rm{f}}}}} = - \frac{1}{a},\frac{{\partial {p_{{\rm{Ld}}}}}}{{\partial {x_1}}} = \frac{1}{a}\left( { - {{\hat \theta }_{{\rm{a}}2}} - 2{{\hat \theta }_{{\rm{a}}3}}{x_1} - } \right.\\ \left. {3{{\hat \theta }_{{\rm{a}}4}}x_1^2 - 4{{\hat \theta }_{{\rm{a}}5}}x_1^3 - {k_1}\left( {{k_2} + \frac{{h_2^2(t)}}{{4{\eta _2}}}} \right)} \right),\frac{{\partial {p_{{\rm{Ld}}}}}}{{\partial {x_2}}} = \frac{1}{a}\left( { - {{\hat \theta }_{{\rm{a}}6}} - } \right.\\ \left. {{{\hat \theta }_{{\rm{a}}7}}\frac{2}{{\rm{\pi }}}\frac{{1000}}{{1 + {{\left( {1000{x_2}} \right)}^2}}} - \left( {m{k_1} + {k_2} + \frac{{h_2^2(t)}}{{4{\eta _2}}}} \right)} \right),\frac{{\partial {p_{{\rm{Ld}}}}}}{{\partial t}} = \\ \frac{1}{a}\left( {m{k_1}{{\ddot x}_{1{\rm{d}}}} + m{x_{1{\rm{d}}}} - \left( {{k_2} + \frac{{h_2^2(t)}}{{4{\eta _2}}}} \right)\left( { - {k_1}{{\dot x}_{1{\rm{d}}}} - {{\ddot x}_{1{\rm{d}}}}} \right)} \right)。\end{array} $ |
| $ \begin{aligned} \dot{p}_{\mathrm{Ldu}}=& \frac{1}{m} \frac{\partial p_{\mathrm{Ld}}}{\partial x_{2}}\left\{\tilde{\theta}_{\mathrm{a} 1}+\tilde{\theta}_{\mathrm{a} 2} x_{1}+\tilde{\theta}_{\mathrm{a} 3} x_{1}^{2}+\tilde{\theta}_{\mathrm{a} 4} x_{1}^{3}+\right.\\ &\left.\tilde{\theta}_{\mathrm{a} 5} x_{1}^{4}+\tilde{\theta}_{\mathrm{a} 6} x_{2}+\tilde{\theta}_{\mathrm{a} 7} S_{\mathrm{f}}\left(x_{2}\right)+\tilde{f}_{0}\right\} \end{aligned} $ | (30) |
对于
| $ \begin{aligned} \dot{p}_{\mathrm{Ldu}} \leqslant & \frac{1}{m}\left|\frac{\partial p_{\mathrm{Ld}}}{x_{2}}\right|\left\{\left\|\left[1, x_{1}, x_{1}^{2}, x_{1}^{3}, x_{1}^{4}, x_{2}, S_{\mathrm{f}}\left(x_{2}\right)\right]\right\| \times\right.\\ &\| \left.\boldsymbol{\theta}_{\mathrm{amax}}-\boldsymbol{\theta}_{\mathrm{amin}} \|+f_{\max }\right\} \end{aligned} $ | (31) |
注 2 单根气动肌肉关节系统模型是由足够光滑的非线性模态项组成,虽然
定义另一个Lyapunov函数为
| $ V_{3}=V_{2}+\frac{1}{2} \omega_{3} s_{3}^{2} $ | (32) |
式中ω3>0为遗忘因子。结合式(22)和式(28),微分V3可得
| $ \begin{array}{l} \dot{V}_{3}=\dot{V}_{2 \mathrm{~d}}+\omega_{2} s_{2} a s_{3}+\omega_{3} s_{3}\left[q_{\mathrm{L}}+G_{\mathrm{p}}\left(x_{1}, x_{2}, x_{3}\right)+\right. \\ \ \ \ \ \ \ \ \ \ \ \left.\theta_{\mathrm{b}}+\tilde{d}_{0}-\dot{p}_{\mathrm{Ldc}}-\dot{p}_{\mathrm{Ldu}}\right] \end{array} $ | (33) |
式中
与步骤一类似,设计如下期望虚拟控制输入qLd,即步骤二控制律:
| $ \left\{\begin{array}{l} q_{\mathrm{Ld}}=q_{\mathrm{Lda} 1}+q_{\mathrm{Lda} 2}+q_{\mathrm{Lds} 1}+q_{\mathrm{Lds} 2} \\ q_{\mathrm{Lda}}=-G_{\mathrm{p}}-\frac{\omega_{2}}{\omega_{3}} a s_{2}-\hat{\theta}_{\mathrm{b}}+{\dot p}_{\mathrm{Ldc}} ,\\ q_{\mathrm{Lds} 1}=-k_{3} s_{3} \end{array}\right. $ | (34) |
式中:k3>0为正反馈增益,qLda1为关于参数估计
将式(34)带入式(33)可得
| $ \begin{aligned} \dot{V}_{3}=& \dot{V}_{2 \mathrm{~d}}-\omega_{3} k_{3} s_{3}^{2}+\omega_{3} s_{3}\left(q_{\mathrm{Lda} 2}+q_{\mathrm{Lds} 2}+\right.\\ &\left.\tilde{\theta}_{\mathrm{b}}+\tilde{d}_{0}-\dot{p}_{\mathrm{Ldu}}\right). \end{aligned} $ | (35) |
与步骤一类似,将式(35)括号内的压力动态参数不确定性估计误差、建模误差及外界干扰高频分量进一步分为低频分量dc和高频分量Δ2(t),即
| $ d_{\mathrm{c}}+\varDelta_{2}(t)=\tilde{\theta}_{\mathrm{b}}+\tilde{d}_{0}-\dot{p}_{\mathrm{Ldu}} $ | (36) |
qLda2选择为
| $ q_{\mathrm{Lda} 2}=-\hat{d}_{\mathrm{c}} $ | (37) |
更新率
| $ \begin{aligned} \dot{\hat{d}}_{\mathrm{c}}=& \operatorname{proj}_{\hat{d}_{\mathrm{c}}}\left(\gamma_{2} s_{3}\right)=\\ &\left\{\begin{array}{l} 0,\left|\hat{d}_{\mathrm{c}}(t)\right|=d_{\mathrm{cM}} \text { and } \hat{d}_{\mathrm{c}}(t) s_{2}>0 \\ \gamma_{2} s_{3}, \text { otherwise } \end{array}\right. \end{aligned} $ | (38) |
式中:γ2>0为自适应率,dcM>0是
将式(36)和式(37)带入式(35)可得
| $ \dot{V}_{3}=\dot{V}_{2 \mathrm{d}}-\omega_{3} k_{3} s_{3}^{2}+\omega_{3} s_{3}\left[q_{\mathrm{Lds} 2}+\varDelta_{2}(t)-\tilde{d}_{\mathrm{c}}\right] $ | (39) |
鲁棒反馈项qLds2选择为
| $ q_{\mathrm{Lds} 2}=-\frac{h_{3}^{2}(t)}{4 \eta_{3}} s_{3} $ | (40) |
式中η3>0为边界层厚度,h3(t)为压力动态系统剩余不确定性得边界函数。结合式(31),A2,A4及式(38)的有界投影映射性质,h3(t)选择为
| $ \begin{array}{r} h_{3}(t)=\frac{1}{m}\left|\frac{\partial p_{\mathrm{Ld}}}{x_{2}}\right|\left\{\left\|\left[1, x_{1}, x_{1}^{2}, x_{1}^{3}, x_{1}^{4}, x_{2}, S_{f}\left(x_{2}\right)\right]\right\| \times\right. \\ \left.\left\|\boldsymbol{\theta}_{\mathrm{amax}}-\boldsymbol{\theta}_{\mathrm{amin}}\right\|+f_{\max }\right\}+d_{\mathrm{cM}}+\theta_{\mathrm{bmax}}+d_{\max } \end{array} $ | (41) |
类似地,鲁棒反馈项qLds2满足下列2个条件:
| $ \left\{\begin{array}{l} s_{3} q_{\mathrm{Lds}2} \leqslant 0 \\ s_{3}\left\{q_{\mathrm{Lds}2}-\left[\tilde{\theta}_{\mathrm{b}}+\dot{p}_{\mathrm{Ldu}}-\tilde{d}_{0}\right]\right\} \leqslant \eta_{3} \end{array}\right. $ | (42) |
将式(42)带入式(39)可得
| $ \dot{V}_{3} \leqslant-\omega_{2} k_{2} s_{2}{}^{2}+\omega_{2} \eta_{2}-\omega_{3} k_{3} s_{3}{}^{2}+\omega_{3} \eta_{3} \leqslant-\lambda V_{3}+\eta $ | (43) |
式中λ=min(2k2/m, 2k3),η=ω2η2+ω3η3。求解式(43)可得
| $ V_{3}(t) \leqslant V_{3}(0) \mathrm{e}^{-\lambda t}+\frac{\eta}{\lambda}\left(1-\mathrm{e}^{-\lambda t}\right) $ | (44) |
由此误差向量
| $ \|\boldsymbol{s}(t)\|^{2} \leqslant\|\boldsymbol{s}(0)\|^{2} \mathrm{e}^{-\lambda t}+\frac{2 \eta}{\lambda}\left(1-\mathrm{e}^{-\lambda t}\right) $ | (45) |
综上分析,所提出控制器设计算法确保输出跟踪有确定的暂态响应,且保证s1最终有界;s2和s3指数收敛于一个确定大小的球域,且该球域大小通过η2,η3,k2,k3调节。
最后通过比例方向阀的质量流量方程由获得的虚拟控制输入qLd计算出控制电压u。
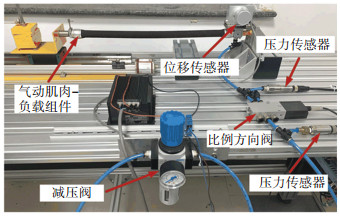
4 对比实验结果 4.1 实验装置及性能指标设计的控制算法在图 8展示的单根气动肌肉关节伺服系统实验台上进行测试。气动肌肉(Festo DMSP-20-480N-RM-CM)由比例方向阀(Festo MPYE-5-1/8-HF-010-B)控制。比例方向阀进出口压力由2个压力传感器(FESTO SDET-22T-D10-G14- I-M12)测量。气动肌肉的收缩量由位移传感器(MIRAN MPS-S-100MM-P)测量。系统各种信号的产生和读取利用dSPACE DS1103完成。
|
图 8 单根气动肌肉关节伺服系统实验台 Fig. 8 Experimental setup |
采用下列数字指标衡量控制器性能优劣:
1) em=max{|s1|}0≤t≤40,前40 s最大绝对跟踪误差,用来衡量控制器的暂态性能。
2)
3) emd=max{|s1|}T1≤t≤T2,干扰测试时的最大绝对跟踪误差,T1、T2为干扰测试实验开始结束时间。
4)
为了验证所设计的DIARC控制器的优越性,同时给出如下几种类型控制器作为对比。
(C1) DIARC:设定控制器参数为k1=150,k2=140,h2(t)=50,η2=0.4,k3=130,h3(t)=50,η3=2,τf=0.02,ωf=100,ξ=1,γ1=10,γ2=1 200;设定系统参数向量初值为θa(0)=[-16.5, -24.6, 55.3, -34.3, 101.3, -70.5, -26.5]T,θb(0)=0;设定系统参数的界为θamax= [0, 0, 200, 0, 200, 0, 0]T, θamin=[-200, -200, 0, -200, 0, -200-200]T, θbmax= 500 000, θbmin=-500 000;设定自适应率矩阵的初值为Γa(0)=diag{10, 10, …, 10}7×7,Γb(0)=1 000;相关快速动态补偿项参数设定为dfM=500,dcM=600 000,df(0)=0,dc(0)=0;其余相关自适应参数设定为αa=αb=0.1,νa=νb=0.1,ρMa=500,ρMb=500 000,
(C2) 间接自适应鲁棒控制(IARC):与DIARC相比,控制器算法不包含快速动态补偿项,即设定γ1=γ2=0。
(C3) 确定性鲁棒控制(DRC):与DIARC相比,控制器算法不包含参数自适应及快速动态补偿项。设定控制器参数为k1=250,k2=300,h2(t)=50,η2=0.4,k3=300,h3(t)=50,η3=2。
(C4) PD控制器:设定比例增益kp=15,微分增益为kd=0.1。
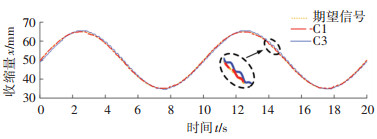
图 9给出了跟踪期望轨迹xd=15sin(0.2πt) +50时控制器C1(DIARC)和C3(DRC)的稳态响应,同时表 1给出了C1~C4的性能指标。可以看出,采用C1控制器,气动肌肉整体运动平稳,颤振几乎可以忽略,能满足一些精度要求较高场合的控制要求,而采用C3控制器,虽然系统也能达到一定控制精度,但稳态时相邻两时钟周期控制电压的平均切换量uvel远远大于C1,运行过程中出现明显颤振。
|
图 9 跟踪正弦信号的稳态响应(C1和C3) Fig. 9 Steady-state response of C1 and C3 for a simusoidal signal |
| 表 1 跟踪正弦时的控制器性能指标 Tab. 1 Tracking performance indexes for a simusoidal signal |
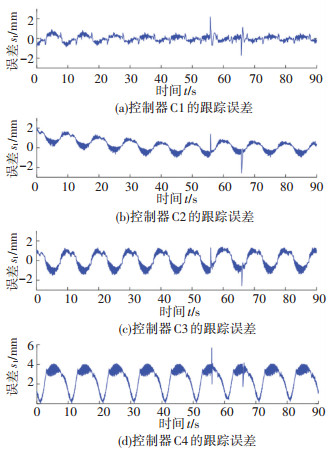
为进一步具体分析系统不确定性补偿的作用,图 10~11给出了90 s内C1~C4的跟踪误差曲线及对应输入电压曲线。结果表明所设计的控制器C1性能最好,具有良好的暂态性能和稳态性能,前40 s最大绝对跟踪误差em不超过0.94 mm,后20 s跟踪误差均方差erms不超过0.21 mm,相比传统PD控制器分别提高了77.1%和92.5%,同时也明显看出传统PD控制器(C4)精度很差,系统会出现"跟不上"的现象。图 10也表明C1和C2的稳态跟踪性能优于C3,C1和C2的erms相比C3分别提高了73.8%和48.7%,由此验证了系统参数不确定性补偿对提高控制器稳态精度有着显著作用。
|
图 10 对正弦信号的跟踪误差(C1~C4) Fig. 10 Tracking error of C1-C4 for a simusoidal signal |
|
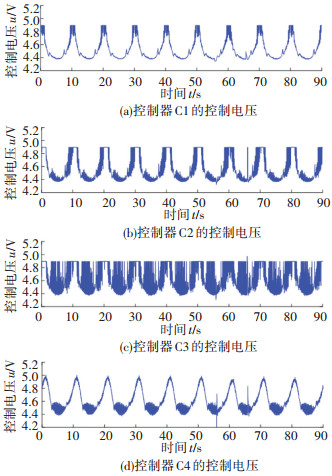
图 11 跟踪正弦信号时的控制电压(C1~C4) Fig. 11 Valve input voltages of C1-C4 for a simusoidal signal |
同时,从图 11中也可以看出,为了追求相对更好的稳态精度,C3控制器增益调节相对较大,将造成控制电压频繁切换,气动肌肉在运动过程的出现颤振。与之相比,C1和C2的颤振明显较小,尤其是C1,颤振现象几乎不存在,此时参数不确定性补偿使得系统剩余不确定性减少,从而仅需要相比C3较小的控制器参数即可获得不错的稳态精度,同时又减少了颤振。
为验证所提出控制器C1的抗干扰能力,在系统运行56 s处给位移传感器施加一个2 mm的阶跃干扰,并于66 s处撤除干扰。图 10结果表明C1控制器只在扰动信号加入和消失瞬间会产生尖峰,系统没有产生振荡或不稳定,可见所加的干扰并没有明显影响整体轨迹跟踪性能,证明了所设计的自适应鲁棒控制器继承了传统确定性鲁棒控制器的抗干扰能力。
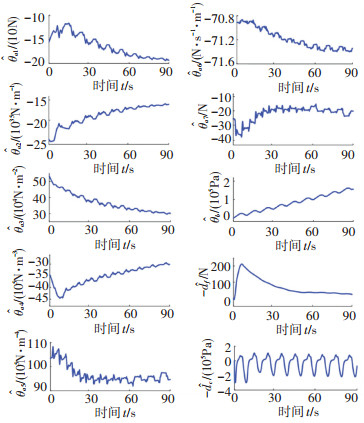
图 12给出了C1控制器系统参数的自适应结果,结果表明系统参数最终收敛到某个确定值附近或者缓慢变化,这证明了基于递归最小二乘法设计的参数在线更新算法的有效性。
|
图 12 跟踪正弦信号时的C1控制器系统参数估计 Fig. 12 Parameter estimation of C1 for a simusoidal signal |
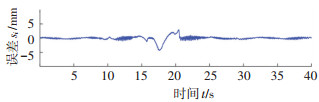
为进一步验证所设计自适应鲁棒控制器C1的有效性,测试其跟踪弦波叠加的周期信号xd=12sin(0.25πt)+12sin(0.2πt)+12sin(0.15πt)+43.5的跟踪效果,其稳态跟踪响应及去全程跟踪误差如图 13~14所示。宏观而言,系统跟踪过程中整体上运行平稳,颤振很小,能实现不同行程的轨迹跟踪控制,特别是在行程不大的工况下,稳态性能良好。但明显地,系统在行程过大的工况下,特别是在气动肌肉收缩过程(a点附近)及换向(b点附近)时,会出现较大的跟踪误差。究其原因,在大行程工况下,气动肌肉在收缩和拉伸时的输出力出现明显的差别,即迟滞现象,此时控制器无法辨别气动肌肉处于拉伸或收缩状态,参数的自适应会偏向拉伸状态下系统参数的真值,从而造成a点附近的跟踪误差较大。再者所用实验气动肌肉可用收缩量在95~120 mm之间,而系统在换向点b附近已经接近可用收缩量,此时气动肌肉的输出力特性因蠕变等因素变得更加复杂,现有模型几乎无法描述此时系统的动态,因而b点附近出现较大的跟踪误差。

|
图 13 跟踪不同行程周期信号的稳态响应(C1) Fig. 13 Steady-state response of C1 for a period signal with varying strokes |
|
图 14 跟踪周期信号的稳态跟踪误差(C1) Fig. 14 Tracking error of C1 for a period signal with varying strokes |
1) 上肢外骨骼助力机器人采用单根肌肉关节结构驱动,使得气动肌肉安装位置灵活,避免了传感器的装配干涉,降低了经济成本,释放了机器人内部空间。对普适性的单根气动肌肉关节伺服系统设计了基于反步法的直接/间接自适应鲁棒控制器,采用递归最小二乘法在线估计系统参数,补偿系统的参数不确定性,进一步由基于梯度法设计的动态快速补偿项补偿系统的参数估计误差、建模误差及外界干扰可估计部分,最后将剩余的系统不确定性通过鲁棒反馈抑制,保证了控制器具有确定的暂态响应及良好的稳态性能。
2) 对比实验表明所设计的控制器具有良好的暂态及稳态性能。跟踪不同行程的轨迹时,系统运行平稳,颤振很小,特别是跟踪幅值为15 mm正弦信号时,其暂态最大绝对跟踪误差为0.94 mm,稳态跟踪误差均方差为0.21 mm,几乎没有颤振现象。同时,干扰测试实验验证了所设计的自适应鲁棒控制器继承了传统鲁棒控制器的抗干扰能力。
3) 间接自适应鲁棒控制器稳态跟踪误差比传统鲁棒控制器提高了48.7%,证明了参数自适应具有提高稳态精度的作用,同时所设计直接/间接自适应控制器的暂态最大绝对跟踪误差与稳态跟踪误差均方差相比间接自适应鲁棒控制器分别提高了55.2%和47.5%,说明快速动态补偿项具有提高暂态性能和进一步减少稳态误差的作用。
| [1] |
OUYANG X, DING S, FAN B, et al. Development of a novel compact hydraulic power unit for the exoskeleton robot[J]. Mechatronics, 2016, 38(3): 68. |
| [2] |
YANG Y, MA L, HUANG D. Development and repetitive learning control of lower limb exoskeleton driven by electro-hydraulic actuators[J]. IEEE Transactions on Industrial Electronics, 2017, 64(5): 4169. DOI:10.1109/TIE.2016.2622665 |
| [3] |
LEE Y, KIM Y, LEE J, et al. Biomechanical design of a novel flexible exoskeleton for lower extremities[J]. IEEE/ASME Transactions on Mechatronics, 2017, 22(5): 2058. DOI:10.1109/TMECH.2017.2718999 |
| [4] |
许祥, 侯丽雅, 黄新燕, 等. 基于外骨骼的可穿戴式上肢康复机器人设计与研究[J]. 机器人, 2014, 36(02): 147. XU Xiang, HOU Liya, HUANG Xinyan, et al. Design and research of a wearable robot for upper limbs rehabilitation based on exoskeleton[J]. Robot, 2014, 36(02): 147. |
| [5] |
PARK Y, CHEN B, PÉREZ-ARANCIBIA N, et al. Design and control of a bio-inspired soft wearable robotic device for ankle-foot rehabilitation[J]. Bioinspiration & Biomimetics, 2014, 9(1). |
| [6] |
隋立明, 张立勋. 气动肌肉驱动步态康复训练外骨骼装置的研究[J]. 哈尔滨工程大学学报, 2011, 32(9): 1244. SUI Liming, ZHANG lixun. Development of an actuated exoskeleton with pneumatic muscles for gait rehabilitation training[J]. Journal of Harbin Engineering University, 2011, 32(9): 1244. |
| [7] |
BEYL P, VAN DAMME M, VAN HAM R, et al. Pleated pneumatic artificial muscle-based actuator system as a torque source for compliant lower limb exoskeletons[J]. IEEE/ASME Transactions on Mechatronics, 2014, 19(3): 1046. DOI:10.1109/TMECH.2013.2268942 |
| [8] |
杨钢, 李宝仁. 基于CMAC的气动人工肌肉变结构位置控制研究[J]. 机械工程学报, 2004, 40(10): 92. YANG Gang, LI Baoren. Pneumatic muscle variable structure position control based on CMAC[J]. Journal of Mechanical Engineering, 2004, 40(10): 92. |
| [9] |
吴军, 王永骥, 黄剑, 等. 新型可穿戴式多自由度气动上肢康复机器人[J]. 华中科技大学学报(自然科学版), 2011, 39(S2): 279. WU Jun, WANG Yongji, HUANG Jian, et al. Novel wearable multi-DOF upper limb rehabilitation robot driven by pneumatic muscle[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2011, 39(S2): 279. |
| [10] |
ANDRIKOPOULOS G, NIKOLAKOPOULOS G, MANESIS S. Advanced nonlinear PID-based antagonistic control for pneumatic muscle actuators[J]. IEEE Transactions on Industrial Electronics, 2014, 61(12): 6926. DOI:10.1109/TIE.2014.2316255 |
| [11] |
ZHAO L, CHENG H, WANG T. Sliding mode control for a two-joint coupling nonlinear system based on extended state observer[J]. ISA Transactions, 2018, 73: 130. DOI:10.1016/j.isatra.2017.12.027 |
| [12] |
LILLY J, YANG L. Sliding mode tracking for pneumatic muscle actuators in opposing pair configuration[J]. IEEE Transactions on Control Systems Technology, 2005, 13(4): 550. DOI:10.1109/TCST.2005.847333 |
| [13] |
LIN C, LIN C, YU S, et al. Hysteresis modeling and tracking control for a dual pneumatic artificial muscle system using Prandtl-Ishlinskii model[J]. Mechatronics, 2015, 28(6): 35. |
| [14] |
王斌锐, 王涛, 郭振武, 等. 气动肌肉四足机器人建模与滑模控制[J]. 机器人, 2017, 39(5): 620. WANG Binrui, WANG Tao, GUO Zhenwu, et al. Modeling and sliding mode control of quadruped robot driven by pneumatic muscles[J]. Robot, 2017, 39(5): 620. |
| [15] |
ASCHEMANN H, SCHINDELE D. Sliding-mode control of a high-speed linear axis driven by pneumatic muscle actuators[J]. IEEE Transactions on Industrial Electronics, 2008, 55(11): 3855. DOI:10.1109/TIE.2008.2003202 |
| [16] |
王杨, 张强, 肖晓晖. 基于鲁棒建模的气动人工肌肉驱动仿生关节的轨迹跟踪控制[J]. 机器人, 2016, 38(2): 248. WANG Yang, ZHANG Qiang, XIAO Xiaohui. Trajectory tracking control of the bionic joint actuated by pneumatic artificial muscle based on robust modeling[J]. Robot, 2016, 38(2): 248. |
| [17] |
鲍春雷, 王斌锐, 金英连, 等. 气动肌肉关节的无模型自适应CMAC迟滞补偿控制[J]. 机器人, 2015, 37(3): 298. BAO Chunlei, WANG Binrui, JIN Yinglian, et al. Model free adaptive CMAC hysteresis compensation control of the pneumatic muscle joint[J]. Robot, 2015, 37(3): 298. |
| [18] |
刘昱, 王涛, 范伟, 等. 气动肌肉群驱动球关节机器人的无模型自适应控制[J]. 机器人, 2013, 35(2): 129. LIU Yu, WANG Tao, FAN Wei, et al. Model-free adaptive control for the ball-joint robot driven by PMA group[J]. Robot, 2013, 35(2): 129. |
| [19] |
ZHU X, TAO G, YAO B, et al. Adaptive robust posture control of a parallel manipulator driven by pneumatic muscles[J]. Automatica, 2008, 44(9): 2248. DOI:10.1016/j.automatica.2008.01.015 |
| [20] |
RICHER E, HURMUZLU Y. A high performance pneumatic force actuator system: Part Ⅰ—nonlinear mathematical model[J]. Transactions of the ASME Journal of Dynamic Systems, Measurement, and Control, 2000, 122(3): 416. DOI:10.1115/1.1286336 |
| [21] |
MENG D, TAO G, CHEN J, et al. Modeling of a pneumatic system for high-accuracy position control[C]// International Conference on Fluid Power and Mechatronics. Beijing: IEEE, 2011: 505
|
| [22] |
YAO B, TOMIZUKA M. Adaptive robust control of MIMO nonlinear systems in semi-strict feedback forms[J]. Automatica, 2001, 37(9): 1305. DOI:10.1016/S0005-1098(01)00082-6 |
| [23] |
YAO B, JIANG C. Advanced motion control: from classical PID to nonlinear adaptive robust control[C]// IEEE international Workshop on Advanced Motion Control. Nagaoka: IEEE, 2010: 815
|
 2021, Vol. 53
2021, Vol. 53


