几何误差在整个机床生命周期中都影响着机床精度。研究表明,几何误差和热误差占机床总误差的65%[1]。因此,有必要建立可靠的误差模型用于量化各零部件误差与机床误差的影响机理,进而辨识关键误差项用于预防和补偿。几十年来,大量研究提出了三角函数模型[2]、Denavit-Hartenberg模型[3]、神经网络模型[4]、变分运动矩阵[5]、多体系统理论[6]等机床误差建模方法,然而这些建模方法只能分析各轴运动误差和整机加工误差的传递关系,无法研究零部件的制造和装配误差对单轴装配精度的影响机理。并且现阶段的机床装配时多依靠工人经验试凑,公差设计多采用一维/二维尺寸链计算法,难以有效表达几何要素的形位公差特征及其相互间的耦合关系。因此,采用属于三维公差分析的雅可比旋量模型定量描述各几何要素表达和传递几何要素在公差域的变动,该模型结合了适合公差表达的旋量模型和适合公差传递的雅克比矩阵,已应用于齿轮泵[7]和发动机[8]等装配过程,而对位置可变的机床双驱Z轴进给系统的装配过程研究较少,也没有考虑双丝杠误差的制约关系。
对误差模型进行敏感性分析能够量化各误差项对双驱Z轴装配精度的影响权重。目前的敏感性分析包括基于一阶偏导数形式[9-10]的局部敏感性分析和包含元效应方法[11]、基于方差方法[12]的全局敏感性分析。其中,基于方差的Sobol法[13-14]能够计算任意维数输入参数的敏感性系数及参数间的耦合效应的影响,同时在处理非线性等复杂模型方面具有较大的优越性,因此非常适用于机床几何误差敏感性分析并得到广泛应用[12, 15]。然而这些研究只是鉴别出各轴运动误差对整机精度的敏感性系数,没有进一步分析零部件在零部件制造和装配过程中对单轴运动误差的影响程度,而且只是根据加工条件选择一个或几个关键位置进行敏感性分析,没有对整个运动过程进行研究。
本文将雅可比旋量模型拓展到双驱Z轴装配体的误差建模,并考虑双丝杠的耦合作用和运动条件下的机床双驱Z轴误差敏感性分析。首先,利用雅可比旋量理论建立误差模型;其次,根据装配流程和几何误差的类型和约束条件,调整雅可比旋量模型以适用于双驱Z轴装配的误差建模;然后,对比仿真和实测数据验证模型的准确性;最后,采用Sobol方法求解不同位置的局部和全局敏感性系数,得到关键误差项。
1 雅可比旋量模型雅可比旋量模型包含用于描述几何公差的小位移旋量和用于公差传递计算的雅克比矩阵两部分。
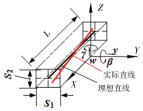
1.1 小位移旋量刚体运动产生的位移可以用3个平移分量和3个转动分量表示,当位移值为公差等级或更小时,6个运动分量构成的矢量即为小位移旋量[16](Small Displacement Torsors,SDT)。由于制造误差和装配误差相对于零件尺寸都足够小,因此可以用小位移旋量表示。其表达式为
| $ \boldsymbol{T}=\left[\begin{array}{llllll} u & v & w & \alpha & \beta & \gamma \end{array}\right]^{\mathrm{T}} $ | (1) |
式中:v、u、w分别为x、y、z方向的平移误差,α、β、γ分别为绕x、y、z轴的角度误差。
构成零件几何特征的点、线、面称为几何要素(如圆心、轴线、圆柱面等)。几何要素有多种公差特征(如平面度、直线度、圆柱度等),决定小位移旋量的参数变化范围。以直线度和平面度为例,在表 1中列出线和面几何要素的小位移旋量形式。其中,同一几何要素上可能会有2种或2种以上的组合公差约束,如导轨面的平行度和直线度。此时要根据几何要素和公差类型,将单个零件上受到多个公差约束的旋量参数进行合并。
| 表 1 两种几何要素的公差要求及其小位移旋量形式 Tab. 1 Tolerance requirements of two geometric features and corresponding SDTs |
雅克比矩阵源自于机器人运动学,用于传递各关节的位姿和速度[17]。雅克比矩阵分为2个部分,分别用于传递几何要素的平动和转动。其形式如下:
| $ [\boldsymbol{J}]_{i}=\left[\begin{array}{cc} {\left[\boldsymbol{R}_{\bf{0}}^{i}\right]_{3 \times 3}} & {\left[\boldsymbol{W}_{i}^{n}\right]_{3 \times 3} \cdot\left[\boldsymbol{R}_{0}^{i}\right]_{3 \times 3}} \\ {[0]_{3 \times 3}} & {\left[\boldsymbol{R}_{0}^{i}\right]_{3 \times 3}} \end{array}\right]_{6 \times 6} $ | (2) |
式中:R0i为第i个几何要素的局部坐标系相对于绝对坐标系之间的方向变换矩阵;Win为第n个几何要素的局部坐标系相对于第i个几何要素的局部坐标系的位置变换矩阵,即
| $ \left[\boldsymbol{W}_{i}^{n}\right]_{3 \times 3}=\left[\begin{array}{ccc} 0 & d z_{i}^{n} & -d y_{i}^{n} \\ -d z_{i}^{n} & 0 & d x_{i}^{n} \\ d y_{i}^{n} & -d x_{i}^{n} & 0 \end{array}\right] $ | (3) |
式中dxin=dxn-dxi,dyin=dyn-dyi,dzin=dzn-dzi。
利用雅可比矩阵将各个几何要素的公差转换到绝对坐标系中进行累加,得到雅可比旋量模型:
| $ [\boldsymbol{E}]=\sum\limits_{i=1}^{n}[\boldsymbol{J}]_{i}[\boldsymbol{T}]_{i} $ | (4) |
式中:T为对应几何要素公差的小位移旋量,E为目标几何要素公差的小位移旋量。
1.3 统计方法本文基于蒙特卡洛算法,将旋量中各矢量的变动和约束方程引入到雅克比旋量模型中,实现准确可靠的公差分析。算法流程有6个步骤[18]:
1) 建立雅可比旋量模型。根据装配流程建立各几何要素的局部坐标系和全局坐标系,建立各要素的雅可比矩阵,根据公差类型确定各要素的几何特征的旋量表达式。
2) 确定各旋量参数的取值范围。根据公差要求,建立各要素的旋量参数的变动区间和约束方程,并将其代入到雅可比旋量模型中。
3) 生成随机数。假设几何要素的旋量参数呈正态分布,根据第二步的旋量参数取值范围和6σ理论,计算各旋量参数的均值和标准差,并生成随机数。
4) 筛选随机数。利用约束方程筛选第三步生成的随机数,确保参与计算的随机数都符合公差要求。
5) 模型计算。将符合要求的随机数代入到雅可比旋量模型中进行计算,重复上述步骤获取大量数据。
6) 结果分析。对仿真结果进行统计分析。
以上就是雅可比旋量模型的统计分析过程。通过旋量模型的统计计算,可以定量预测装配过程中的误差变动范围,为公差分配提供参考。
2 基于雅克比旋量模型的Z轴几何误差建模以MCH63卧式加工中心的双驱Z轴为例,建立Z轴几何误差模型,研究Z轴装配过程中零部件的制造误差和装配误差对Z轴进给系统几何误差的影响机理。
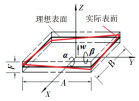
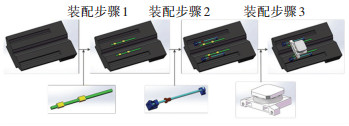
2.1 装配流程和误差辨识Z轴的误差传递过程可由图 1所示的装配流程确定,详细尺寸和公差要求列在表 2中。从图 1可知,所有零部件安装在床身上,其中导轨和轴承座安装于床身上表面。床身作为装配的基体,本身存在表 2所示的制造误差。
|
图 1 双驱Z轴的装配流程 Fig. 1 Assembly process of dual-drive z-axis |
| 表 2 Z轴进给系统的主要参数 Tab. 2 Major parameters of z-axis feed system |
根据Z轴装配过程,可以看到误差存在"床身-滑块"和"床身-螺母"2条传递路径,然后通过安装工作台进行耦合。因此,将误差传递分成3个部分——2个误差子链(导轨-滑块子链和丝杠-螺母子链)及其在工作台处的耦合。其装配实体图和误差传递路径如图 2和图 3所示。

|
图 2 双驱Z轴进给系统结构 Fig. 2 Configuration of dual-drive z-axis feed system |
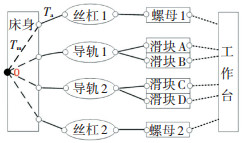
|
图 3 双驱Z轴的误差传递示意图 Fig. 3 Schematic of error transfer of dual-drive z-axis |
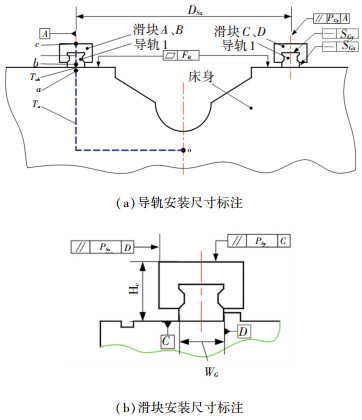
根据图 3,该部件存在4个误差传递链,对应4个滑块。以滑块A的误差传递过程为例,其他3个滑块的分析过程类似。导轨-滑块子链的误差源有FB、SGx、SGy、PRx和PRy,具体含义见表 2和图 4。图 4(a)中,符号o、a、b、c分别表示床身的基准位置、床身上的导轨安装面、导轨1的安装面和滑块A的安装面,对应的雅可比矩阵为Ja、Jab、Jc。为了计算方便,局部坐标系建立在各几何要素的中心。根据各零件的具体尺寸可以建立该子装配链误差传递的雅克比矩阵JA,见式(5)。
|
图 4 导轨滑块装配链的尺寸标注 Fig. 4 Dimensions of guide-slide subassembly |
根据各种公差类型的小位移旋量表达式和对应的公差值,可以计算出几何要素的误差变动范围,表 3详细列出了有关旋量及其约束。其中,导轨面受直线度和平行度公差的共同约束,而形状公差的公差带一般要小于方向公差,且此例中的平行度和直线度的公差带均为两平行平面所限定的区域。所以,满足直线度的变量区间也适用于平行度的变量区间。
| 表 3 导轨滑块装配链的误差源约束方程及偏差范围 Tab. 3 Variations and constraints of error source of guide-slide subassembly |
将雅可比矩阵J_A和表 3中对应的旋量代入公式(4),可推导出由装配链上的各几何要素公差表示的滑块A上工作台安装面的公差要求,见式(6)。同理可得滑块B、C、D的公差要求。
| $ \begin{array}{l} {\mathit{\boldsymbol{J}}_A} = \left[ {{{\left[ {\begin{array}{*{20}{c}} 1&0&0&0&{z + \frac{{{D_{Rz}}}}{2}}&{ - {H_G}}\\ 0&1&0&{ - z - \frac{{{D_{Rz}}}}{2}}&0&{ - \frac{{{D_{Rx}}}}{2}}\\ 0&0&1&{{H_G}}&{\frac{{{D_{Rx}}}}{2}}&0\\ 0&0&0&1&0&0\\ 0&0&0&0&1&0\\ 0&0&0&0&0&1 \end{array}} \right]}_a}{{\left[ {\begin{array}{*{20}{c}} 1&0&0&0&{z + \frac{{{D_{Rz}}}}{2}}&{ - {H_G}}\\ 0&1&0&{ - z - \frac{{{D_{Rz}}}}{2}}&0&{ - \frac{{{D_{Rx}}}}{2}}\\ 0&0&1&{{H_G}}&{\frac{{{D_{Rx}}}}{2}}&0\\ 0&0&0&1&0&0\\ 0&0&0&0&1&0\\ 0&0&0&0&0&1 \end{array}} \right]}_{ab}}} \right.\\ \left. {{{\left[ {\begin{array}{*{20}{c}} 1&0&0&0&{z + \frac{{{D_{Rz}}}}{2}}&0\\ 0&1&0&{ - z - \frac{{{D_{Rz}}}}{2}}&0&0\\ 0&0&1&0&0&0\\ 0&0&0&1&0&0\\ 0&0&0&0&1&0\\ 0&0&0&0&0&1 \end{array}} \right]}_c}} \right] \end{array} $ | (5) |
| $ \boldsymbol{E}_{A}=\left[\begin{array}{c} u_{A} \\ v_{A} \\ w_{A} \\ \alpha_{A} \\ \beta_{A} \\ \gamma_{A} \end{array}\right]=\left[\begin{array}{c} u_{a b}+u_{c}-\gamma_{a} H_{G}+\beta_{c}\left(z+D_{R z} / 2\right)+\beta_{a b}\left(z+D_{R z} / 2\right) \\ v_{a}+v_{a b}+v_{c}-\gamma_{a} D_{R x} / 2-\left(\alpha_{a}+\alpha_{a b}+\alpha_{c}\right)\left(z+D_{R z} / 2\right) \\ \beta_{a b} D_{R z} / 2+\alpha_{a} H_{G}+\alpha_{a b} H_{G} \\ \alpha_{a}+\alpha_{a b}+\alpha_{c} \\ \beta_{a b}+\beta_{c} \\ \gamma_{a} \end{array}\right] $ | (6) |
在Z轴装配的误差链中,滚珠丝杠部件的误差传递不同于导轨滑块部件,但依然可以用雅克比旋量理论进行误差子链的建模。
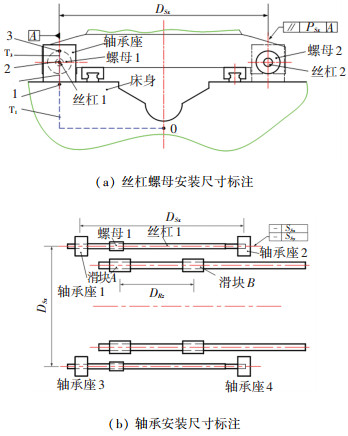
根据图 1的装配流程,丝杠通过轴端的两组轴承安装在床身上,其误差传递路径如图 5所示。图 5中,代号0、1、2、3分别表示床身的基准位置、床身上的轴承座安装面、丝杠1的轴承安装面和螺母1的工作台安装面,对应的雅可比矩阵为J1、J12、J3。根据各零件尺寸可以建立该子装配链的误差传递的雅克比矩阵JN1,见式(7)。
|
图 5 丝杠螺母装配链的尺寸标注 Fig. 5 Dimensions of ball screw subassembly |
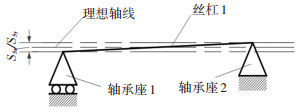
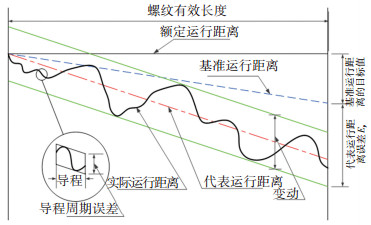
装配过程误差包括床身、轴承、丝杠、螺母的误差:床身的制造误差对丝杠有一定影响;由于支撑轴承的同轴度不可能完全一致,丝杆在安装过程中存在图 6中的X向和Y向的直线度误差;丝杠的导程精度也是影响工作台运动精度的重要原因,一般选择代表运行距离误差EP进行研究,如图 7所示。
|
图 6 丝杠安装的直线度要求 Fig. 6 Straightness of ball screw in axis assembly |
|
图 7 丝杠导程误差的累积效应 Fig. 7 Illustration of cumulative lead error of ball screw |
根据上述误差的定义和取值,可以确定各几何要素的小位移旋量,见式(8)。将雅可比矩阵JN1和式(8)中对应的旋量代入公式(4),可得到螺母1的工作台安装面的公差要求,该误差子链的雅可比旋量模型为式(9)。
| $ \begin{array}{l} {\mathit{\boldsymbol{J}}_{N1}} = \left[ {{{\left[ {\begin{array}{*{20}{c}} 1&0&0&0&{z + \frac{{{D_{Rz}}}}{2}}&{ - {H_{Sy}}}\\ 0&1&0&{ - z - \frac{{{D_{Rz}}}}{2}}&0&{ - \frac{{{D_{Sx}}}}{2}}\\ 0&0&1&{{H_{Sy}}}&{\frac{{{D_{Sx}}}}{2}}&0\\ 0&0&0&1&0&0\\ 0&0&0&0&1&0\\ 0&0&0&0&0&1 \end{array}} \right]}_a}{{\left[ {\begin{array}{*{20}{c}} 1&0&0&0&{z + \frac{{{D_{Rz}}}}{2}}&{ - {H_{Sy}}}\\ 0&1&0&{ - z - \frac{{{D_{Rz}}}}{2}}&0&{ - \frac{{{D_{Sx}}}}{2}}\\ 0&0&1&{{H_{Sy}}}&{\frac{{{D_{Sx}}}}{2}}&0\\ 0&0&0&1&0&0\\ 0&0&0&0&1&0\\ 0&0&0&0&0&1 \end{array}} \right]}_{ab}}} \right.\\ \left. {{{\left[ {\begin{array}{*{20}{c}} 1&0&0&0&{z + \frac{{{D_{Rz}}}}{2}}&0\\ 0&1&0&{ - z - \frac{{{D_{Rz}}}}{2}}&0&0\\ 0&0&1&0&0&0\\ 0&0&0&1&0&0\\ 0&0&0&0&1&0\\ 0&0&0&0&0&1 \end{array}} \right]}_c}} \right] \end{array} $ | (7) |
| $ {\mathit{\boldsymbol{T}}_1} = \left[ {\begin{array}{*{20}{c}} 0\\ {{v_1}}\\ 0\\ {{\alpha _1}}\\ 0\\ {{\gamma _1}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0\\ {\left( { - \frac{{{F_B}}}{2},\frac{{{F_B}}}{2}} \right)}\\ 0\\ {\left( { - \frac{{{F_B}}}{{{L_B}}},\frac{{{F_B}}}{{{L_B}}}} \right)}\\ 0\\ {\left( { - \frac{{{F_B}}}{{{W_B}}},\frac{{{F_B}}}{{{W_B}}}} \right)} \end{array}} \right],{\mathit{\boldsymbol{T}}_{12}} = \left[ {\begin{array}{*{20}{c}} {{u_{12}}}\\ {{v_{12}}}\\ 0\\ {{\alpha _{12}}}\\ {{\beta _{12}}}\\ 0 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\left( { - \frac{{{S_{Sx}}}}{2},\frac{{{S_{Sx}}}}{2}} \right)}\\ {\begin{array}{*{20}{c}} {\left( { - \frac{{{S_{Sy}}}}{2},\frac{{{S_{Sy}}}}{2}} \right)}\\ 0\\ {\left( { - \frac{{{S_{Sy}}}}{{{D_{Sz}}}},\frac{{{S_{Sy}}}}{{{D_{Sz}}}}} \right)} \end{array}} \\ {\begin{array}{*{20}{c}} {\left( { - \frac{{{S_{Sx}}}}{{{D_{Sz}}}},\frac{{{S_{Sx}}}}{{{D_{Sz}}}}} \right)}\\ 0 \end{array}} \end{array}} \right],\\{\mathit{\boldsymbol{T}}_3} = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ {{w_3}}\\ 0\\ 0\\ 0 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ {\left( { - \frac{{ - z + {L_H}/2}}{{{L_H}}}\frac{{{E_p}}}{2},\frac{{ - z + {L_H}/2}}{{{L_H}}}\frac{{{E_p}}}{2}} \right)}\\ 0\\ 0\\ 0 \end{array}} \right] $ | (8) |
| $ \boldsymbol{E}_{N 1}=\left[\begin{array}{c} u_{N 1} \\ v_{N 1} \\ w_{N 1} \\ \alpha_{N 1} \\ \beta_{N 1} \\ \gamma_{N 1} \end{array}\right]=\left[\begin{array}{c} u_{12}-\gamma_{1} D_{S y}+\beta_{12}\left(z+D_{R z} / 2\right) \\ v_{1}+v_{12}-\gamma_{1} D_{S x} / 2-\alpha_{1}\left(z+D_{R z} / 2\right)-\alpha_{12}\left(z+D_{R z} / 2\right) \\ w_{3}+\beta_{12} D_{S z} / 2+\alpha_{1} D_{S y}+\alpha_{12} D_{S y} \\ \alpha_{1}+\alpha_{12} \\ \beta_{12} \\ \gamma_{1} \end{array}\right] $ | (9) |
工作台通过4个滑块和2个螺母与导轨和丝杠连接。所有误差子链通过安装工作台进行耦合,则工作台各个位置的误差可以用6个连接支点的变动表示,如图 8所示。

|
图 8 误差子链的误差耦合 Fig. 8 Error synthesis of all error subchains |
以4个滑块的对称中心为工作台的参考点。基于前面的分析,进给方向上导轨滑块无约束,丝杠的螺距误差为主要影响因素,需与滑块误差分别取均值相加,工作台的平移误差可以表示为
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{u_P}}\\ {{v_P}}\\ {{w_P}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{1}{4}\left( {{u_B} + {u_D} + \frac{1}{2}\left( {{u_A} + {u_C} + {u_{N1}} + {u_{N2}}} \right)} \right)}\\ {\frac{1}{4}\left( {{v_B} + {v_D} + \frac{1}{2}\left( {{v_A} + {v_C} + {v_{N1}} + {v_{N2}}} \right)} \right)}\\ {\frac{1}{2}\left( {{w_{N1}} + {w_{N2}}} \right) + \frac{1}{4}\left( {{w_A} + {w_C} + {w_B} + {w_D}} \right)} \end{array}} \right] = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {\frac{{{u_{12}} + 3{u_{ab}} + 3{u_c}}}{4} + \frac{{{D_{Rz}}\left( {{\beta _{12}} - {\beta _{ab}} - {\beta _c}} \right) - 2{D_{Sy}}{\gamma _1} - 6{H_G}{\gamma _a}}}{8} + \frac{{z\left( {{\beta _{12}} + 3{\beta _{ab}} + 3{\beta _c}} \right)}}{4}}\\ {\frac{{{v_1} + {v_{12}} + 3{v_a} + 3{v_{ab}} + 3{v_c}}}{4} - \frac{{{D_{Rz}}\left( {{\alpha _1} + {\alpha _{12}} - {\alpha _a} - {\alpha _{ab}} - {\alpha _c}} \right)}}{8} - \frac{{z\left( {{\alpha _1} + {\alpha _{12}} + 3{\alpha _a} + 3{\alpha _{ab}} + 3{\alpha _c}} \right)}}{4}}\\ {{w_3} + {D_{Sy}}{\alpha _1} + {D_{Sy}}{\alpha _{12}} + {H_G}{\alpha _a} + {H_G}{\alpha _{ab}}} \end{array}} \right] \end{array} $ | (10) |
式中,[uk vk wk]T, k=A, B, C, D, N1, N2为滑块和螺母的平移误差。
工作台的转动误差可以由滑块和螺母的相互位置关系求出:
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{\alpha _P}}\\ {{\beta _P}}\\ {{\gamma _P}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{1}{4}\left( {\frac{{2{v_B} + 2{v_D} - {v_A} - {v_C} - {v_{N1}} - {v_{N2}}}}{{{D_{Rz}}}}} \right)}\\ {\frac{1}{4}\left( {\frac{{{u_C} - {u_D}}}{{{D_{Rz}}}} + \frac{{{w_B} - {w_D}}}{{{D_{Rx}}}} + \frac{{{u_A} - {u_B}}}{{{D_{Rz}}}} + \frac{1}{2}\left( {\frac{{{w_A} - {w_C}}}{{{D_{Rx}}}} + \frac{{{w_{N1}} - {w_{N2}}}}{{{D_{Sx}}}}} \right)} \right)}\\ {\frac{1}{4}\left( {\frac{{{v_C} + 2{v_D} - {v_A} - 2{v_B}}}{{{D_{Rx}}}} + \frac{{{v_{N2}} - {v_{N1}}}}{{{D_{Sx}}}}} \right)} \end{array}} \right] = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {\frac{{{\alpha _1} + {\alpha _{12}} + 3{\alpha _a} + 3{\alpha _{ab}} + 3{\alpha _c}}}{4} - \frac{{{v_1} + {v_{12}} - {v_a} - {v_{ab}} - {v_c}}}{{2{D_{Rz}}}} + \frac{{z\left( {{\alpha _1} + {\alpha _{12}} - {\alpha _a} - {\alpha _{ab}} - {\alpha _c}} \right)}}{{2{D_{Rz}}}}}\\ {\frac{{{\beta _{12}}}}{8} + \frac{{7{\beta _{ab}}}}{8} + \frac{{{\beta _c}}}{2}}\\ {\frac{{{\gamma _1}}}{4} + \frac{{3{\gamma _a}}}{4}} \end{array}} \right] \end{array} $ | (11) |
至此,最终装配功能需求与丝杠螺母副和导轨滑块副的几何要素要求相关联。
3 几何误差模型的有效性验证为了验证雅可比旋量模型的准确性,在此模型的基础上,通过仿真得到最终误差的变化范围。同时,根据国家标准GB/T 20957,需要在机床验收前测量轴向的定位误差。因此,选择Z轴定位误差用于比较基于雅克比旋量的几何误差模型的仿真数据和实际测量数据。此处以南通机床厂生产的10台同类型卧式加工中心的定位误差为参照。
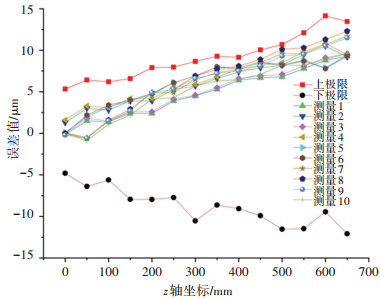
Z轴定位误差的实测数据和仿真数据极值结果列于图 9。从图中可以看到:所有实测误差数据均在仿真数据区间内,且误差变动趋势相同,模型预测较准确;在坐标值较小时,丝杠的螺距误差较小,角度误差对工作定位误差的影响较大,而仿真与实测数据相差较大,说明螺距误差为影响定位误差的主要因素。测量结果表明雅可比旋量法用于误差分析的实用性,该模型也可以定量地描述机床零部件误差在装配过程中的传递方式。
|
图 9 定位误差的仿真与测量结果对比 Fig. 9 Comparison of simulation and measurement data of the positioning error |
机床工作台的运动精度受到零部件几何误差耦合而成的空间误差的影响,每一项误差对运动精度影响程度不同。为了确定各个误差元素对运动精度的影响程度,采用Sobol方法进行几何误差敏感性分析。采用Sobol法进行几何误差敏感性分析的基本流程为:
1) 构造一个与实际问题或系统相对应的数学模型,数学模型是实现敏感性系数计算的必要基础;
2) 明确各输入变量的定义域区间,可通过几何误差测量及合理缩放得到;
3) 对输入变量的定义域空间进行采样,并生成相应的采样矩阵;
4) 利用MATLAB软件进行仿真分析及计算,便可求得敏感性系数。
4.1 基于误差模型的公式推导首先,利用雅可比旋量模型,最终装配体的6个误差分量可以用各零部件几何要素的公差要求进行表示。具体公式如下:
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{u_P}}\\ {{v_P}}\\ {{w_P}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{{{u_{12}} + 3{u_{ab}} + 3{u_c}}}{4} + \frac{{{D_{Rz}}\left( {{\beta _{12}} - {\beta _c} - {\beta _{ab}}} \right) - 2{D_{Sy}}{\gamma _1} - 6{H_G}{\gamma _a}}}{8} + \frac{{z\left( {{\beta _{12}} + 3{\beta _c} + 3{\beta _{ab}}} \right)}}{4}}\\ {\frac{{{v_1} + {v_{12}} + 3{v_a} + 3{v_{ab}} + 3{v_c}}}{4} - \frac{{{D_{Rz}}\left( {{\alpha _1} + {\alpha _{12}} - {\alpha _a} - {\alpha _{ab}} - {\alpha _c}} \right)}}{8} - \frac{{z\left( {{\alpha _1} + {\alpha _{12}} + 3{\alpha _a} + 3{\alpha _{ab}} + 3{\alpha _c}} \right)}}{4}}\\ {{w_3} + {D_{Sy}}{\alpha _1} + {D_{Sy}}{\alpha _{12}} + {H_G}{\alpha _a} + {H_G}{\alpha _{ab}}} \end{array}} \right] = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {\frac{{927 + z}}{{5\;080}}{S_{Sx}} + \frac{{2\;183 + 3z}}{{6\;600}}{S_{Gx}} + \frac{{1\;958 + 3z}}{{6\;000}}{P_{Rx}} - \frac{{61}}{{960}}{F_B}}\\ {\frac{{343 - z}}{{5\;080}}{S_{Sy}} + \frac{{2767 - 3z}}{{6\;600}}{S_{Gy}} + \frac{{2\;542 - 3z}}{{6\;000}}{P_{Ry}} + \frac{{1\;000 + z}}{{2\;000}}{F_B}}\\ {\frac{{19}}{{254}}{S_{Sy}} + \frac{7}{{165}}{S_{Gy}} + \frac{{500 - z}}{{2\;000}}{E_p} + \frac{{33}}{{400}}{F_B}} \end{array}} \right] \end{array} $ | (12) |
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{\alpha _P}}\\ {{\beta _P}}\\ {{\gamma _P}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{{{\alpha _1} + {\alpha _{12}} + 3{\alpha _a} + 3{\alpha _{ab}} + 3{\alpha _c}}}{4} - \frac{{{v_1} + {v_{12}} - {v_a} - {v_{ab}} - {v_c}}}{{2{D_{Rz}}}} + \frac{{z\left( {{\alpha _1} + {\alpha _{12}} - {\alpha _a} - {\alpha _{ab}} - {\alpha _c}} \right)}}{{2{D_{Rz}}}}}\\ {{\beta _{12}} + {\beta _{ab}} + \frac{{{\beta _c}}}{2}}\\ {\frac{{{\gamma _1}}}{4} + \frac{{3{\gamma _a}}}{4}} \end{array}} \right] = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {\frac{{ - 343 + z}}{{1\;483\;360}}{S_{Sy}} + \frac{{1\;117 - z}}{{1\;927\;200}}{S_{Cy}} + \frac{{1\;042 - z}}{{1\;752\;000}}{P_{Ry}} + \frac{1}{{4\;000}}{F_B}}\\ {\frac{1}{{1\;270}}{S_{Sx}} + \frac{1}{{1\;650}}{S_{Gx}} + \frac{1}{{3\;000}}{P_{Rx}}}\\ {\frac{1}{{1\;200}}{F_B}} \end{array}} \right] \end{array} $ | (13) |
式中各参数含义见表 2,其中螺距误差变量Ep的变动范围定为[-0.02 mm, 0.02 mm],其他变量的变动范围为[-0.01 mm, 0.01 mm]。则进给系统综合误差的标量形式为
| $ E_{\mathrm{tot}}=\sqrt{u_{P}{ }^{2}+v_{P}{ }^{2}+w_{P}{ }^{2}} $ | (14) |
根据误差模型参数个数进行蒙特卡洛采样,生成2个相互独立的k×n采样矩阵A和B,其中k为采样个数,n为误差参数个数。再建立2个矩阵AB(j)和BA(j),分别以矩阵A和B为主体,只将第j列元素替换为矩阵B和A的第j列元素。选取不同列数j, 代入以下公式[13-14]即可计算各个误差元素的局部敏感性系数
| $ \hat{E}=\frac{1}{k} \sum\limits_{i=1}^{k} f(A)_{i} $ | (15) |
| $ \hat{V}=\frac{1}{k} \sum\limits_{i=1}^{k} f(A)_{i}^{2}-\left[\frac{1}{k} \sum\limits_{i=1}^{k} f(A)_{i}\right]^{2} $ | (16) |
| $ \hat{V}_{j}=\frac{1}{k} \sum\limits_{i=1}^{k} f(A)_{i}\left(f\left(B_{A}^{(j)}\right)_{i}-f(B)_{i}\right) $ | (17) |
| $ \hat{V}_{T_{j}}=\frac{1}{2 k} \sum\limits_{i=1}^{k}\left(f(A)_{i}-f\left(A_{B}^{(j)}\right)_{i}\right)^{2} $ | (18) |
式中: i代表相应采样矩阵的第i行,
| $ \hat{S}_{j}=\frac{\hat{V}_{j}}{\hat{V}} $ | (19) |
| $ \hat{S}_{T{j}}=\frac{\hat{V}_{T{j}}}{\hat{V}} $ | (20) |
由进给系统的配置参数可知,Z轴的最大有效行程为650 mm,以50 mm为间隔选取14个位置进行敏感性分析。各位置的误差项对综合误差的敏感性系数如图 10所示,图中实线空心点代表局部敏感性系数,虚线实心点代表全局敏感性系数。

|
图 10 Z轴变化时各误差项对综合误差的局部和全局敏感性系数 Fig. 10 Local and global sensitivity indexes of each geometric error source for comprehensive error with varying z-axis |
从图中可以看出:
1) 由于丝杠导程误差的累积效应,代表运行距离误差Ep的局部和全局敏感性系数随着运行距离的增加而同步增大,并在300 mm之后成为主要误差源。说明丝杠导程误差对工作台综合误差的影响是动态的,需要根据加工位置进行补偿。
2) 床身平面度FB的敏感性系数在原点处最大且随着位置的增加而减小,其中全局敏感性系数的降幅远大于局部敏感性系数。说明在坐标原点即安装定位基准附近,平面度对综合误差的影响较大,由于床身是其他部件的安装基座,所以由平面度导致的误差项间的耦合效应较大。
3) 导轨Y向的直线度SGy和运行平行度PRy的敏感性系数不随位置变化,其中全局敏感性系数远大于局部敏感性系数。说明单个导轨对工作台综合误差的影响程度较小,但安装到工作台后,导轨的Y向误差通过误差项间的耦合效应对工作台综合误差产生了较大影响。
4) 其他误差项的敏感性系数基本都小于0.1,随着位置的增加而减小并在300 mm之后趋近于0,只有丝杠Y向的直线度的敏感性系数有小幅度增加。这是由于双驱进给系统结构的对称性,导轨和丝杠在X方向上的误差传递到工作台时会有一定程度的抵消,从而降低X向误差项的敏感性系数。
5 结论1) 在明确双驱进给系统装配流程的基础上,将雅可比旋量模型应用于Z轴装配的误差传递过程。合并平行度和直线度的公差带区域,确定多种公差约束下的旋量表达式及其变量范围。对比基于雅可比旋量模型的仿真结果与相似条件下的实测数据,验证了误差模型的准确性和适用性。
2) 根据误差模型,采用Sobol方法进行了进给系统的几何误差敏感性分析,量化各误差项对进给系统运动误差的影响权重,确定了Ep、FB、SGy、PRy是对进给系统运动空间范围内的运动精度有重要影响的几何误差项。其中Ep、FB的敏感性系数在运动过程中会发生变化,需要根据实际加工位置进行动态误差防止和误差补偿。
3) 几何误差敏感性分析不但能够为进给系统在精密设计、制造、装配调试过程中的几何误差指标分配和几何误差精度优化提供理论依据,而且能够在误差补偿阶段明确误差补偿顺序的优先权。根据敏感性分析结果对重要敏感误差项进行有针对性的补偿和修正可快速地降低重要敏感误差项对运动精度的影响,可有效地提高进给系统的运动精度。
| [1] |
SHEN Hongyao, FU Jianzhong, HE Yong, et al. On-line asynchronous compensation methods for static/quasi-static error implemented on CNC machine tools[J]. International Journal of Machine Tools and Manufacture, 2012, 60: 14. DOI:10.1016/j.ijmachtools.2012.04.003 |
| [2] |
FRENCH D, HUMPHRIES S H. Compensation for the backlash and alignment errors in a numerically controlled machine tool by a digital computer programme[J]. Advances in Machine Tool Design & Research, 1967, 8: 707. |
| [3] |
LAMIKIZ A, LÓPEZ DE LACALLE L N, OCERIN O, et al. The Denavit and Hartenberg approach applied to evaluate the consequences in the tool tip position of geometrical errors in five-axis milling centres[J]. The International Journal of Advanced Manufacturing Technology, 2008, 37(1/2): 122. DOI:10.1007/s00170-007-0956-5 |
| [4] |
谢春, 张为民. 车铣复合加工中心综合误差检测及补偿策略[J]. 光学精密工程, 2014, 22(4): 1004. XIE Chun, ZHANG Weimin. Comprehensive measurement errors of 5-axis turning-milling centers and their compensation strategies[J]. Editorial Office of Optics and Precision Engineering, 2014, 22(4): 1004. |
| [5] |
FERREIRA P M, LIU C R. An analytical quadratic model for the geometric error of a machine tool[J]. Journal of Manufacturing Systems, 1986, 5(1): 51. DOI:10.1016/0278-6125(86)90067-1 |
| [6] |
WU Changjun, FAN Jinwei, WANG Qiaohua, et al. Machining accuracy improvement of non-orthogonal five-axis machine tools by a new iterative compensation methodology based on the relative motion constraint equation[J]. International Journal of Machine Tools and Manufacture, 2018, 124: 80. DOI:10.1016/j.ijmachtools.2017.07.008 |
| [7] |
张为民, 陈灿, 李鹏忠, 等. 基于雅可比旋量法的实际工况公差建模[J]. 计算机集成制造系统, 2011, 17(1): 77. ZHANG Weimin, CHEN Can, LI Pengzhong, et al. Tolerance modeling in actual working condition based on Jacobian-Torsor theory[J]. Computer Integrated Manufacturing Systems, 2011, 17(1): 77. |
| [8] |
CHEN Hua, JIN Sun, LI Zhimin, et al. A modified method of the unified Jacobian-Torsor model for tolerance analysis and allocation[J]. International Journal of Precision Engineering and Manufacturing, 2015, 16(8): 1789. DOI:10.1007/s12541-015-0234-7 |
| [9] |
LI JIE, XIE FUGUI, LIU Xinjun. Geometric error modeling and sensitivity analysis of a five-axis machine tool[J]. The International Journal of Advanced Manufacturing Technology, 2016, 82(9/10/11/12): 2037. |
| [10] |
ZHONG Xuemin, LIU Hongqi, MAO Xinyong, et al. An optimal method for improving volumetric error compensation in machine tools based on squareness error identification[J]. International Journal of Precision Engineering and Manufacturing, 2019, 20(10): 1653. DOI:10.1007/s12541-019-00191-0 |
| [11] |
MIRO S, HARTMANN D, SCHANZ T. Global sensitivity analysis for subsoil parameter estimation in mechanized tunneling[J]. Computers and Geotechnics, 2014, 56: 80. DOI:10.1016/j.compgeo.2013.11.003 |
| [12] |
ZOU Xicong, ZHAO Xuesen, LI Guo, et al. Sensitivity analysis using a variance-based method for a three-axis diamond turning machine[J]. The International Journal of Advanced Manufacturing Technology, 2017, 92(9/10/11/12): 4429. |
| [13] |
SOBOL I M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates[J]. Mathematics and Computers in Simulation, 2001, 55(1): 271. |
| [14] |
SOBOL I M, TARANTOLA S, GATELLI D, et al. Estimating the approximation error when fixing unessential factors in global sensitivity analysis[J]. Reliability Engineering & System Safety, 2007, 92(7): 957. |
| [15] |
CHENG Qiang, ZHAO Hongwei, ZHANG Guojun, et al. An analytical approach for crucial geometric errors identification of multi-axis machine tool based on global sensitivity analysis[J]. The International Journal of Advanced Manufacturing Technology, 2014, 75(1/2/3/4): 107. DOI:10.1007/s00170-014-6133-8 |
| [16] |
吴兆强. 基于小位移旋量的公差模拟建模及公差分析[J]. 机械设计与制造, 2010(1): 205. WU Zhaoqiang. Stimulated tolerances modeling based on small displacement torsors and tolerances analysis[J]. Machinery Design & Manufacture, 2010(1): 205. DOI:10.3969/j.issn.1001-3997.2010.01.087 |
| [17] |
蒋志宏. 机器人学基础[M]. 北京: 北京理工大学出版社, 2018: 43. JIANG Zhihong. Fundamentals of robotics[M]. Beijing: Beijing Institute of Technology Press, 2018: 43. |
| [18] |
陈华. 基于雅克比旋量模型的三维公差分析方法研究及在发动机装配中的应用[D]. 上海: 上海交通大学, 2015 CHEN Hua. Study on three dimensional tolerance analysis method based on Jacobian-Torsor Model and its application in engine assembly[D]. Shanghai: Shanghai Jiao Tong University, 2015 |
 2021, Vol. 53
2021, Vol. 53