薄壁球壳是航空、船舶、车辆和建筑等工业领域的一种重要结构,由于其在受到环境激励后易发生振动和噪声问题,直接影响工业装备的稳定性和工作可靠性,因此对球壳的有效减振成为工业生产中一个亟待解决的问题。应用于板梁和柱壳结构的约束阻尼减振也是球壳的一种主要减振方法,但是由于球壳结构的变形更加复杂,所以球壳的局部约束阻尼减振仍有待深入研究。
针对球壳应用中减振问题,许多学者进行了深入探索。Aleksandr K等[1]利用能量法和有限元法建立了锯齿形阻尼夹层旋转壳体的自由振动模型,分析了圆柱、锥形和球形夹层壳的振动特性,并证明了该方法的准确性。Panda S K等[2]基于有限元法和高阶剪切变形理论,建立了Green-Lagrange意义上的层合扁球壳的几何非线性模型,采用直接迭代法对系统进行了求解,分析了不同参数对等温载荷作用下球壳系统自由振动特性的影响。Ye T G等[3]提出一种求解层合旋转壳体的通用Chebyshev-Ritz公式,通过与试验的比较,验证了该公式的收敛性和准确性,并对不同曲率和任意约束条件下的圆柱、圆锥和球面壳体振动问题进行了研究。Gong Q T等[4]基于Ritz法和一阶剪切变形理论建立了功能梯度球壳模型的动力学模型,采用Jacobi多项式和Fourier级数表示位移函数,分析了各种复杂边界下截球壳的振动特性。Biswal D K[5]基于一阶剪切变形理论,利用哈密顿原理和有限元方法建立了5层夹层球壳的动力学模型,研究了约束层厚度、芯层厚度、粘弹性材料损耗因子和长径比对结构固有频率和系统损耗因子的影响。
但是目前主要针对球壳被动减振问题进行的研究,为了增加减振的有效性,利用压电材料的球壳主动振动控制也被广泛关注。Mao Y Q等[6]基于Talreja张量损伤模型和几何非线性理论推演了具有损伤厚扁球壳的本构关系,建立了考虑损伤效应的压电层合薄球壳的动力学模型,并综合运用正交点位配置法和Newmark法对整个问题进行了求解,分析了损伤、压电效应和结构几何参数对扁球壳动态响应和振动控制的影响。Wang J J等[7]提出了一种简化的环氧树脂包覆径向极化压电陶瓷球壳理论模型,研究了谐波激励作用下单侧半球形压电陶瓷的动态特性。杨颖等[8]利用最优有界参数控制策略对介电弹性体球壳在冲击载荷作用下的振动进行了控制,研究表明该方法具有较好的控制效果及较高的鲁棒性。
虽然球壳的动力学特性已有很多学者进行了研究,一些减振控制方法也被应用于球壳的振动控制中,但是由于球壳结构的复杂性,一些理论成果主要针对被动、全敷设球壳,对于局部敷设主动约束阻尼的球壳振动特性的研究还不够深入。因此本文针对开球壳采用局部主动约束阻尼结构,研究建立和求解该结构动力学模型的有效方法,分析局部主动约束阻尼结构参数变化对球壳振动特性的影响,研究压电层激励电压对球壳振动影响的一般规律。
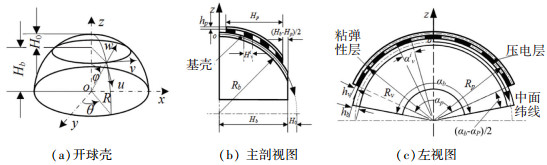
1 局部主动约束阻尼开球壳模型局部主动约束阻尼开球壳结构如图 1所示。主要由压电约束层、粘弹性层和基壳组成,约束层阻尼结构沿坐标系φ和θ方向敷设于基壳中部,粘弹性层等间距均匀设置于约束层和基壳之间。距球顶H0处截取半径为Rb、高度为Hb的球壳为研究对象,αb、αv和αp分别为基壳、粘弹性层和压电层沿θ向角度,Hv和hp分别为粘弹性层和压电层竖向的敷设高度,与坐标φ对应,hb、hv和hp为基层、粘弹性层和压电层厚度,下标b、v和p分别表示基层、粘弹性层和压电层。
|
图 1 局部主动约束阻尼球壳结构 Fig. 1 Spherical shell structure with local ACLD |
根据一阶剪切变形理论,球壳位移场可表示为
| $ \left\{\begin{array}{l} u_{i}(\varphi, \theta, z, t)=u_{0 i}(\varphi, \theta, t)+z_{0 i} \lambda_{i}(\varphi, \theta, t) \\ v_{i}(\varphi, \theta, z, t)=v_{0 i}(\varphi, \theta, t)+z_{0 i} \gamma_{i}(\varphi, \theta, t) \\ w(\varphi, \theta, z, t)=w_{0 i}(\varphi, \theta, t) \end{array}\right. $ | (1) |
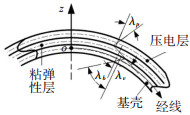
其中u是球壳经线方向上位移,对应角变量φ;角变量θ对应球壳纬线方向上的位移为v,径向z轴对应的位移为w,z0表示距离坐标原点o的距离,u0、v0和w0为中面上点对应的位移矢量。λ和γ是绕纬线方向和经线方向的转角,i=b、v、p,各层绕经线的相对变形关系如图 2所示。
|
图 2 各层的转动变形关系 Fig. 2 Rotational deformation relation of each layer |
假设基壳层与压电层变形前后垂直于中曲面的直法线仍为直线,由于球壳沿经纬线相互对称,所以绕经线的变形关系与纬线一致。则基壳和压电层的横向剪切变形为零,因此有
| $ \lambda_{b} =-\frac{1}{R_{c}} \frac{\partial w_{0}}{\partial \varphi}, \gamma_{b}=-\frac{1}{R_{c} \sin \varphi} \frac{\partial w_{0}}{\partial \theta} $ | (2) |
| $ \lambda_{p} =-\frac{1}{R_{p}} \frac{\partial w_{0}}{\partial \varphi}, \gamma_{p}=-\frac{1}{R_{p} \sin \varphi} \frac{\partial w_{0}}{\partial \theta}. $ | (3) |
若各层之间无相对滑动,位移连续性,顺时针方向为正。根据图 2及式(2)和式(3),可以将粘弹性层的中面位移及横向转角表示为
| $ \left\{\begin{array}{c} u_{0 v}=\frac{1}{2}\left[u_{0 b}+u_{0 p}-\frac{1}{2}\left(\frac{h_{b}}{R_{b}}-\frac{h_{p}}{R_{p}}\right) \frac{\partial w_{0}}{\partial \varphi}\right] \\ v_{0 v}=\frac{1}{2}\left[v_{0 b}+v_{0 p}-\frac{1}{2 \sin \varphi}\left(\frac{h_{b}}{R_{b}}-\frac{h_{p}}{R_{p}}\right) \frac{\partial w_{0}}{\partial \theta}\right] \\ \lambda_{v}=\frac{1}{h_{v}}\left[u_{0 p}-u_{0 b}+\frac{1}{2}\left(\frac{h_{b}}{R_{b}}+\frac{h_{p}}{R_{p}}\right) \frac{\partial w_{0}}{\partial \varphi}\right] \\ \gamma_{v}=\frac{1}{h_{v}}\left[v_{0 p}-v_{0 b}+\frac{1}{2 \sin \varphi}\left(\frac{h_{b}}{R_{b}}+\frac{h_{p}}{R_{p}}\right) \frac{\partial w_{0}}{\partial \theta}\right] \end{array}\right. $ | (4) |
利用Donnell壳体理论,可以将主动约束阻尼球壳各层的应变-位移关系表示为
| $ {\mathit{\boldsymbol{\varepsilon }}^i} = \mathit{\boldsymbol{\varepsilon }}_0^i + {\mathit{\boldsymbol{Z}}_i}{\mathit{\boldsymbol{\chi }}^i} $ | (5) |
其中,εi表示i层应变,ε0i表示i层中曲面膜应变矢量,χi为中曲面弯曲应变矢量,Zi为i层应变变换矩阵。它们的具体形式为
| $ \begin{array}{c} \boldsymbol{\varepsilon}^{i}=\left[\begin{array}{lllll} \varepsilon_{\varphi \varphi}^{i} & \varepsilon_{\theta \theta}^{i} & \varepsilon_{\varphi \theta}^{i} & \varepsilon_{\varphi z}^{i} & \varepsilon_{\theta z}^{i} \end{array}\right]^{\mathrm{T}} ; \\ \boldsymbol{\varepsilon}_{0}^{i}=\left[\begin{array}{lllll} \varepsilon_{\varphi \varphi}^{0 i} & \varepsilon_{\theta \theta}^{0 i} & \varepsilon_{\varphi \theta}^{0 i} & \varepsilon_{\varphi z}^{0 i} & \varepsilon_{\theta z}^{0 i} \end{array}\right]^{\mathrm{T}} ; \\ \boldsymbol{\chi}^{i}=\left[\begin{array}{lllll} \chi_{\varphi \varphi}^{i} & \chi_{\theta \theta}^{i} & \chi_{\varphi \theta}^{i} & \chi_{\varphi z}^{i} & \chi_{\theta z}^{i} \end{array}\right]^{\mathrm{T}} ;\\ \boldsymbol{Z}_{i}=\operatorname{diag}\left[z_{i} \quad z_{i} \quad z_{i} \quad 1 \quad 1\right], i=b, v, p ; \\ \varepsilon_{\theta \theta}^{0 i}=\frac{1}{R_{i} \sin \varphi} \frac{\partial v_{0 i}}{\partial \theta}+\frac{\cot \varphi}{R_{i}} u_{0 i}+\frac{1}{R_{i}} w_{0} ; \\ \varepsilon_{\varphi \theta}^{0 i}=\frac{1}{R_{i} \sin \varphi} \frac{\partial u_{0 i}}{\partial \theta}+\frac{1}{R_{i}} \frac{\partial v_{0 i}}{\partial \varphi}-\frac{v_{0 i}}{R_{i}} \cot \varphi ; \\ \varepsilon_{\varphi z}^{0 i}=\frac{1}{R_{i}} \frac{\partial w_{0}}{\partial \varphi} ; \\ \varepsilon_{\varphi \varphi}^{0 i}=\frac{1}{R_{i}} \frac{\partial u_{0 i}}{\partial \varphi}+\frac{w_{0}}{R_{i}} ; \\ \varepsilon_{\theta z}^{0 i}=\frac{1}{R_{i} \sin \varphi} \frac{\partial w_{0}}{\partial \theta}, i=b, v, p ;\\ \chi_{\varphi \varphi}^{i}=-\frac{1}{R_{i}^{2}} \frac{\partial^{2} w_{0}}{\partial \varphi^{2}}; \\ \chi_{\theta \theta}^{i}=-\left(\frac{1}{R_{i}{ }^{2} \sin ^{2} \varphi} \frac{\partial^{2} w_{o}}{\partial \theta^{2}}+\frac{\cot \varphi}{R_{i}{ }^{2}} \frac{\partial w_{0}}{\partial \varphi}\right) ;\\ \chi_{\varphi \theta}^{i}=\frac{\cot \varphi}{R_{i}^{2} \sin \varphi} \frac{\partial w_{0}}{\partial \theta}-\frac{2}{R_{i}^{2} \sin \varphi} \frac{\partial^{2} w_{0}}{\partial \theta \partial \varphi};\\ \chi_{\varphi z}^{i}=-\frac{1}{R_{i}} \frac{\partial w_{0}}{\partial \varphi}; \\ \chi_{\theta z}^{i}=-\frac{1}{R_{i} \sin \varphi} \frac{\partial w_{0}}{\partial \theta}, i=c, p; \\ \chi_{\varphi \varphi}^{v}=\frac{1}{R_{v}} \frac{\partial \lambda_{v}}{\partial \varphi};\\ \chi_{\theta \theta}^{v}=\frac{1}{R_{v} \sin \varphi} \frac{\partial \gamma_{v}}{\partial \theta}+\frac{\cot \varphi}{R_{v}} \lambda_{v}; \\ \chi_{\varphi \theta}^{v}=\frac{1}{R_{v} \sin \varphi} \frac{\partial \lambda_{v}}{\partial \theta}+\frac{1}{R_{v}} \frac{\partial \gamma_{v}}{\partial \varphi}-\frac{\gamma_{v}}{R_{v}} \cot \varphi;\\ \chi_{\varphi z}^{v}=\lambda_{v}=\frac{1}{h_{v}}\left[u_{0 p}-u_{0 b}+\left(\frac{h_{b}}{2 R_{b}}+\frac{h_{p}}{2 R_{p}}\right) \frac{\partial w_{0}}{\partial \varphi}\right]; \\ \chi_{\theta z}^{v}=\gamma_{v}=\frac{1}{h_{v}}\left[v_{0 p}-v_{0 b}+\frac{1}{2 \sin \varphi}\left(\frac{h_{b}}{R_{b}}+\frac{h_{p}}{R_{p}}\right) \frac{\partial w_{0}}{\partial \theta}\right] \end{array} $ | (6) |
根据应力-应变关系,将总应力σi表示如下:
| $ \left\{\begin{array}{l} \boldsymbol{\sigma}^{i}=\overline{\boldsymbol{Q}}_{i} \boldsymbol{\varepsilon}_{i}-\boldsymbol{e}_{i} \boldsymbol{E}_{i} \\ \boldsymbol{D}_{i}=\boldsymbol{e}_{i}^{\mathrm{T}} \boldsymbol{\varepsilon}_{i}+\boldsymbol{\xi}_{i} \boldsymbol{E}_{i} \end{array}\right. $ | (7) |
其中σi=[σφφi σθθi σφθi σφzi σθzi]T, σφφi、σθθi为i层的正应力,σφθi为i层面内剪切应力,σφzi、σθzi为i层横向剪切应力;Qi表示i层弹性刚度常数矩阵,e,E,ξ,D分别代表压电常数矩阵、电场矢量、介电常数矩阵和电位移矢量,各矩阵和矢量的具体形式为
| $ \left\{\begin{array}{l} \overline{\boldsymbol{Q}}_{i}=\left[\begin{array}{ccccc} \bar{Q}_{11}^{i} & \bar{Q}_{12}^{i} & \bar{Q}_{16}^{i} & 0 & 0 \\ \bar{Q}_{12}^{i} & \bar{Q}_{22}^{i} & \bar{Q}_{26}^{i} & 0 & 0 \\ \bar{Q}_{16}^{i} & \bar{Q}_{26}^{i} & \bar{Q}_{66}^{i} & 0 & 0 \\ 0 & 0 & 0 & \bar{Q}_{44}^{i} & \bar{Q}_{45}^{i} \\ 0 & 0 & 0 & \bar{Q}_{45}^{i} & \bar{Q}_{55}^{i} \end{array}\right], \boldsymbol{e}=\left[\begin{array}{ccc} 0 & 0 & e_{31} \\ 0 & 0 & e_{32} \\ 0 & 0 & e_{36} \\ e_{14} & e_{24} & 0 \\ e_{15} & e_{25} & 0 \end{array}\right] \\ \boldsymbol{E}=\left[\begin{array}{c} E_{1} \\ E_{2} \\ E_{3} \end{array}\right], \boldsymbol{\xi}=\left[\begin{array}{ccc} \xi_{11} & \xi_{12} & 0 \\ \xi_{12} & \xi_{22} & 0 \\ 0 & 0 & \xi_{33} \end{array}\right], \boldsymbol{D}=\left[\begin{array}{c} D_{1} \\ D_{2} \\ D_{3} \end{array}\right] \end{array}\right. $ | (8) |
其中刚度矩阵中各参数具体形式如下:
| $ \left\{\begin{array}{l} \bar{Q}_{11}^{i} =Q_{11}^{i} c^{4}+2\left(Q_{12}^{i}+2 Q_{66}^{i}\right) c^{2} s^{2}+Q_{22}^{i} s^{4} \\ \bar{Q}_{12}^{i} =\left(Q_{11}^{i}+Q_{22}^{i}-4 Q_{66}^{i}\right) c^{2} s^{2}+Q_{12}^{i}\left(c^{4}+s^{4}\right) \\ Q_{22}^{i} =\left(Q_{11}^{i} s^{4}+2\left(Q_{12}^{i}+2 Q_{66}^{i}\right) c^{2} s^{2}+Q_{22}^{i} c^{4}\right.\\ \bar{Q}_{16}^{i} =\left(Q_{11}^{i}+Q_{12}^{i}-2 Q_{66}^{i}\right) c^{3} s+\left(Q_{12}^{i}-Q_{22}^{i}+\right.\\ \ \ \ \ \ \ \ \ \ \ \left.2 Q_{66}^{i}\right) c s^{3} \\ \bar{Q}_{26}^{i} =\left(Q_{11}^{i}-Q_{12}^{i}-2 Q_{66}^{i}\right) c s^{3}+\left(Q_{12}^{i}-Q_{22}^{i}+\right.\\ \ \ \ \ \ \ \ \ \ \ \left.2 Q_{66}^{i}\right) c^{3} s \\ \bar{Q}_{66}^{i} =\left(Q_{11}^{i}+Q_{22}^{i}-2 Q_{12}^{i}-2 Q_{66}^{i}\right) c^{2} s^{2}+\\ \ \ \ \ \ \ \ \ \ \ Q_{66}^{i}\left(c^{4}+s^{4}\right) \\ \bar{Q}_{44}^{i}= Q_{44}^{i} c^{2}+Q_{55}^{i} s^{2}, \bar{Q}_{45}^{i}=\left(Q_{55}^{i}-Q_{44}^{i}\right) c s \\ \bar{Q}_{55}^{i}= Q_{55}^{i} c^{2}+Q_{44}^{i} s^{2}, c=\cos \alpha_{\text {fiber }}^{i}, s=\sin \alpha_{\text {fiber }}^{i} \end{array}\right. $ | (9) |
式中αfiberi为纤维方向角,Qiji为刚度系数。对于各向异性的压电层,Qiji可以被表示为
| $ \begin{array}{l} Q_{11}^{i}=C_{11}^{i}-\frac{C_{13}^{i} C_{13}^{i}}{C_{33}^{i}}, Q_{12}^{i}=C_{12}^{i}-\frac{C_{13}^{i} C_{13}^{i}}{C_{33}^{i}}, Q_{22}^{i}=C_{22}^{i}- \\ \frac{C_{23}^{i} C_{23}^{i}}{C_{33}^{i}}, Q_{44}^{i}=\kappa C_{44}^{i}, Q_{55}^{i}=\kappa C_{55}^{i}, Q_{66}^{i}=\kappa C_{66}^{i}. \end{array} $ | (10) |
对于各向同性的基壳和粘弹性层,Qiji为
| $ \begin{aligned} Q_{11}^{i}=& \frac{E_{1}^{i}}{1-\upsilon _{12}^{i} \upsilon _{21}^{i}}, Q_{12}^{i}=\frac{\upsilon _{12}^{i} E_{1}^{i}}{1-\upsilon _{12}^{i} \upsilon _{21}^{i}}, Q_{22}^{i}=\frac{E_{2}^{i}}{1-\upsilon _{12}^{i} \upsilon _{21}^{i}} ;\\ &Q_{44}^{i}=G_{23}^{i}, Q_{55}^{i}=G_{13}^{i}, Q_{66}^{i}=G_{12}^{i} \end{aligned} $ | (11) |
其中i=b、v、p,κ为剪切修正系数,考虑到剪切应变在径向分布的不均匀性,设κ=π2/12,Cmni为各层的弹性材料常数,Ei为弹性模量,Gi为剪切模量,υ为泊松比。对于基壳和粘弹性层,e和ξ为零。
电势的变化可以被近似认为是余弦和线性变化的组合,满足Maxwell方程,所以电势
| $ \tilde{\varphi}(\varphi, \theta, z, t)=-\cos \left(\beta z_{p}\right) \varphi_{p}(\varphi, \theta, t)+2 \frac{z_{p}}{h_{p}} \varphi_{0}(t) $ | (12) |
其中β=π/hp,φ0为外加电势,φp为球壳经、纬线方向上的根据空间和时间变化的电势,则电场E和电势
| $ \left\{\begin{array}{l} E_{1}=-\frac{1}{R_{p}} \frac{\partial \tilde{\varphi}}{\partial \theta}=\frac{\cos \left(\beta z_{p}\right)}{R_{p}} \frac{\partial \varphi_{p}}{\partial \theta} \\ E_{2}=-\frac{1}{R_{p}} \frac{\partial \tilde{\varphi}}{\partial \varphi}=\frac{\cos \left(\beta z_{p}\right)}{R_{p}} \frac{\partial \varphi_{p}}{\partial \varphi} \\ E_{3}=-\frac{\partial \tilde{\varphi}}{\partial z}=-\beta \sin \left(\beta z_{p}\right) \varphi_{p}-\frac{2 \varphi_{0}}{h_{p}} \end{array}\right. $ | (13) |
假设以压电层球壳内表面为零电势平面,根据文献[10]可令φ0(t)=V0=vcejωt,其中vc是压电层激励电压幅值,角频率ω=2πf,f是压电层激励电压频率。
1.3 边界条件由薄壳理论知,简化后的薄膜应力Nφφ、Nθθ、Nφθ和弯曲应力Mφφ、Mθθ、Mφθ及剪切应力Qφz、Qθz可以表示为
| $ \begin{aligned} \left\{\begin{array}{c} N_{\varphi \varphi}^{i} \\ N_{\theta \theta}^{i} \\ N_{\varphi \theta}^{i} \end{array}\right\}=&\left[\begin{array}{lll} A_{11} & A_{12} & A_{16} \\ A_{12} & A_{22} & A_{26} \\ A_{16} & A_{26} & A_{66} \end{array}\right]\left\{\begin{array}{c} \varepsilon_{\varphi \varphi}^{0 i} \\ \varepsilon_{\theta \theta}^{0 i} \\ \varepsilon_{\varphi \theta}^{0 i} \end{array}\right\}+\\ &\left[\begin{array}{lll} B_{11} & B_{12} & B_{16} \\ B_{12} & B_{22} & B_{26} \\ B_{16} & B_{26} & B_{66} \end{array}\right]\left\{\begin{array}{l} \chi_{\varphi \varphi}^{i} \\ \chi_{\theta \theta}^{i} \\ \chi_{\varphi \theta}^{i} \end{array}\right\} \end{aligned} $ | (14a) |
| $ \begin{aligned} \left\{\begin{array}{l} M_{\varphi \varphi}^{i} \\ M_{\theta \theta}^{i} \\ M_{\varphi \theta}^{i} \end{array}\right\}=&\left[\begin{array}{lll} B_{11} & B_{12} & B_{16} \\ B_{12} & B_{22} & B_{26} \\ B_{16} & B_{26} & B_{66} \end{array}\right]\left\{\begin{array}{c} \varepsilon_{\varphi \varphi}^{0 i} \\ \varepsilon_{\theta \theta}^{0 i} \\ \varepsilon_{\varphi \theta}^{0 i} \end{array}\right\}+\\ &\left[\begin{array}{lll} D_{11} & D_{12} & D_{16} \\ D_{12} & D_{22} & D_{26} \\ D_{16} & D_{26} & D_{66} \end{array}\right]\left\{\begin{array}{c} \chi_{\varphi \varphi}^{i} \\ \chi_{\theta \theta}^{i} \\ \chi_{\varphi \theta}^{i} \end{array}\right\} \end{aligned} $ | (14b) |
| $ \left\{\begin{array}{l} Q_{\varphi z}^{i} \\ Q_{\theta z}^{i} \end{array}\right\}=\left[\begin{array}{ll} A_{44} & A_{45} \\ A_{45} & A_{55} \end{array}\right]\left\{\begin{array}{c} \varepsilon_{\varphi z}^{0 i} \\ \varepsilon_{\theta z}^{0 i} \end{array}\right\} $ | (14c) |
其中Aij、Bij、Dij为应力变换系数,具体表达式如下:
| $ \left\{\begin{array}{l} A_{i j}=C_{i j}^{\xi}\left(Z_{k}^{\xi}-Z_{k-1}^{\xi}\right) \\ B_{i j}=\frac{1}{2} C_{i j}^{\xi}\left[\left(Z_{k}^{\xi}\right)^{2}-\left(Z_{k-1}^{\xi}\right)^{2}\right] \\ D_{i j}=\frac{1}{3} C_{i j}^{\xi}\left[\left(Z_{k}^{\xi}\right)^{3}-\left(Z_{k-1}^{\xi}\right)^{3}\right] \end{array}\right. $ | (15) |
式中ξ=b、v、p,Zkξ与Zk-1ξ分别代表各层上、下表面距中面的高度。
本文对基壳的经线方向两端采用固支边界条件,纬线方向两端采用自由边界条件,因此有
| $ u=w=\frac{\partial w}{\partial \theta}=0, \quad \text { 当 } \theta=\theta_{0} \text { 和 } \theta=\theta_{1} $ | (16a) |
| $ N_{\varphi}=M_{\varphi}=Q_{\varphi}=0, \text { 当 } \varphi=\varphi_{0} \text { 和 } \varphi=\varphi_{1} $ | (16b) |
压电约束层和阻尼层无约束:
| $ M_{\theta}^{i}=M_{\varphi}^{i}=N_{\theta}^{i}=N_{\varphi}^{i}=Q_{\theta}^{i}=Q_{\varphi}^{i}=0 $ | (17) |
其中i=p,v。
1.4 动力学模型根据伽辽金法,可将位移表示为
| $ \boldsymbol{U}=\left[\begin{array}{lllllll} u_{0 b} & v_{0 b} & u_{0 p} & v_{0 p} & w_{0} & \varphi_{p} & \varphi_{0} \end{array}\right]=\boldsymbol{\varphi} \cdot \boldsymbol{q} $ | (18a) |
| $ \begin{aligned} \boldsymbol{\varphi}=&\operatorname{diag}\left[\varphi_{u b}(\varphi, \theta) \quad \varphi_{v b}(\varphi, \theta) \quad \varphi_{u p}(\varphi, \theta)\right.\\ &\left.\varphi_{u p}(\varphi, \theta) \quad \varphi_{w}(\varphi, \theta) \quad \varphi_{p}(\varphi, \theta) \quad v_{c}\right] \end{aligned} $ | (18b) |
| $ \boldsymbol{q}=\left[\begin{array}{llllll} q_{u b}(t) & q_{v b}(t) & q_{u p}(t) & q_{v p}(t) & q_{w}(t) & q_{p}(t) & q_{0}(t) \end{array}\right]^{\mathrm{T}} $ | (18c) |
位移形函数φ分别由雅可比多项式和傅里叶级数组合而成,分别表征纬线和经线方向形变,其形式和参数确定方法与文献[8, 11]一致。
由于球壳扭转变形较小,因此忽略球壳绕经、纬线的转动变形对系统动能的影响,可以将局部主动约束层阻尼球壳结构的动能T表示为
| $ \begin{aligned} T=& \frac{1}{2} \int\limits_{V_{b}} \rho_{b}\left(\dot{\boldsymbol{q}}^{\mathrm{T}} \boldsymbol{\varphi}^{\mathrm{T}} \boldsymbol{\psi}_{1} \boldsymbol{\varphi} \dot{\boldsymbol{q}}\right) \mathrm{d} V_{b}+\\ & \frac{1}{2} \sum\limits_{i=1}^{N_{v}} \int\limits_{V_{v i}} H^{*}\left(\theta_{i}, \boldsymbol{\varphi}_{i}\right) \rho_{v}\left(\dot{\boldsymbol{q}}^{\mathrm{T}} \boldsymbol{\varphi}^{\mathrm{T}} \boldsymbol{\psi}_{2} \varphi \dot{\boldsymbol{q}}+\right.\\ &\left.\dot{\boldsymbol{q}}^{\mathrm{T}} \boldsymbol{\psi}_{3}^{\mathrm{T}} \boldsymbol{\varphi}^{\mathrm{T}} \boldsymbol{\psi}_{4} \boldsymbol{\varphi} \boldsymbol{\psi}_{3} \dot{\boldsymbol{q}}\right) \mathrm{d} V_{v i}+\frac{1}{2} \int\limits_{V_{p}} \rho_{p}\left(\dot{\boldsymbol{q}}^{\mathrm{T}} \boldsymbol{\varphi}^{\mathrm{T}} \boldsymbol{\psi}_{5} \boldsymbol{\varphi} \dot{\boldsymbol{q}}\right) \mathrm{d} V_{p} \end{aligned} $ | (19) |
将式(18)代入式(5)和式(7),并根据应力应变与应变能关系,系统的总势能U表示为
| $ \begin{array}{l} U=\frac{1}{2} \int\limits_{V_{b}} \boldsymbol{q}^{\mathrm{T}} \boldsymbol{n}_{b}^{\mathrm{T}} \bar{\boldsymbol{Q}}_{b} \boldsymbol{n}_{b} \boldsymbol{q} \mathrm{d} V_{b}+\frac{1}{2} \sum\limits_{i=1}^{N_{v}} \int\limits_{V_{v i}} H^{*}\left(\theta_{i}, \boldsymbol{\varphi}_{i}\right) \boldsymbol{q}^{\mathrm{T}} \boldsymbol{n}_{v i}^{\mathrm{T}} \boldsymbol{Q}_{v} \boldsymbol{n}_{v i} \boldsymbol{q} \mathrm{d} V_{v i}+\\ \ \ \ \ \ \ \ \ \frac{1}{2} \int\limits_{V_{p}}\left(\boldsymbol{q}^{\mathrm{T}} \boldsymbol{n}_{p}^{\mathrm{T}} \bar{\boldsymbol{Q}}_{p} \boldsymbol{n}_{p} \boldsymbol{q}-\boldsymbol{q}^{\mathrm{T}} \boldsymbol{n}_{p}^{\mathrm{T}} \boldsymbol{e} \boldsymbol{n}_{e} \boldsymbol{q}-\boldsymbol{q}^{\mathrm{T}} \boldsymbol{n}_{e}^{\mathrm{T}} \boldsymbol{e}^{\mathrm{T}} \boldsymbol{n}_{p} \boldsymbol{q}-\right. \\ \ \ \ \ \ \ \ \ \left.\boldsymbol{q}^{\mathrm{T}} n_{e}^{\mathrm{T}} \xi^{\mathrm{T}} \boldsymbol{n}_{e} \boldsymbol{q}\right) \mathrm{d} V_{p} \end{array} $ | (20) |
其中ρ表示密度,Nv=nhnj是粘弹性弹片的总数,nh和nj分别为纬度和经度方向分段数,H*(θi, φi)为第i个粘弹性阻尼贴片的位置识别函数:
| $ \begin{array}{c} H^{*}\left(\theta_{i}, \varphi_{i}\right)=\left[H\left(\theta-\theta_{i 2}\right)-H\left(\theta-\theta_{i 1}\right)\right]\cdot \\ {\left[H\left(\varphi-\varphi_{i 2}\right)-H\left(\varphi-\varphi_{i 1}\right)\right]} \end{array} $ | (21) |
式中H为单位阶梯函数,θi2和θi1分别为第i个粘弹性贴片沿θ轴的上、下限,φi2和φi1分别为第i个粘弹性贴片沿φ轴的上、下限。
考虑系统粘弹性层阻尼影响,同时将式(19)和式(20)代入Lagrange方程,可以得到系统的动力学方程为
| $ \boldsymbol{M} \ddot{\boldsymbol{q}}+\boldsymbol{K} \boldsymbol{q}=\boldsymbol{f}_{s}+\boldsymbol{f}_{e} $ | (22) |
式中,M=Mb+Mv+Mp,K=Kb+Kv+Kp;Mb、Mv、Mp与Kb、Kv、Kp分别为基壳层、粘弹性层和压电层的质量矩阵与刚度矩阵,fs=∫Vφ·fdV为结构外载荷矢量,f=[fuc fvc fup fvp fw 0 0]T为单位载荷;fe=V0φψ0为电场力矢量,表达式如下:
| $ \left\{\begin{array}{l} \boldsymbol{M}_{b}=\int\limits_{V_{b}} \rho_{b}\left(\boldsymbol{\varphi}^{\mathrm{T}} \boldsymbol{\psi}_{1} \boldsymbol{\varphi}\right) \mathrm{d} V_{b}, \boldsymbol{M}_{p}=\int\limits_{V_{p}} \rho_{p}\left(\boldsymbol{\varphi}^{\mathrm{T}} \boldsymbol{\psi}_{5} \boldsymbol{\varphi}\right) \mathrm{d} V_{p} \\ \boldsymbol{M}_{v}=\sum\limits_{i=1}^{N_{v}} \int\limits_{V_{v i}} H^{*}\left(\theta_{i}, \boldsymbol{\varphi}_{i}\right) \rho_{v}\left(\boldsymbol{\varphi}^{\mathrm{T}} \boldsymbol{\psi}_{2} \boldsymbol{\varphi}+\boldsymbol{\psi}_{3}^{\mathrm{T}} \boldsymbol{\varphi}^{\mathrm{T}} \boldsymbol{\psi}_{4} \boldsymbol{\varphi} \boldsymbol{\psi}_{3}\right) \mathrm{d} V_{v i} \\ \boldsymbol{K}_{b}=\int\limits_{V_{b}} \boldsymbol{n}_{b}^{\mathrm{T}} \bar{\boldsymbol{Q}}_{b} \boldsymbol{n}_{b} \mathrm{~d} V_{b}, \boldsymbol{K}_{v}=\sum\limits_{i=1}^{N_{v}} \int\limits_{V_{v i}} H^{*}\left(\theta_{i}, \varphi_{i}\right) \boldsymbol{n}_{v i}^{\mathrm{T}} \bar{\boldsymbol{Q}}_{v} \boldsymbol{n}_{v i} \mathrm{~d} V_{v i} \\ \boldsymbol{K}_{p}=\int\limits_{V_{p}}\left(\boldsymbol{n}_{p}^{\mathrm{T}} \bar{\boldsymbol{Q}}_{p} \boldsymbol{n}_{p}-\boldsymbol{n}_{p}^{\mathrm{T}} \boldsymbol{e} \boldsymbol{n}_{e}-\boldsymbol{n}_{e}^{\mathrm{T}} \boldsymbol{e}^{\mathrm{T}} \boldsymbol{n}_{p}-\boldsymbol{n}_{e}^{\mathrm{T}} \boldsymbol{\xi}^{\mathrm{T}} \boldsymbol{n}_{e}\right) \mathrm{d} V_{p} \end{array}\right. $ | (23) |
其中矩阵中各参数可以根据边界条件(14)~(17)确定,各变换矩阵可表示为
| $ {\mathit{\boldsymbol{n}}_e} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0&0&{\frac{{\cos \left( {\beta {z_p}} \right)}}{{{R_p}}}\frac{{\partial {\varphi _p}}}{{\partial \theta }}}&0\\ 0&0&0&0&0&{\frac{{\cos \left( {\beta {z_p}} \right)}}{{{R_p}}}\frac{{\partial {\varphi _p}}}{{\partial \varphi }}}&0\\ 0&0&0&0&0&{ - \beta \sin \left( {\beta {z_p}} \right){\varphi _p}}&{ - \frac{{2{v_c}}}{{{h_p}}}} \end{array}} \right],\\{\mathit{\boldsymbol{\psi }}_3} = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0&0&1&0\\ 0&0&0&1\\ 1&0&0&0\\ 0&1&0&0 \end{array}}&{{0_{4 \times 3}}}\\ {{0_{3 \times 4}}}&{{0_{3 \times 3}}} \end{array}} \right],{\mathit{\boldsymbol{\psi }}_0} = {\left[ {\begin{array}{*{20}{l}} 0&0&0&0&0&0&1 \end{array}} \right]^{\rm{T}}}, $ |
| $ \begin{array}{l} \boldsymbol{\psi}_{4}=\frac{1}{4} \boldsymbol{\psi}_{3}, \boldsymbol{\psi}_{1}=\operatorname{diag}\left[\begin{array}{lllllll} 1 & 1 & 0 & 0 & 1 & 0 & 0 \end{array}\right], \boldsymbol{\psi}_{2}=\operatorname{diag}\left[\begin{array}{ccccccc} \frac{1}{4} & \frac{1}{4} & \frac{1}{4} & \frac{1}{4} & 1 & 0 & 0 \end{array}\right], \boldsymbol{\psi}_{5}= \\ \operatorname{diag}\left[\begin{array}{lllll} 0 & 0 & 1 & 1 & 1 & 0 & 0 \end{array}\right], \end{array} $ |
| $ \boldsymbol{n}_{b}=\left[\begin{array}{ccccccc} \frac{1}{R_{b}} \frac{\partial \varphi_{u b}}{\partial \varphi} & 0 & 0 & 0 & \frac{\varphi_{w}}{R_{b}}-\frac{z_{b}}{R_{b}^{2}} \frac{\partial^{2} \varphi_{w}}{\partial \varphi^{2}} & 0 & 0 \\ \frac{\cot \varphi}{R_{b}} \varphi_{u c} & \frac{1}{R_{b} \sin \varphi} \frac{\partial \varphi_{v b}}{\partial \theta} & 0 & 0 & \frac{\varphi_{w}}{R_{b}}-\frac{z_{b}}{R_{b}^{2}}\left(\frac{1}{\sin ^{2} \varphi} \frac{\partial^{2} \varphi_{w}}{\partial \theta^{2}}+\cot \varphi \frac{\partial \varphi_{w}}{\partial \varphi}\right) & 0 & 0 \\ \frac{1}{R_{b} \sin \varphi} \frac{\partial \varphi_{u b}}{\partial \theta} & \frac{1}{R_{b}} \frac{\partial \varphi_{v b}}{\partial \varphi}-\frac{\varphi_{v b}}{R_{b}} \cot \varphi & 0 & 0 & -\frac{z_{b}}{R_{b}^{2} \sin \varphi}\left(2 \frac{\partial^{2} \varphi_{w}}{\partial \theta \partial \varphi}-\cot \varphi \frac{\partial \varphi_{w}}{\partial \theta}\right) & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right], $ |
| $ \boldsymbol{n}_{v}=\left[\begin{array}{cccccc} c_{1} \frac{\partial \varphi_{u c}}{\partial \varphi} & 0 & c_{2} \frac{\partial \varphi_{u p}}{\partial \varphi} & 0 & \frac{1}{R_{v}} \varphi_{w}+c_{3} \frac{\partial^{2} \varphi_{w}}{\partial \varphi^{2}} & 0 & 0 \\ c_{1} \cot \varphi \varphi_{u c} & \frac{c_{1}}{\sin \varphi} \frac{\partial \varphi_{v c}}{\partial \theta} & c_{2} \cot \varphi \varphi_{u p} & \frac{c_{2}}{\sin \varphi} \frac{\partial \varphi_{v p}}{\partial \theta} & \frac{1}{R_{v}} \varphi_{w}+\frac{c_{3}}{\sin ^{2} \varphi} \frac{\partial^{2} \varphi_{w}}{\partial \theta^{2}}+c_{3} \cot \varphi \frac{\partial \varphi_{w}}{\partial \varphi} & 0 & 0 \\ \frac{c_{1}}{\sin \varphi} \frac{\partial \varphi_{v c}}{\partial \theta} & c_{1} \frac{\partial \varphi_{v c}}{\partial \varphi}-c_{1} \cot \varphi \varphi_{v c} & \frac{c_{2}}{\sin \varphi} \frac{\partial \varphi_{u p}}{\partial \theta} & c_{2} \frac{\partial \varphi_{vp}}{\partial \varphi}-c_{2} \cot \varphi \varphi_{vp} & \frac{2 c_{3}}{\sin \varphi} \frac{\partial^{2} \varphi_{w}}{\partial \theta \partial \varphi}-\frac{2 c_{3}}{\sin \varphi} \cot \varphi \frac{\partial \varphi_{w}}{\partial \theta} & 0 & 0 \\ -\frac{1}{h_{v}} \varphi_{u c} & 0 & \frac{1}{h_{v}} \varphi_{u p} & 0 & \left(\frac{1}{R_{v}}+\frac{c_{s}}{h_{v}}\right) \frac{\partial \varphi_{w}}{\partial \varphi} & 0 & 0 \\ 0 & -\frac{1}{h_{v}} \varphi_{v c} & 0 & \frac{1}{h_{v}} \varphi_{vp} & \left(\frac{1}{R_{v}}+\frac{c_{s}}{h_{v}}\right) \frac{1}{\sin \varphi} \frac{\partial \varphi_{w}}{\partial \theta} & 0 & 0 \end{array}\right] \text { , } $ |
其中
| $ \boldsymbol{n}_{p}=\left[\begin{array}{cccccc} 0 & 0 & \frac{1}{R_{p}} \frac{\partial \varphi_{u p}}{\partial \varphi} & 0 & \frac{\varphi_{w}}{R_{p}}-\frac{z_{p}}{R_{p}^{2}} \frac{\partial^{2} \varphi_{w}}{\partial \varphi^{2}} & 0 & 0 \\ 0 & 0 & \frac{\cot \varphi}{R_{p}} \varphi_{u p} & \frac{1}{R_{p} \sin \varphi} \frac{\partial \varphi_{v p}}{\partial \theta} & \frac{\varphi_{w}}{R_{p}}-\frac{z_{p}}{R_{p}^{2}}\left(\frac{1}{\sin ^{2} \varphi} \frac{\partial^{2} \varphi_{w}}{\partial \theta^{2}}+\cot \varphi \frac{\partial \varphi_{w}}{\partial \varphi}\right) & 0 & 0 \\ 0 & 0 & \frac{1}{R_{p} \sin \varphi} \frac{\partial \varphi_{u p}}{\partial \theta} & \frac{1}{R_{p}} \frac{\partial \varphi_{v p}}{\partial \varphi}-\frac{\varphi_{v p}}{R_{p}} \cot \varphi & -\frac{z_{p}}{R_{p}^{2} \sin \varphi}\left(2 \frac{\partial^{2} \varphi_{w}}{\partial \theta \partial \varphi}-\cot \varphi \frac{\partial \varphi_{w}}{\partial \theta}\right) & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right] $ | (24) |
求解方程(22)可得系统第n阶复模态频率ωn,则模态阻尼比ξn可表示为
| $ \xi_{n}=\operatorname{Re}\left(\omega_{n}\right) / 2 \operatorname{Im}\left(\omega_{n}\right) $ | (25) |
其中Re(·)和Im(·)分别为实部和虚部计算函数。
1.5 压电球壳模态分析比较利用本文提出的压电球壳动力学方法对文献[12]中厚径比为0.005,球壳厚度为0.005 m的45°、60°和90°固定约束冒型开球壳进行模态分析,得到经度方向波数为1的前六阶模态频率由表 1给出。由表 1可以看出,除45°开球壳的第四阶模态和90°开球壳的第一阶模态频率本文结果与文献[12]相差超过10 Hz外,其余球壳结构的模态频率均相差较小,因此本文所给出的方法能够对压电球壳的动力学行为进行准确计算。
| 表 1 模态频率 Tab. 1 Modal frequency |
初步设定本次分析参数,在球顶向下H0=0.4R处向下截取Hb=0.5 m,西经0° ~150°的开球壳作为研究对象,球壳基层中面半径R=0.6 m,基层厚度hb=2 mm;本文针对开球壳敷设主动约束阻尼,约束层沿经度和纬度方向对称,敷设于球壳中部,约束层敷设角αp=100°,hp=0.4 m厚度hp=0.000 5 m,压电层初始电压为20 V;粘弹性材料在整个阻尼层中均匀相间布置,初始粘弹性层厚度hv=2 mm,沿经度方向分段数mv=12,纬度方向分段数为nv=12,占空比χ=0.4,基壳在αb=0°和150°的两端采用固定约束。后续分析中未作特别说明各参数与初始值一致,各层材料参数分别由表 2和表 3给出。
| 表 2 基层和粘弹性层材料属性 Tab. 2 Material properties of base layer and viscoelastic layer |
| 表 3 压电层材料属性 Tab. 3 Material properties of piezoelectric layer |
设主动约束层阻尼球壳中引入质量比为∈=MACLD/Mb,MACLD=Mv+Mp,Mb、Mv和Mp分别为基层球壳、粘弹性阻尼层和压电约束层的质量。为了准确表示阻尼层有效面积在敷设区域的占比,本文定义占空比χ=AviNv/αpHp,其中Avi为第i个粘弹性阻尼单元在压电层的敷设面积Avi,Avi=αviHviAvi=αpl/mvnv,令
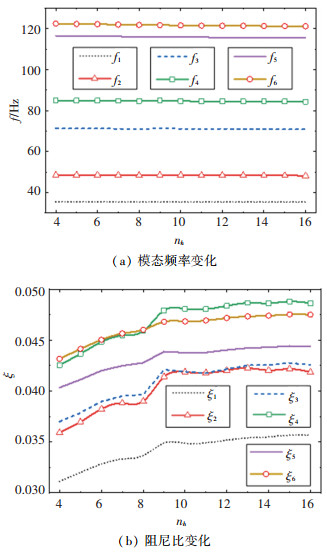
图 3是阻尼层纬度方向分段数对结构振动特性的影响。图 3 (a)中显示,随着分段数nh的增加,1到6阶模态固有频率逐渐下降,但是下降幅度较小;由图 3(b)可以看出,随着分段数的增加,前6阶模态阻尼比逐渐增大,且当nh>9后,阻尼比增加趋势变缓,近似保持不变。
|
图 3 纬度方向分段数对振动特性的影响 Fig. 3 Influence of segment number in latitude on vibration characteristics |
经度方向分段数对结构振动特性的影响如图 4所示。在图 4(a)中可以看出,球壳的前6阶模态固有频率随分段数nj增大而逐渐增加,但增幅较小;图 4(b)显示,随着nj的增加,前6阶模态阻尼比逐渐增大,但当nj>11后,阻尼比增幅变小,而且低频模态几乎保持不变。

|
图 4 经度方向分段数对振动特性的影响 Fig. 4 Influence of segment number in longitude on vibration characteristics |
由此可知,阻尼层分段数变化对系统固有频率和阻尼比影响较小,这可能是由于分段数变化不会较大地影响约束层和阻尼层的耦合特性。虽然由于本文给出的截球壳在经、纬度方向波动幅度不同,阻尼比的变化幅度略有不同,但适当增加阻尼层分段数可以增加截球壳的阻尼比;而且分段数变化时引入约束阻尼质量比几乎不变。
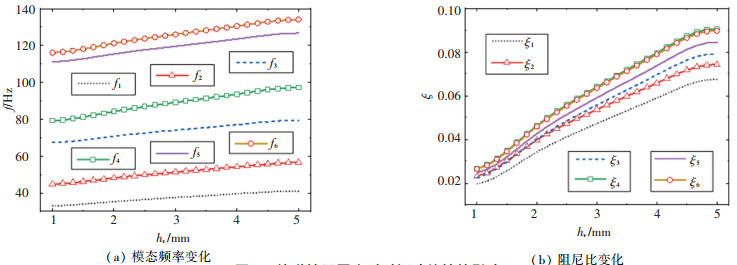
2.2 粘弹性层厚度对结构减振特性的影响当粘弹性层厚度hv在1~5 mm范围内变化时,前6阶模态固有频率和阻尼比的变化曲线如图 5所示。由图 5(a)可见,粘弹性层厚度的增加会导致模态固有频率逐渐增大,而且高频模态沿经度方向波数较大,增大hv会使球壳抗弯曲能力增加,因此高频模态频率增幅较大。在图 5(b)中,阻尼比ζ随hv的增大而增大,而且由于高频率模态较大的弯曲变形使得阻尼层具有更大的剪切变形,因此高频模态阻尼比增加更显著,但是随着hv的增大引入质量比∈将增大,当hv=5 mm时,∈将达到54.25%。
|
图 5 粘弹性层厚度对对振动特性的影响 Fig. 5 Influence of viscoelastic layer thickness on vibration characteristics |
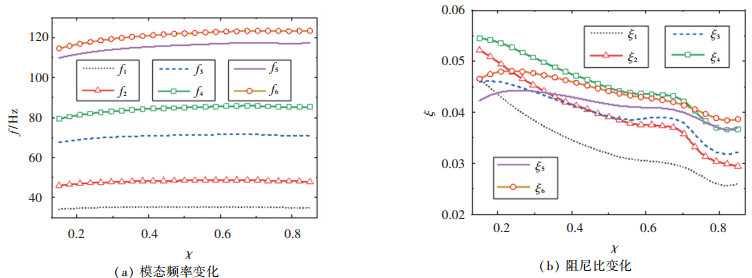
图 6给出了占空比χ对约束阻尼部分球壳的振动特性影响曲线。由图 6(a)可以看出,随占空比χ的增大第1~4阶模态频率呈现先增大后减小趋势,而5、6阶模态固有频率呈现单调上升趋势,由于高、低频模态振型不同,因此阻尼结构设置对低频模态固有频率影响较小。图 6(b)表明,随着占空比χ的增加,虽然阻尼单元与基层接触面积增加,但不同模态阻尼层剪切变形产生耗散能相对总应变能变化趋势不同,第5、6阶模态在χ接近0.25附近时模态阻尼比最大,其余模态阻尼比随χ的增大而逐渐减小;而且较大的χ会导致引入质量增加,当χ=85%时,∈为51.3%。
|
图 6 占空比对振动特性的影响 Fig. 6 Influence of duty ratio on vibration characteristics |
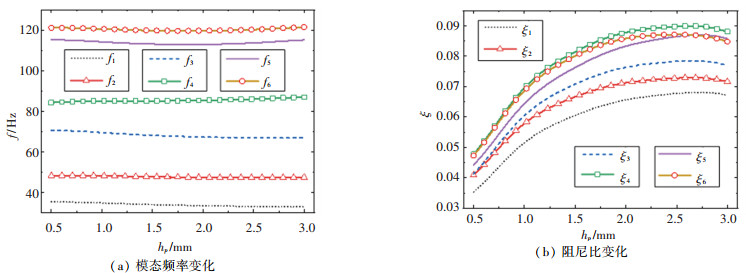
当压电层厚度hp在0.5~3 mm范围内变化时,前6阶模态阻尼比和固有频率的变化曲线如图 7所示。由图 7(a)可见,由于约束层密度较大,因此随着hp的增加,系统的质量增大,使得前三阶模态的固有频率逐渐减小;而高频模态经度方向波动较大,约束层具有较高的弹性模量,因此hp增加会引起4~6阶模态频率增大。从图 7(b)看出,随着hp增加,各阶模态阻尼比先快速增大而后又缓慢减小,这可能是因为一定厚度的约束层可以增加阻尼层剪切变形,但厚度较大时,使系统质量大幅增加,引起系统总应变能大幅增加,从而使阻尼比减小;而且太大的hp会使系统质量大幅增加,当hp=3 mm时,∈=198.7%,这将会严重影响球壳应用要求。
|
图 7 约束层厚度对振动特性的影响 Fig. 7 Influence of constraint layer thickness on vibration characteristics |
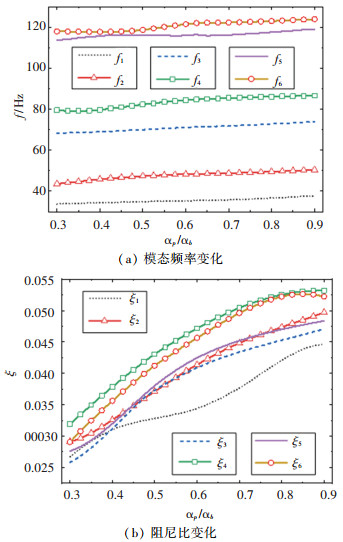
约束层经度方向敷设角对部分球壳振动特性的影响如图 8所示。从图 8(a)看出,随αp的增加约束阻尼层敷设面积增加,因此模态固有频率随之增加,但由于约束层厚度较小,对模态频率影响有限。图 8(b)表明,随着αp的增加,阻尼比ξ逐渐增大,但当αp/αb超过0.8后,高频模态的阻尼比ξ4、ξ5和ξ6的增幅减小,几乎保持不变;而且随着αp的增加,引入阻尼结构的质量也会随之增加,但当约束层厚度较小时,引入质量有限,如当αp=135 °时,引入质量比仅为62.9%,η1因此对于αp的选择,应综合考虑球壳工程应用和减振效果,可在保证使用要求的条件下选择较大的约束层敷设角αp。
|
图 8 约束层敷设角对振动特性的影响 Fig. 8 Influence of laying angle of constraint layer thickness on vibration characteristics |
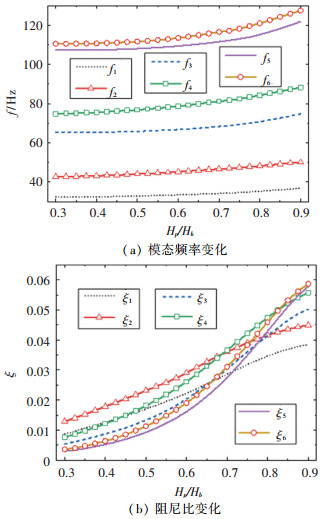
图 9为约束层敷设高度对振动特性的影响。由图 9(a)可以看出,当约束层高度hp增加时,引入的约束层增加,使得系统模态频率增大。从图 9(b)可知,随着hp的增加模态阻尼比也随之逐渐增大,而且当hp超过0.25 m后,模态3~6的阻尼增速变大。同理当约束层敷设高度增大也会导致系统引入质量增加,但是当hp=0.45 m时,引入质量比仅为46.6%,相对增加约束层厚度和敷设角,引入质量较少。
|
图 9 约束层敷设高度对振动特性的影响 Fig. 9 Influence of laying height of constraint layer thickness on vibration characteristics |
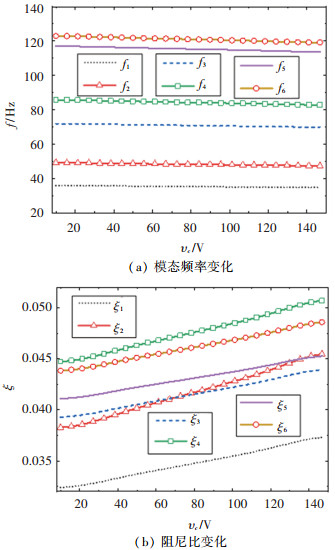
图 10是激励电压对振动特性的影响曲线。由图 10(a)可见,当压电层施加的激励电压vc增加时,模态固有频率小幅下降,而且在激励电压10~150 V变化时,各阶模态频率波动范围仅为1.5 Hz,因此激励电压不会严重影响系统工作频率范围。图 10(b)表明,压电层受到激励电压vc后,由于压电材料的逆压电效应,约束层会沿经度和纬度方向变形,使得粘弹性层的剪切应变能增加,而且电压越大,压电层形变越大,耗散应变能越大,因此模态阻尼比随电压的增加而增加。由此可见,合理施加激励电压能够增加模态阻尼比,能够使主动约束阻尼球壳减振更加有效。
|
图 10 激励电压对振动特性的影响 Fig. 10 Influence of excitation voltage on vibration characteristics |
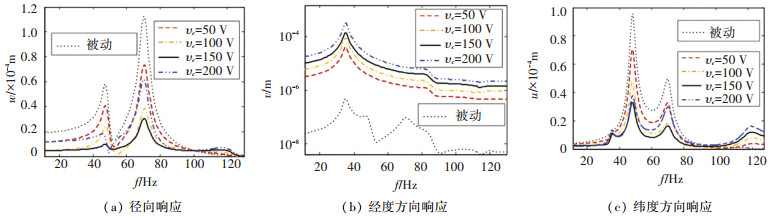
当在球壳中点施加10 N的径向载荷,其频域特性如图 11所示。由图 11(a)可见,施加激励电压的主动约束阻尼结构,较被动约束阻尼结构在第二和第三模态的径向振幅有效缩减,但对于径向振动激励电压为150 V时能够获得较大的幅值缩减,较小电压或较大电压均可能导致47.5 Hz和69.7 Hz附近较大幅值的径向振动。在图 11(b)中可以看出,由于压电层逆压电效应,虽然控制电压较大时压电层形变会使粘弹性层剪切变形增加,但由于压电层与基壳的耦合作用,球壳经度方向变形增加仍然很大,因此较大的控制电压会增加经度方形的振动。图 11(c)表明,相对于被动减振,主动约束阻尼结构在经、纬度方向仍然具有较好的减振特性,而且当vc=150 V时,在低频模态峰值仍然最小,但高频模态的减振性能有限。由上可得,对于球壳不同的工作频带以及不同方向的减振要求,可以施加不同的激励电压,而且特定电压只对特定模态减振效果较好,因此通过合理设计实时控制算法,可以在多种工况实现比较高效的减振。
|
图 11 不同vc下的频域响应 Fig. 11 Frequency domain response under different vc |
1) 取nh>9,nj>11时可以在固有频率变化较小的情况下增大阻尼比;特定粘弹性层厚度能够有效增加模态阻尼比,模态频率在一定范围内随粘弹性层厚度增加而增加;增加占空比会导致模态频率增大,但在一定程度上使损耗因子减小。
2) 增加压电层厚度会导致高频模态频率增加,而使低频模态频率减小,在hp<2 mm时,hp增加能够快速增大阻尼比;增加其经纬度方向尺寸能够导致球壳模态频率和阻尼比增大,但敷设较大尺寸的压电层会使引入质量大幅增加。
3) 压电层激励电压对模态频率影响较小,增加激励电压能够增加系统振动能量损耗;固定幅值的激励电压可使特定振动方向模态幅值有效缩减。
| [1] |
ALEKSANDR K, ROLANDS R, HOLM A, et al. Free damped vibrations of sandwich shells of revolution[J]. Journal of Sandwich Structures and Materials, 2001, 3(3): 171. DOI:10.1106/LB2E-22L4-7JA6-CAED |
| [2] |
PANDA S K, MAHAPATRA T R. Nonlinear finite element analysis of laminated composite spherical shell vibration under uniform thermal loading[J]. Meccanica, 2014, 49(1): 191. DOI:10.1007/s11012-013-9785-9 |
| [3] |
YE T G, JIN G Y, SU Z, et al. A unified Chebyshev-Ritz formulation for vibration analysis of composite laminated deep open shells with arbitrary boundary conditions[J]. Archive of Applied Mechanics, 2014, 84(4): 441. DOI:10.1007/s00419-013-0810-1 |
| [4] |
GONG Q T, LI H C, CHEN H L, et al. Application of Ritz method for vibration analysis of stepped functionally graded spherical torus shell with general boundary conditions[J]. Composite Structures, 2020, 243: 112215. DOI:10.1016/j.compstruct.2020.112215 |
| [5] |
BISWAL D K, MOHANTY S C. Free vibration study of multilayer sandwich spherical shell panels with viscoelastic core and isotropic/laminated face layers[J]. Composites Part B: Engineering, 2019, 159: 72. DOI:10.1016/j.compositesb.2018.09.075 |
| [6] |
MAO Y Q, FU Y M, TIAN Y P. Nonlinear dynamic response and active control of piezoelastic laminated shallow spherical shells with damage[J]. International Journal of Damage Mechanics, 2012, 21(6): 783. DOI:10.1177/1056789511417751 |
| [7] |
WANG J J, KONG Q Z, SHI Z F, et al. A theoretical model for designing the novel embeddable spherical smart aggregate[J]. IEEE Access, 2018, 6: 48403. DOI:10.1109/ACCESS.2018.2851454 |
| [8] |
杨颖, 金肖玲, 王永, 等. 介电弹性体球壳瞬态振动的最优参数控制[J]. 振动工程学报, 2019, 32(5): 778. YANG Y, JIN X L, WANG Y, et al. Optimal parametric control for transient vibration of dielectric elastomer spherical shell[J]. Journal of Vibration Engineering, 2019, 32(5): 778. |
| [9] |
BODAGHI M, SHAKERI M. An analytical approach for free vibration and transient response of functionally graded piezoelectric cylindrical panels subjected to impulsive loads[J]. Composite Structures, 2012, 94(5): 1721. DOI:10.1016/j.compstruct.2012.01.009 |
| [10] |
WANG J J, QIN L, WEI P J, et al. Modeling and analysis of multilayer piezoelectric-elastic spherical transducers[J]. Journal of Intelligent Material Systems and Structures, 2018, 29(11): 2437. DOI:10.1177/1045389X18770868 |
| [11] |
DU Y, SUN L P, LI S, et al. Vibration analysis of truncated spherical shells under various edge constraints[J]. Thin-Walled Structures, 2020, 147: 106544. DOI:10.1016/j.tws.2019.106544 |
| [12] |
WU Y C, HEYLIGER P. Free vibration of layered piezoelectric spherical caps[J]. Journal of Sound and Vibration, 2001, 245(3): 527. DOI:10.1006/jsvi.2001.3569 |
 2021, Vol. 53
2021, Vol. 53


