在对DCT车辆换挡品质进行客观评价时,合适的评价指标是其基础,没有一套可信的、科学的指标就无法得出合理的评价结果。目前,在DCT车辆换挡品质评价指标方面已有较多的研究。宋世欣等[1]从控制的角度出发,以结合转速波动量等10个参数作为换挡舒适性与使用寿命的评价指标,最后以AHP法确定指标权重。褚天争[2]以烦恼度、冲击度、换挡响应时间等11个指标作为换挡品质评价指标,并使用相关性分析精简指标。孙亚斌[3]以换挡时间、冲击度、加速度振动量等9个指标作为DCT车辆换挡动力性、使用寿命和舒适性评价指标,并通过熵权法确定了各个指标权重。王会义[4]以冲击度幅值和均方根值作为换挡舒适性评价指标,并进行了试验验证。国外研究中,Chalmers University of Technology课题组[5-6]对汽车换挡过程中的低频振荡现象进行了深入的研究,利用振动剂量值VDV对换挡舒适性进行量化评价。AVL公司基于神经网络构建了车辆各个工况评价模型,模型采用车辆纵向加速度、冲击度、换档时间等指标作为神经网络的输入,输出为车辆该工况下的评分。Volvo公司[7]采用车辆纵向加速度峰值、冲击度峰值等4个客观参数以及驾驶员的主观评价值作为换挡品质指标,从客观数据和主观得分来反映换挡过程的平稳性。
以上文献对DCT车辆换挡品质的各个方面进行较为全面的研究,但普遍存在着以下问题:指标数目较多,可能包含大量冗余信息,从而增加评价工作的复杂度与评价结果的可信度。另一方面,对于指标权重的确定,现有的研究采用基于专家知识的主观赋权法或者基于数据的客观赋权法,前者需要专家对指标的重要度进行打分从而忽略了数据本身包含的信息,后者则没有考虑评价主体的知识与经验。
针对以上问题,本文提出了一种基于粗糙集理论的DCT车辆换挡品质评价指标约简与赋权方法。该方法利用遗传算法优化的粗糙集知识约简方法对初选指标进行约简,同时基于属性重要度的概念确定约简后指标的权重。最后通过整车试验验证了该方法的可行性和合理性,为DCT车辆换挡品质评价及优化奠定了基础。
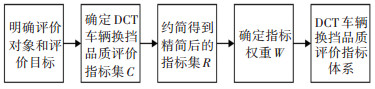
1 DCT车辆换挡品质指标体系构建步骤与指标初选 1.1 DCT车辆换挡品质指标体系构建步骤指标体系的建立过程是一个由具体到抽象再到具体的思维过程,在这一过程中评价者对评价目标和评价对象的认识逐渐深入、完善、系统化[8]。遵循以上原则,首先建立了DCT车辆换挡动力学模型,之后结合模型从换挡的动力性与平顺性角度出发完成对换挡品质指标集C的初选,在此基础之上结合专家知识D并利用遗传知识约简算法删除冗余指标,得到约简后的指标集R,最后基于属性重要度的概念确定评价指标权重W,完成指标体系的建立。其过程如图 1所示。
|
图 1 指标体系构建步骤 Fig. 1 Construction steps of index system |
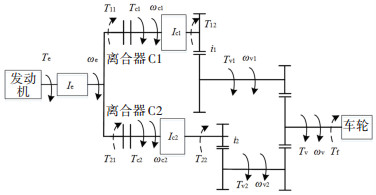
DCT车辆传动系统是个多自由度的复杂系统,假设各个部件都以集中质量的形式,对DCT车辆传动系统的建模如图 2所示[9]。
|
图 2 DCT车辆传动系动力学模型 Fig. 2 Dynamic model of DCT vehicle transmission system |
图 2中:Te为发动机输出扭矩;Ie为发动机曲轴、飞轮及离合器主动部分的转动惯量;ωe为发动机输出转速;T11、T21为离合器C1、C2输入轴反作用转矩;Tc1、Tc2为离合器C1、C2传递转矩;ωc1、ωc2为离合器C1、C2输出轴转速;Ic1、Ic2为离合器C1、C2输出轴转动惯量;T12、T22为离合器C1、C2输出轴反作用转矩;离合器C1输出轴连接奇数档和倒档,离合器C2连接偶数档,其中i1、i2为奇数档、偶数挡各个挡位传动比;Tv1、Tv2传动轴1、2传递转矩;ωv1、ωv2传动轴1、2转速;Tv为变速器输出转矩;ωv为变速器输出转速;Tf车辆总阻力矩。
以湿式离合器为例,在换挡过程中自动变速箱控制单元通过控制离合器C1,C2的结合油压间接控制其结合或者分离,配合换挡机构完成挡位的切换。以1升2档为例,其过程可以分为4个阶段:低挡运行阶段、转矩相、惯性相以及高挡运行阶段。
低挡运行阶段:低档位运行阶段时车辆位于1档,离合器C1处于结合状态,C2处于分离状态。此时,发动机扭矩全部经过离合器C1输出,整车处于一个稳定的工作状态。该阶段的动力学方程描述如下:
| $ \left\{ {\begin{array}{*{20}{l}} {\left( {{I_{\rm{e}}} + {I_{{\rm{cl}}}}} \right){{\dot \omega }_{\rm{e}}} = {T_{\rm{e}}} - {T_{12}}}\\ {{I_{{\rm{c}}2}}{{\dot \omega }_{{\rm{c}}2}} = {T_{22}}} \end{array}} \right. $ | (1) |
转矩相:在转矩相阶段,离合器C1主从动盘之间的压紧力降低,但仍旧处于结合状态;离合器C2主从动盘之间的压紧力上升,其处于滑摩状态。离合器C1和C2同时参与发动机扭矩的分配。
| $ \left\{ {\begin{array}{*{20}{l}} {\left( {{I_{\rm{e}}} + {I_{{\rm{cl}}}}} \right){{\dot \omega }_{\rm{e}}} = {T_{\rm{e}}} - {T_{12}} - {T_{21}}}\\ {{I_{{\rm{c}}2}}{{\dot \omega }_{{\rm{c}}2}} = {T_{{\rm{c}}2}} + {T_{22}}} \end{array}} \right. $ | (2) |
惯性相:在惯性相阶段,离合器C1主从动盘之间的压紧力持续降低,进入滑摩状态;离合器C2主从动盘之间的压紧力不足,仍处于滑摩状态。此时,发动机输出扭矩与离合器传递扭矩之间不一定能够匹配,可能会产生较大的冲击。该过程下动力学方程为
| $ \left\{ {\begin{array}{*{20}{l}} {{I_{\rm{e}}}{{\dot \omega }_{\rm{e}}} = {T_{\rm{e}}} + {T_{11}} - {T_{21}}}\\ {{I_{{\rm{cl}}}}{{\dot \omega }_{{\rm{c}}1}} = {T_{12}} - {T_{{\rm{cl}}}}}\\ {{I_{{\rm{c}}2}}{{\dot \omega }_{{\rm{c}}2}} = {T_{{\rm{c}}2}} - {T_{22}}} \end{array}} \right. $ | (3) |
高挡运行阶段:在高挡运行阶段,离合器C1主从动盘之间完全分离,离合器C2完全结合。发动机扭矩全部经过离合器C2输出,整车位于2档行驶并重新回归稳定状态。
| $ \left\{ {\begin{array}{*{20}{l}} {\left( {{I_{\rm{e}}} + {I_{{\rm{c}}2}}} \right){{\dot \omega }_{\rm{e}}} = {T_{\rm{e}}} - {T_{22}}}\\ {{I_{{\rm{cl}}}}{{\dot \omega }_{{\rm{c}}1}} = {T_{12}}} \end{array}} \right. $ | (4) |
换挡品质的含义是在保证汽车传动系耐久性和整车的动力性的前提下,实现换挡过程的平顺无冲击[10]。换挡品质在整车层面的表现会影响驾乘人员的主观感受,从而影响到消费者的购买意愿。当换挡品质较差时会出现以下现象:换挡响应慢持续时间长,驾驶员的动力性需求得不到满足;在换挡过程中,离合器C1、C2结合参数控制不合理导致的整车纵向抖动大、冲击与噪声明显,恶化驾乘人员的舒适感。因此确定从换挡平顺性和动力性2个评价维度出发对换挡品质进行评价,并初选了10个与之相关的参数作为初选指标集合C={c1, c2, ..., c10}。按照c1~c10的顺序,各个指标的物理含义如下。
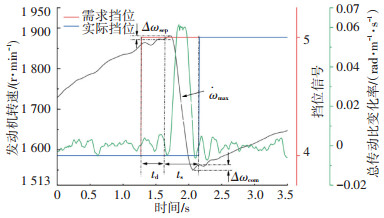
1.3.1 与时间及发动机转速相关的指标c1~c5(图 3)
|
图 3 与时间及发动机转速相关的评价指标 Fig. 3 Evaluation indexes related to time and engine speed |
1) 换挡时间ts/s。当车辆在某挡位稳定行驶时,其总传动比的变化率为0。因此将换挡时间ts定义为一次换挡过程中,总传动比变化率两次不为0时中间经历时间。换挡时间可用来衡量换挡过程的动力性,换挡时间越长动力性评价越差。
2) 换挡响应时间td/s。换挡响应时间td表示一次换挡过程中,从需求挡位发生变化到总传动比变化率发生改变所经历的时间。换挡响应时间越长,换挡动力性评价越差。
3) 发动机转速变化率ω·max/(r·min-1·s-1)。发动机转速变化率ω·max定义为:惯性相中,发动机转速对时间一阶导数绝对值的最大值。发动机转速变化率越大,换挡过程的冲击越大,车辆换挡平顺性越低。
4) 离合器分离转速超调Δωsep/(r·min-1)。在换挡过程中,由于离合器的分离使得发动机负载减少,从而导致的发动机转速瞬间变大产生超调。离合器分离转速超调越大换挡噪声与发动机轰响也就越大,换挡平顺性评价也就越差。
5) 离合器结合转速超调Δωcom/(r·min-1)。在离合器结合过程中,离合器从动盘与发动机转速逐渐接近,此时会引起发动机转速的波动。离合器结合转速超调越大说明换挡结束时发动机转速波动越大,换挡平顺性也就越差。
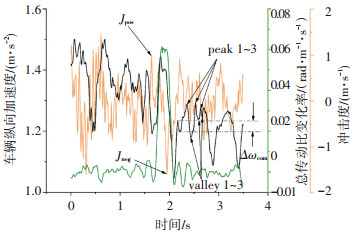
1.3.2 与车辆纵向加速度相关的指标c6~c10(图 4)
|
图 4 与车辆纵向加速度相关的评价指标 Fig. 4 Evaluation indexes related to vehicle longitudinal acceleration |
1) 离合器结合加速度幅值Δacom/(m·s-2)。离合器结合加速度幅值Δacom是指离合器结合阶段车辆纵向加速度最大值与最小值之差。该值越大则换挡平顺性越差,主观评价越低。
2) 加速度振荡Δa/(m·s-2)。加速度振荡Δa为换挡结束之后车辆纵向加速度曲线连续3个波峰与波谷之间高度的和,该值反映了离合器结合之后车辆的耸动情况。加速度振荡越大说明耸车越严重,平顺性也就越差。
3) 加速度均方根值arms/(m·s-2)。在换挡时间ts内,车辆纵向加速度的均方根值可以用来衡量换档过程中加速度的波动情况,该值越大说明换挡过程中加速度波动越大,平顺性也就越差。
4) 负向冲击度Jneg/(m·s-3)。负向冲击度Jneg表示换挡时间ts内,车辆纵向加速度对时间一阶导数的最小值。负向冲击度越小,驾驶员的前倾感越强,换挡平顺性越差。
5) 正向冲击度Jpos/(m·s-3)。正向冲击度Jpos表示在换挡时间ts内,车辆纵向加速度对时间的一阶导数的最大值。正向冲击度越大,驾驶员的后仰感越强,换挡平顺性越差。
2 基于粗糙集理论的指标约简及权重模型 2.1 粗糙集理论粗糙集理论在1982年由波兰数学家Pawlak.Z提出,是一种可以处理不完备和不确定信息的数学工具[11-12]。目前粗糙集理论已经被应用到机器学习、数据挖掘、知识发现等多个领域。
定义1:信息系统。
定义S=(U, A, V, f)是一个信息系统,或称之为知识表达系统。其中U为论域、A为属性集、V为属性A的值域集、f为信息函数。令C为条件属性,D为决策属性,则有A=C∪D且C∩D=Ø。同时定义条件属性C和决策属性D组成的系统称为决策表。
定义2:不可分辨关系。
设R为任意一个非空属性集合,即R⊆A且R≠Ø,定义不可分辨关系IND(R)为
| $ \begin{array}{l} {\mathop{\rm IND}\nolimits} (R) = \{ (x, y) \in U \times U\mid \forall a \in R, f(x, a) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;f(y, a)\} \end{array} $ | (5) |
定义3:上下近似集。
为了定义知识的近似程度,粗糙集理论引入下近似集的概念。下近似集R(X)定义为U中所有必定属于集合X的对象的集合,即
| $ \underline R (X) = \left\{ {x\mid {{[x]}_R} \subseteq X} \right\} $ | (6) |
同时,定义上近似集R(X)为U中所有必定属于和可能属于集合X的对象的集合,即
| $ \bar R(X) = \left\{ {x\mid {{[x]}_R} \cap X \ne \emptyset } \right\} $ | (7) |
其中,X的R下近似集也称为正域记作posR(X)。
定义4:条件属性对决策属性的支持度。
令C为条件属性,D为决策属性,且A=C∪D、C∩D=Ø。定义条件属性C对决策属性D的支持度γC(D)表示为
| $ {\gamma _C}(D) = \frac{{{\mathop{\rm card}\nolimits} \left( {{{{\mathop{\rm pos}\nolimits} }_C}(D)} \right)}}{{{\mathop{\rm card}\nolimits} (U)}} $ | (8) |
式中,card(*)表示集合的基。由定义可知0≤γC(D)≤1,当γC(D)=1表示决策属性完全由条件属性决定,当0<γC(D)<1时表示决策属性部分决定于条件属性,γC(D)=0则称决策属性完全独立于条件属性。
定义5:条件属性对决策属性的重要度。
定义条件属性的子集Ci对于决策属性D的重要度为
| $ {{\mathop{\rm Sig}\nolimits} _D}\left( {{C_i}} \right) = {\gamma _C}(D) - {\gamma _{C - {C_i}}}(D), {C_i} \subseteq C $ | (9) |
定义6:知识约简。
知识约简是粗糙集理论中的核心部分。知识约简就是对信息系统中规则的抽取的过程,通常包括属性约简和属性值约简两部分[13],本研究只涉及属性约简。设S=(U, A, V, f)是一个信息系统,R⊆C,若有γC(D)=γR(D),且不存在P⊆R使得γC(D)=γP(D),则称R为C相对于D的一个相对约简。
2.2 遗传知识约简算法由于知识约简已经被证明属于NP-hard问题[14],而遗传算法作为一种启发式优化算法具有高效、隐含并行及全局性的特点,因此适用于粗糙集知识约简问题。遗传算法的基本原理已经有较多文献涉及,本小节仅就与粗糙集知识约简相关的步骤进行论述。
2.2.1 染色体编码方法设条件属性集合C有n个元素, 对应n个条件属性,即有C={c1, c2, ..., cn}。使用n位二进制染色体r来对每个条件属性进行编码。其中二进制码"0"表示在染色体r中不包含对应的条件属性,"1"则相反。
2.2.2 适应度函数设计适应度函数用来评判不同个体的优劣程度,控制着不同个体的遗传行为。适应度函数一般由目标函数变换而来,其应满足非负的特点。本研究中约简效果的评判标准有两个。
1) 约简掉的条件属性个数ns(r),对应染色体r中"0"的个数。从指标体系的精简程度来看,约简掉的条件属性越多越好,即ns(r)越大越好。
2) 约简后条件属性对决策属性的支持度γC(r)(D),对应染色体r中编码为"1"的条件属性对决策属性的支持度。从指标体系的完备程度来看,决策属性应该尽可能完全由条件属性决定,即γC(r)(D)越大越好。
经过上述分析,设目标函数为max{ns+γ(r)C(r)(D)},同时由粗糙集理论知识可知0≤ns(r)≤n、0≤γC(D)≤1,所以ns(r)和γC(r)(D)对目标函数的权重并不相同。因此将ns(r)值域映射到和γC(r)(D)值域相同的范围内,并引入平衡系数α来构造染色体r的适应度函数Fr:
| $ {F_r} = \alpha \cdot \frac{{n_{\rm{s}}^{(r)}}}{n} + (1 - \alpha ) \cdot \gamma _{\rm{C}}^{(r)}(D), \alpha \in [0, 1] $ | (10) |
在遗传算子的选择方面,采用锦标赛的策略进行选择,即从上一代种群中任意挑选一组个体,并将这组个体中适应度最优的个体纳入到下一代种群中去,重复挑选直到下一代种群数目满足设定值。交叉算子采用单点交叉,该算子以概率Pc在染色体中随机的一处交叉点互换2个个体的基因。变异算子采用均匀变异,该算子以概率Pm随机反转某位基因的二进制码。
2.2.4 遗传知识约简步骤设置算法终止条件为总遗传代数达到T0或者连续T代适应度函数值不再变化,遗传知识约简算法伪代码如表 1所示。
| 表 1 遗传知识约简算法 Tab. 1 Knowledge reduction of genetic algorithm |
对于一个信息系统S=(U, A, V, f)来讲,一个属性的重要度体现在去掉该属性时知识库分类的变化程度[15]。变化程度越大说明该属性重要度越大。基于以上思路,可以通过属性的重要程度来衡量指标的权重。
设R={r1, r2, ..., rm}为经过约简后的指标集合,D为决策属性。指标ri对于决策属性D的重要度为
| $ {{\mathop{\rm Sig}\nolimits} _D}\left( {{r_i}} \right) = {\gamma _R}(D) - {\gamma _{R - {r_i}}}(D), i = 1, 2, \ldots , m $ | (11) |
对指标重要度进行归一化处理,定义指标ri的权重wi为
| $ {w_i} = \frac{{{{{\mathop{\rm Sig}\nolimits} }_D}\left( {{r_i}} \right)}}{{\sum\limits_{i = 1}^m {{{{\mathop{\rm Sig}\nolimits} }_D}} \left( {{r_i}} \right)}}, i = 1, 2, \ldots , m $ | (12) |
实验车辆选用装配有DCT的国内某款乘用车,以该车辆4档升5档不同油门开度为试验工况。试验数据采集于整车CAN信号及外接速度、加速度传感器。试验数据经过片段截取、预处理后提取换挡品质评价指标。同时为了获得不同油门开度下换挡品质评价分数,邀请5位专业整车主观评价人员对换挡过程进行独立打分,评分方式借鉴于SAEJ1060十分制,最终以5位主观评分师加权平均值作为最终换挡品质的主观评分。
3.2 换挡品质指标约简以10个初选指标作为条件属性集合C={c1, c2, ..., c10},整车主观评价人员打分作为决策属性D={d1},16组换挡样本作为原始数据。首先,通过平均相关系数rC衡量指标体系的冗余度:
| $ {r_C} = \frac{{\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\left| {{r_{ij}}} \right|} } - n}}{{{n^2} - n}} $ | (13) |
式中,rij为指标体系相关系数矩阵第i行j列的元素, n为指标数量。通常情况下平均相关系数0≤rC≤1,且越接近1表示当前指标体系的冗余度越大。由于实际整车系统的复杂性,指标间之间完全独立是不可能的,一般认为当RC≤0.5时指标之间相关度较低[16]。计算10个初选指标之间的平均相关系数rC=0.534 9,说明指标之间存在交多的冗余信息,应该进行指标约简。
由于粗糙集工具只适用于离散数据,所以还需对原始指标值进行离散化处理。首先通过Min-max规范化处理将相同属性的数据线性映射到0-1范围内,接着由Sturges经验公式确定分组数,最终通过一维K-means算法聚类后得到如表 2所示的决策表。其中,按照聚类簇中心值从小到大的顺序将各个簇中的成员赋予标签1、2、3、4。
| 表 2 换挡品质决策表 Tab. 2 Shift quality decision table |
按照本文的算法对换挡品质决策表进行约简。令适应度函数Fr中平衡系数α=0.5,并设置种群中个体总数为100、Pm=0.01、Pc=0.8、T=20、T0=200。经过计算得到最优个体的染色体r为"0100001010"、ns(r)=7、γC(r)(D)=1。
由ns(r)=7、染色体编码为"0100001010"可知,遗传知识约简算法约简掉了7个冗余指标从而只保留了3个指标{c2, c7, c9}。其中,c2为换挡响应时间td、c7为加速度振荡Δa、c9为负向冲击度Jneg。且由γC(r)(D)=1说明精简后的这3个指标对评价结论的支持度为1,即本试验中主观人员的评价结论完全由这3个指标决定。并设约简后的指标集合R={c2, c7, c9}={r1, r2, r3}。
3.3 指标约简有效性验证首先计算约简后指标集合R的平均相关系数rR=0.442 6,对比rC=0.534 9说明约简算法在数理统计意义上消除了部分冗余信息,降低了指标体系内的冗余。
考虑到粗糙集知识约简是在保持原有知识库中的分类能力不变的情况下删除冗余属性[17],因此还需对数据的分类能力进行验证。分别使用约简前指标集合C、约简后指标集合R对评价结果D进行分类预测。如果使用集合R的预测准确率优于或者等于使用集合C的,则说明约简算法在保持原有知识分类能力下约简掉了一些冗余不相关的属性,即约简模型是有效的。
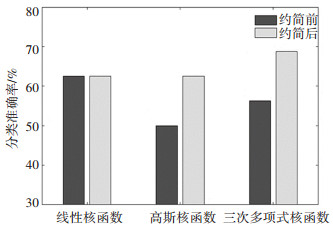
支持向量机(Support Vector Machine, SVM)作为一种有监督的机器学习算法,通过核函数将低维线性不可分问题映射到高维空间内变换为线性可分问题,因此SVM具有较高的预测准确率,尤其是在面对样本特征数目比较多而样本数目偏少的数据集时。为了验证约简有效性,分别使用线性、三次多项式、高斯核函数SVM分类模型对决策属性进行10折交叉训练验证,计算分类准确率。不同类型的核函数SVM分类模型分类准确率如图 5所示。
|
图 5 SVM分类准确率 Fig. 5 Classification accuracy of SVM |
SVM分类模型分类准确率显示,约简后的指标集合对评价结果的预测效果普遍较好。其中,基于高斯核函数的SVM分类模型准确率提升最大,相对于使用未约简的指标集合准确率上升了25%。SVM分类模型验证结果说明,遗传知识约简算法可以在保证知识分类能力的前提下删除冗余指标,保留了3个可以表征当前工况下评价人员主观感受的核心品质指标:换挡响应时间td、加速度振荡Δa、负向冲击度Jneg,提升了DCT车辆换挡品质评价指标体系的合理性。同时,对比目前整车厂通过换挡时间、冲击度、换挡后车辆纵向加速度线性程度这3个指标来衡量换挡品质,说明遗传约简算法的约简结果不但与实际工程经验较为吻合,而且可以有效地将评价主体的经验认识和整车客观试验数据结合起来挖掘出新的核心指标。
3.4 指标权重分析由公式(11)和(12)计算换挡响应时间td、加速度振荡Δa、负向冲击度Jneg的属性重要度和权重,如表 3所示。
| 表 3 属性重要度与指标权重 Tab. 3 Attribute importance and index weight |
由表 3可以看出,加速度振荡Δa权值最大,负向冲击度Jneg其次,换挡响应时间td最小。指标权重排序反映出在当前试验工况下,加速度振荡对驾驶员主观感受的影响最大、换挡响应时间最小,为DCT车辆换挡品质控制优化及评价提供了参考依据。
4 结论1) 本文从DCT车辆换挡平顺性和动力性2个评价维度出发,初步选取了以换挡时间ts、换挡响应时间td、负向冲击度Jneg、加速度振荡Δa等10个参数作为DCT车辆换挡品质评价指标。
2) 基于遗传知识约简算法对初选指标进行指标约简,得到了以换挡响应时间td、负向冲击度Jneg、加速度振荡Δa作为DCT车辆4升5档工况下换挡品质评价核心指标。通过对比3种核函数SVM分类模型在约简前后的分类准确率,实现了对约简结果进行合理性验证。结果表明,遗传知识约简算法可以有效挖掘主要品质指标,提升指标的合理性。
3) 使用基于属性重要度的定权法确定了4升5档工况下换挡品质评价指标权重,最终建立了该工况下的DCT车辆换挡品质评价指标体系。
| [1] |
宋世欣, 张元侠, 刘科, 等. 双离合器自动变速器控制品质评价指标分析[J]. 汽车工程, 2015, 37(8): 925. SONG Shixin, ZHANG Yuanxia, LIU Ke, et al. An analysis on the evaluation metrics of control quality for vehicles with dual clutch transmission[J]. Automotive Engineering, 2015, 37(8): 925. DOI:10.3969/j.issn.1000-680X.2015.08.011 |
| [2] |
褚天争. DCT换挡品质主客观评价一致性研究[D]. 长春: 吉林大学, 2020 CHU Tianzheng. Research on the consistency of subjective and objective evaluation for DCT shift quality[D]. Changchun: Jilin University, 2020 |
| [3] |
孙亚斌. 双离合自动变速器换挡品质评价方法研究[D]. 合肥: 合肥工业大学, 2017 SUN Yabin. Study on the evaluation method of shift quality for the DCT[D]. Hefei: Hefei University of Technology, 2017 |
| [4] |
HUANG Quanan, WANG Huiyi. Fundamental study of jerk evaluaion of shift quality and ride comfort[C]//SAE Automotive Dynamics, Stability & Controls Conference and Exhibition. Detroit: SAE, 2004
|
| [5] |
JOHANSSON S, LANGJORD E, PETTERSSON S. Objective evaluation of shunt and shuffle in vehicle powertrains[C]//7th International Symposium on Advanced Vehicle Control. Arnhem: [s. n. ], 2004
|
| [6] |
PERSSON J. Integrated powertrain control-a literature survey on longitudinal vibrations, drivability aspects and future challenges[D]. Gothenburg: Chalmers University of Technology, 2004
|
| [7] |
SCHNETZLER S, PETTERSSON J, MURTONEN P. Quality assurance of driver comfort for automatic transmissions[C]//SAE 200 World Congress. Detroit: SAE, 2000
|
| [8] |
李远远. 基于粗糙集的指标体系构建及综合评价方法研究[D]. 武汉: 武汉理工大学, 2009 LI Yuanyuan. Research on the construction of indicator system and comprehensive evaluation method based on rough set[D]. Wuhan: Wuhan University of Technology, 2009 |
| [9] |
付尧. 基于客观评价的双离合器自动变速器换挡控制技术研究[D]. 长春: 吉林大学, 2015 FU Yao. Research on gearshift control for dual clutch transmission based on objective evaluation[D]. Changchun : Jilin University, 2020 |
| [10] |
孙迎波. 六速DCT换挡模型及换挡品质评价体系研究[D]. 合肥: 合肥工业大学, 2015 SUN Yingbo. Study on shift models and evaluation system of shift quality for the six speed DCT[D]. Hefei: Hefei University of Technology, 2015 |
| [11] |
PAWLAK Z. Rough sets[J]. International Journal of Computer and Information Sciences, 1982, 11(5): 341. DOI:10.1007/BF01001956 |
| [12] |
张文修, 吴伟志. 粗糙集理论与方法[M]. 北京: 科学出版社, 2001. ZHANG Wenxiu, WU Weizhi. Rough set theory and method[M]. Beijing: Science Press, 2001. |
| [13] |
伞冶, 叶玉玲. 粗糙集理论及其在智能系统中的应用[J]. 智能系统学报, 2007(2): 40. SAN Zhi, YE Yuling. Rough set theory and its application in the intelligent systems[J]. CAAI Transactions on Intelligent Systems, 2007(2): 40. |
| [14] |
ZHAO H, MIN F, ZHU W. Test-cost-sensitive attribute reduction based on neighborhood rough set[C]//Proceedings of the 2011 IEEE International Conference on Granular Computing. Piscat-away, NJ: IEEE, 2011: 802
|
| [15] |
肖劲森, 孙立民. 改进的粗糙集属性重要度[J]. 计算机工程与应用, 2017, 53(3): 174. XIAO Jinsen, SUN Limin. Improved attribute significance degree based on rough set[J]. Computer Engineering and applications, 2017, 53(3): 174. |
| [16] |
付允, 刘怡君. 指标体系有效性的RST评价方法及应用[J]. 管理评论, 2009, 21(7): 91. FU Yun, LIU Yijun. The RST evaluation method of indicator system validity and its application[J]. Management Review, 2009, 21(7): 91. |
| [17] |
CHANG S. A novel attribute reduction method based on rough setsand its application[J]. International Journal of Advancements in Computing Technology, 2012, 4(3): 99. DOI:10.4156/ijact.vol4.issue3.13 |
 2021, Vol. 53
2021, Vol. 53


