2. 中国科学院大学,北京 100049;
3. 哈尔滨工业大学(深圳) 国际人工智能研究院,广东 深圳 518055
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. International Research Institute of Artificial Intelligence, Harbin Institute of Technology, Shenzhen, Shenzhen 518055, Guangdong, China
自深度学习技术兴起以来,神经网络架构设计一直是计算机视觉中最重要的基础研究之一,人类专家手工设计了大量优秀的神经网络架构(如AlexNet[1]、ResNet[2]、DenseNet[3]、SENet[4]等)。手工设计的神经网络架构,往往需要专家进行大量的试错实验。因此在限定的搜索空间中,采用网络架构搜索(neural architecture search, NAS)方法模拟专家自动设计更好神经网络架构的研究,受到了越来越多的关注[5-13]。
不同于采用强化学习[6](reinforcement learning, RL) 和进化算法[7](evolutional algorithm, EA)作为优化策略的NAS方法,文献[8]提出了可微分架构搜索算法(differentiable architecture search, DARTS),创造性地把离散空间的架构搜索问题转化为连续空间的参数优化问题[8]。在相同的搜索空间中,采用性能相近的图形处理单元(graphics processing unit, GPU),该方法可更高效地搜索架构。例如,后者计算资源需求仅为4 GPU · d,前两者则分别需要2 000 GPU · d[6]和3 150 GPU · d[7]。同时,在CIFAR-10[14]和ImageNet数据集上,后者搜得架构的性能也能达到前两种方法相近的水平[8],且3种方法搜得的架构都超越了先前人类专家设计的架构。
DARTS算法高效的架构搜索能力,吸引了众多学者的关注,并出现了一系列的改进方法[15-20]。文献[15]提出了渐进的可微分架构搜索算法(progressive differentiable architecture search, P-DARTS),以改善搜索架构的超网络与架构评测网络在网络深度上存在“鸿沟”(depth gap)的问题。文献[16]提出了随机神经网络架构搜索算法(stochastic neural architecture search, SNAS),通过限制架构参数为独热(one-hot)编码形式构建超网络,以改善DARTS因派生cell的方法而导致超网络与派生架构出现性能“鸿沟”的问题。文献[17]注意到,DARTS算法中各级cell共享架构参数的超网络本身可能存在潜在问题。本文通过跟踪超网络各级cell的skip数量变化趋势,进一步发现,共享架构参数容易造成各级cell通过架构参数相互耦合。在超网络优化后期,耦合会导致各级cell的skip操作通过架构参数叠加,并产生包含过多skip操作的cell,从而严重影响搜得架构的性能[15, 17]。
针对上述的后两项问题,本文提出了改进算法: 熵启发的分级可微分网络架构搜索。首先,针对DARTS的耦合问题,设计了新颖的分级超网络,对DARTS超网络的耦合问题进行解耦。其次,针对超网络与派生架构间的“鸿沟”问题,引入架构熵作为超网络目标函数的损失项,促使目标函数缩小超网络与派生架构因派生引起的“鸿沟”,以启发超网络在巨大的搜索空间中搜得更好的架构。最后,在图像分类数据集CIFAR-10上进行了实验,搜索阶段算法耗时仅11 h,最终构建的评测网络在该数据集上的分类错误率仅为2.69%,优于DARTS[8]、高效的网络架构搜索(efficient neural architecture search, ENAS)[13]和SNAS[16]等算法。同时其参数量仅为2.95×106,比性能相近的架构少约10%。在大规模图像分类数据集ImageNet上,本文所得架构的分类错误率仅为25.9%(对应评测网络的参数量为4.3×106),优于MobileNets[21]等手工设计的架构,也优于DARTS[8]、SNAS[16]等算法自动设计的架构,该结果表明本文搜得的架构具有较好的图像分类能力和良好的可迁移性。综合性能与参数量两项指标来看,本文搜得的架构达到了领先水平。
1 分级可微分网络架构搜索 1.1 DARTS算法简介DARTS算法以cell[6-7]为搜索的基本单元。cell由若干有序结点组成的有向无环图(directed acyclic graph, DAG)表示[8],见图 1。DAG中的结点表示特征图,连接结点的有向边表示候选操作。DARTS定义的cell共包含7个结点。其中,前两个结点为输入结点,分别代表最近临的前两个cell的输出;中间的4个结点,每个都通过有向边与其所有前序结点相连,如式(1)所示[8];最后一个结点按通道合并(concatenation,concat)4个中间结点代表的特征图[8],作为该cell的输出(output)。
| $ x^{(j)}=\sum\limits_{i<j} o^{(i, j)}\left(x^{(i)}\right) $ | (1) |

|
图 1 DARTS算法的cell图示 Fig. 1 Schematic of cell in DARTS |
式中: x(j)为cell的中间结点,x(i)为输入结点或中间结点, o(i, j)为连接x(j)和x(i)的混合操作,i和j均为结点序号。
有向边关联的候选操作集合O,共包含8个操作函数,分别是3×3/5×5可分离卷积(sep_conv)、3×3/5×5空洞可分离卷积(dil_conv)、3×3平均/最大池化(avg/max_pool)、跳跃连接(skip)和无连接(none)。
DARTS创造性地在cell中引入了架构参数α,把离散的架构搜索问题转化为连续参数空间的参数优化问题[8],并以可学习的架构参数作为候选操作的权重,构建了加权的混合操作,最终把架构搜索简化为对候选操作权重的学习。该算法还采用软最大(softmax)函数对架构参数进行松弛化操作,把架构参数的值归一化到(0, 1)区间。松弛化操作后,式(1)中的混合操作o(i, j)变形为[8]
| $ \bar{o}^{(i, j)}(x)=\sum\limits_{o \in O} \frac{\exp \left(\alpha_{o}^{(i, j)}\right)}{\sum\nolimits_{o^{\prime} \in O} \exp \left(\alpha_{o^{\prime}}^{(i, j)}\right)} * o(x) $ | (2) |
式中:
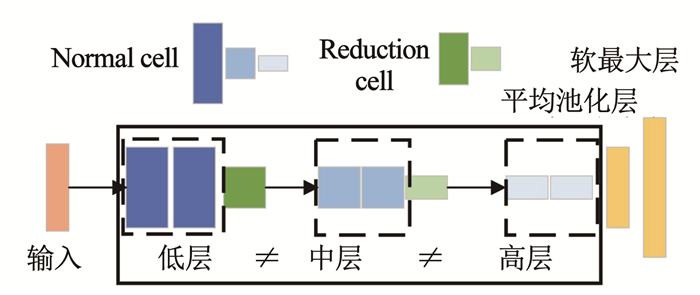
为了高效地学习cell中的参数,DARTS构建了以cell为模块的超网络(深度记为d),见图 2。超网络含有两种类型的cell,分别是常规元胞(normal cell)和降维元胞(reduction cell)[8]。Reduction cell位于超网络d/3和2d/3,步幅为2,起降维作用;normal cell特征图维度保持不变,主要起特征提取作用。超网络被reduction cell分为3个层级,每级包含M个堆叠的normal cell,后级normal cell的特征图大小则是前一级的1/2。该超网络中各级cell共享架构参数,即超网络中不同层级的cell结构完全相同[8]。超网络训练完成后,算法根据架构参数由完整cell保留部分候选操作得到派生的cell,再以派生的cell构建评测网络对架构进行性能评测。

|
图 2 DARTS构建的超网络 Fig. 2 Super network constructed by DARTS |
DARTS算法中不同层级的cell共享架构参数,意味着同一个架构参数会出现在超网络的不同深度。而超网络目标函数关于参数的梯度,是逐层求导累积得到的,那么超网络中不同深度的同一架构参数的梯度也不同。架构参数共享的设置,导致超网络优化位于不同层级cell的相同架构参数时,不同趋势的更新要在同一套架构参数中共享。这就造成不同层级cell学习到的架构参数相互影响,即产生了耦合效应。
架构参数耦合容易带来两方面的影响:1)同一架构参数,在超网络不同位置的梯度有很大差异,当不同层级cell的架构参数变化趋势不同时,造成共享的架构参数主要体现了梯度较大处的选择;2)随着超网络的训练,混合操作中含有卷积的候选操作逐渐被优化,超网络便逐渐偏向skip和pooling这类容易优化的无参数操作,由于架构参数共享,这种偏好被叠加,容易造成最后学到的架构包含大量的skip操作,导致其性能欠佳(文献[17]也注意到了这种现象)。
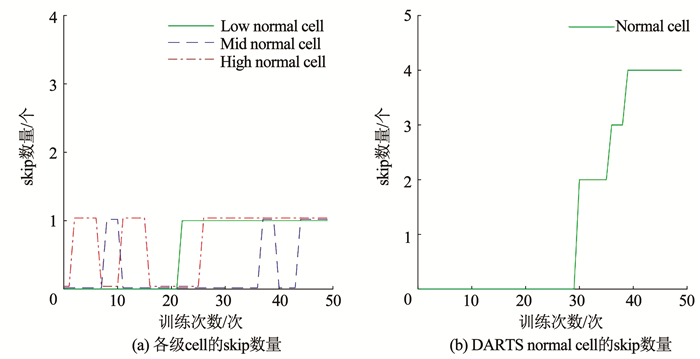
以normal cell的skip为例,本文分别跟踪各级cell的skip数量变化,发现随着超网络的优化,其数量都有所增长,如图 3(a)所示。初始化相同情况下,共享架构参数的normal cell在超网络训练的后期,由于耦合效应,造成skip数量大幅增加。该cell中skip占据操作总数的4/8(如图 3(b)所示,CIFAR-10上测试错误率为3.10%)。这导致cell中含有卷积参数的候选操作数量偏少,从而影响了cell的表征能力。
|
图 3 相同初始化,架构搜索过程cell包含的skip数量对比 Fig. 3 Comparison of skip numbers during architecture search with identical initialization |
针对DARTS算法构建的超网络出现的耦合问题,本文基于DARTS的超网络,设计了cell分级的超网络,以避免不同层级间cell的相互影响。如图 4所示,该超网络被reduction cell分为3个层级,分别为低层次常规(low normal)、中层次常规(mid normal)和高层次常规(high normal)层级。每级包含M个堆叠的normal cell,各级cell的搜索空间相同,但各自拥有独立的结构。由于reduction cell的降维作用,不同层级的normal cell对应的特征图维度则依次减小,更深一级cell中的候选操作提取的特征也更加抽象。本文超网络的设置,既允许各层级cell搜索到相同的结构,也允许更深的cell在更抽象的特征图上搜索到不同于低层cell的结构。
|
图 4 cell分级的超网络 Fig. 4 Super network constructed by multi-level cells |
与分级的超网络结构相对应,本文分别设置了低(low)、中(mid)和高(high)3个层级cell对应的架构参数:αl={αl(i, j)},αm={αm(i, j)},αh={αh(i, j)}。超网络需要学习的架构参数矩阵则为αall=(αl αm αh)T。本文超网络的训练沿用DARTS的策略,即在训练集上更新候选操作的卷积核参数w,在验证集上更新架构参数α[8],并采用DARTS的一阶近似优化算法训练超网络。超网络待优化的目标函数定义如下式所示:
| $ \min \limits_{\boldsymbol{\alpha}_{\text {all }}}\left(L_{\text {val }}\left(w^{*}\left(\boldsymbol{\alpha}_{\text {all }}\right), \boldsymbol{\alpha}_{\text {all }}\right)\right) $ | (3) |
| $ \text { s.t. } \quad w^{*}\left(\boldsymbol{\alpha}_{\text {all }}\right)=\underset{w}{\arg \min } L_{\text {train }}\left(w, \boldsymbol{\alpha}_{\text {all }}\right) $ | (4) |
式中:w为卷积核参数,Ltrain为训练集损失,Lval为验证集损失,w*为使当前训练集损失最小的卷积核参数。超网络训练完成后,按式(5)保留各级cell有向边中权重最大的候选操作。并沿用DARTS的派生策略,保留中间结点含有候选操作权重top-2的边[8],得到最终的派生架构,以构建评测网络。
| $ o_k^{(i, j)} = \mathop {\arg \max }\limits_{{o_k} \in O} \alpha _{{o_k}}^{(i, j)} $ | (5) |
式中:αo(i, j)为候选操作的权重,ok(i, j)为权重最大的候选操作。k∈{l, m, h},为cell处于低、中、高层级的表示。O代表候选操作集合,与DARTS算法一样包含8个候选操作[8],ok代表集合O中的候选操作之一。
本文设计的cell分级的超网络,从根本上改变了网络架构搜索空间的设置。按照文献[8]的计算方法,本文超网络的搜索空间包含约1063种形态的网络架构(文献[8]为1025种);由派生cell构建的评测网络形成的空间,包含约1045种(文献[8]为1018种)。从搜索空间的规模上看,本文远多于文献[8]。
这种设计的优点有:1)解除不同层级cell间的耦合;2)增加架构的多样性;3)超网络在架构搜索出现问题时,有利于定位来源,以便进一步优化。
当然,搜索空间的指数级增涨,也为搜索算法带来了巨大的挑战,这便要求更有启发性的搜索策略以应对该挑战。
1.3 熵启发正则项DARTS算法搜索架构时,超网络中各候选操作和架构参数以加权求和的方式对特征图作变换计算,并在反向传播时被更新。搜索完成后,根据该算法的派生规则[8],权重最大的架构参数对应的候选操作被认为对超网络的贡献最大,因而在派生cell中保留下来,其他候选操作则被遗弃。文献[16]指出,这种派生操作造成了超网络与派生得到的架构在验证集上的表现出现“鸿沟”(gap)问题,即超网络在验证集上的准确率较高,但派生得到的架构(未重新训练时)在验证集上的准确率与前者相差很大。文献[16]认为出现这种情况的原因是,DARTS的超网络在搜索训练完成后, 每条边的架构参数分布仍然拥有相对较高的熵,较高的熵意味着搜索方法对搜索到架构的确定性偏低。从这个环节看来,以Lval优化超网络的架构参数α的过程中,超网络中结点对之间的架构参数呈现独热向量形态时,熵最低,是最理想的优化结果。
本文构建的超网络,沿用了DARTS算法的派生策略[8],所以架构派生也存在类似问题。受文献[16]启发,本文将已归一化的架构参数向量与熵联系起来,定义了架构熵,见式(6)。该指标衡量了搜索算法对搜索结果的确定性,降低架构熵能提升超网络与派生架构在验证集上表现的相关性。
| $ L_{\text {entropy }}=-\sum \bar{\alpha}_{k}^{(i, j)} \times \ln \left(\bar{\alpha}_{k}^{(i, j)}\right) $ | (6) |
式中:Lentropy为架构熵,
以Lentropy作为该目标函数的损失项,可启发超网络在逐渐更新架构参数时,兼顾架构参数的分布,使架构参数在参数空间中向独热向量收敛。架构搜索环节,超网络的目标函数由式(3)变为式(7)。
| $ \min \limits_{\boldsymbol{\alpha}_{\mathrm{all}}}\left(L_{\mathrm{val}}\left(w^{*}\left(\boldsymbol{\alpha}_{\mathrm{all}}\right), \boldsymbol{\alpha}_{\mathrm{all}}\right)+\gamma \times L_{\text {entropy }}\right) $ | (7) |
式中γ为平衡Lval和Lentropy的超参数,其他变量与以上公式定义一致。γ值的选择见2.2节。
2 实验及结果本文搜索阶段实验采用的操作系统为Windows 10,处理器为Intel i7-7800X,GPU为NVIDIA GeForce GTX 1080Ti。评测阶段实验采用的操作系统为Ubuntu 16.04,处理器为Xeon E5,训练和测试CIFAR-10使用的显卡为NVIDIA GeForce GTX 1080Ti,训练和测试ImageNet使用的显卡为NVIDIA Titan RTX。编程语言均为Python 3.6,深度学习框架均为Pytorch。
2.1 实验数据集如DARTS等算法一样,本文采用图像分类数据集CIFAR-10[14]和ImageNet作为实验数据集。算法的架构搜索环节在CIFAR-10上完成,并分别在CIFAR-10和ImageNet对进行架构评测。
CIFAR-10数据集包含60 000张分辨率为32×32的图像,共10类。其中训练集包含50 000张图像,测试集包含10 000张图像。搜索架构时,把训练集均分为两个子集(分别为Strain和Sval),Strain用于更新超网络中候选操作的卷积核参数w,Sval用于更新超网络中的架构参数α[8]。搜索架构完成后,以完整cell得到派生的cell,再以后者构建评测网络[8]。评测网络在训练集上重新开始训练,结束后在测试集上进行评测,并以该测试准确率作为搜得架构的性能评价指标。在超网络训练和评测网络训练时,测试集均未使用,仅在测试评测网络时,测试集才被使用。
ImageNet是图像分类研究中最权威的常用数据集之一。其训练集包含约128万张图像,验证集包含50 000张图像,共1 000类。在该数据集上,本文采用与DARTS等算法一样的实验设置,通过剪切原图像得到分辨率为224×224的样本,并将这些样本作为评测网络的输入,对其进行训练和测试。
2.2 熵启发损失项的超参数选择本文设计了实验,以确定式(7)中熵启发损失项的超参数如何设置。如表 1所示,本文分别设置了γ= 0、0.1、1、5、10,共5组实验。每组重复进行4次完整的架构搜索与评测实验,以评测结果的平均值作为该超参数选择的依据。由实验结果可知,熵启发项的系数为0时,超网络在1063搜索空间中,仅依靠可微分方法搜索网络架构具有一定的难度;γ=1时,搜得的架构表现最好;当熵启发项的系数增大到5时,损失函数中熵启发损失项所占比重过大,影响了可微分方法的搜索。因此,本文以γ= 1作为熵启发项的超参数值。
| 表 1 γ不同取值在CIFAR-10平均性能 Tab. 1 Average performance of different values of γ on CIFAR-10 |
本文的超网络按不同层级分级设置cell,相应地搜得的各级cell也可能不同。DARTS搜得的架构仅包含一个normal cell和一个reduction cell[8],而本文算法搜得的架构包含3个层级的cell,各级cell如图 5所示。由于高层级cell与池化层相接,所以不包含reduction cell。

|
图 5 分级超网络搜得的各级cell(搜索采用了熵启发损失项) Fig. 5 Cell architectures searched by proposed algorithm (search algorithm with entropy loss term) |
由图 5所示,本文采用分级超网络后,搜得的架构解除了参数共享带来的耦合效应,不同层级cell包含的skip操作仅影响本层级的cell结构。如图 5(a)所示,该cell不包含skip操作,而图 5(b)、图 5(c)各cell都含有两个skip操作。此外,DARTS搜得的normal cell包含的候选操作类别较少,分别是sep_conv_3×3、dil_conv_3×3和skip_connect。而本文搜得的cell,包含的候选操作更加多样,能提取更丰富的特征。
2.4 实验结果 2.4.1 CIFAR-10实验结果沿用DARTS算法的架构筛选策略[8],本文也重复了4次架构搜索实验,并分别构建评测网络。在CIFAR-10上随机初始化卷积参数w后,训练评测网络,以最优测试结果的架构作为算法的最终架构。如表 2所示,以人工设计的DenseNet[3]为基准,NAS算法搜得的网络架构在CIFAR-10上都超越了该基准架构,这表明了网络架构搜索算法的潜力。与其他自动搜索网络架构方法相比,本文搜得的网络架构取得了具有竞争力的结果。
| 表 2 搜得架构在CIFAR-10上与其他NAS算法搜得架构的性能对比 Tab. 2 Performannce comparison of architectures searched by proposed algorithm and other NAS methods on CIFAR-10 |
从测试错误率上看,仅采用本文分级策略构建的超网络搜得的架构,在CIFAR-10上的错误率为2.88%,优于DARTS_V1[8]搜得的架构,并与SNAS[16]相近;增加熵启发损失项后,本文搜得架构的错误率进一步降低到2.69%,与NASNet-A[6]相近。从参数量指标看,与性能相近的NASNet-A[6]相比,本文架构的参数量更低。其原因是本文分级设置cell的超网络构建方法,得到的mid normal和high normal两级cell的参数量都较低。同时,本文采用DARTS算法的一阶近似优化策略,搜索时间远低于NASNet-A[6],且与P-DARTS[15]相近。综上,实验结果证明了本文所提方法的有效性,并且本文所提方法计算资源需求低、分类表现好、搜得架构的参数量少。
2.4.2 ImageNet实验结果为了验证本文搜得架构的可迁移性,本文进一步在ImageNet上进行了评测实验。构建评测网络的方式与DARTS算法保持一致,即网络深度d=14,网络初始通道数C0=48。该评测网络的训练采用与文献[15]相同的策略。沿用DARTS算法的限制条件,本文也选择输入样本分辨率为224×224时,运算乘加次数<600×106(移动设备运算要求)的网络进行对比。本文架构及对比算法所得架构在ImageNet上的性能表现见表 3。其中,“≈”表示约等于。
| 表 3 搜得架构在ImageNet与其他NAS算法搜得架构的性能对比 Tab. 3 Performance comparison of architectures searched by proposed algorithm and other NAS methods on ImageNet |
以本文搜得架构构建的评测网络,在ImageNet上取得了25.9%的分类错误率,不仅优于Inception[22]、MobileNet[21]、ShuffleNet[23]等手工设计的网络架构,还优于DARTS[8]、SNAS[16]等算法自动设计的网络架构,这表明了本文架构的可迁移性。同时本文评测网络的参数量仅为4.3×106,比参数量相同的SNAS[16]分类错误率低1.4%。与分类错误率相近的NASNet-A[6]相比,本文评测网络的参数量低1.0×106。本文评测网络的乘加次数也只有533×106,但比乘加次数相近的ShuffleNet[23]和SNAS[16]有更好的分类性能。结合分类错误率、参数量和乘加次数3项指标,ImageNet上的实验结果表明,本文搜得的架构具有更好的特征提取和图像分类能力。
3 结论设计了cell分级的超网络,对DARTS算法各层级cell存在耦合的现象进行了解耦。实验结果表明,采用本文设计的超网络,避免了架构参数共享引起的耦合效应,并提升了搜得架构的性能。引入熵启发的损失项后,降低了超网络与派生架构的“鸿沟”,进一步提升了搜得架构的表现。最后,本文按层级构建超网络和评测网络的设计,可启发探索新的网络架构搜索范式。
| [1] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks[J]. Communications of the ACM, 2017, 60(6): 84. DOI:10.1145/3065386 |
| [2] |
HE K, ZHANG X, REN S, et al. Deep residual learning for image recognition[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016: 770. DOI: 10.1109/CVPR.2016.90
|
| [3] |
HUANG G, LIU Z, VAN DER MAATEN L, et al. Densely connected convolutional networks[C]//Proceedings of the IEEE Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017: 4700. DOI: 10.1109/CVPR.2017.243
|
| [4] |
HU J, SHEN L, SUN G. Squeeze-and-excitation networks[C]//Proceedings of the IEEE Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 7132. DOI: 10.1109/CVPR.2018.00745
|
| [5] |
ZOPH B, LE Q V. Neural architecture search with reinforcement learning[EB/OL]. [2017-02-15]. https://arxiv.org/pdf/1611.01578
|
| [6] |
ZOPH B, VASUDEVAN V, SHLENS J, et al. Learning transferable architectures for scalable image recognition[C]//Proceedings of the IEEE Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 8697. DOI: 10.1109/CVPR.2018.00907
|
| [7] |
REAL E, AGGARWAL A, HUANG Y, et al. Regularized evolution for image classifier architecture search[C]//Proceedings of the AAAI Conference on Artificial Intelligence. Honolulu: AAAI, 2019, 33: 4780. DOI: 10.1609/aaai.v33i01.33014780
|
| [8] |
LIU H, SIMONYAN K, YANG Y. DARTS: differentiable architecture search[EB/OL]. [2019-04-23]. https://arxiv.org/abs/1806.09055
|
| [9] |
LIU H, SIMONYAN K, VINYALS O, et al. Hierarchical representations for efficient architecture search[EB/OL]. [2018-02-22]. https://arxiv.org/abs/1711.00436
|
| [10] |
BROCK A, LIM T, RITCHIE J M, et al. SMASH: one-shot model architecture search through HyperNetworks[EB/OL]. [2017-08-17]. https://arxiv.org/abs/1708.05344
|
| [11] |
BAKER B, GUPTA O, RASKAR R, et al. Accelerating neural architecture search using performance prediction[EB/OL]. [2017-11-08]. https://arxiv.org/abs/1705.10823
|
| [12] |
RADOSAVOVIC I, KOSARAJU R P, GIRSHICK R, et al. Designing network design spaces[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020: 10428. DOI: 10.1109/CVPR42600.2020.01044
|
| [13] |
PHAM H, GUAN M Y, ZOPH B, et al. Efficient neural architecture search via parameter sharing[EB/OL]. [2018-02-12]. https://arxiv.org/abs/1802.03268
|
| [14] |
KRIZHEVSKY A, HINTON G. Learning multiple layers of features from tiny images[R]. Toronto: University of Toronto, 2009
|
| [15] |
CHEN X, XIE L, WU J, et al. Progressive differentiable architecture search: bridging the depth gap between search and evaluation[C]//Proceedings of the IEEE International Conference on Computer Vision. Long Beach: IEEE, 2019: 1294. DOI: 10.1109/ICCV.2019.00138
|
| [16] |
XIE S, ZHENG H, LIU C, et al. SNAS: stochastic neural architecture search[EB/OL]. [2019-01-12]. https://arxiv.org/abs/1812.09926
|
| [17] |
LIANG H, ZHANG S, SUN J, et al. DARTS+: Improved differentiable architecture search with early stopping[EB/OL]. [2020-10-20]. https://arxiv.org/abs/1909.06035
|
| [18] |
XU Y, XIE L, ZHANG X, et al. PC-DARTS: partial channel connections for memory-efficient differentiable architecture search[EB/OL]. [2020-04-07]. https://arxiv.org/abs/1907.05737
|
| [19] |
FANG J, SUN Y, ZHANG Q, et al. Densely connected search space for more flexible neural architecture search[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020: 10628. DOI: 10.1109/CVPR42600.2020.01064
|
| [20] |
WU B, DAI X, ZHANG P, et al. FBNet: hardware-aware efficient ConVnet design via differentiable neural architecture search[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019: 10734. DOI: 10.1109/CVPR.2019.01099
|
| [21] |
HOWARD A G, ZHU M, CHEN B, et al. MobileNets: efficient convolutional neural networks for mobile vision applications[EB/OL]. [2017-04-17]. https://arxiv.org/abs/1704.04861
|
| [22] |
SZEGEDY C, LIU W, JIA Y, et al. Going deeper with convolutions[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Boston: IEEE, 2015: 1. DOI: 10.1109/CVPR.2015.7298594
|
| [23] |
ZHANG X, ZHOU X, LIN M, et al. ShuffleNet: an extremely efficient convolutional neural network for mobile devices[C]//Proceedings of the IEEE conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 6848. DOI: 10.1109/CVPR.2018.00716
|
 2021, Vol. 53
2021, Vol. 53


