2. 西北工业大学 无人机系统国家工程研究中心,西安 710072
2. UAV National Engineering Research Center, Northwestern Polytechnical University, Xi'an 710072, China
海雾是一种常常发生于中国沿海的灾害天气现象,在海面、岛屿和滨岸低层大气中积聚大量水滴和冰晶,其能见度往往小于1 km[1]。海雾形成包括两个环节——水汽凝结和雾滴低空积聚。分析雾滴残存物发现,水汽凝结核由燃烧核、盐微粒和土壤粒子组成,其比例是5∶ 4∶ 1[2-5]。其中,燃烧核半径为1 μm左右,表面包裹着吸湿凝结性很强的膜。因此,海面空气中吸湿性粒子的浓度较高,导致海边比内陆更容易起雾。雾滴低空积聚后一般直径为10 μm左右,尺寸较小,悬浮在近海空气中,致使大气能见度较低。海雾粒子散射作用会导致可见光摄像头采集的视频图像对比度低、颜色失真,严重影响海上场景监控、舰船视觉导航、渔船作业、军事活动以及沿海交通的正常运行。
现有去雾方法从原理上大致可分为图像增强去雾方法和物理模型图像复原方法。前者主要是提高对比度,但未考虑导致图像降质的因素,并未实质消除雾,效果非常有限[6-8]。而在物理模型图像复原方法中,Oakley等[9-10]建立了多参数统计退化模型,对灰度场景进行可见性复原。Tan等[11]改进了统计退化模型,对雾天彩色图像进行可见性复原。这些方法必须已知场景深度,其详细深度信息需要利用高精度测距设备才能获得,应用成本较高。Narasimhan等[12-13]利用多幅不同天气的同一场景退化图像作为辅助信息,从多个角度研究利用场景深度复原图像。这种方法在实际应用中对条件要求比较苛刻,适用范围有局限。近年来,很多学者[14-16]开始着手研究基于先验知识的单幅图像去雾方法。He等[17]统计分析大量图像,发现不含天空的图像区域中,取像素R、G、B的最小值,该值总是趋向于0,定义为暗通道。利用暗通道作为先验信息估计大气光和透射率,同时通过软抠图获取透射率的粗估计并滤波,得到精确透射率,从而利用雾天成像模型复原图像[18]。海面监控画面中天空相对较多,暗通道方法一般不适用于海雾情况。朱青松等[16]在2015年提出了一种颜色衰减先验理论,即雾天条件下,景物的亮度变高而色彩饱和度降低,经过大量统计证实了这一理论,并给出了亮度和饱和度之间定性和定量的关系。
海上监控画面获取的含雾图像与一般含雾图像不同,由于拍摄场景本身因素,图片中含有大量的天空等明朗区域,且这些区域通常与含雾区域混杂。在这些明亮区域中,暗通道先验在一定程度上失去作用,导致全局大气光值选取出现偏差,使用雾天降质模型对图像复原效果变差,图像中的部分信息因为图像复原过程中场景透射率等的偏移而丢失,图像亮度较低且色彩失真严重,对海面场景监控、海上目标跟踪与识别以及海上行为分析等带来了负面影响。
通过分析海雾图像降质机理,针对传统依赖单一先验知识的去雾算法往往存在估计大气光值不够精确致使还原图像颜色失真、比较昏暗的问题,提出了一种基于最小方差中值引导滤波融合变差函数和颜色衰减先验理论的去海雾图像算法,使用变差函数[19]可以较快地判别出像素点是否隶属于白色或高亮区域,从而标记出图像中的天空区域,但其易将近景区域中物体本身为白色的区域囊括在内;使用颜色衰减先验理论则可以有效去除图像中近景部分本身存在的纯白色区域,但其对图片中的高亮天空区域估计较差。因此使用二者同时对图像中的非天空区域进行估计,并对获得区域取并运算, 以相互弥补各自估计错误的区域,得到较为准确的非天空区域,最终获得较好的复原效果。
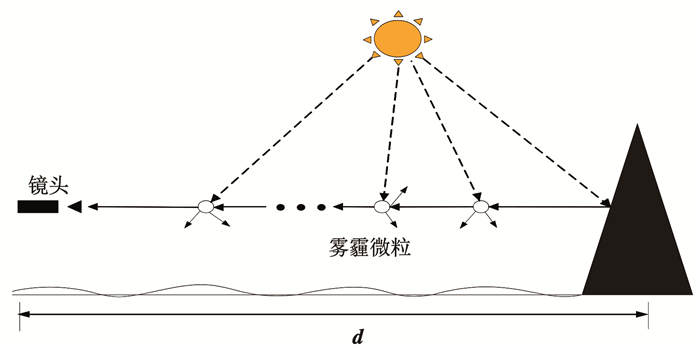
1 含海雾图像降质模型借鉴文献[20-23],建立海雾天图像降质模型见图 1,镜头获取参与成像的光线由场景中目标物的反射光与大气中悬浮雾霾颗粒散射作用后的环境光组成,其中目标物的反射光在传输过程中会受到大气中微粒的散射和吸收作用从而导致衰减,分析该模型可知海雾颗粒对光线的作用以及对成像的影响。含海雾图像的模型为
| $ \mathit{\boldsymbol{L}}(x,y) = {\mathit{\boldsymbol{L}}_0}(x,y){{\rm{e}}^{ - k\mathit{\boldsymbol{d}}(x,y)}} + {\mathit{\boldsymbol{L}}_{\rm{s}}}\left( {1 - {{\rm{e}}^{ - k\mathit{\boldsymbol{d}}(x,y)}}} \right) $ | (1) |
|
图 1 海雾颗粒对成像影响过程 Fig. 1 Influence process of sea fog particles on imaging |
式中:采集的含雾降质图像为L (x, y),d (x, y) 为场景深度,L0(x, y)e-kd (x, y)为入射光衰减模型,Ls(1-e-kd(x, y)) 为大气光成像模型,Ls为环境光亮度,e-kd(x, y)为透射分布率。L0(x, y)为反射光强度。k为大气散射系数,微粒大小为γ,波长为λ,计算如式(2)所示。
| $ k(\lambda) \propto \frac{1}{\lambda^{y}} $ | (2) |
通过对上述模型的分析可以得出图像降质的成因:低空积聚后形成的海雾颗粒直径为10 μm左右,尺寸远远大于晴朗条件下直径为10-4 μm左右的正常空气微粒。因此,在海雾条件下,可认为相比于波长,颗粒大小作为影响大气散射系数的主要因素,致使对不同颜色光线近似等量散射,因此获取的海雾图像呈现灰白。同时,从式(1)中入射光衰减模型的计算公式可知,图像亮度也会受到景深影响呈指数衰减。海雾颗粒的折射和散射作用还会在成像中引入噪声,引起离焦模糊,图像质量较差。
2 融合变差函数和颜色衰减先验理论的大气光估计在基于物理模型的含雾图像复原过程中,大气光估计值是否准确决定了去雾后图像的亮暗程度。在求解全局大气光时,传统暗通道去雾方法通常直接选取暗通道图像中最亮的1‰像素点对应含雾图像中像素点的亮度值作为大气光值。该方法受图像中白色或高亮区域的影响,估计的大气光值不够准确,存在较大局限性。因此,为了剔除出图像中的白色(高亮区域),本文提出了一种融合变差函数和颜色衰减先验理论的方法来得到较为准确的全局大气光估计值。通常直接采用暗通道图像中最亮的1‰像素点亮度值作为大气光值。实际情况中该方法受图像中白色或高亮区域的影响,估计的大气光值往往偏离实际大气光值。
2.1 变差函数文献[24]经过大量实验提出了一种可判断暗通道图像中像素点是否来自高亮区域的函数,即变差函数。用公式描述如下:
| $ \left\{\begin{array}{l} \boldsymbol{S}(x, y)=\lambda\left(\sum\nolimits_{i \in\{\mathrm{R}, \mathrm{G}, \mathrm{B}\}} \frac{\left(\boldsymbol{I}_{i}(x, y)-\boldsymbol{m}(x, y)\right)^{2}}{3}\right)^{\frac{1}{2}} \\ \boldsymbol{m}(x, y)=\frac{\sum\nolimits_{i \in\{\mathrm{R}, \mathrm{G}, \mathrm{B}\}} \boldsymbol{I}_{i}(x, y)}{3} \end{array}\right. $ | (3) |
式中:Ii(x, y)表示像素点(x, y)在某一颜色通道的值; m(x, y)为对应位置像素点在3个通道的均值; S(x, y)为对应位置的变差函数值; λ为引入的比例系数,经过大量实验这里取经验值为18。
由变差函数的定义可见,S(x, y)在高亮区域非常小,在其他区域比较大。
计算含雾图像对应的暗通道图像,根据变差函数判断像素点是否隶属于白色或高亮区域(Δ为阈值)。若S ≥Δ,则将该点作为一个有效全局环境光值依据,并基于变差函数求得图像暗部,记为IVAM_dark;若S<Δ,认为其来源于白色或高亮区域并舍弃像素点数据。
2.2 颜色衰减先验理论颜色衰减先验理论是对大量含雾图像统计后得到的规律。对于海上含雾监控图像来说,场景深度越大的区域,雾的浓度越高。根据颜色衰减先验理论,图像中任意区域雾的浓度与该区域像素点的明度和饱和度之差成正相关,因而可以得到含雾图像中不同区域景深的差异,用数学公式描述为
| $ \boldsymbol{d}(x, y) \propto \boldsymbol{c}(x, y) \propto \boldsymbol{v}(x, y)-\boldsymbol{s}(x, y) $ | (4) |
式中:d(x, y)表示图像中坐标为(x, y)处的像素点对应的场景深度,c (x, y)为该点处的雾气浓度,v (x, y)和s (x, y)分别代表该像素点的明度和色彩饱和度。
场景深度同亮度与饱和度之差的相关性见图 2。左边为含雾图像,分别截取近景、薄雾、浓雾3个30×30像素单位大小的矩形区域,统计其色彩明度和饱和度之差如图 2右边从上到下3个小图所示,可以看出场景深度越大,色彩明度和饱和度的差值越大。

|
图 2 颜色衰减先验示意 Fig. 2 Schematic of color attenuation prior |
从大气散射模型的角度来看,颜色衰减先验理论是指:一方面目标场景光线在穿过空气悬浮的微粒进入图像采集设备时发生了折射和散射,导致光线的明度和饱和度均产生了衰减;另一方面空气中的微粒的折射作用,将非目标场景中的光线引入图像采集设备中,参与成像过程(即大气光成像过程),导致含雾图像的色彩明度增强,由于大气光影响较大导致最终采集到的含雾图像色彩明度增强而饱和度降低,且随着雾气浓度越大(即场景深度越大),像素的色彩明度和饱和度之差越大。
2.3 融合变差函数和颜色衰减先验理论的大气光估计含雾图像中天空及白色区域会影响对大气光的准确估计。针对这个问题,提出了一种融合变差函数和颜色衰减先验理论的估计大气光方法。首先求出含雾图像对应的暗通道图像。本文结合拍摄的含海雾图像一般包括较多天空区域的特点,同时经过大量实验,实验中设置阈值取经验值Δ=35,求出IVAM_dark。再根据颜色衰减先验理论,将含雾图像转换到HSV颜色空间,求解各个像素点的色彩明度和饱和度之差,即
| $ \boldsymbol{D}(i, j)=\boldsymbol{I}^{\mathrm{v}}(i, j)-\boldsymbol{I}^{\mathrm{s}}(i, j) $ | (5) |
式中Iv(i, j)和Is(i, j) 分别为像素点(i, j)处的色彩明度和饱和度,D(i, j)为该像素点对应的颜色衰减率。
求解整幅含雾图像对应的颜色衰减率图像,并将其值按降序进行排序,取前10%的颜色衰减率作为颜色衰减先验变换的亮暗部分界阈值,根据该阈值得到原雾化降质图像的暗部,记为IHSV_dark。
对由变差函数得到的图像暗部IVAM_dark和颜色衰减先验理论得到的暗部IHSV_dark取并集,得到用于估计暗区域大气环境光值Adark的暗部图像Imark_dark,进行递减排序,选取像素值排在前1‰的含雾降质图像像素点集合的平均值作为Adark的值。
3 基于多级权重相对总变差模型的透射率估计根据雾天图像成像模型和大气对光线的散射特性,含雾图像中每个像素点所对应的大气耗散函数均为0到各颜色通道的最小值之间的正值,因此可以利用3通道的最小颜色分量即最小通道图对大气耗散函数值V进行估计
| $ \boldsymbol{I}_{\min }(i, j)=\min \limits_{c \in\{\mathrm{R}, \mathrm{G}, \mathrm{B}\}} \boldsymbol{I}_{c}(i, j) $ | (6) |
式中Ic(i, j) 为含雾图像中坐标(i, j)处R、G、B某一颜色通道的值。
计算的大气耗散函数值包含了丰富的纹理和边缘信息。而Tan[7]认为大气耗散函数跟场景深度数据有关,仅在景深突变的区域可能会产生边缘,因此,去除纹理信息对准确估计大气耗散函数十分重要。
3.1 相对总变差模型相对总变差模型(relative total variation model,RTV)是一种不依赖纹理先验知识和人工干预,仅利用函数的总变差区分纹理和结构信息的方法,其公式描述为
| $ \begin{gathered} \arg \min \sum\limits_{\boldsymbol{p}}\left(S_{\boldsymbol{p}}-I_{\boldsymbol{p}}\right)^{2}+ \\ \lambda\left[\frac{D_{x}(\boldsymbol{p})}{L_{x}(\boldsymbol{p})+\psi}+\frac{D_{y}(\boldsymbol{p})}{L_{y}(\boldsymbol{p})+\psi}\right] \end{gathered} $ | (7) |
式中:p为某一局部区域,Sp和Ip分别为分解出的结构图和原图在该区域的值,(Sp-Ip)2表示结构图和原图的相似度,λ为权重系数。Dx、Dy和Lx、Ly分别为x和y方向上区分纹理和结构信息的正则化系数,ψ是用来预防分母为0的调整系数。
由于相对总变差模型本身的固定性,对于实际含雾降质图像而言,在多样的气象条件及拍摄方式影响下,无法适应去雾模型中大气透射率的粗略估计,因而必须改进模型。
3.2 多级权重相对总变差模型针对相对总变差模型的局限性,本文提出一种新的多级权重相对总变差模型(multi-level weight relative total variation model,MWRTV)。权重相对总变差在RTV基础上引入平滑权重系数η,用于对平滑程度修正,其公式为
| $ \begin{aligned} &\arg \min \sum\limits_{\boldsymbol{p}}\left\{\left(S_{\boldsymbol{p}}-f_{\boldsymbol{p}}\right)^{2}+\right. \\ &\left.\lambda \sum\limits_{i}\left[a_{x, \boldsymbol{p}(i)}\left(\frac{\partial S}{\partial x}\right)^{2}+a_{y, \boldsymbol{p}(i)}\left(\frac{\partial S}{\partial y}\right)^{2}\right]\right\} \end{aligned} $ | (8) |
其中:
| $ a_{x, \boldsymbol{p}(i)}=w_{x} \cdot u_{x} $ | (9) |
| $ a_{y, \boldsymbol{p}(i)}=w_{y} \cdot u_{y} $ | (10) |
| $ w_{x}=\left[\max \left(\left|\frac{\partial f}{\partial x}\right|, \psi\right)\right]^{-1} $ | (11) |
| $ w_{y}=\left[\max \left(\left|\frac{\partial f}{\partial y}\right|, \psi\right)\right]^{-1} $ | (12) |
| $ u_{x}=\left[\max \left(\left|g_{\boldsymbol{p}} * \frac{\partial f}{\partial x}\right|^{\eta}, \psi\right)\right]^{-1} $ | (13) |
| $ u_{y}=\left[\max \left(\left|g_{\boldsymbol{p}} * \frac{\partial f}{\partial y}\right|^{\eta}, \psi\right)\right]^{-1} $ | (14) |
式中:p,Sp,Ip,(Sp-Ip)2,λ,ψ与式(7)相同; ax, p(i)和ay, p(i)为平滑项权重系数,其目的是在x和y方向上区分纹理和结构信息的正则化系数。平滑权重系数η用于修正纹理和结构信息对最终结果的影响。
MWRTV根据不同平滑权重系数η下对图像纹理及边界的不同影响,采用不同η取值多级处理图像。首先,对于输入的暗通道图像进行去纹理信息处理,即使用较小的平滑权重系数η,以减少图像内无用的纹理信息;然后,对上述处理后的图像进行边界增强处理,以突出图像内的边界景深信息,即使用较大的平滑权重系数η。

|
图 3 多级权重相对总变差流程图 Fig. 3 Flow chart of multi-level weight relative total variation model |
使用多级权重相对总变差对最小值图像进行滤波,去除最小通道图中包含的纹理信息得到大气耗散函数的粗估计W。根据大气散射模型,则可得透射率的粗估计,表示为
| $ {\mathit{\boldsymbol{t}}_{{\rm{estimate }}}} = 1 - \varphi \times \frac{W}{A} $ | (15) |
式中φ为去雾系数。考虑到空间透视现象的存在,如果完全移除雾霾,图像看起来会不自然并且可能丢失景深信息,所以需要对远处的对象保留少量的雾霾,此外,雾霾的存在是人类感知深度的基本线索[25],并且He等[17]对此进行了详细论述。因此,为防止去雾过于彻底,且复原后图片需符合真实人类视觉感受,经过大量数据实验测试后,φ在此取值为0.9。
4 基于最小方差中值引导滤波的透射率二次估计 4.1 引导滤波器引导滤波本质是基于最小二乘法的最优化过程,避免了求最优解过程中的迭代运算。通过滤波器能够融合引导图像特征,对滤波图像进行修正。计算公式如下:
| $ \boldsymbol{q}_{i}=a_{k} \boldsymbol{I}_{i}+b_{k}, \forall i \in \boldsymbol{\omega}_{k} $ | (16) |
式中:I为输入引导图像,q为输出图像,ωk为局部滤波窗口,ak和bk是以像素k为中心的窗口系数,Ii及qi分别为引导图像及输出图像窗口内临近像素点。对式(16)求梯度得
| $ \nabla \boldsymbol{q}=a \nabla \boldsymbol{I} $ | (17) |
通过式(17)可以看出,I与q的梯度相关性能够说明该滤波器的边缘保持能力。定义
| $ \mathrm{E}\left(a_{k}, b_{k}\right)=\sum\limits_{i \in \boldsymbol{\omega}_{k}}\left(\left(a_{k} \boldsymbol{I}_{i}+b_{k}-\boldsymbol{p}_{i}\right)^{2}+\varepsilon a_{k}^{2}\right) $ | (18) |
式中ε为正则化平滑因子,防止ak过大。计算ak和bk最优解,保证I和q差异最小,即式(18)的值最小,就能使得q具有I的边缘特征。求解ak和bk及式(16)可得滤波输出q即为平滑后的区域大气光,利用最小二乘法计算最优解可得
| $ a_{k}=\frac{\frac{1}{|\boldsymbol{\omega}|} \sum\nolimits_{i \in \boldsymbol{\omega}_{k}} \boldsymbol{I}_{i} \boldsymbol{p}_{i}-\boldsymbol{\mu}_{k} \overline{\boldsymbol{p}}_{k}}{\boldsymbol{\sigma}_{k}^{2}+\varepsilon} $ | (19) |
| $ b_{k}=\overline{\boldsymbol{p}}_{k}-a_{k} \mu_{k} $ | (20) |
式中:μk和σk2分别为引导图像I在ωk内的像素均值和方差; |ω|是ωk的像素数量; pk是输入图像p在窗口内的像素均值。
4.2 最小方差中值引导滤波器的设计本文设计了一种新的最小方差中值引导滤波器,其工作原理是:计算图像模板邻域内的方差,选择图像灰度值较均匀的区域中值替代模板中心像素灰度值。而模板较均匀的区域所对应的方差是最小的。为了获取图像模板中较均匀区域的中值,滤波区域R被划分为k个重叠的子区域R1,R2, …, Rk。位于图像中位置为(u, v)处的每一个像素,所对应的每一个模板子区域的均值和方差通过式(21)和式(22)来计算。
| $ \begin{aligned} \boldsymbol{\mu}_{k}(u, v)=& \frac{1}{\left|\boldsymbol{R}_{k}\right|} \cdot \sum\limits_{(i, j) \in \boldsymbol{R}} \boldsymbol{I}(u+i, v+j)=\\ & \frac{1}{n_{k}} \cdot \boldsymbol{S}_{1, k}(u, v) \end{aligned} $ | (21) |
| $ \begin{aligned} \boldsymbol{\sigma}_{k}^{2}(u, v)=& \frac{1}{\left|\boldsymbol{R}_{k}\right|} \cdot \sum\limits_{(i, j) \in R}\left(\boldsymbol{I}(u+i, v+j)-\boldsymbol{\mu}_{k}(u, v)^{2}\right)=\\ & \frac{1}{\left|\boldsymbol{R}_{k}\right|} \cdot\left[\boldsymbol{S}_{2, k}(u, v)-\frac{S_{1, k}^{2}(u, v)}{\left|\boldsymbol{R}_{k}\right|}\right] \end{aligned} $ | (22) |
对k=1, …, k,有式(23)、(24)成立
| $ \boldsymbol{S}_{1, k}(u, v) =\sum\limits_{(i, j) \in \boldsymbol{R}_{k}} \boldsymbol{I}(u+i, v+j) $ | (23) |
| $ \boldsymbol{S}_{2, k}(u, v) =\sum\limits_{(i, j) \in \boldsymbol{R}_{k}} \boldsymbol{I}^{2}(u+i, v+j) $ | (24) |
对应方差最小子区域的中值替代模板中心像素的灰度值, 即
| $ \boldsymbol{I}^{\prime}(u, v) \leftarrow \operatorname{median}_{k^{\prime}}(u, v) $ | (25) |
| $ k^{\prime}=\arg \min \sigma_{k}^{2}(u, v) $ | (26) |
设计最小方差中值引导滤波器时,结合式(17)、(19)、(20)可得,在求解ak和bk过程中,同一个像素会被多个窗口包含计算,从而计算可得多个系数。为解决这个问题,将该像素点的系数定义改进为
| $ q_{i}=\frac{1}{|\boldsymbol{\omega}|} \sum\limits_{k: i \in \boldsymbol{\omega}_{k}}\left(a_{k} \boldsymbol{I}_{i}+b_{k}\right) $ | (27) |
式中, i表示为位于局部线性窗口ωk的中心像素索引,k为ωk中其他像素点的索引。
式(27)可简化为
| $ q_{i}=\bar{a}_{i} \boldsymbol{I}_{i}+\bar{b}_{i} $ | (28) |
即在具体计算某一点的系数时,使用该点在不同窗口中的系数均值作为该点系数。系数ai和bi随窗口位置不同而变化,也就是说式(15)中滤波输出图像和引导图像之间的梯度不是单一成比例关系,而是变化相关的。设计新的引导滤波的最优解公式为:
| $ a_{k}=\frac{\left(\boldsymbol{I}_{k}^{\mathrm{m}}-\boldsymbol{p}_{k}^{\mathrm{m}}\right)^{2}}{\left(\boldsymbol{I}_{k}^{\mathrm{m}}\right)^{2}-\left(\boldsymbol{p}_{k}^{\mathrm{m}}\right)^{2}+\varepsilon^{\prime}} $ | (29) |
| $ b_{k}=\boldsymbol{p}_{k}^{\mathrm{m}}-a_{k} * \boldsymbol{p}_{k}^{\mathrm{m}} $ | (30) |
式中: Ikm和Pkm分别为I和P在窗口ωk的中值; ε′为正则化调节系数,防止分母为0, 此处取ε′=10-6; 实验中ωk的大小为3×3。
提出算法计算出某一子域的方差后,将该子域向外扩展一个像素,计算新的子域方差并与原方差进行比较。若新的子域方差值小于原方差值,则继续进行新一轮扩展并寻找下一个子域方差进行比较,否则将该值作为该子域的最小方差值。寻找到最小方差子域后使用其中值进行滤波。这样,引导图与被滤波图经过自适应8子区域最小方差中值引导滤波处理,即可得到经过边界增强的图片。
4.3 透射率的二次估计透射率t (x) 与距离和雾的浓度有关,其大小表征了光线在大气中的穿透能力。透射率数值越大,表示较多光线能够穿过海雾进入图像采集设备,散射越少。实验发现,传统优化透射率图的方法不区分像素点来源于目标场景还是天空,在目标场景去雾力度不足导致还原图像不够清晰,而在天空等明亮区域去雾过度会造成颜色失真。为了解决这一问题,本文提出了融合变差函数和颜色衰减先验理论的算法来区分图像中高亮区域和目标场景,根据本文所得暗部图像区域Imark_dark对初步估计的透射率进行调整,弱化亮部图像的去雾,增强暗部图像的去雾。调整函数用公式表示为
| $ \boldsymbol{t}_{\text {modify }}= \begin{cases}\boldsymbol{t}_{\text {light }}=\min \left(\boldsymbol{t}_{\text {constraint }}, 0.9\right), & \boldsymbol{I} \notin \boldsymbol{I}_{\text {mark_dark }} \\ \boldsymbol{t}_{\text {dark }}=\max \left(\boldsymbol{t}_{\text {estimate }}, t_{0}\right), & \boldsymbol{I} \in \boldsymbol{I}_{\text {mark_dark }}\end{cases} $ | (31) |
其中,
| $ \boldsymbol{t}_{\text {constraint }}=\max \left(\frac{\varDelta}{|\boldsymbol{I}-\boldsymbol{A}|}, 1\right) \times \max \left(\boldsymbol{t}_{\text {estimate }}, t_{0}\right) $ | (32) |
式中: t0为定义的透射率下阈值, tconstraint为场景透射率约束矩阵,testimate为场景透射率粗估计矩阵,tlight为亮部场景透射率,tdark为暗部场景透射率,Δ为定义的变差函数阈值。最后利用最小方差中值引导滤波对调整后的透射率进行处理,得到最终的透射率图tfilter。
5 算法流程设计按照前文所述的融合变差函数和颜色衰减先验原理求得大气光Adark以及结合透射率调整函数和中值引导滤波优化后的透射率tfilter,根据雾天图像复原公式
| $ \boldsymbol{J}(i, j)=\frac{\boldsymbol{I}(i, j)-\boldsymbol{A}}{\max \left(\boldsymbol{t}_{\mathrm{filter}}(i, j), t_{0}\right)}+\boldsymbol{A} $ | (33) |
式中t0取值为0.1, J为求得去雾后的图像。算法流程见图 4。

|
图 4 算法流程图 Fig. 4 Algorithm flow chart |
本文实验采用GPU硬件平台NVIDIA GeForce GTX1080Ti,使用一组不同场景下的无人机航拍海雾图片,分别采用暗通道去雾算法(DCP)[17]、基于融合的变分图像去雾算法(FVID)[26]、基于色彩衰减先验的快速单图像去雾算法(CAP)[27]、基于深度学习的DehazeNet方法[28]、基于改进梯度相似度核的交通图像去雾算法(IGSK)[29]、多尺度窗口的自适应透射率修复交通图像去雾方法(MSW)[30]及本文算法进行处理。这里选取4幅不同场景下关键帧图片的实验结果, 见图 5。同时,表 1中引入了信息熵、平均梯度、灰度图像对比度及雾感知密度评估(FADE)等参数,客观评价去雾效果。

|
图 5 图像去雾效果1 Fig. 5 Effect of image defogging 1 |
| 表 1 去雾图像参数评价 Tab. 1 Evaluation of defogging image parameters |
信息熵是图像特征的一种统计形式,反映了图像中的平均信息量。信息熵越大,表示图像包含的信息越多[22, 28, 31]。其计算公式为
| $ H=\sum\limits_{i=0}^{255} \frac{f(i, j)}{N^{2}} \log \frac{f(i, j)}{N^{2}} $ | (34) |
式中:i表示像素的灰度值,j表示邻域灰度值,f(i, j) 为特征二元组(i, j)出现的频数,N为图像尺度。
平均梯度可以直观反映出图像边缘信息的完整性[20, 22]。其计算公式为
| $ G=\frac{1}{M \times N} \sum\limits_{i=1}^{M} \sum\limits_{j=1}^{N} \sqrt{\frac{\left(\frac{\partial f}{\partial x}\right)^{2}+\left(\frac{\partial f}{\partial y}\right)^{2}}{2}} $ | (35) |
式中:M×N表示图像的大小,∂f/∂x表示水平方向的梯度,∂f/∂y表示垂直方向的梯度。
灰度图像对比度是一幅图像中明暗区域最亮的白和最暗的黑之间不同亮度层级的测量,较大的对比度可以体现图像中更多的信息,且更符合人眼视觉感受[22]。其计算公式为
| $ C=\sum\limits_{\delta} \delta(i, j)^{2} P_{\delta}(i, j) $ | (36) |
式中, δ(i, j)= |i-j|,即相邻像素间的灰度差; Pδ(i, j)为相邻像素间的灰度差的像素分布概率。
本文采用的FADE评价指标是由Choi等[25]在2015年提出的图像去雾专用指标,其全称为fog aware density evaluator,即雾霾浓度评价指标,是目前最权威的图像去雾评价指标。FADE评价指标是一种无参考评价指标,无需参考额外的清晰图像,无需依赖局部特征等信息,而是通过统计雾霾图像及其对应的清晰图像差异,对雾霾图像的特征进行学习,建立一种雾霾浓度评价模型,能准确评价复原图像中的雾霾浓度。
6.1 主观评价图 5为包含较多细节特征且含有大量天空区域的入海口建筑物图像及其复原图像,较大的天空区域及水面上较为浓烈的雾霾区域对丰富的海岸建筑细节的复原带来了较大困难。采用DCP算法虽然较好地复原出近景区域的建筑物与道路,但是远景天空区域仍残留一定浓度的雾霾;FVID与CAP方法对近景建筑物区域均有不同程度的提升,但对远景区域及天空区域的复原较差;基于深度学习的DehazeNet方法虽然在图像色调上与原图相似度较好,但可以看到整幅图像上存在一定的薄雾;IGSK方法与DCP方法处理效果相近,即对建筑物、道路等近景部分复原效果良好,但海面与远景部分仍含有大量雾霾噪声;MSW方法处理后图像较为明亮,但整图雾霾噪声去除效果较差,建筑物、海面等区域仍有大量雾霾噪声存在;本文方法得到的复原图像与原始场景相似,饱和度有较大程度的提升,且图像远景区域及天空区域雾霾去除效果良好,近景区域建筑物纹理细节清晰,色彩饱和鲜艳。
图 6包含大量水面区域的海面船艇浓雾图像及其复原图像,图像中含有大量水面浓雾区域以及相对较小的水面船艇细节区域。DCP方法较好复原了船艇区域细节信息,但同时大量损失了水面纹理特征;FVID算法在水面区域的复原上有所提升,但可以看到图中船艇区域仍有薄雾存在;CAP方法虽然将两个区域的信息都有所复原,但复原效果较差;DehazeNet方法得到的复原图像亮度较低且饱和度较低;IGSK方法处理后图像较暗,且占图像较大面积的海面仍存在雾霾噪声,导致整体图像视觉效果较差;MSW方法处理后图像明亮,但图像中船艇区域存在薄雾,与FVID方法处理后效果相近;而本文方法得到的复原图像可以清楚看到水面上的纹理信息,且船艇区域的颜色、纹理都得到了较好复原。

|
图 6 图像去雾效果2 Fig. 6 Effect of image defogging 2 |
图 7为浓雾环境下海岛建筑物监控图像及去雾复原图像。相比于其他图像,最大难点在于过于厚重雾霾噪声严重影响了原图像中的细节信息,图像去雾难度较大。DCP方法得到的复原图像对岛上建筑进行了良好的复原,但图像的色彩饱和度较低;FVID方法得到的复原图像可以明显看到图像整体亮度偏低,复原质量较差;CAP方法得到的复原图像虽然亮度有所提升,但整幅图像上仍覆盖有一定浓度的雾霾;DehazeNet方法得到的复原图像整体色调偏蓝,且整幅图片仍然存留有雾霾;IGSK方法对建筑物的细节复原效果较好,但图片整体亮度较低;MSW方法得到的复原图片虽亮度有所提升,但图片整体仍存在薄雾;本文方法在保证天空、建筑物及水面区域不失真的前提下,有效地提升了建筑物区域的色彩饱和度,相对于DCP方法,色彩更加鲜艳,且整体图像亮度较高。

|
图 7 图像去雾效果3 Fig. 7 Effect of image defogging 3 |
图 8为海面船艇含雾图像。场景中的雾霾区域主要集中于水面区域。DCP方法对船艇的上半部分细节复原效果较好,但船艇下半部分及水面区域有雾霾存在,复原效果较差;FVID方法得到的复原图像整体色调偏暗;CAP方法虽然对水面区域的复原效果有所提升,但提升并不明显,仍可看到雾霾的存在;DehazeNet方法得到的复原图像与含雾图像亮度、色调相似,但船艇下半部分及水面区域雾霾去除不彻底;IGSK方法较好地复原出水面舰船的边缘信息,但对雾霾噪声处理效果较差;MSW方法复原后图片的水面区域仍残留有大量雾霾噪声;本文方法得到的复原图像有效解决了其他方法的问题,在保证船体区域细节的前提下,有效地去除了水面的浓雾区,水面上船只倒影清晰可见。

|
图 8 图像去雾效果4 Fig. 8 Effect of image defogging 4 |
根据图像去雾评价标准,采用信息熵、平均梯度、灰度图像对比度及FADE等客观评价指标对复原图像质量进行评价,见表 1,图 9为客观评价指标的柱状图。

|
图 9 去雾图像参数评价直方图 Fig. 9 Histogram of evaluation of dehazing image parameters |
结合图 5~8及表 1分析实验结果可以看出,经过基于融合的变分图像去雾算法(FVID)得到的复原图像与原图像相比,图像的信息熵、平均梯度、FADE等评价指标有所提升,但灰度图像对比度较小,图像整体颜色产生偏差且由于海雾情况图片整体受天空大海影响过大,造成整体亮度估计过高,去雾后图像偏暗,去雾效果差。经暗通道去雾算法(DCP)得到的复原图像所测得的评价指标虽然都有所提升,但其灰度图像对比度仍然较低,造成整体图像色调偏暗。基于深度学习的DehazeNet方法得到的复原图像虽然在平均梯度这一项指标上表现良好,但仍然存在图像整体色调偏暗的问题,且由于其原有训练数据集为大量室内图像及人工合成雾霾图像,对于自然浓雾及包含景深较大的区域复原效果较差。基于色彩衰减先验的快速单图像去雾算法(CAP)得到的复原图像在灰度图像对比度这一评价参数上表现良好,获得的复原图像整体亮度较高,该方法在其他几个评价参数下的表现较差,结合实际去雾效果也会发现图像中有部分区域仍含有大量雾霾噪声。基于改进梯度相似度核的交通图像去雾算法(IGSK)处理后图像测得的评价参数相较于DCP算法均有不同程度提升,且平均梯度这一项指标高于前几种算法,但在处理海面较多的图片时(如图 6、8),所测得的信息熵与灰度图像对比度数值较低。多尺度窗口的自适应透射率修复交通图像去雾方法(MSW)处理后图像测得的各项评价参数均表现良好,结合复原图像可观察出该方法虽对图片整体雾霾噪声进行去除,但仍然存有薄雾,雾霾噪声去除不彻底。本文算法得到复原图像与原图像相比信息熵最大,图像内含有的细节信息最多,平均梯度及灰度图像对比度较高,评价参数FADE较低可说明图像的整体色调与原始场景相似度较高,结合实际复原图像可以发现对于海面上一些雾霾较重区域处理效果较好,得到图像色彩更加鲜艳。
7 结论现有图像去雾算法虽然能取得一定的效果,但是去雾后图像存在色调偏暗、色彩饱和度较低、颜色畸变的问题,适用环境有限,给海上和舰船作业中图像监控、目标识别和目标跟踪等处理过程带来了极大难度。针对这些问题,本文提出了一种融合变差函数和颜色衰减先验理论的海雾图像去雾方法。与传统算法相比,本文算法的复原图像在信息熵、平均梯度、对比度及FADE等评价指标方面均有较大幅度提升,对恶劣海雾天气条件下,海上监控与舰船作业过程中改善复原图像质量有着积极的意义。
| [1] |
王峥, 滕骏华, 蔡文博, 等. 基于GOCI影像的黄海海雾提取方法研究[J]. 海洋环境科学, 2018, 37(6): 941. WANG Zheng, TENG Junhua, CAI Wenbo, et al. Yellow Sea fog extraction method based on GOCI image[J]. Marine Environmental Science, 2018, 37(6): 941. DOI:10.13634/j.cnki.mes.2018.06.021 |
| [2] |
SINGH D, KUMAR V. Single image haze removal using integrated dark and bright channel prior[J]. Modern Physics Letters B, 2018, 1850051. DOI:10.1142/S0217984918500513 |
| [3] |
FATTAL R. Single image dehazing[J]. ACM Transactions on Graphics, 2008, 27(3): 721. DOI:10.1145/1360612.1360671 |
| [4] |
HWANG B M, SANG H L, LIM W T, et al. A fast spatial-domain terahertz imaging using block-based compressed sensing[J]. Journal of Infrared Millimeter and Terahertz Waves, 2011, 32(11): 1328. DOI:10.1007/s10762-011-9822-5 |
| [5] |
HERMAN M A, STROHMER T. High-resolution radar via compressed sensing[J]. IEEE Transactions on Signal Processing, 2009, 57(6): 2275. DOI:10.1109/TSP.2009.2014277 |
| [6] |
ZHANG Z, FENG W, WANG T, et al. An improved aerial remote sensing image defogging method based on dark channel prior information[J]. Journal of Geomatics Science and Technology, 2018, 35(2): 182. DOI:10.5194/isprs-archives-XLⅡ-2-W7-1025-2017 |
| [7] |
TAN R T. Visibility in bad weather from a single image[C]//IEEE Conference Computer Vision and Pattern Recognition. Anchorage: IEEE, 2008: 1
|
| [8] |
KIM J Y, KIM L S, HWANG S H. An advanced contrast enhancement using partially overlapped Sub-Block histogram equalization[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2001, 11(4): 475. DOI:10.1109/76.915354 |
| [9] |
OAKLEY J P, SATHERLEY B L. Improving image quality in poor visibility conditions using a physical model for contrast degradation[J]. IEEE Transactions on Image Processing: A Publication of the IEEE Signal Processing Society, 1998, 7(2): 167. DOI:10.1109/83.660994 |
| [10] |
OAKLEY J P. Enhancement of color images in poor visibility conditions[C]//2000 International Conference Image Processing. Vancouver: IEEE, 2000: 788
|
| [11] |
TAN K K, OAKLEY J. Enhancement of color images in poor visibility conditions[C]//International Conference Image Processing. Vancouver: IEEE, 2000: 788
|
| [12] |
NARASIMHAN S G, NAYAR S K. Vision and the atmosphere[J]. International Journal of Computer Vision, 2002, 48(3): 233. DOI:10.1023/A:1016328200723 |
| [13] |
NARASIMHAN S G, NAYAR S K. Contrast restoration of weather degraded images[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25(6): 720. DOI:10.1109/TPAMI.2003.1201821 |
| [14] |
TAN R T. Visibility in bad weather from a single image[C]//IEEE Conference Computer Vision and Pattern Recognition. Anchorage: IEEE, 2008: 1
|
| [15] |
LI Z, ZHENG J, YAO W, et al. Single image haze removal via a simplified dark channel[C]//IEEE International Conference Acoustics, Speech & Signal Processing. Brisbane: IEEE, 2015: 1608
|
| [16] |
ZHU Q, MAI J, SHAO L. A fast single image haze removal algorithm using color attenuation prior[J]. IEEE Transactions on Image Processing, 2015, 24(11): 3522. DOI:10.1109/TIP.2015.2446191 |
| [17] |
HE K M, SUN J, TANG X O. Single image haze removal using dark channel prior[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2011, 33(12): 2341. DOI:10.1109/TPAMI.2010.168 |
| [18] |
HE K M, SUN J, TANG X O. Guided image filtering[C]//11th Eurpean Conferemce on Computer Vision. Greece: Springer Science, 2010: 1
|
| [19] |
XU L, YAN Q, XIA Y, et al. Structure extraction from texture via relative total variation[J]. ACM Transactions on Graphics, 2012, 31(6): 1. DOI:10.1145/2366145.2366158 |
| [20] |
黄鹤, 宋京, 郭璐, 等. 基于新的中值引导滤波的交通视频去雾算法[J]. 西北工业大学学报, 2018, 36(3): 414. HUANG He, SONG Jing, GUO Lu, et al. A novel dehazing algorithm based on median guide filter for traffic video[J]. Journal of Northwestern Polytechnical University, 2018, 36(3): 414. DOI:10.3969/j.issn.1000-2758.2018.03.002 |
| [21] |
黄鹤, 宋京, 王会峰, 等. 雾霾天气下基于二次滤波的交通图像去雾算法[J]. 科学技术与工程, 2016, 30(16): 274. HUANG He, SONG Jing, WANG Huifeng, et al. The traffic image defogging algorithm based on twice filter in haze weather[J]. Science Technology and Engineering, 2016, 30(16): 274. DOI:10.3969/j.issn.1671-1815.2016.30.048 |
| [22] |
HUANG H, SONG J, GUO L, et al. Haze removal method based on a variation function and colour attenuation prior for UAV remote-sensing images[J]. Journal of Modern Optics, 2019, 66(12): 1282. DOI:10.1080/09500340.2019.1615141 |
| [23] |
CHOI L K, YOU J, BOVIK A C. Referenceless prediction of perceptual fog density and perceptual image defogging[J]. IEEE Transactions on Image Processing, 2015, 24(11): 3888. DOI:10.1109/TIP.2015.2456502 |
| [24] |
刘万军, 赵庆国, 曲海成. 变差函数和形态学滤波的图像去雾算法[J]. 中国图像图形学报, 2016, 21(12): 1609. LIU Wanjun, ZHAO Qingguo, QU Haicheng. Image defog algorithm based on variogram and morphological filter[J]. Journal of Image and Graphics, 2016, 21(12): 1609. DOI:10.11834/jig.20161206 |
| [25] |
PREETHAN A J, SHIRLEY P, SMITS B. A practical analytic model for daylight[C]//ACM Conference SIGGRAPH. Angeles: ACM, 1999, 91
|
| [26] |
ZHU Qingsong, MAI Jiaming, SHAO Ling. A fast single image haze removal algorithm using color attenuation prior[J]. IEEE Transactions on Image Processing, 2015, 24(11): 3522. DOI:10.1109/TIP.2015.2446191 |
| [27] |
ADRIAN G, JAVIER V C, DAVID P M, et al. Fusion-based variational image dehazing[J]. IEEE Transactions on Image Processing, 2017, 24(2): 151. DOI:10.1109/LSP.2016.2643168 |
| [28] |
CAI B, XU X, JIA K, et al. DehazeNet: an end-to-end system for single image haze removal[J]. IEEE Transactions on Image Processing, 2016, 25(11): 5187. DOI:10.1109/TIP.2016.2598681 |
| [29] |
汪贵平, 宋京, 杜晶晶, 等. 基于改进梯度相似度核的交通图像去雾算法[J]. 中国公路学报, 2018, 31(6): 264. WANG Guiping, SONG Jing, DU Jingjing, et al. Haze defogging algorithm for traffic images based on improved gradient similarity kernel[J]. China Journal of Highway and Transport, 2018, 31(6): 264. |
| [30] |
黄鹤, 李昕芮, 宋京, 等. 多尺度窗口的自适应透射率修复交通图像去雾方法[J]. 中国光学, 2019, 12(6): 1311. HUANG He, LI Xinrui, SONG Jing, et al. A traffic image dehaze method based on adaptive transmittance estimation with multi-scale window[J]. Chinese Optics, 2019, 12(6): 1311. |
| [31] |
杨红, 崔艳. 基于开运算暗通道和优化边界约束的图像去雾算法[J]. 光子学报, 2018, 47(6): 244. YANG Hong, CUI Yan. Image defogging algorithm based on opening dark channel and improved boundary constraint[J]. Acta Photonica Sinica, 2018, 47(6): 244. DOI:10.3788/gzxb20184706.0610004 |
 2021, Vol. 53
2021, Vol. 53


