2. 海军工程大学 管理工程与装备经济系,武汉 430033
2. Department of Management Engineering and Equipment Economics, Naval University of Engineering, Wuhan 430033, China
部件发生劣化,对其余部件寿命造成影响,这样的现象称为失效相关[1]。关于多状态系统可靠性理论的现有研究大多假设系统部件间的失效规律相互独立,忽视了部件之间失效相关问题对系统整体可靠性的影响,这虽然简化了模型,降低了解析难度,但往往会对系统可靠性估计过高,影响技术人员决策,导致维修保障力量及备件储存等不能很好地适用于实际问题。随着复杂多状态系统大量应用于科学研究,尤其是在航空航天、核工业等高精尖领域,对系统可靠性评估提出了越来越高的要求,失效相关问题不容忽视。
鉴于此,人们越来越重视系统中的失效相关现象,并对此展开研究[2-4]。Zuo等[5]研究了基于证据网络的共因失效系统,并对模型参数的不确定性进行了分析。Zhang等[6]研究了载荷共享机制下存在失效相关的并联系统可靠性。Parkinson[7]基于单元失效相关性推导出串联系统可靠性区间,计算出任意两子单元的联合可靠性指标。Levitin在失效相关方面做了大量工作,对系统部件失效独立和失效扩展并存而引起共因失效的二态系统可靠性进行了研究[8],针对存在共因失效的串并联不可修多状态系统,基于通用发生函数方法提出了一个两阶段的隐性方法评估系统可靠性[9],并且针对多状态系统组件之间失效传播时间具有随机性的特点,利用通用发生函数以及广义可靠性框图对系统可靠性进行评估[10]。刘宇等[11]考虑单元载荷动态变化对单元失效规律的影响,针对二态单元构成的并联多状态不可修系统建立了马尔可夫模型,得到了系统可靠度,并分析了系统的组成结构和单元的载荷动态分配策略对系统可靠度的影响规律。张卓琦等[12]在考虑部件间失效率相关的基础上,为降低两部件系统的维修成本,研究了年龄预防性维修与机会维修相结合的维修策略。唐家银等[13]为解决可修表决系统中部件的失效相关问题,根据部件之间寿命的正相关关系,运用Copula函数,建立了失效相关表决系统可靠性模型,并全面考虑了共因失效、部件工作寿命及维修时间分布的一般性。周志刚等[14]在研究风力发电机齿轮传动系统动态可靠性时以应力-强度干涉模型刻画齿轮间的失效相关性。姚运志等[15]为解决存在失效相关现象的多部件系统预防性维修问题,引入失效相关系数,对复杂装备预防性维修模型进行研究。
目前,针对两状态单元构成的失效相关系统已有较为深入的研究,但由于多状态可修系统的失效相关问题较为复杂,现有研究大多考虑运用特定函数或明确的失效相关机理对这一性质进行描述,较少考虑环境时变、部件状态性能波动、外部冲击等导致失效相关性不明确的情况,造成模型适用性有所降低[16]。
基于此,Ding和Lisnianski[17]首先提出了模糊多状态系统的概念,并对传统的通用发生函数进行改进,引入了模糊通用发生函数对系统可靠性进行研究。随后,模糊多状态理论被广泛应用于模糊可用度、模糊概率及模糊可靠性等方面[18-22]。目前,虽然模糊可靠性理论已有较为丰富的研究,但在考虑系统参数模糊性的同时,考虑部件之间失效相关现象及其模糊性的研究却少有涉及。而忽略失效相关现象时常会导致可靠性指标估计过高、区间过窄的情况,难以满足工程实际需求。
作为一类常见的多状态系统,主辅单元并联的形式广泛存在于工程实际中,结构功能具有鲜明特点。主单元承担了系统的主要功能,辅单元起到配合作用,除分担小部分功能外,还能使系统运行更加稳定,减缓主单元的失效进程,从而提高系统可靠性[23]。对于这类系统,根据辅单元主要功能的不同可以进行分类,如辅单元的作用为协助主单元进行功率输出,此类系统可称为“协同型”主辅并联系统;或是减缓主单元劣化速度,代替主单元承受外部冲击,这类可称为“保护型”主辅并联系统。考虑到上述两类主辅并联系统大量应用于工程实践,分别对其进行可靠性研究具有一定意义。
因此,本文主要针对外部环境复杂程度高、时变性强导致系统部件性能水平、劣化规律存在不确定性,且又对可靠性指标等评估具有较高要求的系统进行分析研究,从部件性能模糊性及失效相关性入手,着重分析了两类典型的主辅并联系统。将系统各部件的失效转移率、修复转移率及状态性能水平均视为模糊数的同时,考虑了系统的失效相关问题。对两类系统分别建模后运用Zadeh扩张原理分析了系统模糊状态概率的隶属函数,采用参数规划技术得到了系统的稳态指标,并通过实际算例给出了系统稳态指标随部件参数模糊性变动的情况,验证了模型的适用性。
1 协同型主辅并联系统 1.1 系统介绍 1.1.1 模型描述及失效相关规则建立假设系统由主、辅单元并联构成,此处的“并联”并不仅仅是传统意义上的结构并联,更体现出“协同”的特点,即主单元A承担系统主要性能输出,辅单元B对系统性能输出具有一定促进作用。
考虑主单元A内组成部件存在失效率相关,即某一部件发生劣化,可能会导致剩余工作件的失效率增大。此类情况在工程实际中较为普遍,例如某电子元器件失效瞬间产生瞬时电流冲击,对一定范围内的工作件产生影响,又如常见的流量传输系统,其中一条路径失效后,载荷将转移到剩余路径,导致剩余路径加速劣化。
对于此类失效率相关的问题,相关系数的确定仍旧是一个较为困难的问题。尤其是对于大型复杂系统,各组成部件之间的失效率相关系数更加难以确定,而且经常会随着外部环境、自身性态的变化而出现波动。因此,为说明问题,在一定程度的误差允许范围内,以模糊数刻画部件之间的失效率相关系数是较为合理的。
同时,辅单元B除了确保系统平稳运行,减缓主单元失效进程外,主要功能为协同主单元进行一定的性能输出,此为协同型主辅并联系统的典型特征。注意到辅单元B与主单元A之间存在协同关系,因此辅单元发生失效的瞬间也可能对主单元产生一定载荷冲击,使得主单元加速劣化。这样的情况很常见,如电子系统内部,某元器件失效,导致电路内瞬时电流增大,可能会烧毁主板。
基于上述分析,对“协同型”主辅并联系统作进一步描述并建立失效相关规则如下:
a) 主单元A各组成部件为逐级劣化,每次维修时都将主单元修复到完好态,且修复如新;
b) 部件之间存在失效相关阈值,即某一部件劣化后不一定引起剩余部件失效率增大,而是存在一定的条件,如失效件劣化的程度、剩余工作件的状态性能水平、复杂多变的外部环境等。典型的例子有承重系统,某承重梁发生失效,将自身载荷转移到剩余承重梁,若未超过应力极限,则可忽略此影响,否则可能导致承重梁出现裂痕,并迅速引发劣化,甚至出现折断的现象;
c) 失效率相关具有叠加性,即多个部件劣化后产生的失效相关影响大于单个部件失效相关的影响,失效相关影响函数为φsi(·),视系统功能、结构、状态等因素具有不同的形式;
d) 同一时刻主单元内部有多个部件发生劣化的概率极小,暂忽略不计;
e) 辅单元B为逐级劣化,每次维修都将其修复至前一状态,完全失效时直接修复到完好态,且能修复如新;
f) 每次进入完全失效态,辅单元B都会对主单元A造成一定冲击,冲击载荷具有累积性,当遭受k次冲击后主单元瞬间劣化,性能水平输出乘以一个随机的模糊数
g) 主单元A独立失效模式与遭受载荷冲击发生劣化的模式相互独立,构成多模失效,拥有各自的失效转移率、修复转移率及状态空间;
h) 系统所有部件失效时间、修复时间均服从指数分布且相互独立。
1.1.2 重要参数定义及符号说明| 表 1 模型1参数符号及定义 Tab. 1 Parameters and definitions of model 1 |
模型1 主单元内部失效相关建模。根据上述分析,可得模型1(即主单元内各部件)的状态转移图,见图 1。
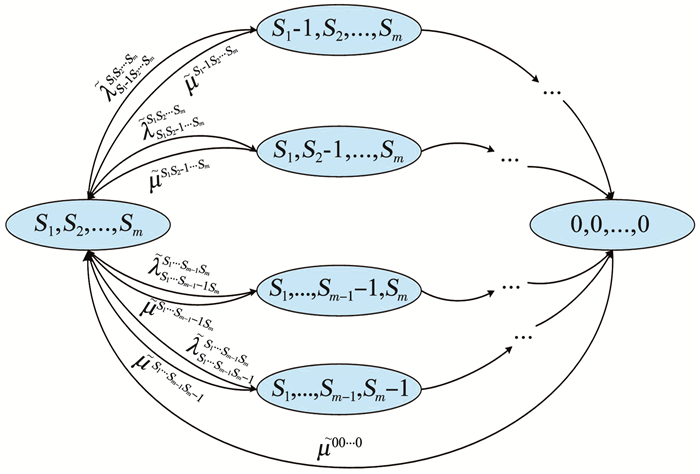
|
图 1 主单元模糊状态转移 Fig. 1 Fuzzy state transition diagram of main unit |
其中:S1, S2, …, Sm表示系统第一个部件至第m个部件的状态为S1至Sm;
由图 1可得主单元状态转移的Kolmogorov微分方程组
| $ \begin{gathered} \frac{\mathrm{d} \tilde{p}_{S_{1} S_{2} \cdots S_{m}}(t)}{\mathrm{d} t}= \\ -\tilde{p}_{S_{1} S_{2} \cdots S_{m}}(t) \cdot\left[\tilde{\lambda}_{S_{1}-1 S_{2} \cdots S_{m}}^{S_{1} S_{2} \cdots S_{m}}+\cdots+\widetilde{\lambda}_{S_{1} S_{2} \cdots S_{m}-1}^{S_{1} S_{2} \cdots S_{m}}\right]+ \\ \sum \tilde{p}_{i_{1} i_{2} \cdots i_{m}} \cdot \tilde{\mu}^{i_{1} i_{2} \cdots i_{m}} \end{gathered} $ | (1) |
| $ \begin{gathered} \frac{\mathrm{d} \tilde{p}_{i_{1} i_{2} \cdots i_{m}}(t)}{\mathrm{d} t}= \\ -\tilde{p}_{i_{1} i_{2} \cdots i_{m}}(t) \cdot\left[\widetilde{\lambda}_{i_{1}-1 i_{2} \cdots i_{m}}^{i_{i} i_{2} \cdots i_{m}}+\cdots+\right. \\ \left.\widetilde{\lambda}_{i_{1} i_{2} \cdots i_{m}-1}^{i_{1} i_{2} \cdots i_{m}}+\widetilde{\mu}^{i_{1} i_{2} \cdots i_{m}}\right]+ \\ \tilde{p}_{i_{1}+1 i_{2} \cdots i_{m}}(t) \cdot \tilde{\lambda}_{i_{1} i_{2} \cdots_{m}}^{i_{1}+1 i_{2} \cdots i_{m}}+\cdots+ \\ \tilde{p}_{i_{1} i_{2} \cdots i_{m}+1}(t) \cdot \widetilde{\lambda}_{i_{1} i_{2} \cdots i_{m}}^{i_{1} i_{2} \cdots i_{m}+1} \end{gathered} $ | (2) |
| $ \begin{gathered} \frac{\mathrm{d} \tilde{p}_{00} \cdots_{0}(t)}{\mathrm{d} t}= \\ \tilde{p}_{10 \cdots 0}(t) \cdot \widetilde{\lambda}_{00 \cdots 0}^{10 \cdots 0}+\cdots+\tilde{p}_{00 \cdots 1}(t) \cdot \widetilde{\lambda}_{00 \cdots 0}^{00 \cdots 1}- \\ \tilde{p}_{00 \cdots 0}(t) \cdot \tilde{\mu}^{00 \cdots 0} \end{gathered} $ | (3) |
其中0≤ij≤Sj,1≤j≤m,且当ij-1 < 0或ij+1>Sj时,对应的参数值均为零。
由模糊数
| $ \tilde{x}_{\alpha}=\left[\min \limits_{x \in X}\left\{x \mid \eta_{\tilde{x}}(x) \geqslant \alpha\right\}, \max \limits_{x \in X}\left\{x \mid \eta_{\tilde{x}}(x) \geqslant \alpha\right\}\right] $ |
再根据Zadeh扩张原理,可得
| $ \begin{gathered} \left(\tilde{p}_{i_{1} i_{2} \cdots i_{m}}(t)\right)_{\alpha}=\left[\min f _ { i _ { 1 } i _ { 2 } \cdots i _ { m } } \left(\tilde{\lambda}^{i_{1} i_{2} \cdots i_{m}}, \tilde{\mu}^{i_{1} i_{2} \cdots i_{m}}, t ;\right.\right. \\ \left.\eta_{\tilde{\lambda}_{1} i_{2} \cdots i_{m}}\left(\lambda^{i_{1} i_{2} \cdots i_{m}}\right) \geqslant \alpha, \eta_{\tilde{\mu}^{i_{1} i_{2} \cdots i_{m}}}\left(\mu^{i_{1} i_{2} \cdots i_{m}}\right) \geqslant \alpha\right) ,\\ \max f_{i_{1} i_{2} \cdots i_{m}}\left(\widetilde{\lambda}^{i_{1} i_{2} \cdots i_{m}}, \widetilde{\mu}^{i_{1} i_{2} \cdots i_{m}}, t;\right.\\ \left.\left.\eta_{\tilde{\lambda}^{i_{1} i_{2} \cdots i_{m}}}\left(\lambda^{i_{1} i_{2} \cdots i_{m}}\right) \geqslant \alpha, \eta_{\tilde{\mu}^{i_{1} 12 \cdots i_{m}}}\left({\mu}^{i_{1} i_{2} \cdots i_{m}}\right) \geqslant \alpha\right)\right]= \\ {\left[\left(\tilde{p}_{i_{1} i_{2} \cdots i_{m}}\right)_{\alpha}^{\mathrm{L}},\left(\tilde{p}_{i_{1} i_{2} \cdots i_{m}}\right)_{\alpha}^{\mathrm{U}}\right], 0 \leqslant \alpha \leqslant 1} \end{gathered} $ | (4) |
结合主单元各项参数,可得状态概率的下边界为
| $ \begin{gathered} \left(\tilde{p}_{i_{1} i_{2} \cdots i_{m}}(t)\right)_{\alpha}^{\mathrm{L}}= \\ \min f_{i_{1} i_{2} \cdots i_{m}}\left(\lambda^{i_{1} i_{2} \cdots i_{m}}, \mu^{i_{1}i_{2} \cdots i_{m}}, t\right), \quad 0 \leqslant \alpha \leqslant 1 \\ \text { s. t. }\left(\lambda_{i_{1}-1 i_{2} \cdots i_{m}}^{i_{1} i_{2} \cdots i_{m}}\right)_{\alpha}^{\mathrm{L}} \leqslant \lambda_{i_{1}-1 i_{2} \cdots i_{m}}^{i_{1} i_{2} \cdots i_{m}} \leqslant\left(\lambda_{i_{1}-1 i_{2} \cdots i_{m}}^{i_{1} i \cdots i_{m}}\right)_{\alpha}^{\mathrm{U}}\\ \vdots \\ \left(\lambda_{i_{1} i_{2} \cdots i_{m}-1}^{i_{1} i_{2} \cdots i_{m}}\right)_{\alpha}^{\mathrm{L}} \leqslant \lambda_{i_{1} i_{2} \cdots i_{m}-1}^{i_{1} i_{2} \cdots i_{m}} \leqslant\left(\lambda_{i_{1} i_{2} \cdots i_{m}-1}^{i_{1} i_{2} \cdots i_{m}}\right)_{\alpha}^{\mathrm{U}} \\ \left(\mu^{i_{1} i_{2} \cdots i_{m}}\right)_{\alpha}^{\mathrm{L}} \leqslant \mu^{i_{1} i_{2} \cdots i_{m}} \leqslant\left(\mu^{i_{1} i_{2} \cdots i_{m}}\right)_{\alpha}^{\mathrm{U}} \end{gathered} $ | (5) |
上边界为
| $ \begin{gathered} \left(\tilde{p}_{i_{1} i_{2} \cdots i_{m}}(t)\right)_{\alpha}^{\mathrm{U}}= \\ \max f_{i_{1} i_{2} \cdots i_{m}}\left(\lambda^{i_{1} i_{2} \cdots i_{m}}, \mu^{i_{1} i_{2} \cdots i_{m}}, t\right), 0 \leqslant \alpha \leqslant 1 \\ \text { s.t. }\left(\lambda_{i_{1}-1 i_{2} \cdots i_{m}}^{i_{i} i_{2} \cdots i_{m}}\right)_{\alpha}^{\mathrm{L}} \leqslant \lambda_{i_{1}-1 i_{2} \cdots i_{m}-1}^{i_{1} i_{2} \cdots i_{m}} \leqslant\left(\lambda_{i_{1}-1 i_{2} \cdots i_{m}}^{i_{1} i_{2} \cdots i_{m}}\right)_{\alpha}^{\mathrm{U}}\\ \vdots \\ \left(\lambda_{i_{1} i_{2} \cdots i_{m}}^{i_{1} i_{2} \cdots i_{m}}\right)_{\alpha}^{\mathrm{L}} \leqslant \lambda_{i_{1} i_{2} \cdots i_{m}-1}^{i_{1} i_{2} \cdots i_{m}} \leqslant\left(\lambda_{i_{1} i_{2} \cdots i_{m}-1}^{i_{1} i_{2} \cdots i_{m}}\right)_{\alpha}^{\mathrm{U}} \\ \left(\mu^{i_{1} i_{2} \cdots i_{m}}\right)_{\alpha}^{\mathrm{L}} \leqslant \mu^{i_{1} i_{2} \cdots i_{m}} \leqslant\left(\mu^{i_{1} i_{2} \cdots i_{m}}\right)_{\alpha}^{\mathrm{U}} \end{gathered} $ | (6) |
其中
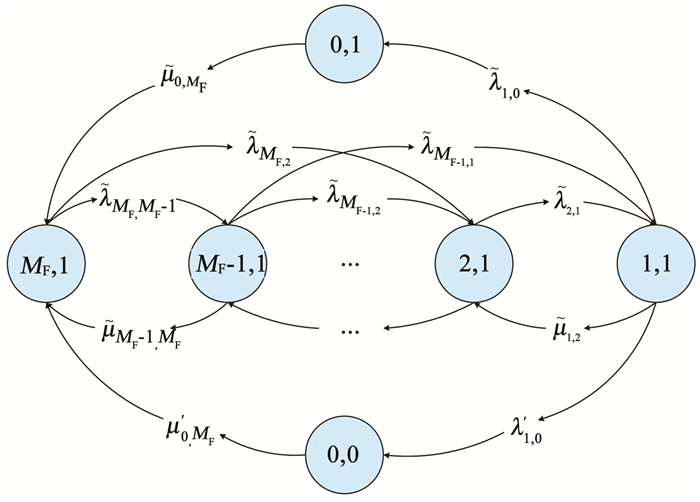
模型2 辅单元对主单元存在失效冲击建模。考虑辅单元对主单元存在失效冲击时,模型的状态转移过程见图 2,由此可得模型状态转移的Kolmogrov微分方程组。

|
图 2 考虑失效冲击的系统模糊状态转移 Fig. 2 Fuzzy state transition diagram of system with failure |
当i=0时:
| $ \frac{\mathrm{d} \tilde{v}_{01}(t)}{\mathrm{d} t}=-\tilde{v}_{01}(t) \cdot\left(\tilde{\theta}_{0}^{1}+\widetilde{\sigma}_{2}^{1}\right)+\tilde{v}_{02}(t) \cdot \tilde{\theta}_{1}^{2} $ | (7) |
| $ \begin{aligned} \frac{\mathrm{d} \tilde{v}_{0 j}(t)}{\mathrm{d} t}=&-\tilde{v}_{0 j}(t) \cdot\left(\widetilde{\theta}_{j-1}^{{j}}+\widetilde{\sigma}_{j+1}^{j}\right)+\tilde{v}_{0(j+1)}(t) \cdot \tilde{\theta}_{j}^{j+1}+\\ & \tilde{u}_{0(j-1)}(t) \cdot \widetilde{\sigma}_{j}^{j-1}, \quad 2 \leqslant j \leqslant N_{F}-1 \end{aligned} $ | (8) |
| $ \begin{gathered} \frac{\mathrm{d} \tilde{v}_{0 N_{\mathrm{F}}}(t)}{\mathrm{d} t}=-\tilde{v}_{0 N_{\mathrm{F}}}(t) \cdot \widetilde{\theta}_{N_{\mathrm{F}}-1}^{N_{\mathrm{F}}}+ \\ \tilde{v}_{0\left(N_{\mathrm{F}}-1\right)}(t) \cdot \widetilde{\sigma}_{N_{\mathrm{F}}}^{\left(N_{\mathrm{F}}-1\right)}+\tilde{v}_{m 0}(t) \cdot \tilde{\sigma} \end{gathered} $ | (9) |
当1≤i≤k-1时:
| $ \frac{\mathrm{d} \tilde{v}_{i 0}(t)}{\mathrm{d} t}=-\tilde{v}_{i 0}(t) \cdot \widetilde{\sigma}_{N_{\mathrm{F}}}^{0}+\tilde{v}_{(i-1) 1}(t) \cdot \tilde{\sigma}_{0}^{1} $ | (10) |
| $ \frac{\mathrm{d} \tilde{v}_{i 1}(t)}{\mathrm{d} t}=-\tilde{v}_{i 1}(t) \cdot\left(\tilde{\theta}_{0}^{1}+\widetilde{\sigma}_{2}^{1}\right)+\tilde{v}_{i 2}(t) \cdot \tilde{\theta}_{1}^{2} $ | (11) |
| $ \begin{gathered} \frac{\mathrm{d} \tilde{v}_{i j}(t)}{\mathrm{d} t}=-\tilde{v}_{i j}(t) \cdot\left(\tilde{\theta}_{j-1}^{j}+\widetilde{\sigma}_{j+1}^{j}\right)+ \\ \tilde{v}_{i(j+1)}(t) \cdot \tilde{\theta}_{j}^{j+1}+ \\ \tilde{v}_{i(j-1)}(t) \cdot \widetilde{\sigma}_{j}^{j-1}, 2 \leqslant j \leqslant N_{F}-1 \end{gathered} $ | (12) |
| $ \begin{gathered} \frac{\mathrm{d} \tilde{v}_{i N_{\mathrm{F}}}(t)}{\mathrm{d} t}=-\tilde{v}_{i N_{\mathrm{F}}}(t) \cdot \tilde{\theta}_{N_{\mathrm{F}}-1}^{N_{\mathrm{F}}}+\tilde{v}_{i 0}(t) \cdot \widetilde{\sigma}_{N_{\mathrm{F}}}^{0}+ \\ \tilde{v}_{i\left(N_{\mathrm{F}}-1\right)}(t) \cdot \widetilde{\sigma}_{N_{\mathrm{F}}}^{N_{\mathrm{F}}-1} \end{gathered} $ | (13) |
当i=k时:
| $ \frac{\mathrm{d} \tilde{v}_{k 0}(t)}{\mathrm{d} t}=-\tilde{v}_{k 0}(t) \cdot \widetilde{\sigma}+\tilde{v}_{(k-1) 1}(t) \cdot \tilde{\theta}_{0}^{1} $ | (14) |
| $ \frac{\mathrm{d} \tilde{v}_{k 1}(t)}{\mathrm{d} t}=-\tilde{v}_{k 1}(t) \cdot\left(\hat{\theta}_{0}^{1}+\widetilde{\sigma}_{2}^{1}\right)+\tilde{v}_{k 2}(t) \cdot \hat{\theta}_{1}^{2} $ | (15) |
| $ \begin{gathered} \frac{\mathrm{d} \tilde{v}_{k j}(t)}{\mathrm{d} t}=-\tilde{v}_{k j}(t) \cdot\left(\tilde{\theta}_{j-1}^{j}+\widetilde{\sigma}_{j+1}^{j}\right)+ \\ \tilde{v}_{k(j+1)}(t) \cdot \widetilde{\theta}_{j}^{j+1}+ \\ \tilde{v}_{k(j-1)}(t) \cdot \widetilde{\sigma}_{j}^{j-1}, 2 \leqslant j \leqslant N_{\mathrm{F}} \end{gathered} $ | (16) |
| $ \begin{gathered} \frac{\mathrm{d} \tilde{v}_{k N_{F}}(t)}{\mathrm{d} t}=-\tilde{v}_{k N_{\mathrm{F}}}(t) \cdot \tilde{\theta}_{N_{\mathrm{F}}-1}^{N_{\mathrm{F}}}+\tilde{v}_{k 0}(t) \cdot \widetilde{\sigma}_{N_{\mathrm{F}}}^{0}+ \\ \tilde{v}_{k\left(N_{\mathrm{F}}-1\right)}(t) \cdot \widetilde{\sigma}_{N_{\mathrm{F}}}^{N_{\mathrm{F}}-1} \end{gathered} $ | (17) |
同理, 由Zadeh扩张原理,可得
| $ \begin{gathered} \left(\tilde{v}_{i j}(t)\right)_{\alpha}=\left[\min f _ { i j } \left(\widetilde{\theta}_{j}^{i}, \widetilde{\sigma}_{j}^{i}, t ;\right.\right. \\ \left.\eta_{\widetilde{\theta}_{j}^{i}}\left(\theta_{j}^{i}\right) \geqslant \alpha, \eta_{\widetilde{\sigma}_{j}^{i}}\left(\sigma_{j}^{i}\right) \geqslant \alpha\right),\\ \max f_{i j}\left(\tilde{\theta}_{j}^{i}, \widetilde{\sigma}_{j}^{i}, t ;\right. \\ \left.\left.\eta_{\tilde{\theta}_{j}^{i}}\left(\theta_{j}^{i}\right) \geqslant \alpha, \eta_{\tilde{\sigma}_{j}^{i}}\left(\sigma_{j}^{i}\right) \geqslant \alpha\right)\right]= \\ {\left[\left(\tilde{v}_{i j}\right)_{\alpha}^{\mathrm{L}},\left(\tilde{v}_{i j}\right)_{\alpha}^{\mathrm{U}}\right], 0 \leqslant \alpha \leqslant 1} \end{gathered} $ | (18) |
下边界为
| $ \begin{gathered} \left(\tilde{v}_{i j}(t)\right)_{\alpha}^{\mathrm{L}}=\min f_{i j}\left(\theta_{j}^{i}, \sigma_{j}^{i}, t\right), 0 \leqslant \alpha \leqslant 1 \\ \text { s.t. }\left(\theta_{j}^{i}\right)_{\alpha}^{\mathrm{L}} \leqslant \theta_{j}^{i} \leqslant\left(\theta_{j}^{i}\right)_{\alpha}^{\mathrm{U}} \\ \left(\sigma_{j}^{i}\right)_{\alpha}^{\mathrm{L}} \leqslant \sigma_{j}^{i} \leqslant\left(\sigma_{j}^{i}\right)_{\alpha}^{\mathrm{U}} \end{gathered} $ | (19) |
上边界为
| $ \begin{gathered} \left(\tilde{v}_{i j}(t)\right)_{\alpha}^{\mathrm{U}}=\max f_{i j}\left(\theta_{j}^{i}, \sigma_{j}^{i}, t\right), 0 \leqslant \alpha \leqslant 1 \\ \text { s.t. } \quad\left(\theta_{j}^{i}\right)_{\alpha}^{\mathrm{L}} \leqslant \theta_{j}^{i} \leqslant\left(\theta_{j}^{i}\right)_{\alpha}^{\mathrm{U}} \\ \left(\sigma_{j}^{i}\right)_{\alpha}^{\mathrm{L}} \leqslant \sigma_{j}^{i} \leqslant\left(\sigma_{j}^{i}\right)_{\alpha}^{\mathrm{U}} \end{gathered} $ | (20) |
1) 系统模糊稳态可用度
现在对系统的稳态可用度进行计算。一般情况下,只有当系统的状态性能水平不低于使用者需求时,才视为可用的。记系统处于状态i的模糊状态性能水平为
定义
| $ \begin{gathered} p\left(\tilde{z}_{i} \geqslant 0\right)=\frac{\sum\limits_{z_{i} \in Z_{i}\atop {{z}_{i} \geqslant 0\atop \eta_{\tilde{z}_{i}}\left(z_{i}\right)\geqslant \alpha}} \eta_{\tilde{z}_{i}}\left(z_{i}\right)}{\sum\limits_{z_{i} \in Z_{i}\atop \eta_{\tilde{z}_{i}}\left(z_{i}\right)\geqslant \alpha}\eta_{\tilde{z}_{i}}\left(z_{i}\right)} \end{gathered} \atop $ | (21) |
其中0≤α≤1。
因此,由清晰集下系统可用度定义,可得系统模糊稳态可用度
| $ \widetilde{A}=\sum \tilde{p}_{i} \cdot p, \tilde{z}_{i} \geqslant 0 $ | (22) |
考虑系统模糊稳态可用度的α水平截集
| $ \begin{gathered} A_{\alpha}^{\mathrm{L}}=\min \sum p_{i} \cdot p, \tilde{z}_{i} \geqslant 0 \\ \text { s. t. }\left(p_{i}\right)_{\alpha}^{\mathrm{L}} \leqslant p_{i} \leqslant\left(p_{i}\right)_{\alpha}^{\mathrm{U}} \\ \sum p_{i}=1 \\ A_{\alpha}^{\mathrm{U}}=\max \sum p_{i} \cdot p, \tilde{z}_{i} \geqslant 0 \end{gathered} $ | (23) |
| $ \begin{gathered} \text { s.t. }\left(p_{i}\right)_{\alpha}^{\mathrm{L}} \leqslant p_{i} \leqslant\left(p_{i}\right)_{\alpha}^{\mathrm{U}} \\ \sum p_{i}=1 \end{gathered} $ | (24) |
2) 系统平均稳态性能输出
| $ \widetilde{E}_{\mathrm{W}}=\sum \tilde{p}_{i} \cdot \tilde{g}_{i} $ | (25) |
考虑系统平均稳态性能输出的α水平截集
| $ \begin{gathered} \left(E_{\mathrm{W}}\right)_{\alpha}^{\mathrm{L}}=\min \sum p_{i} \cdot g_{i} \\ \text { s.t. }\left(p_{i}\right)_{\alpha}^{\mathrm{L}} \leqslant p_{i} \leqslant\left(p_{i}\right)_{\alpha}^{\mathrm{U}} \\ \sum p_{i}=1 \end{gathered} $ | (26) |
| $ \begin{gathered} \left(E_{\mathrm{W}}\right)_{\alpha}^{\mathrm{U}}=\max \sum p_{i} \cdot g_{i} \\ \text { s.t. }\left(p_{i}\right)_{\alpha}^{\mathrm{L}} \leqslant p_{i} \leqslant\left(p_{i}\right)_{\alpha}^{\mathrm{U}} \\ \sum p_{i}=1 \end{gathered} $ | (27) |
3) 主、辅单元处于完好态的稳态概率
由于主单元较为重要,很多时候除了对系统整体可用度提出要求外,使用者还要求主、辅单元满足一定性能。因此掌握主、辅单元处于完好状态的稳态概率对合理进行系统可靠性评估、维护保养及结构优化具有重要意义。
4) 系统必然可用度
考虑到模糊系统的特点,部件参数模糊程度的大小对系统可用度有直接影响。而必然可用度则是衡量所有部件处于最低性能时系统可用的概率,即无论部件参数模糊程度如何,系统都能满足使用者需求的概率,这是模糊系统可靠性中不容忽视的指标之一。
2 保护型主辅并联系统 2.1 模型描述 2.1.1 模型描述及失效相关规则建立工程实际中,除了前面研究的功率输出协同型系统外,还存在大量“保护型”主辅并联系统。即主单元承担了系统的全部功能,辅单元的主要作用为保护主单元不受外部环境等因素的影响,使得主单元处在一个尽量平稳的工作环境中,借此延缓主单元的失效进程,大到航空发动机的外层防护装置,小如晶体管的密封层,实际上都起到了保护主要单元,减缓主要单元退化进程的作用。本节对此类“保护型”系统进行研究,为工程实际提供一些参考。
考虑某主辅单元构成的“保护型”系统,其中主单元承担系统功能,辅单元为保护单元,主要作用为防止主单元因外部侵蚀(如高温、高湿、高盐或强电磁环境等),或是遭受随机的外部冲击而导致主单元瞬间失效的情形。此时认为系统的失效相关主要由两部分构成,一是主单元内部之间的失效相关。结合工程实际,对于存在载荷共享机制的系统,常用Power Law规则描述部件之间的失效相关关系,认为系统承受的总载荷平均分配给组成部件[11]。
此外,由于辅单元的保护作用,可以代替主单元承受来自系统外部的随机冲击,起到保护主单元的作用,但辅单元承受的累积冲击超过承受能力时便会进入完全失效态,且此次外部冲击的剩余载荷会导致主单元一定概率发生劣化。
根据上述分析,现假设主单元由m种不同部件并联而成,第i类部件的数量为Ni个(1≤i≤m),则主单元总的部件数目为Z=N1+N2+…+Nm。辅单元共有MF+1个不同状态,其中MF为完好态,0为完全失效态,且辅单元的固有失效模式为逐级劣化。下面对问题作进一步描述。
1) 主单元
a) 主单元由不同类型部件构成,为并联结构;
b) 主单元所有组成部件均只有“完好”和“失效”两个状态,部件的失效时间服从指数分布;
c) 任意时刻系统中有两个及两个以上部件同时发生失效的概率极小,暂忽略不计;
d) 任意时刻系统总载荷均平均分配给处于完好态的部件,且认为部件失效率只与当前承担的载荷l有关,满足Power Law规则,即
e) 主单元构成部件为逐级劣化,考虑到主单元相对重要,若发生劣化则直接将其修复到完好态,且修复如新。
2) 辅单元
a) 辅单元的固有失效模式为逐级劣化,且每次维修都将其修复到前一状态;
b) 外部环境对系统产生随机冲击时,由辅单元承受冲击载荷,对主单元不产生影响,每次冲击都可能以概率
c) 辅单元能够承受的外部冲击有限,进入完全失效态时此次冲击的剩余载荷将以一定几率
d) 辅单元完全失效后直接将其修复到完好态,此时若主单元也因外部冲击而劣化,则也对主单元进行维修,消除外部冲击造成的损伤(不包括主单元自然失效产生的影响);
e) 所有部件的失效时间均服从指数分布且相互独立。
2.1.2 重要参数定义及符号说明| 表 2 模型2参数符号及定义 Tab. 2 Parameters and definitions of model 2 |
模型1 主单元内部失效相关建模。由假设可知,主单元组成部件均为二态部件,故主单元状态转移过程仍可用图 1表示,在求解状态转移微分方程组时只需将同型部件归类即可。其中任一状态(i1, …, im)表示主单元中1型完好部件的数量为i1,2型完好部件的数量为i2,…,m型完好部件的数量为im。
模型2 辅单元承受冲击失效相关建模。根据假设,令Z(t)={0, 1, …, MF}、L(t)={0, 1}分别表示此过程中辅单元状态及主单元状态。L(t)=1表示主单元因辅单元保护未受到外部冲击引发劣化,L(t)=0表示因辅单元完全失效,外部冲击剩余载荷导致主单元发生劣化,进入不可用状态。此时,由于引发劣化的影响因素不同,故可认为外部冲击失效与主单元的固有失效相互独立,构成多模失效。
由此可得模型状态转移图见图 3。
|
图 3 承受外部冲击时系统状态转移 Fig. 3 State transition diagram of system subject to external impact |
相应的Kolmogrov状态转移微分方程组为
| $ \begin{gathered} \frac{\mathrm{d} \tilde{v}_{M_{\mathrm{F}}, 1}(t)}{\mathrm{d} t}=-\tilde{v}_{M_{\mathrm{F}}, 1}(t) \cdot \sum\limits_{i=1}^{M_{\mathrm{F}}-1} \tilde{\lambda}_{M_{\mathrm{F}}, i}+ \\ \tilde{v}_{M_{\mathrm{F}}-1,1}(t) \cdot \tilde{\mu}_{M_{\mathrm{F}}-1, M_{\mathrm{F}}}+ \\ \tilde{v}_{0,1}(t) \cdot \tilde{\mu}_{0, M_{\mathrm{F}}}+\tilde{v}_{0,0}(t) \cdot \tilde{\mu}_{0, M_{\mathrm{F}}}^{\prime} \end{gathered} $ | (28) |
| $ \begin{gathered} \frac{\mathrm{d} \tilde{v}_{j, 1}(t)}{\mathrm{d} t}=-\tilde{v}_{j, 1}(t) \cdot\left(\sum\limits_{i=1}^{j-1} \tilde{\lambda}_{j, i}+\tilde{\mu}_{j, j+1}\right)+ \\ \tilde{v}_{j+1,1}(t) \cdot \tilde{\lambda}_{j+1, j}+\tilde{v}_{j-1,1}(t) \cdot \tilde{\mu}_{j-1, j}+ \\ \sum\limits_{l=j+1}^{M_{\mathrm{F}}} \tilde{v}_{l, 1} \cdot \tilde{\lambda}_{l, j}, 2 \leqslant j \leqslant M_{\mathrm{F}}-1 \end{gathered} $ | (29) |
| $ \begin{gathered} \frac{\mathrm{d} \tilde{v}_{1,1}(t)}{\mathrm{d} t}=-\tilde{v}_{1,1}(t) \cdot\left(\tilde{\lambda}_{1,0}+{\tilde{\lambda}^{\prime}}_{1,0}+\tilde{\mu}_{1,2}\right)+ \\ \sum\limits_{l=2}^{M_{\mathrm{F}}} \tilde{v}_{l, 1} \cdot \tilde{\lambda}_{l, 1} \end{gathered} $ | (30) |
| $ \frac{\mathrm{d} \tilde{v}_{0,1}(t)}{\mathrm{d} t}=-\tilde{v}_{0,1}(t) \cdot \tilde{\mu}_{0, M_{\mathrm{F}}}+\tilde{v}_{1,1}(t) \cdot \tilde{\lambda}_{1,0} $ | (31) |
| $ \frac{\mathrm{d} \tilde{v}_{0,0}(t)}{\mathrm{d} t}=-\tilde{v}_{0,0}(t) \cdot \tilde{\mu}_{0, {M^{\prime}}_{\mathrm{F}}}+\tilde{v}_{1,1}(t) \cdot {\tilde{\lambda}^{\prime}}_{1,0} $ | (32) |
1) 模糊稳态可靠度
假设主单元中有至少C个部件完好时系统正常工作,由清晰集下系统可靠度的定义可得模糊条件下系统稳态可靠度。
| $ \widetilde{R}=\left(\sum\limits_{i=C}^{Z} \widetilde{P}_{i}\right) \cdot\left(1-\tilde{v}_{0,0}\right) $ | (33) |
其中
2) 主单元j型部件的平均故障数量得到每种类型部件的稳态平均故障数量,有利于更好制定维修保障方案。
| $ \widetilde{E}_{\mathrm{F}}^{j}=\sum\limits_{k=1}^{i_{j}} k \cdot \tilde{p}_{i_{1} \cdots i_{j}-k \cdots i_{m}} $ | (34) |
3) 系统平均工作件数量
工作件数量代表了系统遂行任务的能力,对于表决系统,这一指标尤为重要。
| $ \widetilde{E}_{\mathrm{W}}=\sum\left(i_{1}+\cdots+i_{m}\right) \cdot \tilde{p}_{i_{1} \cdots i_{m}} $ | (35) |
考虑主辅单元协同的雷达系统。主单元A负责产生初始功率,辅单元B的主要功能为放大A产生的功率(如电子设备中常见的功率放大器等)。其中主单元A由部件A1、A2构成,A1为四状态部件,A2为两状态部件,此时假设主单元A的总功率为两个子部件的性能输出之和。辅单元B为三状态部件,状态性能水平对应于不同的放大倍率,可将主单元产生的功率进行放大输出,使用者对系统的总需求功率为
| 表 3 模型1部件模糊失效(修复)转移率 Tab. 3 Fuzzy failure(repair)transfer rate of components in model 1 |
| 表 4 模型1部件状态性能水平 Tab. 4 Performance level of components in model 1 |
| 表 5 模型1模糊失效相关阈值(系数) Tab. 5 Fuzzy failure-correlation threshold (coefficient) of model 1 |
限于篇幅,这里直接给出数学软件计算后系统稳态指标随水平截集α变动的情况(见图 4)。此处α的实际意义是代表了部件参数的模糊程度,当α=0时,部件参数的取值区间最为宽泛,即模糊程度最大,也即表明系统部件的性能状态较为模糊;当α趋近于1时,参数的取值范围越来越精确,即参数的模糊程度越来越小,系统部件的状态性能就越来越明确;当α=1时,代表部件参数的取值范围为一精确数,系统部件状态性能水平是确定的。
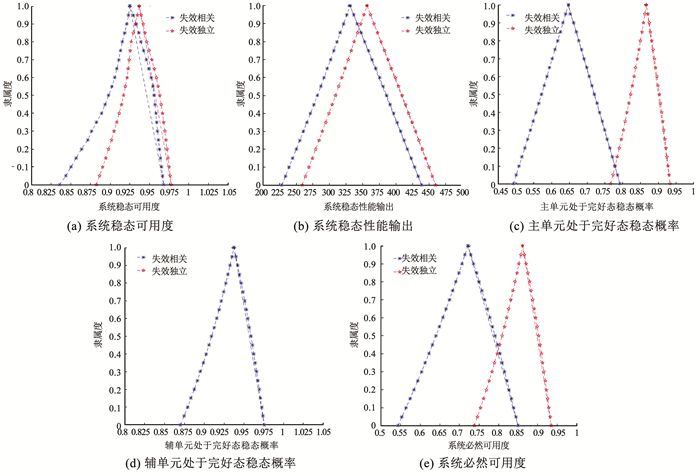
|
图 4 模型1系统模糊稳态指标 Fig. 4 System fuzzy steady state features of model 1 |
由图 4(a)可知,若考虑部件之间的失效相关性,得到的稳态可用度约为0.833~0.958之间,忽略部件失效相关带来的影响,则在0.885~0.98之间,若使用者对设备的要求为长期运行后的可用度不低于0.85,则忽略失效相关会导致出现判断错误的情况,甚至在高强度的环境下运行,可能导致部件的参数性能降至最低,系统可用度无法满足需求。更进一步地,若使用者的可用度需求为不低于0.9,则进行系统升级时需将失效相关纳入考虑范畴,以免出现返工,造成资源浪费。
图 4(b)为系统的稳态性能输出,由于使用者的需求功率为
从图 4(c)及4(d)中可以得到主单元、辅单元各自处于完好态的稳态概率,由于在整个系统中主单元占据主导地位,掌握主单元的状态性能情况至关重要,且对于维修和保养具有一定策略支持。考虑失效相关时,主单元处于完好态的稳态概率约为0.495~0.795,忽略失效相关时的稳态概率约为0.77~0.93,两者的区间下界相差较大,达到0.275,可见是否进行失效相关的预计对主单元的可靠性评估具有较大影响。对于辅单元,稳态时其处于完好态的概率较高,约为0.869~0.975。
系统在恶劣环境下满足使用者需求的能力是值得考虑的重要指标。尤其是对于受到外部环境等因素影响导致状态性能水平及部件参数具有不确定性的系统,这个指标代表了系统在最差状态性能水平时都能满足使用者需求的概率,即系统的必然可用度。图 4(e)给出了稳态时系统的必然可用度,分别为0.538~0.85和0.738~0.935。显然,提高这个指标对提升恶劣环境下系统的可靠性具有重要意义。
3.2 保护型主辅并联系统考虑某恒定功率的负载系统(例如大型装置的电力供应系统、舰船装备综合电力系统等),该系统由主单元A和辅单元B构成。主单元A担负恒定载荷,由A1、A2两种类型子部件并联而成,其中A1、A2型部件的数量均为2,其中A1型子部件的固有失效率及修复率为
| 表 6 模型2部件模糊失效(修复)转移率及辅单元随机劣化概率 Tab. 6 Fuzzy failure(repair)transfer rate of components and failure probability of auxiliary unit in model 1 |
辅单元除保护主单元免受恶劣环境影响之外,还能够代替主单元承受随机的外部冲击,且每次遭受冲击后辅单元随机进入某一劣化态,概率如下(见表 6)。
随机外部冲击的到达服从参数为
由假设,主单元内部的自然失效与外部冲击导致的劣化构成主单元的多模失效,当遭受外部冲击且发生劣化时主单元被认为是不可用的。
此时,将辅单元修复至完好态且认为同时将主单元遭受冲击引发的劣化损伤消除,主单元内部有至少两个部件工作时,系统正常工作,则可得系统的主要稳态指标(见图 5)。
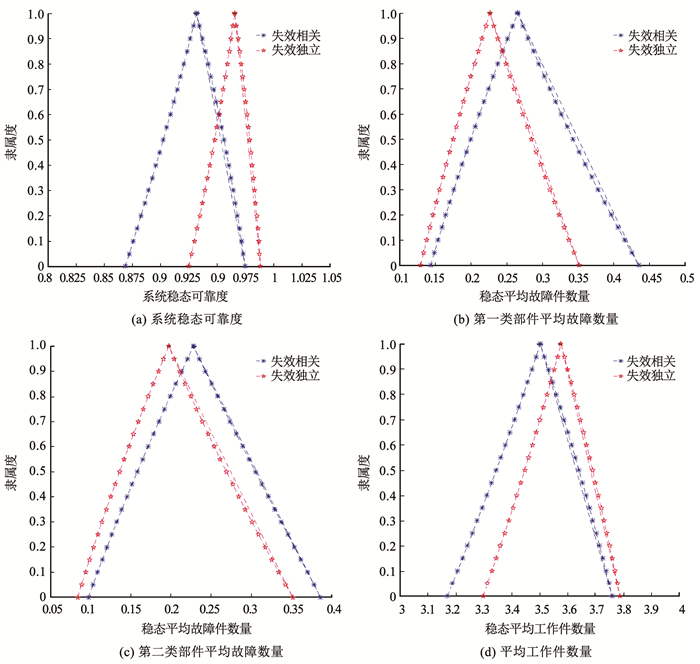
|
图 5 模型2系统模糊稳态指标 Fig. 5 System fuzzy steady state features of model 2 |
从图 5(a)可以看出在系统可靠度评估时将部件之间的失效相关关系纳入建模中,系统的稳态可靠度约为0.868~0.974,若不考虑部件之间的载荷动态分配情况,则系统稳态可靠度区间为0.925~0.988。不难发现,是否考虑失效相关关系,对系统可靠度区间下界影响较大,两者差值为0.057。若使用者(即用户)要求设备长期运行后的可靠度不低于0.9,那么假如不考虑部件之间的失效相关性无疑会产生误判,甚至导致更为严重的后果。
图 5(b)及(c)给出稳态时主单元中A1部件和A2部件的平均故障数量,由此可以对系统长期运行时所需维修力量及维修经费作出合理安排,同时也便于备件保障方及时准备库存,合理进行备件采购。
图 5(d)中给出考虑部件失效相关和忽略部件失效相关时主单元的平均工作件数量,分别为3.18~3.76和3.3~3.78,那么从长远考虑,在一个时期内准备一个部件的完全维修费用相对经济,且为了应对紧急情况,确保在任意时刻均有一个备用件(A1或A2均可) 可供更换是较为合理的。
4 结论1) 与传统可靠性模型相比,考虑了外部环境导致系统部件性能水平及退化特性出现不确定性的情况,运用模糊数对部件参数进行刻画,同时将部件间大量存在的失效相关现象纳入建模之中,避免了对系统可靠性指标估计过高、区间过窄的情形。
2) 复杂环境下,部件的失效相关关系有时并不明确,以精确函数或明确机理描述部件间的失效相关性可能并不适用,对此采用模糊数对失效相关关系进行刻画,通过数据收集等方式,可以避免多状态系统失效相关复杂性带来的困扰,同时对于历史数据缺乏的新型装备也具有良好的评估作用,更为贴近工程实际。
3) 建立了“协同型”和“保护型”两类典型的主辅并联系统,分别从主单元的内部失效相关关系,及辅单元对主单元存在失效相关影响的情况进行描述,研究了系统部件的失效率相关及系统间的失效冲击现象,同时区别于一般研究中直接考虑失效相关性而忽略失效相关发生条件的问题,分析了存在失效相关阈值的情况,通过算例验证了是否考虑部件失效相关对系统可靠性指标产生的影响。
4) 运用α水平截集和Zadeh扩张原理对系统可靠性指标进行求解分析,得到了稳态指标随部件参数性能模糊程度的变动情况,便于及时掌握不同环环境条件下系统各项性能指标的波动范围。
5) 能够得到系统长期运行后的换件需求,制定相应的保障计划,相比传统可靠性评估,便于更为合理地进行备件储存及维修力量分配,为研究复杂条件下的主辅并联系统提供了参考,同时有利于对工程实际中的此类模型进行优化,节约资源与人工。
6) 如何在复杂环境下更为合理、精准地描述多状态系统中的失效相关性,在模糊中把握准确性是下步研究的重点,同时对于可修系统,将维修力量,如修理工人数、维修台数质量、维修前的准备期等纳入考虑,进行全保障任务的可靠性建模研究对工程实际具有重要指导意义。
| [1] |
HOYLANDA, RAUSAND M. System reliability theory: models and statistical methods[M]. New York: Wiley, 1994.
|
| [2] |
SHAO Qi, YANG Shunkun, GOU Xiaodong. Formal analysis of multiple-cell upset failure based on common cause failure theory[J]. IEEE Transactions on Reliability, 2020. DOI:10.1109/TR.2020.3010937 |
| [3] |
WEN Jiakun, CAO Yuan, MA Lianchuan, et al. Design and analysis of double one out of two with a hot standby safety redundant structure[J]. Chinese Journal of Electronics, 2020, 29(3): 586. DOI:10.1049/cje.2020.03.015 |
| [4] |
CAO Yingsai, LIU Sifeng, FANG Zhigeng. Reliability improvement allocation method considering common cause failures[J]. IEEE Transactions on Reliability, 2020, 69(2): 571. DOI:10.1109/TR.2019.2935633 |
| [5] |
ZUO Lin, XIAHOU Tangfan, LIU Yu. Evidential network-based failure analysis for systems suffering common cause failure and model parameter uncertainty[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2019, 233(6): 2225. DOI:10.1177/0954406218781407 |
| [6] |
ZHANG Chao, ZHANG Yuan. Common cause and load-sharing failures-based reliability analysis for parallel systems[J]. Maintenance and Reliability, 2019, 22(1): 26. DOI:10.17531/ein.2020.1.4 |
| [7] |
PARKINSON D B. Reliability bounds for dependent failures[J]. IEEE Transactions on Reliability, 1988, 37(1): 54. DOI:10.1109/24.3713 |
| [8] |
LEVITIN G, XING Liudong. Reliability and performance of multi-state systems with propagated failure having selective effect[J]. Reliability Engineering & System Safety, 2010, 95(6): 655. |
| [9] |
LEVITIN G. Incorporating common-cause failures into non-repairable multi-state series-parallel system analysis[J]. IEEE Transactions on Reliability, 2001, 50(4): 380. DOI:10.1109/24.983398 |
| [10] |
LEVITIN G, XING Liudong, BEN-HAIM H, et al. Reliability of series-parallel systems with random failure propagation time[J]. IEEE Transactions on Reliability, 2013, 62(3): 637. DOI:10.1109/TR.2013.2270415 |
| [11] |
刘宇, 李翔宇, 张小虎. 考虑载荷动态分配机制的多状态系统可靠性建模及优化[J]. 机械工程学报, 2016, 52(6): 198. LIU Yu, LI Xiangyu, ZHANG Xiaohu. Multi-state system reliability modeling and optimization with considering dynamic load distribution mechanism[J]. Journal of Mechanical Engineering, 2016, 52(6): 198. DOI:10.3901/JME.2016.06.197 |
| [12] |
张卓琦, 吴甦, 李斌锋. 考虑故障相关的两部件系统机会维修策略[J]. 清华大学学报(自然科学版), 2012, 52(1): 122. ZHANG Zhuoqi, WU Su, LI Binfeng. Opportunistic maintenance policy for a two-unit system with failure interactions[J]. Journal of Tsinghua University (Science and Technology), 2012, 52(1): 122. |
| [13] |
唐家银, 何平, 李裕奇, 等. 故障相关的表决可修系统可用度计算[J]. 数学的实践与认识, 2013, 43(1): 108. TANG Jiayin, HE Ping, LI Yuqi, et al. Availability calculation model for repairable voting systems considering failure correlation[J]. Mathematics in Practice and Theory, 2013, 43(1): 108. DOI:10.3969/j.issn.1000-0984.2013.01.014 |
| [14] |
周志刚, 秦大同, 杨军, 等. 考虑失效相关性的风力发电机齿轮传动系统动态可靠性分析[J]. 太阳能学报, 2013, 34(7): 1212. ZHOU Zhigang, QIN Datong, YANG Jun, et al. Time-dependent reliability analysis of gear transmission system of wind turbine considering dependent failure[J]. Acta Energiae Solaris Sinica, 2013, 34(7): 1212. DOI:10.3969/j.issn.0254-0096.2013.07.018 |
| [15] |
姚运志, 孟晨, 王成. 考虑失效相关的多部件系统最优预防维修策略[J]. 计算机集成制造系统, 2013, 19(12): 2976. YAO Yunzhi, MENG Chen, WANG Cheng. Optimal preventive maintenance policies for multi-unit system considering failure interactions[J]. Computer Integrated Manufacturing System, 2013, 19(12): 2976. |
| [16] |
李彦锋, 黄洪钟, 黄意贤. 太阳翼驱动机构的故障模式影响分析与时变可靠性研究[J]. 机械工程学报, 2020, 56(5): 108. LI Yanfeng, HUANG Hongzhong, HUANG Yixian. Failure mode and effects analysis and time varying reliability of solar array drive assembly[J]. Journal of Mechanical Engineering, 2020, 56(5): 108. |
| [17] |
DING Y, LISNIANSKI A. Fuzzy universal generating functions for multi-state system reliability assessment[J]. Fuzzy Sets and Systems, 2008, 159(3): 307. DOI:10.1016/j.fss.2007.06.004 |
| [18] |
YU Hongping, ZHAO Yue, MO Li. Fuzzy Reliability assessment of safety instrumented systems accounting for common cause failure[J]. IEEE Access, 2020, 8: 135371. DOI:10.1109/ACCESS.2020.3010878 |
| [19] |
ZHOU Jian, HAN Yulin, LIU Jing, et al. New approached for optimizing standby redundant systems with fuzzy lifetimes[J]. Computer & Industrial Engineering, 2018, 123: 263. |
| [20] |
TEH J. Uncertainty analysis of transmission line end-of-life failure model for bulk electric system reliability studies[J]. IEEE Transactions on Reliability, 2018, 67(3): 1261. DOI:10.1109/TR.2018.2837114 |
| [21] |
HU Linmin, SU Peng. Fuzzy availability assessment for a discrete time repairable multi-state series-parallel system[J]. Journal of Intelligent & Fuzzy Systems, 2016, 30(5): 2663. |
| [22] |
LI Zhigang, ZHOU Jungang, LIU Boying. System reliability analysis method based on fuzzy probability[J]. International Journal of Fuzzy Systems, 2017, 19(6): 1759. DOI:10.1007/s40815-017-0363-5 |
| [23] |
高文科, 张志胜, 周一帆, 等. 存在失效相关及不完备检测的主辅并联系统可靠性建模与维修策略[J]. 自动化学报, 2015, 41(12): 2100. GAO Wenke, ZHANG Zhisheng, ZHOU Yifan, et al. Reliability modeling and maintenance policy for main and supplementary parallel system with failure interaction and imperfect detection[J]. Acta Automatica Sinica, 2015, 41(12): 2100. DOI:10.16383/j.aas.2015.c140735 |
 2021, Vol. 53
2021, Vol. 53


