2. 武汉理工大学 智能交通系统研究中心,武汉 430063;
3. 武汉理工大学 航运学院,武汉 430063;
4. 内河航运技术湖北省重点实验室(武汉理工大学),武汉 430063
2. Intelligent Transportation Systems Research Center, Wuhan University of Technology, Wuhan 430063, China;
3. School of Navigation, Wuhan University of Technology, Wuhan 430063, China;
4. Hubei Key Laboratory of Inland Shipping Technology (Wuhan University of Technology), Wuhan 430063, China
船舶行为是指船舶在内部或外部条件影响下产生的活动。对船舶行为进行认知是分析和判断水上交通态势[1]的关键。从认知论的角度,作为一个时空对象,船舶行为本质上是对船舶时空位置及其关联活动的语义理解[2]。传统的船舶行为建模和分析侧重于从船舶活动的时空数据出发,实现时间、空间维度的模式识别和表达。这种表达能够准确地描述船舶在时空间的活动特征(如位置随时间的变化,速度随时间的变化等),但往往忽略了语义维度的信息挖掘和表达。如,当描述船舶在环境中的行为时,此时是船舶与环境进行的交互行为,单纯从船舶轨迹的时空特征进行分析无法准确辨识船舶行为,需要融合航行环境的数据来对船舶轨迹进行辅助建模与表达,实现对船舶行为的深层认知。
目前,围绕船舶行为的数据模型构建与轨迹的语义丰富两方面,学者们开展了相应的研究。
基于轨迹数据驱动的船舶行为认知方面,主要包括通过船舶自动识别系统(automatic identification system, AIS)轨迹数据所反映的运动特征进行行为建模与基于轨迹的空间分布来挖掘船舶的典型活动模式及检测异常行为两方面。
在微观层面,有学者采用轨迹特征建模的方式对船舶轨迹单元或基本行为进行建模及表达[3-4],但存在轨迹划分方法不一致或划分粒度较大而无法满足细粒度行为分析的问题。有学者基于物体的运动特征提出了一种轨迹基元的划分方法,并建立了基于轨迹基元的时间序列的行为模型[5],为船舶轨迹单元的划分与行为建模提供了理论借鉴。
在宏观层面,学者们注重于对船舶行为模式的挖掘研究。有学者通过船舶AIS数据对船舶轨迹进行聚类分析,挖掘船舶的运动模式及对异常轨迹进行识别[6-8]。这种基于统计学的方法通过对大规模船舶数据进行分析,可以区分出不同行为模式[9-11]的船舶,以及为船舶航行轨迹的预测提供依据。
在语义层,考虑到利用轨迹数据对船舶行为进行认知时会存在信息丢失,部分学者尝试对轨迹进行了语义丰富[12-14],并探索行为的语义表达方法[15-16]。在此基础上,结合机器学习与语义行为进行模式识别[17]与行为预测[18],在语义层对船舶行为进行了分析与挖掘,提高了海事监管人员对水上交通态势的认知。
前人所做的工作在不同程度上提高了对船舶行为的认知,为机器自动辨识船舶行为提供了多种方法。但是还存在一些不足之处:
首先,基于数据驱动的船舶行为认知从智能识别的角度解决了对船舶当前所处航行状态的智能识别,实现了对船舶轨迹在时空区域中的辨识。但是船舶轨迹受物理环境的约束,仅从时空角度对船舶轨迹进行认知无法对轨迹所隐含的物理意义进行表达。因此需要结合船舶所处的环境信息对船舶行为进行分析与描述。
其次,目前的行为语义分析大部分围绕宏观的轨迹特征进行语义分析与建模,很少对船舶语义单元构建进行研究,使得船舶行为在知识层的认知推理能力受到局限。
因此,针对轨迹分割与行为建模中存在的问题,提出了一种船舶行为的语义建模方法,探索了船舶行为语义基本单元的构建方法。首先,根据船舶的运动特征,提出原子行为的概念,将船舶轨迹划分为10种轨迹单元;在此基础上,将船舶轨迹划分为原子轨迹,并融合航行的地理信息,计算原子轨迹与交通规则或基础设施之间的空间拓扑关系,对船舶轨迹进行拓扑语义丰富。其次,结合原子行为与拓扑行为,对船舶的行为语义单元——交通行为, 进行语义组合,构建船舶行为语义模型的基础。最后,以港口为航行环境对船舶行为进行语义表达为例,验证本文提出的模型与方法。
1 船舶行为的语义特征分析船舶行为语义认知是通过模拟人类对船舶轨迹的思维架构来构建计算机对船舶轨迹的语义表达模型,图 1为船舶轨迹到船舶行为的语义建模框架。

|
图 1 船舶轨迹到行为的语义建模框架 Fig. 1 Semantic modeling framework from ship trajectory to behavior |
首先,船舶轨迹是由一连串动作组合而成,而相同的船舶动作在同样的环境中可能表示不同的行为。如图 1所示,直行匀速轨迹段与航道进行空间交互后可能表示船舶正在顺航道航行,也可能表示船舶正在穿越航道。因此,需要对船舶轨迹进行动作划分,对船舶轨迹单元进行建模,实现对船舶行为的抽象提取。船舶轨迹自身具有的运动特征可通过船舶AIS数据记录的位置、速度与航向3个运动属性对船舶运动的基本单元进行特征建模,划分船舶的运动空间。
其次,考虑到船舶航行环境对船舶行为的影响,需要结合船舶航行环境的空间特征,对船舶轨迹运动单元与航行环境存在的交互特征进行建模,对船舶轨迹进行拓扑语义丰富,挖掘船舶轨迹中隐含的语义信息[14]。
最后,为了对船舶行为进行语义表达,需要对船舶的轨迹单元模型及其与航行环境的交互模型进行语义组合,实现对船舶行为的语义建模和语义表达。
2 船舶轨迹单元建模轨迹被认为是在给定的时空区域中为实现某一目标的物体位置的演变记录[4]。其中船舶轨迹T定义为每一时刻下位置序列对的有序组合。
| $ \boldsymbol{T}=\left\{\left(s_{l}, t_{l}\right), \cdots,\left(s_{n}, t_{n}\right)\right\} $ | (1) |
式中: sl= (xl, yl), l∈[1, n],n为轨迹点的个数,sl是轨迹点的经纬度序列对,表示每个时间索引tl的轨迹点所在位置。xl与yl分别表示轨迹点的纬度值与经度值。
2.1 原子行为定义1 运动状态向量:可以反应物体的运动状态,包括停留、变速及转向等状态。
船舶的运动状态向量用一个四元组来表征
| $ \boldsymbol{p}_{l}=\left\{s_{l}, v_{l}, c_{l}, t_{l}\right\} $ | (2) |
式中vl为船对地航速,cl为船舶对地航向。
定义2 船舶原子行为是指在一段时间内,船舶的运动状态不发生变化的行为。
因此,船舶原子行为定义为
| $ \boldsymbol{B}^{\mathrm{a}}=\left\{p_{1}, p_{2}, \cdots, p_{m}\right\} $ | (3) |
式中m为原子行为包含轨迹点的个数。原子行为对应的船舶轨迹即为原子轨迹,是由对应轨迹下每一个时刻下的船舶运动向量组成的有序集合。每个原子轨迹Ta都包含一个起始点与一个终止点,表示如式(4)所示:
| $ \boldsymbol{T}^{\mathrm{a}}=\left\{\left(p_{1}^{\mathrm{b}}, t_{1}\right),\left(s_{2}, t_{2}\right), \cdots,\left(s_{m-1}, t_{m-1}\right),\left(p_{m}^{\mathrm{e}}, t_{m}\right)\right\} $ | (4) |
式中: p1b与pme分别为Ta的起始点与终止点。
根据船舶的运动状态属性,将船舶的原子行为根据位置是否变化、速度及航向是否发生变化两特征划分为10种类型,包括停止、直行加速及右转减速等,见图 2。

|
图 2 船舶原子行为划分 Fig. 2 Classification of ship atomic behaviors |
为方便对船舶行为进行研究,将船舶轨迹视为在二维空间中的一系列点,利用船舶AIS数据实现船舶运动状态向量的建模并进行轨迹的运动空间划分。
通过划分的10种原子行为来划分船舶轨迹,任何时空轨迹都可被视为是轨迹运动单元的有序组合。因此,将船舶轨迹T划分为p个包含起点与终点的原子轨迹,则轨迹T可以表示为
| $ \boldsymbol{T}=\left\{\boldsymbol{T}_{1}^{\mathrm{a}}, \cdots, \boldsymbol{T}_{p}^{\mathrm{a}}\right\} $ | (5) |
式中Tia(i∈[1, p])表示轨迹T划分后的第i个原子轨迹,其反映的原子行为表示为Bia,即
船舶航向差:
| $ \Delta c=\left\{\begin{array}{l} 360^{\circ}-(c(t)-c(t-1)), c(t)-c(t-1) \geqslant 180^{\circ} \\ 360^{\circ}+(c(t)-c(t-1)), c(t)-c(t-1) \leqslant-180^{\circ} \\ c(t)-c(t-1),-180^{\circ}<c(t)-c(t-1)<180^{\circ} \end{array}\right. $ |
船舶加速度:
船舶转向率:
停留速度阈值:vε
加速度阈值:aε
单位航向差阈值:δ
2.2.2 原子轨迹的特征建模根据原子行为及船舶运动状态向量的定义,可对船舶原子轨迹进行特征建模,速度与航向的结合可用两者参数相结合进行确定。
1) 停留
| $ \begin{gathered} \boldsymbol{T}^{\text {stop }}=F\left\{\exists \boldsymbol{T}_{i}^{\mathrm{a}}, \boldsymbol{B}_{i}^{\mathrm{a}},\right. \\ \left.\forall \boldsymbol{p}_{l} \in \boldsymbol{B}_{i}^{\mathrm{a}} \cap 0 \leqslant v_{l} \leqslant v_{\varepsilon}\right\}=1 \end{gathered} $ | (6) |
式中: F{*}是Boolean函数,如果*为真,则F{*}=1,否则,F{*}=0。
2) 运动
| $ \begin{gathered} \boldsymbol{T}^{\text {move }}=F\left\{\exists \boldsymbol{T}_{i}^{\mathrm{a}}, \boldsymbol{B}_{i}^{\mathrm{a}},\right. \\ \left.\forall \boldsymbol{p}_{l} \in \boldsymbol{B}_{i}^{\mathrm{a}} \cap v_{l}>v_{\varepsilon}\right\}=1 \end{gathered} $ | (7) |
3) 直行
| $ \begin{gathered} \boldsymbol{T}^{\mathrm{kc}}=F\left\{\exists \boldsymbol{T}_{i}^{\mathrm{a}}, \boldsymbol{B}_{i}^{\mathrm{a}},\left(\boldsymbol{T}_{i}^{\mathrm{a}}=\boldsymbol{T}^{\mathrm{move}}\right) \cap\right. \\ \left.\left(\forall p_{l} \in \boldsymbol{B}_{i}^{\mathrm{a}} \cap 0 \leqslant \tau_{l} \leqslant \delta\right)\right\}=1 \end{gathered} $ | (8) |
4) 转向
| $ \begin{gathered} \boldsymbol{T}^{\mathrm{tc}}=F\left\{\exists \boldsymbol{T}_{i}^{\mathrm{a}}, \boldsymbol{B}_{i}^{\mathrm{a}},\left(\boldsymbol{T}_{i}^{\mathrm{a}}=T^{\mathrm{move}}\right) \cap\right. \\ \left.\left(\forall p_{l} \in \boldsymbol{B}_{i}^{\mathrm{a}} \cap \tau_{l}>\delta\right)\right\}=1 \end{gathered} $ | (9) |
5) 变速
| $ \begin{gathered} \boldsymbol{T}^{\mathrm{as}}=F\left\{\exists \boldsymbol{T}_{i}^{\mathrm{a}}, \boldsymbol{B}_{i}^{\mathrm{a}},\left(\boldsymbol{T}_{i}^{\mathrm{a}}=T^{\mathrm{move}}\right) \cap\right. \\ \left.\left.\forall p_{l} \in \boldsymbol{B}_{i}^{\mathrm{a}},\left|a_{l}\right|>a_{\varepsilon}\right)\right\}=1 \end{gathered} $ | (10) |
6) 匀速
| $ \begin{gathered} \boldsymbol{T}^{\mathrm{cs}}=F\left\{\exists \boldsymbol{T}_{i}^{\mathrm{a}}, \boldsymbol{B}_{i}^{\mathrm{a}},\left(\boldsymbol{T}_{i}^{\mathrm{a}}=\boldsymbol{T}^{\mathrm{move}}\right) \cap\right. \\ \left.\left(\forall \boldsymbol{p}_{l} \in \boldsymbol{B}_{i}^{\mathrm{a}} \cap 0 \leqslant\left|a_{l}\right| \leqslant a_{\varepsilon}\right)\right\}=1 \end{gathered} $ | (11) |
定义3 船舶拓扑行为:船舶原子轨迹与航行环境中的交通规则或实体设施产生空间拓扑关系所隐含的语义行为。
| $ \boldsymbol{T}^{\mathrm{o}}=\left\{\boldsymbol{T}_{i}^{\mathrm{a}} \cap r_{k}\right\}, k \in[1, K] $ | (12) |
式中: Tia为第i个原子轨迹,rk为第k个交通规则,K为交通规则的数量。
基于维数扩展的9交模型(DE-9IM)能够很好地将两个空间目标的交集是空、点、线或面4种情况区分开[19],可用于分析船舶轨迹与航行环境之间的拓扑关系。
| $ R_{\mathrm{DE-9IM }}(A, B)=\left(\begin{array}{lll} \operatorname{DIM}(\partial A \cap \partial B) & \operatorname{DIM}\left(\partial A \cap B^{\circ}\right) & \operatorname{DIM}\left(\partial A \cap B^{-}\right) \\ \operatorname{DIM}\left(A^{\circ} \cap \partial B\right) & \operatorname{DIM}\left(A^{\circ} \cap B^{\circ}\right) & \operatorname{DIM}\left(A^{\circ} \cap B^{-}\right) \\ \operatorname{DIM}\left(A^{-} \cap \partial B\right) & \operatorname{DIM}\left(A^{-} \cap B^{\circ}\right) & \operatorname{DIM}\left(A^{-} \cap B^{-}\right) \end{array}\right) $ | (13) |
式中: ∂A表示A的内部,A°表示A的边界,A-表示A的外部区域,维扩展9交模型分别计算了两个空间实体3个区域之间的交集,得出DIM的值,值为0表示两者相交结果为点,1表示两者相交结果为线,2表示两者相交结果为面,F表示两者相交为空集。
根据船舶轨迹与航行环境之间形成的拓扑关系,结合DE-9IM,构建了常用的船舶拓扑行为集合Tseto,共15种,包括点-线、点-面、线-线及线-面4种类型。船舶在航行环境中所具有的拓扑行为均可表示为拓扑集合中的一种。
| $ \boldsymbol{T}_{\mathrm{set}}^{\mathrm{o}}=\left\{\boldsymbol{T}_{\mathrm{PL} 1}^{\mathrm{\mathrm{o}}}, \boldsymbol{T}_{\mathrm{PL} 2}^{\mathrm{o}}, \cdots, \boldsymbol{T}_{\mathrm{LA} 5}^{\mathrm{o}}\right\} $ | (14) |
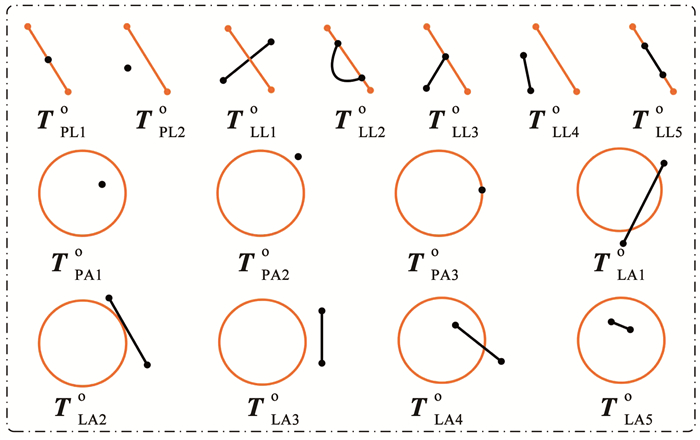
|
图 3 船舶与航行环境的空间拓扑关系 Fig. 3 Spatial topology relation representation between ship and navigation environment |
在船舶原子轨迹对船舶轨迹进行划分的基础上,计算船舶原子轨迹与周围环境中交通规则或基础设施的拓扑关系,对船舶原子行为进行拓扑语义丰富。
3.2.1 地理空间建模将船舶所处航行环境中的交通规则或基础设施视为二维空间中的实体,包括点、线及面3种,根据实体的空间特征对实体进行数学建模。
1) 点位置: p=(x0, y0),(x0, y0)是点的坐标。
2) 圆形区域建模: (x-x0)2+(y-y0)2 < r2,(x, y)为圆形区域内的点,(x0, y0)为锚地或掉头区域的中心,r为半径。
3) 椭圆区域建模:
4) 线段或折线建模:
5) 多边形区域建模:对于由线段组成的闭合或非闭合水域,可以根据线段特征对多边形区域构建线性方程组进行建模。
3.2.2 船舶拓扑关系计算在对船舶航行环境进行数学建模的前提下,结合DE-9IM可对船舶轨迹与航行的环境进行空间拓扑计算。
根据DE-9IM对两个空间实体拓扑计算的定义,对15种船舶拓扑行为对应的拓扑计算结果进行表示,见表 1。
| 表 1 船舶拓扑行为对应的计算矩阵 Tab. 1 Calculation matrix corresponding to topological behavior of ship |
由于一条船舶轨迹包含了起始点与终止点,在计算空间拓扑关系时,不止需要计算轨迹段存在的拓扑关系,也需要计算起止点与周围环境存在的拓扑关系。因此,船舶原子轨迹与航行环境中的交通规则或基础设施之间进行空间拓扑计算之后一般都包含两种或两种以上拓扑行为。
为了对船舶轨迹进行拓扑语义丰富,在船舶原子轨迹划分的基础上,计算轨迹中每一段原子轨迹与周围环境的空间拓扑关系,计算过程见算法1。
| 表 |
船舶原子行为与拓扑行为分别描述了船舶轨迹在时空中的运动特征与航行环境中交通规则或基础设施的空间关系,描述了船舶的时空行为。但是同样的原子行为与不同类型的空间实体之间的交互可能会表达不同的语义行为。如船舶原子轨迹与航道边界有相交(intersection)关系,表示船舶可能发生驶入航道行为,也可能是发生驶出航道行为。因此需要结合原子行为与相应的拓扑行为来对船舶行为进行组合判断。
定义4 船舶交通行为是指船舶原子轨迹在航行环境中所表达的语义行为。交通行为作为船舶语义行为的基本单元,符合人类对船舶行为的认知基础。船舶的复杂行为可由交通行为有序组合而成。
| $ \mathit{\boldsymbol{T}}_l^{\rm{r}} = \left\{ {\underline {\underline {\underline {\mathit{\boldsymbol{T}}_i^{\rm{a}}} } } \cap \underline {\mathit{\boldsymbol{T}}_j^0} \cap \mathop {\ \ {r_k}\ \ }\limits_{\sim\sim\sim} \cap \left[ {\mathit{\boldsymbol{B}}_i^{\rm{a}}} \right]} \right\} $ | (15) |
船舶交通行为的语义表达可参考句子的表达,如式(15)所示。假定交通行为表示为一个独立的句子,则句子的主语是原子轨迹,谓语为拓扑行为,宾语为船舶所处的航行环境,状语为原子行为,表示船舶的进行状态,句子表达的意思即为交通行为。
5 模型实例如图 4所示,以某一港口为例,基于船舶行为语义模型探索船舶在具体的航行水域中行为的抽象提取与语义表达方法。

|
图 4 港口水域船舶轨迹与航行环境交互 Fig. 4 Interaction of ship trajectory and navigation environment in port waters |
港口水域的交通规则或基础设施主要包括锚地、航道、码头、禁航区等,对不同空间特征的航行区域进行特征建模。
1) 线状区域。港口水域单纯的线状区域较少,但是判断船舶的交通行为时也需要对面状区域包含的线段进行拓扑计算。线段用来对港口水域用直线段组成的区域进行建模,包括停泊区域、航道边界以及多边形区域的边界等。船舶在单纯线状区域的交通行为包括3种:靠泊、离泊及停泊。
2) 面状区域。港口水域的大部分水域为圆形水域或被线段划分的多边形水域或半封闭区域,面状水域包括锚地、航道及管制区域等。
船舶在面状区域的交通行为包括驶入行为、驶出行为、航经行为以及横越行为等。
5.2 港口水域船舶交通行为的形式化表达在港口水域船舶交通行为划分的基础上,可对船舶交通行为进行形式化表达,如式(16)~(20)所示。
1) 码头停泊、锚泊
| $ \begin{array}{c} \exists \boldsymbol{T}_{i}^{\mathrm{a}}, F\left\{( \boldsymbol { T } _ { i } ^ { \mathrm { a } } = \text { 停留 } ) \cap \left(R_{\mathrm{DE}-9 \mathrm{IM}}\left(\boldsymbol{T}_{i}^{\mathrm{a}}, \text { 泊位/锚地 }\right)=\right.\right. \\ \left.\left.\boldsymbol{T}_{\mathrm{LL5}}^{\mathrm{o}} / \boldsymbol{T}_{\mathrm{LA} 5}^{\mathrm{o}}\right)\right\}=1 \end{array} $ | (16) |
2) 靠泊、离泊行为
| $ \begin{gathered} \exists \boldsymbol{T}_{i}^{\mathrm{a}} \cap\left(p_{m}^{\mathrm{e}} \cup p_{1}^{\mathrm{b}}\right) \in \boldsymbol{T}_{i}^{\mathrm{a}}, F\left\{\left(\boldsymbol{T}_{i}^{\mathrm{a}}=\boldsymbol{T}^{\mathrm{as}}\right) \cap\right. \\ \left(R_{\mathrm{DE}-9 \mathrm{IM}}\left(\boldsymbol{T}_{i}^{\mathrm{a}}, \text { 泊位 }\right)=\boldsymbol{T}_{\mathrm{LL} 3}^{0}\right) \cap \\ \left.\left(R_{\mathrm{DE}-9 \mathrm{IM}}\left(p_{m}^{\mathrm{e}} / p_{1}^{\mathrm{b}}, \text { 泊位 }\right)=\boldsymbol{T}_{\mathrm{PL} 1}^{\mathrm{o}}\right)\right\}=1 \end{gathered} $ | (17) |
3) 驶入、驶出行为
| $ \begin{aligned} &\exists \boldsymbol{T}_{i}^{\mathrm{a}} \cap\left(p_{m}^{\mathrm{e}} \cup p_{1}^{\mathrm{b}}\right) \in \boldsymbol{T}_{i}^{\mathrm{a}}, F\left\{\left(\boldsymbol{B}_{i}^{\mathrm{a}}=\boldsymbol{T}^{\mathrm{move}}\right) \cap\right.\\ &\left(R_{\mathrm{DE}-9 \mathrm{IM}}\left(\boldsymbol{T}_{i}^{\mathrm{a}}, \text { 面状区域/线状区域 }\right)=\right.\\ &\begin{gathered} \left.\boldsymbol{T}_{\mathrm{LA4}}^{\mathrm{o}} / \boldsymbol{T}_{\mathrm{LL1}}^{\mathrm{o}}\right) \cap\left(R _ { \mathrm { DE } - 9 \mathrm { IM } } \left(p_{m}^{\mathrm{e}} / p_{1}^{\mathrm{b}},\right.\right. \\ \text { 面状区域 } \left.\left.)=\boldsymbol{T}_{\mathrm{PL} 1}^{\mathrm{o}}\right)\right\}=1 \end{gathered} \end{aligned} $ | (18) |
4) 横越行为
| $ \begin{gathered} \exists \boldsymbol{T}_{i}^{\mathrm{a}}, F\left\{\left(\boldsymbol{B}_{i}^{\mathrm{a}}=\boldsymbol{T}^{\text {move }}\right) \cap\right. \\ \left.\left(R_{\mathrm{DE}-9 \mathrm{IM}}\left(\boldsymbol{T}_{i}^{\mathrm{a}}, \text { 面状区域 }\right)=\boldsymbol{T}_{\mathrm{LA1}}^{\mathrm{o}}\right)\right\}=1 \end{gathered} $ | (19) |
5) 航经行为
| $ \begin{array}{c} \exists \boldsymbol{T}_{i}^{\mathrm{a}}, F\left\{( \boldsymbol { T } _ { i } ^ { \mathrm { a } } = \boldsymbol { T } ^ { \mathrm { move } } ) \cap \left(R _ { \mathrm { DE } - 9 \mathrm { IM } } \left(\boldsymbol{T}_{i}^{\mathrm{a}},\right.\right.\right. \text { 面状区域/ } \\ \text { 线状区域 } \left.\left.)=\left(\boldsymbol{T}_{\mathrm{LA} 2}^{\mathrm{o}} / \boldsymbol{T}_{\mathrm{LA3}}^{\mathrm{o}}\right) / \boldsymbol{T}_{\mathrm{LLA}}^{\mathrm{o}}\right)\right\}=1 \end{array} $ | (20) |
如图 5所示,利用语义组合的方式对港口船舶交通行为进行建模,最终对行为进行形式化表达后,提高了船舶交通行为的语义表达能力,为探索大尺度的船舶行为奠定了基础。

|
图 5 港口水域船舶行为语义单元建模 Fig. 5 Behavior semantic unit modeling of ship in port waters |
1) 模型定义了船舶原子行为、拓扑行为及交通行为的概念,对船舶轨迹的运动分割提供了新的思路与方法。利用原子轨迹作为轨迹单元计算船舶的拓扑行为、交通行为,并通过形式化的表达方法构建了3种行为的表达模型,构建了船舶语义行为的底层框架,为分析及推理深层次、大尺度的船舶行为提供支撑。
2) 模型对行为进行了语义建模及表达,首先,模型考虑了船舶航行环境的空间特征,根据不同的空间特征对航行环境中的交通实体进行数学建模,利用维扩展9交模型对船舶原子轨迹与其进行空间拓扑计算,对船舶行为进行拓扑语义丰富;其次,利用船舶行为的语义描述,对船舶原子轨迹、原子行为及拓扑行为进行语义组合,实现了船舶交通行为的语义表达。
3) 该模型对船舶行为进行了抽象提取与语义建模,下一步需要结合船舶的AIS数据与航行的具体场景,探索不同航行场景下船舶原子行为的语义构建标准,如停留时的速度阈值、船舶的转向阈值等,进而通过构建船舶行为的本体模型,实现不同场景中船舶轨迹到行为的语义转化,运行推理机,对船舶行为进行语义推理,辨识船舶的不同行为,对知识驱动的船舶行为检测能力进行验证。
4) 在此基础上,为了对不同时间、空间范围内船舶行为进行自动监管,如“进港”“靠离泊”“锚泊”行为等,考虑到船舶行为的时空多尺度特性,需要对船舶不同时空尺度下的行为进行时序建模,构建不同行为间的时序关系。借助本体的知识表达能力,搭建船舶行为的时空多尺度表达模型,将海事领域中船舶行为的知识转化为具体的本体模型,在语义层对船舶行为进行建模、计算及查询,实现机器对船舶的“半自动”监管。
| [1] |
杜磊, 文元桥, 李正强, 等. 水上交通宏观态势评估模型[J]. 大连海事大学学报, 2016, 42(1): 27. DU Lei, WEN Yuanqiao, LI Zhengqiang, et al. Marine traffic macroscopic situation assessment model[J]. Journal of Dalian Maritime University, 2016, 42(1): 27. DOI:10.16411/j.cnki.issn1006-7736.2016.01.006 |
| [2] |
高惠君. 城市规划空间数据的多尺度处理与表达研究[D]. 北京: 中国矿业大学(北京), 2012 GAO Huijun. Research on multi-scale handline and representation of urban planning spatial data[D]. Beijing: China University of Mining and Technology (Beijing), 2012 |
| [3] |
马文耀, 吴兆麟, 李伟峰, 等. AIS数据中单船操纵模式辨识[J]. 中国航海, 2017, 40(4): 51. MA Wenyao, WU Zhaolin, LI Weifeng, et al. Recognition of individual ship maneuvering pattern from AIS data[J]. Navigation of China, 2017, 40(4): 51. DOI:10.3969/j.issn.1000-4653.2017.04.011 |
| [4] |
NOGUEIRA T P, BRAGA R B, MARTIN H. An ontology-based approach to represent trajectory characteristics[C]//2014 Fifth International Conference on Computing for Geospatial Research and Application. Washington DC: IEEE, 2014: 102
|
| [5] |
曾珍珍, 蔡盛腾, 吕明琪. 基于3D运动轨迹解析与隐马尔可夫模型的动作识别算法[J]. 光学技术, 2018, 44(6): 747. ZENG Zhenzhen, CAI Shengteng, LV Mingqi. The motion recognition algorithm based on 3D trajectory analysis coupled with hidden Markov model[J]. Optical Technique, 2018, 44(6): 747. DOI:10.13741/j.cnki.11-1879/o4.2018.06.020 |
| [6] |
肖潇, 邵哲平, 潘家财, 等. 基于AIS信息的船舶轨迹聚类模型及应用[J]. 中国航海, 2015, 38(2): 82. XIAO Xiao, SHAO Zheping, PAN Jiacai, et al. Ship trajectory clustering model based on AIS data and its application[J]. Navigation of China, 2015, 38(2): 82. DOI:10.3969/j.issn.1000-4653.2015.02.020 |
| [7] |
彭祥文, 高曙, 初秀民, 等. 基于Spark的船舶航行轨迹聚类方法[J]. 中国航海, 2017, 40(3): 49. PENG Xiangwen, GAO Shu, CHU Xiumin, et al. Clustering method of ship's navigation trajectory set based on spark[J]. Navigation of China, 2017, 40(3): 49. DOI:10.3969/j.issn.1000-4653.2017.03.011 |
| [8] |
朱姣, 刘敬贤, 陈笑, 等. 基于轨迹的内河船舶行为模式挖掘[J]. 交通信息与安全, 2017, 35(3): 107. ZHU Jiao, LIU Jingxian, CHEN Xiao, et al. Mining behavior pattern mining of inland vessels based on trajectories[J]. Journal of Transport Information and Safety, 2017, 35(3): 107. DOI:10.3963/j.issn.1674-4861.2017.03.014 |
| [9] |
茅晨昊, 潘晨, 尹波, 等. 基于高斯过程回归的船舶航行轨迹预测[J]. 科技创新与应用, 2017(31): 28. MAO Chenhao, PAN Chen, YIN Bo, et al. Ship trajectory prediction based on Gaussian process regression[J]. Technology Innovation and Application, 2017(31): 28. |
| [10] |
黄亮, 刘益, 文元桥, 等. 基于航行经验的内河稀疏AIS轨迹估计方法[J]. 大连海事大学学报, 2017, 43(3): 7. HUANG Liang, LIU Yi, WEN Yuanqiao, et al. Inland waterway sparse AIS trajectory estimation method based on navigation experience[J]. Journal of Dalian Maritime University, 2017, 43(3): 7. DOI:10.16411/j.cnki.issn1006-7736.2017.03.002 |
| [11] |
黄亮, 刘益, 文元桥, 等. 内河渡船异常行为识别[J]. 大连海事大学学报, 2017, 43(1): 8. HUANG Liang, LIU Yi, WEN Yuanqiao, et al. Abnormal behavior recognition of inland river ferryboat[J]. Journal of Dalian Maritime University, 2017, 43(1): 8. DOI:10.16411/j.cnki.issn1006-7736.2017.01.002 |
| [12] |
VAN HAGE W R, MALAISÉ V, DE VRIES G, et al. Combining ship trajectories and semantics with the simple event model (SEM)[C]//Proceedings of the 1st ACM International Workshop on Events in Multimedia. New York: ACM, 2009: 73. DOI: 10.1145/1631024.1631039
|
| [13] |
GÓMEZ-ROMERO J, SERRANO M A, GARCÍA J, et al. Context-based multi-level information fusion for harbor surveillance[J]. Information Fusion, 2015, 21: 173. DOI:10.1016/j.inffus.2014.01.011 |
| [14] |
PARENT C, SPACCAPIETRA S, RENSO C, et al. Semantic trajectories modeling and analysis[J]. ACM Computing Surveys, 2013, 45(4): 1. DOI:10.1145/2501654.2501656 |
| [15] |
WEN Yuanqiao, ZHANG Yimeng, HUANG Liang, et al. Semantic modelling of ship behavior in harbor based on ontology and dynamic Bayesian network[J]. ISPRS International Journal of Geo-Information, 2019, 8(3): 107. DOI:10.3390/ijgi8030107 |
| [16] |
文元桥, 张义萌, 黄亮, 等. 基于语义的船舶行为动态推理机制[J]. 中国航海, 2019, 42(3): 34. WEN Yuanqiao, ZHANG Yimeng, HUANG Liang, et al. Mechanism of ship behavior dynamic reasoning based on semantics[J]. Navigation of China, 2019, 42(3): 34. |
| [17] |
HUANG Liang, WEN Yuanqiao, GUO Wei, et al. Mobility pattern analysis of ship trajectories based on semantic transformation and topic model[J]. Ocean Engineering, 2020, 201107092. DOI:10.1016/j.oceaneng.2020.107092 |
| [18] |
ADIBI P, PRANOVI F, RAFFAETÁ A, et al. Predicting fishing effort and catch using semantic trajectories and machine learning[C]//International Workshop on Multiple-Aspect Analysis of Semantic Trajectories. Cham: Springer, 2019: 83
|
| [19] |
吴华意, 刘波, 李大军, 等. 空间对象拓扑关系研究综述[J]. 武汉大学学报(信息科学版), 2014, 39(11): 1269. WU Huayi, LIU Bo, LI Dajun, et al. Topological relations of spatial objects: a review[J]. Geomatics and Information Science of Wuhan University, 2014, 39(11): 1269. DOI:10.13203/j.whugis20130642 |
 2021, Vol. 53
2021, Vol. 53


