由于多智能体系统理论在各种工程领域中具有巨大的实际应用价值,近年来多智能体系统的分布式协同控制问题引起了大量专家学者的注意,很多实用有趣的成果见诸报道。例如通过多自主无人车辆的智能感知与协同控制,可以实现无人车之间的间距控制,达到减少交通拥堵、降低尾气排放和保护环境等目标[1-2]。通过多无人机编队控制[3]、多移动舞台机器人协同控制[4]等可以变换出许多有意义的图案或者保持某种队形运动,给观众带来无与伦比的视觉体验。另外,在无线传感网络中通过多智能体系统协同控制理论和方法可以对目标的状态进行更好的探测、定位和预测[5]。
通常多智能体系统中各个智能体之间都是基于网络传输,因此可能会存在复杂的网络攻击和不确定环境干扰等问题[6-7]。例如,Feng等[8]研究了基于事件触发安全协同控制策略下遭受DoS攻击的线性多智能体系统,并分析了安全平均一致问题下DoS攻击的频率和持续时间。Ni等[9]提出了针对存在DoS攻击下连续时间异构线性多智能体网络基于鲁棒随机采样数据的输出反馈一致控制器设计方法。然而以上研究中攻击行为的统计概率信息都是确定已知的,但在实际情况下往往很难精确地获取相关攻击信息,因此研究不确定的DoS攻击下系统协同控制问题将更具现实意义。另外,当攻击发生时,多智能体之间的通信将被阻塞甚至完全打断,各个智能体之间的通信连接情况不再是某一单一的状态,而是在不断发生变化。马尔可夫切换系统方法通常被用来描述此类参数突变的实际系统,关于马尔可夫切换系统的研究已经有了很多重要的结果,其涵盖的领域有系统稳定性分析、滤波器设计和控制器合成等[10-12]。例如,Lam等[13]和Wu等[14]分别研究了基于马尔可夫切换系统方法的$\mathscr{H}$∞鲁棒控制和滑模控制问题,Zhang等[15]针对DoS攻击下的异构线性多智能体系统提出了一种新的切换系统方法并给出了攻击强度和一致性能之间的数量关系。然而,大部分已知的关于马尔可夫切换系统工作无论是应用于控制还是滤波都基于一个重要的假设,那就是控制器/滤波器始终可以完全获取设备的状态信息以确保控制器/滤波器模式始终与系统模式同步运行。因此,所设计的控制器被称为模式相关控制器或同步控制器,然而在实际应用中,这种理想的假设是很难成立的。
基于对上述问题的观察和分析,针对在复杂网络攻击下的基于有向通信传输的异构线性多智能体系统, 设计了一个异步输出反馈控制器来解决:1)不确定发生的DoS攻击导致基于固定数据采样周期通信的系统模型发生不确定的变化从而造成系统失控和2)由于攻击行为的复杂以及网络诱导时延、丢包等产生的系统模型-控制器异步现象。首先通过使用马尔可夫切换系统方法来构建系统模型,并将攻击发生的不确定性描述为在一个凸包面上分布的状态转移概率矩阵,然后设计一个静态输出反馈控制器并引入马尔可夫链来描述系统和控制器之间的异步现象。本文所提出方法主要有两个益处:1)所遭受的攻击信息可以是确定、不确定甚至是完全未知的,因此在实际应用中能够取得更好的效果;2)所设计的异步控制器包含了常见的模型独立控制器($\mathfrak{M}$ ={1})和同步控制器($\mathfrak{M}$=$\mathfrak{N}$且μsφ=1),具有更为广泛的通用性,实际应用中限制更小。
符号:$\mathbb{R}$n表示n维欧几里得空间,X>0表示矩阵X是正定矩阵,角标T表示矩阵的转置,(X)y=X+XT。$\mathbb{E}${·}和Pr{·}分别表示事件·的期望和概率。‖·‖表示矩阵二范数,*表示矩阵的对称项,⊗表示克罗内克积。diag{…}描述块对角矩阵。λmin{Ω}表示矩阵Ω的最小特征值。Re(λ)和Im(λ)分别表示特征值λ的实部和虚部。I和0分别代表适当维度的单位阵和零矩阵。
1 预备知识和问题引入 1.1 图论基础首先介绍一些图论中的基本概念。由集合(v,ε)构成一个有向图G,其中V={v1, v2, …, vn}表示具有n个节点的集合,ε⊆V×V是有序节点对构成的边集合。如果在图G中的任意两个节点都是连通的,则可以称此有向图G是连通图。邻接矩阵定义为A=[aij],当(νi, νj)∈ε时aij>0,表示节点i可以从节点j获得信息,否则aij=0。节点i的邻居集合被定义为Ni={j∶aij>0}。矩阵D=diag{di}称为入度矩阵,其中
假设1 有向图G是连通图并且其中没有孤立的点。
假设2[17] DoS攻击持续的时间是有界的并且攻击行为的变化满足马尔可夫过程。
1.2 攻击描述和系统建模在本文中,假定有一个领导者和n个跟随者,领导者模型为:
| $ \left\{\begin{array}{l} \dot{\boldsymbol{x}}_{0}(t)=\overline{\boldsymbol{M}} \boldsymbol{x}_{0}(t) \\ \boldsymbol{y}_{0}(t)=\overline{\boldsymbol{R}} \boldsymbol{x}_{0}(t) \end{array}\right. $ | (1) |
式中:x0(t)∈$\mathbb{R}$m,y0(t)∈$\mathbb{R}$q分别是领导者的状态变量和测量输出,M∈$\mathbb{R}$m×m和R∈$\mathbb{R}$q×m是两个常数矩阵。
跟随者的模型描述为:
| $ \left\{\begin{array}{l} \dot{\boldsymbol{x}}_{i}(t)=\boldsymbol{A}_{i} \boldsymbol{x}_{i}(t)+\boldsymbol{B}_{i} \boldsymbol{u}_{i}(t)+\boldsymbol{D}_{i} \boldsymbol{\omega}_{i}(t) \\ \boldsymbol{y}_{i}(t)=\boldsymbol{C}_{i} \boldsymbol{x}_{i}(t), i=1, \cdots, n \end{array}\right. $ | (2) |
式中:xi(t)∈$\mathbb{R}$ni、ui(t)∈$\mathbb{R}$pi、ωi(t)∈$\mathbb{R}$mi和yi(t)∈$\mathbb{R}$q分别是第i个智能体的状态、输入、扰动和输出,在异构多智能体系统中,常数矩阵Ai,Bi,Ci,Di一般各不相同。
由于所设计的控制系统通常都是采用数字方式,因此本文假定每一个智能体都能够周期地触发采样过程,类似基于数据采样通信过程可参考文献[18]。正常情况下系统以T0为固定采样周期进行采样,然而由于DoS攻击的存在导致通信连接被破坏,由于每一个智能体采用保持输入机制来更新状态,因此随着攻击持续的时间不同,采样周期hk=tk+1-tk将会变为2T0,3T0,4T0, …,假设hk取值于一个有限集合$\mathfrak{R}$,即hk∈$\mathfrak{R}$={δ1T0, δ2T0, …, δNT0},其中δj, j=1, 2, …, N是正整数。将采样时刻tk简记为k,定义马尔可夫链{ρ(k), k∈$\mathbb{N}$+}用来描述DoS攻击过程,
领导者为
| $ \left\{\begin{array}{l} \boldsymbol{x}_{0}(k+1)=\overline{\boldsymbol{M}}_{\rho(k)} \boldsymbol{x}_{0}(k) \\ \boldsymbol{y}_{0}(k)=\overline{\boldsymbol{R}} \boldsymbol{x}_{0}(k) \end{array}\right. $ | (3) |
跟随者为
| $ \left\{\begin{array}{l} \boldsymbol{x}_{i}(k+1)=\boldsymbol{A}_{i \rho(k)} \boldsymbol{x}_{i}(k)+\boldsymbol{B}_{i \rho(k)} \boldsymbol{u}_{i}(k)+\boldsymbol{D}_{i \rho(k)} \boldsymbol{\omega}_{i}(k) \\ \boldsymbol{y}_{i}(k)=\boldsymbol{C}_{i} x_{i}(k), \quad i=1, \cdots, n \end{array}\right. $ | (4) |
上述式中有:
| $ \left\{\begin{array}{l} \boldsymbol{A}_{i \rho(k)}=\left(\boldsymbol{A}_{i 0}\right)^{\delta_{\rho(k)}}, \boldsymbol{B}_{i \rho(k)}=\sum\limits_{t=1}^{\delta_{\rho(k)}}\left(\boldsymbol{A}_{i 0}\right)^{t-1} \boldsymbol{B}_{i 0} \\ \boldsymbol{D}_{i \rho(k)}=\sum\limits_{t=1}^{\delta_{\rho(k)}}\left(\boldsymbol{A}_{i 0}\right)^{t-1} \boldsymbol{D}_{i 0}, \overline{\boldsymbol{M}}_{\rho(k)}=\left(\overline{\boldsymbol{M}}_{0}\right)^{\delta_{\rho(k)}} \end{array}\right. $ | (5) |
| $ \left\{\begin{array}{l} \boldsymbol{A}_{i 0}=e^{A_{i} T_{0}}, \boldsymbol{B}_{i 0}=\boldsymbol{B}_{i} \int_{0}^{T_{0}} e^{A_{i} \tau} \mathrm{d} \tau \\ \boldsymbol{D}_{i 0}=\boldsymbol{D}_{i} \int_{0}^{T_{0}} e^{A_{i} \tau} \mathrm{d} \tau, \bar{M}_{0}=e^{\bar{M} T_{0}} \end{array}\right. $ | (6) |
但是在实际中由于攻击者会刻意隐藏其攻击行为导致很难精确获取相关攻击信息,因此转移概率矩阵Λ={πst}中的某些元素可能是不确定甚至完全未知的,为此本文将用一个凸多面体来描述概率转移矩阵中有界但不确定的元素,具体形式为
| $ \boldsymbol{P}_{\boldsymbol{\varLambda}} \triangleq\left\{\boldsymbol{\varLambda} \mid \boldsymbol{\varLambda}=\sum\limits_{r=1}^{\mathbb{Z}} \alpha_{r} \boldsymbol{\varLambda}_{r} ; \alpha_{r} \geqslant 0, \sum\limits_{r=1}^{\mathbb{Z}} \alpha_{r}=1\right\} $ | (7) |
其中Λr=[πst], s, t∈$\mathfrak{N}$, r=1, …, $\mathbb{Z}$是包含不确定元素的状态转移概率矩阵,αr∈[0, 1],$\mathbb{Z}$是凸多面体中面的个数。为便于分析,定义$\mathfrak{N}$=$\mathfrak{N}$k(s)∪$\mathfrak{N}$uc(s)∪$\mathfrak{N}$uk(s),其中:
| $ \left\{\begin{array}{l} \mathfrak{N}_{\mathrm{k}}^{(s)} \triangleq\left\{t: \pi_{s t}\right\}, \mathfrak{N}_{\mathrm{uc}}^{(s)} \triangleq\left\{t: \tilde{\pi}_{s t}\right\} \\ \mathfrak{N}_{\mathrm{uk}}^{(s)} \triangleq\left\{t: \hat{\pi}_{s t}\right\}, \pi_{\mathrm{k}}^{(s)} \triangleq \sum\nolimits_{t \in \mathfrak{N}_{\rm{k}}^{(s)}} \pi_{s t} \\ \pi_{\mathrm{uc}}^{(s)} \triangleq \sum\nolimits_{\mathrm{t} \in \mathfrak{N}_{\mathrm{uc}}^{(s)}} \widetilde{\pi}_{s t}^{r}, \forall r=1, \cdots, \mathbb{Z} \end{array}\right. $ | (8) |
不确定和未知的元素分别用上标“~”和“^”表示。
此外,由于攻击行为过于复杂以及各种网络传输问题,控制器所获取的模型信息往往是不准确的,因此控制器模态可以视为是系统模态的观测值,两者之间存在异步现象。本文设计的控制器为
| $ \left\{\begin{array}{l} \boldsymbol{\zeta}_{i}(k+1)=\overline{\boldsymbol{M}}_{\rho(k)} \boldsymbol{\zeta}_{i}(k)+\boldsymbol{F}_{\sigma(k)} \tilde{\sum} \\ \boldsymbol{u}_{i}(k)=\boldsymbol{K}_{i \sigma(k)}\left(y_{i}(k)-\boldsymbol{C}_{i} \boldsymbol{\varPi}_{i} \boldsymbol{\zeta}_{i}(k)\right)+\boldsymbol{\varGamma}_{i \rho(k)} \boldsymbol{\zeta}_{i}(k) \end{array}\right. $ | (9) |
式中:
| $ \left\{\begin{array}{l} \boldsymbol{A}_{i \rho(k)} \boldsymbol{\varPi}_{i}+\boldsymbol{B}_{i \rho(k)} \boldsymbol{\varGamma}_{i \rho(k)}=\boldsymbol{\varPi}_{i} \bar{M}_{\rho(k)} \\ \boldsymbol{C}_{i} \boldsymbol{\varPi}_{i}=\overline{\boldsymbol{R}}, i=1, \cdots, n \end{array}\right. $ | (10) |
上述调节器方程(10)存在解是异构输出同步问题可解的充要条件[19],如果对于任意
定义下列误差信号:
| $ \left\{\begin{array}{l} \boldsymbol{e}_{i}(k)=\boldsymbol{y}_{i}(k)-\boldsymbol{y}_{0}(k) \\ \boldsymbol{\varepsilon}_{i}(k)=\boldsymbol{x}_{i}(k)-\boldsymbol{\varPi}_{i} \boldsymbol{\zeta}_{i}(k) \\ \boldsymbol{\eta}_{i}(k)=\boldsymbol{\zeta}_{i}(k)-\boldsymbol{x}_{0}(k) \end{array}\right. $ | (11) |
和下列符号:
| $ \left\{\begin{array}{l} \boldsymbol{e}(k)=\left[\boldsymbol{e}_{1}^{\mathrm{T}}(k), \cdots, \boldsymbol{e}_{n}^{\mathrm{T}}(k)\right]^{\mathrm{T}} \\ \boldsymbol{\varepsilon}(k)=\left[\boldsymbol{\varepsilon}_{1}^{\mathrm{T}}(k), \cdots, \boldsymbol{\varepsilon}_{n}^{\mathrm{T}}(k)\right]^{\mathrm{T}} \\ \boldsymbol{\eta}(k)=\left[\boldsymbol{\eta}_{1}^{\mathrm{T}}(k), \cdots, \boldsymbol{\eta}_{n}^{\mathrm{T}}(k)\right]^{\mathrm{T}} \\ \boldsymbol{x}_{c}(k)=\left[\boldsymbol{\varepsilon}^{\mathrm{T}}(k), \boldsymbol{\eta}^{\mathrm{T}}(k)\right]^{\mathrm{T}} \\ \boldsymbol{\omega}(k)=\left[\boldsymbol{\omega}_{1}^{\mathrm{T}}(k), \cdots, \boldsymbol{\omega}_{n}^{\mathrm{T}}(k)\right]^{\mathrm{T}} \\ \boldsymbol{A}_{\rho(k)}=\operatorname{diag}\left(\boldsymbol{A}_{i \rho(k)}\right), \boldsymbol{B}_{\rho(k)}=\operatorname{diag}\left(\boldsymbol{B}_{i \rho(k)}\right), \\ \boldsymbol{D}_{\rho(k)}=\operatorname{diag}\left(\boldsymbol{D}_{i \rho(k)}\right) \\ \boldsymbol{C}=\operatorname{diag}\left(\boldsymbol{C}_{i}\right), \boldsymbol{K}_{\sigma(k)}=\operatorname{diag}\left(\boldsymbol{K}_{i \sigma(k)}\right), \boldsymbol{\varPi}=\operatorname{diag}\left(\boldsymbol{\varPi}_{i}\right) \end{array}\right. $ | (12) |
于是可以得到闭环系统
| $ \left\{\begin{array}{l} \boldsymbol{x}_{c}(k+1)=\boldsymbol{A}_{c} \boldsymbol{x}_{c}(k)+\boldsymbol{D}_{c} \boldsymbol{\omega}(k) \\ \boldsymbol{e}(k)=\boldsymbol{C}_{c} \boldsymbol{x}_{c}(k) \end{array}\right. $ | (13) |
其中:
| $ \begin{aligned} &\boldsymbol{A}_{c}=\left[\begin{array}{cc} \boldsymbol{A}_{\rho(k)}+\boldsymbol{B}_{\rho(k)} \boldsymbol{K}_{\sigma(k)} \boldsymbol{C} & \boldsymbol{\varPi}(\boldsymbol{L}+\boldsymbol{G}) \otimes \boldsymbol{F}_{\sigma(k)} \\ \mathit{\pmb{0}} & \boldsymbol{I} \otimes \bar{M}_{\rho(k)}-(\boldsymbol{L}+\boldsymbol{G}) \otimes \boldsymbol{F}_{\sigma(k)} \end{array}\right]\\ &\boldsymbol{C}_{c}=\left[\begin{array}{ll} \boldsymbol{C} & \bar{R}_{c} \end{array}\right], \boldsymbol{D}_{c}=\left[\begin{array}{ll} \boldsymbol{D}_{\rho(k)}^{\mathrm{T}} & \mathit{\pmb{0}} \end{array}\right]^{\mathrm{T}}, \overline{\boldsymbol{R}}_{c}=\boldsymbol{I} \otimes \overline{\boldsymbol{R}} \end{aligned} $ | (14) |
输出一致性问题描述如下:
问题1[21] 设计控制器(9)使得:
1) 当ωi(k)=0且在非零初始条件下有
| $ \left\{\begin{array}{l} \mathbb{E}\left\{\sum\limits_{k=0}^{\infty}\left\|\boldsymbol{\eta}_{i}(k)\right\|^{2} \mid \chi(0)\right\}<\infty \\ \mathbb{E}\left\{\sum\limits_{k=0}^{\infty}\left\|\boldsymbol{\varepsilon}_{i}(k)\right\|^{2} \mid \chi(0)\right\}<\infty \end{array}\right. $ | (15) |
成立,其中χ(0)={ηi(0), εi(0), ρ(0), σ(0)}表示初始条件。
2) 当ωi(k)∈l[0, ∞)且在零初始条件下有
| $ \mathbb{E}\left\{\sum\limits_{k=0}^{\infty}\left\|\boldsymbol{e}_{i}(k)\right\|^{2}\right\} \leqslant \gamma^{2} \sum\limits_{k=0}^{\infty}\left\|\boldsymbol{\omega}_{i}(k)\right\|^{2} $ | (16) |
成立,其中γ是一个正数(鲁棒增益)。
为了解决问题1,本文需要一个合适的引理来处理有向图,根据假设1可知L+G为正定矩阵[22],首先引入一个非奇异矩阵U∈$\mathbb{R}$n×n使得
| $ \boldsymbol{U}^{-1}(\boldsymbol{L}+\boldsymbol{G}) \boldsymbol{U}=\mathfrak{J} $ | (17) |
其中$\mathfrak{J}$是L+G的约旦标准型,λi是它的对角元素且有Re(λ1)≤Re(λ2)≤…Re(λn)。对于任意复数特征值λ,定义分解形式为
| $ \boldsymbol{\varPi}_{\lambda}=\left[\begin{array}{lr} \operatorname{Re}(\lambda) \boldsymbol{I} & -\operatorname{Im}(\lambda) \boldsymbol{I} \\ \operatorname{Im}(\lambda) \boldsymbol{I} & \operatorname{Re}(\lambda) \boldsymbol{I} \end{array}\right] $ | (18) |
λ1, 2=Re(λ1)±jφ,λ3, 4=Re(λn)±jφ,其中φ=max{Im(λi)},据此给出引理1。
引理1[23] 如果对于p={1, 2, 3, 4},有Ξ0+Re(λp)Ξ1+Im(λp)Ξ2 < 0,那么对于所有的p={1, 2, …, n}都有不等式
| $ \varXi_{0}+\operatorname{Re}\left(\lambda_{p}\right) \varXi_{1}+\operatorname{Im}\left(\lambda_{p}\right) \varXi_{2}<0 $ | (19) |
成立,其中Ξ0,Ξ1和Ξ2是与特征值无关的实对称矩阵。
在得出主要结论之前,还需要引入以下几个引理:
引理2 对于具有适当维度的矩阵T,M,U和W,T+(MW)y<0成立充分条件为
| $ \left[\begin{array}{cc} \boldsymbol{T} & * \\ \boldsymbol{M}^{\mathrm{T}}+\boldsymbol{U} \boldsymbol{W} & -\boldsymbol{U}-\boldsymbol{U}^{\mathrm{T}} \end{array}\right]<0 $ | (20) |
引理3 存在正定矩阵Q使得不等式-QTⅡ-1Q≤-Q-QT+Ⅱ对于任意实矩阵Ⅱ≥0都成立。
引理4(舒尔补):若给定对称矩阵
| $ \begin{gathered} \Delta<0 \\ \Delta_{11}<0, \Delta_{22}-\Delta_{12}^{\mathrm{T}} \Delta_{11}^{-1} \Delta_{12}<0 \\ \Delta_{22}<0, \Delta_{11}-\Delta_{12} \Delta_{22}^{-1} \Delta_{12}^{\mathrm{T}}<0 \end{gathered} $ | (21) |
定理1 问题1可解,即异构多智能体系统一致性得到保证等价于低阶闭环系统
| $ \hat{\boldsymbol{\eta}}_{i}(k+1)=\left(\overline{\boldsymbol{M}}_{\rho(k)}-\lambda_{i} \boldsymbol{F}_{\sigma(k)}\right) \hat{\boldsymbol{\eta}}_{i}(k), i=1, \cdots, n $ | (22) |
均方渐近稳定和低阶闭环系统
| $ \left\{\begin{array}{l} \hat{\boldsymbol{\varepsilon}}_{i}(k+1)=\left(\boldsymbol{A}_{i \rho(k)}+\boldsymbol{B}_{i \rho(k)} \boldsymbol{K}_{i \sigma(k)} \boldsymbol{C}_{i}\right) \hat{\boldsymbol{\varepsilon}}_{i}(k)+\boldsymbol{D}_{i \rho(k)} \boldsymbol{\omega}_{i}(k) \\ \boldsymbol{e}_{i}(k)=\boldsymbol{C}_{i} \hat{\boldsymbol{\varepsilon}}_{i}(k), i=1, \cdots, n \end{array}\right. $ | (23) |
均方渐近稳定且具有鲁棒增益γ≥0,其中λi是拓扑矩阵L+G的非零特征值。
证明 可以找到一个非奇异矩阵U∈$\mathbb{R}$n×n使得
| $ \boldsymbol{U}^{-1}(\boldsymbol{L}+\boldsymbol{G}) \boldsymbol{U}=\mathfrak{J}=\left(\begin{array}{ccc} \lambda_{1} & \cdots & * \\ \vdots & & \vdots \\ \mathit{\pmb{0}} & \cdots & \lambda_{n} \end{array}\right) $ | (24) |
定义
| $ \left\{\begin{array}{l} \hat{\boldsymbol{x}}_{c}(k+1)=\boldsymbol{A}_{c}^{\prime} \hat{\boldsymbol{x}}_{c}(k)+\boldsymbol{D}_{c}^{\prime} \boldsymbol{\omega}(k) \\ \boldsymbol{e}(k)=\boldsymbol{C}_{c}^{\prime} \hat{\boldsymbol{x}}_{c}(k) \end{array}\right. $ | (25) |
其中:
| $ \boldsymbol{A}_{c}^{\prime}=\left[\begin{array}{cc} \boldsymbol{A}_{\rho(k)}+\boldsymbol{B}_{\rho(k)} \boldsymbol{K}_{\sigma(k)} \boldsymbol{C} & \boldsymbol{\varPi}(\boldsymbol{L}+\boldsymbol{G}) \boldsymbol{U}^{-1} \otimes \boldsymbol{F}_{\sigma(k)} \\ \mathit{\pmb{0}} & I \otimes \bar{M}_{\rho(k)}-\boldsymbol{U}(\boldsymbol{L}+\boldsymbol{G}) \boldsymbol{U}^{-1} \otimes \boldsymbol{F}_{\sigma(k)} \end{array}\right] $ |
| $ \boldsymbol{C}_{c}^{\prime}=\left[\begin{array}{ll} \boldsymbol{C} & \boldsymbol{U}^{-1} \otimes \overline{\boldsymbol{R}}_{c} \end{array}\right], \boldsymbol{D}_{c}^{\prime}=\boldsymbol{D}_{c} $ |
易知,上式等价于如下的n个低阶系统
| $ \left\{\begin{array}{l} \hat{\boldsymbol{x}}_{c_{i}}(k+1)=\left[\begin{array}{l} \hat{\boldsymbol{\varepsilon}}_{i}(k) \\ \hat{\boldsymbol{\eta}}_{i}(k) \end{array}\right]=\boldsymbol{A}_{c_{i}}^{\prime} \hat{\boldsymbol{x}}_{c_{i}}(k)+\boldsymbol{D}_{c_{i}}^{\prime} \boldsymbol{\omega}_{i}(k) \\ \boldsymbol{e}_{i}(k)=\boldsymbol{C}_{c_{i}}^{\prime} \hat{\boldsymbol{x}}_{c_{i}}(k) \end{array}\right. $ | (26) |
同步渐近稳定,其中:
| $ \begin{aligned} &\boldsymbol{A}_{c_{i}}^{\prime}=\left[\begin{array}{cc} \boldsymbol{A}_{i \rho(k)}+\boldsymbol{B}_{i \rho(k)} \boldsymbol{K}_{i \sigma(k)} \boldsymbol{C}_{i} & \mathit{\boldsymbol{\aleph}} \\ \mathit{\pmb{0}} & \bar{M}_{\rho(k)}-\lambda_{i} \boldsymbol{F}_{\sigma(k)} \end{array}\right]\\ &\boldsymbol{C}_{c_{i}}^{\prime}=\left[\begin{array}{ll} \boldsymbol{C}_{i} & \mathfrak{J} \end{array}\right], \boldsymbol{D}_{c_{i}}^{\prime}=\left[\begin{array}{c} \boldsymbol{D}_{i \rho(k)} \\ \mathit{\pmb{0}} \end{array}\right] \end{aligned} $ | (27) |
上式中$\mathit{\boldsymbol{\aleph}}$和$\mathfrak{I}$是不影响分析的无关项,其中输入ωi(k)不会影响
定理2 如果对于任意的s∈$\mathfrak{N}$和φ∈$\mathfrak{M}$存在鲁棒系数γ≥0,一系列正定对称矩阵Pρ(k)以及控制器增益Fσ(k)和Kiσ(k)使得下列不等式
| $ \sum\limits_{\varphi=1}^{M} \mu_{s \varphi} \boldsymbol{M}_{\Pi}^{\mathrm{T}} \mathscr{P}_{\Omega}^{(s)} \boldsymbol{M}_{\Pi}-\boldsymbol{P}_{s}<0 $ | (28) |
| $ \sum\limits_{\varphi=1}^{M} \mu_{s \varphi}\left(\psi_{i s \varphi}^{\mathrm{T}} \mathscr{P}_{\Omega}^{(s)} \boldsymbol{\psi}_{i s \varphi}-\boldsymbol{X}_{\psi}\right)-\boldsymbol{P}_{s}+\boldsymbol{C}_{i}^{\mathrm{T}} \boldsymbol{C}_{i}<0 $ | (29) |
成立,那么问题1可解,其中:
| $ \begin{array}{l} \boldsymbol{X}_{\psi}=\psi_{i s \varphi}^{\mathrm{T}} \mathscr{P}_{\Omega}^{(s)} \boldsymbol{D}_{i s}\left(\boldsymbol{D}_{i s}^{\mathrm{T}} \mathscr{P}_{\Omega}^{(s)} \boldsymbol{D}_{i s}-\gamma^{2} \boldsymbol{I}\right)^{-1} \boldsymbol{D}_{i s}^{\mathrm{T}} \mathscr{P}_{\Omega}^{(s)} \boldsymbol{\psi}_{i s \varphi}\\ \left\{\begin{array}{l} \mathscr{P}_{k}^{(s)} \triangleq \sum\nolimits_{t \in \mathfrak{N}_\mathcal{K}^{(s)}} \pi_{s t} \boldsymbol{P}_{t}, \mathscr{P}_\mathcal{UC}^{(s)} \triangleq \sum\nolimits_{t \in \mathfrak{N}_\mathcal{\mathcal{UC}}^{(s)}} \widetilde{\pi}_{s t}^{r} \boldsymbol{P}_{t}\\ \mathscr{P}_\mathcal{UK}^{(s)} \triangleq \sum\nolimits_{t \in \mathfrak{N}_\mathcal{UK}^{(s)}} \hat{\pi}_{s t} \boldsymbol{P}_{t}\\ \mathscr{P}^{s} \triangleq \mathscr{P}_{k}^{(s)}+\sum\nolimits_{t \in \mathfrak{N}_{\mathcal{UC}}^{{s}}}\left(\sum\nolimits_{r=1}^{\mathbb{Z}} \alpha_{r} \widetilde{\pi}_{s t}^{r}\right) \boldsymbol{P}_{t}+\mathscr{P}_{\mathcal{UK}}^{(s)}\\ \mathscr{P}_{\Omega}^{(s)} \triangleq \mathscr{P}_{\mathcal{K}}^{(s)}+\mathscr{P}_{\mathcal{UC}}^{(s)}+\left(1-\pi_{\mathcal{K}}^{(s)}-\pi_{\mathcal{UC}}^{(s)}\right) \boldsymbol{P}_{t}, \forall t \in \mathfrak{N}_{\mathcal{UK}}^{(s)} \end{array}\right. \end{array} $ | (30) |
| $ \left\{\begin{array}{l} \hat{\boldsymbol{M}}_{s}=\operatorname{diag}\left\{\overline{\boldsymbol{M}}_{s}, \overline{\boldsymbol{M}}_{s}\right\} \\ \hat{\boldsymbol{F}}_{\varphi}=\operatorname{diag}\left\{\boldsymbol{F}_{\varphi}, \boldsymbol{F}_{\varphi}\right\} \\ \boldsymbol{\psi}_{i s \varphi}=\boldsymbol{A}_{i s}+\boldsymbol{B}_{i s} \boldsymbol{K}_{i \varphi} \boldsymbol{C}_{i} \\ \boldsymbol{M}_{\Pi}=\hat{\boldsymbol{M}}_{s}-\boldsymbol{\Pi}_{\lambda} \hat{\boldsymbol{F}}_{\varphi} \end{array}\right. $ | (31) |
证明 1)首先对于随机系统(22),令
| $ \boldsymbol{z}_{i}(k+1)=\left(\hat{\boldsymbol{M}}_{s}-\boldsymbol{\varPi}_{\lambda} \hat{\boldsymbol{F}}_{\varphi}\right) \boldsymbol{z}_{i}(k) $ | (32) |
渐近随机稳定。为了表达简便,令
| $ \begin{aligned} \mathbb{E}\left\{\Delta V\left(\boldsymbol{z}_{i}(k), k\right)\right\} &=\sum\limits_{\varphi=1}^{M} \mu_{s \varphi} \boldsymbol{z}_{i}^{\mathrm{T}}(k) \boldsymbol{M}_{\Pi}^{\mathrm{T}} \mathscr{P}^{s} \boldsymbol{M}_{\Pi} \boldsymbol{z}_{i}(k)-\\ & \boldsymbol{z}_{i}^{\mathrm{T}}(k) \boldsymbol{P}_{s} \boldsymbol{z}_{i}(k) \end{aligned} $ | (33) |
定义
| $ \left\{\begin{array}{l} \boldsymbol{\varPhi}_{i}=\sqrt{\sum\limits_{\varphi=1}^{M} \mu_{s \varphi} \boldsymbol{M}_{\Pi}} \boldsymbol{z}_{i}(k) \\ \boldsymbol{\varOmega}_{i}=-\boldsymbol{z}_{i}^{\mathrm{T}}(k) \boldsymbol{P}_{s} \boldsymbol{z}_{i}(k) \end{array}\right. $ | (34) |
那么可得
| $ \mathbb{E}\left\{\Delta V\left(\boldsymbol{z}_{i}(k), k\right)\right\}=\boldsymbol{\varPhi}_{i}^{\mathrm{T}} \mathscr{P}^{s} \boldsymbol{\varPhi}_{i}+\boldsymbol{\varOmega}_{i} $ | (35) |
其中有:
| $ \begin{gathered} \mathscr{P}^{s}=\sum\limits_{t=1}^{N} \pi_{s t} \boldsymbol{P}_{t}= \\ \mathscr{P}_{K}^{(s)}+\sum\nolimits_{t \in \mathfrak{N}_{\mathcal{UC}}^{(s)}}\left(\sum\limits_{r=1}^{\mathbb{Z}} \alpha_{r} \tilde{\pi}_{\mathrm{st}}^{r}\right) \boldsymbol{P}_{t}+\mathscr{P}_{\mathcal{UK}}^{(s)} \end{gathered} $ | (36) |
根据实际存在关系
| $ \begin{gathered} E\left\{\Delta V\left(\boldsymbol{z}_{i}(k), k\right)\right\}=\sum\limits_{r=1}^{\mathbb{Z}} \alpha_{r}\left(\boldsymbol{\varPhi}_{i}^{\mathrm{T}} \widetilde{\boldsymbol{\varTheta}}_{1} \boldsymbol{\varPhi}_{i}+\boldsymbol{\varOmega}_{i}\right)= \\ \boldsymbol{\varPhi}_{i}^{\mathrm{T}}\left(\mathscr{P}_{k}^{(s)}+\mathscr{P}_{u c}^{(s)}+\widetilde{\boldsymbol{\varTheta}}_{2}\right) \boldsymbol{\varPhi}_{i}+\boldsymbol{\varOmega}_{i}=\boldsymbol{\varPhi}_{i}^{\mathrm{T}} \mathscr{P}_{\Omega}^{s)} \boldsymbol{\varPhi}_{i}+\boldsymbol{\varOmega}_{i} \end{gathered} $ | (37) |
其中有
| $ \widetilde{\boldsymbol{\varTheta}}_{1}=\mathscr{P}_{k}^{(s)}+\sum\limits_{t \in \mathfrak{N}_{\mathcal{UC}}^{(s)}} \tilde{\pi}_{s t}^{r} \boldsymbol{P}_{t}+\mathscr{P}_{\mathcal{UK}}^{(s)} $ | (38) |
| $ \widetilde{\boldsymbol{\varTheta}}_{2}=\left(1-\pi_{k}^{(s)}-\pi_{u c}^{(s)}\right) \sum\limits_{t \in \mathfrak{N}_{\mathcal{UK}}^{(s)}} \frac{\hat{\pi}_{s t}}{1-\pi_{k}^{(s)}-\pi_{u c}^{(s)}} \boldsymbol{P}_{t} $ | (39) |
| $ \mathscr{P}_{\Omega}^{(s)} \triangleq \mathscr{P}_{k}^{(s)}+\mathscr{P}_{u c}^{(s)}+\left(1-\pi_{k}^{(s)}-\pi_{u c}^{(s)}\right) \boldsymbol{P}_{t}, \forall t \in \mathfrak{N}_{\mathcal{UK}}^{(s)} $ | (40) |
于是可得
| $ \begin{gathered} \mathbb{E}\left\{\Delta V\left(\boldsymbol{z}_{i}(k), k\right)\right\}= \\ \boldsymbol{z}_{i}^{\mathrm{T}}(k)\left(\sum\limits_{\varphi=1}^{M} \mu_{s \varphi} \boldsymbol{M}_{\Pi}^{\mathrm{T}} \mathscr{P}_{\Omega}^{(s)} \boldsymbol{M}_{\Pi}-\boldsymbol{P}_{s}\right) \boldsymbol{z}_{i}(k) \end{gathered} $ | (41) |
根据式(28)可知E{ΔV(zi(k), k)}≤0。
定义
| $ \mathbb{E}\left\{\Delta V\left(\boldsymbol{z}_{i}(k), k\right)\right\} \leqslant-\lambda_{\min }\{\overline{\boldsymbol{\varTheta}}\} \boldsymbol{z}_{i}^{\mathrm{T}}(k) \boldsymbol{z}_{i}(k) $ | (42) |
将不等式两边从0累加到∞有
| $ \begin{aligned} &\mathbb{E}\left\{\sum\limits_{k=0}^{\infty}\left\|\boldsymbol{z}_{i}(k)\right\|^{2}\right\} \leqslant \frac{1}{-\lambda_{\min }\{\overline{\boldsymbol{\varTheta}}\}} \mathbb{E}\{V(\infty)\}+ \\ &\frac{1}{\lambda_{\min }\{\overline{\boldsymbol{\varTheta}}\}} \mathbb{E}\{V(0)\} \leqslant \frac{1}{\lambda_{\min }\{\overline{\boldsymbol{\varTheta}}\}} \mathbb{E}\{V(0)\}<\infty \end{aligned} $ | (43) |
2) 对于随机系统(23),分别考虑ωi(k)=0和ωi(k)≠0两种情况。
a) 当ωi(k)=0时,令ψisφ=Ais+BisKiφCi,定义Lyapunov函数
| $ \begin{gathered} \mathbb{E}\left\{\Delta V\left(\hat{\varepsilon}_{i}(k), k\right)\right\}= \\ \hat{\varepsilon}_{i}^{\mathrm{T}}(k)\left(\sum\limits_{\varphi=1}^{M} \mu_{s \varphi} \boldsymbol{\psi}_{i s \varphi}^{\mathrm{T}} \mathscr{P}_{\Omega}^{(s)} \boldsymbol{\psi}_{i s \varphi}-\boldsymbol{P}_{s}\right) \hat{\varepsilon}_{i}(k) \end{gathered} $ | (44) |
根据(29)可知
| $ \mathbb{E}\left\{\sum\limits_{k=0}^{\infty}\left\|\hat{\varepsilon}_{i}(k)\right\|^{2}\right\}<\infty $ | (45) |
b) 当ωi(k)≠0时,有
| $ \begin{gathered} \mathbb{E}\left\{\Delta V\left(\hat{\varepsilon}_{\iota}(k), k\right)\right\}= \\ \hat{\varepsilon}_{i}^{\mathrm{T}}(k)\left(\sum\limits_{\varphi=1}^{M} \mu_{s \varphi} \boldsymbol{\psi}_{i s \varphi}^{\mathrm{T}} \mathscr{P}_{\Omega}^{(s)} \boldsymbol{\psi}_{i s \varphi}-\boldsymbol{P}_{s}\right) \hat{\varepsilon}_{i}(k)+ \\ \left(\hat{\varepsilon}_{i}^{\mathrm{T}}(k) \sum\limits_{\varphi=1}^{M} \mu_{s \varphi} \boldsymbol{\psi}_{i s \varphi}^{\mathrm{T}} \mathscr{P}_{\Omega}^{(s)} \boldsymbol{D}_{i s} \boldsymbol{\omega}_{i}(k)\right)_{\mathrm{y}}+ \\ \boldsymbol{\omega}_{i}^{\mathrm{T}}(k) \boldsymbol{D}_{i s}^{\mathrm{T}} \mathscr{P}_{\Omega}^{(s)} \boldsymbol{D}_{i s} \boldsymbol{\omega}_{i}(k) \end{gathered} $ | (46) |
定义
| $ \begin{gathered} \mathbb{H}=\mathbb{E}\left\{\Delta V\left(\hat{\varepsilon}_{i}(k), k\right)\right\}+ \\ \boldsymbol{e}_{i}^{\mathrm{T}}(k) \boldsymbol{e}_{i}(k)-\gamma^{2} \boldsymbol{\omega}_{i}^{\mathrm{T}}(k) \boldsymbol{\omega}_{i}(k) \end{gathered} $ | (47) |
于是可以得到
| $ \mathbb{H}=\boldsymbol{\zeta}_{k}\left[\begin{array}{cc} \sum\limits_{\varphi=1}^{M} \mu_{s \varphi} \boldsymbol{\psi}_{i s \varphi}^{\mathrm{T}} \mathscr{P}_{\Omega}^{(s)} \boldsymbol{\psi}_{i s \varphi}-\boldsymbol{P}_{s}+\boldsymbol{C}_{i}^{\mathrm{T}} \boldsymbol{C}_{i} & \sum\limits_{\varphi=1}^{M} \mu_{s \varphi} \boldsymbol{\psi}_{i s \varphi}^{\mathrm{T}} \mathscr{P}_{\Omega}^{(s)} \boldsymbol{D}_{i s} \\ * & \boldsymbol{D}_{i s}^{\mathrm{T}} \mathscr{P}_{\Omega}^{(s)} \boldsymbol{D}_{i s}-\boldsymbol{\gamma}^{2} \boldsymbol{I} \end{array}\right] \boldsymbol{\zeta}_{k}^{\mathrm{T}} $ | (48) |
根据式(29)并使用引理4可知$\mathbb{H}$≤0,对Hamiltonian函数两边从k=0累加到∞有
| $ \begin{gathered} \mathbb{E}\{V(\infty)-V(0)\}+ \\ \mathbb{E}\left\{\sum\limits_{k=0}^{\infty}\left\|\boldsymbol{e}_{i}(k)\right\|^{2}\right\}-\gamma^{2} \sum\limits_{k=0}^{\infty}\left\|\boldsymbol{\omega}_{i}(k)\right\|^{2} \leqslant 0 \end{gathered} $ | (49) |
由于零初始条件V(0)=0和V(∞)>0可以得
| $ \mathbb{E}\left\{\sum\limits_{k=0}^{\infty}\left\|\boldsymbol{e}_{i}(k)\right\|^{2}\right\}-\gamma^{2} \sum\limits_{k=0}^{\infty}\left\|\boldsymbol{\omega}_{i}(k)\right\|^{2} \leqslant 0 $ | (50) |
也就是
| $ \mathbb{E}\left\{\sum\limits_{k=0}^{\infty}\left\|\boldsymbol{e}_{i}(k)\right\|^{2}\right\} \leqslant \gamma^{2} \sum\limits_{k=0}^{\infty}\left\|\omega_{i}(k)\right\|^{2} $ | (51) |
定理2虽然给出了解决问题1的充分条件,然而并不能直接方便的用来求解控制器(9),为了克服这个困难,本文通过运用一系列矩阵变换方法得出定理3。
2.3 基于LMI求解控制器增益定理3 如果存在一系列正定对称矩阵Pρ(k)、G、G、H、Q、Rsφ、Risφ和适维矩阵Hφ、Liφ、Viφ、Ξiφ、$\mathit{\pmb{Ƴ}}$以及鲁棒系数γ≥0使得下列矩阵不等式(52)、(53)对于任意的s∈$\mathfrak{N}$和φ∈$\mathfrak{M}$有可行解,那么问题1可解,即异构多智能体系统输出一致性得到保证。
| $ \left\{\begin{array}{l} {\left[\begin{array}{cc} -\boldsymbol{P}_{s} & \varDelta_{12} \\ * & \varDelta_{22} \end{array}\right]<0} \\ {\left[\begin{array}{cc} -\boldsymbol{R}_{s \varphi} & \boldsymbol{\lambda}^{\prime} \\ * & -\boldsymbol{H}-\boldsymbol{H}^{\mathrm{T}}+\mathscr{P}_{\Omega}^{(s)} \end{array}\right]<0} \end{array}\right. $ | (52) |
| $ \left\{\begin{array}{l} {\left[\begin{array}{cc} \boldsymbol{C}_{i}^{\mathrm{T}} \boldsymbol{C}_{i}-\boldsymbol{P}_{s} & \bar{\varDelta}_{12} \\ * & \bar{\varDelta}_{22} \end{array}\right]<0} & \\ {\left[\begin{array}{cccc} -\boldsymbol{Q}-\boldsymbol{Q}^{\mathrm{T}}+\mathscr{P}_{\Omega}^{s)} & * & * & * \\ \boldsymbol{A}_{i s}^{\mathrm{T}} \boldsymbol{Q}+\boldsymbol{C}_{i}^{\mathrm{T}} \boldsymbol{L}_{i \varphi} \boldsymbol{Y} & -\overline{\boldsymbol{R}}_{i s \varphi} & * & * \\ \boldsymbol{D}_{i s}^{\mathrm{T}} \boldsymbol{Q} & \boldsymbol{0} & -\gamma^{2} \boldsymbol{I} & * \\ \boldsymbol{B}_{i s}^{\mathrm{T}} \boldsymbol{Q}-\boldsymbol{V}_{i \varphi} \boldsymbol{Y} & \boldsymbol{\varXi}_{i \varphi}^{T} \boldsymbol{L}_{i \varphi}^{\mathrm{T}} \boldsymbol{C}_{i} & \mathit{\pmb{0}} & \boldsymbol{V}_{\varXi} \end{array}\right]<0} \end{array}\right. $ | (53) |
其中Ξiφ、$\mathit{\pmb{Ƴ}}$为自行设定的参数矩阵,且有:
| $ \left\{\begin{array}{l} \mathscr{P}_{\Omega}^{(s)}=\mathscr{P}_{\mathcal{K}}^{(s)}+\mathscr{P}_{\mathcal{UC}}^{(s)}+\left(1-\pi_{\mathcal{K}}^{(s)}-\pi_{\mathcal{UC}}^{(s)}\right) \boldsymbol{P}_{t}, \forall t \in \mathfrak{N}_{\mathcal{UK}}^{(s)} \\ \mathscr{P}_{\mathcal{K}}^{(s)}=\sum\nolimits_{t \in \mathfrak{N}_{\mathcal{K}}^{(s)}} \pi_{s t} \boldsymbol{P}_{t}, \mathscr{P}_{\mathcal{UC}}^{(s)}=\sum\nolimits_{t \in \mathfrak{N}_{\mathcal{UC}},} \tilde{\pi}_{s t}^{r} \boldsymbol{P}_{t} \end{array}\right. $ | (54) |
| $ \varDelta_{12}=\left[\sqrt{\mu_{s 1}} \boldsymbol{G} \quad \sqrt{\mu_{s 2}} \boldsymbol{G} \quad \cdots \quad \sqrt{\mu_{s M}} \boldsymbol{G}\right] $ | (55) |
| $ \varDelta_{22}=\left[\begin{array}{ccc} -\boldsymbol{G}-\boldsymbol{G}^{\mathrm{T}}+\boldsymbol{R}_{s 1} & & \\ & \ddots & \\ & & -\boldsymbol{G}-\boldsymbol{G}^{\mathrm{T}}+\boldsymbol{R}_{s M} \end{array}\right] $ | (56) |
| $ \boldsymbol{\lambda}^{\prime}=\left[\begin{array}{cc} \overline{\boldsymbol{M}}_{s}^{\mathrm{T}} \boldsymbol{H}-\operatorname{Re}\left(\overline{\lambda_{p}}\right) \overline{\boldsymbol{H}}_{\varphi} & \operatorname{Im}\left(\bar{\lambda}_{p}\right) \overline{\boldsymbol{H}}_{\varphi} \\ -\operatorname{Im}\left(\lambda_{p}\right) \overline{\boldsymbol{H}}_{\varphi} & \overline{\boldsymbol{M}}_{s}^{\mathrm{T}} \boldsymbol{H}-\operatorname{Re}\left(\overline{\lambda_{p}}\right) \overline{\boldsymbol{H}}_{\varphi} \end{array}\right] $ | (57) |
| $ \bar{\varDelta}_{12}=\left[\sqrt{\mu_{s 1}} \bar{\boldsymbol{G}} \quad \sqrt{\mu_{s 2}} \bar{\boldsymbol{G}} \quad \cdots \quad \sqrt{\mu_{s M}} \bar{\boldsymbol{G}}\right] $ | (58) |
| $ \bar{\varDelta}_{22}=\left[\begin{array}{lll} -\overline{\boldsymbol{G}}-\overline{\boldsymbol{G}}^{\mathrm{T}}+\overline{\boldsymbol{R}}_{i s 1} & & \\ & \ddots & \\ & & -\overline{\boldsymbol{G}}-\overline{\boldsymbol{G}}^{\mathrm{T}}+\overline{\boldsymbol{R}}_{i s M} \end{array}\right] $ | (59) |
| $ \boldsymbol{V}_{\varXi}=-\boldsymbol{V}_{i \varphi} \tilde{\boldsymbol{\varXi}}_{i \varphi}-\boldsymbol{\varXi}_{i \varphi}^{T} \boldsymbol{V}_{i \varphi}^{\mathrm{T}} $ | (60) |
控制器增益Kiφ=(LiφViφ-1)T, Fφ=(HφH-1)T。
证明 1)如果存在正定对称矩阵Ps使得
| $ \sum\limits_{\varphi=1}^{M} \mu_{s \varphi}\left(\boldsymbol{M}_{\varPi}^{\mathrm{T}} \mathscr{P}_{\Omega}^{(s)}\ \boldsymbol{M}_{\varPi}+\varepsilon \boldsymbol{I}\right)-\boldsymbol{P}_{s}<0 $ | (61) |
令Rsφ=ΜΠT$\mathscr{P}$Ω(s)ΜΠ+εI则有
| $ \left\{\begin{array}{l} \sum\limits_{\varphi=1}^{M} \mu_{s \varphi} \boldsymbol{R}_{s \varphi}-\boldsymbol{P}_{s}<0 \\ \boldsymbol{M}_{\varPi}^{\mathrm{T}} \mathscr{P}_{\Omega}^{(s)} \boldsymbol{M}_{\varPi}-\boldsymbol{R}_{s \varphi}<0 \end{array}\right. $ | (62) |
应用引理4有
| $ \left\{\begin{array}{l} \left[\begin{array}{ccccc}-\boldsymbol{P}_{s} & \sqrt{\mu_{s 1}} & \sqrt{\mu_{s 2}} & \cdots & \sqrt{\mu_{s M}} \\ * & -\boldsymbol{R}_{s 1}^{-1} & \boldsymbol{0} & \cdots & \boldsymbol{0} \\ * & * & -\boldsymbol{R}_{s 2}^{-1} & \cdots & \boldsymbol{0} \\ \vdots & \vdots & \vdots & & \vdots \\ * & * & * & \cdots & -\boldsymbol{R}_{s M}^{-1} \end{array}\right]<0\\ \left[\begin{array}{cc} -\boldsymbol{R}_{s \varphi} & \left(\hat{\boldsymbol{M}}_{s}-\boldsymbol{\varPi}_{\lambda} \hat{\boldsymbol{F}}_{\varphi}\right)^{\mathrm{T}} \\ * & -\left(\mathscr{P}_{\Omega}^{(s)}\right)^{-1} \end{array}\right]<0 \end{array}\right. $ | (63) |
上、下矩阵不等式分别左、右乘以对角矩阵diag{I, G, …, G}T,diag{I, H}T和它们的转置后,应用引理3可得
| $ \left\{\begin{array}{l} {\left[\begin{array}{cc} -\boldsymbol{P}_{s} & \varDelta_{12} \\ * & \varDelta_{22} \end{array}\right]<0} \\ {\left[\begin{array}{cc} -\boldsymbol{R}_{s \varphi} & \left(\hat{\boldsymbol{M}}_{s}-\boldsymbol{\varPi}_{\lambda} \hat{\boldsymbol{F}}_{\varphi}\right)^{\mathrm{T}} \boldsymbol{H} \\ * & -\boldsymbol{H}-\boldsymbol{H}^{\mathrm{T}}+\mathscr{P}_{\Omega}^{(s)} \end{array}\right]<0} \end{array}\right. $ | (64) |
令
| $ \boldsymbol{\lambda}^{\prime}=\left[\begin{array}{cc} \overline{\boldsymbol{M}}_{s}^{\mathrm{T}} \boldsymbol{H}-\operatorname{Re}\left(\bar{\lambda}_{p}\right) \overline{\boldsymbol{H}}_{\varphi} & \operatorname{Im}\left(\bar{\lambda}_{p}\right) \overline{\boldsymbol{H}}_{\varphi} \\ -\operatorname{Im}\left(\bar{\lambda}_{p}\right) \overline{\boldsymbol{H}}_{\varphi} & \overline{\boldsymbol{M}}_{s}^{\mathrm{T}} \boldsymbol{H}-\operatorname{Re}\left(\bar{\lambda}_{p}\right) \overline{\boldsymbol{H}}_{\varphi} \end{array}\right] $ | (65) |
2) 同理存在ε>0使得
| $ \sum\limits_{\varphi=1}^{M} \mu_{s \varphi}\left(\boldsymbol{\psi}_{i s \varphi}^{\mathrm{T}} \mathscr{P}_{\Omega}^{(s)} \boldsymbol{\psi}_{i s \varphi}-\boldsymbol{X}_{\psi}+\varepsilon \boldsymbol{I}\right)-\boldsymbol{P}_{s}+\boldsymbol{C}_{i}^{\mathrm{T}} \boldsymbol{C}_{i}<0 $ | (66) |
令Risφ=ψisφT$\mathscr{P} $Ω(s)ψisφ-Χψ+εI,则有
| $ \left\{\begin{array}{l} \sum\limits_{\varphi=1}^{M} \mu_{s \varphi} \overline{\boldsymbol{R}}_{i s \varphi}-\boldsymbol{P}_{s}+\boldsymbol{C}_{i}^{\mathrm{T}} \boldsymbol{C}_{i}<0 \\ \boldsymbol{\psi}_{i s \varphi}^{\mathrm{T}} \mathscr{P}_{\Omega}^{(s)} \boldsymbol{\psi}_{i s \varphi}-\boldsymbol{X}_{\psi}-\overline{\boldsymbol{R}}_{i s \varphi}<0 \end{array}\right. $ | (67) |
应用引理4可得
| $ \left\{\begin{array}{l} {\left[\begin{array}{cccc} \boldsymbol{C}_{i}^{\mathrm{T}} \boldsymbol{C}_{i}-\boldsymbol{P}_{s} & \sqrt{\mu_{s 1}} & \sqrt{\mu_{s 2}} & \cdots & \sqrt{\mu_{s M}} \\ * & -\overline{\boldsymbol{R}}_{i s 1}^{-1} & \mathit{\pmb{0}} & \cdots & \mathit{\pmb{0}} \\ * & * & -\overline{\boldsymbol{R}}_{i s 2}^{-1} & \cdots & \mathit{\pmb{0}} \\ \vdots & \vdots & \vdots & & \vdots \\ * & * & * & \cdots & -\overline{\boldsymbol{R}}_{i s M}^{-1} \end{array}\right]<0} \\ {\left[\begin{array}{cc} \boldsymbol{\psi}_{i s \varphi}^{\mathrm{T}} \mathscr{P}_{\Omega}^{(s)} \boldsymbol{\psi}_{i s \varphi}-\overline{\boldsymbol{R}}_{i s \varphi} & \boldsymbol{\psi}_{i s \varphi}^{\mathrm{T}} \mathscr{P}_{\Omega}^{(s)} \boldsymbol{D}_{i s} \\ * & \boldsymbol{D}_{i s}^{\mathrm{T}} \mathscr{P}_{\Omega}^{(s)} \boldsymbol{D}_{i s}-\gamma^{2} \boldsymbol{I} \end{array}\right]<0} \end{array}\right. $ | (68) |
再一次应用引理4有
| $ \left\{\begin{array}{l} \left[\begin{array}{ccccc}\boldsymbol{C}_{i}^{\mathrm{T}} \boldsymbol{C}_{i}-\boldsymbol{P}_{s} & \sqrt{\mu_{s 1}} & \sqrt{\mu_{s 2}} & \cdots & \sqrt{\mu_{s M}} \\ * & -\overline{\boldsymbol{R}}_{i s 1}^{-1} & \mathit{\pmb{0}} & \cdots & \mathit{\pmb{0}} \\ * & * & -\overline{\boldsymbol{R}}_{i s 2}^{-1} & \cdots & \mathit{\pmb{0}} \\ \vdots & \vdots & \vdots & & \vdots \\ * & * & * & \cdots & -\overline{\boldsymbol{R}}_{i s M}^{-1} \end{array}\right]<0\\ \left[\begin{array}{ccc} -\left(\mathscr{P}_{\Omega}^{(s)}\right)^{-1} & * & * \\ \boldsymbol{\psi}_{i s \varphi}^{\mathrm{T}} & -\overline{\boldsymbol{R}}_{i s \varphi} & * \\ \boldsymbol{D}_{i s}^{\mathrm{T}} & \mathit{\pmb{0}} & -\gamma^{2} \boldsymbol{I} \end{array}\right]<0 \end{array}\right. $ | (69) |
上、下矩阵不等式分别左、右乘以对角矩阵diag{I, G, …, G}T,diag{Q, I, I}T和它的转置后,据引理3可得
| $ \left\{\begin{array}{l} {\left[\begin{array}{ccc} \boldsymbol{C}_{i}^{\mathrm{T}} \boldsymbol{C}_{i}-\boldsymbol{P}_{s} & \bar{\varDelta}_{12} \\ * & \bar{\varDelta}_{22} \end{array}\right]<0} & \\ {\left[\begin{array}{ccc} -\boldsymbol{Q}-\boldsymbol{Q}^{\mathrm{T}}+\mathscr{P}_{\Omega}^{(s)} & * & * \\ \boldsymbol{\psi}_{i s \varphi}^{T} \boldsymbol{Q} & -\overline{\boldsymbol{R}}_{i s \varphi} & * \\ \boldsymbol{D}_{i s}^{\mathrm{T}} \boldsymbol{Q} & \mathit{\pmb{0}} & -\gamma^{2} \boldsymbol{I} \end{array}\right]<0} \end{array}\right. $ | (70) |
由于ψisφ=Ais+BisKiφCi,那么
| $ \left[\begin{array}{ccc} -\boldsymbol{Q}-\boldsymbol{Q}^{\mathrm{T}}+\mathscr{P}_{\Omega}^{(s)} & * & * \\ \boldsymbol{\psi}_{i s \varphi}^{\mathrm{T}} \boldsymbol{Q} & -\overline{\boldsymbol{R}}_{i s \varphi} & * \\ \boldsymbol{D}_{i s}^{\mathrm{T}} \boldsymbol{Q} & \mathit{\pmb{0}} & -\gamma^{2} \boldsymbol{I} \end{array}\right]<0 $ | (71) |
可以写成
| $ \begin{gathered} {\left[\begin{array}{ccc} -\boldsymbol{Q}-\boldsymbol{Q}^{\mathrm{T}}+\mathscr{P}_{\Omega}^{(s)} & * & * \\ \boldsymbol{A}_{i s}^{\mathrm{T}} \boldsymbol{Q} & -\overline{\boldsymbol{R}}_{i s \varphi} & * \\ \boldsymbol{D}_{i s}^{\mathrm{T}} \boldsymbol{Q} & \mathit{\pmb{0}} & -\boldsymbol{\gamma}^{2} \boldsymbol{I} \end{array}\right]+} \\ \left(\left[\begin{array}{c} \mathit{\pmb{0}} \\ \boldsymbol{I} \\ \mathit{\pmb{0}} \end{array}\right] \boldsymbol{C}_{i}^{\mathrm{T}} \boldsymbol{K}_{i \varphi}^{\mathrm{T}} \boldsymbol{B}_{i s}^{\mathrm{T}} \boldsymbol{Q}\left[\begin{array}{lll} \boldsymbol{I} & \mathit{\pmb{0}} & \mathit{\pmb{0}} \end{array}\right]\right)_{\rm{y}}<0 \end{gathered} $ | (72) |
令KiφT=LiφViφ-1,并引入可调参数矩阵Ξiφ,$\mathit{\pmb{Ƴ}}$可得
| $ \begin{array}{c} &{\left[\begin{array}{ccc} -\boldsymbol{Q}-\boldsymbol{Q}^{\mathrm{T}}+\mathscr{P}_{\Omega}^{(s)} & * & * \\ \boldsymbol{A}_{i s}^{\mathrm{T}} \boldsymbol{Q}+\boldsymbol{C}_{i}^{\mathrm{T}} \boldsymbol{L}_{i \varphi} \mathit{\pmb{Ƴ}} & -\overline{\boldsymbol{R}}_{i s \varphi} & * \\ \boldsymbol{D}_{i s}^{\mathrm{T}} \boldsymbol{Q} & \mathit{\pmb{0}} & -\gamma^{2} \boldsymbol{I} \end{array}\right]+} \\ &\left(\left[\begin{array}{l} \mathit{\pmb{0}} \\ \boldsymbol{I} \\ \mathit{\pmb{0}} \end{array}\right] \boldsymbol{C}_{i}^{\mathrm{T}} \boldsymbol{L}_{i \varphi} \boldsymbol{\varXi}_{i \varphi} \boldsymbol{\varXi}_{i \varphi}^{-1} \boldsymbol{V}_{i \varphi}^{-1}\left(\boldsymbol{B}_{i s}^{\mathrm{T}} \boldsymbol{Q}-\boldsymbol{V}_{i \varphi} \boldsymbol{Y}\right)\left[\begin{array}{lll} \boldsymbol{I} & \mathit{\pmb{0}} & \mathit{\pmb{0}} \end{array}\right]\right)_{\rm{y}}<0 \end{array} $ | (73) |
定义:
| $ \left\{\begin{array}{l} \boldsymbol{T}=\left[\begin{array}{ccc} -\boldsymbol{Q}-\boldsymbol{Q}^{\mathrm{T}}+\mathscr{P}_{\Omega}^{(s)} & * & * \\ \boldsymbol{A}_{i s}^{\mathrm{T}} \boldsymbol{Q}+\boldsymbol{C}_{i}^{\mathrm{T}} \boldsymbol{L}_{i \varphi} \mathit{\pmb{Ƴ}} & -\overline{\boldsymbol{R}}_{i s \varphi} & * \\ \boldsymbol{D}_{i s}^{\mathrm{T}} \boldsymbol{Q} & \mathit{\pmb{0}} & -\gamma^{2} \boldsymbol{I} \end{array}\right] \\ \boldsymbol{M}=\left[\begin{array}{l} \mathit{\pmb{0}} \\ \boldsymbol{I} \\ \mathit{\pmb{0}} \end{array}\right] \boldsymbol{C}_{i}^{\mathrm{T}} \boldsymbol{L}_{i \varphi} \boldsymbol{\varXi}_{i \varphi} \\ \boldsymbol{W}=\boldsymbol{\varXi}_{i \varphi}^{-1} \boldsymbol{V}_{i \varphi}^{-1}\left(\boldsymbol{B}_{i s}^{\mathrm{T}} \boldsymbol{Q}-\boldsymbol{V}_{i \varphi} \boldsymbol{Y}\right)\left[\begin{array}{lll} \boldsymbol{I} & \mathit{\pmb{0}} & \mathit{\pmb{0}} \end{array}\right] \\ \boldsymbol{U}=\boldsymbol{V}_{i \varphi} \boldsymbol{\varXi}_{i \varphi} \end{array}\right. $ | (74) |
通过使用引理2可知(53)成立。
为了便于更清晰地理解本文算法整体思想,见表 1,给出了异步控制器具体设计求解的步骤。
| 表 1 异步控制器求解过程 Tab. 1 Solving process of asynchronous controller |
本章基于移动舞台机器人系统进行了仿真研究,证明所提出方法的有效性。现在常用的移动舞台机器人系统一般采用轮式结构,可以很方便的建立数学模型用来研究协同控制问题。
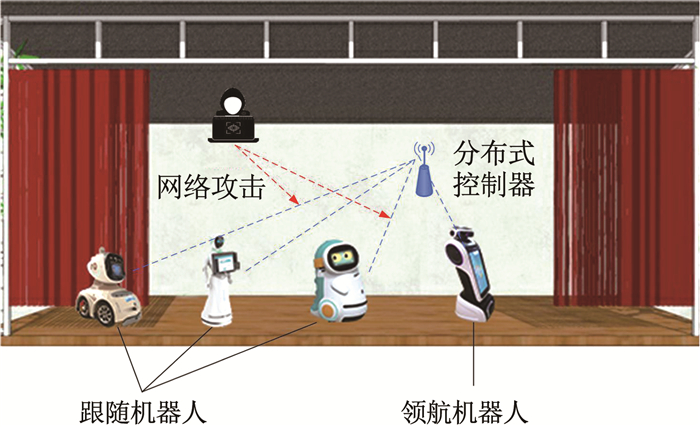
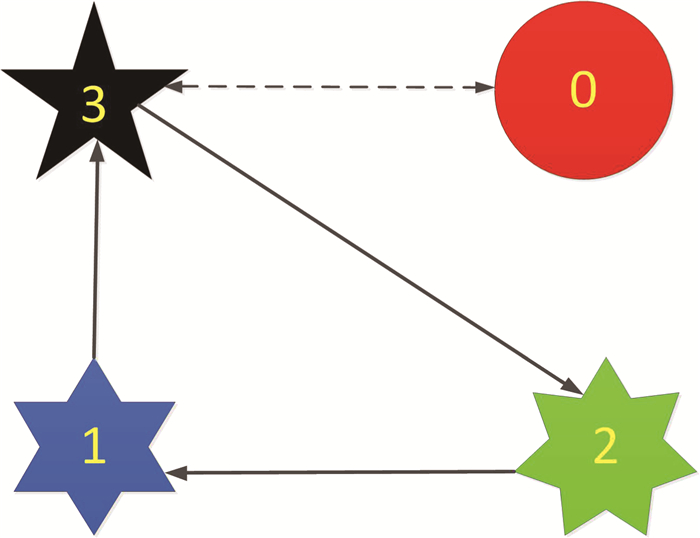
图 1所示为网络攻击下的移动舞台机器人系统整体结构。在本例中,采用一个三阶线性时不变系统来描述移动舞台机器人的运动学模型,其中xi(t)=x1i(t) x2i(t) x3i(t)T,并且x1i(t)、x2i(t)、x3i(t)分别表示位置、速度、加速度。本例假设在1个领导者和3个跟随者的移动舞台机器人系统中进行,其拓扑结构如图 2所示,3个跟随者机器人的运动学模型分别为
| $ \left\{\begin{array}{l} \dot{\boldsymbol{x}}_{i}(t)=\left[\begin{array}{r} 0 & 1 & 0 \\ 0 & 0 & c_{i} \\ 0 & -d_{i} & -a_{i} \end{array}\right] \boldsymbol{x}_{i}(t)+\left[\begin{array}{c} 0 \\ 0 \\ b_{i} \end{array}\right] \boldsymbol{u}_{i}(t)+\left[\begin{array}{c} 0 \\ 0 \\ e_{i} \end{array}\right] \boldsymbol{\omega}_{i}(t) \\ \boldsymbol{y}_{i}(t)=\left[\begin{array}{lll} 1 & 0 & 0 \end{array}\right] \boldsymbol{x}_{i}(t), i=1,2,3 \end{array}\right. $ | (75) |
|
图 1 舞台机器人系统结构 Fig. 1 Structure of stage robot system |
|
图 2 通信连接拓扑 Fig. 2 Communication connection topology |
其中{ai, bi, ci, di, ei}分别取值为{2, 1, 1, 10, 1},{2, 1, 1, 3, 1},{2, 2, 1, 10, 1}。领导机器人模型见式(76)。
| $ \left\{\begin{array}{l} \dot{\boldsymbol{x}}_{0}(t)=\left[\begin{array}{ll} 0 & 1 \\ 0 & 0 \end{array}\right] \boldsymbol{x}_{0}(t) \\ \boldsymbol{y}_{0}(t)=\left[\begin{array}{ll} 1 & 0 \end{array}\right] \boldsymbol{x}_{0}(t) \end{array}\right. $ | (76) |
假设3个跟随机器人受到的干扰信号分别为0.5sin(k),sin(k),-sin(k)。根据式(10)可以计算得到:
| $ \left\{\begin{array}{l} \boldsymbol{\varPi}_{i}=\left[\begin{array}{lll} 1 & 0 & 0 \\ 0 & 1 & 0 \end{array}\right]^{\mathrm{T}} \\ \boldsymbol{\varGamma}_{11}=\boldsymbol{\varGamma}_{12}=\boldsymbol{\varGamma}_{13}=\left[\begin{array}{ll} 0 & 10 \end{array}\right] \\ \boldsymbol{\varGamma}_{21}=\boldsymbol{\varGamma}_{22}=\boldsymbol{\varGamma}_{23}=\left[\begin{array}{ll} 0 & 3 \end{array}\right] \\ \boldsymbol{\varGamma}_{31}=\boldsymbol{\varGamma}_{32}=\boldsymbol{\varGamma}_{33}=\left[\begin{array}{ll} 0 & 5 \end{array}\right] \end{array}\right. $ | (77) |
正常情况下系统的采样周期设定为T0=0.01,设定最大攻击持续时间为2T0,DoS攻击持续时长的概率转移矩阵为
| $ \boldsymbol{\varLambda}=\left[\begin{array}{ccc} 0.5 & 0.2 & 0.3 \\ ? & {\left[\begin{array}{ccc} 0.5 & 0.6 \end{array}\right]} & ? \\ 0.4 & 0.1 & 0.5 \end{array}\right] $ | (78) |
控制器和系统模态异步的概率转移矩阵为
| $ \boldsymbol{\varOmega}=\left[\begin{array}{ccc} 0.2 & 0.1 & 0.7 \\ 0.36 & 0.6 & 0.04 \\ 0.1 & 0.1 & 0.8 \end{array}\right] $ | (79) |
根据通信拓扑计算得到λi, i=1, 2, 3分别为0.245 1, 1.877 4±j0.744 9,所以Re(λp)=0.245 1和1.877 4,Im(λp)=0.744 9,进一步,取γ=2, Ξiφ=0.6,$\mathit{\pmb{Ƴ}}$=[1 0 0], 通过定理3求得控制器增益如下:
| $ \left\{\begin{array}{l} \boldsymbol{F}_{1}=\left[\begin{array}{rrrr} 0.430\ 1 & 0.006\ 1 \\ -0.001\ 6 & 0.430\ 1 \end{array}\right] \\ \boldsymbol{F}_{2}=\left[\begin{array}{rrrrr} 0.428\ 1 & 0.006\ 4 \\ -0.002\ 0 & 0.428\ 1 \end{array}\right] \\ \boldsymbol{F}_{3}=\left[\begin{array}{rrrrr} 0.419\ 8 & 0.005\ 5 \\ -0.002\ 8 & 0.420\ 3 \end{array}\right] \end{array}\right. $ | (80) |
| $ \left\{\begin{array}{lll} K_{11}=-1.647\ 9 & K_{12}=-1.648\ 0 & K_{13}=-1.643\ 7 \\ K_{21}=-1.606\ 9 & K_{22}=-1.607\ 2 & K_{23}=-1.583\ 8 \\ K_{31}=-1.632\ 1 & K_{32}=-1.632\ 9 & K_{33}=-1.630\ 8 \end{array}\right. $ | (81) |
在仿真中,选择初始条件为
| $ \begin{cases}\boldsymbol{x}_{0}(0)=\left[\begin{array}{lll} 6 & 1 \end{array}\right]^{\mathrm{T}} & \boldsymbol{x}_{1}(0)=\left[\begin{array}{lll} 7.8 & 1 & 1 \end{array}\right]^{\mathrm{T}} \\ \boldsymbol{x}_{2}(0)=\left[\begin{array}{lll} 3.8 & 1 & 1 \end{array}\right]^{\mathrm{T}} & \boldsymbol{x}_{3}(0)=\left[\begin{array}{lll} 4.6 & 1 & 1 \end{array}\right]^{\mathrm{T}} \\ \boldsymbol{\zeta}_{1}(0)=\left[\begin{array}{lll} -10 & -20 \end{array}\right]^{\mathrm{T}} & \boldsymbol{\zeta}_{2}(0)=\left[\begin{array}{ll} 10 & 20 \end{array}\right]^{\mathrm{T}} \\ \boldsymbol{\zeta}_{3}(0)=\left[\begin{array}{ll} -8 & -10 \end{array}\right]^{\mathrm{T}}\end{cases} $ | (82) |
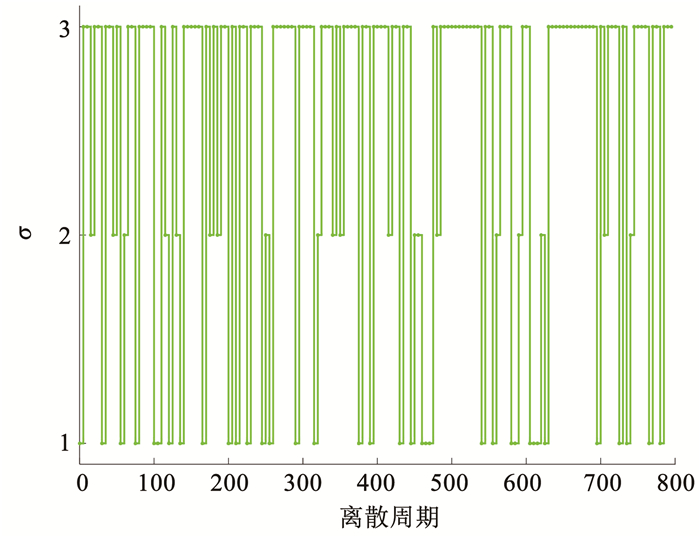
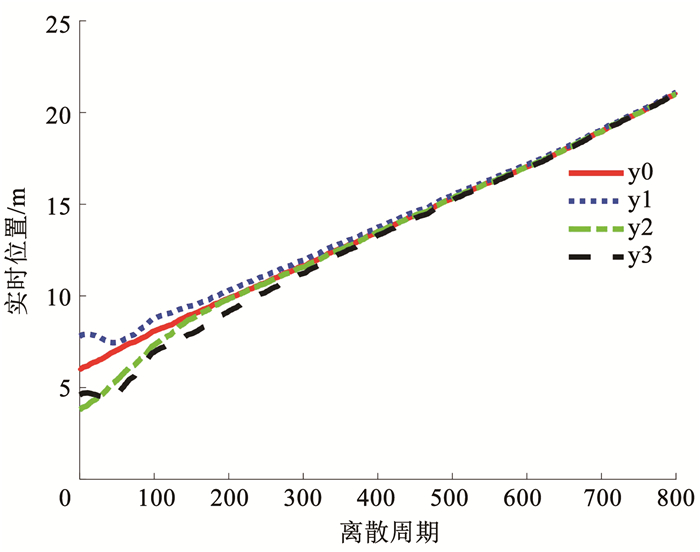
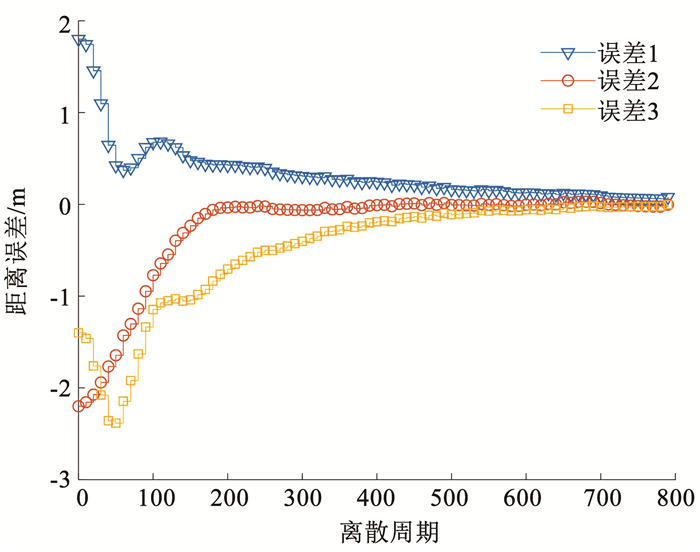
DoS攻击的触发和控制器异步状态分别见图 3、4,从图 5(位置跟踪)和图 6(跟踪误差)可以看出异构移动舞台机器人系统的一致性基本能够被满足。

|
图 3 系统状态 Fig. 3 System state |
|
图 4 控制器状态 Fig. 4 Controller state |
|
图 5 实时位置跟踪 Fig. 5 Real-time location tracking |
|
图 6 跟踪距离误差 Fig. 6 Tracking distance error |
鲁棒性是衡量系统性能的一个重要指标,其体现了系统对抗外界干扰的能力,本文所设计的异步控制器具有较好的兼容性,包含了普通的模式独立控制器和同步控制器。在完全相同的系统模型和初始条件下,分别采用普通的模式独立控制器和同步控制器以及本文所设计的异步控制器,仿真计算得出其系统鲁棒性系数γ分别为1.293 1、1.106 8和0.915 5。可以验证使用本文所设计的异步控制器时系统具有更好(小)的鲁棒性能,表现为抗干扰能力更强,即系统鲁棒性能更优。
4 结论本文考虑了不确定DoS攻击下由于系统模态获取困难引起的控制器-系统模型异步问题。引入马尔可夫过程来描述系统所遭受的攻击以及与控制器之间的异步现象,给出了更为全面的系统建模方法,然后结合所设计的输出反馈控制器通过解耦技术将原高维系统转换为两个低维的闭环误差系统,并且通过应用Lyapunov稳定性理论得到了保证异构多智能体系统输出一致性的充分条件。进一步,结合相关矩阵变换方法给出了通过求解一系列矩阵不等式来获得控制器增益的方法。最后,通过基于移动舞台机器人系统的仿真研究验证了本文所提出方法的有效性。
| [1] |
ZHENG Yang, LI Shengbo, LI Keqiang, et al. Platooning of connected vehicles with undirected topologies: robustness analysis and distributed H-infinity controller synthesis[J]. IEEE Transactions on Intelligent Transportation Systems, 2018, 19(5): 1353. DOI:10.1109/TITS.2017.2726038 |
| [2] |
FAX J, MURRAY R. Information flow and cooperative control of vehicle formations[J]. IEEE Transactions on Automatic Control, 2004, 49(9): 1465. DOI:10.1109/TAC.2004.834433 |
| [3] |
DASGUPTA P. A multiagent swarming system for distributed automatic target recognition using unmanned aerial vehicles[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part A: Systems and Humans, 2008, 38(3): 549. DOI:10.1109/TSMCA.2008.918619 |
| [4] |
YU Wenhai, NI Hongjie, DONG Hui, et al. Consensus of heterogeneous multi-agent systems with uncertain DoS attack: application to mobile stage vehicles[J]. Kybernetika, 2020, 56(2): 278. DOI:10.14736/kyb-2020-2-0278 |
| [5] |
臧传治, 于海斌, 梁韦华, 等. 基于多智能体理论实现无线传感器网络的目标监视与追踪的策略[J]. 高技术通讯, 2006, 16(3): 257. ZANG Chuanzhi, YU Haibin, LIANG Weihua, et al. Target tracking based on multi-agent theory in wireless sensor network[J]. High Technology Letters, 2006, 16(3): 257. DOI:10.3321/j.issn:1002-0470.2006.03.008 |
| [6] |
伍益明. 恶意攻击下的多智能体系统安全一致性问题研究[D]. 杭州: 浙江工业大学, 2016 WU Yiming. Research on secure consensus for multi-agent systems under malicious attacks[D]. Hangzhou: Zhejiang University of Technology, 2016 |
| [7] |
吴治海. 网络环境下的多智能体系统一致性问题研究[D]. 武汉: 华中科技大学, 2011 WU Zhihai. Research on the consensus of multi-agent systems in network environment[D]. Wuhan: Huazhong University of Science and Technology, 2011. DOI: 10.7666/d.d186214 |
| [8] |
FENG Zhi, HU Guoqiang. Distributed secure average consensus for linear multi-agent systems under DoS attacks[C]//2017 American Control Conference (ACC). Seattle: IEEE, 2017: 2261. DOI: 10.23919/ACC.2017.7963289
|
| [9] |
NI Hongjie, XU Zhenhua, CHENG Jun, et al. Robust stochastic sampled-data-based output consensus of heterogeneous multi-agent systems subject to random DoS attack: a Markovian jumping system approach[J]. International Journal of Control Automation & Systems, 2019, 17(7): 1687. DOI:10.1007/s12555-018-0658-9 |
| [10] |
ZHANG Lixian, WANG Shun, KARIMI H R, et al. Robust finite-time control of switched linear systems and application to a class of servomechanism systems[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(5): 2476. DOI:10.1109/TMECH.2014.2385796 |
| [11] |
ZHANG Lixian, ZHUANG Songlin, SHI Peng, et al. Uniform tube based stabilization of switched linear systems with mode-dependent persistent dwell-time[J]. IEEE Transactions on Automatic Control, 2015, 60(11): 2994. DOI:10.1109/TAC.2015.2414813 |
| [12] |
WU Ligang, ZHENG Weixing, GAO Huijun. Dissipativity-based sliding mode control of switched stochastic systems[J]. IEEE Transactions on Automatic Control, 2013, 58(3): 785. DOI:10.1109/TAC.2012.2211456 |
| [13] |
LAM J, SHU Z, XU S, et al. Robust H∞ control of descriptor discrete-time Markovian jump systems[J]. International Journal of Control, 2007, 80(3): 374. DOI:10.1080/00207170600999322 |
| [14] |
WU Ligang, SU Xiaojie, SHI Peng. Sliding mode control with bounded L2 gain performance of Markovian jump singular time-delay systems[J]. Automatica, 2012, 48: 1929. DOI:10.1016/j.automatica.2012.05.064 |
| [15] |
ZHANG Dan, FENG Gang. A new switched system approach to leader-follower consensus of heterogeneous linear multiagent systems with DoS attack[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems. DOI:10.1109/TSMC.2019.2895097 |
| [16] |
MESBAHI M, EGERSTEDT M. Graph theoretic methods in multiagent networks[M]. Princeton: Princeton University Press, 2010.
|
| [17] |
FENG Zhi, WEN Guanghui, HU Guoqiang. Distributed secure coordinated control for multiagent systems under strategic attacks[J]. IEEE Transactions on Cybernetics, 2017, 47(5): 1273. DOI:10.1109/TCYB.2016.2544062 |
| [18] |
WEN Guanghui, YU Wenwu, CHEN M Z Q, et al. H∞ pinning synchronization of directed networks with aperiodic sampled-data communications[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2014, 61(11): 3245. DOI:10.1109/TCSI.2014.2334871 |
| [19] |
WIELAND P, SEPULCHRE R, ALLGOWER F. An internal model principle is necessary and sufficient for linear output synchronization[J]. Automatica, 2011, 47(5): 1068. DOI:10.1016/j.automatica.2011.01.081 |
| [20] |
HUANG Jie. Nonlinear output regulation: theory and applications[M]. Philadelphia: Society for Industrial and Applied Mathematics, 2004: 5.
|
| [21] |
YANG Fuwen, WANG Zidong, HUNG Y S, et al. H∞ control for networked systems with random communication delays[J]. IEEE Transactions on Automatic Control, 2006, 51(3): 511. DOI:10.1109/TAC.2005.864207 |
| [22] |
JIAO Qiang, MODARES H, LEWIS F L, et al. Distributed L2-gain output-feedback control of homogeneous and heterogeneous systems[J]. Automatica, 2016, 71: 361. DOI:10.1016/j.automatica.2016.04.025 |
| [23] |
XI Jianxiang, SHI Zongying, ZHONG Yisheng. Consensus analysis and design for high-order linear swarm systems with time-varying delays[J]. Physica A: Statistical Mechanics and its Applications, 2011, 390: 4114. DOI:10.1016/j.physa.2011.06.045 |
 2021, Vol. 53
2021, Vol. 53


