2. 陕西科技大学 设计与艺术学院,西安 710021;
3. 中国船舶科学研究中心,江苏 无锡 214082
2. College of Art and Design, Shaanxi University of Science and Technology, Xi'an 710021, China;
3. China Ship Scientific Research Center, Wuxi 214082, Jiangsu, China
狭小、密闭舱室空间的优化布局,通常是以操作员为中心,建立仿真模拟器来进行系列优化研究与评估,广泛用于航空宇航、飞行器及载人潜水器空间布局中。国外的波音公司早在1969年研发的BOEMAN项目,创建人体模型进行工效分析,用于飞机舱室布局。进入21世纪,随着虚拟仿真技术的发展,美国NASA航空宇航的A3I项目、北约飞行器的AGARD项目以及荷兰NLR实验室的GRACE飞机驾驶舱项目[1],都是通过仿真模拟器来研究如何优化空间布局,达到降低人为因素导致失误率的目的。国内的研究起步相对较晚,研究主体是国内的航空航天类大学,代表性的研究有科技部973项目、工信部十二五计划民机专项,主要是针对驾驶舱人机工效综合仿真及评估方面的研究。
载人潜水器是探索深海、开发海洋的一种神兵利器,需要潜航员在密闭、狭小的潜水器舱室进行高强度、高精度作业。如何在极度压缩的空间里进行舱室布局,符合诸多人机工程学要求,让潜航员们高效、舒适的完成潜水器作业任务,一直以来就是海洋强国研究的热门课题。本文基于虚拟仿真技术,构建潜水器舱室虚拟场景,以潜水器任务为导向,仿真实际工作中潜航员的人体生物力学参数及作业行为,经多方博弈后达到潜航员的最佳均衡状态,得到系列动态仿真数据用于人机工效综合分析与评估,为优化舱室布局提高人因可靠性提供一种探讨途径。
1 载人潜水器舱室布局 1.1 载人潜水器深潜与任务载人潜水器深潜的操作流程简化为下潜、坐底、巡航、工作、上浮5个部分。蛟龙号潜水器采用无动力上浮下潜方式,出水带自动定位功能[2],如图 1所示。潜水器任务可简化为测量、取样、设备布放、检测等多种作业任务。

|
图 1 “蛟龙号”总布置图 Fig. 1 General layout of Jiaolong |
载人潜水器舱室近似椭圆形球体,如图 1的粗线框球形。球形舱内径2.1 m,能容纳包括一名操作员、两名科学家共3名潜航员,以及座椅、监视器、操纵器等其他设备。工作舱按功能可分为主控区、显示区、生保区、工作区及其他设备区,如图 2(a)所示。3名潜航员工作区域重叠,其任务活动空间集中在舱室前部,一人主操作,一人辅助观察,一人监视。舱室后半部分用于放置大型设备,舱室壁放置显示器和监视器等,如图 2(b)所示就是基于潜航员的舱室分割布局。

|
图 2 基于潜航员的舱室分割布局 Fig. 2 Cabin layout decomposition based on submariners |
博弈论又称为对策论(Game Theory),主要分为合作博弈与非合作博弈,是研究具有竞争性质个体之间相互作用的数学理论和方法。1956年Blackwell将向量函数的零和博弈称为多目标博弈模型,1959年Shapley在多目标博弈问题中定义了均衡点[3]。博弈论常根据多个个体行为来研究其优化策略,广泛应用于现代科学中。构建多目标博弈下的潜航员作业姿态仿真模型,得到舱室环境、潜水器任务与潜航员人机工学诸多要素之间相互作用的动态仿真数据,是评估潜航员人因可靠性的一种有效方法[4]。
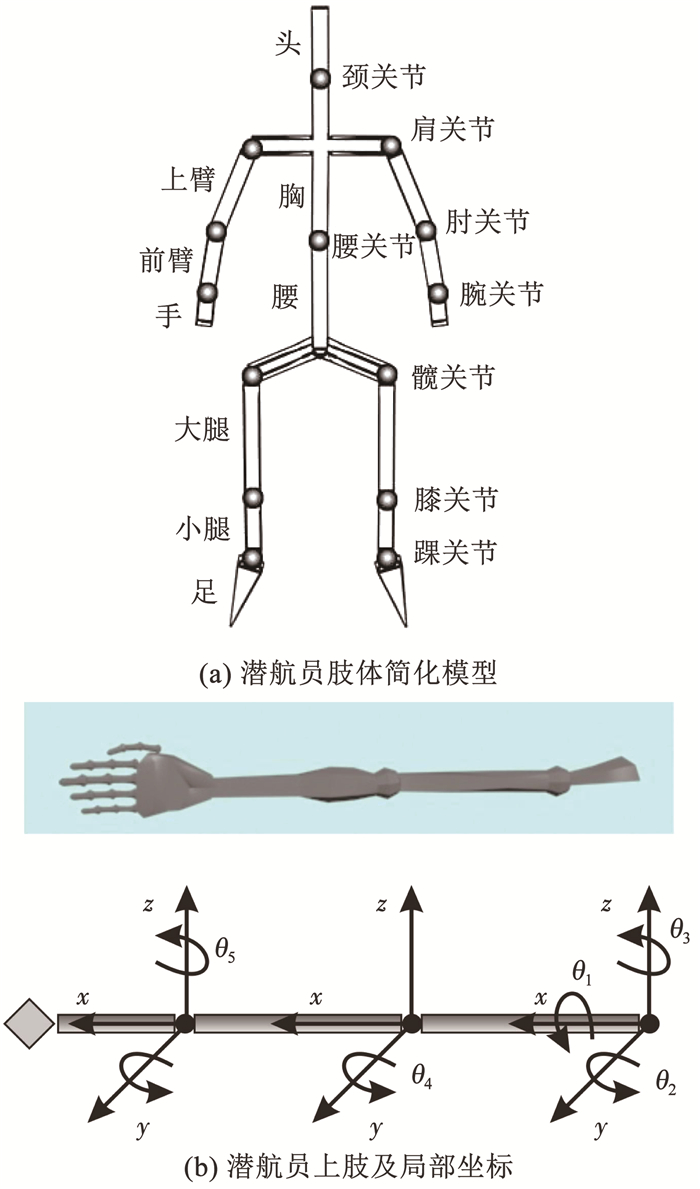
2.1 潜航员肢体系统简化模型构建作业姿态仿真模型,首先把潜航员肢体可以看作是自由度很高的多关节链状结构,肢体运动通过相邻肢体转动来实现,不同范围运动肢体的舒适度不同。潜航员肢体模型简化为15个刚体、14个关节[5],如图 3(a)所示,潜航员上肢及局部坐标如图 3(b)所示。
|
图 3 潜航员肢体系统简化模型 Fig. 3 Simplified model of submariner body system |
载人潜水器舱室布局依据图 2构建仿真模型如图 4(a)所示,舱室的底部是连体座椅,座椅内部是能源及电子设备,舱室后面是氧气及储物柜,最上面是生命保障物资及进出口。根据潜水器任务,将舱室作业路线规划成4个阶段(因为舱室空间狭小,作业主要由一个潜航员来操作,其余两位科学家在仿真中隐去)。为避免在其他空间的随机搜索,有效提高作业效率,本文把潜航员作业路线集中在4个阶段。1)操作台操控、作业及监视;2)打开座椅维修、取放物品;3)打开后部维修、取放物品;4)打开顶部取放物品及进出舱室,运动规划路线图如图 4(b)所示。

|
图 4 潜航员在潜水器舱室空间路线规划 Fig. 4 Route planning of submariners in the cabin space of the submersible |
潜水器球型舱室内白色区域是虚拟潜航员的活动空间,实线是规划路线,灰色区域是约束空间。虚拟潜航员沿实线在白色区域内进行运动规划,分别可以得到路径点M和N。重复上述步骤,最终完成4个阶段路径的整个运动规划。
2.3 构建潜航员舱室作业姿态仿真模型假定潜水器舱室布局非常完美:既能完成潜水器任务,又能满足潜航员可视性、可达性、舒适性等人因工程要求。把潜航员的最佳舒适状态作为一个多目标博弈模型来研究,即构建多目标博弈下的潜航员作业姿态仿真模型解空间,也就是潜航员在潜水器舱室完成任务的过程中,包含所有可能影响潜航员作业姿态因素所组成的集合[6]。
| $X = \{ \mathit{\boldsymbol{x}}|{f_i}(\mathit{\boldsymbol{x}}) \le 0, i = 1, 2, 3, \cdots , m\} \subset {R^m} $ | (1) |
式中:X为潜航员在载人潜水器舱室的作业姿态集合,是一组m维空间;x=[x1, x2, …, xm]为潜航员作业姿态向量;分量xi∈x(i=1, 2, 3, …,m)为潜航员工作状态参数,如潜航员的舒适性、平衡性、可达性及关节弯曲等。潜航员舱室作业姿态x⊂X应满足约束条件fi(x)≤0(i=1, 2, 3, …, m),约束包括潜航员肩、肘、腕关节的活动范围、可视性、舒适度、平衡性等。
由此构建基于潜航员作业的多目标博弈模型,潜航员在潜水器舱室作业姿态的数学模型[7]可表述如下:
| $\left\{ \begin{array}{l} \max \{ \mathit{\boldsymbol{\omega }} \cdot \mathit{\boldsymbol{\mu }}(\mathit{\boldsymbol{x}})\} = \mathop {\max }\limits_{X \in D} \{ \sum\limits_{i = 1}^m {{\omega _i} \times {u_i}({x_i})\} } \\ {\rm{s}}{\rm{.t}}\;\;{f_i}(\mathit{\boldsymbol{x}}) \le 0, i = 1, 2, 3, \cdots , m\\ \mathit{\boldsymbol{\omega }} = [{\omega _1}, {\omega _2}, \cdots , {\omega _m}]且\sum\limits_{i = 1}^m {{\omega _i}} = 1({\omega _i} \ge 0)\\ \mathit{\boldsymbol{\mu }}(\mathit{\boldsymbol{x}}) = {[{u_1}({x_1}), {u_2}({x_2}), \cdots , {u_m}({x_m})]^{\rm{T}}} \in {[0, 1]^m} \end{array} \right. $ | (2) |
式中:潜航员作业姿态x的舒适度函数设为μ,也就是说分量ui(xi)∈μ(x)是xi∈x(i=1,2,…,m)的舒适度评估函数,用来评判潜航员在舱室作业姿态的舒适程度;
| 表 1 不同偏好下各项人机因素指标权重 Tab. 1 Weight of human-machine factors under different preferences |
潜航员连续维持长达十几个小时高强度的作业姿态,需要克服人体生理因素的影响。由人机工学可知,关节是通过肌肉的运动实现的,与运动量和作业时间成正比。在人因工程的约束下,基于模糊多目标博弈理论[8],将式(2)中各评估函数ui(xi)∈μ表示为潜航员在载人潜水器舱室工作状态分量xi∈x的舒适度模糊最优集,关节舒适度的评估函数为
| ${u_i}({x_i}) = 1 - \frac{{\int_0^{{T_{\lim }}} {{g_i}({x_i}, t){\rm{d}}t} }}{{g_i^{\max } \cdot {T_{\lim }}}} \in [0, 1] $ | (3) |
由式(3)可以得出,当t=0时,即潜航员刚开始执行任务时,舒适度ui=1,也就是潜航员保持最舒适状态(超常状态舒适度也看成是1);当t趋近Tlim时,即疲劳等生理数值达到潜航员的极限值时,舒适度ui=0,也就是潜航员不能再工作。因此,舒适度评估函数ui的评估范围为[0, 1],关节承受的负荷gi是肩、肘、腕关节转动角度xi和时间t的函数,式(3)通常时间越长,由疲劳等生理因素导致的gi是递减的,关节负荷gi在一定时间范围内的积分表达疲劳效应。gimax是肩、肘、腕关节能承受的最大负荷,Tlim是潜航员在完成某一项潜水器任务所需的时间。
μ的模糊Pareto最优解集简化为梯形模糊函数[9],如图 5(a)所示,关节转角为横坐标;关节舒适度为纵坐标。潜航员肩、肘、腕关节梯形函数见式(4)。具体关系如图 5(b)所示,舒适度值越高则说明关节转角呈现的姿态越好。

|
图 5 关节舒适度评估函数与范围 Fig. 5 Joint comfort assessment function and its range |
| ${u_i}({x_i}) = \left\{ {\begin{array}{*{20}{c}} {\frac{{{x_i} - {\theta _{\min }}}}{{{\theta _{c\min }} - {x_i}}},}&{{\theta _{\min }} \le {x_i} \le {\theta _{c\min }}}\\ {1,}&{{\theta _{c\min }} \le {x_i} \le {\theta _{c\max }}}\\ {\frac{{{\theta _{\max }} - {x_i}}}{{{x_i} - {\theta _{c\max }}}},}&{{\theta _{c\max }} \le {x_i} \le {\theta _{\max }}} \end{array}} \right. $ | (4) |
式中:θmin、θmax分别为关节转角的最小值和最大值;θcmin、θcmax分别为关节转角处于舒适状态的最小值和最大值。潜航员作业姿态的舒适性优化模型具有以下优点:①将潜航员在载人潜水器舱室作业姿态设定为一个多目标优化模型,其目的是提高潜航员的人因可靠性,向量x代表潜航员的多种行为状态。②量纲一的处理各分量函数ui,在一个模型内整合不同类型的潜航员作业姿态参数,线性加权方式评估潜航员作业姿态效果。③由于不同潜航员在潜水器舱室完成作业任务时带有自身等主观因素,所以引进权向量ω,表征个体的差异性,权向量的取值差异用来协调参数之间均衡[10],见表 1。
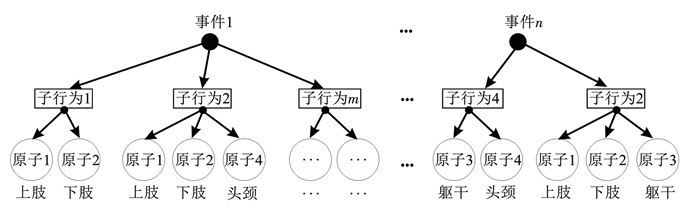
3 虚拟潜航员作业姿态的优化算法 3.1 3层虚拟潜航员作业姿态结构虚拟潜航员作业姿态优化到最佳,要分类研究潜航员在潜水器舱室的动作特点与行为方式。构建3层结构的虚拟潜航员行为模型,在密闭狭小舱室特殊环境下,从潜水器作业任务入手,将潜航员的行为动作分解成3个层级:即原子动作层级、子行为层级以及行为模式层级[11]。原子动作作为最小的行为单元,代表潜航员肢体的运动,基本形式有两种:正向运动和逆向运动。一组原子动作组合就构成一个子行为;完成一次子行为层级动作,也就是说在多个原子动作目标中完成了一次博弈算法。将相同潜水器作业任务的子行为再归类到同一行为模式,具体关系如图 6所示。
|
图 6 3层虚拟潜航员作业姿态结构 Fig. 6 Three-level virtual submariner operating attitude structure |
基于MAS虚拟潜航员优化作业行为仿真框架[12],构建载人潜水器舱室模型,如图 7所示。

|
图 7 MAS合作式博弈框架 Fig. 7 Cooperative game framework based on MAS |
虚拟潜航员作业姿态算法基于MAS合作式博弈框架,是潜航员在潜水器舱室进行多个目标和任务之间的博弈与平衡;包括潜航员必须完成的多个作业任务、潜航员在潜水器舱室的作业姿态、舒适性、平衡性等因素的博弈[13];让虚拟潜航员状态达到最优是所有博弈的最终目标。由MAS合作式博弈框架得知,一个子行为层级动作就可以看做是完成了一次微分博弈,一个行为模式层级动作就意味着完成多次微分博弈,同理,多次行为模式博弈结果累加可得虚拟潜航员最终行为状态。
根据MAS合作博弈框架模型,因为多目标冲突的问题,虚拟潜航员所有目标评估值μi∈x(i=1,2,…,m)不可能同时达到最佳,其最佳作业姿态是多元目标在协商的基础上达到最佳均衡[14]。因此,所有参与博弈的目标Xi∈x(i=1,2,…,m)都必须遵守的谈判底线可以表示为
| $\bar \mu = {[{{\bar \mu }_1}, {{\bar \mu }_2}, \cdots , {{\bar \mu }_m}]^{\rm{T}}} \in {[0, 1]^m} $ | (5) |
所谓潜航员作业姿态评估博弈的Pareto最优解是指:存在x*∈X,使得μ(x*)≥μ, 即
| ${\mathit{\boldsymbol{\mu }}_i}({\mathit{\boldsymbol{x}}^\mathit{\boldsymbol{*}}}) \ge {{\bar \mu }_i}, (i = 1, 2, \cdots m) $ | (6) |
则μ(x*)是潜航员姿态评估的Pareto最优解,而x*是一个满意的潜航员作业姿态,也是潜航员作业状态的Pareto最优解。
3.4 潜航员作业姿态在MAS合作式博弈下的优化算法求解多目标决策,也就是寻求潜航员最佳的行为状态,是一组动态博弈[15]。本文博弈算法采用梯度下降的方法,搜索步长以前一次的子行为为基准,这样就能以最快的速度得到虚拟潜航员的最佳工作状态。
步骤1 潜航员舱室工作舒适度评估。博弈参与者分别为潜航员上肢、下肢、躯干、头颈等舒适度评估。综合评估结果表示为μi(x)=[μ1,μ1,…,μm],由博弈仲裁(虚拟潜航员)计算总体舒适度ω∙μi(x)。
步骤2 潜航员工作满意程度的评判。潜航员舱室工作满意程度的评判标准是:潜航员姿态评估μi(x)满足μ(x*)≥μ所有的Pareto最优解。当潜航员行为状态x满足需求时,结束算法。判断潜航员总体舒适度是否最佳,通常是令潜航员总体舒适度C(x)=ω∙μi(x),若下式成立:
| $|C(\mathit{\boldsymbol{x}}) - C({\mathit{\boldsymbol{x}}^\mathit{\boldsymbol{*}}})| \le \varepsilon $ | (7) |
则算法结束。x*为潜航员舱室最佳作业姿态;ε为潜航员在潜水器舱室作业姿态舒适度评估的容许误差。
步骤3 确定梯度搜索步长。虚拟潜航员最佳的作业姿态x*∈X, 则梯度搜索步长为:
1) 假设当前潜航员工作状态x*的评估结果为μi(xi)≤μi,则触发博弈各方的谈判底线,按照MAS合作博弈框架,博弈各方xi请求调整其自身的行为状态,达到改善潜航员舱室工作状态,提高其舒适度。
2) 博弈仲裁根据各目标权向量的重要程度,将参与博弈的各方(潜航员员上肢、下肢、躯干、头颈)组成谈判序列。
3) 确定梯度搜索步长,并按照优先权原则从队列xi的议题中,来寻找提高潜航员舱室作业舒适度ω∙μi(x)最佳的子行为。
步骤4 执行上面寻找的子行为, 博弈参与者被博弈仲裁分配给相应功能的原子动作任务,让参与博弈的各方完成一次博弈合作。
步骤5 在子行为执行完毕后,如步骤1一样对新的潜航员舱室工作状态进行评估, 并分析得到的结果。假如合作失败,则子行为博弈失败,返回重新进入博弈流程。假如合作成功,则子行为博弈成功,显示博弈动画。
然后返回步骤2循环执行, 直到满足式(6)、(7)的条件为止。也就是说虚拟潜航员舱室作业姿态达到满意,得到一组Pareto最优解。
4 虚拟潜航员仿真实验及结果分析 4.1 虚拟潜航员仿真实验基于虚拟潜航员的作业姿态仿真,在windows/VC6.0/OpenGL平台上开发了虚拟潜航员作业姿态仿真系统。本系统提供了如图 4(a)所示的虚拟载人潜水舱室,在舱室内创建了潜水器舱室设备、3名潜航员的几何模型及人体骨骼控制系统[16]。这此基础上,构建基于多目标博弈下的虚拟潜航员作业姿态仿真模型,可以实现虚拟潜航员博弈参与者的自动协调[17]。
系统还能对虚拟潜航员的不同作业姿态进行比较评估,并得出其优劣的具体数据,如图 4(b)所示,4个阶段虚拟潜航员要完成的作业任务,系统为4个阶段的作业姿态进行评估并得出结论。
4.2 虚拟潜航员仿真实验结果分析为保证算法的稳定性,本文选取图 4中4个阶段的规划路线,用它们的仿真实例来验证。如图 8所示,每个阶段的仿真能生成100~300帧动画,从动画序列帧中选取代表性关键帧来展示虚拟潜航员的典型作业姿态。在每组实例中, 完成的工作任务不同,潜航员的作业姿态也不一样。

|
图 8 4组虚拟潜航员作业姿态仿真 Fig. 8 Simulation of operating attitudes of four groups of virtual submariners |
尽管仿真平台和潜水器舱室潜航员实际作业之间存在不同,但仿真系统能生成真实感较强的虚拟潜航员作业仿真动画,它展示了潜航员作业行为的基本姿态,跟现实中潜航员在舱室完成的任务一样,最终工作姿态合理自然。
仿真实例选择仿真动画c组,如图 8、9所示,c阶段仿真共生成195帧动画,c阶段仿真包括潜航员在舱室后部,执行开箱、维修和取放物品等作业的仿真动画。由图 9(c)所示,自0~195帧, 仿真算法处于打开后部物品储存箱进行维修和取放物品模式,实现了虚拟潜航员来到潜水器舱室后部,打开物品储存箱,进行维修和取出所需物品作业。在仿真实例c阶段,系统测评虚拟潜航员舒适度及参与博弈分量的舒适度,在开始阶段保持舒适状态,一段时间后都呈下降趋势。拐点在135帧, 潜航员总体舒适度、肩关节、膝关节和潜航员平衡性为相对低位,分别是0.683 5,0.796 2,0.425 3和0.405 8。从仿真动画得到的数据看,人体平衡性和膝关节状态是导致影响潜航员舱室作业总体舒适度不高的主要原因。随后,c阶段的仿真动画从相对低点的135帧到195帧结束为止,虚拟潜航员处于自动优化模式,优化算法导致总体舒适度、肩关节、膝关节和潜航员平衡性曲线呈上升趋势。最终,参与博弈的各分量数值为:总体舒适度为0.824 4、肩关节为0.883 6、膝关节为0.850 6和平衡性为0.781 6。由数据可知参与博弈的各分量状态都得到很大改善。潜航员在载人潜水器舱室的工作状态满足博弈论的预设条件,是一组多目标博弈下的Pareto最优解。

|
图 9 潜航员舒适度评估变化趋势 Fig. 9 Change trend of submariner comfort assessment |
1) 仿真模型在潜航员自身参数、行为感知及模糊决策基础上得到的结果,不需要潜航员复杂生理及动作数据,大大简化和缩短仿真周期。
2) 根据MAS合作式博弈框架模型,经多次行为模式的微分博弈达到最佳均衡,其结果累加最终获得满足多种利益的最佳均衡状态Pareto最优解集。
3) 多个目标与任务之间建立的博弈机制,搜索步长以前一次的子行为为基准,能快速得到潜航员随时间变化的各种参数趋势曲线,行为动画和仿真数据能直观评估人因可靠性,也为优化舱室空间布局提供一种思路和途径。
4) 仿真博弈算法只是主观从潜航员自身行为入手,仿真系统设置不完善,在下一步将加入疲劳等生理约束因素,引进仿生及其他算法来完善此方法,能得到更精确更实际的虚拟潜航员仿真。
| [1] |
ABATE A F, GUIDA M, LEONCINI P, et al. A haptic-based approach to virtual training for aerospace industry[J]. Journal of Visual Languages and Computing, 2009, 20: 318. DOI:10.1016/j.jvlc.2009.07.003 |
| [2] |
任玉刚, 刘保华, 丁忠军, 等. 载人潜水器发展现状及趋势[J]. 海洋技术学报, 2018, 37(2): 114. REN Yugang, LIU Baohua, DING Zhongjun, et al. Research on the current status and development trend of manned submersibles[J]. Journal of Ocean Technology, 2018, 37(2): 114. DOI:10.3969/j.issn.1003-2029.2018.02.019 |
| [3] |
QIU Shiguang, HE Qichang, FAN Xiumin, et al. Virtual human hybrid control in virtual assembly and maintenance simulation[J]. International Journal of Production Research, 2014, 52(3/4): 867. |
| [4] |
孙守迁, 吴群, 吴剑锋. 虚拟人技术及应用[M]. 北京: 高等教育出版社, 2010: 6. SUN Shouqian, WU Qun, WU Jianfeng. Virtual human technology and application[M]. Beijing: Higher Education Press, 2010: 6. |
| [5] |
韩端锋, 韩海辉, 刘峰, 等. 载人潜水器驾驶舱三维布局优化研究[J]. 船舶工程, 2013, 35(1): 76. HAN Duanfeng, HAN Haihui, LIU Feng, et al. Research on 3D layout optimization of HOV cabin[J]. Ship Engineering, 2013, 35(1): 76. DOI:10.13788/j.cnki.cbgc.2013.01.018 |
| [6] |
WANG Wenzhong, ZHANG Shusheng, YE Cong, et al. A new method for optimizing the cabin layout of manned submersibles[J]. Complexity, 2020, 2020: 6626602. DOI:10.1155/2020/6626602 |
| [7] |
BOULIC R, MAUPU D, THALMANN D. On scaling strategies for the full-body postural control of virtual mannequins[J]. Interacting with Computers, 2009, 21(1/2): 11. DOI:10.1016/j.intcom.2008.10.002 |
| [8] |
王朝晖, 陈恳, 朱心雄. 一种虚拟人作业行为的自主优化模型[J]. 软件学报, 2012, 23(9): 2358. WANG Zhaohui, CHEN Ken, ZHU Xinxiong. Automatic optimization model for virtual human's working behaviors[J]. Journal of Software, 2012, 23(9): 2358. DOI:10.3724/SP.J.1001.2012.04174 |
| [9] |
张帅, 何卫平, 陈登凯, 等. 载人潜水器舱室空间舒适性复合评估方法[J]. 哈尔滨工业大学学报, 2019, 51(10): 83. ZHANG Shuai, HE Weiping, CHEN Dengkai, et al. Compound evaluation method for the space comfort of manned submersible[J]. Journal of Harbin Institute of Technology, 2019, 51(10): 83. DOI:10.11918/j.issn.0367-6234.201810148 |
| [10] |
王朝晖. 虚拟人自适应行为的多Agent决策模型与人机工程仿真[D]. 北京: 北京航空航天大学, 2009 WANG Zhaohui. Multi-agent based decision making for adaptive behavior of virtual human and ergonomic simulation[D]. Beijing: Beihang University, 2009 |
| [11] |
武维维, 叶林梅, 邵晓东, 等. 基于多目标遗传算法的虚拟人作业姿态仿真[J]. 计算机集成制造系统, 2019, 25(1): 155. WU Weiwei, YE Linmei, SHAO Xiaodong, et al. Working posture simulation method for virtual human based on multi-objective genetic algorithm[J]. Computer Integrated Manufacturing Systems, 2019, 25(1): 155. DOI:10.13196/j.cims.2019.1.015 |
| [12] |
杨宇盟, 聂斌, 方红根, 等. 虚拟人手臂避障抓取运动规划[J]. 计算机辅助设计与图形学学报, 2014, 26(8): 1362. YANG Yumeng, NIE Bin, FANG Honggen, et al. Planning collision-free grasping actions of virtual human[J]. Journal of Computer-Aided Design & Computer Graphics, 2014, 26(8): 1362. |
| [13] |
陈登凯, 范昱, 张帅, 等. 舱内功能及人机工效导向的载人潜水器工作舱布局设计方法[J]. 中国舰船研究, 2018, 13(2): 41. CHEN Dengkai, FAN Yu, ZHANG Shuai, et al. Manned submersible working cabin layout design method under cabin function system constraints and ergonomic constraints[J]. Chinese Journal of Ship Research, 2018, 13(2): 41. DOI:10.3969/j.issn.1673-3185.2018.02.006 |
| [14] |
王文中, 张树生, 余隋怀. 基于粒子群优化的BP神经网络图像复原算法研究[J]. 西北工业大学学报, 2018, 36(4): 709. WANG Wenzhong, ZHANG Shusheng, YU Suihuai. Image restoration by BP neural based on PSO[J]. Journal of Northwestern Polytechnical University, 2018, 36(4): 709. |
| [15] |
叶聪, 宗立成, 陈登凯. 虚拟设计在潜水器舱室布局设计中的研究与应用[J]. 机械设计, 2015, 32(1): 6. YE Cong, ZONG Licheng, CHEN Dengkai. Research and application on virtual design in cabin layout design of deep submergence vehicle[J]. Journal of Machine Design, 2015, 32(1): 6. DOI:10.13841/j.cnki.jxsj.2015.01.002 |
| [16] |
张帅, 叶聪, 何卫平, 等. 载人潜水器坐底过程人因失效预测[J]. 哈尔滨工程大学学报, 2017, 39(2): 290. ZHANG Shuai, YE Cong, HE Weiping, et al. Research on method of human failure prediction in the process of landing manned submersibles[J]. Journal of Harbin Engineering University, 2017, 39(2): 290. DOI:10.11990/jheu.201609053 |
| [17] |
姜健, 赵杰, 臧希喆. 基于并列选择遗传算法的多机器人协作探测[J]. 计算机工程与设计, 2008, 29(5): 1218. JIANG Jian, ZHAO Jie, ZANG Xizhe. Coordinated multi-robot exploration based on parallelism selection genetic algorithm[J]. Computer Engineering and Design, 2008, 29(5): 1218. DOI:10.16208/j.issn1000-7024.2008.05.083 |
 2021, Vol. 53
2021, Vol. 53


