2. 济南城建集团有限公司,济南 250000;
3. 哈尔滨工业大学 土木工程学院,哈尔滨 150090
2. Jinan Urban Construction Group, Jinan 250000, China;
3. School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China
基础冲刷是导致桥梁垮塌事故的重要原因之一,如美国在过去30年发生了1 000多座桥梁倒塌事故,其中约60%与基础冲刷有关[1-2]。因此研究高效、经济和便捷的桥梁基础冲刷检测和监测方法极其必要。由于水下环境复杂,基础冲刷检测难度较大,目前常用的检测方法为人工潜水观察、雷达探测和声纳探测等[3]。但这些水下检测手段存在风险高、耗时长、费用昂贵、水下设备安装和操作难度大等局限,同时易受水文条件、自然环境和气候等因素干扰和限制,对冲刷后的杂物回填现象也无法有效识别[4]。
相关研究表明基础冲刷可导致桥梁动力特性及外部激励下的动力行为发生变化,据此国内外学者在基于动力的基础冲刷诊断和评估方面开展了一些研究工作,并发现该类方法具备实现高效、准确和低成本检测评估的应用潜力[5-6]。目前该类方法采用的外部激励方式主要分为人工强迫振动、环境激励和过桥车辆激励3类[3-4]。文献[7]基于小波分析和模型修正理论,采用数值模拟方法研究了以小波包能量熵为诊断指标的柱式桥墩定量化损伤诊断方法,并分析了病害类型、环境噪声等对诊断结果的影响。文献[8]利用力锤激励钢梁桥模型,基于实测得到的桥面竖向和水平向加速度响应识别上部结构振型,发现竖向振型对冲刷不敏感,部分水平振型对冲刷敏感,提出采用水平振型和动态柔度特征的变化来识别基础冲刷的思路。文献[9]建立了冲刷环境三维数值仿真精细化模型,研究了流速和桥墩参数与桥墩最大冲刷深度的关系。文献[10]基于人工锤击激励响应,利用频响函数的相似性并联合模型修正针对铁路桥梁独柱式桥墩进行了损伤评估。文献[11]基于过桥车辆和环境激励,提出以多次测量的结构振动速度响应平均傅里叶谱频率变化为指标进行基础冲刷的评估方法;并指出等速过桥车辆激励一般仅能激起桥面局部振动,无法激起下部结构振动;而环境激励下结构响应幅值较小,易受干扰,信号易被掩盖。文献[12]基于车桥振动分析,发现基础冲刷对车辆过桥时墩顶横向振动响应影响明显,指出基于该响应指标有望建立一种简便易行的冲刷监测方法。文献[13]基于环境激励下的实测模态,修正杭州湾大桥的基础冲刷模型以得到基础冲刷深度,并通过对比水下地形测绘数据验证了该方法的精度。
综上分析,目前基于动力的桥梁基础冲刷诊断研究所采用的外部激励方式中环境振动引起的结构响应小,且易受环境和噪声等干扰,影响和限制了诊断方法的适用性;人工强迫振动使用力锤、激振器等,需现场安装激励设备,操作不当可能造成桥体破损,主要激起结构的局部振动且方向固定;而过桥车辆激励具有输入参数确定、操作简便且可融入常规荷载试验过程的优点,具备广阔的应用前景,正得到广泛的关注。但现有研究主要关注车辆匀速过桥激励,而较少研究变速与制动等车辆行驶状态下基础冲刷对桥梁动力响应的影响规律。匀速车辆激励下桥梁以竖向振动为主而对基础冲刷敏感的纵横向响应较小;相比而言变速与制动激励可激起更大的纵横向响应。故系统研究基础冲刷对不同车辆激励下结构动力行为特性的影响,对于深入探究基础冲刷与结构动力行为特性变化的内在联系具有重要的意义。
为此,本文采用数值模拟方法,考虑车辆匀速、变速和制动等多种行驶状态,研究基础冲刷对桥梁车载下动力行为特性的影响规律。首先引入不同行驶状态下的惯性力效应建立车桥振动分析模型,然后依托算例分析基础冲刷对桥梁动力特性的影响;进而考虑多种车辆行驶状态,系统分析基础冲刷对桥梁车载下多种动力响应类型的敏感程度及其特征;最后对比确定最适用于冲刷诊断的激励方式与响应类型。研究结果将为基于车激动力响应的桥梁基础冲刷识别提供可行的动力指标和一定的理论基础。
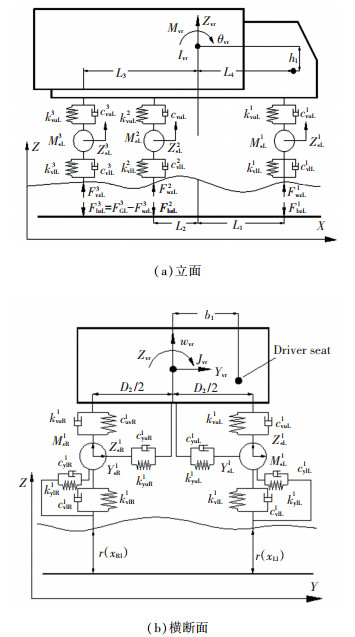
1 多态运行车辆与桥梁耦合振动的分析模型 1.1 车辆模型选取公路桥梁荷载试验常用的三轴重车为车辆的分析模型,其空间计算模型如图 1所示。
|
图 1 车辆模型 Fig. 1 Vehicle model |
该模型包含16个自由度。其中车体有4个自由度,分别为竖向浮沉自由度Zvr、横向移动自由度Yvr、绕Y轴的转动自由度θvr及绕X轴的侧倾自由度φvr。每个悬架刚体有4个自由度,分别为竖向浮沉自由度ZsLi和ZsRi,横向摆动自由度YsLi和YsRi。M表示悬架质量,k、c分别表示悬挂系统与轮胎的弹簧刚度及阻尼。下角标vr表示车体,s表示悬架刚体,L、R表示分别X轴左侧和右侧,u、l分别表示弹簧与阻尼的上、下位置。车辆模型详细参数及运动方程推导等详见文献[14],此不赘述。
1.2 车桥耦合振动分析原理基于模态综合法建立桥梁子系统的运动方程,考虑车辆匀速过桥时轮胎与桥面接触点的位移和力的协调平衡条件,构建车桥系统总体动力方程:
| $ \begin{gathered} {\left[\begin{array}{cc} \boldsymbol{M}_{\mathrm{v}} & \bf{0} \\ \bf{0} & \boldsymbol{M}_{\mathrm{B}} \end{array}\right]\left[\begin{array}{c} \ddot{\boldsymbol{X}}_{\mathrm{v}} \\ \ddot{\boldsymbol{q}}_{\mathrm{B}} \end{array}\right]+\left[\begin{array}{cc} \boldsymbol{C}_{\mathrm{v}} & \boldsymbol{C}_{\mathrm{vB}} \\ \boldsymbol{C}_{\mathrm{Bv}} & \boldsymbol{C}_{\mathrm{B}}+\boldsymbol{C}_{\mathrm{B}}^{\mathrm{v}} \end{array}\right]\left[\begin{array}{c} \dot{\boldsymbol{X}}_{\mathrm{v}} \\ \dot{\boldsymbol{q}}_{\mathrm{B}} \end{array}\right]+} \\ {\left[\begin{array}{cc} \boldsymbol{K}_{\mathrm{v}} & \boldsymbol{K}_{\mathrm{vB}} \\ \boldsymbol{K}_{\mathrm{Bv}} & \boldsymbol{K}_{\mathrm{B}}+\boldsymbol{K}_{\mathrm{B}}^{v} \end{array}\right]\left[\begin{array}{l} \boldsymbol{X}_{\mathrm{v}} \\ \boldsymbol{q}_{\mathrm{B}} \end{array}\right]=\left[\begin{array}{l} \boldsymbol{F}_{\mathrm{v}} \\ \boldsymbol{F}_{\mathrm{B}} \end{array}\right]} \end{gathered} $ | (1) |
式中:M、K、C、F分别表示质量、刚度、阻尼矩阵及荷载向量;$\boldsymbol{X}_{{\mathrm{v}}}、\dot{\boldsymbol{X}}_{{\mathrm{v}}}、\ddot{\boldsymbol{X}}_{\mathrm{v}}$分别表示车辆位移、速度、加速度响应向量;$\boldsymbol{q}_{\mathrm{B}}、\dot{\boldsymbol{q}}_{\mathrm{B}}、\ddot{\boldsymbol{q}}_{\mathrm{B}}$分别表示桥梁位移、速度、加速度响应向量;矩阵下标v和B分别表示车辆项和桥梁项,Bv和vB表示车桥耦合项。利用车桥系统间受力平衡和位移协调条件,可推导得到上述矩阵及荷载向量中各项分量,详细过程见文献[14]。
考虑车辆的制动或变速行驶时,车辆的加速度将产生惯性力,会导致车轴荷载的重新分配。根据车体受力平衡方程,可将车桥系统运动方程式(1)改写为
| $ \begin{aligned} &{\left[\begin{array}{cc} \boldsymbol{M}_{\mathrm{v}} & \bf{0} \\ \bf{0} & \boldsymbol{M}_{\mathrm{B}} \end{array}\right]\left[\begin{array}{l} \ddot{\boldsymbol{X}}_{\mathrm{v}} \\ \ddot{\boldsymbol{q}}_{\mathrm{B}} \end{array}\right]+\left[\begin{array}{cc} \boldsymbol{C}_{\mathrm{v}} & \boldsymbol{C}_{\mathrm{vB}} \\ \boldsymbol{C}_{\mathrm{Bv}} & \boldsymbol{C}_{\mathrm{B}}+\boldsymbol{C}_{\mathrm{B}}^{\mathrm{v}} \end{array}\right]\left[\begin{array}{c} \dot{\boldsymbol{X}}_{\mathrm{v}} \\ \dot{\boldsymbol{q}}_{\mathrm{B}} \end{array}\right]+} \\ & \;\;\;\;{\left[\begin{array}{cc} \boldsymbol{K}_{\mathrm{v}} & \boldsymbol{K}_{\mathrm{vB}} \\ \boldsymbol{K}_{\mathrm{Bv}} & \boldsymbol{K}_{\mathrm{B}}+\boldsymbol{K}_{\mathrm{B}}^{\mathrm{v}} \end{array}\right]\left[\begin{array}{l} \boldsymbol{X}_{\mathrm{v}} \\ \boldsymbol{q}_{\mathrm{B}} \end{array}\right]=\left[\begin{array}{c} \boldsymbol{F}_{\mathrm{v}} \\ \boldsymbol{F}_{\mathrm{B}}+\boldsymbol{F}_{x t} \end{array}\right]} \end{aligned} $ | (2) |
式中Fxt为变速或制动过程产生的惯性力,其具体推导过程见文献[15]。
考虑车辆制动时,Fxt取决于制动力峰值系数及制动力上升时间;考虑车辆变速行驶时,车辆加速度远小于制动状态,且变化时间短,故将加速度设为恒定,采用相同方法计算Fxt;考虑车辆匀速行驶时Fxt为零,原运动方程不变。
根据以上原理编制的车桥耦合振动计算程序已通过多个实桥工程的现场测试结果进行了验证,结果显示该方法和程序具有较好的精度和工程适用性[14-17]。该程序将用于本文后续分析研究。
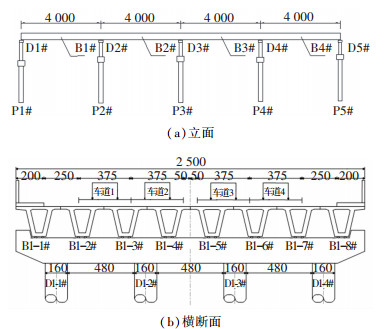
2 桥梁计算模型与基础冲刷模拟 2.1 桥例概况及计算模型依托黑龙江省宁安市宁古塔大桥作为工程背景,该桥跨越牡丹江河道,采用预应力混凝土连续梁桥结构。选取该桥跨主河道的第二联4×40 m预应力混凝土连续梁为对象(见图 2)。上部结构采用混凝土简支转连续小箱梁形式;桥墩为柱式墩,直径为1.6 m,墩长为5.5~8.4 m;基础采用C25钻孔灌注桩,桩径为2.2 m,桩长为17~19 m;支座采用板式橡胶支座和聚四氟乙烯滑板橡胶支座,具体参数见文献[15]。桥位处设计流量为2 200 m3/s,平均水深约为3.13 m,最大水深为3.78 m。地质勘测数据显示,桥位处地层由上而下依次为粗砂、卵石、圆砾等,桩端支承于砂岩中。
|
图 2 桥梁布置(cm) Fig. 2 Layout of the bridge (cm) |
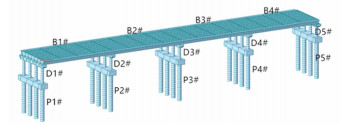
建立该联桥梁空间有限元模型如图 3所示,其中上部结构选用梁格模型模拟,横隔梁、墩柱和桩基础采用梁单元模拟,支座采用三维弹簧单元模拟;边墩上设置节点质量模拟相邻桥跨恒载作用,利用节点弹性支撑模拟相邻跨桥墩的侧向约束。
|
图 3 桥梁有限元模型 Fig. 3 Finite element model of the bridge |
桩土相互作用计算中Winkler地基梁模型应用最为广泛,该方法以垂直于桩柱的等效土弹簧来模拟土体对桩柱的作用,其中M法[18]为基于Winkler地基模型的常用线性方法。本文通过M法分别以水平和竖向弹簧系数模拟周围土体对基础的侧向约束和基底竖向约束。
水流冲刷引起基础埋深线下降,导致基础侧向约束削弱,会影响桥梁整体刚度和动力特性。冲刷状态模拟的本质是桩土作用及其影响范围的模拟。本文依据冲刷深度重新计算桩周土弹簧刚度,通过改变弹簧约束的等效刚度及数量实现不同冲刷状况的模拟。
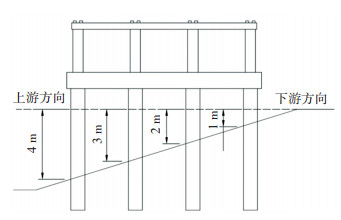
受地质、水文条件差异及桥墩间相对位置关系等影响,纵、横向桥墩间冲刷状态一般存在明显的差异性与时变性,故考虑基础冲刷深度和均匀性设置9种典型冲刷工况(见表 1),用于研究基础冲刷对桥梁车激动力行为特性的影响规律。本文基础冲刷考虑了一般冲刷和局部冲刷的特征,可视为二者的总体作用。表中工况1~4为单排桥墩均匀冲刷;工况5~7为单排桥墩不均匀冲刷;工况8、9为多排墩冲刷。对不均匀冲刷工况,考虑上游桥墩对下游桥墩的屏蔽作用,顺水流方向上桩基冲刷深度一般会递减,故基于数值模拟角度以单排基础自上游向下游方向冲刷按照深度线性递减简化模拟,如图 4所示。桥墩、桩基编号见图 2、3。
| 表 1 基础冲刷工况 Tab. 1 Foundation scour conditions |
|
图 4 不均匀冲刷示意 Fig. 4 Uneven scour simulation |
采用之前建立的桥梁计算模型开展动力特性分析,获得完好状况下该桥的主要振型如图 5所示。考虑表 1给出的9个典型冲刷工况,分析基础冲刷对结构动力特性的影响,结果见表 2。可见,随P3#基础冲刷深度不断增加,D3#墩各阶局部模态频率线性减小,且桥墩局部模态频率变化率远大于全桥。当冲刷深度由1 m增加到4 m时,D3#墩一阶纵弯、扭转和横弯模态频率降幅分别由8.1%、6.3%、6.7%增至28.7%、25.9%、29.6%,且敏感模态由桥墩一阶纵弯变为一阶横弯模态。

|
图 5 桥梁主要振型 Fig. 5 Representative modal shapes |
| 表 2 不同冲刷位置、不同冲刷深度下桥梁自振频率 Tab. 2 Natural vibration frequency of the bridge with various scouring positions and depths |
考虑单墩横向各墩柱1~4 m不均匀冲刷,桥梁模态分析结果表明,D3#墩各阶模态频率变化率介于均匀冲刷2~3 m之间,由此可得频率变化与冲刷深度之和正相关。同时,D3#墩局部振动模态频率仅在P3#桩基冲刷工况下变化显著,表明桥墩局部振动模态频率仅对同位置基础冲刷敏感。
考虑多墩冲刷时桥梁模态分析结果表明,冲刷敏感模态仍为受冲刷基础位置的桥墩局部模态,且桥墩模态频率变化率与对应基础均匀冲刷时相近,以工况1和工况9为例,发现冲刷导致的两者D3#墩一阶纵弯、扭转和横弯模态频率变化率差异微小。
综上分析,基础冲刷一般主要影响同位置桥墩模态频率,为此后续研究中将仅考虑单墩冲刷工况。
4 基础冲刷对多种行驶状态下桥梁车激动力行为特性的影响分析基于前述建立车桥耦合振动分析方法和桥例,考虑P3#基础均匀冲刷1~4 m典型工况,系统分析冲刷对多种车辆行驶状态下(匀速、制动和变速)桥梁动力行为特征的影响。选取D3-1#墩顶和第2跨1#梁B2-1#跨中位置动力响应为对象进行分析。
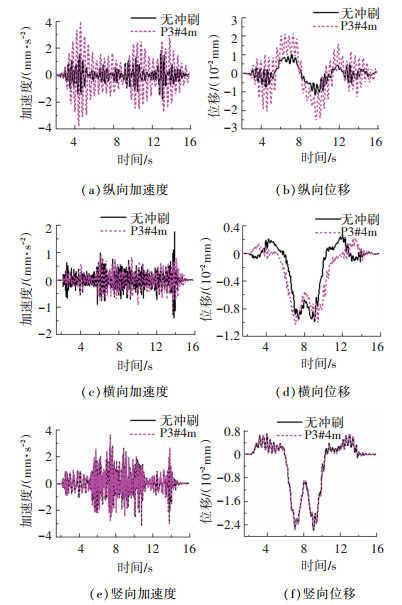
4.1 基础冲刷对匀速车辆激励下桥梁动力响应的影响分析以车速50 km/h、桥面不平整度为“好”、重29.8 t的标准车辆由车道2过桥工况为例,考察冲刷对桥梁典型位置动力响应的影响,结果如图 6、7所示。
|
图 6 匀速车辆激励下D3-1#墩顶动力响应时程 Fig. 6 Response time history on top of D3-1# pier under the excitation of vehicle with uniform speed |
|
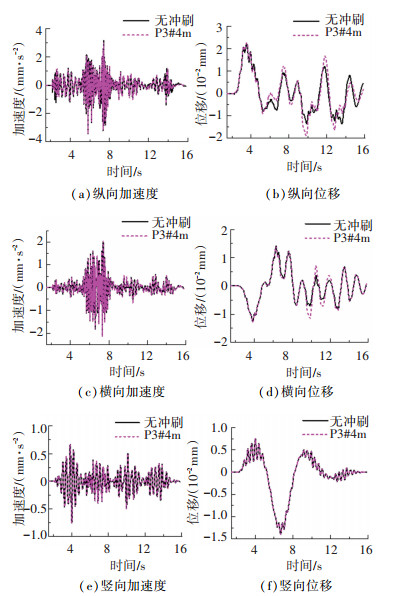
图 7 匀速车辆激励下B2-1#跨中动力响应时程 Fig. 7 Response time history of B2-1# midspan under the excitation of vehicle with uniform speed |
可见,车辆匀速行驶激励下桥梁墩顶纵横向加速度、纵横向位移响应和主梁跨中纵横向位移响应对基础冲刷均较为敏感。为进一步分析上述敏感响应峰值受冲刷的影响情况,现将不同冲刷深度下动力响应峰值列于表 3。
| 表 3 车辆匀速激励下桥梁动力响应峰值 Tab. 3 Peak response of the bridge under the excitation of vehicle with uniform speed |
由表 3可得,车辆匀速行驶激励下,墩顶纵向响应对基础冲刷的敏感性最为显著;随冲刷深度由1 m增加至4 m,墩顶纵向加速度峰值由1.808 mm/s2增至3.977 mm/s2,相较于无冲刷工况,增幅分别为24.66%、87.59%、115.82%、119.95%,纵向位移也呈现类似的趋势,表明纵向响应峰值变化与冲刷程度正相关。此外,随冲刷深度增加,墩顶横向加速度响应峰值变化明显,呈现先减小后增大趋势;横向位移时程产生明显偏移,但曲线形状与峰值基本不变。车辆匀速行驶激励下,受基础冲刷影响,主梁跨中纵、横向位移时程产生明显波动,但峰值基本不变。表明上部结构匀速车辆激励下动力响应对基础冲刷的敏感性弱于桥墩。
下面对墩顶和跨中纵横向和竖向加速度响应进行频谱分析,结果如图 8所示。表明车辆匀速过桥条件下,基础冲刷可导致墩顶纵向加速度响应频谱幅值明显增大,中心频率向低频偏移;横向加速度的频谱曲线也有相似特征,且频带宽度有增大趋势。

|
图 8 车辆匀速激励下桥梁动力响应频谱 Fig. 8 Response spectrum of the bridge under the excitation of vehicle with uniform speed |
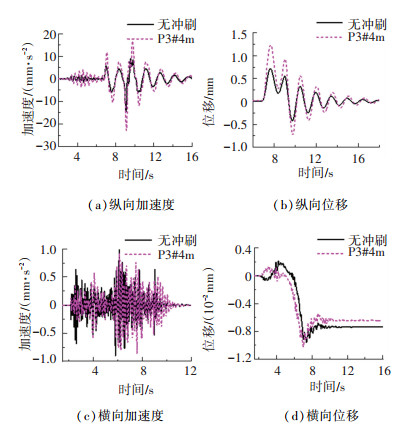
本节研究车辆制动作用下基础冲刷对桥梁动力行为的影响,车辆制动分析参数为:桥面不平度为“好”,车重29.8 t的三轴卡车以50 km/h的初速度在车道2制动,停止时车辆前轴位于D3#墩墩顶,制动力上升时间为0.3 s,制动峰值系数为0.7。桥墩和主梁动力响应时程如图 9、10所示。
|
图 9 车辆制动激励下D3-1#墩顶动力响应时程 Fig. 9 Response time history on top of D3-1# pier under the excitation of vehicle braking |

|
图 10 车辆制动激励下B2-1#跨中动力响应时程 Fig. 10 Response time history of B2-1# midspan under the excitation of vehicle braking |
可见,车辆制动激励下桥梁墩顶纵横向加速度、纵横向位移响应和主梁跨中纵向加速度、纵向位移响应对基础冲刷均较为敏感。为进一步分析上述敏感响应峰值受冲刷的影响情况,现将不同冲刷深度下动力响应峰值列于表 4。
| 表 4 车辆制动激励下桥梁动力响应峰值 Tab. 4 Peak response of the bridge under the excitation of vehicle braking |
由表 4可得,车辆制动激励下墩顶纵向动力响应峰值随冲刷深度的增加线性增大,当冲刷深度由1 m增至4 m时,墩顶纵向加速度响应峰值由14.652 mm/s2增至22.894 mm/s2,相较于无冲刷工况增幅分别为13.03%、30.07%、43.99%、56.26%;纵向位移响应峰值由0.716 mm增加至1.236 mm,增幅分别为14.67%、33.90%、52.75%、72.72%。此外,随冲刷深度增加,墩顶横向加速度响应峰值变化明显,呈先减后增趋势,且变化率小于纵向响应;横向位移时程曲线前半段向左侧偏移,后半段向上偏移,峰值基本无变化。
跨中纵向加速度和位移响应时程产生小幅波动。冲刷深度为4 m时,跨中纵向加速度和位移响应峰值相较于无冲刷工况时的变化率分别为1.324%、4.044%。表明上部结构车辆制动激励下动力响应对基础冲刷的敏感性弱于桥墩。
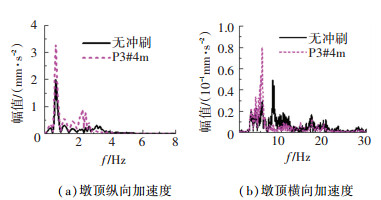
此外,墩顶纵横向加速度频谱分析的结果如图 11所示。发现车辆制动作用下基础冲刷导致两个水平向加速度响应频谱幅值均明显增大,中心频率向低频偏移;且横向加速度频带宽度有增大趋势。与车辆匀速激励下的变化趋势一致。
|
图 11 车辆制动激励下桥梁动力响应频谱 Fig. 11 Response spectrum of the bridge under the excitation of vehicle braking |
设置车辆行驶至D3#墩位置开始匀减速,减速至下桥,加速度为-0.098 m/s2,其他参数同4.1节匀速行驶工况。桥墩和主梁动力响应时程如图 12、13所示。

|
图 12 车辆变速激励下D3-1#墩顶动力响应时程 Fig. 12 Response time history on top of D3-1# pier under the excitation of vehicle with different speeds |
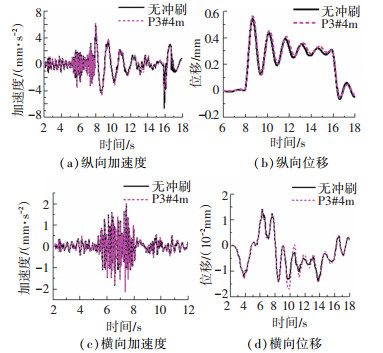
|
图 13 车辆变速激励下B2-1#跨中动力响应时程 Fig. 13 Response time history of B2-1# midspan under the excitation of vehicle with different speeds |
可见,车辆变速行驶激励下桥梁墩顶纵横向加速度、纵横向位移响应和主梁跨中纵横向位移响应对基础冲刷均较为敏感。为进一步分析上述敏感响应峰值受冲刷的影响情况,现将不同冲刷深度下动力响应峰值列于表 5。
| 表 5 车辆变速行驶激励下桥梁响应峰值 Tab. 5 Peak response of the bridge under the excitation of vehicle with different speeds |
由表 5可得,车辆变速行驶激励下,桥墩纵向响应对基础冲刷的敏感度最高。随冲刷深度由1 m增至4 m,墩顶纵向加速度响应峰值由1.915 mm/s2增至5.407 mm/s2,相较于无冲刷工况,其增幅分别为55.56%、148.25%、173.81%、182.38%;纵向位移响应峰值也与加速度响应呈现相同的变化趋势。此外,随冲刷深度增加,墩顶横向加速度响应峰值变化明显,呈先减后增趋势,且变化率小于纵向响应;横向位移时程前半段向左侧偏移,后半段向右偏移,但曲线形状与峰值基本不变。与车辆匀速行驶激励下的变化规律基本一致。
此外,跨中纵横向位移响应时程产生明显波动。冲刷深度为4 m时,跨中纵横位移响应峰值相较于无冲刷工况变化率分别为3.85%、21.43%。表明上部结构车辆变速激励下动力响应对基础冲刷的敏感性仍弱于桥墩。
进一步对墩顶纵向和横向加速度响应进行频谱分析,结果如图 14所示。可见,受冲刷影响,车辆变速激励下墩顶纵横向加速度频谱幅值显著上升,中心频率向低频偏移;且横向加速度频带宽度有增大趋势。与车辆匀速行驶和制动激励下的变化趋势一致。
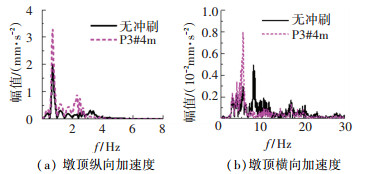
|
图 14 车辆变速行驶激励下动力响应频谱 Fig. 14 Response spectrum on top of pier under the excitation of vehicle with different speeds |
对比3种行驶状态下的桥梁动力响应可得:墩顶纵向位移和加速度响应峰值及变化幅度在车辆制动激励下最大,在车辆匀速行驶激励下最小;且在不同车辆激励状态下随冲刷深度增大,响应峰值均趋于增加。墩顶横向加速度响应峰值和变化幅度在车辆匀速行驶激励下最大,在车辆制动激励下最小,且在车辆不同激励下随冲刷深度增大,响应峰值均呈现先减小后增大的趋势。墩顶横向位移响应在车辆不同激励下峰值基本不变。
跨中纵向位移响应峰值及变化率在车辆制动激励下最大,在车辆匀速行驶激励下最小。考虑到跨中动力响应峰值变化率远小于墩顶,可得上部结构动力响应在车辆不同激励下对基础冲刷的敏感性始终弱于桥墩。
5 结论建立了多态运行车辆作用下的车桥振动计算模型并编制了相应分析程序。依托一座预应力混凝土连续梁桥算例研究了基础冲刷对多种行驶状态下桥梁车激动力行为的影响,得到以下结论:
1) 基础冲刷主要影响冲刷位置桥墩的模态频率,且随冲刷深度增加桥墩局部模态频率逐步减小。
2) 在匀速、制动和变速3种行驶状态车辆激励下,桥梁墩顶纵向动力响应对基础冲刷敏感性最高;且纵向位移和加速度响应峰值随冲刷深度增大线性增大,增幅明显。同时由频谱分析可得,基础冲刷导致结构敏感动力响应频谱幅值显著提高,且中心频率向低频偏移。
3) 比较3种车激状态下桥梁动力行为发现,车辆制动激励下基础冲刷引起的动力响应峰值变化幅度最大。冲刷深度由1 m增加至4 m时,相较于无冲刷工况,制动激励下墩顶纵向加速度与位移响应峰值增幅分别线性增加至56.26%与72.72%,该类激励方式如用于基础冲刷诊断将有更好的抗噪能力和发展潜力。
| [1] |
LAGASSE P F, RICHARDSON E V. ASCE compendium of stream stability and bridge scour papers[J]. Journal of Hydraulic Engineering, 2001, 127(7): 531. DOI:10.1061/(ASCE)0733-9429(2001)127:7(531) |
| [2] |
WARDHANA K, HADIPRIONO F C. Analysis of recent bridge failures in the United States[J]. Journal of Performance of Constructed Facilities, 2003, 17(3): 144. DOI:10.1061/(ASCE)0887-3828(2003)17:3(144) |
| [3] |
熊文, 邹晨, 叶见曙. 基于动力特性识别的桥墩冲刷状态分析[J]. 中国公路学报, 2017, 30(5): 89. XIONG Wen, ZOU Chen, YE Jianshu. Condition assessment of bridge scour by tracing dynamic performance of bridges[J]. China Journal of Highway and Transport, 2017, 30(5): 89. DOI:10.3969/j.issn.1001-7372.2017.05.012 |
| [4] |
BAO Ting, SWARTZ R A, VITTON S, et al. Critical insights for advanced bridge scour detection using the natural frequency[J]. Journal of Sound and Vibration, 2017, 386: 116. DOI:10.1016/j.jsv.2016.06.039 |
| [5] |
FOTI S, SABIA D. Influence of scour of foundations on the dynamic response of an existing bridge[J]. Journal of Bridge Engineering, 2010, 10: 152. |
| [6] |
SABARETHINAM K, JAMIE E P. Parameterized fragility assessment of bridges subjected to pier scour and vehicular loads[J]. Journal of Bridge Engineering, 2018, 23(7): 04018044. DOI:10.1061/(ASCE)BE.1943-5592.0001240 |
| [7] |
刘凯. 基于冲击响应的公路桥梁柱式墩损伤识别方法研究[D]. 北京: 北京交通大学, 2018 LIU Kai. Study on damage identification method for highway column piers based on impact responses[D]. Beijing: Beijing Jiaotong University, 2018 |
| [8] |
ELSAID A, SERACINO R. Rapid assessment of foundation scour using the dynamic features of bridge superstructure[J]. Construction and Building Materials, 2014, 50: 42. DOI:10.1016/j.conbuildmat.2013.08.079 |
| [9] |
熊文, 姚浩, CAIC S, 等. 冲刷环境对桥墩冲刷空间形态影响的仿真分析[J]. 哈尔滨工业大学学报, 2016, 48(3): 108. XIONG Wen, YAO Hao, CAI C S, et al. A simulation analysis on 3D bridge scour developments by various environment parameters[J]. Journal of Harbin Institute of Technology, 2016, 48(3): 108. |
| [10] |
战家旺, 闫宇智, 强伟亮, 等. 一种基于频响函数相似性的铁路桥墩损伤识别方法[J]. 中国铁道科学, 2018, 39(2): 37. ZHAN Jiawang, YAN Yuzhi, QIANG Weiliang, et al. Damage identification method for railway pier based on frequency response function similarity[J]. China Railway Science, 2018, 39(2): 37. DOI:10.3969/j.issn.1001-4632.2018.02.05 |
| [11] |
KO Y Y, LEE W F, CHANG W K, et al. Scour evaluation of bridge foundations using vibration measurement[C]//International Conference on Scour and Erosion 2010(ICSE-5). San Francisco, CA: American Society of Civil Engineers, 2010: 884
|
| [12] |
PRENDERGAST L J, GAVIN K, REALE C. Sensitivity studies on scour detection using vibration-based systems[J]. Transportation Research Procedia, 2016(14): 3982. |
| [13] |
熊文, 魏乐永, 张学峰, 等. 大跨度缆索支承桥梁基础冲刷动力识别方法[J]. 哈尔滨工业大学学报, 2019, 51(3): 92. XIONG Wen, WEI Leyong, ZHANG Xuefeng, et al. Dynamic-based bridge scour identification of super-span cable-supported bridges[J]. Journal of Harbin Institute of Technology, 2019, 51(3): 92. |
| [14] |
LI Yan, CAI C S, LIU Yang, et al. Dynamic analysis of a large span specially shaped hybrid girder bridge with concrete-filled steel tube arches[J]. Engineering Structures, 2016, 106(1): 243. |
| [15] |
杨婷婷, 李岩, 李全林. 汽车制动作用下混凝土梁桥下部结构动力响应分析[J]. 铁道科学与工程学报, 2020, 17(3): 637. YANG Tingting, LI Yan, LI Quanlin. Dynamic performance analysis of substructure for concrete girder bridges under vehicle braking[J]. Journal of Railway Science and Engineering, 2020, 17(3): 637. |
| [16] |
杨婷婷. 基于变速行驶车辆激励的桥梁下部结构损伤诊断方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2018 YANG Tingting. Damage detection method for substructure of bridges based on vehicle excitation with different velocity[D]. Harbin: Harbin Institute of Technology, 2018 |
| [17] |
李岩, 吴志文, 蔡明, 等. 一种随机车流与桥梁耦合振动的分析方法[J]. 哈尔滨工业大学学报, 2018, 50(3): 46. LI Yan, WU Zhiwen, CAI Ming, et al. An analysis method for coupled vibration random traffic flow and bridge[J]. Journal of Harbin Institute of Technology, 2018, 50(3): 46. |
| [18] |
中华人民共和国铁道部. 铁路桥涵地基和基础设计规范: TB 10002.5—2005[S]. 北京: 中国铁道出版社, 2005 Ministry of Railways of the People's Republic of China. Code for design on subsoil and foundation of railway bridge and culvert: TB 10002.5—2005[S]. Beijing: China Railway Press, 2005 |
 2021, Vol. 53
2021, Vol. 53


