2. 中国汽车技术研究中心有限公司,天津 300300
2. China Automotive Technology and Research Center Co., Ltd., Tianjin 300300, China
中国近期发布的《交通强国建设纲要》要求“提升本质安全水平”[1]。虽然中国交通运输安全整体形势已得到了改善,但重特大交通事故时有发生,这就为中国车辆运行安全评估提出了更高要求。伴随着智能网联交通的快速发展,诸如车车通信等一些新技术将会对异质混合交通流的运行规律产生重要影响,使其蕴含的车辆运行风险更加复杂,并可能出现一些未知的道路交通风险。因此,有必要对车车通信环境下的车辆运行安全指标进行研究,以提高智能网联环境下的车辆运行安全[2-3]。
既有研究针对常规车辆和网联车辆在混合交通流下车辆运行安全进行了探讨。一方面,已有研究基于数值仿真数据或一般交通流数据进行研究。例如,文献[4]利用数值仿真,选取多项安全评价指标对异质混合交通流下车辆运行安全进行评估,结果表明智能网联车能够有效地提高车辆运行安全;文献[5]通过数值仿真,在不同CAV渗透率条件下,分析了CAV混合交通流的优化控制法对车辆追尾碰撞风险的影响,结果表明采用该方法可降低车辆追尾碰撞风险;文献[6]提出网联环境下基于安全势场理论的车辆跟驰模型,用于描述考虑加速度参数条件下的跟驰行为,并用NGSIM数据标定模型参数,建立的基于安全势场理论的车辆跟驰模型具有良好的精度。另一方面,由于传统的车辆运行安全评估方法大多依赖于历史事故数据,该类方法存在数据收集时间长、事故记录漏报以及事故记录不准确等诸多局限性[7],相应地,间接安全评价方法(surrogate safety measures,SSMs)随之而生。SSMs是一种基于交通冲突理论的主动车辆运行安全评估方法,目的在于将识别出的非碰撞事件进一步转换为相应的危险程度,不依赖历史碰撞事故数据即可实现对车辆运行安全的评估[8]。目前SSMs方法主要有碰撞时间(time-to-collision,TTC)[9]、后侵占时间(post-encroachment time,PET)[7]、停车距离比例(proportion of stopping distance,PSD)[10]以及避撞减速度(deceleration rate to avoid collision,DRAC)[11]。上述SSMs未同时考虑前后车相对速度及相对加速度。因此,文献[12]基于牛顿运动方程提出MTTC(modified time-to-collision)并确立了其满足的关系等式,并在仿真环境下验证了MTTC能以较高的置信度捕获实际路况下的车辆运行安全特性。
已有研究多基于微观仿真数据或一般环境下实验数据进行研究,鲜有文献以车车通信环境的车辆行驶实测数据为基础进行MTTC混合分布模型研究。此外,已有研究忽略了车辆运行风险等级的差异性对MTTC分布的影响,然而不同风险等级的差异性是影响车辆运行安全的重要因素[13]。因此,本文针对不同车辆运行风险等级,基于车车通信环境下实测数据对MTTC混合分布模型进行研究,并利用一般环境下实测数据对该模型的适应性进行分析。
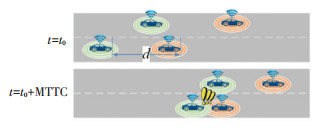
1 MTTC概念鉴于加速度反映了车辆行驶状态趋势,Ozbay等[12]基于牛顿运动学方程定义了MTTC,以预测车辆运行中发生碰撞的可能性。图 1为车辆发生纵向碰撞示意图。其中,t为当前行驶时刻,t0为初始时刻,d为前后车初始间距。
|
图 1 车辆纵向碰撞示意 Fig. 1 Schematic of vehicle longitudinal collision |
在这种情况下,同一车道的前后两车发生碰撞的条件为
| $ v_{\mathrm{f}} t+\frac{1}{2} a_{\mathrm{f}} t^{2} \geqslant d+v_{1} t+\frac{1}{2} a_{1} t^{2} $ | (1) |
| $ \frac{1}{2} \Delta a t^{2}+\Delta v t-d \geqslant 0 $ | (2) |
式中:vf、vl分别为后车和前车的速度,af、al分别为后车和前车的加速度, Δv= vf-vl,Δa=af-al。
令
| $ t_{1}=\frac{-\Delta v-\sqrt{\Delta v^{2}+2 \Delta a d}}{\Delta a} $ | (3) |
| $ t_{2}=\frac{-\Delta v+\sqrt{\Delta v^{2}+2 \Delta a d}}{\Delta a} $ | (4) |
式中t1、t2表示MTTC的两种解。
则MTTC的取值可表示为
| $ \text { MTTC }=\left\{\begin{array}{l} \min \left(t_{1}, t_{2}\right) \text {,当 } t_{1}, t_{2}>0 \text { 且 } \Delta a \neq 0 \text { 时 } \\ t_{1}, \text { 当 } t_{1}>0, t_{2} \leqslant 0 \text { 且 } \Delta a \neq 0 \text { 时 } \\ t_{2}, \text { 当 } t_{2}>0, t_{1} \leqslant 0 \text { 且 } \Delta a \neq 0 \text { 时 } \\ \frac{d}{\Delta v} \text {,当 } \Delta v>0 \text { 且 } \Delta a=0 \text { 时 } \end{array}\right. $ | (5) |
式中min(·)表示求最小值。
MTTC的值越小,前后两车发生追尾碰撞的风险越大。当MTTC>20 s时,驾驶人有充足的时间对突发情况进行反应并采取避让措施[14]。因此,对小于20 s的MTTC进行统计分析是研究的重点。
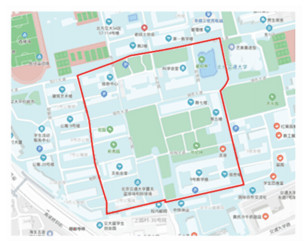
2 实验及数据准备 2.1 实验条件为获取分析MTTC所需的车辆行驶信息,于2019年5月22日在北京交通大学车辆协同实验场进行了车车通信场地实验和一般环境场地实验,实验道路为3.2 km的双向两车道,实车实验路线如图 2所示,实车实验场景如图 3所示。为保证实验安全进行,实验场地无行人及其他社会车辆出现。
|
图 2 实车实验路线 Fig. 2 Field test route |

|
图 3 实车实验场景 Fig. 3 Field test scenario |
以奇瑞和福特两品牌的5座轿车为实验车,分别安装了OBU设备、LTE-V设备、GPS及各类车载传感器,车速测量精度为0.01 km/h,加速度测量精度为0.01 m/s2,差分GPS定位精度为1 cm。每辆实验车上分别有一位驾驶员、一位测量操作员和一位联络员。测量操作员坐在实验车副驾驶位,负责监控设备运行状态,在出现LTE-V通讯连接中断或者卫星定位终端信号中断时,及时进行处理,并通过联络员将异常情况告知其他车辆。为保证两次实验的外界条件相对一致,车车通信场地实验和一般环境场地实验采用相同的实验车及车载传感器设备。另外,一般环境场地实验时,实验车关闭LTE-V通讯设备,其他设备保持开启状态。
2.2 数据获取采集的实验数据包括前后车的差分GPS定位数据、LTE-V设备发送和接收数据、通信延迟数据、事件日志数据等5类信息,主要记录车辆的位置、行驶状态以及通信相关参数,所采集的实验数据见表 1,实验数据的统计特征见表 2。
| 表 1 实验数据类型 Tab. 1 Test data types |
| 表 2 实验数据统计特征 Tab. 2 Statistical characteristics of test data |
在车车通信场地实验和一般环境场地实验获取的实验样本数据中,共选取500条实验数据作为样例数据,前后车的速度、加速度变化规律分别如图 4、5所示。

|
图 4 前后车速度变化规律 Fig. 4 Speed variation of leading and rear cars |

|
图 5 前后车加速度变化规律 Fig. 5 Acceleration variation of leading and rear cars |
由OBU编号区分前车和后车,由两车的速度和加速度计算出前后车的相对速度和相对加速度。实验数据采样时间间隔为1 s,实验采集到车车通信环境下实验数据量为2 800个,一般环境下实验数据量为1 800个,对数据进行预处理并剔除部分无效数据后,车车通信环境下实验数据量为2 562个,一般环境下实验数据量为1 583个,然后筛选出MTTC<20 s的车辆行驶运动学数据后,车车通信环境下实验数据量为1 888个,一般环境下实验数据量为1 194个,将筛选后的数据作为实验样本进行分析。
3 车辆运行风险等级划分为研究车车通信环境下车辆运行风险等级对MTTC分布的影响,需要获取不同风险等级的车车通信车辆行驶运动学数据。利用表 3中MTTC<20 s的车车通信实验样本数据,采用文献[15]提出的驾驶人风格分类类似思路,基于k-means算法对车辆运行风险等级进行划分。
| 表 3 4种风险等级样本描述 Tab. 3 Description of samples for four types of risk levels |
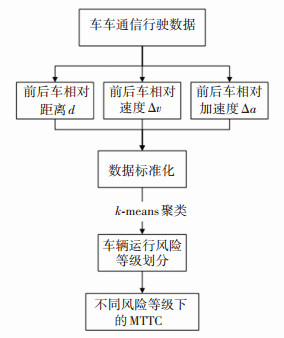
由式(3)~(5)可知,MTTC的计算过程只涉及d、Δv以及Δa,不同风险等级下3个参数具有不同的数值分布,因此,确定上述3个参数作为输入特征进行聚类分析以获得不同风险等级的车辆行驶运动学数据,分类流程如图 6所示。
|
图 6 MTTC数据分类流程图 Fig. 6 Classification flow chart for MTTC data |
为解决各特征之间数值差异过大的问题,在进行聚类分析前,需对特征数据进行标准化处理。采用min-max标准化方式对原始数据进行线性变换,使特征值都映射到[0, 1]内。其转换函数为
| $ x^{*}=\frac{x-\min }{\max -\min } $ | (6) |
式中:x为原始数值;max为样本数据最大值;min为样本数据最小值;x*为归一化转换后的值。
按照式(6)对前后车间距、相对速度以及相对加速度的样本数据均进行归一标准化处理,处理后的各特征数据皆在[0, 1]内,处于同一个数量级。
3.2 k-means聚类k-means算法的任务是将数据集划分成k类,其损失函数通常为误差平方和函数。定义式为
| $ E=\sum\limits_{i=1}^{k} \sum\limits_{X \in C_{i}}\left\|X-\mu_{i}\right\|^{2} $ | (7) |
式中: k为类别数;Ci为第i类聚集中心域的样本集合;X为数据对象;μi为第i类的类中心, 类中心为
| $ \mu_{i}=\frac{1}{N_{i}} \sum\limits_{X \in C_{i}} X $ | (8) |
其中Ni为Ci中的样本数。
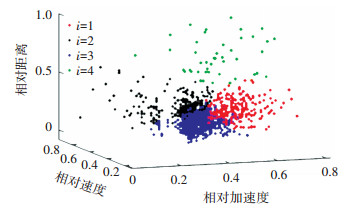
3.3 风险等级分类结果依据《国家突发公共事件总体应急预案》[16]分类方法,将风险等级划分为高、较高、一般、低4个等级。利用k-means聚类方法确定每种风险等级的样本数据,其中类别数k取4。将车车通信环境下获取到的前后车的d、Δv、Δa作为输入特征值,并采用欧几里得距离函数。3个参数聚类的标准化结果如图 7所示。
|
图 7 3个参数聚类标准化结果 Fig. 7 Clustering standardization results of three parameters |
由图 7可知,i=1的样本数据主要集中在前后车间距较小,相对加速度较大的区域;i=2的样本数据主要落在间距较小,相对速度较大,后车相对前车减速或者加速度较小的区域;i=3的样本数据聚集在前后车间距较小,相对速度较小,后车相对前车减速或者加速度较小的区域;i=4的样本数据主要分布在间距较大的区域。借鉴文献[17]中关于风险等级与车辆运行风险发生概率的对应关系,结合实际车辆运行情景,i=1对应高风险,i=2对应较高风险,i=3对应一般风险,i=4对应低风险,4种风险等级的样本描述见表 3。由表 3可知,车辆在场地实验过程中大部分时间都处于一般风险及以下,少部分时间处于较高风险及以上。
为验证不同风险等级下3个参数的分布数值具有差异性,对3个参数分别进行单因素方差分析,方差分析结果见表 4。
| 表 4 3个参数单因素方差分析结果 Tab. 4 One-way analysis of variance results for three parameters |
由表 4可知,相伴概率均小于0.05,表明在0.05的显著性水平下,4种风险等级的d、Δv和Δa存在显著差异,从而验证了不同风险等级下3个参数具有不同的分布数值。
为验证不同风险等级之间存在差异性,基于LSD(least-significant difference)法对4种风险等级下MTTC进行多重比较分析,多重比较结果见表 5,其中,I、J均为组别,代表风险等级。
| 表 5 不同风险等级MTTC多重比较结果 Tab. 5 Multiple comparison results of MTTC under different risk levels |
由表 5可知,4种风险等级之间的相伴概率均小于0.05。说明在0.05的显著性水平下,4种风险等级之间都存在显著差异,表 5中*标出了显著性差别。同样,侧面验证了基于k-means对不同风险等级的MTTC聚类效果良好。
4 不同风险等级的MTTC概率分布拟合 4.1 概率分布模型参数估计选用Weibull分布、Gamma分布、对数正态分布3种经典概率分布模型,针对车车通信4种风险等级的MTTC概率分布进行分析。采用MLE参数估计方法对3种模型的参数进行估计,参数估计结果见表 6。其中,α1、β1分别代表Weibull分布的形状参数和尺度参数;α2、β2分别代表Gamma分布的形状参数和比例参数;μ、σ分别代表对数正态分布的对数均值和对数标准差。
| 表 6 概率分布模型参数估计值 Tab. 6 Estimated values of distribution models parameters |
选取小于20 s的车车通信MTTC实验样本数据,利用上述3种概率分布模型对4种风险等级的MTTC概率分布进行拟合。为了定量比较概率分布模型的拟合效果,选用K-S检验对拟合结果进行检验,其中p值表示在原假设为真的条件下样本观察结果出现的概率。若p很小,则表示原假设情况发生的概率很小。根据小概率原理,拒绝原假设。取0.05作为显著性水平,如果p大于0.05,认为数据总体样本分布符合理论分布模型;否则,理论分布模型不能很好地描述数据分布特性。3种模型的检验结果见表 7。
| 表 7 3种模型的K-S检验结果 Tab. 7 K-S test results for three models |
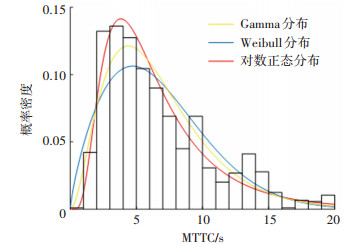
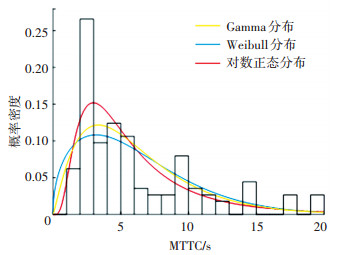
由表 7可知,4种风险等级的对数正态概率分布模型K-S检验的p值均大于0.05。结果表明,车车通信的高风险、较高风险、一般风险、低风险的MTTC都能够用对数正态分布进行拟合,而Weibull和Gamma概率分布模型仅能通过低风险等级情形下的假设检验。4种风险等级的MTTC分布拟合结果如图 8~11所示。

|
图 8 高风险MTTC分布模型拟合效果对比 Fig. 8 Comparison of parameters fitting results of MTTC distribution models under high-risk level |

|
图 9 较高风险MTTC分布模型拟合效果对比 Fig. 9 Comparison of parameters fitting results of MTTC distribution models under second-high risk level |
|
图 10 一般风险MTTC分布模型拟合效果对比 Fig. 10 Comparison of parameters fitting results of MTTC distribution models under general-risk level |
|
图 11 低风险MTTC分布模型拟合效果对比 Fig. 11 Comparison of parameters fitting results of MTTC distribution models under low-risk level |
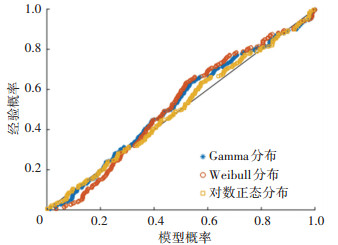
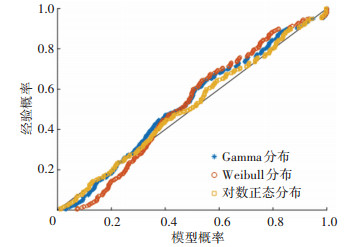
P-P图表示变量的累积概率与理论模型的累积概率之间的关系。P-P图中各点越近似一条直线表明理论模型越接近真实概率分布[18],选择P-P图进一步对3种概率分布模型的拟合效果进行分析。图 12~15为4种不同风险等级的MTTC概率分布函数参数拟合的P-P图。结果表明,对数正态分布优于Weibull分布和Gamma分布,与表 7的K-S检验结果相一致。
|
图 12 高风险P-P图 Fig. 12 P-P graph under high-risk level |
|
图 13 较高风险P-P图 Fig. 13 P-P graph under second-high risk level |

|
图 14 一般风险P-P图 Fig. 14 P-P graph under general-risk level |

|
图 15 低风险P-P图 Fig. 15 P-P graph under low-risk level |
基于上述分析结果可知,对数正态分布对车车通信的4种风险等级的MTTC拟合效果最优。因此,针对4种风险等级,建立描述MTTC总体的对数正态混合分布模型如下:
| $ \begin{aligned} f(t)=& \omega_{1} \frac{1}{\sqrt{2 {\rm{ \mathsf{ π} }}} \sigma_{1}} \exp \left\{-\frac{\left(\ln t-\mu_{1}\right)^{2}}{2 \sigma_{1}^{2}}\right\}+\\ & \omega_{2} \frac{1}{\sqrt{2 {\rm{ \mathsf{ π} }}} \sigma_{2}} \exp \left\{-\frac{\left(\ln t-\mu_{2}\right)^{2}}{2 \sigma_{2}^{2}}\right\}+\\ & \omega_{3} \frac{1}{\sqrt{2 {\rm{ \mathsf{ π} }}} \sigma_{3}} \exp \left\{-\frac{\left(\ln t-\mu_{3}\right)^{2}}{2 \sigma_{3}^{2}}\right\}+\\ & \omega_{4} \frac{1}{\sqrt{2 {\rm{ \mathsf{ π} }}} \sigma_{4}} \exp \left\{-\frac{\left(\ln t-\mu_{4}\right)^{2}}{2 \sigma_{4}^{2}}\right\} \end{aligned} $ | (9) |
式中:f(t)为MTTC概率密度函数;t为MTTC样本;ω1、ω2、ω3、ω4分别为4种风险等级的先验概率,
记MTTC的分布模型参数θ=[ω1, ω2, ω3, ω4, μ1, μ2, μ3, μ4, σ1, σ2, σ3, σ4]。
5.2 参数估计混合分布模型参数估计通常采用EM算法进行求解。
EM算法的迭代分为两部分,即E步和M步。两部分交替进行计算。设γji为隐变量,其表达式为
| $ \gamma_{j i}=\left\{\begin{array}{l} 1, \text { 第 } j \text { 个样本来自第 } i \text { 种分布, } j=1,2, \cdots, n \\ 0, \text { 否则 } \end{array}\right. $ | (10) |
式中:γji为第j个MTTC样本对应的第i类分布的隐变量;n为样本总数。
为方便计算隐变量值,将式(9)记为
| $ f(t)=\sum\limits_{i=1}^{4} \omega_{i} f_{i}(t) $ | (11) |
| $ f_{i}(t)=\frac{1}{\sqrt{2 {\rm{ \mathsf{ π} }}} \sigma_{i}} \exp \left\{-\frac{1}{2 \sigma_{i}^{2}}\left(\ln t-\mu_{i}\right)^{2}\right\} $ | (12) |
EM算法的步骤如下:
1) 选择模型参数θ的初始值θ0,开始迭代。
2) E步是由前一次迭代得到的θm,计算隐变量的新值,即
| $ \hat{\gamma}_{j i}{ }^{(m)}=\frac{\omega_{i} f_{i}\left(t_{j} \mid \theta_{m}\right)}{\sum\limits_{i=1}^{4} \omega_{i} f_{i}\left(t_{j} \mid \theta_{m}\right)} $ | (13) |
3) M步是计算新一轮迭代的模型参数,即
| $ \hat{\mu}_{m+1}=\frac{\sum\limits_{j=1}^{n} \hat{\gamma}_{j i}{ }^{(m)} t_{j}}{\sum\limits_{j=1}^{n} \hat{\gamma}_{j i}{ }^{(m)}} $ | (14) |
| $ \hat{\sigma}_{m+1}=\frac{\sum\limits_{j=1}^{n} \hat{\gamma}_{j i}{ }^{(m)}\left(t_{j}-\mu_{m}\right)^{2}}{\sum\limits_{j=1}^{n} \hat{\gamma}_{j i}{ }^{(m)}} $ | (15) |
| $ \hat{\omega}_{m+1}=\frac{\sum\limits_{j=1}^{n} \hat{\gamma}_{j i}{ }^{(m)}}{n} $ | (16) |
式中:m为迭代次数;tj为第j个样本;
以θm+1作为θm的更新值,重复E步和M步,直至‖θm+1-θm‖小于某个设定值时停止迭代,最终得到分布函数参数的估计值。
5.3 实例验证为验证理论分布模型的合理性和普适性,分别采用车车通信场地实验和一般环境场地实验获取的MTTC<20 s的实验样本数据进行验证。
利用车车通信场地实验采集的车辆行驶运动学数据,采用EM算法估计概率分布模型参数,并选取Weibull分布、Gamma分布、对数正态分布作为对比模型。
采用K-S检验方法对拟合结果进行检验,显著性水平为0.05,车车通信MTTC混合分布模型参数标定及K-S检验结果见表 8。
| 表 8 车车通信MTTC分布模型参数及K-S检验结果 Tab. 8 Parameters and K-S test results of MTTC distribution models in V2V communication |
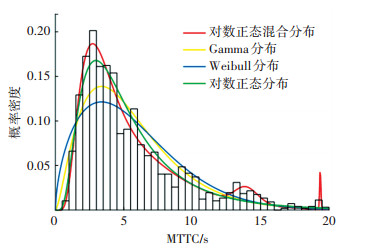
由表 8可知,对数正态混合分布通过检验,说明车车通信MTTC可用对数正态混合分布模型拟合,同时也验证了4种风险等级之间存在差异性。图 16为车车通信的4种MTTC概率分布模型的拟合曲线。
|
图 16 车车通信MTTC分布模型拟合效果对比 Fig. 16 Comparison of fitting results of MTTC distribution models in V2V communication |
由图 16可知,与其他3种概率分布模型相比,对数正态混合分布模型拟合的曲线最接近车车通信MTTC概率分布。
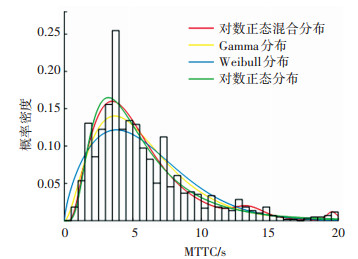
利用4种概率分布模型对一般环境下MTTC<20 s的实验样本数据进行拟合。对数正态混合分布、Weibull分布、Gamma分布以及对数正态分布的K-S检验结果p值分别为0.10、6.28×10-6、4.78×10-3、8.67×10-6。图 17为4种概率分布模型的拟合效果。结果表明,相比其他3种概率分布模型,对数正态混合分布模型也能更好地拟合一般环境下的MTTC分布,进一步验证了理论分布模型的合理性。
|
图 17 一般环境MTTC分布模型拟合效果对比 Fig. 17 Comparison of fitting results of MTTC distribution models in conventional environment |
1) 通过车车通信环境场地实验,获取实际车辆行驶实验数据,利用k-means聚类方法划分了车辆运行风险等级,获得了不同风险等级的车辆行驶运动学数据。
2) 考虑4种车辆运行风险等级,分析了不同类型风险等级的MTTC概率分布规律,对比了3种概率分布模型在不同风险等级下的拟合检验效果。
3) 建立了MTTC对数正态混合概率分布模型,标定了模型参数,对比了4种概率分布模型,通过拟合优度分析验证了混合分布模型的有效性。
4) 本文针对两车行驶场景研究了车车通信环境下MTTC概率分布规律,未来应尝试更高车速多车间的跟驰、换道等驾驶行为的车辆行驶测试实验,进一步探究符合复杂道路MTTC概率分布规律。
| [1] |
卢春房, 张航, 陈明玉. 新时代背景下的交通运输高质量发展[J]. 中国公路学报, 2021, 34(6): 3. LU Chunfang, ZHANG Hang, CHEN Mingyu. Realization of high-quality development of transportation in the new era[J]. China Journal of Highway and Transport, 2021, 34(6): 3. |
| [2] |
DUAN Aowen, ZHOU Mingxia, QIU Jinlong, et al. A 6-year survey of road traffic accidents in Southwest China: emphasis on traumatic brain injury[J]. Journal of Safety Research, 2020, 73: 161. DOI:10.1016/j.jsr.2020.02.010 |
| [3] |
孙平, 宋瑞, 王海霞. 我国道路交通事故成因分析及预防对策[J]. 安全与环境工程, 2007, 14(2): 97. SUN Ping, SONG Rui, WANG Haixia. Analysis of the causes of traffic accidents on roads and countermeasures[J]. Safety and Environmental Engineering, 2007, 14(2): 97. DOI:10.3969/j.issn.1671-1556.2007.02.026 |
| [4] |
蒋阳升, 胡蓉, 姚志洪, 等. 智能网联车环境下异质交通流稳定性及安全性分析[J]. 北京交通大学学报, 2020, 44(1): 27. JIANG Yangsheng, HU Rong, YAO Zhihong, et al. Stability and safety analysis for heterogeneous traffic flow composed of intelligent and connected vehicles[J]. Journal of Beijing Jiaotong University, 2020, 44(1): 27. DOI:10.11860/j.issn.1673-0291.20190045 |
| [5] |
秦严严, 王昊. 智能网联车辆交通流优化对交通安全的改善[J]. 中国公路学报, 2018, 31(4): 202. QIN Yanyan, WANG Hao. Improving traffic safety via traffic flow optimization of connected and automated vehicles[J]. China Journal of Highway and Transport, 2018, 31(4): 202. DOI:10.3969/j.issn.1001-7372.2018.04.024 |
| [6] |
李林恒, 甘婧, 曲栩, 等. 智能网联环境下基于安全势场理论的车辆跟驰模型[J]. 中国公路学报, 2019, 32(12): 76. LI Linheng, GAN Jing, QU Xu, et al. Car-following model based on safety potential field theory under connected and automated vehicle environment[J]. China Journal of Highway and Transport, 2019, 32(12): 76. |
| [7] |
TANG K, KUWAHARA M. Implementing the concept of critical post-encroachment time for all-red clearance interval design at signalized intersections[J]. Journal of Eastern Asia Society for Transportation Studies, 2011, 9: 1485. |
| [8] |
GETTMAN D, PU L, SAYED T, et al. Surrogate safety assessment model and validation: FHWA-HRT-08-051[R]. Washington DC: Federal Highway Administration, 2008
|
| [9] |
HAYWARD J C. Near-miss determination through use of a scale of danger[J]. Highway Research Record, 1972(384): 24. |
| [10] |
ALLEN B L, SHIN B T, COOPER P J. Analysis of traffic conflicts and collisions[J]. Transportation Research Record, 1978(667): 67. |
| [11] |
ARCHER J. Indicators for traffic safety assessment and prediction and their application in micro-simulation modeling: a study of urban and suburban intersections[D]. Stockholm: Royal Institute of Technology, 2005
|
| [12] |
OZBAY K, YANG H, BARTIN B, et al. Derivation and validation of a new simulation-based surrogate safety measure[J]. Transportation Research Record, 2008(2083): 105. |
| [13] |
朱西产, 魏昊舟, 马志雄. 基于自然驾驶数据的跟车场景潜在风险评估[J]. 中国公路学报, 2020, 33(4): 169. ZHU Xichan, WEI Haozhou, MA Zhixiong. Assessment of the potential risk in car-following scenario based on naturalistic driving data[J]. China Journal of Highway and Transport, 2020, 33(4): 169. DOI:10.3969/j.issn.1001-7372.2020.04.017 |
| [14] |
陆建, 张文珺, 杨海飞, 等. 基于碰撞时间的追尾风险分析[J]. 交通信息与安全, 2014, 32(5): 58. LU Jian, ZHANG Wenjun, YANG Haifei, et al. Analysis of rear-end risk based on the indicator of time to collision[J]. Journal of Transport Information and Safety, 2014, 32(5): 58. DOI:10.3963/j.issn.1674-4861.2014.05.011 |
| [15] |
刘通, 付锐, 马勇, 等. 考虑驾驶人风格的跟车预警规则研究[J]. 中国公路学报, 2020, 33(2): 170. LIU Tong, FU Rui, MA Yong, et al. Car-following warning rules considering driving styles[J]. China Journal of Highway and Transport, 2020, 33(2): 170. |
| [16] |
中华人民共和国国务院. 国家突发公共事件总体应急预案[M]. 北京: 中国法制出版社, 2006: 74. The State Council of the People's Republic of China. National overall emergency plan for public emergencies[M]. Beijing: China Legal Press, 2006: 74. |
| [17] |
马艳丽, 范璐洋, 吕天玲, 等. 车辆运行风险贝叶斯网络量化分级方法[J]. 哈尔滨工业大学学报, 2020, 52(3): 36. MA Yanli, FAN Luyang, LÜ Tianling, et al. Quantification classification method for driving risk quantization using Bayesian network[J]. Journal of Harbin Institute of Technology, 2020, 52(3): 36. |
| [18] |
曲昭伟, 段宇洲, 宋现敏, 等. 多车道环形交叉口车头时距分布模型[J]. 吉林大学学报(工学版), 2015, 45(3): 743. QU Zhaowei, DUAN Yuzhou, SONG Xianmin, et al. Analysis of time headway distribution models at multi-lane roundabout[J]. Journal of Jilin University (Engineering and Technology Edition), 2015, 45(3): 743. |
 2021, Vol. 53
2021, Vol. 53


