2. 招商局重庆交通科研设计院有限公司, 重庆 400067;
3. 同济大学 交通运输工程学院, 上海 201804
2. China Merchants Chongqing Communications Research & Design Institute Co., Ltd., Chongqing 400067, China;
3. College of Transportation Engineering, Tongji University, Shanghai 201804, China
长白山脉纵向分布于黑龙江、吉林和辽宁三省的东部地区,属于《公路自然区划标准》[1]中的东北东部山地湿冻区(Ⅱ1区)。公路工程主要面临冬季雪害、夏季水毁的威胁,对路基平衡湿度预估的准确性要求高。湿度指数TMI(Thornthwaite moisture index)是现行《公路路基设计规范》[2]中预估气候因素控制型路基平衡湿度的主要参数,采用TMI模型(Thornthwaite法)计算,主要包括路基土潜在蒸发蒸腾量PE(potential evapotranspiration)估算及年度湿度平衡两部分。但是采用Thornthwaite法计算公路自然区划Ⅱ1区的路基湿度指数时存在一个问题,即当气温低于0 ℃时,认为蒸发蒸腾作用停止,PE计算值为0[3-6]。虽然相对于液态水、森林积雪而言,无覆盖路基边坡和植物边坡(裸土和苔原)积雪的蒸发速率较慢,但并不为0[7]。此外,受路面覆盖效应影响,路基土的蒸发蒸腾量以及降雨入渗量无法准确衡量,现行《公路路基设计规范》和Thornthwaite法也并未对路面的覆盖效应进行定量的修正[8]。另一方面,正温期水分蒸发、负温期雪面蒸发、春季融雪径流再蒸发的现象更为特殊[9-10],年度湿度平衡法在一定程度弱化了Ⅱ1区路基湿度状态的季节性变化特征,致使现行规范中推荐的Ⅱ1区TMI取值可能未涵盖所有可能的干湿状态。为了弥补Ⅱ1区湿度指标计算方法中存在的不足,需建立一种新的计算方法,使PE估算时不受限于温度范围,且湿度平衡算法能够反映路基的阶段性冻结-融化特点。
多年来,学者们发展了多种PE估算模型,包括综合法、辐射法、温度法以及蒸发皿法4大类[11-13]。在综合法估算PE中,最具影响力的是Penman-Monteith法,该法是由联合国粮农组织FAO推荐的参考作物日蒸发蒸腾量计算公式,是PE计算的标准化方法和缺乏实测资料地区评价其他方法的标准,也称FAO-PM法[14-15]。中国现行的《公路自然区划标准》计算蒸腾力所采用的H.L.彭曼公式即是FAO-PM法的原始形式,可见采用该方法计算路基土壤的干湿状况早已得到行业专家的认可。Thornthwaite法的湿度表征指标有两种:一是按年计的湿度指标,二是按月计算湿润指标Ih(humid index)、干旱指标Ia(arid index)。农业学中一般采用月计湿润或干旱指标,以便于统计农作物在不同的生长周期时的需水量,这种周期性统计方法对于分析类似具有阶段性冻融现象的季冻区路基土体湿度状态具有较好的借鉴意义。为此,本文引入FAO-PM法估算Ⅱ1区路基土PE,以月统计法为基础进行分阶段统计,建立Ⅱ1区路基湿度指数计算方法,按照三级区划将计算所得湿度指数补充于现行规范取值范围。研究成果有望细化公路自然区划Ⅱ1区湿度取值范围,提高该区路基湿度指数取值精度。
1 基于FAO-PM法的潜在蒸发蒸腾量蒸发蒸腾量是指在一定时段内,水分经蒸发而散布到空气中的量,通常用蒸发掉的水层厚度表示。FAO-PM计算公式中包含最高气温、最低气温、相对湿度、2 m高处的平均风速以及日照时数5个参数,且最低气温不设限,该法具有较高的精度和较好的通用性,被认为是干旱地区和湿润地区计算效果最好的一种方法,计算公式为
| $ \mathrm{ET}_{0}=\frac{0.408 \varDelta\left(R_{\mathrm{n}}-G\right)+\gamma \frac{900}{T+273} u_{2}\left(e_{\mathrm{s}}-e_{\mathrm{a}}\right)}{\varDelta+\gamma\left(1+0.34 u_{2}\right)} $ | (1) |
式中:ET0为日蒸发蒸腾量,cm,按月累加后以PE表示;es、ea分别为饱和水汽压和实际水汽压,kPa,计算公式为
| $ e_{\mathrm{s}}=\frac{e_{\left(T_{\text {max }}\right)}^{0}+e_{\left(T_{\min }\right)}^{0}}{2} $ | (2) |
| $ e_{\mathrm{a}}=\frac{\mathrm{R} \mathrm{H}_{\operatorname{mean}}}{100}\left[\frac{e_{\left(T_{\max }\right)}^{0}+e_{\left(T_{\min }\right)}^{0}}{2}\right] $ | (3) |
| $ e_{(T)}^{0}=0.610\ 8 \exp \left(\frac{17.27 T}{T+237.3}\right) $ | (4) |
其中T、Tmax、Tmin分别为平均温度、最高温度、最低温度,℃,实测结果;RHmean为平均相对湿度,实测结果;Δ为温度-饱和水汽压关系曲线在T处的斜率,kPa/℃,计算公式为
| $ \varDelta=\frac{4\ 098\left[0.610\ 8 \exp \left(\frac{17.27 T}{T+237.3}\right)\right]}{(T+237.3)^{2}} $ | (5) |
γ为湿度计常数,kPa/℃,计算公式为
| $ \gamma=\frac{c_{P} P}{\varepsilon \lambda}=0.665 \times 10^{-3} P $ | (6) |
其中cP为定压比热,一般取1.013×10-3,MJ·kg-1·℃-1;ε为水汽与干空气的比率,ε=0.622;λ为汽化潜热,一般取2.45 MJ·kg-1;P为当地实际气压,计算公式为
| $ P=101.3\left(\frac{293-0.006\ 5 Z}{293}\right)^{5.26} $ | (7) |
其中Z为计算点海拔高程,m;Rn为净辐射,MJ·m-2·d-1,计算公式为
| $ R_{\mathrm{n}}=R_{\mathrm{ns}}-R_{\mathrm{nl}} $ | (8) |
其中Rns为净短波辐射,MJ·m-2·d-1,计算公式为
| $ R_{\mathrm{ns}}=0.77 R_{\mathrm{s}} $ | (9) |
Rnl为净长波辐射,MJ·m-2·d-1,计算公式为
| $ R_{\mathrm{nl}}=\sigma\left[\frac{T_{\mathrm{max}, \mathrm{K}}^{4}+T_{\mathrm{min}, \mathrm{K}}^{4}}{2}\right]\left(0.34-0.14 \sqrt{e_{\mathrm{a}}}\right)\left(1.35 \frac{R_{\mathrm{s}}}{R_{\mathrm{s} 0}}-0.35\right) $ | (10) |
其中σ为斯蒂芬-玻尔兹曼(Stefan-Boltzmann)常数,σ=4.903×10-9 MJ·K-4·m-2·d-1;Tmax, K为最高绝对温度,Tmax, K=Tmax+273.16;Tmin, K为最低绝对温度,Tmin, K=Tmin+273.16;Rs为到达地球表面的实际太阳辐射,MJ·m-2·d-1,计算公式为
| $ R_{\mathrm{s}}=\left(0.25+0.5 \frac{n}{N}\right) R_{\mathrm{a}} $ | (11) |
其中n为实际日照时数,实测结果;N为最大可能日照时数,计算公式为
| $ N=\frac{24}{{\rm{ \mathsf{ π} }}} \omega_{\mathrm{s}} $ | (12) |
其中ωs为日落时角度,rad,计算公式为
| $ \omega_{\mathrm{s}}=\arccos (-\tan \varphi \tan \delta) $ | (13) |
其中φ为地理纬度,rad;δ为日倾角,rad,计算公式为
| $ \delta=0.409 \sin \left(\frac{2 {\rm{ \mathsf{ π} }}}{365} J-1.39\right) $ | (14) |
其中J为日序数(1月1日为1,逐日增加);Ra
为大气顶太阳辐射,MJ·m-2·d-1,计算公式为
| $ R_{\mathrm{a}}=37.6 d_{\mathrm{r}}\left(\omega_{\mathrm{s}} \sin \varphi \sin \delta+\cos \varphi \cos \delta \sin \omega_{\mathrm{s}}\right) $ | (15) |
其中dr为日地相对距离的倒数,计算公式为
| $ d_{\mathrm{r}}=1+0.033 \cos \left(\frac{2 {\rm{ \mathsf{ π} }}}{365} J\right) $ | (16) |
Rs0为到达地球表面的晴空太阳辐射,MJ·m-2·d-1,计算公式为
| $ R_{\mathrm{s} 0}=\left(0.75+\frac{2}{10^{5}} z\right) R_{\mathrm{a}} $ | (17) |
G为土壤热通量,由于日尺度的土壤热通量相对很小,一般可以忽略;u2为2 m高度平均风速,计算公式为
| $ u_{2}=u_{z} \frac{4.87}{\ln (67.8 z-5.42)} $ | (18) |
uz为风标高度处的实际风速,m/s,实测结果。
2 区分冻结-融化时期的阶段湿度指数 2.1 冻结-融化现象季冻区公路路基的冻结-融化时期一般归纳为冰冻期、完全融化期、融化恢复期和平衡湿度期4个时期。根据气象统计资料显示,Ⅱ1区平均气温<0 ℃时间为3~5个月[16],考虑到路面具有一定的覆盖效应,则该区路基冰冻期约为4个月左右。冻融循环4个时期的持续时长与季节并不完全一致,完全融化期持续时长仅为1个月,冰冻期与平衡湿度期持续时间最长,约4个月[17-20]。Ⅱ1区路基冰冻最早于每年的11月底至12月初开始,融化时间为每年的3月底至4月初,各时期的持续时长及冰冻开始时间见表 1。
| 表 1 季冻区路基冻结-融化现象不同时期持续时长 Tab. 1 Duration of subgrade freezing-thawing phenomenon in seasonal frozen area |
基于上述分析,可将Ⅱ1区路基的冰冻开始时间确定为12月初,则冻结-融化现象的4个时期及其区间为:冰冻期(上年度12月份—本年度3月份),完全融化期(本年度4月份),融化恢复期(本年度5月份—本年度7月份)和平衡期(本年度8月份—本年度11月份)。
2.2 湿度平衡原理湿度平衡或称水分平衡,是土壤学与农业气象学等领域的概念,常用的湿度平衡模型有指数消退模型、人工神经网络模型、水量平衡模型、冻融期土壤水热耦合传输模型和SPAC水热耦合传输模型等[21-22]。Thornthwaite法的湿度平衡原理可归属为水量平衡模型,李迪强等[23]在计算中国潜在植被生产力时,采用的土壤湿度动态的处理方法即参照了Thornthwaite法。当该方法被逐渐引入公路路基湿度预估研究后,国内外学者在进行路基湿度平衡分析时均采用Thornthwaite的湿度平衡原理[24-25]。
土壤由于具有复杂多孔隙结构,因而具有一定的储水能力。它一方面通过大气降水获得水分补充,另一方面通过蒸发蒸腾作用丧失一部分水分。当降雨量小于蒸发量,此时降水全部蒸发,土壤中原有的水分也将蒸发,当原有水分全部蒸发之后仍有进一步蒸发的趋势,这样就形成湿度不足量,即缺水量DF;而当土壤达到最大湿度状态(即饱和含水率状态),多余的降水将以径流的形式流走,1个月产生的径流总量就是该月的径流量R。在以月为统计单位时,若不考虑当月蒸发掉的水来源于当月降雨还是上月储存,则可根据土壤月储水量将湿度平衡后的土壤湿度状态归纳为3种状态:1)有径流,表示的是Si>Smax,土壤月储量Si超过最大储水量Smax,当月未蒸发掉全部水量,富余水量可以形成径流补给次月;2)无径流不干旱,表示的是0<Si≤Smax,土壤月储量介于0与最大储水量之间,当月未蒸发掉全部水量,但也无法形成径流补给次月;3)无径流干旱,表示的是Si≤0,土壤月储水量为0,当月蒸发掉所有水分(包括当月降水量及上月补给量),且有进一步蒸发的趋势。
基于上述分析,本文对现有的湿度平衡计算流程进行一定程度的优化,湿度平衡的计算流程如图 1所示。图中,Si表示土壤月储水量,cm;Si-1表示土壤上月储水量终值,也就是本月储水量初值,cm;Ri为月径流量,cm;DFi为月缺水量,cm;Pi为月降雨量,cm。土壤最大储水量Smax取决于土质类型,其值等于饱和体积含水率θs与土层厚度h之积。降雨影响深度一般在0.6~2.5 m之间[26],考虑到路面结构的防水、阻水效应,本文取路基土层厚度h为1.2 m。在湿度平衡计算中,还需要确定路基的初始储水量S0,它与土壤的初始湿度状况有关,其值等于土壤初始体积含水率θ0(在此,取路基土压实施工时的湿度状态为初始湿度状况,且其施工碾压含水率为土的最佳含水率)与土层厚度h(1.2 m)之积。
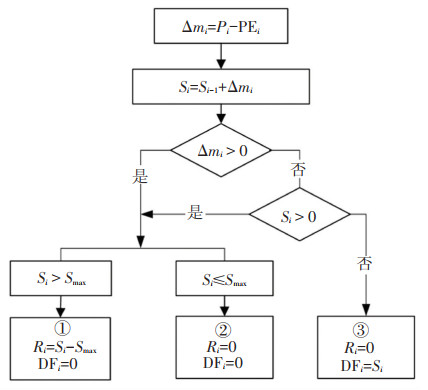
|
图 1 湿度平衡计算流程 Fig. 1 Moisture balance calculation process |
Thornthwaite法计算土壤湿度指标的方法分为月计指标和年计指标两种,湿润指标为
| $ I_{\mathrm{h}}=100 \times \frac{S}{\mathrm{PE}} $ | (19) |
干旱指标为
| $ I_{\mathrm{a}}=100 \times \frac{\mathrm{DF}}{\mathrm{PE}} $ | (20) |
根据全年各月的湿润指标与干旱指标,可以计算当年的年度湿度指数:
| $ I_{\mathrm{m}}=I_{\mathrm{h}}-0.6 I_{\mathrm{a}}=\frac{100\left(R_{y}-0.6 \mathrm{DF}_{y}\right)}{\mathrm{PE}_{y}} $ | (21) |
式中:Ry为第y年年度径流量,cm;DFy为第y年年度缺水量,cm;PEy为第y年年度蒸发蒸腾总量,cm。上述各值均由各月的值累加获得。
月计指标以一个月为一个考察单元,分析当月降水量和蒸发蒸腾量的平衡关系,评价当月土壤湿度状态。年计指标以12个月为一个考察单元,将12个月的降水量和蒸发蒸腾量简单均值化,评价全年土壤湿度状态,这种方法在一定程度上抵消了径流积聚和负温下的土壤蒸发蒸腾,无法揭示最不利时期的真实湿度状态。
根据上述对Ⅱ1区路基土的冻结-融化时期开始时间与持续时长的分析结论,建立冰冻期、完全融化期、融化恢复期和平衡湿度期4个时期的阶段湿度指数Ism(staged moisture index)计算公式为
| $ I_{\mathrm{sm}}=\frac{100\left(R_{\mathrm{st}}-0.6 \times \mathrm{DF}_{\mathrm{st}}\right)}{\mathrm{PE}_{\mathrm{st}}} $ | (22) |
式中:Rst为各个时期的累积径流量,cm;DFst为各个时期的累积缺水量,cm;PEst为各个时期的累积蒸发蒸腾总量,cm。
按此公式计算出的Ism为4组数值,分别表示公路路基冻结-融化各个时期的平衡湿度情况:IsmⅠ为冰冻期湿度指数,IsmⅡ为完全融化期湿度指数,IsmⅢ为融化恢复期湿度指数,IsmⅣ为平衡湿度期湿度指数。湿度指数TMI为4组数值的平均值。
2.4 算例以任一气象站点——延吉站为例,详细介绍采用FAO-PM法计算PE的具体过程。延吉站位于东经126.28°,北纬42.53°,高程为176.8 m。路基初始体积含水率θ0为0.18,饱和体积含水率θs为0.24。气象数据来源于中国气象局公布的中国国际交换站地面气候标准值月值数据集(1971年—2000年),见表 2。
| 表 2 气象站点数据 Tab. 2 Meteorological data |
FAO-PM法的PE计算过程见表 3,湿度平衡与阶段湿度指数Ism计算过程与结果列于表 4、5中。根据表 4数据可计算得到:S0=θ0h=0.18×120 cm=21.6 cm;Smax=θsh=0.24×120 cm=28.8 cm。根据表 5数据可计算得到TMI=-9.7。
| 表 3 潜在蒸发蒸腾量计算过程 Tab. 3 Calculation process of PE |
| 表 4 湿度平衡过程 Tab. 4 Moisture balance process |
| 表 5 阶段湿度指数计算过程 Tab. 5 Calculation process of staged moisture index |
通过上述计算流程求得Ⅱ1区不同土组的潜在蒸发蒸腾量。气象数据来源同上,位于Ⅱ1区的气象站共7个。表 6为各站PE计算结果,结果表明:负温下的PE占全年总蒸发蒸腾量的9.8%~15.7%,其中,绥芬河站为14.2%、牡丹江站为12%、鸡西站为13.2%、临江站为12.4%、延吉站为15.7%、丹东站为9.8%、本溪站为12.3%。可见,忽略负温下蒸发蒸腾能力将导致湿度指数估算值偏高。
| 表 6 Ⅱ1区不同站点潜在蒸发蒸腾量 Tab. 6 PE at different weather stations in zone Ⅱ1 |
以延吉站为例说明逐月PE与气象因素的关系,如图 2~5所示,结果表明:正负温同时参与统计时,PE与平均气温显著正相关,与其他气候因素的线性相关性不显著。
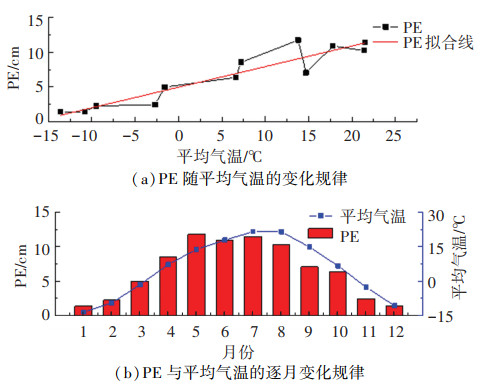
|
图 2 平均气温与潜在蒸发蒸腾量关系 Fig. 2 Relationship between PE and average temperature |
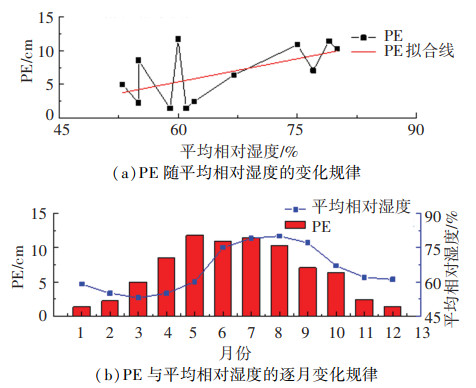
|
图 3 平均相对湿度与潜在蒸发蒸腾量关系 Fig. 3 Relationship between PE and average relative humidity |
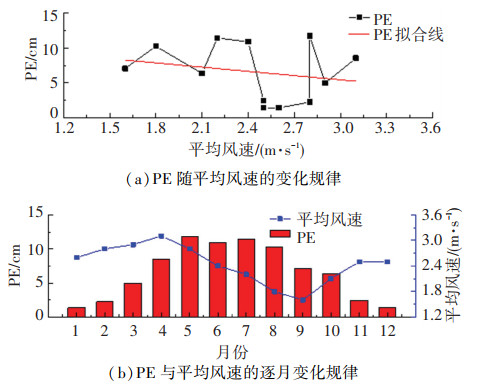
|
图 4 平均风速与潜在蒸发蒸腾量关系 Fig. 4 Relationship between PE and average wind speed |
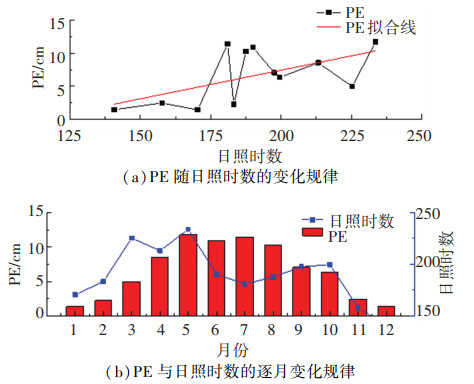
|
图 5 日照时数与潜在蒸发蒸腾量关系 Fig. 5 Relationship between PE and sunshine hours |
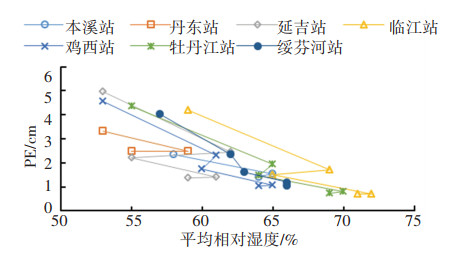
图 6~9为负温时(11月份至次年3月份),PE随各气象因素的变化规律,可以看出,PE与平均日照时数、平均气温和平均风速正相关,PE随之增加而增加;PE与平均相对湿度负相关,相对湿度越大,则PE越小。
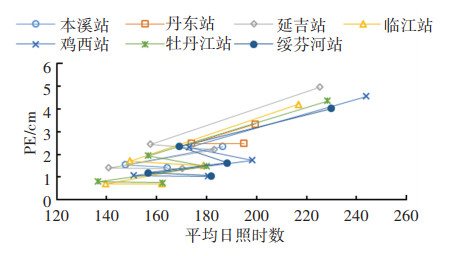
|
图 6 负温下PE与平均日照时数的关系 Fig. 6 Relationship between PE and average sunshine hours at negative temperature |
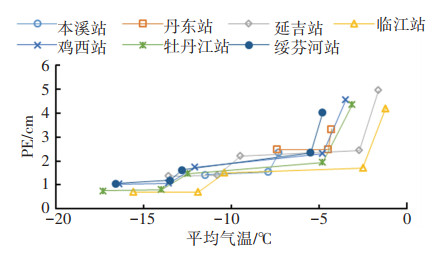
|
图 7 负温下PE与平均气温的关系 Fig. 7 Relationship between PE and average temperature at negative temperature |
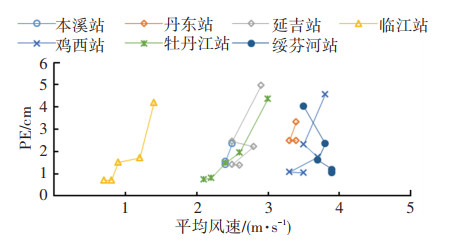
|
图 8 负温下PE与平均风速的关系 Fig. 8 Relationship between PE and average wind speed at negative temperature |
|
图 9 负温下PE与平均相对湿度的关系 Fig. 9 Relationship between PE and average relative humidity at negative temperature |
将FAO-PM法、Thornthwaite法[18]计算所得PE结果与中国气象局公布的累年各月蒸发量(小型)数值进行对比,如图 10所示。

|
图 10 PE计算结果对比 Fig. 10 Comparison of PE calculation results |
总体而言,FAO-PM法计算模型所得的PE值偏小,但与各地气象站数值的逐月变化趋势基本保持一致,误差为0.47~13.22 cm,88%的误差介于0.47~ 7.07 cm之间;Thornthwaite法计算模型所得的PE与气象站数值相比偏差较大,表现为冬季PE为0,年峰值与气象站数值相比延迟2个月出现,误差为-1.85~16.88 cm,88%的误差介于-1.85~10.55 cm之间。
值得关注的是,FAO-PM法未能准确模拟5月份至6月份间的PE突增现象,模型计算值虽有增加,但增幅远小于气象站数值。出现这种差异的原因是由于FAO-PM法采用平均气温直接参与PE计算,而不是最高气温。在Ⅱ1区,根据气象原始数据可知,5月份和6月份的昼夜温差较大,平均气温往往仅为最高气温的65%左右,而气温是与PE高度正相关的影响因素,因此导致了模型计算值比气象站数值偏小。
4 Ⅱ1区路基湿度指数取值范围 4.1 Ⅱ1区公路路基湿度指数本文通过上述计算流程求得Ⅱ1区的不同土组湿度指数,其中,不同土组的θ0与θs取值见表 7,阶段湿度指数计算结果见表 8,湿度指数计算结果见表 9。
| 表 7 Ⅱ1区不同土组的特征体积含水率值[18] Tab. 7 Characteristic values of volumetric water content for different soil groups in zone Ⅱ1 [18] |
| 表 8 Ⅱ1区不同土组的阶段湿度指数 Tab. 8 Staged moisture index of different soil groups in zone Ⅱ1 |
| 表 9 Ⅱ1区不同土组的湿度指数 Tab. 9 TMI of different soil groups in zone Ⅱ1 |
1986年颁布的《公路自然区划标准》一直沿用至今,对中国公路建设事业的发展起到了一定的推进作用。2008年王彩霞等[27]对东部温润季冻区公路三级自然区划进行了研究,将Ⅱ1区东北东部山地湿润冻区划分为Ⅱ1-a、Ⅱ1-b、Ⅱ1-c及Ⅱ1-d 4个三级区划。该方法是通过数学模型的理论法和相关分析的半经验法相结合确定的分区界限,使区域划分更具客观性。本研究中计算的7个气象站分别位于Ⅱ1-a区(鸡西站)、Ⅱ1-b区(牡丹江站、绥芬河站)、Ⅱ1-c区(本溪站、临江站、延吉站)及Ⅱ1-d区(丹东站)。
本文在此三级区划的基础上,将Ⅱ1区内不同土组的湿度指数进行归并,得到了三级区划路基湿度指数最大值、最小值。具体方法:1)按4类土组进行归并,分别为砂、其他砂类土、粉质土及黏质土;2)归并所得最小值按照各站湿度指数计算值与《公路路基设计规范》推荐最小值二者中的最小值进行选取;3)归并所得最大值按照三级区划内各站湿度指数计算值与规范推荐最大值二者中的最大值进行选取。三级区划补充细化后的Ⅱ1区路基湿度指数推荐取值范围由-8.1~35.1扩大至-16.5~35.1,具体见表 10。
| 表 10 Ⅱ1区不同土组的TMI范围 Tab. 10 TMI range of different soil groups in zone Ⅱ1 |
PE的准确估算是Ⅱ1区路基湿度指数预估的重点也是难点,本文引入FAO-PM法进行Ⅱ1区路基土PE估算,有效解决了Thornthwaite法中负温下PE为零的问题,优化建立了阶段湿度指数计算方法,并补充细化了Ⅱ1区路基湿度指数取值范围,取得了以下主要研究结论:
1) 负温下路基土的PE不为零,其总量可达年蒸发蒸腾总量的9.8%~15.7%,采用FAO-PM法估算Ⅱ1区路基土的PE精度相对更高,但该方法在模拟5、6月份期间的PE突增现象时精度不足,其原因是FAO-PM法忽略昼夜温差而采用平均气温计算PE所引起的低估。负温下路基土PE与平均日照时数、平均风速和平均气温为正相关,与平均相对湿度为负相关;当统计时长扩大至全年时,PE与气象因子相关性不一致,主要归因于平均气温与PE高度正相关,夏季高温使PE显著增加,抵消了平均相对湿度的负相关影响。
2) 通过比较当月储水量与最大储水量、最小储水量之间的大小关系,将路基土各月湿度平衡后的状态简化归纳为有径流、无径流不干旱和无径流干旱3种状态,可根据当月路基土状态计算径流量R和缺水量DF。优化后,在进行湿度平衡计算时,无需考虑无径流蒸发的水分的来源,简化了计算过程。
3)Ⅱ1区不同土组的湿度指数差异明显,自西南向东北由正变负、逐渐减小,取值范围较规范推荐值较宽,扩大后的取值为-16.7~35.1,按照三级区划重新归并路基湿度指数,从地域上进一步细化取值范围,更便于取值。
4) 本文在研究过程中还发现,铺面覆盖效应对路基降雨入渗和蒸发蒸腾能力有较大影响,由于缺乏实测数据支撑,现阶段未将铺面覆盖效应考虑在内。若要从根本上明确铺面覆盖效应的影响规律,则应从室内外试验和仿真模拟等方面进行深入研究。
| [1] |
中华人民共和国交通运输部. 公路自然区划标准: JTJ 003—1986[S]. 北京: 人民交通出版社, 1986 Ministry of Transport of the People's Republic of China. Standard of climatic zoning for highway: JTJ 003—1986[S]. Beijing: China Communications Press, 1986 |
| [2] |
中华人民共和国交通运输部. 公路路基设计规范: JTJ D30—2015[S]. 北京: 人民交通出版社, 2015 Ministry of Transport of the People's Republic of China. Specifications for design of highway subgrade: JTJ D30—2015[S]. Beijing: China Communications Press, 2015 |
| [3] |
THORNTHWAITE C W. An approach toward a rational classification of climate[J]. Geographical Review, 1948, 38(1): 55. DOI:10.2307/210739 |
| [4] |
BHASKAR V V. Hydro-climatic characteristics of hill stations of India[J]. Meteorology & Atmospheric Sciences, 2015, 66(1): 129. DOI:10.1134/S0097807815020098 |
| [5] |
ZAREIA A, AMIN M S R, AMADOR-JIMENEZ L E. Thornthwaite moisture index modeling to estimate the implication of climate change on pavement deterioration[J]. Journal of Transportation Engineering, 2016, 142(4): 04016007. DOI:10.1061/(ASCE)TE.1943-5436.0000840 |
| [6] |
张新时. 植被的PE(可能蒸散)指标与植被-气候分类(二)——几种主要方法与PEP程序介绍[J]. 植物生态学与地植物学学报, 1989, 13(3): 197. CHANG Hsinshih. The potential evapotranspiration (PE) index for vegetation and vegetation-climatic classification (2)—an introduction of main methods and PEP program[J]. Acta Phytoecologica et Geobotanica Sinica, 1989, 13(3): 197. DOI:10.1007/BF02009745 |
| [7] |
李辉东, 关德新, 金昌杰, 等. 森林积雪蒸发测算方法及研究进展[J]. 应用生态学报, 2013, 24(12): 3603. LI Huidong, GUAN Dexin, JIN Changjie, et al. Measurement and estimation methods and research progress of snow evaporation in forests[J]. Chinese Journal of Applied Ecology, 2013, 24(12): 3603. |
| [8] |
CHRISTNER E, KOHLER M, SCHNEIDER M. The influence of snow sublimation and meltwater evaporation on delta D of water vapor in the atmospheric boundary layer of central Europe[J]. Atmospheric Chemistry and Physics, 2017, 17(2): 1207. DOI:10.5194/acp-17-1207-2017 |
| [9] |
冉武平, 李玲. 考虑路面覆盖效应的路基平衡湿度分布及预估[J]. 重庆交通大学学报(自然科学版), 2015, 34(6): 58. RAN Wuping, LI Ling. Distribution and prediction of equilibrium moisture of subgrade considering pavement blanketing effect[J]. Journal of Chongqing Jiaotong University (Natural Science), 2015, 34(6): 58. DOI:10.3969/j.issn.1674-0696.2015.06.11 |
| [10] |
杨倩. 东北地区积雪时空分布及其融雪径流模拟[D]. 长春: 吉林大学, 2015 YANG Qian. Study on spatio-temporal distribution of snow cover in northeast China and its simulation on snowmelt runoff[D]. Changchun: Jilin University, 2015 |
| [11] |
徐俊增, 彭世彰, 丁加丽, 等. 基于蒸渗仪实测数据的日参考作物蒸发腾发量计算方法评价[J]. 水利学报, 2010, 41(12): 1497. XU Junzeng, PENG Shizhang, DING Jiali, et al. Evaluation of methods for estimation daily reference crop evapotranspiration based on lysimeter grass experiments[J]. Journal of Hydraulic Engineering, 2010, 41(12): 1497. DOI:10.13243/j.cnki.slxb.2010.12.016 |
| [12] |
冯克鹏, 田军仓. Hargreaves公式计算宁夏地区参考作物腾发量的研究[J]. 干旱区资源与环境, 2014, 28(9): 100. FENG Kepeng, TIAN Juncang. Estimation of evapotranspiration in Ningxia by Hargreaves equation[J]. Journal of Arid Land Resources and Environment, 2014, 28(9): 100. DOI:10.13448/j.cnki.jalre.2014.09.026 |
| [13] |
MCKEEN R G, JOHNSON L D. Climate-controlled soil design parameters for mat foundations[J]. Journal of Geotechnical Engineering, 1990, 116(7): 1073. DOI:10.1061/(ASCE)0733-9410(1990)116:7(1073) |
| [14] |
孙亮, 陈仲新. 应用Penman-Monteith公式和土壤湿度指数估算区域地表蒸散[J]. 农业工程学报, 2013, 29(10): 101. SUN Liang, CHEN Zhongxin. Estimation of regional evapotranspiration based on Penman-Monteith equation and soil moisture index[J]. Transactions of the Chinese Society of Agricultural Engineering, 2013, 29(10): 101. |
| [15] |
ZHAO Liwen, ZHAO Wenzhi. Evapotranspiration of an oasis-desert transition zone in the middle stream of Heihe River, Northwest China[J]. Journal of Arid Land, 2014, 6(5): 529. DOI:10.1007/s40333-014-0061-1 |
| [16] |
张海娜, 侯依玲, 赵春雨, 等. CCSM4模式对东北气温和降水的模拟及预估[J]. 气象与环境学报, 2019, 35(1): 72. ZHANG Haina, HOU Yiling, ZHAO Chunyu, et al. Simulation and projection of temperature and precipitation by CCSM4 model in Northeast China[J]. Journal of Meteorology and Environment, 2019, 35(1): 72. DOI:10.3969/j.issn.1673-503X.2019.01.010 |
| [17] |
曹长伟. 路基湿度状况及模量调整系数研究[D]. 上海: 同济大学, 2007 CAO Changwei. Study on humidity condition and modulus adjustment factor for subgrade[D]. Shanghai: Tongji University, 2007 |
| [18] |
MASON M. Guide for mechanistic-empirical design of new and rehabilitated pavement structures: NCHRP 1-37A[J]. Washington DC: Transportation Research Board, 2004. |
| [19] |
李聪, 凌建明, 官盛飞. 基于路基湿度预估的综合湿度指数[J]. 同济大学学报(自然科学版), 2012, 40(11): 1672. LI Cong, LING Jianming, GUAN Shengfei. Prediction-based subgrade moisture Thornthwaite moisture index[J]. Journal of Tongji University (Natural Science), 2012, 40(11): 1672. |
| [20] |
王书娟, 陈志国, 秦绪喜, 等. 季节性冻土地区公路路基冻融过程实时监测分析[J]. 路基工程, 2015(1): 39. WANG Shujuan, CHEN Zhiguo, QIN Xuxi, et al. Analysis on real-time monitoring for freezing and thawing process of highway subgrade in seasonal frozen soil area[J]. Subgrade Engineering, 2015(1): 39. DOI:10.13379/j.issn.1003-8825.2015.01.09 |
| [21] |
周健民. 土壤学大辞典[M]. 北京: 科学出版社, 2013. ZHOU Jianmin. Dictionary of soil science[M]. Beijing: Science Press, 2013. |
| [22] |
TIAN S, TREGONING P, RENZULLO L J, et al. Improved water balance component estimates through joint assimilation of GRACE water storage and SMOS soil moisture retrievals[J]. Water Resources Research, 2017, 53(3): 1820. DOI:10.1002/2016WR019641 |
| [23] |
李迪强, 孙成永, 张新时. 中国潜在植被生产力的分布与模拟[J]. 植物学报, 1998(6): 77. LI Diqiang, SUN Chengyong, ZHANG Xinshi. Modeling the net primary productivity of the natural potential vegetation in China[J]. Journal of Integrative Plant Biology, 1998(6): 77. DOI:10.3321/j.issn:1672-9072.1998.06.013 |
| [24] |
JAVID A H, BULUT R. Evaluating equilibrium matric suctions under pavement system based on Thornthwaite moisture index (TMI)[C]//International Airfield and Highway Pavements Conference 2019: Testing and Characterization of Pavement Materials. Chicago: American Society of Civil Engineers, 2019: 511
|
| [25] |
ZAREIE A, AMIN M S R, AMADOR-JIMENEZ L E. Thornthwaite moisture index modeling to estimate the implication of climate change on pavement deterioration[J]. Journal of Transportation Engineering, 2016, 142(4): 04016007. DOI:10.1061/(ASCE)TE.1943-5436.0000840 |
| [26] |
邹维列, 李聪, 汪建峰, 等. 非饱和路堤对加载和降雨入渗响应的模型试验研究[J]. 岩土工程学报, 2009, 31(10): 1512. ZOU Weilie, LI Cong, WANG Jianfeng, et al. Model tests on responses of unsaturated road-embankments to loading and rainfall infiltration[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(10): 1512. DOI:10.3321/j.issn:1000-4548.2009.10.006 |
| [27] |
王彩霞, 马兆有, 冯德成, 等. 东部温润季冻区公路三级自然区划方法[J]. 哈尔滨工业大学学报, 2008, 40(2): 250. WANG Caixia, MA Zhaoyou, FENG Decheng, et al. Method of the third rank division of highway in east seasonal frost region[J]. Journal of Harbin Institute of Technology, 2008, 40(2): 250. DOI:10.3321/j.issn:0367-6234.2008.02.019 |
 2021, Vol. 53
2021, Vol. 53


