2. 牵引动力国家重点实验室(西南交通大学),成都 610036
2. State Key Laboratory of Traction Power (Southwest Jiaotong University), Chengdu 610036, China
轮轨关系是列车-轨道-桥梁动力相互作用研究中的重要部分,直接受到轮轨界面激励的影响。从不平顺的角度来看,影响轮轨关系的因素包括轨道几何不平顺以及轨道刚度不平顺[1]。轮轨几何不平顺对车轨桥系统的影响经过多年研究已经相对清晰,但是目前对轨道刚度不平顺的关注较少。
轨道刚度不平顺这一概念首先在翟婉明院士的专著《车辆-轨道耦合动力学》[1]中以“动力型轨道刚度不平顺”的概念被提出,根据形成原因不同可分为两类:1)常规型轨道刚度不平顺,主要由扣件间距、轨道板长度等结构周期性分布所引起的轨道刚度变化。这种刚度不平顺主要表现为周期性激励,严重时可能导致列车零件或轨下结构共振,危害系统稳定;2)缺陷型轨道刚度不平顺,主要由轨下结构劣化导致,比如扣件失效、轨枕空吊、无砟轨道层间脱空等,这种不平顺会引起列车通过时轨下结构脱空或局部畸变,导致轮轨冲击,加剧轨下结构损伤并大幅度恶化结构稳定性,更可能威胁列车安全平稳运行[2]。
目前关于缺陷型轨道刚度不平顺对系统的影响已有一些研究。比如在轨枕空吊方面,文献[3]考虑货车非线性因素,建立了重载货车-轨道耦合动力学模型,研究了重载货车通过轨枕空吊时的动态特性;在过渡段方面,文献[4]基于车辆-线路相互作用理论,研究了高速铁路路桥过渡段对列车动态特性的影响规律,研究表明该区域对列车运行性能有较大影响;在无砟轨道层间损伤方面,文献[5]针对CRTS III板式轨道,建立了考虑层间离缝的列车-轨道耦合动力学模型,研究了离缝尺寸对系统的影响;文献[6-7]也针对缺陷型轨道刚度不平顺对系统的影响开展了研究。相比之下,目前关于常规型轨道刚度不平顺的研究较少,只有部分学者研究了桥梁跨径引起的车桥系统共振[8-9],本文作者也曾考虑桥墩沉降及桥跨长度的影响,研究了系统力学行为随轨道刚度的变化[2, 10],另外,既有研究表明轨道模型的精细程度对刚度不平顺的仿真有较大影响[11],目前无砟轨道建模主要存在如下问题:1)轨道的结构弹性未充分考虑,既有研究大多考虑了钢轨、轨道板等结构的弯曲变形,但是对其结构自身的弹性压缩变形考虑的并不完善;2)填充层大多模拟为弹簧,以至于其参振质量未能充分考虑。这些简化均可能导致对轨道刚度不平顺的研究存在一定的误差。
针对常规型和缺陷型两种轨道刚度不平顺,首先建立考虑结构弹性的轨道模型,提出轨道刚度不平顺的计算方法,并基于列车-轨道-桥梁动力相互作用理论建立高速车轨桥耦合动力学模型,从时域和频域角度研究两种刚度不平顺对系统的影响。
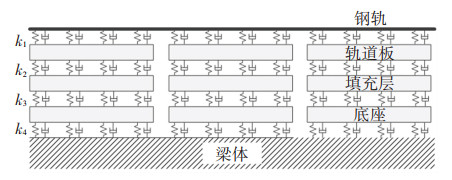
1 轨道刚度不平顺的解析表达以中国高速铁路最常用的板式无砟轨道为例进行轨道刚度不平顺的解析推导。图 1为考虑结构弹性的板式轨道模型,图中k1为扣件刚度、k2为轨道板结构弹性压缩所等效的弹簧刚度、k3为填充层结构弹性所等效的弹簧刚度、k4为底座板结构弹性压缩所等效的弹簧与桥轨关系的联合刚度。其中根据结构自身弹性等效弹簧刚度的计算流程为:1)对结构顶部施加大小为F的竖向力;2)根据材料力学中结构拉伸效应可知上述力引起的结构变形为Fh0/(E0A0),其中h0为结构原始高度,E0为结构弹性模量,A0为结构底面积;3)将结构弹性等效为刚度为K0的弹簧,该弹簧在荷载F作用下的变形为F/K0;4)根据等效原理,第2步和第3步中得到的变形应相等,因此可得到结构自身弹性的等效刚度为K0=E0A0/h0;5)理论分析中常需要将结构弹性的等效为多个弹簧,则每个弹簧的刚度为K0/n0,其中n0为弹簧数量。
|
图 1 考虑结构弹性的板式轨道模型 Fig. 1 Slab track model considering structural elasticity |
借助上述模型,在钢轨上某一位置xF施加一恒载F,并计算该荷载下的钢轨变形,即可得到该位置轨道刚度K(xF)。
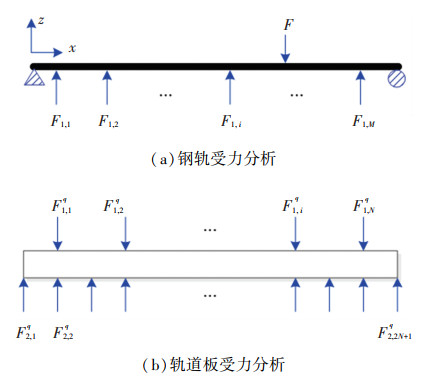
钢轨模拟为长度为lr的简支梁,其受到上部载荷F及下部弹簧力的作用,如图 2(a)所示。其中F1, i为第i个扣件力,M为轨下扣件数,坐标原点位于梁最左端。需要说明的是,钢轨两端实际并非简支约束,但是根据文献[1]的研究:钢轨两端采用不同约束主要影响3个扣件长度范围内的钢轨力学行为,若钢轨的计算长度足够长,则可以用简支梁近似模拟。本研究中钢轨计算长度为130 m,远大于3个扣件长度,因此可采用简支梁近似模拟钢轨。
|
图 2 轨道结构受力分析 Fig. 2 Forces applied on track structures |
钢轨变形zr由两部分叠加而成,即由上部载荷F引起的变形zr1和下部弹簧引起的变形zr2组成。根据简支梁挠度方程可以得到:
| $ z_{\mathrm{r} 1, i}=\left\{\begin{array}{l} \frac{F x_{\mathrm{r}, i}\left(l_{\mathrm{r}}-x_{F}\right)}{6 E_{\mathrm{r}} I_{\mathrm{r}} l_{\mathrm{r}}}\left(2 l_{\mathrm{r}} x_{F}-x_{F}^{2}-x_{\mathrm{r}, i}^{2}\right), i \leqslant P \\ \frac{F\left(l_{\mathrm{r}}-x_{F}\right)}{6 E_{\mathrm{r}} I_{\mathrm{r}} l_{\mathrm{r}}}\left[\frac{l_{\mathrm{r}}}{l_{\mathrm{r}}-x_{F}}\left(x_{\mathrm{r}, i}-x_{F}\right)^{3}-\right. \\ \ \ \ \ \ \left.\left(2 l_{\mathrm{r}} x_{F}-x_{F}^{2}\right) x_{\mathrm{r}, i}-x_{\mathrm{r}, i}^{3}\right], P<i \leqslant M \end{array}\right. $ | (1) |
| $ \begin{aligned} z_{\mathrm{r} 2, i}=& \sum\limits_{j=1}^{i} \frac{F_{1, j}\left(l_{\mathrm{r}}-x_{\mathrm{r}, j}\right)}{6 E_{\mathrm{r}} I_{\mathrm{r}} l_{\mathrm{r}}}\left[\frac{l_{\mathrm{r}}}{l_{\mathrm{r}}-x_{\mathrm{r}, j}}\left(x_{\mathrm{r}, i}-x_{\mathrm{r}, j}\right)^{3}-\right.\\ &\left.\left(2 l_{\mathrm{r}} x_{\mathrm{r}, j}-x_{\mathrm{r}, j}^{2}\right) x_{\mathrm{r}, i}-x_{\mathrm{r}, i}^{3}\right]+\\ & \sum\limits_{j=i+1}^{M} \frac{F_{1, j} x_{\mathrm{r}, i}\left(l_{\mathrm{r}}-x_{\mathrm{r}, j}\right)}{6 E_{\mathrm{r}} I_{\mathrm{r}} l_{\mathrm{r}}}\left(2 l_{\mathrm{r}} x_{\mathrm{r}, j}-x_{\mathrm{r}, j}^{2}-x_{\mathrm{r}, i}^{2}\right) \end{aligned} $ | (2) |
其中:zr1, i为由F引起的第i个扣件位置处钢轨变形,zr2, i为由弹簧力引起的第i个扣件位置处钢轨变形,F1, i为第i个弹簧力,xF为力F的坐标,P为坐标[0, xF]内的扣件数,M为计算长度内的轨下扣件总数,xr, i为第i个扣件的坐标,Er和Ir分别为钢轨的弹性模量和惯量。
因此,第i个扣件位置处的钢轨总变形为
| $ z_{\mathrm{r}, i}=z_{\mathrm{r} 1, i}+z_{\mathrm{r} 2, i} $ | (3) |
将其表示为矩阵形式:
| $ \boldsymbol{Z}_{\mathrm{r}}=\boldsymbol{R} \cdot F+\boldsymbol{A} \cdot \boldsymbol{F}_{1} $ | (4) |
式中R和A为关系矩阵,其表达式为
| $ \boldsymbol{R}=\left[\begin{array}{llllll} R_{1} & R_{2} & \cdots & R_{i} & \cdots & R_{M} \end{array}\right]^{\mathrm{T}} $ | (5) |
| $ \boldsymbol{A}=\left[\begin{array}{cccccc} A_{1,1} & A_{1,2} & \cdots & A_{1, j} & \cdots & A_{1, M} \\ A_{2,1} & A_{2,2} & \cdots & A_{2, j} & \cdots & A_{2, M} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ A_{i, 1} & A_{i, 2} & \cdots & A_{i, j} & \cdots & A_{i, M} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ A_{M, 1} & A_{M, 2} & \cdots & A_{M, j} & \cdots & A_{M, M} \end{array}\right] $ | (6) |
其中:
| $ R_{i}=\left\{\begin{array}{l} \frac{x_{\mathrm{r}, i}\left(l_{\mathrm{r}}-x_{F}\right)}{6 E_{\mathrm{r}} I_{\mathrm{r}} l_{\mathrm{r}}}\left(2 l_{\mathrm{r}} x_{F}-x_{F}^{2}-x_{\mathrm{r}, i}^{2}\right), \quad i \leqslant P \\ \frac{l_{\mathrm{r}}-x_{F}}{6 E_{\mathrm{r}} I_{\mathrm{r}} l_{\mathrm{r}}}\left[\frac{l_{\mathrm{r}}}{l_{\mathrm{r}}-x_{F}}\left(x_{\mathrm{r}, i}-x_{F}\right)^{3}-\left(2 l_{\mathrm{r}} x_{F}-\right.\right. \\ \ \ \ \ \ \ \left.\left.x_{F}^{2}\right) x_{\mathrm{r}, i}-x_{\mathrm{r}, i}^{3}\right], P<i \leqslant M \end{array}\right. $ | (7) |
| $ A_{i, j}=\left\{\begin{array}{l} \frac{l_{\mathrm{r}}-x_{\mathrm{r}, j}}{6 E_{\mathrm{r}} I_{\mathrm{r}} l_{\mathrm{r}}}\left[\frac{l_{\mathrm{r}}}{l_{\mathrm{r}}-x_{\mathrm{r}, j}}\left(x_{\mathrm{r}, i}-x_{\mathrm{r}, j}\right)^{3}-\left(2 l_{\mathrm{r}} x_{\mathrm{r}, j}-\right.\right. \\ \ \ \ \ \ \ \left.\left.x_{\mathrm{r}, j}^{2}\right) x_{\mathrm{r}, i}-x_{\mathrm{r}, i}^{3}\right], i \geqslant j \\ \frac{x_{\mathrm{r}, i}\left(l_{\mathrm{r}}-x_{\mathrm{r}, j}\right)}{6 E_{\mathrm{r}} I_{\mathrm{r}} l_{\mathrm{r}}}\left(2 l_{\mathrm{r}} x_{\mathrm{r}, j}-x_{\mathrm{r}, j}^{2}-x_{\mathrm{r}, i}^{2}\right), i<j \end{array}\right. $ | (8) |
轨道板受力情况如图 2(b)所示,图中上标q代表第q块轨道板,F1, iq和F2, jq分别表示第q块轨道板上第i个扣件力和板下第j个砂浆力。既有研究大多将轨道板模拟为弹性支撑的自由梁进行求解[1],但是该求解过程较为复杂。相对而言,简支梁的求解技术较为完善与便捷,因此本文将自由梁考虑为整体可发生刚性位移的简支梁模型,即两端支撑点可以竖向移动的简支梁结构,该方法的具体推导过程可以参考文献[10]。
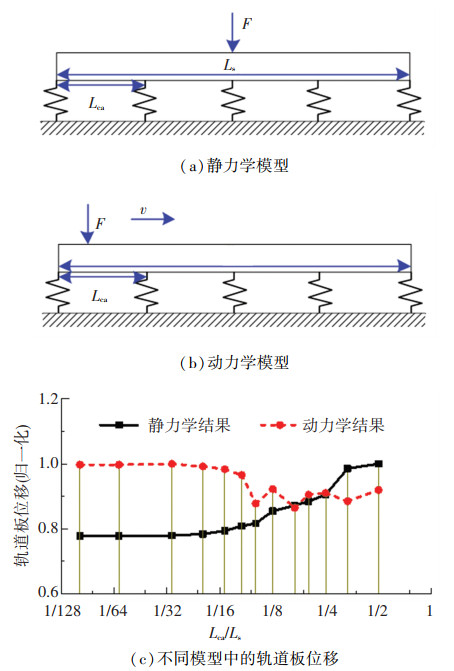
另外,轨道板下面为砂浆连续支撑,而既有研究为了便于计算则将连续支撑的砂浆模拟为离散砂浆弹簧[11],但是如何确定合适的砂浆弹簧间距则成为了影响研究结果精度的一个关键问题。针对该问题,本文建立了两个简单模型(图 3(a)、3(b)),从静力学和动力学的角度研究砂浆弹簧间距对计算结果的影响,如图 3(c)所示。静力学模型中将一集中力作用于轨道板中间位置;动力学模型则将一恒定载荷以速度v匀速通过轨道板。Ls和Lca分别表示轨道板长度以及砂浆离散弹簧间距,因此横坐标(Lca/Ls)即代表砂浆弹簧间距与轨道板长度的比值;所提取的观测指标为轨道板中间位置处的竖向位移;纵坐标为归一化处理后的轨道板位移,即将各工况下的轨道板位移除以所有工况下的最大计算值。
|
图 3 砂浆离散弹簧间距对轨道板位移的影响 Fig. 3 Influence of distance between mortar springs on slab displacement |
由图 3可以清楚看出,Lca和Ls的比值越小,计算结果越收敛、越准确;而随着Lca/Ls的增大,静力学和动力学计算结果均出现不同程度的发散;综合考虑计算效率和计算精度,建议Lca/Ls不大于1/15,即离散后的砂浆弹簧间距不应大于板长的1/15。
在确定了砂浆弹簧数量之后,即可根据上文中的等效弹簧刚度计算方法确定砂浆弹簧的刚度。
采用上述方法,轨道板位移以矩阵形式表示为
| $ \boldsymbol{Z}_{\mathrm{s}}=\boldsymbol{B} \cdot \boldsymbol{F}_{1}+\boldsymbol{C} \cdot \boldsymbol{F}_{2} $ | (9) |
其中:
| $ \boldsymbol{B}=\left[\begin{array}{c} \boldsymbol{B}^{1} & & & & & {{\bf{0}}} \\ & \boldsymbol{B}^{2} & & & & \\ & & \ddots & & & \\ & & & \boldsymbol{B}^{q} & & \\ & & & & \ddots & \\ {{\bf{0}}} & & & & & \boldsymbol{B}^{Q} \end{array}\right] $ | (10) |
| $ \boldsymbol{C}=\left[\begin{array}{c} \boldsymbol{C}^{1} & & & & & {{\bf{0}}} \\ & \boldsymbol{C}^{2} & & & & \\ & & \ddots & & & \\ & & & \boldsymbol{C}^{q} & & \\ & & & & \ddots & \\ {{\bf{0}}} & & & & & \boldsymbol{C}^{Q} \end{array}\right] $ | (11) |
| $ \boldsymbol{B}^{q}=\left[\begin{array}{c} \boldsymbol{B}_{1}^{q} \\ \boldsymbol{B}_{j}^{q} \\ \boldsymbol{B}_{2 N+1}^{q} \end{array}\right]=\left[\begin{array}{c} {\left[{\omega}_{1, j}^{b}\right]} \\ {\left[{\omega}_{i, j}^{b}\right]} \\ {\left[{\omega}_{2 N+1, j}^{b}\right]} \end{array}\right] $ | (12) |
| $ \boldsymbol{C}^{q}=\left[\begin{array}{c} \boldsymbol{C}_{1}^{q} \\ \boldsymbol{C}_{j}^{q} \\ \boldsymbol{C}_{2 N+1}^{q} \end{array}\right]=\left[\begin{array}{c} {\left[{\omega}_{1, j}^{c}\right]} \\ {\left[{\omega}_{i, j}^{c}\right]} \\ {\left[{\omega}_{2 N+1, j}^{c}\right]} \end{array}\right] $ | (13) |
| $ \left\{\begin{aligned} &\omega_{1, j}^{b}=\frac{2 N-2 j+1}{2 N k_{2}} \\ &\omega_{2 N+1, j}^{b}=\frac{2 j-1}{2 N k_{2}} \\ &\omega_{i, j}^{b}=\omega_{i, j}+\frac{2-(i-1) l_{\mathrm{f}} l_{\mathrm{s}}}{2} \cdot \omega_{1, j}^{b}+\frac{(i-1) l_{\mathrm{f}} l_{\mathrm{s}}}{2} \cdot \omega_{2 v+1, j}^{b} \\ &{\omega}_{1, j}^{c}=\left\{\begin{array}{l} 0, j=1,2 N+1 \\ -\frac{2 N+j-1}{2 N k_{2}}, j=2, \cdots, 2 N \end{array}\right. \\ &{\omega}_{2 N+1, j}^{c}=\left\{\begin{array}{l} 0, j=1,2 N+1 \\ -\frac{j-1}{2 N k_{2}}, j=2, \cdots, 2 N \end{array}\right. \\ &\omega_{i, j}^{c}=\omega_{i, j}+\frac{2-(i-1) l_{\mathrm{f}} l_{\mathrm{s}}}{2} \cdot \omega_{1, j}^{c}+\frac{(i-1) l_{\mathrm{f}} l_{\mathrm{s}}}{2} \cdot \omega_{2 N+1, j}^{c} \end{aligned}\right. $ | (14) |
式中:B和C为关系矩阵;F1和F2为扣件力和砂浆力向量;Q为轨道板数;N为每块轨道板上的扣件数;砂浆离散弹簧间距设为扣件间距的一半,按照本文计算参数(见第3节),此时Lca/Ls约为1/18,满足Lca/Ls不大于1/15的精度要求,因此每块轨道板下的砂浆弹簧个数为2N+1;ωi, jb和ωi, jc分别为矩阵B和C中的元素;k2为砂浆弹簧刚度;lf和ls分别为扣件间距与单块轨道板长度。
同理,填充层和底座板也可以用上述方法进行表示,因此板式轨道各层结构的变形可以用以下矩阵形式表示:
| $ \left\{\begin{array}{l} \boldsymbol{Z}_{\mathrm{r}}=\boldsymbol{R} \cdot \boldsymbol{F}+\boldsymbol{A} \cdot \boldsymbol{F}_{1} \\ \boldsymbol{Z}_{\mathrm{s}}=\boldsymbol{B} \cdot \boldsymbol{F}_{1}+\boldsymbol{C} \cdot \boldsymbol{F}_{2} \\ \boldsymbol{Z}_{\mathrm{f}}=\boldsymbol{D} \cdot \boldsymbol{F}_{2}+\boldsymbol{G} \cdot \boldsymbol{F}_{3} \\ \boldsymbol{Z}_{\mathrm{b}}=\boldsymbol{H} \cdot \boldsymbol{F}_{3}+\boldsymbol{J} \cdot \boldsymbol{F}_{4} \end{array}\right. $ | (15) |
式中:Zr、Zs、Zf、Zb分别为钢轨、轨道板、砂浆填充层以及底座的变形向量;F1、F2、F3、F4分别为图 1中轨道各层间弹簧力向量,表示为
| $ \left\{\begin{array}{l} \boldsymbol{F}_{1}=k_{1}\left(\boldsymbol{Z}_{\mathrm{r}}-\boldsymbol{Z}_{\mathrm{s}}\right) \\ \boldsymbol{F}_{2}=k_{2}\left(\boldsymbol{Z}_{\mathrm{s}}-\boldsymbol{Z}_{\mathrm{f}}\right) \\ \boldsymbol{F}_{3}=k_{3}\left(\boldsymbol{Z}_{\mathrm{f}}-\boldsymbol{Z}_{\mathrm{b}}\right) \\ \boldsymbol{F}_{4}=k_{4} \boldsymbol{Z}_{\mathrm{b}} \end{array}\right. $ | (16) |
联立求解式(15)、(16),轨道各层弹簧力及层间结构变形可以分别表示为
| $ \left[\begin{array}{c} \boldsymbol{F}_{1} \\ \boldsymbol{F}_{2} \\ \boldsymbol{F}_{3} \\ \boldsymbol{F}_{4} \end{array}\right]=\boldsymbol{T}^{-1}\left[\begin{array}{c} -k_{1} \boldsymbol{R} F \\ {\bf{0}} \\ {\bf{0}} \\ {\bf{0}} \end{array}\right] $ | (17) |
| $ \left[\begin{array}{c} \boldsymbol{Z}_{\mathrm{r}} \\ \boldsymbol{Z}_{\mathrm{s}} \\ \boldsymbol{Z}_{\mathrm{f}} \\ \boldsymbol{Z}_{\mathrm{b}} \end{array}\right]=\boldsymbol{S}^{-1}\left[\begin{array}{c} -\boldsymbol{R} F \\ {\bf{0}} \\ {\bf{0}} \\ {\bf{0}} \end{array}\right] $ | (18) |
其中:
| $ \boldsymbol{T}=\left[\begin{array}{cccc} k_{1} \boldsymbol{A}-k_{1} \boldsymbol{B}-1 & -k_{1} \boldsymbol{C} & {\bf{0}} & {\bf{0}} \\ k_{2} \boldsymbol{B} & k_{2} \boldsymbol{C}-k_{2} \boldsymbol{D}-1 & -k_{2} \boldsymbol{G} & {\bf{0}} \\ {\bf{0}} & k_{3} \boldsymbol{D} & k_{3} \boldsymbol{G}-k_{3} \boldsymbol{H}-1 & -k_{3} \boldsymbol{J} \\ {\bf{0}} & {\bf{0}} & k_{4} \boldsymbol{H} & k_{4} \boldsymbol{J} \end{array}\right] $ | (19) |
| $ \boldsymbol{S}=\left[\begin{array}{cccc} \boldsymbol{A} k_{1}-1 & -\boldsymbol{A} k_{1} & {\bf{0}} & {\bf{0}} \\ \boldsymbol{B} k_{1} & -\boldsymbol{B} k_{1}+\boldsymbol{C} k_{2}-1 & -\boldsymbol{C} k_{2} & {\bf{0}} \\ {\bf{0}} & \boldsymbol{D} k_{2} & -\boldsymbol{D} k_{2}+\boldsymbol{G} k_{3}-1 & -\boldsymbol{G} k_{3} \\ {\bf{0}} & {\bf{0}} & \boldsymbol{H} k_{3} & -\boldsymbol{H} k_{3}+\boldsymbol{J} k_{4}-1 \end{array}\right] $ | (20) |
通过式(17)~(20)即可得到载荷F作用位置处的钢轨位移Zr(xF),因此该位置处的轨道刚度可以表示为
| $ \boldsymbol{K}\left(x_{F}\right)=\frac{F}{\boldsymbol{Z}_{\mathrm{r}}\left(x_{F}\right)} $ | (21) |
将所有位置处的轨道刚度沿纵向排列即可得到轨道刚度不平顺。
需要说明的是,上述表达式可以直接用来描述常规型轨道刚度不平顺,如果要模拟缺陷型刚度不平顺,则要改变缺陷位置的弹簧刚度并进行计算。
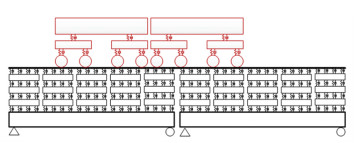
2 高速列车-轨道-桥梁动力学模型高速列车-板式轨道-桥梁动力学模型见图 4,该模型包括列车子模型、轨道子模型以及桥梁子模型。列车子模型由一系列等距离放置的车辆模型构成,每节车辆由7个刚体组成:1个车体、两个构架以及4个轮对,每个刚体考虑伸缩、沉浮、横移、摇头及侧滚等5个自由度。钢轨采用连续欧拉梁进行模拟,扣件考虑为离散支撑弹簧-阻尼元件,轨道板等结构考虑为自由梁。桥梁子结构采用有限元法进行模拟。模型的具体推导过程和求解方法见文献[1, 12-13]。该模型也经过了现场试验验证,试验相关内容及验证结果见文献[2, 13]。
|
图 4 高速列车-板式轨道-桥梁动力学模型 Fig. 4 High-speed train-track-bridge dynamic model |
本节针对常规型轨道刚度不平顺,从时域和频域角度研究其对车轨桥系统动态特性的影响。研究中选择CRH380B、CRTS I板式轨道以及32 m简支箱梁作为研究对象。
列车关键参数:车体、构架、轮对质量分别为38.8、2.9、1.5 t;车体、构架惯量分别为1 905、1.293 t·m2;轴距为2.5 m;定距为17.375 m;车轮半径为0.46 m;一系、二系悬挂刚度分别为0.886 5、0.195 MN/m。
轨道动力学参数如下:计算长度为130 m;扣件间距为0.63 m;扣件刚度为30 kN/m;轨道板混凝土为C60;轨道板长、宽、厚分别为5.6、2.4、0.19 m;砂浆弹性模量为100~300 MPa;底座混凝土为C40。桥梁参数见文献[14]。
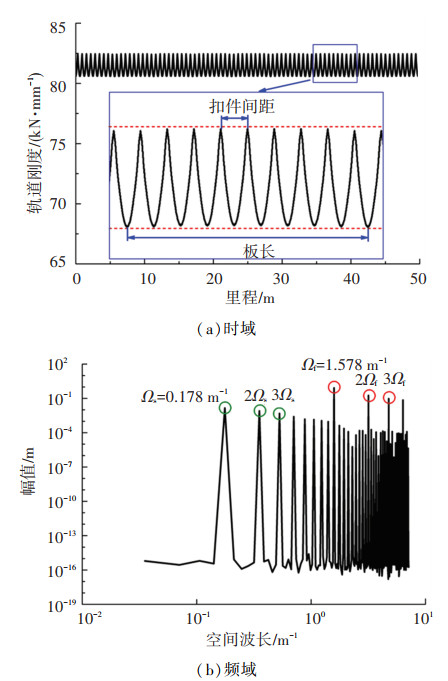
3.1 常规型轨道刚度不平顺特征研究CRTS I型板式无砟轨道的刚度不平顺如图 5所示。从图 5(a)的时域结果中可以清晰看出,轨道刚度不平顺包括两个周期成分,分别为扣件间距所引起的波动以及由轨道板长度所引起的波动。相比而言,由扣件间距所引起的轨道刚度变化(变化幅值约为1.5 kN/mm)要远大于板长所引起的刚度变化。
图 5(b)进一步从频域角度给出了轨道刚度不平顺的特征,从中可以看到规律的空间频率。其中空间频率的主频为1.587 m-1,这是由扣件间距(0.63 m)所引起的。同时,在该频率的倍频处也出现了明显的峰值,证明了扣件间距对刚度不平顺的影响是极大的。另外,在0.178 m-1处也出现了一个峰值,该空间频率是由轨道板长所引起的,在其倍频处仍然出现了一系列的峰值。需要说明的是,虽然扣件间距所引起的频率处的幅值较大,但是其频率成分相比板长引起的频率则少了很多,也就是说板长所引起的基频及其倍频的频带较宽。
|
图 5 CRTS I型板式无砟轨道的刚度不平顺 Fig. 5 Track stiffness irregularity of CRTS I track |
经过大量计算后发现,常规型轨道刚度不平顺对桥梁的振动影响较小,因此着重探讨刚度不平顺对桥上列车和轨道振动的影响。
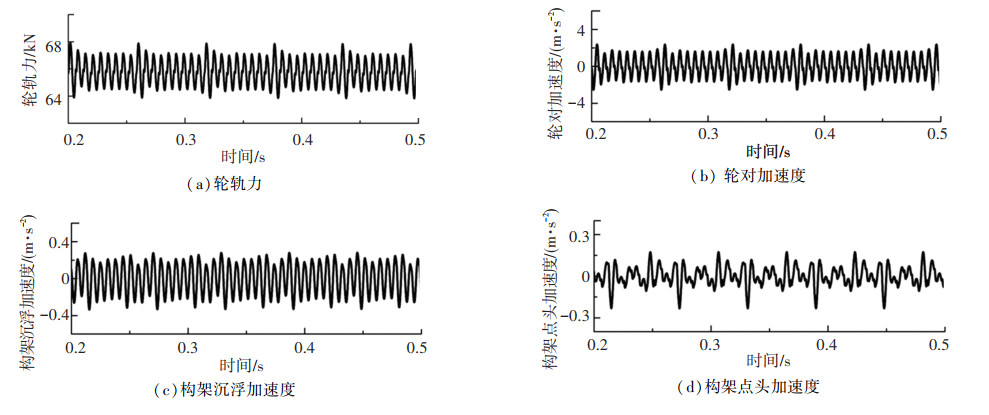
当列车以350 km/h的速度运行时,车辆振动如图 6所示。从图 6中可以看出,轮轨力、轮对加速度、构架加速度均呈现出了规律性,且扣件间距和板长的规律性分布均明显地呈现出来。对于轮轨力、轮对加速度以及构架沉浮加速度来说,波形较为一致,均为固定间距的小幅振动后出现一次幅值较大的波动,其分别显现出了扣件间距和板长的影响。但是对于构架点头加速度,其振动情况有较大不同,在每通过一个板长间距内,构架出现一次点头的振动,但是扣件间距并不能很明确地反映在点头振动中。另外,从幅值的角度来看,轨道刚度不平顺对构架点头运动影响较大,这是由于列车在运行的时候,转向架会周期地运行在两块轨道板上,即同一转向架前后轮的支撑刚度不同,导致点头振动会明显受到板长的影响。
|
图 6 轨道刚度不平顺对列车振动的影响 Fig. 6 Influence of track stiffness irregularity on train vibrations |
更进一步,图 7给出了上述列车振动的频域特性。从该结果中也能看出轮轨力、轮对加速度、构架沉浮加速度的频率分布较为一致,均在154 Hz处出现峰值,该频率即列车350 km/h速度通过0.63 m扣件间距时所产生的激励频率。在此基础上,该频率的倍频成分处(309、463 Hz等)均出现了明显的振动增大。而对于构架点头加速度来说,除了扣件间距引起的振动频率外,由板长引起的频率极大地出现在该结果中,列车通过每块板时受到的激励为17.44 Hz,该频率的多阶倍频均大幅度影响了构架点头振动,且该频率对振动的贡献要高于扣件间距导致的周期激励。表明即使板长导致的刚度不平顺幅值远低于扣件间距导致的刚度变化,但是其引起的系统振动不可忽略,尤其是对于车辆的点头运动。

|
图 7 列车振动的频域特性 Fig. 7 Vibrations of train in frequency domain |
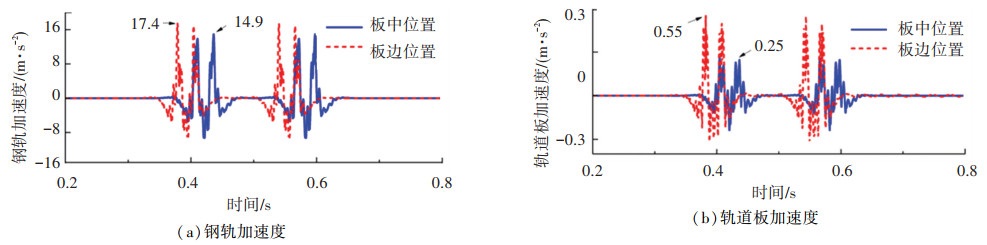
不同位置处轨道动态特性见图 8。从中可以看出,在考虑轨道结构弹性的情况下,轨道板中部及边缘位置处的钢轨和轨道板振动具有较大不同,板边位置处由于其自由边的力学特性而振动较大,两位置处钢轨加速度幅值比为1.17,而轨道板的加速度比值则达到了2.2,从而更加说明详细考虑轨道结构才能更准确反应系统的振动。
|
图 8 不同位置处的轨道振动 Fig. 8 Track vibrations at different locations |
另外,图 9更进一步给出了考虑与不考虑轨道结构弹性时的轨道系统振动。从图 9中可以看出,考虑了轨道结构弹性后,钢轨的振动没有明显变化,但是轨道板的振动差别较为明显,特别是从频域结果中可以看出,考虑了结构弹性后在几乎全频段都与不考虑结构弹性有所区别,这说明考虑结构自身弹性的重要性。

|
图 9 考虑与不考虑轨道结构弹性时的轨道振动 Fig. 9 Track vibrations with or without structural elasticity |
诸多轨道损伤均会产生缺陷型轨道刚度不平顺,本节选取扣件失效这种缺陷型轨道刚度不平顺为例开展研究。
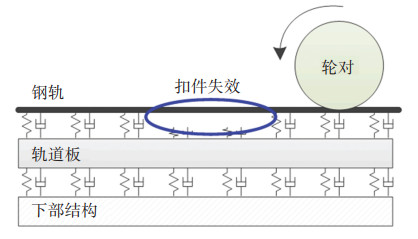
扣件失效是指扣件作为联结钢轨和轨道板的重要结构失去了其工作效能,具体表现一般为断裂或疲劳失效。该现象一般从表面上很难看出,但是当列车通过时会产生明显的轨道变形及轮轨冲击现象(见图 10)。从力学角度来看,扣件失效可视为该位置处扣件弹簧刚度为0。
|
图 10 扣件失效模型 Fig. 10 Model of fastener failure |
为研究扣件失效对高速轮轨系统动力学性能的影响,分析不同失效扣件数量及不同运行速度下系统的动力特性。根据高速铁路的实际运营状况,设定分析的运行速度为200~350 km/h,失效扣件集中分布在轨道某一区段,扣件失效数量0~3个。
图 11反映了高速车辆以350 km/h速度运行时扣件失效对轮轨垂向力和钢轨位移的影响,可以看出,扣件失效区段的轮轨作用力和钢轨位移明显增大,轮轨垂向力甚至接近了170 kN的标准限值。

|
图 11 列车以350 km/h速度运行时扣件失效对系统的影响 Fig. 11 Influence of fastener failure on system with train operation speed of 350 km/h |
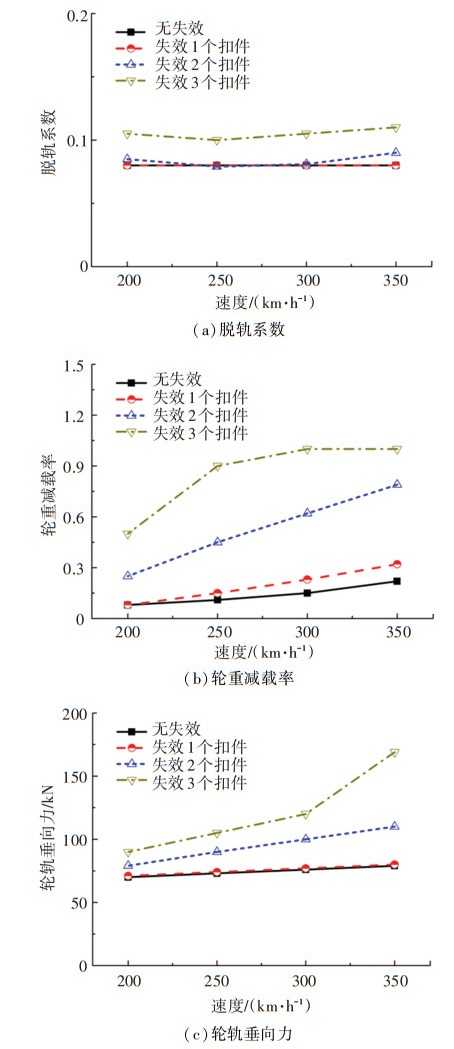
图 12进一步给出了列车不同运行速度下扣件失效个数对桥上列车运行性能的影响,包括脱轨系数、轮重减载率和轮轨垂向力。该冲击荷载同样使轨道和桥梁的振动出现了增加,但是由于轨下结构安全系数较高,因此本文主要给出了列车的动态特性。从图 12中可以看出,不同运行速度下,扣件失效主要是对轮轨垂向动力学性能产生影响,而对横向动力学性能影响较小,不同的失效扣件数量对脱轨系数影响不大,而对轮重减载率及轮轨垂向力影响明显。其中,由图 12(b)可知,3个扣件同时失效时,车辆运行速度高于250 km/h时,轮重减载率超过了0.8的动态限值,速度达到300 km/h及以上时,车轮已完全跳离钢轨;2个扣件同时失效时,车辆运行速度达到300 km/h时,轮重减载率已超过0.65的准静态限值。另外,由图 12(c)可知,在分析的参数取值范围内,最大轮轨垂向力小于170 kN。因此,从轮重减载率不超过规定限值的角度而言,车辆在以250~350 km/h的速度运行时,失效扣件的数量最多应为1个。
|
图 12 扣件失效对高速列车的影响 Fig. 12 Influence of fastener failure on high-speed train |
将轨道刚度不平顺分为常规型及缺陷型两种,推导了轨道刚度不平顺的计算方法,并建立了高速车轨桥动力学模型,从时域和频域角度研究了两种轨道刚度不平顺对系统的影响。通过研究得到了如下结论:
1) 轨道结构弹性对系统动态特性有明显影响;建议离散后的砂浆弹簧间距不应大于板长的1/15;当考虑结构弹性后,轨道板边缘位置处的振动较板中位置处的振动大,两位置处钢轨加速度幅值比为1.17,而轨道板的加速度比值则达到了2.2。
2) 常规型轨道刚度不平顺主要引起结构周期振动,可能导致系统共振,加速结构损伤;列车通过时的振动响应明显表现出扣件间距及轨道板长度的周期性影响;在所考察的指标中,构架点头加速度对常规型轨道刚度不平顺最为敏感。
3) 缺陷型轨道刚度不平顺会造成轮轨冲击,严重时导致轮轨垂向力和轮重减载率超标,威胁行车安全;列车在以250~350 km/h的速度运行时,失效扣件的数量最多为1个。
4) 轨道板长度导致的刚度不平顺幅值远低于扣件间距导致的轨道刚度变化,但是其引起的系统振动不可忽略,尤其是对于车辆的点头运动。
| [1] |
翟婉明. 车辆-轨道耦合动力学[M]. 4版. 北京: 科学出版社, 2015. ZHAI Wanming. Vehicle-track coupled dynamics[M]. 4th ed. Beijing: Science Press, 2015. |
| [2] |
CHEN Zhaowei, ZHAI Wanming, YIN Qiang. Analysis of structural stresses of tracks and vehicle dynamic responses in train-track-bridge system with pier settlement[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2018, 232(2): 421. DOI:10.1177/0954409716675001 |
| [3] |
张大伟, 王开云, 翟婉明, 等. 重载铁路轨枕空吊对轮轨动力相互作用的影响研究[J]. 振动与冲击, 2017, 36(18): 1. ZHANG Dawei, WANG Kaiyun, ZHAI Wanming, et al. Effect of unsupported sleepers on the wheel/rail dynamic interaction on heavy-haul railway lines[J]. Journal of Vibration and Shock, 2017, 36(18): 1. |
| [4] |
罗强, 蔡英, 翟婉明. 高速铁路路桥过渡段的动力学性能分析[J]. 工程力学, 1999(5): 65. LUO Qiang, CAI Ying, ZHAI Wanming. Dynamic performance analyses on high speed railway bridge-subgrade transition[J]. Engineering Mechanics, 1999(5): 65. |
| [5] |
娄平, 赵晨, 宫凯伦. 层间离缝对车辆-CRTSⅢ板式轨道系统响应影响[J]. 铁道工程学报, 2019, 36(9): 6. LOU Ping, ZHAO Chen, GONG Kailun. Influences of interlayer separation on the dynamic responses of vehicle-CRTS Ⅲ slab track system[J]. Journal of Railway Engineering Society, 2019, 36(9): 6. DOI:10.3969/j.issn.1006-2106.2019.09.002 |
| [6] |
杨荣山, 段玉振, 刘学毅. 双块式无砟轨道轨枕松动对轮轨系统动力性能影响研究[J]. 中国铁道科学, 2014, 35(5): 13. YANG Rongshan, DUAN Yuzhen, LIU Xueyi. Influence induced by sleeper looseness of bi-block slab track on dynamic property of wheel-track system[J]. China Railway Science, 2014, 35(5): 13. DOI:10.3969/j.issn.1001-4632.2014.05.03 |
| [7] |
周文涛, 涂鹏, 陈宪麦. CRTS Ⅱ型板式无砟轨道路桥过渡段动力响应研究[J]. 铁道科学与工程学报, 2018, 15(12): 3050. ZHOU Wentao, TU Peng, CHEN Xianmai. Study on dynamic response of CRTS Ⅱ slab track of bridge-subgrade transition section[J]. Journal of Railway Science and Engineering, 2018, 15(12): 3050. |
| [8] |
夏禾, 郭薇薇, 张楠. 车桥系统共振机理和共振条件分析[J]. 铁道学报, 2006(5): 52. XIA He, GUO Weiwei, ZHANG Nan. Analysis of resonance mechanism and conditions of train-bridge system[J]. Journal of the China Railway Society, 2006(5): 52. |
| [9] |
时瑾, 姚忠达, 王英杰. 二轴列车行经序列等跨桥时车辆共振响应分析[J]. 振动与冲击, 2019, 38(5): 237. SHI Jin, YAO Zhongda, WANG Yingjie. Resonance responses of vehicle during a two-axle train passing through sequential equal-span bridges[J]. Journal of Vibration and Shock, 2019, 38(5): 237. |
| [10] |
陈兆玮, 孙宇, 翟婉明. 高速铁路桥墩沉降与钢轨变形的映射关系(I): 单元板式无砟轨道系统[J]. 中国科学: 技术科学, 2014, 44(7): 770. CHEN Zhaowei, SUN Yu, ZHAI Wanming. Mapping relationship between pier settlement and rail deformation of high-speed railways—part(I): the unit slab track system[J]. Scientia Sinica: Technologica, 2014, 44(7): 770. |
| [11] |
ZHAI Wanming, HAN Zhaoling, CHEN Zhaowei, et al. Train-track-bridge dynamic interaction: a state-of-the-art review[J]. Vehicle System Dynamics, 2019, 57(7): 984. |
| [12] |
CHEN Zhaowei, FANG Hui. Dynamic evaluation of elastic bar in track transition section of fast-metro system[J]. Advances in Mechanical Engineering, 2019, 11(12): 1687814019895740. |
| [13] |
CHEN Zhaowei, FANG Hui. An alternative solution of train-track dynamic interaction[J]. Shock and Vibration, 2019(2019): 1859261. |
| [14] |
CHEN Zhaowei, ZHAI Wanming, TIAN Guoying. Study on the safe value of multi-pier settlement for simply supported bridges in high-speed railways[J]. Structure and Infrastructure Engineering, 2018, 14(3): 400. |
 2021, Vol. 53
2021, Vol. 53


