2. 深圳信息职业技术学院 智能制造与装备学院,广东 深圳 518000;
3. 深圳市腾讯计算机系统有限公司, 广东 深圳518000
2. School of Intelligent Manufacturing and Equipment, Shenzhen Institute of Information Technology, Shenzhen 518000, Guangdong, China;
3. Shenzhen Tencent Computer Systems Company Limited, Shenzhen 518000, Guangdong, China
全球不可再生能源迅速消耗,使用清洁能源代替燃烧汽油的电动汽车是环境保护的重要组成部分。电动汽车应用领域的关键技术之一是用于锂离子电池充电和放电的车载充电机(on-board charger, OBC)技术。OBC通常具有6.6 kW、11 kW和22 kW的单相三相充电能力。OBC正向运行时电网能量向高压电池充电,OBC反向运行时高压电池的能量向交流负载放电或为其他电动车提供动力辅助。由于电动汽车的特殊应用背景,要求OBC具有高功率密度,低成本和宽范围输出特性。现有的OBC内部最常用的是两级结构:功率因数矫正PFC(power factor correction)与高压直流DC/DC(direct current)变换器级联。第1级PFC级实现功率因数校正并生成稳定的母线电压。第2级DC/DC将高压总线转换为宽范围的电池电压,并在AC(alternating current)侧和DC侧之间提供隔离。用于OBC的DCDC拓扑最具竞争力的是双向软开关DAB(dual active bridge)变换器和CLLC(电容-电感-电感-电容)谐振变换器。由于DAB的满载环流和关断损耗大,在车载充电机应用中,该拓扑的满载效率低于谐振转换器[1]。CLLC谐振变换器通过在LLC的副边增加谐振电容实现正向和反向的升降压运行,同时保留宽范围软开关的优势[2-6],因此CLLC变换器更适用于车载充电机中。可将目前现有的CLLC拓扑应用于OBC的方案分成两类:第1类是可调节的直流母线方案,由第1级PFC产生宽范围可变的高压直流母线电压,后级CLLC谐振变换器主要在谐振频率点工作损耗最小,并使用SiC器件提高整机的效率和功率密度,这类方案避开CLLC复杂的参数设计过程,经对比,变母线方案较固定总线方案,效率可以提高2%[7-12],文献[13-14]提出一种在直流微电网中应用的开环CLLC参数的容错设计方法,同样设计谐振变换器在谐振点工作,输出宽范围的变化主要由前一级PFC实现,这种宽范围调节母线的方案,由于采用了高压宽禁带器件,整机成本会大大增加,而且使用高压母线电容也将具有较大的体积和成本。第2类方案是不调节母线电压方案,由PFC输出的母线电压一般稳定在400 V,使拓扑应用的开关管和母线电容耐压规格较低,为实现宽范围的电池充电电压,文献[15-18]提出将不同的控制策略相结合的方法以扩展谐振转换器的工作范围,控制方式通常采用频率调制,脉冲宽度调制和相移控制相结合的策略,这些新颖的控制策略通常根据不同的工作区域而具有复杂的控制模式,这增加了整个系统的复杂性并降低了软件的可靠性,根据拓扑使用区间的定制化方案,不利于功率从单相扩展到三相。
由于OBC超宽的电池电压充电范围,以及CLLC拓扑的多个谐振参数耦合特性,使CLLC变换器的设计过程复杂且困难。上述两种方案分别利用变母线和控制策略实现宽范围充电,而不是拓扑自身特性。文献[19-22]中提到CLLC的详细参数设计方法,但是通常设计的样机传输功率低,满负载工作范围窄,正反向对称运行,设计方法较难满足实际车载充电机产品的应用。本文设计一种基于固定母线电压的OBC实现方法,采用PFC级联CLLC变换器。通过研究CLLC之间谐振参数的相互作用,提出双向运行时的高效超宽输出的参数设计和优化方法,并采用简单的调频+打嗝模式控制。同时基于谐振拓扑单元的串联和并联,谐振网络可以直接扩展到11 kW和22 kW充电机应用。本文的第1节提出了车载充电机的整机拓扑结构,第2节提出了CLLC拓扑的归一化双向增益模型并分析了不同谐振参数对正向和反向增益的影响,第3节提出了基于增益模型的参数设计和优化方法,基于所提出的方法设计具有充电6.6 kW和放电3.3 kW的宽输出范围的样机,第4节中给出实验结果,最后给出了本文的结论。
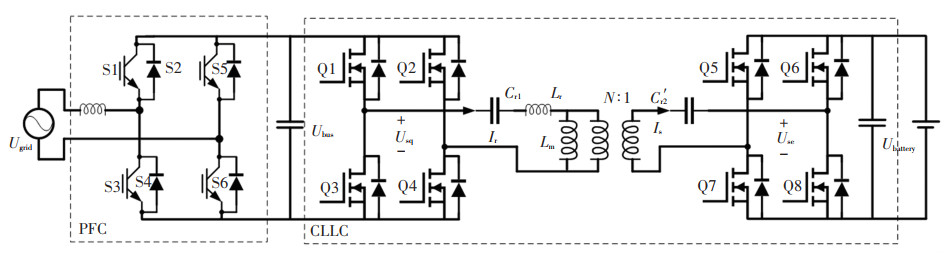
1 提出的双向车载充电机拓扑结构OBC的两级级联结构如图 1所示。第1级是双向AC-DC整流器和逆变器,将85~265 V(AC)的单相电网电压整流为400 V的固定总线,充电机具有的宽范围AC输入以满足不同国家和地区的电网要求。第2级是双向CLLC谐振变换器将母线电压转换为200~480 V的超宽电池电压。
|
图 1 双向车载充电机原理 Fig. 1 Schematic diagram of bidirectional on-board charger |
第1级的PFC运行于CCM(continuous current mode)模式,其中S1和S3采用IGBT(insulated gate bipolar transistor),工作频率为67 kHz,S2和S4是并联的SiC二极管,用作高频整流,同时作为宽禁带器件可消除反向恢复损耗。S5和S6是IGBT组成的低频整流开关管。由于母线电压固定,在CCM模式下的PFC仅在AC侧具有较大范围的变化,设计容易实现。双向CLLC变换器在母线侧和电池侧均具有全桥结构。图中Lr是谐振电感,Lm是励磁电感,Cr1和C′r2是谐振电容,变压器匝数比N。最大充电功率为DC 6.6 kW,交流侧放电功率为AC 3.3 kW。对于谐振变换器,正反向运行是不对称的工况,固定的低母线电压是400 V,而CLLC变换器可选择普通的Si MOSFET(metal-oxide-semiconductor field-effect transistor),整机的实现成本较低。
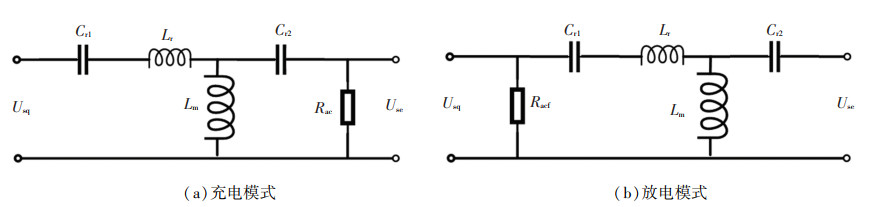
2 CLLC拓扑的双向数学模型基波分析法(fundamental harmonic analysis, FHA)是分析谐振变换器最有效而又简单的方法。使用FHA方法仅考虑电压和电流的基波分量,忽略了所有高次谐波分量。谐振变换器是通过在次级增加电容Cr2使反向可以作升压运行,因此Cr2的值决定反向运行的特性。双向谐振变换器通常可等效为两种数学模型:CLLC和CLLLC(电容-电感-电感-电感-电容)模型[18]。两种模型的参数可相互转换,但CLLLC对称模型更适合用于谐振变换器仅在谐振点附近工作,对称的参数可获得相同的充电和放电特性。当谐振变换器用于非对称的工况中,因为待定的参数少,CLLC模型更加适合。因此本文采用CLLC模型设计谐振参数。基于FHA,可得到充放电模式下CLLC的等效数学模型如图 2所示[18]。为更好地分析,将CLLC模型的参数在充放电运行时都等效到母线端,Rac和Racf分别是基波交流等效充放电负载, 其表达式可从文献[18]中获得,见式(1)、(2),其中RL和RLf是直流端负载。
|
图 2 双向CLLC变换器的等效数学模型 Fig. 2 Equivalent mathematical model of bidirectional CLLC converter |
充电模式:
| $ R_{\mathrm{ac}}=\frac{8 \times N^{2} \times R_{\mathrm{L}}}{{\rm{ \mathsf{ π} }}^{2}}, R_{\mathrm{L}}=\frac{V_{\mathrm{bat}}^{2}}{P_{\mathrm{bat}}} $ | (1) |
放电模式:
| $ R_{\mathrm{acf}}=\frac{8 \times N^{2} \times R_{\mathrm{Lf}}}{{\rm{ \mathsf{ π} }}^{2}}, R_{\mathrm{Lf}}=\frac{V_{\mathrm{bus}}^{2}}{P_{\mathrm{bus}}} $ | (2) |
根据FHA的等效模型,可推导出充放电谐振网络的增益Mg和Mgf的计算公式如下。
充电模式:
| $ \begin{aligned} &\ \ \ \ M_{\mathrm{g}}=\frac{V^{\prime}{}_{\mathrm{se}}}{V_{\mathrm{sq}}}= \\ &\left|\frac{\frac{1}{\frac{1}{R_{\mathrm{ac}}+\frac{1}{\mathrm{j} \omega C_{\mathrm{r} 2}}}+\frac{1}{\mathrm{j} \omega L_{\mathrm{m}}}}}{\frac{1}{\frac{1}{R_{\mathrm{ac}}+\frac{1}{\mathrm{j} \omega C_{\mathrm{r} 2}}}+\frac{1}{\mathrm{j} \omega L_{\mathrm{m}}}}+\mathrm{j} \omega L_{\mathrm{r}}+\frac{1}{\mathrm{j} \omega C_{\mathrm{r} 1}}} \times \frac{R_{\mathrm{ac}}}{R_{\mathrm{ac}}+\frac{1}{\mathrm{j} \omega C_{\mathrm{r} 2}}} \right| \end{aligned} $ | (3) |
放电模式:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {M_{{\rm{gf}}}} = \frac{{{V_{{\rm{sq}}}}}}{{{V^\prime }_{{\rm{se}}}}} = \\ \left| {\frac{{\frac{1}{{\frac{1}{{{R_{{\rm{acf}}}} + \frac{1}{{{\rm{j}}\omega {C_{{\rm{r1}}}} + {\rm{j}}\omega {L_{\rm{r}}}}}}} + \frac{1}{{{\rm{j}}\omega {L_{\rm{m}}}}}}}}}{{\frac{1}{{\frac{1}{{{R_{{\rm{acf}}}} + \frac{1}{{{\rm{j}}\omega {C_{{\rm{r1}}}} + {\rm{j}}\omega {L_{\rm{r}}}}}}} + \frac{1}{{{\rm{j}}\omega {L_{\rm{m}}}}}}} + \frac{1}{{{\rm{j}}\omega {C_{{\rm{r}}2}}}}}} \times \frac{{{R_{{\rm{acf}}}}}}{{{R_{{\rm{acf}}}} + \frac{1}{{{\rm{j}}\omega {C_{{\rm{r}}1}}}} + {\rm{j}}\omega {L_{\rm{r}}}}}} \right| \end{array} $ | (4) |
为简化分析,将式中的变量作如下等效变换:
| $ \omega=2 {\rm{ \mathsf{ π} }} f_{\mathrm{sw}} $ | (5) |
| $ f=\frac{f_{\mathrm{sw}}}{f_{0}} $ | (6) |
| $ f_{0}=\frac{1}{2 {\rm{ \mathsf{ π} }} \sqrt{L_{\mathrm{r}} C_{\mathrm{r} 1}}} $ | (7) |
式中fsw是谐振变换器的开关频率,f0是归一化的高频谐振点。
| $ L_{\mathrm{n}}=\frac{L_{\mathrm{m}}}{L_{\mathrm{r}}} $ | (8) |
| $ Q_{\mathrm{e}}=\frac{\sqrt{L_{\mathrm{r}} / C_{\mathrm{r} 1}}}{R_{\mathrm{ac}}} $ | (9) |
| $ Q_{\mathrm{ef}}=\frac{\sqrt{L_{\mathrm{r}} / C_{\mathrm{r} 1}}}{R_{\mathrm{acf}}} $ | (10) |
| $ C_{\mathrm{n}}=\frac{C_{\mathrm{r} 2}}{C_{\mathrm{r} 1}} $ | (11) |
将式(5)~(11)代入式(3)、(4)中,推导归一化的增益模型见式(12)、(13),变换增益与f、Ln、Qe(Qef)和Cn的值有关。
| $ \begin{aligned} &\ \ \ \ M_{\text {g_charging }}= \\ &\left|\frac{C_{\mathrm{n}} L_{\mathrm{n}} f^{3}}{C_{\mathrm{n}} f\left(L_{\mathrm{n}} f^{2}+f^{2}-1\right)+\mathrm{j} Q_{\mathrm{e}}\left(C_{\mathrm{n}} L_{\mathrm{n}} f^{4}-C_{\mathrm{n}} L_{\mathrm{n}} f^{2}-L_{\mathrm{n}} f^{2}-f^{2}+1\right)} \right| \end{aligned} $ | (12) |
| $ \begin{aligned} &\ \ \ \ M_{\mathrm{g}\_{\text {discharging }}}= \\ &\left|\frac{C_{\mathrm{n}} L_{\mathrm{n}} f^{3}}{f\left(C_{\mathrm{n}} L_{\mathrm{n}} f^{2}-1\right)+\mathrm{j} Q_{\mathrm{ef}}\left(C_{\mathrm{n}} L_{\mathrm{n}} f^{4}-C_{\mathrm{n}} L_{\mathrm{n}} f^{2}-L_{\mathrm{n}} f^{2}-f^{2}+1\right)}\right| \end{aligned} $ | (13) |
将式(12)、(13)的虚部设置为零,可以求解出充放电的谐振频率点。
高频解:
| $ \begin{aligned} &\ \ \ \ f_{0\_{h}}=\\ &{\sqrt{\frac{L_{\mathrm{n}}+\sqrt{C_{\mathrm{n}}^{2} L_{\mathrm{n}}^{2}+2 C_{\mathrm{n}} L_{\mathrm{n}}^{2}-2 C_{\mathrm{n}} L_{\mathrm{n}}+L_{\mathrm{n}}^{2}+2 L_{\mathrm{n}}+1}+C_{\mathrm{n}} L_{\mathrm{n}}+1}{2 C_{\mathrm{n}} L_{\mathrm{n}}}}} \end{aligned} $ | (14) |
低频解:
| $ \begin{aligned} &\ \ \ \ f_{0\_{1}}=\\ &{\sqrt{\frac{L_{\mathrm{n}}-\sqrt{C_{\mathrm{n}}^{2} L_{\mathrm{n}}^{2}+2 C_{\mathrm{n}} L_{\mathrm{n}}^{2}-2 C_{\mathrm{n}} L_{\mathrm{n}}+L_{\mathrm{n}}^{2}+2 L_{\mathrm{n}}+1}+C_{\mathrm{n}} L_{\mathrm{n}}+1}{{2 C_{\mathrm{n}} L_{\mathrm{n}}}}}} \end{aligned} $ | (15) |
双向谐振变换器在高频谐振点处的增益推导见式(16)、(17)。
充电模式:
| $ \text { Gain}_\text {_charging }=\frac{L_{\mathrm{n}} f_{0\_\mathrm{h}}^{2}}{L_{\mathrm{n}} f_{0\_{\mathrm{h}}}^{2}+f_{0\_{\mathrm{h}}}^{2}-1} $ | (16) |
放电模式:
| $ \text { Gain}_\text {_discharging }=\frac{C_{\mathrm{n}} L_{\mathrm{n}} f_{0\_{\mathrm{h}}}^{2}}{C_{\mathrm{n}} L_{\mathrm{n}} f_{0\_{\mathrm{h}}}^{2}-1} $ | (17) |
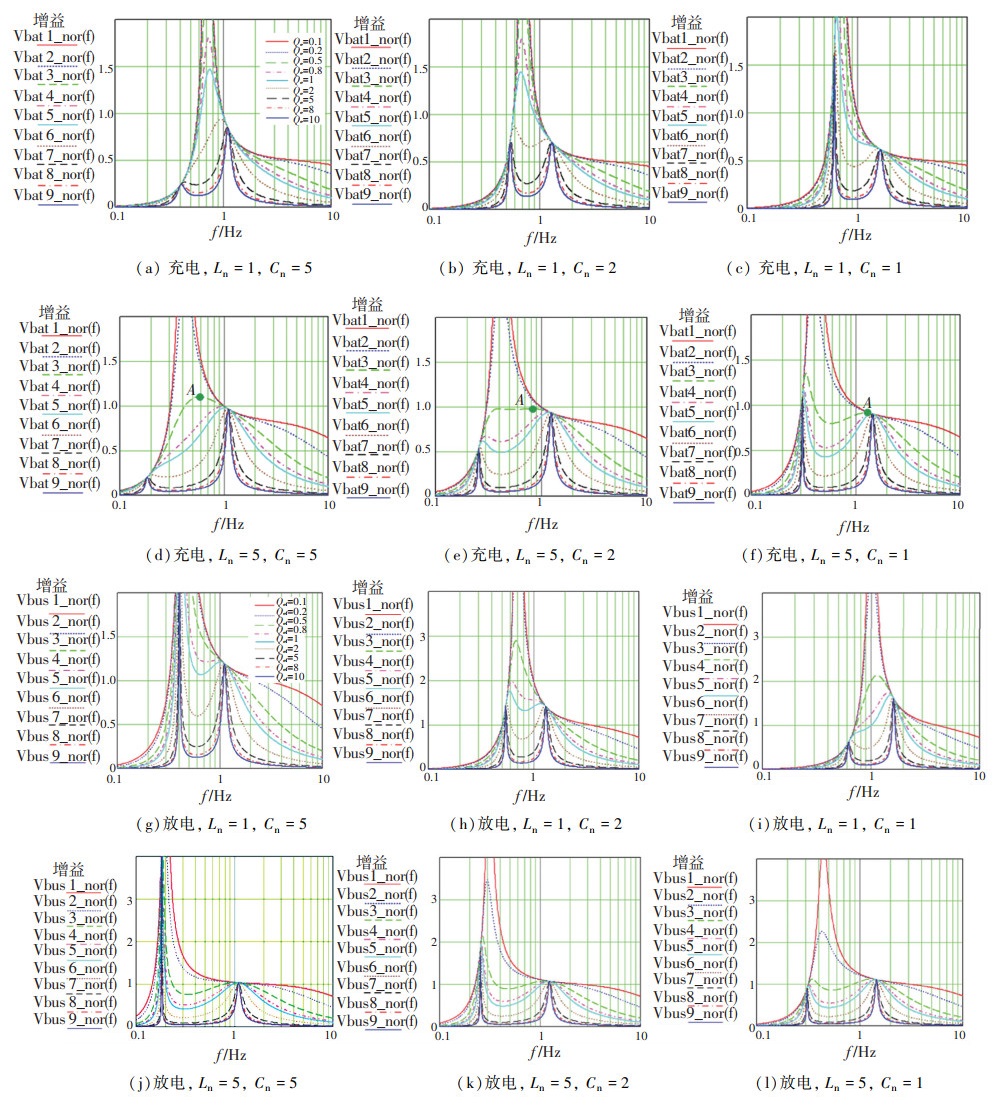
影响CLLC变换器增益的参数为Ln、Qe(Qef)、N和Cn。以归一化的开关频率作为变量,画出充放电增益曲线随不同谐振参数变化的趋势如图 3所示,其中Vbat1_nor~Vbat9_nor和Vbus1_nor~Vbus9_nor分别是Qe和Qef的值逐渐增大的曲线,对应的Qe和Qef的值为0.1~10,图例标注在充电和放电曲线图 3(a)和3(g)中。根据图 3中参数变化对增益的影响,可以总结出以下3点规律:
|
图 3 随Ln,Cn和Qe(Qef)变化充放电模式的增益曲线 Fig. 3 Variation of charging and discharging mode gains with Ln, Cn, and Qe (Qef) |
1) 从图 3中所有充放电的增益曲线中均可看到,随着Qe的增加,增益的趋势是减小的。影响Qe的因素有两种情况,一种是负载Rac的值减小,Qe增加,即负载变重时增益会下降,满载情况是最恶劣的工作点;另一种是Lr与Cr1的比值减小, 可减小Qe的值,当发现负载太重增益无法满足要求时,需要调整谐振电感与电容的比值来提高整机输出功率的能力。
2) 观察图 3(a)和3(d)发现随Ln值的减小曲线变窄,增益逐渐增加,CLLC变换器具有更好的输出电压能力和更小的频率变化范围。因此在输出功率能力不足时需要调整参数Ln的值使其减小,以上Ln和Qe的参数选取原则与LLC变换器一致。
3) 双向CLLC谐振变换器与单相的LLC谐振变换器主要的区别是电池端多一个谐振电容,该谐振电容主要影响传输特性,Cn的值决定了CLLC充电和放电的增益能力。从图 3(a)和3(d)中可看到Cn的值越大,Cr2的阻抗对充电电压增益的影响越小,并且充电增益曲线越接近LLC。Cn的值影响低频谐振点和低频谐振点的增益,当Cn较小时,充电模式下低频谐振点处增益越大,导致高频谐振点附近的增益损失越多。如图 3(d)~3(f)中的A点所示,随着Cn的减小,A点的最大输出电压逐渐降低。当Cn较大时,放电增益曲线高频谐振点附近的增益更平滑,工作点频率更高,这是特性较差的工作区。Cn对充电和放电方向的影响是相反的,因此需要根据实际的需求综合选择Cn值。从图 3(c)和图 3(f)中能够看到,当Cn的值等于1时,充电模式下增益损失幅度较大。在双向应用中,Cn的值应大于1。在Cn≥5的情况下,图 3(g)和图 3(i)放电模式f0_h处的增益变得过于平滑,可以升压运行的区间较小,因此Cn的值应小于5。综合充放电的增益情况,在双向传输功率相当的需求时,Cn的值选择2~3是较为合适的。
2.2 变压器匝数比对充电和放电增益的影响在宽范围应用谐振变换器参数选取过程中,效率是最重要的优化量。CLLC拓扑运行于软开关模式,因此MOSFET的损耗主要是导通损耗,导通损耗是由谐振腔的环流值决定的,变压器的匝数比决定充放电的环流值分布,也就是系统最佳工作点的分布。推导充电模式下母线侧的环流有效值iacp为
| $ i_{\mathrm{acp}}=\frac{{\rm{ \mathsf{ π} }}}{2} \frac{1}{N} I_{\mathrm{o}_{-} \mathrm{cha}} \sin \left(2 {\rm{ \mathsf{ π} }} f_{\mathrm{sw}} t-\varphi_{\mathrm{i}}\right) $ | (18) |
式中:Io_cha为充电模式下的充电电流,φi为输出充电电流的相角。
端口的电压Vm电流有效值Iacp为
| $ I_{\mathrm{acp}}=\frac{\sqrt{2}}{4} \frac{{\rm{ \mathsf{ π} }}}{N} I_{\mathrm{o}\_\mathrm{cha}} $ | (19) |
| $ V_{\mathrm{m}}=I_{\mathrm{acp}}\left|\mathrm{j} \frac{1}{\omega C_{\mathrm{r} 2}}+R_{\mathrm{ac}}\right|=I_{\mathrm{acp}} \sqrt{R_{\mathrm{ac}}^{2}+\left(\frac{1}{\omega C_{\mathrm{r} 2}}\right)^{2}} $ | (20) |
励磁电流的有效值Im推导公式为
| $ I_{\mathrm{m}}=\frac{I_{\mathrm{acp}} \sqrt{R_{\mathrm{ac}}^{2}+\left(\frac{1}{\omega C_{\mathrm{r} 2}}\right)^{2}}}{\omega L_{\mathrm{m}}} $ | (21) |
根据式(19)~(21)充电模式母线侧环流的有效值Ip表达式为
| $ I_{\mathrm{p}}=\frac{\sqrt{2}}{4} \frac{{\rm{ \mathsf{ π} }}}{N} I_{\mathrm{o}\_\mathrm{cha}} \sqrt{\frac{R_{\mathrm{ac}}^{2}+\left(\frac{1}{\omega C_{\mathrm{r} 2}}\right)^{2}}{\left(\omega L_{\mathrm{m}}\right)^{2}}+1} $ | (22) |
同样地,推导出放电模式电池侧环流的有效值Is表达式为
| $ I_{\mathrm{s}}=\frac{\sqrt{2}}{4} N {\rm{ \mathsf{ π} }} I_{\mathrm{o}\_\mathrm{discha}} \sqrt{\frac{R_{\mathrm{acf}}^{2}+\left(\omega L_{\mathrm{r}}+\frac{1}{\omega C_{\mathrm{r} 1}}\right)^{2}}{\left(\omega L_{\mathrm{m}}\right)^{2}}+1} $ | (23) |
式中Io_discha是放电时的电池电流。
根据循环电流有效值的表达式,主要的影响参数是变压器匝数比N和Lm。其中,Lm的选择与输出功率能力相关。一般Lm的值越大输出功率能力越小,环流越小效率越高,即在额定的输出功率下,设计的Lm使功率域量越小效率将越高,通常这一优化过程对效率的影响有限。当N的值选择越大时,充电模式下母线侧的环流值越大,母线线侧的MOSFET和谐振电容器的损耗较大。在充电模式下,电池侧的MOSFET用作二极管,环流对损耗的影响较小,放电模式具有相同趋势。当N的值选择较小时,放电模式下电池侧的环电流较大,电池侧MOSFET和谐振电容的损耗较大。即无论在充电工况还是放电工况,调节N的值可以设置较高的效率。通常充电模式是典型的工作区域,因此N值的设置往往会考虑优化提高充电效率。此外,N还将宽范围的工作点划分成升压区(频率小于谐振频率)和降压区(频率大于谐振频率),其中升压区运行频率较低,增益曲线效率高易于控制, 是较好的工作区。N对工作区划分的影响在下一节中详细讨论。
3 CLLC变换器的参数设计方法通过上文谐振参数对充电和放电增益曲线的影响分析,本节详细讨论参数的设计和优化方法。谐振变换器采用FHA分析方法,只考虑了基波分量,因此基于FHA方法对谐振变换器的分析在谐振频率附近的结果是较为准确的,偏离谐振频率的结果存在误差。设计过程基于FHA方法,并且结合仿真软件对参数作进一步修改。设计CLLC输入母线电压为400 V,电池电压为270~480 V,充电功率为6 600 W,AC放电功率为3 300 W,母线侧的MOSFET型号为STW65N65DM2AG,电池侧MOSFET的型号为STW50N65DM2AG。
3.1 谐振频率的选择谐振变换器的设计从选择谐振频率f0_h开始。综合考虑开关损耗、变压器体积以及EMC的测试范围,CLLC的工作频率在100~200 kHz之间是较为合适的,在本文中,将f0设置为100 kHz。确定谐振频率后,变换器的工作点将接近谐振频率。CLLC系统的高频谐振点f0_h由4个谐振参数确定,为了简化参数设计过程,将选定的谐振频率近似等于f0,实际的充电谐振频率将略大于f0,而放电谐振频率将略小于f0。
3.2 初步选择变压器匝数比CLLC变换器的输入电压和输出电压转换公式分别为
| $ V_{\text {battery }}=V_{\text {bus }} \times \frac{1}{N} \times M_{\text {g_forward }} $ | (24) |
| $ V_{\text {bus }}=V_{\text {battery }} \times N \times M_{\text {g_reverse }} $ | (25) |
当输入和输出具有较宽范围变化时,首先根据额定电压的工作点设置变压器的匝数比。从上一节可以看出,CLLC转换器在高频谐振点处的增益将略低于1,初始设计可以暂时将增益值Mg_f0设为1。系统额定的工作点是母线400 V转换为充电电压360 V,据此初步选取变压器的匝数比为
| $ N=\frac{V_{\mathrm{o}\_{\mathrm{nor}}} M_{\mathrm{g}\_\mathrm{f0}}}{V_{\text {in_nor }}}=0.9 $ | (26) |
根据所选的变压器匝数比,可计算出所需充电增益的最大值和最小值分别为Mg_c_min = 0.6和Mg_c_max = 1.08, 所需放电增益的最大值和最小值分别为Mg_d_min = 0.92和Mg_d_max=1.64。
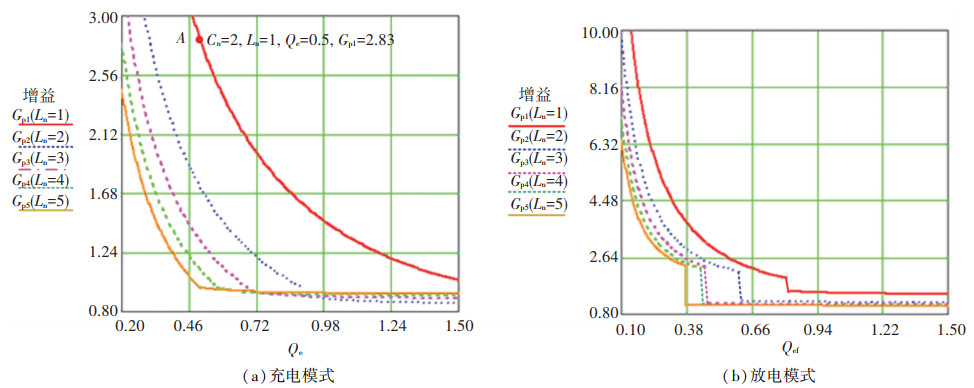
3.3 选择Ln和Qe选择合适的Ln和Qe的值,可保证系统获得所需的充放电最大和最小增益。根据上文对Cn取值的分析,Cn=2时,正反向工作的增益可较好地满足双向功率传输。在图 4中给出了随着Ln和Qe的变化增益峰值的变化曲线,其中Cn=2。例如,图 4中的A点表明Ln=1、Qe=0.5、Cn=2时充电增益曲线上感性区最大的增益值是2.83。比较图 4(a)和图 4(b),可以看到一些曲线是不连续的。增益曲线上具有两个峰值,只有频率较高的峰值点才处于可应用的感性区。随着Qe(或Qef)的值增加,增益的峰值会逐渐降低,并在两个谐振频率点之间出现一个容性区,导致感性区的峰值突变到高频谐振点的增益值。
|
图 4 Cn=2,随Ln,Qe变换的CLLC变换器充放电增益峰值曲线 Fig. 4 Variation of charging and discharging peak gains of CLLC converter with Ln and Qe, when Cn=2 |
充电工况下输出是恒功率的,因此Qe值最低的点是480 V。可以暂且将Qe=0.5时设置为480 V,从图中看到如果Qe=0.5时的增益要大于所需的1.08,则Ln的值必须小于3。选择Ln = 3,然后继续检查Qe=1.58(电池电压为270 V),增益为0.85(即接近所需的增益0.6),则所选参数符合要求。根据正向增益,Ln=3,Qe=0.5(480 V)。
3.3.2 根据放电需求选择Ln和Qe的值放电工况下输出是恒定电压值,负载不变。在这种情况下,电压和直流功率值分别为400 V和3 600 W,即Qef=0.39。逆变时电池电压270 V需要满足增益1.64的要求,从放电曲线可以看出,当Qef=0.39时,Ln=3的增益值比较临界,进一步调整Ln=2。最终根据充放电增益要求选择参数Ln=2,Qe=0.5(充电480 V)。
3.4 优化变压器匝数比N根据上述步骤选择的参数可以满足充电和放电的功率转换要求,但在超宽的输出范围下,电池电压较低时会具有较大的环流值,MOSFET的导通损耗较其他工作点大,这不利于整机的器件选型。需要通过增加N的值降低充电模式下低压部分的环流有效值,降低MOSFET的损耗。本文选择Q1~Q4的导通电阻为40 mΩ,选择的Q5~Q8的导通电阻为70 mΩ。谐振参数相同,不同N值下对比充放电模式下的开关损耗如图 5所示。通过图中对比,给出了两个极限工作点270 V/6.6 kW和480 V/6.6 kW的损耗值。如果根据额定工作点将N选择为0.9,那么在270 V/6.6 kW时损耗将高达36 W。增加N的值可以显著减小充电损耗,但同时会增加放电工况的损耗。通常充电效率是更被关注的指标,而N值的选取倾向于提高充电效率。

|
图 5 不同变压器匝数比MOSFET的损耗 Fig. 5 Loss of MOSFET under different transformer turns ratios |
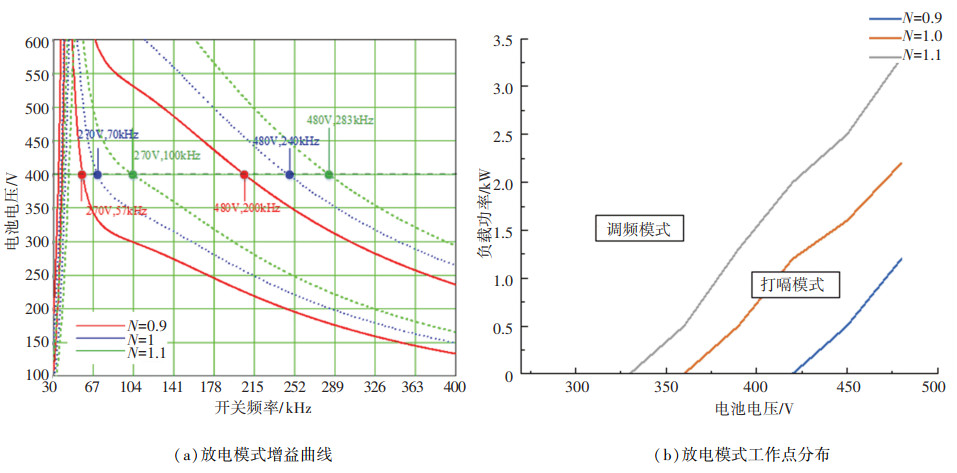
此外随着N值的增加,高频谐振点对应的电池电压逐步降低,充电工况具有更多工作点处在升压区域。同时放电工况更多的工作点位于降压区域,并且放电模式的工作频率将提高。绘制在不同匝数比和不同电池电压下放电模式的增益曲线,如图 6所示,曲线中的负载对应的是母线电压400 V/3.6 kW。该图表明随着N的增加,放电模式的工作点频率将显著增加。本文设计的OBC采用调频和打嗝模式结合的控制策略,当CLLC的工作频率超过300 kHz后从调频状态进入到300 kHz的打嗝状态。工作点频率的增加将使更多的工况位于打嗝区,由于占空比是间隙性发波,电池电流的纹波会较大,不是较好的工作区,因此调整N时同时要考虑放电工作点的划分。图 6(b)描述了负载变化时放电工作点的分布情况,N的值越大,放电工况打嗝的区域越大。因此综合考虑整机充电效率和放电工作点的分布,将N确定为1更合适,结合软件仿真及器件的选型微调谐振参数,最终优化后的谐振参数和器件选型如下所列。PFC中的电感值为260 μH,S1和S3的型号是AIGW40N65H5,S2和S4的型号是STPSC20H065CWY,S5和S6的型号是AIKW50N60CT,CLLC变换器母线侧的谐振电容为90 nF,电池测谐振电容为198 nF,谐振电感为25 μH,励磁电感为50 μH,变压器的原副边匝数均是10。
|
图 6 不同变压器匝数比下放电模式工作点分布 Fig. 6 Distribution of operating points in discharging mode under different transformer turns ratios |
谐振变换器的特性受谐振参数的影响,因此在器件选型时要考虑硬件参数随时间、温度和环境的变化所产生的影响。通常磁性器件的制造误差在8%~15%之间,电容器件的误差在10%~20%之间,应尽可能选择误差较小的器件。在选用的器件确定后,需要对参数差异的最坏情况进行评估,谐振电感和电容对特性的显著影响主要是工作点的偏移。谐振参数变化后使谐振频率点偏移,从而正反向所有的工作点进一步平移。在充电机宽范围的应用中,充电电压在最低和最高是两个极限点,充电时电池电压270 V时工作频率最高,环流有效值最大,效率最低,因此充电时电池电压最低点是最苛刻的工作点。充电480 V时工作频率最低,验证在该点的最低频率是否会超出最低频率的限制。放电运行时,480 V时的频率最高,环流有效值最大,效率最低,因此在放电过程480 V是最苛刻的工作点。放电运行270 V时工作频率最大,确保参数差异下该点的最低运行频率不会超出限制。确定以上最恶劣的工作点后,挑选参数偏差较大的几组磁性元件和电容对最恶劣工作点进行验证,确保极限点的指标仍在要求内。
4 实验结果根据前文设计的谐振参数,搭建了OBC样机,由第1级PFC级联后级的CLLC变换器。本节对整机的特性及CLLC拓扑特性进行测试,验证提出的设计方法。
4.1 软启动策略CLLC拓扑在启动过程中,输出电压为零,谐振变换器的输出等效于短路。启动时会有较大的谐振电流损坏MOSFET。推导启动时峰值电流Ipeak为
| $ I_{\mathrm{peak}}=\frac{V_{\mathrm{in}} \Delta t}{L_{\mathrm{r}}} $ | (27) |
式(27)表明,只有谐振电感和占空比时间才能限制启动电流。当谐振变换器在400 V母线下传输6.6 kW的大功率时,谐振电感的值通常是较小的。因此本文提出了一种软启动方案,通过控制脉冲宽度来限制起机电流,如图 7所示。最开始输出电压以400 kHz的打嗝模式分段发波。随着输出电压的升高,打嗝模式的频率逐渐降低至打嗝模式与PFM (pulse frequency modulation)的分界点300 kHz,然后系统进入稳态PFM模式。此外,如果在保证输出功率的基础上,尽量增加谐振电感的值可有效抑制启动电流的峰值。

|
图 7 软启动控制策略 Fig. 7 Soft start control strategy |
测试充电电池电压360 V时的启动波形如图 8所示。输出端采用电压电流环的双环控制方式,启动过程逐渐释放输出电压的参考值,并使用高频脉冲串建立输出电压。直到输出电压达到所需的电池电压,然后逐渐释放输出电流参考值,直到输出功率达到6.6 kW。反向启动过程与正向相同:首先通过高频打嗝模式对母线电容充电。在电容电压达到380 V后,PFC启动开始逐渐建立交流输出电压。通过软启动控制策略,可以确保谐振腔的峰值电流不超过35 A,确保开关器件的可靠运行。

|
图 8 软启动测试波形 Fig. 8 Soft start test waveform |
为了完全覆盖电池电压的充电范围,本文设计的样机具有超宽范围的输出电压,不同电池电压下的充电功率和电流曲线如图 9所示。

|
图 9 充电模式输出功率及电流曲线 Fig. 9 Charging mode output power and current curve |
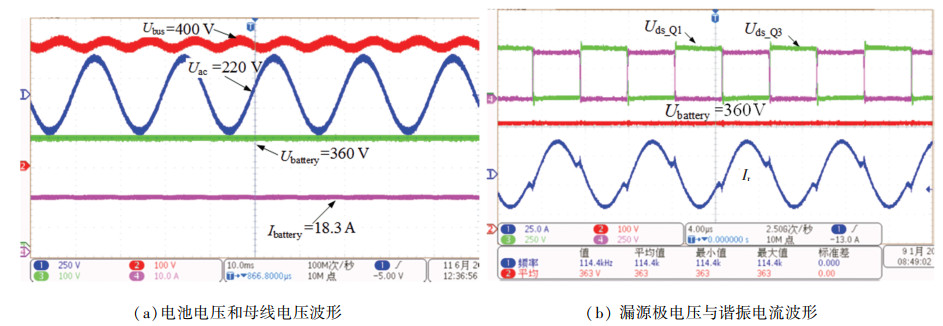
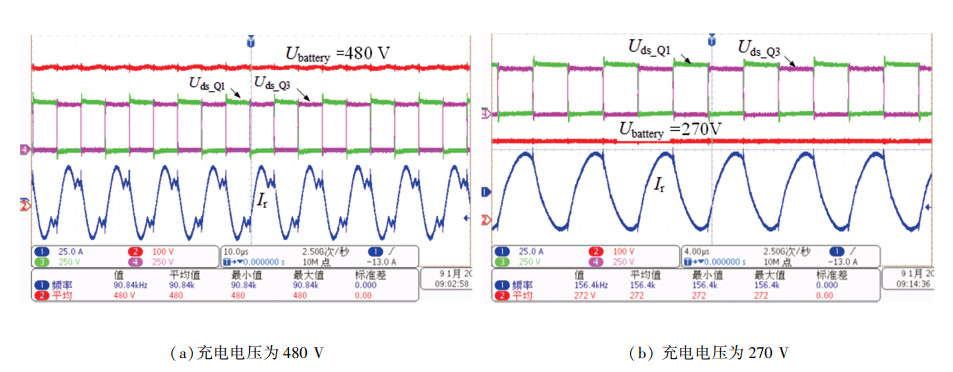
由图 9能够看到,满载充电电压为270~480 V,充电功率为6.6 kW,最大输出电流为24 A,在低电池电压200~270 V时充电限流为10 A。图 10展示了额定输入为220 V(AC)充电电压为360 V的满载测试波形。图 10表明CLLC的工作频率为114 kHz,母线电压稳定在400 V,纹波为30 V。图 11为充电电压分别为270、480 V时稳态细节测试波形。由于输出范围大,运行的频率在91~156 kHz之间变化。
|
图 10 充电电压360 V的测试波形 Fig. 10 Tested waveforms of charging voltage 360 V |
|
图 11 充电电压为270 V和480 V时的测试波形 Fig. 11 Tested waveforms of charging voltage 270 V and 480 V |
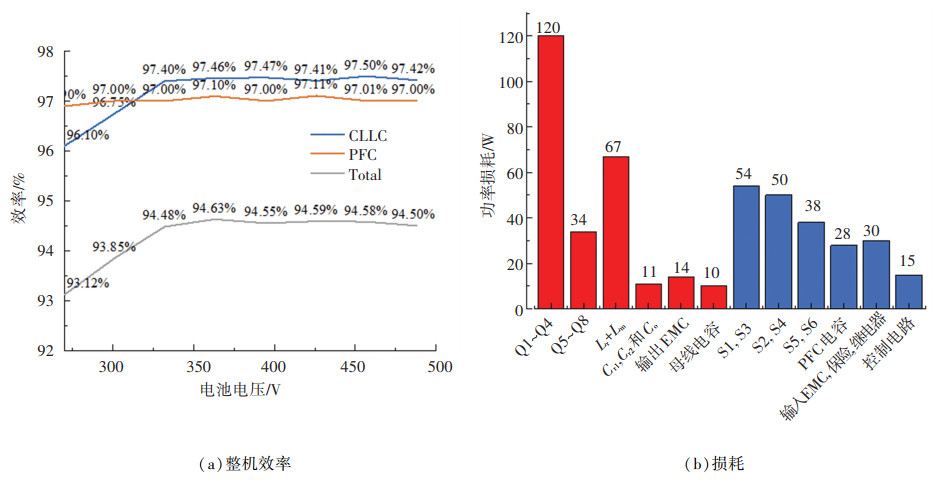
车载充电器主要在满载充电条件下工作,因此测试了不同电池电压满载的效率曲线,如图 12所示。母线电压在不同的充电电压下保持恒定,PFC的效率基本不变,整个样机的效率随CLLC拓扑的变化而变化。从曲线中能够看到谐振频率点附近的效率最高,这是因为该工作点中环流的有效值最小,并且波形是较好的正弦波, 变压器损耗也较小。在图 12(b)中分析了效率最低点270 V的器件损耗。CLLC变换器中损耗最高的两种器件是MOSFET Q1~Q4和磁性元件。通过优化匝数比N的值,可以进一步降低谐振电流,从而减少变压器的铜损和MOSFET的导通损耗,优化充电效率。
|
图 12 OBC充电模式的整机效率及损耗 Fig. 12 Overall efficiency and loss of OBC in charging mode |
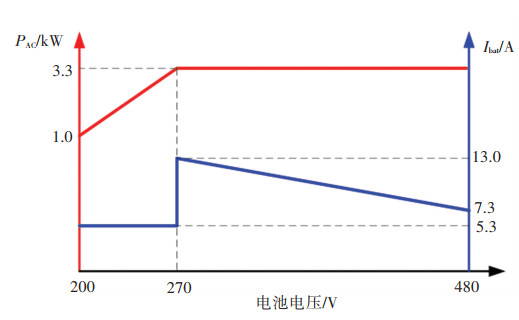
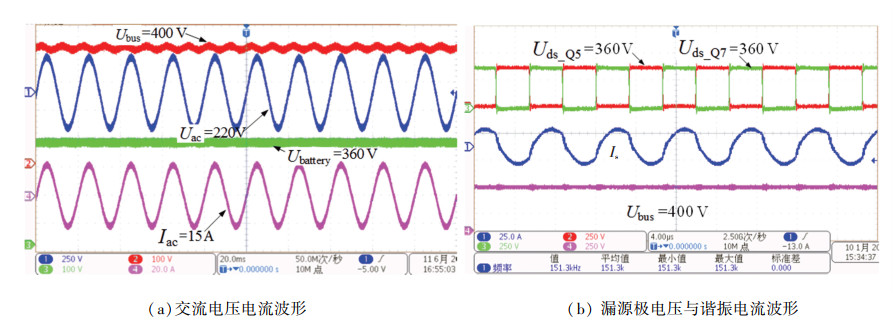
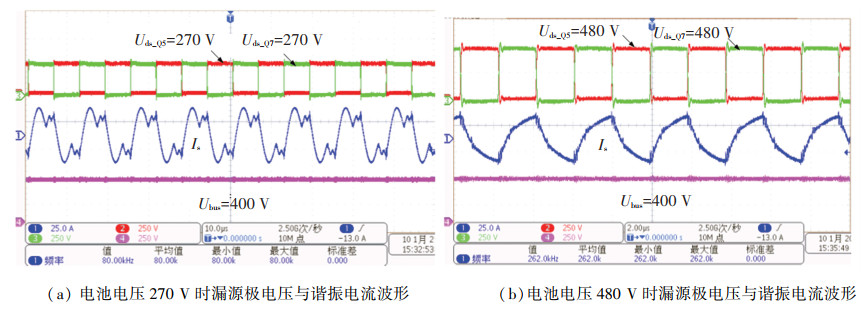
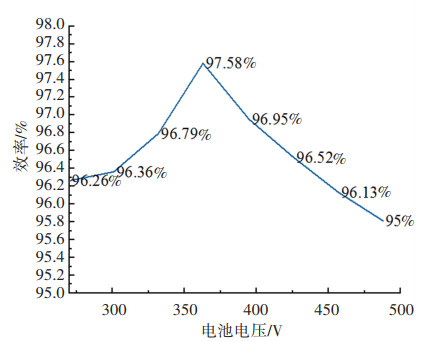
放电模式的输出功率和电流曲线如图 13所示,最大交流端放电功率为3.3 kW。分别测试270、360、480 V时的CLLC变换器的放电波形,如图 14、15所示。从图中能看出,放电运行时整机的工作频率会更高,最高频率可以达到260 kHz。在交流输出功率为3.3 kW的情况下,测试CLLC放电操作的效率曲线如图 16所示,放电效率略低于充电模式。放电模式对效率的要求并不苛刻。通过对充放电运行模式的测试表明,搭建的OBC样机能够完成超宽的双向功率变换,并具有较高的效率,满载整机充电效率最高为94.5%,CLLC单级满载充电效率可达97.5%。
|
图 13 放电模式输出功率及电流曲线 Fig. 13 Discharging mode output power and current curve |
|
图 14 放电电压360 V的测试波形 Fig. 14 Tested waveforms of discharging voltage 360 V |
|
图 15 放电电压270 V和480 V的测试波形 Fig. 15 Tested waveforms of discharging voltage 270 V and 480 V |
|
图 16 OBC放电模式的整机效率及损耗 Fig. 16 Overall efficiency and loss of OBC in discharging mode |
本文设计一款输入输出超宽范围的高效双向车载充电机,采用PFC级联CLLC谐振变换器。提出一种CLLC谐振变换器的双向归一化增益模型,分析了拓扑正反向功率传输能力和增益特性。并提出了通用的谐振参数设计方法指导CLLC变换器的参数设计与优化。基于车载充电机高效率和低成本的要求,采用固定母线方案,通过分析谐振变换器的增益和损耗表明,谐振电容和变压器匝数比是双向运行的主要影响参数。合理设置谐振电容与变压器匝数比可使谐振变换器在宽范围运行中获得最佳的充电效率。设计了一台充放电额定功率分别为6.6 kW(DC)和3.3 kW(AC)的实验样机,验证所提出的参数设计方法,结果表明,谐振变换器可实现双向宽范围功率变换,满载充电效率达到97.5%,整机充电效率可达94.5%。
| [1] |
HE Peiwen, KHALIGH A. Comprehensive analyses and comparison of 1 kW isolated DC-DC converters for bidirectional EV charging systems[J]. IEEE Transactions on Transportation Electrification, 2017, 3(1): 147. DOI:10.1109/TTE.2016.2630927 |
| [2] |
HU Zhiyuan, WANG Laili, WANG Hongliang, et al. An accurate design algorithm for LLC resonant converters—part I[J]. IEEE Transactions on Power Electronics, 2016, 31(8): 5435. DOI:10.1109/TPEL.2015.2496333 |
| [3] |
HU Zhiyuan, WANG Laili, QIU Yajie, et al. An accurate design algorithm for LLC resonant converters—part Ⅱ[J]. IEEE Transactions on Power Electronics, 2016, 31(8): 5448. DOI:10.1109/TPEL.2015.2496179 |
| [4] |
JIN Ke, RUAN Xinbo. Hybrid full-bridge three-level LLC resonant converter—a novel DC-DC converter suitable for fuel-cell power system[J]. IEEE Transactions on Industrial Electronics, 2006, 53(5): 1492. DOI:10.1109/TIE.2006.882020 |
| [5] |
LEE J, JEONG Y, HAN B. An isolated DC/DC converter using high-frequency unregulated LLC resonant converter for fuel cell applications[J]. IEEE Transactions on Industrial Electronics, 2011, 58(7): 2926. DOI:10.1109/TIE.2010.2076311 |
| [6] |
BEIRANVAND R, RASHIDIAN B, ZOLGHADRI M, et al. Using LLC resonant converter for designing wide-range voltage source[J]. IEEE Transactions on Industrial Electronics, 2011, 58(5): 1746. DOI:10.1109/TIE.2010.2052537 |
| [7] |
LI Bin, LI Qiang, LEE F, et al. A high efficiency high density wide band gap device based bi-directional on board charger[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 6(3): 1627. DOI:10.1109/JESTPE.2018.2845846 |
| [8] |
LIU Zhengyang, LI Bin, LEE F, et al. High efficiency high density critical mode rectifier/inverter for WBG device based on board charger[J]. IEEE Transactions on Industrial Electronics, 2017, 64(11): 9114. DOI:10.1109/TIE.2017.2716873 |
| [9] |
LI Bin, LEE F, LI Qiang, et al. Bi-directional on board charger architecture and control for achieving ultra-high efficiency with wide battery voltage range[C]// IEEE Applied Power Electronics Conference and Exposition. Tampa: IEEE, 2017: 3688
|
| [10] |
ZOU Shenli, LU Jiangheng, MALLIK A, et al. Bi-directional CLLC converter with synchronous rectification for plug-in electric vehicles[J]. IEEE Transactions on Industry Applications, 2018, 54(2): 998. DOI:10.1109/TIA.2017.2773430 |
| [11] |
Bidirectional CLLLC resonant dual active bridge (DAB) reference design for HEV/EV on board charger[EB/OL]. (2020-03-12)[2020-05-10]. https://www.ti.com/tool/TIDM-02002
|
| [12] |
KIM H, RYU M, BAEK J, et al. High-efficiency isolated bidirectional AC-DC converter for a DC distribution system[J]. IEEE Transactions on Power Electronics, 2013, 28(4): 1642. DOI:10.1109/TPEL.2012.2213347 |
| [13] |
HUANG Jinging, ZHANG Xin, SHUAI Zhikang, et al. Robust circuit parameters design for the CLLC type DC transformer in the hybrid AC-DC microgrid[J]. IEEE Transactions on Industrial Electronics, 2019, 66(3): 1906. DOI:10.1109/TIE.2018.2835373 |
| [14] |
HUANG Jingjing, ZHANG Xin, ZHAO Bin. Simplified resonant parameters design of the asymmetrical CLLC type DC transformer in the renewable energy system via semi-artificial intelligent optimal scheme[J]. IEEE Transactions on Power Electronics, 2019, 35(2): 1548. |
| [15] |
LIU Gang, JANG Y, ZHANG Jianqiu. Over 300 kHz GaN device based resonant bi-directional DCDC converter with integrated magnetics[C]// IEEE Applied Power Electronics Conference and Exposition. Long Beach: IEEE, 2016: 595
|
| [16] |
KHALID U, SHU Dongdong, WANG Haoyu. Hybrid modulated reconfigurable bidirectional CLLC converter for V2G enabled PEV charging applications[C]// IEEE Applied Power Electronics Conference and Exposition. Anaheim: IEEE, 2019: 3332
|
| [17] |
LEE B, KIM J, KIM S, et al. An isolated/bidirectional PWM resonant converter for V2G(H) EV on-board charger[J]. IEEE Transactions on Vehicular Technology, 2017, 66(9): 7741. DOI:10.1109/TVT.2017.2678532 |
| [18] |
BAI C, HAN B, KWON B, et al. Highly efficient bidirectional series-resonant DC/DC converter over wide range of battery voltages[J]. IEEE Transactions on Power Electronics, 2020, 35(4): 3636. DOI:10.1109/TPEL.2019.2933408 |
| [19] |
ZAHID Z, DALALA Z, CHEN Rui. Design of bidirectional DCDC resonant converter for vehicle to grid applications[J]. IEEE Transactions on Transportation Electrification, 2015, 1(3): 232. DOI:10.1109/TTE.2015.2476035 |
| [20] |
JUNG J, KIM H, RYU M, et al. Design methodology of bidirectional CLLC resonant converter for high frequency isolation of DC distribution systems[J]. IEEE Transactions on Power Electronics, 2013, 28(4): 1741. DOI:10.1109/TPEL.2012.2213346 |
| [21] |
LV Zheng, YAN Xiangwu, FANG Yukang, et al. Mode analysis and optimum design of bidirectional CLLC resonant converter for high frequency isolation of DC distribution systems[C]//IEEE Energy Conversion Congress and Exposition. Montreal: IEEE, 2015: 1513
|
| [22] |
CHEN Wei, RONG Ping, LU Zhengyu. Snubberless bidirectional DC-DC converter with new CLLC resonant tank featuring minimized switching loss[J]. IEEE Transactions on Industrial Electronics, 2010, 57(9): 3075. DOI:10.1109/TIE.2009.2037099 |
 2021, Vol. 53
2021, Vol. 53


