2. 苏州科技大学 机械工程学院,江苏 苏州 215009
2. School of Mechanical Engineering, Suzhou University of Science and Technology, Suzhou 215009, Jiangsu, China
随着人类对海洋开发的深入,面临的水下作业环境也愈发险恶。自主水下机器人(autonomous underwater vehicle, AUV)作为海洋探测的重要工具,对其性能也提出了更高的要求。传统的水下机器人因采用螺旋桨推进而存在效率低、噪声大、机动性差等缺陷,已无法适应日益发展的水下作业要求。近年来,受鱼类优越的游动性能启发,科研人员对鱼类的游动机理进行了深入的研究,模仿并研发了各类高性能的仿生机器鱼[1]。作为自主水下作业装备,仿生机器鱼需要对周围流场环境进行有效地感知和识别。然而,受水质浑浊度和复杂非结构的水下地形环境影响,传统的光学成像和声呐探测技术应用受到限制,严重制约了仿生水下机器人的作业能力。
侧线系统是鱼类长期适应水下环境进化出来的一类特有感觉系统,它使鱼类能够在漆黑、浑浊的水下环境中通过感知水流、水压和微弱电场的动态变化进而有效识别环境中的障碍物,造就了鱼类趋流、集群、捕食、避障等众多奇妙行为[2]。鱼类侧线系统神奇的环境感知能力引起了研究人员的广泛关注,国内外学者主要从侧线感知机理、仿生人工侧线(artificial lateral line, ALL)和信号处理等3个方面对其展开了研究。Hofer最早进行了侧线功能的研究[3], 并推测侧线在感受水体刺激的过程中发挥了感受器的功能。文献[4]通过微观分析和行为实验研究了两类洞穴鱼的侧线系统结构及工作机理。受侧线感知系统启发,研究人员构建了形式多样的ALL系统,其结构主要分为两类,一类是基于微机电系统(MEMS)技术开发的人工纤毛传感器[5],另一类是利用压力传感器阵列来实现流场感知功能[6]。此外,研究人员还提出了多种数据处理算法,对获取的流场压力信息进行融合处理[7-8]。
综合现有文献研究可知,ALL在流场流速检测和运动物体位置识别等方面获得了较好的应用。ALL阵列被安装在刚性的载体上,通过采集周围流场的压力变化信息实现对来流速度或运动物体位置的预测[9-10]。然而在基于仿生机器鱼的水下作业中,如:海底石油管道漏油检测、海底地形地貌测绘、水下桥墩或大坝健康状态监测等,ALL需要安装在柔性波动的机器鱼体表面且同时需要对流场速度和靠近作业对象壁面的距离进行检测,以便调整自身游动模式实现高效稳定地对目标近距离作业。本文通过研究仿鲹科机器鱼近壁面游动的体表压力变化特性,提出了一种基于ALL和多层前馈神经网络的近壁面流场识别方法,实现了仿生机器鱼近壁面游动的来流速度和靠壁距离预测,为水下复杂非结构环境感知提供了一种新思路。
1 理论分析鱼类侧线系统包含表面神经丘和侧线管神经丘,分别用于感知流体的速度和加速度(与压力相关)信号,并将该时空动态变异的微小信息传导至中枢神经,提供给鱼体即时的位向和环境水动态信息,助其调整身体的行为模式,达到适应环境的目的。考虑不可压缩、等温的牛顿流体(密度ρ,黏度μ),Navier-Stokes(N-S)方程可表示为
| $ \rho \frac{{D\mathit{\boldsymbol{V}}}}{{Dt}} = - \nabla \mathit{\boldsymbol{P}} + \rho g + \mu {\nabla ^2}\mathit{\boldsymbol{V}}, \mathit{\boldsymbol{V}} = (u, v, w) $ | (1) |
由上式可知,压力-∇P和动量∇2V之间存在函数关联,速度减少会导致压力值的上升,因此通过分析鱼体体表压力值的变化可对来流速度进行估计。此外,鱼体主动对称波动变形和受流体作用下的被动运动会导致周围流场的周期性变化,进而影响鱼体体表压力分布。作用于单位长度鱼体的侧向力R可表示为
| $ R = \left( {\frac{\partial }{{\partial t}} + U\frac{\partial }{x}} \right)(m(x)w(x, t)) $ | (2) |
其中:m(x)为单位长度鱼体的虚质量,w(x, t)为鱼体相对于流体的侧向运动速度。
靠近壁面波动时,鱼体推动流体流向侧壁时,流体因受到侧壁面的阻挡,速度下降,从而导致w(x, t)的值上升,侧向力R增大。因此,通过检测鱼体两侧对称位置的体表压力差值可对靠壁距离进行预测估计。
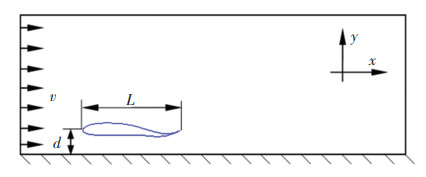
2 数据采集及处理 2.1 仿真建模仿真计算模型如图 1所示,左侧为流场入口边界,来流速度为v,右侧为压力出口边界,上/下边界和鱼体表面定义为无滑壁面边界。采用基于非结构化网格的非定常N-S求解器对流场进行仿真,其中N-S方程见式(1)。时间离散采用一阶隐格式,黏性项采用标准态离散,压力-速度耦合项用SIMPLE方式,而对流项则用二阶迎风格式离散。通过编写UDF程序控制机器鱼进行波动运动,采用弹簧光顺和局部重构的动网格技术对网格进行更新。
|
图 1 仿真模型 Fig. 1 Simulation model |
利用长度为L的二维Joukowski翼型模拟机器鱼在距离侧壁面为d的位置做波动运动,采用的鲹科波动方程[11]表示为
| $ \left\{ {\begin{array}{*{20}{l}} {y(x, t) = A(x)\sin (kx - 2\pi ft)}\\ {A(x) = {a_0} + {a_1}x + {a_2}{x^2}} \end{array}} \right. $ | (3) |
其中:x为体长方向的坐标;A(x)为横向运动的波幅包络,为确保在鱼体尾部具有最大位移,依据文献[12]的实验数据可确定波幅包络系数a0=0.02、a1=-0.008、a2=0.16;y(x, t)为t时刻x处的横向位移;
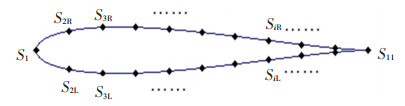
为了采集流场压力变化信息,如图 2所示,在仿生机器鱼体表配置了一系列虚拟压力传感器,构建流场识别ALL系统用于提取仿生机器鱼波动推进过程中的实时体表压力数据。其中头部压力传感器记为S1,沿体长方向均匀对称分布的压力传感器组记为Si
|
图 2 ALL传感器布局 Fig. 2 ALL sensor arrangement |
考虑来流速度v、靠壁距离d以及波动频率f对仿生机器鱼体表压力的影响,本文进行了一系列的参数化仿真实验。仿真实验中设置来流速度为0~1.0 m/s、靠壁距离为0.1L~2L、波动频率为0.5~2.5 Hz、ALL采样频率为0.5~2.5 kHz,开展了277次仿真实验。其中d=2L表示无壁面效应状态。ti时刻,头部压力传感器S1采集的压力数据记为P(s1, ti),压力传感器组Si采集的压力数据表示为P(Si, ti)
| $ \mathit{\boldsymbol{P}}(t) = \left( {\begin{array}{*{20}{c}} {P\left( {{s_1}, {t_0}} \right)}&{P\left( {{s_1}, {t_1}} \right)}& \cdots &{P\left( {{s_1}, {t_T}} \right)}\\ {P\left( {{s_2}, {t_0}} \right)}&{P\left( {{s_2}, {t_1}} \right)}& \cdots &{P\left( {{s_2}, {t_T}} \right)}\\ \vdots & \vdots & \vdots & \vdots \\ {P\left( {{s_{11}}, {t_0}} \right)}&{P\left( {{s_{11}}, {t_1}} \right)}& \cdots &{P\left( {{s_{11}}, {t_T}} \right)} \end{array}} \right) $ | (4) |
为了消除鱼体自身波动运动对侧向压力分量的影响,对头部压力传感器S1采集的压力数据在运动周期T内取均值,同时对传感器组Si采集的压力数据求和并取均值,可得
| $ \left\{ {\begin{array}{*{20}{l}} {\bar P\left( {{s_1}} \right) = \frac{1}{T}\int_0^T p \left( {{s_1}, t} \right){\rm{d}}t}\\ {\bar P\left( {{s_i}} \right) = \frac{1}{T}\int_0^T {\left[ {{p_{\rm{L}}}\left( {{s_{i{\rm{L}}}}, t} \right) + {p_R}\left( {{s_{i{\rm{R}}}}, t} \right)} \right]} {\rm{d}}t, i = 2, \cdots , 11} \end{array}} \right. $ | (5) |
由于鱼体自身波动运动的对称性,无壁面效应时,P(si)应趋于0;而在壁面效应作用下,P(si)则不为0,且与靠壁距离相关。
进一步,对各压力传感器采集的压力数据进行无量纲化处理,可得到归一化压力系数表示为
| $ {C_p}\left( {{s_i}} \right) = \frac{{\bar P\left( {{s_i}} \right)}}{{2\rho {U^2}}}, i = 1, 2, \cdots , 11 $ | (6) |
其中U=λf。
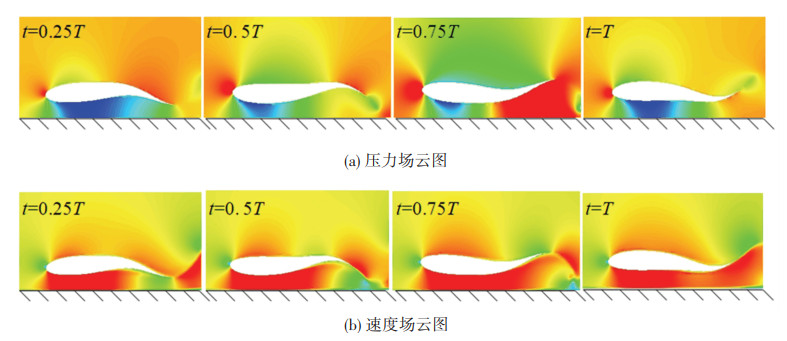
2.2 仿真结果分析图 3为仿生机器鱼近壁面游动(d=0.2L)时,不同时刻的流场结构分布云图。由图 3(a)压力场云图可知,在整个运动周期内,鱼体和壁面之间始终存在一个低压区。受壁面效应的影响,鱼体对称波动形成的压力场呈现出非对称分布。同理,如图 3(b)所示的速度场云图,由于壁面效应的存在,鱼体和壁面之间始终出现一个高速区且速度场也呈现出非对称分布。压力场和速度场的非对称分布为近壁面环境的识别提供了依据。
|
图 3 流场分布云图 Fig. 3 Flow field distribution |
对头部传感器S1和传感器组Si(i=2, …, 11)在不同靠壁距离d和来流速度v下采集并处理得到的压力系数求方差,可得到如图 4所示的压力系数方差曲线。由图 4(a)可知,在给定的来流速度v=0.2~1.0 m/s,头部传感器S1在不同靠壁距离下采集的压力系数方差值随来流速度增大而增大,沿着体长方向中部的传感器组S2, …, S6采集的压力系数方差值保持较低的水平,尾部传感器组S7, …, S11采集的压力系数方差值呈上升趋势变化。由图 4(b)可知,在给定的靠壁距离d=0.2L~0.8L内,传感器阵列在不同来流速度下采集的压力系数方差值沿体长方向的变化趋势与图 4(a)保持一致。数据样本方差体现了数据的离散程度,利用传感器采集的压力系数方差值可衡量传感器对流场参数的辨识度,方差值越大表示该传感器组对流场参数变化越敏感,传感器组在整个阵列中的信息权值也越大。由此可根据传感器组采集的压力数据方差值对传感器的布局和数量进行优化。

|
图 4 压力系数方差曲线 Fig. 4 Pressure coefficient variance curves |
利用仿真实验采集的压力数据,训练并建立基于多层前馈神经网络的来流速度和靠壁距离预测回归模型。多层前馈神经网络的结构参数包括输入数据特征数量、隐藏层数量、隐藏层神经元数量、隐藏层/输出层激活函数的选择。如表 1所示,建立来流速度和靠壁距离两个预测回归模型,采用ReLU函数作为隐藏层激活函数,输出层采用线性激活函数。为了寻找优化的神经网络结构,将隐藏层层数从1逐步递增到5,第1隐藏层的神经元数量从输入特征数量逐步递增到3倍,每次步进为1。各隐藏层神经元数量呈递减规律配置,后一层神经元数量是前一层的2/3。
| 表 1 多层前馈神经网络结构参数 Tab. 1 Structural parameters of multilayer feed forward neural network |
采用均方误差(mean-square error, MSE)和决定系数R2对不同配置的网络结构进行性能评估:
| $ {\rm{MSE}} = \frac{{\sum\nolimits_{i = 1}^n {{{\left( {{{\hat Y}_i} - {Y_i}} \right)}^2}} }}{n}, {R^2} = 1 - \frac{{\sum\nolimits_{i = 1}^n {{{\left( {{Y_i} - {{\hat Y}_i}} \right)}^2}} }}{{\sum\nolimits_{i = 1}^n {{{\left( {{Y_i} - \bar Y} \right)}^2}} }} $ | (7) |
式中Ŷi, Yi, Y分别表示预测值、观测值和均值。
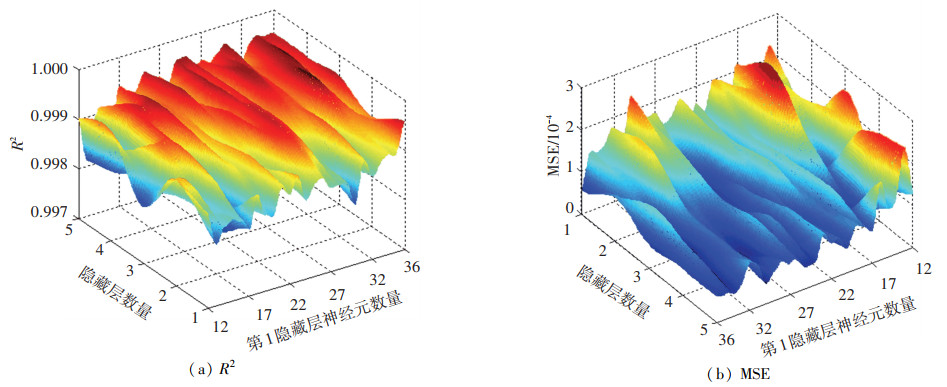
来流速度预测回归模型取不同结构参数时的评价指标,如图 5所示。隐藏层数量和隐藏层神经元数量决定了神经网络的容量,网络容量越大,时间复杂度越大且越容易过拟合,因此在保证模型性能指标的情况下应尽量减小网络容量。由图 5可知,在给定的结构参数范围内,隐藏层数量和隐藏层神经元数量对R2和MSE的影响都很小,为减小网络容量首先可确定采用1个隐藏层。进一步由图 5(b)可知,采用1个隐藏层且隐藏层神经元为36时,MSE的取值最小。因此综合考虑模型性能指标和网络容量,可确定最优的来流速度神经网络预测回归模型的结构为12-36-1。
|
图 5 来流速度预测回归模型评价指标 Fig. 5 Evaluation indexes of regression model for inflow velocity prediction |
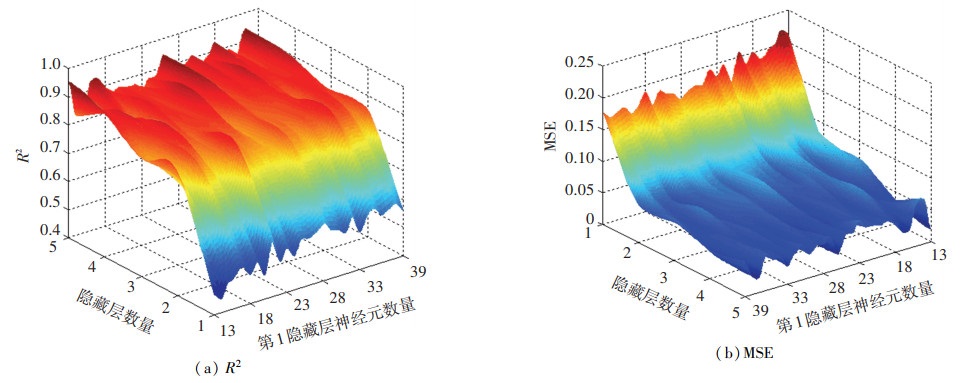
靠壁距离预测回归模型取不同结构参数的评价指标,如图 6所示,由图 6可知,在给定的参数范围内,随隐藏层数量增多,R2首先呈增大趋势变化而MSE呈下降趋势变化,当隐藏层数量大于等于4时,R2和MSE基本都保持不变,为保证模型性能指标,可确定隐藏层数量的取值为4。此外,隐藏层神经元数量对R2和MSE的影响都很小,为减小网络容量,第1隐藏层神经元数量应取最小值13。综上所述,可获得最优的靠壁距离预测回归模型的结构为13 - 13 - 8 - 5 - 3 - 1。
|
图 6 靠壁距离预测回归模型评价指标 Fig. 6 Evaluation indexes of regression model for near wall distance prediction |
依据2.2节对人工侧线采集的压力系数方差值的分析结果,采用特征变量逐步消除法对输入数据特征进行缩减。如表 3所示,对压力传感器采集的压力系数方差值按照从小到大的顺序逐步消除对应的输入数据特征。
| 表 3 数据特征消除顺序列表 Tab. 3 Data feature elimination order |
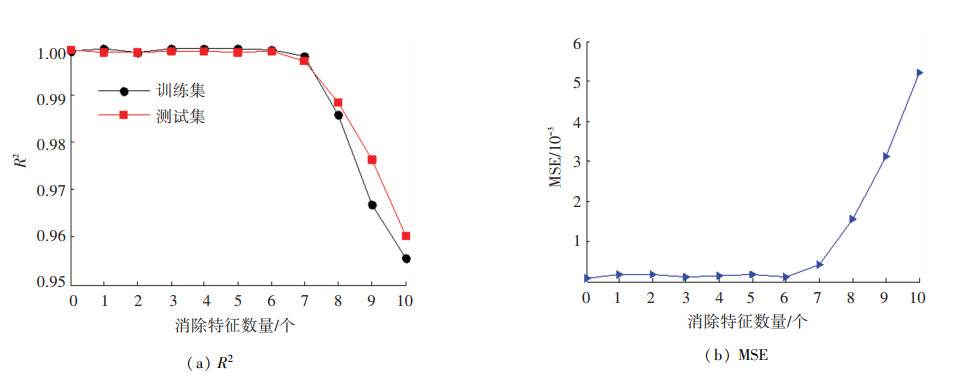
图 7为来流速度预测回归模型中数据特征消除数量对评价指标的影响关系曲线。由图 7(a)可知,当消除数据特征数量小于等于6个时,在训练集和测试集上的R2基本保持平稳,随着消除数据特征数量的进一步增大,R2呈快速下降趋势变化。对于MSE由图 7(b)同样可以看出,当消除数据特征数量小于等于6个时变化很小,而大于6个时呈快速增长趋势变化。由此可知,数据特征序列{ S5, S6, S4, S7, S3, S8}对来流速度预测回归模型的预测效果影响很小,特征消除后的优化特征集为{ S1, S2, S9, S10, S11, f}。
|
图 7 来流速度预测回归模型数据特征消除的评价指标 Fig. 7 Evaluation indexes of data feature elimination in regression model of inflow velocity prediction |
图 8为靠壁距离预测回归模型数据特征消除数量对评价指标的影响关系。由图 8(a)可知,当消除数据特征数量小于等于5个时,在训练集和测试集上的R2变化很小,而当消除数据特征数量大于5个时,在训练集和测试集上的R2呈快速下降趋势变化。同理,由图 8(b)可知,当消除数据特征数量大于5个时,在测试集上的MSE呈快速上升趋势变化。由此可知,数据特征序列{S3, S4, S2, S5, S6}对靠壁距离预测回归模型的预测效果影响甚微,应予以消除,最终可获得优化的模型输入数据特征集为{ S7, S8, S9, S1, S10, S11, f, v }。

|
图 8 靠壁距离预测回归模型数据特征消除的评价指标 Fig. 8 Evaluation indexes of data feature elimination in regression model of near wall distance prediction |
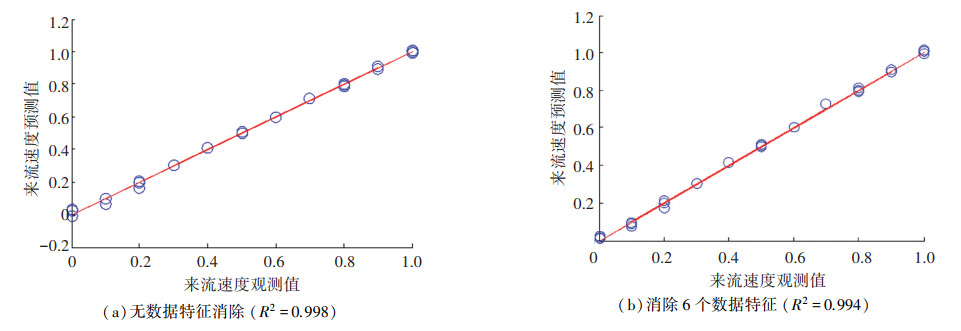
图 9、10分别为来流速度和靠壁距离预测回归模型在数据特征消除前后的预测效果对比。由图 9可知,来流速度预测回归模型对给定范围内的来流速度预测效果很好(R2=0.998),消除6个数据特征后,预测效果基本保持不变(R2=0.994)。由图 10可知,靠壁距离预测回归模型对靠近壁面时的状态预测效果较好,而远离壁面状态(d=2L)的预测效果变差(R2=0.912)。消除5个弱相关的数据特征后,预测效果变化不大(R2=0.883)。
|
图 9 来流速度预测回归模型数据特征消除预测效果对比 Fig. 9 Comparison of prediction effects of data feature elimination in regression model of inflow velocity |

|
图 10 靠壁距离预测回归模型数据特征消除预测效果对比 Fig. 10 Comparison of prediction effects of data feature elimination in regression model of near wall distance |
提出了一种基于人工侧线的近壁面波动推进仿生机器鱼流场识别方法,采用计算流体动力学方法开展了参数化仿真实验,采集了不同流场状况下仿生机器鱼的体表压力数据,训练并建立了基于多层前馈神经网络的流场参数预测回归模型,并进行了模型结构优化和数据特征缩减。得出主要结论如下:
1) 仿生机器鱼近壁面波动推进将导致周围流场结构的非对称分布,为基于人工侧线的流场参数识别提供了依据。
2) 获得了侧线压力传感器阵列在不同来流速度和靠壁距离下的压力系数方差值,揭示了不同位置压力传感器对流场参数变化的辨识度。
3) 隐藏层数量和隐藏层神经元数量对来流速度预测回归模型的评价指标影响很小,而靠壁距离预测回归模型的隐藏层数量增多将导致R2增大,MSE减小。
4) 沿体长方向中部的压力传感器组对来流速度和靠壁距离的预测效果影响小,应予以消除,计算结果表明所提出的方法对来流速度和靠壁距离具有较好的预测效果。
| [1] |
王安忆, 刘贵杰, 王新宝, 等. 身体/尾鳍推进模式仿生机器鱼研究的进展与分析[J]. 机械工程学报, 2016, 52(17): 137. WANG Anyi, LIU Guijie, WANG Xinbao, et al. Development and analysis of body and/or caudal fin biomimetic robot fish[J]. Journal of Mechanical Engineering, 2016, 52(17): 137. |
| [2] |
李超, 王晓杰, 宋佳坤. 鱼类的侧线机械感受系统和仿生学等应用研究[J]. 科学通报, 2017, 62: 2509. LI Chao, WANG Xiaojie, SONG Jiakun. Structure and function of the mechanosensory lateral line system in fish and biomimetic[J]. Chinese Science Bulletin, 2017, 62: 2509. |
| [3] |
PARKER G H. The function of the lateral-line organs in fishes[J]. Bulletin of the Bureau Fisheries, 1904, 24: 185. |
| [4] |
JIANG Y G, FU J C, ZHANG D Y, et al. Investigation on the lateral line systems of two cavefish: Sinocyclocheilus macrophthalmus and S. microphthalmus (Cypriniformes: Cyprinidae)[J]. Journal of Bionic Engineering, 2016, 13: 108. DOI:10.1016/S1672-6529(14)60164-5 |
| [5] |
YAUL F M, BULOVIC V, LANG J H. A flexible underwater pressure sensor array using aconductive elastomer strain gauge[J]. Journal of Microelectromechanical Systems, 2012, 21(4): 897. DOI:10.1109/JMEMS.2012.2190714 |
| [6] |
ZHENG X, WANG C, FAN R, et al. Artificial lateral line based local sensing between two adjacent robotic fish[J]. Bioinspiration & Biomimetics, 2018, 13: 016002. |
| [7] |
TUHTAN J A, FUENTES-PEREZ J F, TOMING G, et al. Flow velocity estimation using a fish-shaped lateral line probe with product moment correlation features and a neural network[J]. Flow Measurement and Instrumentation, 2017, 54: 1. DOI:10.1016/j.flowmeasinst.2016.10.017 |
| [8] |
吴乃龙, 吴超, 葛彤, 等. 基于鱼类体线感知机理的水下机器人水流场识别研究[J]. 机械工程学报, 2016, 52(13): 54. WU Nailong, WU Chao, GE Tong, et al. Flow recognition of underwater vehicle based on the perception mechanism of lateral line[J]. Journal of Mechanical Engineering, 2016, 52(13): 54. |
| [9] |
刘钰, 胡桥, 赵振轶, 等. 基于EMD与SVM的仿生机器鱼人工侧线智能探测方法[J]. 水下无人系统学报, 2019, 27(2): 174. LIU Yu, HU Qiao, ZHAO Zhenyi, et al. Intelligent detection of artificial lateral line for biomimetic robotic fish based on EMD and SVM[J]. Journal of Unmanned Undersea Systems, 2019, 27(2): 174. |
| [10] |
XU D, LV Z Y, ZENG H L, et al. Sensor placement optimization in the artificial lateral line using optimal weight analysis combining feature distance and variance evaluation[J]. ISA Transactions, 2018, 75: 110. |
| [11] |
BORAZJANI I, SOTIROPOULOS F. Numerical investigation of the hydrodynamics of carangiform swimming in the transitional and inertial flow regimes[J]. Journal of Experimental Biology, 2008, 211: 1541. DOI:10.1242/jeb.015644 |
| [12] |
VIDELER J J, HESS F. Fast continuous swimming of two pelagic predators, saithe (Pollachius virens) and mackerel (Scomber scombrus): a kinematic analysis[J]. Journal of Experimental Biology, 1984, 109: 209. DOI:10.1242/jeb.109.1.209 |
 2021, Vol. 53
2021, Vol. 53



