2. 智能机器人教育部工程研究中心(复旦大学),上海 200433
2. Engineering Research Center of AI & Robotics, Ministry of Education (Fudan University), Shanghai 200433, China
随着工作环境的日益复杂,对于工业机器人的定位性能提出了更高的要求。通常使用工业机器人的重复定位精度和绝对定位精度来评价它的定位性能[1]。在实际的工业环境中,由于工业机器人连杆变形等自身因素引起的几何误差占定位误差的90%,所以将其作为机器人定位误差研究的重点。常用的补偿法为软件法[2-3],补偿通常分为误差建模、数据测量、参数辨识、误差补偿4步。建立合适的误差模型可以对工业机器人的几何误差进行分析,常用的误差模型有D-H模型[4];误差测量法可分为开环法、闭环法和轴线测量法,测量工具有三坐标测量仪和激光测距仪[5];误差辨识法有最小二乘法,还有Levenberg-Marquardt算法[6-7]。随着智能算法的高速发展,近年来许多学者对智能算法在机器人定位误差的应用进行了探索。粒子群算法尤其受到学者青睐,Wang等[8]将改进粒子群算法用于机器人运动标定中最佳位姿选择,实验证明了提出算法的有效性。房立金等[9]针对并联机器人与串联机器人,提出一种通用的运动学标定方法,通过量子粒子群算法进行了误差求解,最后实验验证了所提算法的有效性。总结现有研究发现,工业机器人几何误差方程是一个高维的非线性方程,粒子群算法在求解过程中迭代所需要的粒子群数目较大,导致粒子群算法的迭代效率降低。但是工业机器人对速率的要求却越来越高。
有学者指出,粒子群数目对于算法的迭代时间影响很大,受此启发,本文首先对标准粒子群算法的数目进行线性递减,同时由于粒子群算法迭代后期大多数粒子都聚集在最优解附近,所以按照算法的迭代规律对标准粒子群算法的速度更新公式进行了更改,并进行了仿真实验,证明了所提算法在保证收敛精度同时大幅提高了运算效率[10]。
1 几何误差参数标定的数学模型 1.1 DH模型建立机器人常用的模型是DH模型,目前,DH模型已被广泛应用于工业机器人中[11],由DH模型可得到工业机器人相邻连杆的转换公式:
| $\begin{array}{l} \mathit{\boldsymbol{A}}{_i} = {\rm{rot}}\left( {{Z_i}, {\theta _i}} \right){\rm{trans}}\left( {{Z_i}, {d_i}} \right){\rm{trans}}\left( {{X_i}, {a_i}} \right){\rm{rot}}\left( {{X_i}, {\alpha _i}} \right) = \\ \;\;\;\left[ {\begin{array}{*{20}{c}} {\cos {\theta _i}}&{ - \sin {\theta _i}\cos {\alpha _i}}&{\sin {\theta _i}\sin {\alpha _i}}&{{a_i}\cos {\theta _i}}\\ {\sin {\theta _i}}&{\cos {\theta _i}\cos {\alpha _i}}&{ - \cos {\theta _i}\sin {\alpha _i}}&{{a_i}\sin {\theta _i}}\\ 0&{\sin {a_i}}&{\cos {\alpha _i}}&{{d_i}}\\ 0&0&0&1 \end{array}} \right] \end{array}$ | (1) |
式中:ai为工业机器人第i个关节的连杆长度;θi为关节角;di为连杆偏距;αi为关节扭角, i=1,2,…,n, n为关节数目。机器人名义位姿为
| ${\mathit{\boldsymbol{T}}_{\rm{n}}} = {\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{A}}_2}{\mathit{\boldsymbol{A}}_3}{\mathit{\boldsymbol{A}}_4}{\mathit{\boldsymbol{A}}_5}{\mathit{\boldsymbol{A}}_6}{\mathit{\boldsymbol{A}}_{{\rm{tool}}}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_n}}&{{\mathit{\boldsymbol{P}}_n}}\\ 0&1 \end{array}} \right]$ | (2) |
式中:Rn∈R3×3为名义姿态旋转矩阵,Pn∈R3×1为位置平移矩阵。同理,当机器人的几何参数存在误差Δθi、Δdi、Δai、Δαi时,机器人的实际姿态可以表示为
| ${\mathit{\boldsymbol{T}}_{\rm{r}}} = \mathit{\boldsymbol{A}}_1^{\rm{r}}\mathit{\boldsymbol{A}}_2^{\rm{r}}\mathit{\boldsymbol{A}}_3^{\rm{r}}\mathit{\boldsymbol{A}}_4^{\rm{r}}\mathit{\boldsymbol{A}}_5^{\rm{r}}\mathit{\boldsymbol{A}}_6^{\rm{r}}\mathit{\boldsymbol{A}}_{{\rm{tool}}}^{\rm{r}}$ | (3) |
令ΔP=Pr-Pn,ΔP=(δpx, δpy, δpz)T表示工业机器人实际位置与名义位置的误差。
1.2 目标函数| $f = \min (\sum\limits_{i = 1}^N {\sqrt {({{\left( {\delta {p_{xi}}} \right)}^2} + {{\left( {\delta {p_{yi}}} \right)}^2} + {{\left( {\delta {p_{zi}}} \right)}^2}} }) $ | (4) |
式中:N为机器人误差标定点的数目,f是几何参数误差集(Δai, Δdi, Δαi, Δθi, )的函数,当工业机器人处于不同的关节角位置时刻,获取实际位置与名义位置的误差,然后通过优化算法求解(Δai, Δdi, Δαi, Δθi, )的真实值,进而减小实际误差。由于在D-H模型中,需要求解的参数有24个,属于高维非线性方程求解问题,可以用仿生算法求解。
2 改进粒子群算法的几何参数标定将传统的粒子群算法用于工业机器人的几何误差标定耗时较长,因为获取工业机器人6个关节的几何误差参数多达24个,参数的求解属于高维函数优化问题。粒子群迭代求解的粒子数目较大,迭代所需时间较长,所以提出改进算法。
粒子群的每个粒子代表问题的一个潜在解,标准的粒子群算法更新公式可表示为[12].
| $\begin{array}{*{20}{c}} {{v_{ij}}\left( {t + 1} \right) = w{v_{ij}}\left( t \right) + {c_1}{r_1}\left( {{p_{ij}}\left( t \right) - {x_{ij}}\left( t \right)} \right) + }\\ {{c_2}{r_2}\left( {{g_{ij}}\left( t \right) - {x_{ij}}\left( t \right)} \right)} \end{array}$ | (5) |
| ${x_{ij}}\left( {t + 1} \right) = {x_{ij}}\left( t \right) + {v_{ij}}\left( {t + 1} \right)$ | (6) |
从时间复杂度的角度看,传统PSO算法每一次迭代的粒子数目不变,假设每次迭代的粒子数目都是N,Max dt表示最大迭代次数,每一个粒子每次迭代需运行时间为T,则传统PSO算法的每次迭代需要的总时间为N*Max dt*T。在求解工业机器人的几何参数标定这种高维函数问题时,由于粒子群数目较大且持续不变,就会导致算法迭代时间较长, 所以本文提出将粒子群的粒子数目进行线性递减:
| $\begin{array}{l} N = {\rm{round}}({N_{{\rm{max}}}} - \left( {t - 1} \right)*\left( {{N_{{\rm{max}}}} - {N_{{\rm{min}}}}} \right)/\\ \;\;\;\;\;\;\;\;\left( {{\rm{Max}}\;{\rm{d}}t - 1} \right)) \end{array}$ | (7) |
式中:Nmax为粒子数目最大值,Nmin为粒子数目最小值, Max dt为粒子设定的迭代次数,t为当前的迭代次数。传统粒子群算法中,随着t的变化,粒子群中粒子的数目N=Nmax始终不变;而改进粒子群算法中,当t=1时,N=Nmax,当t>1以后,每次迭代的粒子数目N逐渐线性递减,则改进粒子群算法迭代总时间为(Nmax+Nmin)/2*Max dt*T, 由于(Nmax+ Nmin)/2小于Nmax,所以改进粒子群算法的整体迭代时间减少。
2.2 粒子群算法的分段迭代 2.2.1 DSPSO算法简介传统粒子群算法早期收敛速度高,但是在算法后期,求解精度降低。李洪亮等[13]借鉴协同进化算法思想,提出了改进粒子群算法DSPSO。DSPSO算法将粒子群分为“开发者”与“探索者”,将标准的粒子群体更改为3个子群s1、s2和s3,采用不同的进化方程为
| $\left\{ \begin{array}{l} {v_{ij}}\left( {t + 1} \right) = {\rm{ }}w{v_{ij}}\left( t \right) + {c_1}{r_1}({p_{ij}}\left( t \right) - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{x_{ij}}\left( t \right)) + {c_2}{r_2}\left( {{g_{ij}}\left( t \right) - {x_{ij}}\left( t \right)} \right)\\ w = 0.3 \end{array} \right.$ | (8) |
| $\left\{ \begin{array}{l} {v_{ij}}\left( {t + 1} \right) = w{v_{ij}}\left( t \right) + {c_2}{r_2}({g_{ij}}\left( t \right) -{x_{ij}}\left( t \right)) \\ w = 0.7 \end{array} \right.$ | (9) |
| $\left\{ \begin{array}{l} {v_{ij}}\left( {t + 1} \right) = {\rm{ }}w{v_{ij}}\left( t \right) + {c_1}{r_1}({p_{ij}}\left( t \right) - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{x_{ij}}\left( t \right)) + {c_2}{r_2}\left( {{g_{ij}}\left( t \right) - {x_{ij}}\left( t \right)} \right)\\ w = 0.9 \end{array} \right.$ | (10) |
其中子群体s2是开采者,它的搜索区域主要在当前群体最优位置的小范围内。
2.2.2 改进的粒子群速度更新公式在求解机器人几何参数标定的前期,粒子群速度迭代是采用标准粒子群算法进行迭代;而在改进粒子群算法的粒子数目线性递减后期,粒子群的粒子数目变少,同时大多数粒子聚集在最优解附近。则受DSPSO算法中式(9)启发, 采用式(11)进行迭代,
| $\left\{ \begin{array}{l} {v_{ij}}\left( {t + 1} \right) = w{v_{ij}}\left( t \right) + {c_2}{r_2}\left( {{g_{ij}}\left( t \right) - {x_{ij}}\left( t \right)} \right)\\ w = 0.4 \end{array} \right.$ | (11) |
同时按照Shi等[14]的研究,在算法后期对w取值为0.4,使得改进粒子群算法在迭代后期更集中于最优解附近的局部。
2.3 改进粒子群算法几何参数标定流程本文所提算法简称为基于两段式的动态粒子群算法(LDPSO-BT算法),求解工业机器人几何参数标定流程为:
1) 在工业机器人几何参数误差范围内对算法初始化。
2) 按照式(4)求得粒子的个体适应度值与全局适应度值。
3) 按照式(7)更新粒子群的数目,以便提高几何参数标定的迭代效率。
4) 判断当前迭代次数t是否>K*Max dt,若否,则按照式(5)对粒子群速度进行更新;否则,按照式(11)对粒子群速度进行更新。
5) 更新种群的个体与全局极值。
6) 判断是否满足结束条件,若不满足,则转到第2步;若满足,则结束,进而获取几何参数误差。
3 实验与结果 3.1 位姿产生采用库卡(KUKA)机器人有限公司生产的KUKA KR5 arc机器人验证所提算法的有效性。KUKA KR5 arc机器人DH模型参数见表 1[11]。几何参数误差如表 2。
| 表 1 KR5 arc机器人名义参数 Tab. 1 Nominal geometric parameters of KR5 arc robot |
| 表 2 KR5 arc机器人几何参数误差 Tab. 2 Geometric parameters errors of KR5 arc robot |
在[-0.25, 0.25](mm)和[-0.05, 0.05](rad)区间范围内,随机均匀产生30组理论关节角,将之前设定的几何误差加入到机器人的名义几何参数中,代入式(3)中,同时通过式(2)求出理论关节角,再将30组关节误差代入式(4),便可得到相应的适应度值公式。
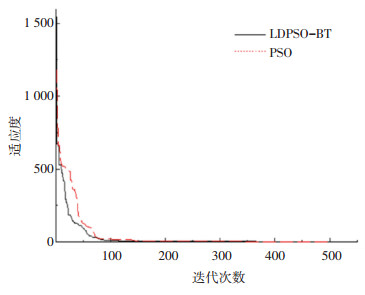
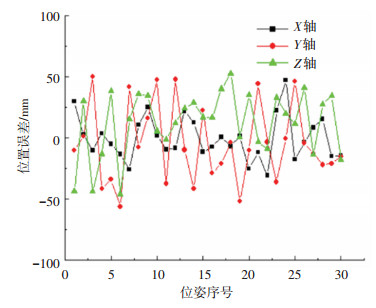
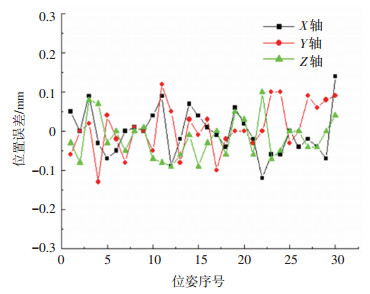
3.2 结果与讨论设定改进的LDPSO-BT粒子群算法初始最大粒子数Nmax为240,最小粒子数Nmin为40,迭代次数Max dt为500,w1为0.8, w2为0.4,参数k为0.8,加速系数c1和c2都为1.49[15]。表 3是传统PSO和LDPSO-BT算法分别迭代10次的平均适应度、最佳适应度和平均耗时。图 1为两种粒子群算法在Intel(R)Core(TM)i7-8550U主频4.00 GHz计算机上采用Matlab9.1迭代500次的最佳收敛曲线图。图 2是机器人标定前沿X、Y、Z轴方向的末端位置误差,图 3和图 4分别是工业机器人经过传统PSO算法和LDPSO-BT算法标定后的沿X、Y、Z轴方向的末端位置误差。
| 表 3 LDPSO-BT和PSO实验结果 Tab. 3 LDPSO-BT and PSO experiment results |
|
图 1 进化过程 Fig. 1 Evolution process |
|
图 2 补偿前位置误差 Fig. 2 Errors before compensation |
|
图 3 补偿后位置误差(PSO方法) Fig. 3 Errors after compensation (PSO) |

|
图 4 补偿后位置误差(LDPSO-BT方法) Fig. 4 Errors after compensation (LDPSO-BT) |
从表 3中可以看出,与传统PSO算法相比,LDPSO-BT算法平均适应度与最佳适应度都基本相差不大,但LDPSO-BT算法在确保收敛精度的同时,迭代时间减少了41.85%,可以有效地提高算法的迭代效率。
从图 1中可以看出,两种粒子群算法的收敛趋势相近,收敛精度也相当。
从图 2中可以看出,在标定前,X、Y、Z轴的最大误差绝对值分别为47.1、51.8、52.8 mm。由图 3可知,经过传统PSO算法标定后,X、Y、Z轴的最大误差绝对值降低为0.14、0.13、0.10 mm。从图 4中可以看出,经过LDPSO-BT算法标定后,X、Y、Z轴的最大误差绝对值降低为0.18、0.18、0.15 mm,可见经过标定后,传统PSO算法和LDPSO-BT算法均可大幅减小沿X、Y、Z轴方向的末端位置误差,同时LDPSO-BT拥有更高的收敛速度。
4 结语1) 本文提出了一种新的LDPSO-BT算法,结合标准粒子群算法的迭代规律,对粒子群数目进行线性递减,同时在算法后期,使用改进的速度迭代公式进行迭代,仿真实验表明,所提算法可以大幅提升工业机器人的定位精度,同时具备高效、快速的优势。
2) 工业机器人末端定位误差主要由于其几何连杆参数误差引起,通过辨识出实际的几何连杆参数值,可以大幅提高工业机器人定位精度。
3) 本文的研究为工业机器人动力学参数辨识提供了新的思路,适用于工业机器人离线或者在线动力学参数的辨识,但还需要进行相关实验,以验证本文所提算法在实际动力学参数辨识的效果。
| [1] |
周煦武. 六自由度串联机器人静态位姿误差及其补偿研究[D]. 杭州: 浙江理工大学, 2018 ZHOU Xuwu. Research on static pose error and compensation of six degrees of freedom serial robot[D]. Hangzhou: Zhejiang Sci-Tech University, 2018 http://cdmd.cnki.com.cn/Article/CDMD-10338-1019023540.htm |
| [2] |
CHEN Yonghua, DONG Fenghua. Robot machining: recent development and future research issues[J]. The International Journal of Advanced Manufacturing Technology, 2013, 66(9/10/11/12): 1489. DOI:10.1007/s00170-012-4433-4 |
| [3] |
CHEN Gang, LI Tong, CHU Ming, et al. Review on kinematics calibration technology of serial robots[J]. International Journal of Precision Engineering and Manufacture, 2014, 15(8): 1759. DOI:10.1007/s12541-014-0528-1 |
| [4] |
张旭, 郑泽龙, 齐勇. 6自由度串联机器人D-H模型参数辨识及标定[J]. 机器人, 2016, 38(3): 360. ZHANG Xu, ZHENG Zelong, QI Yong. Parameter identification and calibration of D-H model for 6-DOF serial robots[J]. Robot, 2016, 38(3): 360. DOI:10.13973/j.cnki.robot.2016.0360 |
| [5] |
HOLLERBACH J M, WAMPLER C W. The calibration index and taxonomy for robot kinematic calibration methods[J]. The International Journal of Robotics Research, 1996, 15(6): 573. DOI:10.1177/027836499601500604 |
| [6] |
VEITSCHEGGER W K, WU C H. Robot calibration and compensation[J]. IEEE Journal on Robotics and Automation, 1988, 4(6): 643. DOI:10.1109/56.9302 |
| [7] |
GROTJAHN M, DAEMI M, HEIMANN B. Friction and rigid body identification of robot dynamics[J]. International Journal of Solids and Structures, 2001, 38(10/11/12/13): 1889. DOI:10.1016/S0020-7683(00)00141-4 |
| [8] |
WANG Weidong, SONG Huajian, YAN Zhiyuan, et al. A universal index and an improved PSO algorithm for optimal pose selection in kinematic calibration of a novel surgical robot[J]. Robotics and Computer-Integrated Manufacturing, 2018, 50: 90. DOI:10.1016/j.rcim.2017.09.011 |
| [9] |
房立金, 党鹏飞. 基于量子粒子群优化算法的机器人运动学标定方法[J]. 机械工程学报, 2016, 52(7): 23. FANG Lijin, DANG Pengfei. Kinematic calibration method of robots based on quantum-behaved particle swarm optimization[J]. Journal of Mechanical Engineering, 2016, 52(7): 23. DOI:10.3901/JME.2016.07.023 |
| [10] |
王沁, 李磊, 陆成勇, 等. 平均计算时间复杂度优化的动态粒子群优化算法[J]. 计算机科学, 2010, 37(3): 191. WANG Qin, LI Lei, LU Chengyong, et al. Average computational time complexity optimized dynamic particle swarm optimization algorithm[J]. Computer Science, 2010, 37(3): 191. DOI:10.3969/j.issn.1002-137X.2010.03.046 |
| [11] |
史晓佳. 工业机器人在线误差测量与实时控制补偿技术研究[D]. 天津: 天津大学, 2016 SHI Xiaojia. Research on online error measurement and real-time control compensation technology for industrial robots[D]. Tianjin: Tianjin University, 2016 http://cdmd.cnki.com.cn/Article/CDMD-10056-1018059049.htm |
| [12] |
ENGELBRECHT A P. Fundamentals of computational swarm intelligence[M]. New York: Wiley, 2009.
|
| [13] |
李洪亮, 侯朝桢, 周绍生. 一种高效的改进粒子群优化算法[J]. 计算机工程与应用, 2008, 44(1): 14. LI Hongliang, HOU Chaozhen, ZHOU Shaosheng. High efficient algorithm of modified particle swarm optimization[J]. Computer Engineering and Applications, 2008, 44(1): 14. DOI:10.3778/j.issn.1002-8331.2008.01.005 |
| [14] |
SHI Yuhui, EBERHART R C. Empirical study of particle swarm optimization[C]//Proceedings of the 1999 Congress on Evolutionary Computation. Washington DC: IEEE Computer Society. 1999: 1945-1950. DOI: 10.1109/CEC.1999.785511
|
| [15] |
GAO Guanbin, LIU Fei, SAN Hongjun, et al. Hybrid optimal kinematic parameter identification for an industrial robot based on BPNN-PSO[J]. Complexity, 2018, 2018: 4258676. DOI:10.1155/2018/4258676 |
 2022, Vol. 54
2022, Vol. 54


