2. 哈尔滨工业大学 航天科学与力学系,哈尔滨 150090
2. Department of Aerospace Science and Mechanics, Harbin Institute of Technology, Harbin 150090, China
传统的车辆半主动悬架传感器架构以4个车身加速度传感器和4个高度传感器或4个簧下位置处加速度传感器为主,但这种方案线束复杂,而且成本较高。单车身惯性测量单元(Inertial Measurement Unit, IMU)与适当的姿态解算算法结合可以替代传统的4加速度计方案[1],但需要对其解算方法和安装位置进行理论推导和敏感性分析。IMU能够获得其自身定义坐标系下三轴方向的角速度和加速度,从而获得所需要的姿态和位置信息,因此在汽车、医学等领域得到了广泛应用[2-3]。
IMU在汽车上的应用主要集中在对传感器的信号解析和信号噪声处理上,如对车辆姿态与速度等信息的估计[4],设计平滑估计器提高定位精度[5],利用卡尔曼滤波消除解算误差[6]及降低传感器噪声[7]等。针对IMU安装位置及解算方法的研究主要包括Berkane等[8]提出了一种基于IMU/GPS的加速刚体系统的姿态软测量计算方法,但是其主要针对陀螺等惯性元件进行分析,未给出针对车身姿态估计的一般公式和旋转角次序。Jørgensen等[9]利用IMU软测量技术进行车身姿态估计并进行实验,比较了不同滤波器的效果,但是未给出针对安装位置的敏感性进行分析。意大利米兰理工Savaresi团队[1, 10]在半主动悬架领域享有盛名,该团队利用机器学习方法比较了不同IMU安装位置对车身姿态解算结果的影响。结果表明,针对不同安装位置的解算方法存在差异和不同程度的误差,但是未给出原因说明及理论推导。马亚平等[11]对IMU安装位置的误差提出了一种新的正交补偿方误差法,在存在零偏的大角度安装误差的情况下提高了标定效率;对IMU安装角度进行分析和误差补偿,有一定工程意义以及启发作用。目前的研究主要聚焦于传感器的信号解析,缺乏对IMU安装位置的优化及敏感性分析。
本文专注于研究车身姿态解算及IMU安装位置对解算结果的影响,提出一种新的IMU布置方案及精确的解算方法,并在此基础上利用最优化理论进行参数敏感性分析及布置优化。最后通过实验验证解算公式和布置方案的合理性,对理论研究及工程布置有一定指导意义。
1 半主动悬架传感器新方案传统的半主动悬架传感器布置方案如图 1(a)所示[1, 12]。一般悬架控制器位于车辆后部,导致高度和加速度传感器与悬架控制器之间的线束连接复杂,布置困难,成本高。本文提出一种基于IMU的半主动悬架软测量技术及IMU传感器布置优化方法(见图 1(b)),只需用一个IMU传感器就可以精确计算半主动悬架控制所需要的簧上位置处加速度信息,简化了半主动悬架电气架构和电子控制单元(Electronic Control Unit, ECU)开发流程。IMU与ECU之间仅需要一根电缆连接,节约了开发成本。除此之外只需要4个高度传感器进行悬架高度的闭环控制即可,各传感器通过CAN或其他总线方式与整车网络连接。通过IMU和4个高度传感器就可以用一定的解算方法进行4个悬架簧上位置的高度和加速度的信息识别。相比传统布置方案,新方案可以减少布置难度,节省成本,电器架构简明。但是,只用一个IMU传感器来估算4个悬架位置处的运动学信息依赖于精确的解算方法。为了使该新方案可行,本文提出了由IMU信号获取4个悬架位置处运动学信号的解算方法。
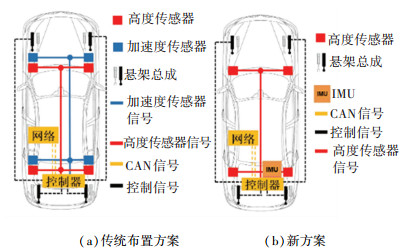
|
图 1 传感器布置方法 Fig. 1 Arrangement methods of sensors |
为了方便后续运动学公式推导,结合实际物理情况,假设整个车身为刚体。并且为了减小由于粘接产生的误差,IMU以及加速度传感器均使用氰基丙烯酸盐(502胶水)进行粘接[13]。无约束刚体运动可以通过6个自由度描述,如图 2所示。OXYZ为与地面固连的绝对坐标系(惯性参考系);OiXmYmZm为原点与IMU安装位置重合、三轴方向与绝对坐标系相同的中间坐标系;OiXiYiZi为与IMU固连的坐标系,其三轴方向为IMU直接测量的加速度方向;P点为需要测量的点。
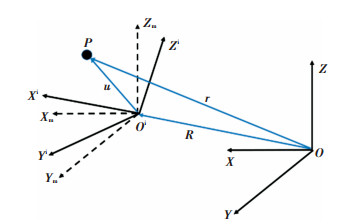
|
图 2 坐标系及矢量定义 Fig. 2 Coordinate system and vector definition |
由刚体一般运动的欧拉定理[14-15]可知,绝对坐标系下P点的运动可分为随基点的平动位移R与绕基点转动的矢量和,即
| $\left\{ \begin{array}{l} \mathit{\boldsymbol{r}} = \mathit{\boldsymbol{R}} + \mathit{\boldsymbol{u}}\\ \mathit{\boldsymbol{u}} = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{u}}^{\rm{i}}}, {\mathit{\boldsymbol{u}}^{\rm{i}}} = {\rm{ }}{[{x^{\rm{i}}}, {\rm{ }}{y^{\rm{i}}}, {\rm{ }}{z^{\rm{i}}}]^{\rm{T}}} \end{array} \right.$ | (1) |
式中:A为旋转坐标矩阵,u为在固连坐标系下P点的位置,ui为u在各坐标轴上的投影。由于车身刚体假设,故该位置是个确定的值。结合车辆运动学特点,在进行旋转矩阵A的计算时先考虑绕固连坐标系下Z轴旋转(横摆角α),再绕Y轴旋转(俯仰角β),最后绕X轴旋转(侧倾角γ)。可得旋转矩阵A表达式为:
| $\mathit{\boldsymbol{A}}\left( {\alpha , \beta , \gamma } \right) = \mathit{\boldsymbol{A}}{_\gamma }{\mathit{\boldsymbol{A}}_\beta }{\mathit{\boldsymbol{A}}_\alpha }$ | (2) |
| $\left\{ \begin{array}{l} {\mathit{\boldsymbol{A}}_\gamma } = \left( {\begin{array}{*{20}{c}} {\cos \gamma }&{ - \sin \gamma }&0\\ {\sin \gamma }&{\cos \gamma }&0\\ 0&0&1 \end{array}} \right)\\ {\mathit{\boldsymbol{A}}_\beta } = \left( {\begin{array}{*{20}{c}} {\cos \beta }&0&{\sin \beta }\\ 0&1&0\\ { - \sin \beta }&0&{\cos \beta } \end{array}} \right)\\ {\mathit{\boldsymbol{A}}_\alpha } = \left( {\begin{array}{*{20}{c}} 1&0&0\\ 0&{\cos \alpha }&{ - \sin \alpha }\\ 0&{\sin \alpha }&{\cos \alpha } \end{array}} \right) \end{array} \right.$ | (3) |
在计算P点速度时,将式(1)两侧对时间求导。由于旋转矩阵A是正则矩阵,由线性代数易知其随时间的导数为
| $\mathit{\boldsymbol{\dot A = \tilde \omega A}}$ | (4) |
式中
| $\begin{array}{l} \mathit{\boldsymbol{\tilde \omega }} = \left( {\begin{array}{*{20}{c}} 0&{ - {\omega _z}}&{{\omega _y}}\\ {{\omega _z}}&0&{ - {\omega _x}}\\ { - {\omega _y}}&{{\omega _x}}&0 \end{array}} \right) \end{array}$ | (5) |
则可得到P点速度及加速度表达式为
| $\left\{ \begin{array}{l} \mathit{\boldsymbol{\dot r}} = \mathit{\boldsymbol{\dot R}} + \mathit{\boldsymbol{\dot A}}{\mathit{\boldsymbol{u}}^{\rm{i}}} = \mathit{\boldsymbol{\dot R}} + \mathit{\boldsymbol{\tilde \omega A}}{\mathit{\boldsymbol{u}}^{\rm{i}}} = \\ \;\;\;\;\;\mathit{\boldsymbol{\dot R}} + \mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{u}} = \mathit{\boldsymbol{\dot R}} + \mathit{\boldsymbol{A}}\left( {{\mathit{\boldsymbol{\omega }}^{\rm{i}}} \times {\mathit{\boldsymbol{u}}^{\rm{i}}}} \right)\\ \mathit{\boldsymbol{\ddot r}} = \mathit{\boldsymbol{\ddot R}} + \mathit{\boldsymbol{\alpha }} \times \mathit{\boldsymbol{u}} + \mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{u}} = \\ \;\;\;\;\;\mathit{\boldsymbol{\ddot R}} + \mathit{\boldsymbol{A}}\left( {{\mathit{\boldsymbol{\alpha }}^{\rm{i}}} \times {\mathit{\boldsymbol{u}}^{\rm{i}}} + {\mathit{\boldsymbol{\omega }}^{\rm{i}}} \times {\mathit{\boldsymbol{\omega }}^{\rm{i}}} \times {\mathit{\boldsymbol{u}}^{\rm{i}}}} \right) \end{array} \right.$ | (6) |
结合物理意义可知,加速度表达式由基点平移矢量加速度(
| $\begin{array}{l} {\mathit{\boldsymbol{z}}_\mathit{\boldsymbol{A}}} = \mathit{\boldsymbol{A}} \times \mathit{\boldsymbol{z}}_\mathit{\boldsymbol{A}}^{\rm{i}} = \mathit{\boldsymbol{A}} \times {\left[ {\begin{array}{*{20}{c}} 0&0&1 \end{array}} \right]^{\rm{T}}} = \\ \left( {\begin{array}{*{20}{c}} {\sin \alpha \sin \gamma + \cos \alpha \sin \beta \cos\gamma }\\ {\sin \alpha \sin \beta \sin \gamma - \sin \alpha \cos\gamma }\\ {\cos \alpha \cos \beta } \end{array}} \right) \end{array}$ | (7) |
可得到|zA|=|zAi|=1。根据矢量点乘公式,绝对加速度与Zi轴夹角以及通过IMU加速度(aI)解算在P处垂直于车身平面的加速度为:
| $\left\{ \begin{array}{l} \delta = \arccos \frac{{{\mathit{\boldsymbol{a}}_\mathit{\boldsymbol{A}}} \cdot {\mathit{\boldsymbol{z}}_\mathit{\boldsymbol{A}}}}}{{\left| {{\mathit{\boldsymbol{a}}_\mathit{\boldsymbol{A}}}} \right|\left| {{\mathit{\boldsymbol{z}}_\mathit{\boldsymbol{A}}}} \right|}} = \arccos \frac{{{\mathit{\boldsymbol{a}}_\mathit{\boldsymbol{A}}} \cdot {\mathit{\boldsymbol{z}}_\mathit{\boldsymbol{A}}}}}{{\left| {{\mathit{\boldsymbol{a}}_\mathit{\boldsymbol{A}}}} \right|}}\\ {\mathit{\boldsymbol{a}}_1} = \left| {{\mathit{\boldsymbol{a}}_\mathit{\boldsymbol{A}}}} \right| \cdot \cos \delta = \mathit{\boldsymbol{\ddot r}} \cdot {\mathit{\boldsymbol{z}}_\mathit{\boldsymbol{A}}} \end{array} \right.$ | (8) |
根据式(6),可得
| $\begin{array}{l} \mathit{\boldsymbol{\ddot r}} = \mathit{\boldsymbol{A}}\left( {\begin{array}{*{20}{c}} {a_x^{\rm{i}}}\\ {a_y^{\rm{i}}}\\ {a_z^{\rm{i}}} \end{array}} \right) + \mathit{\boldsymbol{A}}\left( {\begin{array}{*{20}{c}} 0&{ - \alpha _z^{\rm{i}}}&{\alpha _y^{\rm{i}}}\\ {\alpha _z^{\rm{i}}}&0&{ - \alpha _x^{\rm{i}}}\\ { - \alpha _y^{\rm{i}}}&{\alpha _x^{\rm{i}}}&0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x^{\rm{i}}}}\\ {{y^{\rm{i}}}}\\ {{z^{\rm{i}}}} \end{array}} \right) + \\ \mathit{\boldsymbol{A}}\left( {\begin{array}{*{20}{c}} 0&{ - \omega _z^{\rm{i}}}&{\omega _y^{\rm{i}}}\\ {\omega _z^{\rm{i}}}&0&{ - \omega _x^{\rm{i}}}\\ { - \omega _y^{\rm{i}}}&{\omega _x^{\rm{i}}}&0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} 0&{ - \omega _z^{\rm{i}}}&{\omega _y^{\rm{i}}}\\ {\omega _z^{\rm{i}}}&0&{ - \omega _x^{\rm{i}}}\\ { - \omega _y^{\rm{i}}}&{\omega _x^{\rm{i}}}&0 \end{array}} \right) \cdot \\ \left( {\begin{array}{*{20}{c}} {{x^{\rm{i}}}}\\ {{y^{\rm{i}}}}\\ {{z^{\rm{i}}}} \end{array}} \right) \end{array}$ | (9) |
联立式(6)~(9)可得P处垂直于车身平面的加速度为
| $\begin{array}{l} {\mathit{\boldsymbol{a}}_1} = \mathit{\boldsymbol{\ddot r}} \cdot {\mathit{\boldsymbol{z}}_\mathit{\boldsymbol{A}}} = a_z^{\rm{i}} + \left( {\alpha _x^{\rm{i}}{y^{\rm{i}}} - \alpha _y^{\rm{i}}{x^{\rm{i}}}} \right) + [\omega _z^{\rm{i}}\omega _x^{\rm{i}}{x^{\rm{i}}} - \\ \;\;\;\;\;\;\;\;\;\;(\omega _x^{{\rm{i}}\;{\rm{2}}} + \omega _y^{{\rm{i}}\;{\rm{2}}}){z^{\rm{i}}} + \omega _z^{\rm{i}}\omega _x^{\rm{i}}{y^{\rm{i}}}] \end{array}$ | (10) |
在式(10)中,只有俯仰角加速度αyi以及侧倾角加速度αxi需要通过数值方法求得,其他量都可以通过IMU读数直接得到。观察式(10),加速度由平动加速度、角加速度、向心加速度3项组成。定义使得车头向下运动俯仰角速度及角加速度为正方向。且根据垂直轴的定义,对于z轴的向心加速度项取负号是符合物理意义的。但是,由于传感器安装位置与其本身测量误差会对最终结果产生一定或较大影响,针对式(10)的误差和敏感性分析是必要的,将在第4节中讨论。
3 运动学模型的实验验证运动学公式(10)的精度对软测量技术的精度至关重要。为此本节设计了实车实验,验证与标定式(10)的准确性。本次实验采用整车实验,并安装IMU位于3个不同位置的点,安装车型为大众探歌280舒适款。为了检测IMU及解算方法的正确性,在4个轮心正上方对应的车身上的点布置了灵敏度为100 mV/g的加速度传感器;并在车顶中心安装有GPS定位装置,用于记录行驶轨迹及车速等信息,以便明确实验场地工况信息以及不同工况的车速,便于后续分析。加速度传感器与IMU具体安装位置及坐标系见图 3及表 1。
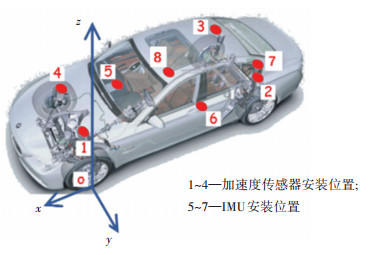
|
图 3 实验IMU安装位置及车身坐标系 Fig. 3 Experimental IMU installation positions and vehicle body coordinate system |
| 表 1 加速度传感器及IMU安装位置 Tab. 1 Acceleration sensors and IMU installation positions |
4个加速度传感器安装位置为1~4,假设车身为刚体,则该加速度传感器直接反映了簧上位置处的加速度信号;IMU安装位置共3个,为副驾驶地板(5)、驾驶后座地板(6)以及后备箱地板一侧后轴正上方(7)。
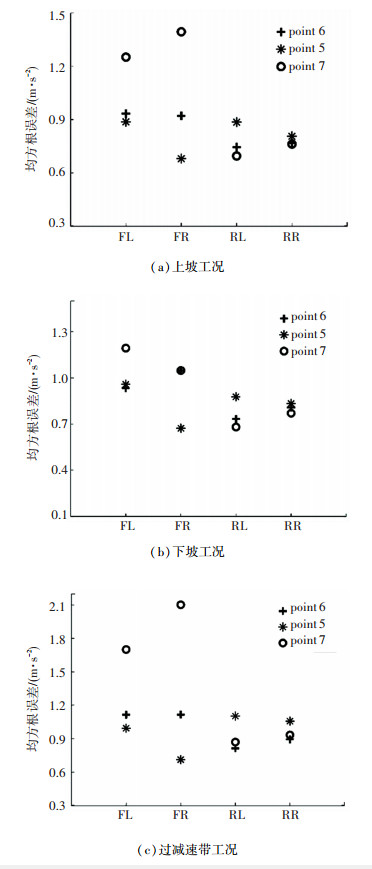
为了验证解算方法及误差分析的合理性,根据式(10)及安装位置坐标信息计算出4个悬架处的加速度,并和安装在该位置的加速度传感器数值进行比较。试验选取了如上坡、下坡及过减速带等典型工况进行验证。以(5)号安装位置(副驾驶地板)为例,图 4为上坡工况下的两个悬架位置处(FL为左前悬架;RR为右后悬架,下同)加速度传感器数据以及从IMU解算之后的数据对比(虚线代表加速度传感器测量的数据,实线代表IMU解算的结果)。需要说明的是,此处选取的两个悬架位置处具有代表性,因为本次实验中不考虑各工况下左右侧车轮行驶轨迹的差别。

|
图 4 IMU安装在(5)号位置上坡时的信号 Fig. 4 Signals for IMU mounted on position (5) (uphill) |
对3个IMU安装位置及3种工况(上坡、下坡及过减速带)分别进行测量,并将4个悬架位置处IMU解算与加速度传感器测量值的均方根误差值作为衡量观测值同真值之间偏差离散程度的评价指标。
图 5给出了IMU安装在(5)号位置下坡和过减速带工况下的信号。
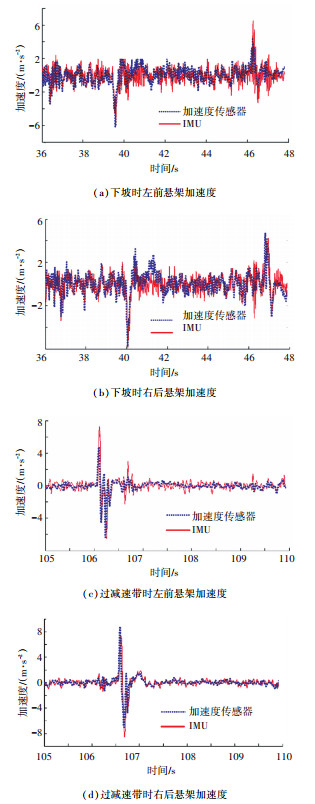
|
图 5 IMU安装在(5)号位置的信号 Fig. 5 Signals for IMU mounted on position (5) (downhill, bump) |
加速度传感器与IMU均存在安装误差与信号传递过程中的干扰,在本文的实验结果及敏感性分析中将不予考虑。从加速度传感器测量的原始数据、IMU解算结果及其加速度均方根值误差可以看出:IMU解算与实际加速度传感器信号吻合度较高,验证了解算理论公式的合理性。综合该解算结论及IMU安装较为简单,可靠性高且维修方便的特点,不难发现IMU作为车身姿态检测器的潜力,同时此结论为工程实际应用提供了理论基础。即单车身IMU方案在不同安装位置处的确可以起到替代4加速度计的方案,且可靠性较高。
3种安装位置的实验及解算结果见图 6。从图 6可以看出,不同安装位置对解算结果影响较大。如位置7处(后备箱地板一侧后轴正上方)测量前轴(FL和FR)的均方根误差值最大而且不同工况下均方根误差波动较大,即测量最不精确;5号位置(副驾驶地板)对右侧前后悬架测量较准,但是对左侧两个悬架测量误差较大;相反,6号测点(驾驶后座地板)对左侧测量较准,对右侧测量误差较大。这两个点在不同工况下均方根误差变化约为20%~30%,比7号位置有所改善。比较3个安装位置的实验数据和几何坐标发现,不同的IMU安装位置(水平和垂向)会对解算精度造成不同程度的影响,进而可能导致后续半主动悬架控制所需运动学参数不准确,造成控制效果变差甚至相反等后果。而观察3个不同的安装位置的测量精度发现,应当存在一个收敛的最佳安装位置,下面通过对安装位置的敏感性分析推导最优安装位置并进行实验验证。
|
图 6 IMU安装位置与均方根误差(3个观测点) Fig. 6 IMU installation positions and RMSE(3 positions) |
理论上看,IMU安装在任何位置都可以起到替代4个加速度传感器的作用,但是由于安装位置不同所导致的误差可能会放大。故需要综合考虑安装位置和4个悬架位置的几何关系,拟定误差指标并进行最优化处理从而得到最佳安置点。除此之外,需要考虑在实际生产安装过程中可能由于其他限制,IMU不能放置在最佳安置点,或者在一定范围内不能放置。故问题被抽象成有约束最优化问题,下面进行有约束最优化问题的求解。
由IMU本身带来的随机误差无法避免,根据用户手册可以得轴向加速度以及角速度的最大误差绝对值为δa和δω。其中角速度和角速度平方的相对误差定义为
| ${\delta _\omega } = \frac{{{\omega _{\rm{m}}} - {\omega _{\rm{r}}}}}{{{\omega _{\rm{r}}}}} = \frac{{\Delta \omega }}{{{\omega _{\rm{r}}}}}, {\rm{ }}{\delta _{{\omega ^2}}} = 2{\delta _\omega }$ | (11) |
下标m、r分别代表测量值和真值。加速度误差需要根据相对误差定义式计算,设加速度信号最大误差绝对值为
| ${\delta _\alpha } = m{\delta _\omega }$ | (12) |
m为一常数。则将式(11)、(12)代入(10),得到最终加速度解算公式的误差为
| $\begin{array}{l} {\delta _{\ddot r}} \le {\delta _a} + m{\delta _\omega }\left( {\left| {{y^{\rm{i}}}} \right| + \left| {{x^{\rm{i}}}} \right|} \right) + (2{\delta _\omega }\left| {{x^{\rm{i}}}} \right| + \\ \;\;\;\;\;4{\delta _\omega }\left| {{z^{\rm{i}}}} \right| + 2{\delta _\omega }\left| {{y^{\rm{i}}}} \right|) = {\delta _a} + {\delta _\omega }[(2 + \\ \;\;\;\;\;m)\left| {{x^{\rm{i}}}} \right| + \left( {2 + m} \right)\left| {{y^{\rm{i}}}} \right| + 4\left| {{z^{\rm{i}}}} \right|] \end{array}$ | (13) |
由于δa和δω均为确定的正值,故引入误差定义新变量为
| $\frac{{{\delta _{\ddot r}} - {\delta _a}}}{{{\delta _\omega }}} = \left( {2 + m} \right)\left| {{x^{\rm{i}}}} \right| + \left( {2 + m} \right)\left| {{y^{\rm{i}}}} \right| + 4\left| {{z^{\rm{i}}}} \right|$ | (14) |
该变换对最终误差分析无影响,但是可以大大简化后续最优性分析。针对具体车辆,L为前后悬架距离(轴距),W为左右悬架距离(轮距),车身平面与IMU安装位置高度之差为c,与左前悬架处沿长度方向(x轴方向)距离为b,沿宽度方向(y轴方向)距离为a。对IMU安装位置与4个悬架的几何关系进行分析,取误差二次项之和为需要优化的指标。根据半主动悬架的实际需求,对前悬架(左前右前)引入加权因子k≥1。则无约束最优化问题为:
| $\left\{ \begin{array}{l} \min J = \sum\limits_{i = 1}^4 {{{\left( {\frac{{{\delta _{\ddot r}} - {\delta _a}}}{{{\delta _\omega }}}} \right)}_{\rm{i}}} = {A_1}{{\left( {a - {a_0}} \right)}^2} + {B_1}(b - } \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{b_0}{)^2} + {C_1}{\left| c \right|^2} + {C_2}\left| c \right| + \mathit{\Delta }\\ {A_1} = {B_1} = 2\left( {k + 1} \right){\left( {m + 2} \right)^2}\\ {C_1} = 32\left( {k + 1} \right) - \frac{{32}}{{k + 1}}\\ {C_2} = 8\left( {m + 2} \right)\left[ {\left( {k + 1} \right)\left( {W + 2L} \right) + \frac{{2L - \left( {k - 1} \right)W}}{{k + 1}}} \right]\\ {a_0} = \frac{W}{2}, {b_0} = \frac{L}{{k + 1}} - \frac{{\left( {k - 1} \right)\left[ {W{{\left( {m + 2} \right)}^2} + 8c\left( {m + 2} \right)} \right]}}{{{A_1}}}\\ \mathit{\Delta } = \mathit{\Delta }\left( {L, W, m, k} \right) = {\rm{const}} \end{array} \right.$ | (15) |
结合最优化指标J与实际物理意义,IMU安装位置在车身平面的投影应当在4个悬架构成的长方形区域内。如果安装在外部,则必能在长方形内部找到一个点,使得该指标小于等于原值。观察式(15),由于C1、C2为正值,故最佳安置处c=0,即处于车身平面内。由于左右侧悬架权重相等,最佳安置位于车辆纵向对称面内。另外,参数a和b二次项系数相等,故不论垂向高度c如何取值,该封闭图形横截面必为圆形,该物理意义在下文中会详述。应当注意的是,由于前后悬架权重不等,故在确定安装位置纵向位置时,存在b和c耦合项。由于此为无约束最优化问题,可先令c=0,讨论k的取值对结果影响。
1) k=1时。此时前后悬架权重相等,可以得到最佳安置点的坐标为
| ${a_0} = \frac{W}{2}, {b_0} = \frac{L}{2}, {c_0} = 0$ | (16) |
与实际物理意义相符,当4个悬架处权重相等,则最佳安置点应当处于悬架构成封闭长方形的几何中心处。
2) k→∞时。此时前悬架权值为无穷,得到的理论位置为
| ${a_0} = \frac{W}{2}, {b_0} = - \frac{W}{2}, {c_0} = 0$ | (17) |
但是由前所述,b应大于0。出现这个问题的主要原因是此时对参数b来说, 其抛物线对称轴位于该区域外,故此时取b=0即可。
3) b=0时。此时最佳安置点位于车身平面与纵向对称面的交线上,且处于前悬架中点处。此时的权重值为
| ${k_{{\rm{max}}}} = \frac{{2L}}{W} + 1$ | (18) |
kmax与m无关,仅与悬架位置有关。此时IMU距离前悬架距离最近,测量误差最小。即当取前悬架权重大于该值时,IMU最佳安置点不变,测量误差也不变。b的取值随着k的增大呈单调下降趋势并存在下限,这对权重选取以及安装位置有一定指导意义。
前文分析了无约束最优化问题的解以及权重取值对最佳安置点的影响,在许多新车型或改装车型上往往最佳安置点条件是很难满足的,需要研究有约束条件下最优化指标及最佳安置点的确定。本文利用方向导数的概念比较直观地给出有约束条件下选取最佳安置点的步骤,比较适用于工程分析及实际安装。反观式(15),求出目标指标J对3个方向的偏导数
| $\left\{ \begin{array}{l} \frac{{\partial J}}{{\partial a}} = 4\left( {k + 1} \right){\left( {m + 2} \right)^2}\Delta a\\ \frac{{\partial J}}{{\partial b}} = 4\left( {k + 1} \right){\left( {m + 2} \right)^2}\Delta b\\ \frac{{\partial J}}{{\partial c}} = \left[ {64\left( {k + 1} \right) - \frac{{64}}{{k + 1}}} \right]\Delta c + 8\left( {m + 2} \right) \cdot \\ \;\;\;\;\;\;\;\left[ {\left( {k + 1} \right)\left( {W + 2L} \right) + \frac{{2L - \left( {k-1} \right)W}}{{k + 1}}} \right] \end{array} \right.$ | (19) |
式中Δa、Δb、Δc为安装点与最佳安装点三轴方向的距离。显然,最终误差指标对安装位置与车身平面的垂向距离十分敏感,应该尽可能保证IMU安装在车身平面内。当确定了垂向距离后即可利用式(15)计算出a0、b0,然后让IMU安装位置尽可能接近该点即可。下面仅给出前后悬架权重相等(k=1)时的结论,其他情况可类推。
根据敏感性分析理论,此时最佳安置点应该位于车身平面上并处于4个悬架位置中心。故在原车上增加了一个靠近最佳安置点的位置(前排扶手箱8)来进行验证,具体位置坐标见表 2。
| 表 2 IMU安装位置8坐标值 Tab. 2 Coordinates of IMU mounted on position 8 |
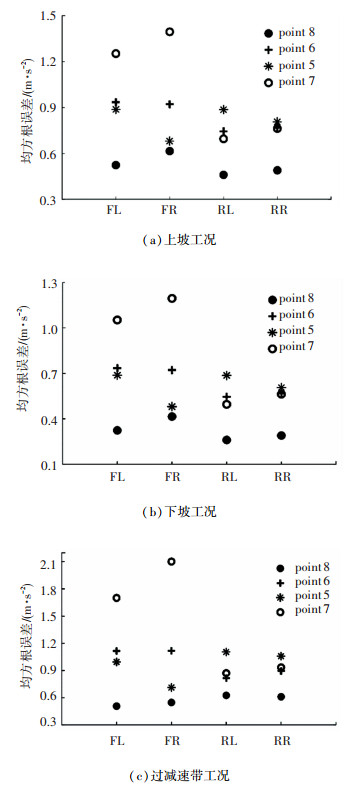
由上述实验步骤及统计量计算,得出4个IMU安装位置的加速度均方根误差值并进行整理,结果见图 7。
|
图 7 IMU安装位置与均方根误差(4个观测点) Fig. 7 IMU installation positions and RMSE(4 positions) |
车身姿态的精确检测和解算对于车身姿态的控制有着重要意义,而解算结果的精度高度依赖于IMU传感器的安装位置。由图 7可以看出,测点8对4个悬架的测量值均方根误差最小,约为0.5~ 0.6且与工况几乎无关,在测量加速度剧烈变化的减速带工况下仍保持此值。结合理论分析,主要是因为该点近似位于车身平面内,根据式(19)可以看出,误差对安装的垂向距离是十分敏感的,实验结果进一步验证了理论的正确性。该测点与4个悬架的距离值近似相等,位于最佳测量点附近,故其测量的加速度均方根误差最小,与理论结论相符。
为了给出直观的解释,在确定最优化指标J(即误差评价指标)、角加速度最大误差系数m与前悬架权重比k后,得出3个坐标之间的等式关系。观察易知,该曲面为空间椭球,该椭球的特点是任意水平截面均为圆形。图 8为取车身平面为基准,m=10与k=2时的椭球面。图 8中透明水平面表示车身平面(c=0),该平面往上即为在车身上误差指标相等的安装位置等值面。由于在理论推导公式中给出的垂向位置是距离车身平面的距离,故整个等值面应该是该椭球位于等值面以上的部分及该部分对车身平面的镜像面。由式(15)可知,该椭球关于a轴(图 3中y轴)的旋转角度只与前悬架权重k有关。
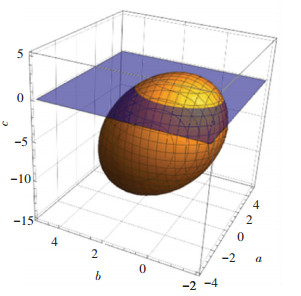
|
图 8 最优化指标的空间表示 Fig. 8 Spatial representation of optimization index |
在k=1时,最佳理论安置点位于车身平面内与4个悬架位置相同的点,可见测点8对4个悬架的测量值应是最准确的,这也与实验结果相符。对于测点5和6,大约位于同一等值椭球面上,故该两点对前后悬架测量值虽然有不同的侧重,但是整体效果相近。测点7处在误差指标较大的椭球等值面上,虽然对后轴测量较好,但是对4个悬架的测量值均方根误差总体较大。用该等值椭球面可以清楚直观地看出较优的安装位置。
5 结论本文基于半主动悬架控制所需传感器架构,提出了一种新的集成式IMU软测量布置方案,基于运动学理论提出了一种精确解算方法,并在此基础上利用最优化理论进行参数敏感性分析及布置优化,最后通过实验验证了解算公式和布置方案的合理性,并给出了在不同悬架权重下安装位置的空间图形,具有一定的工程指导意义。得出的主要结论有:
1) IMU安装位置对最终解算精度影响较大,在同一安装高度下,不同水平安装位置对IMU的测量精度有较大影响。
2) 解算结果的精度强依赖于IMU传感器的安装位置,且总体误差值对IMU与车身平面的垂向距离非常敏感。
3) 利用数形结合思想,给出了一个IMU安装位置误差等值椭球面,可以较为清楚直观地对安装位置进行分析。
4) 本文的理论分析与实验表明,所提出的IMU软测量方案与加速度传感器测量值吻合程度高,用敏感性分析理论给出的有约束情况下较佳安置点与实验相符,可用于指导实际安装位置的选择。
| [1] |
塞吉奥·马泰奥·萨瓦瑞斯, 查尔斯·普索特瓦萨尔, 克里斯蒂亚诺·斯卑尔特, 等. 车辆半主动悬架控制设计[M]. 危银涛, 彭志召, 译. 北京: 清华大学出版社, 2019: 10 SAVARESI M S, POUSSOT-VASSAL C, SPELTA C, et al. Semi-active suspension control design for vehicles[M]. WEI Yintao, PENG Zhizhao, translate. Beijing: Tsinghua University Press, 2019: 10 |
| [2] |
程世超, 高爽, 林铁, 等. 随钻测量用微小型惯性测量单元设计[J]. 传感器与微系统, 2015, 34(4): 95. CHENG Shichao, GAO Shuang, LIN Tie, et al. Design of miniaturized inertial measurement unit used for measurement-while-drilling[J]. Sensors and Microsystems, 2015, 34(4): 95. DOI:10.13873/J.1000-9787(2015)04-0095-04 |
| [3] |
高爽, 焦禹舜, 林铁, 等. 轻小型二位置光纤陀螺测斜仪惯性测量单元设计[J]. 传感器与微系统, 2014, 33(6): 86. GAO Shuang, JIAO Yushun, LIN Tie, et al. Design of two-position miniaturized inclinometer IMU based on FOG[J]. Sensors and Microsystems, 2014, 33(6): 86. DOI:10.3969/j.issn.1000-9787.2014.06.025 |
| [4] |
SCHOLTE W J, MARCO V R, NIJMEIJER H. Experimental validation of vehicle velocity, attitude and IMU bias estimation[J]. IFAC-Papers On Line, 2019, 52(8): 118. DOI:10.1016/j.ifacol.2019.08.058 |
| [5] |
ZHAO Sheng, CHEN Yiming, FARRELL J A. High-precision vehicle navigation in urban environments using an MEM's IMU and single-frequency GPS receiver[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(10): 2854. DOI:10.1109/TITS.2016.2529000 |
| [6] |
COLLIN J. MEMS IMU carouseling for ground vehicles[J]. IEEE Transactions on Vehicular Technology, 2015, 64(6): 2242. DOI:10.1109/TVT.2014.2345847 |
| [7] |
AMIRSADRI A, KIM J, PETERSSON L, et al. Practical considerations in precise calibration of a low-cost MEMS IMU for road-mapping applications[C]//American Control Conference. Piscataway: IEEE, 2012: 101. DOI: 10.1109/ACC.2012.6315131
|
| [8] |
BERKANE S, TAYEBI A. Attitude and gyro bias estimation using GPS and IMU measurements[C]// 2017 IEEE 56th Annual Conference on Decision and Control. Piscataway: IEEE, 2017. DOI: 10.1109/CDC.2017.8264001
|
| [9] |
JØRGENSEN E K, FOSSEN T I, SCHJØLBERG I, et al. Experimental validation of attitude and rate-sensor bias filter using range-difference measurements[J]. Control Engineering Practice, 2018, 73: 118. DOI:10.1016/j.conengprac.2018.01.002 |
| [10] |
GELMINI S, FOUKA M, STRADA S, et al. Self-calibration algorithm for an IMU in two-wheeled vehicles: design and experimental validation[C]//2018 21st International Conference on Intelligent Transportation Systems (ITSC). Piscataway: IEEE, 2018: 1751. DOI: 10.1109/ITSC.2018.8569762
|
| [11] |
马亚平, 魏国, 周庆东. 改进的IMU传感器安装误差正交补偿方法[J]. 传感器与微系统, 2016, 35(9): 9. MA Yaping, WEI Guo, ZHOU Qingdong. An improved method of orthogonal compensation for IMU installation error[J]. Transducer and Microsystem Technologies, 2016, 35(9): 9. DOI:10.13873/J.1000-9787(2016)09-0009-05 |
| [12] |
余志生. 汽车理论[M]. 5版. 北京: 机械工业出版社, 2009: 103. YU Zhisheng. Automobile theory[M]. 5th ed. Beijing: China Machine Press, 2009: 103. |
| [13] |
于雪莲. 加速度传感器安装方式对灵敏度的影响[J]. 中国计量, 2017(2): 114. YU Xuelian. Influence of acceleration sensor installation mode on sensitivity[J]. China Metrology, 2017(2): 114. |
| [14] |
刘延柱. 高等动力学[M]. 北京: 高等教育出版社, 2001: 108. LIU Yanzhu. Advanced dynamics[M]. Beijing: Higher Education Press, 2001: 108. |
| [15] |
TIMOSHENKO S, YOUNG D H. Advanced dynamics[M]. New York: MacGraw-Hill, 1948: 13.
|
 2022, Vol. 54
2022, Vol. 54


