2. 工业装备结构分析国家重点实验室(大连理工大学) 辽宁 大连 116024
2. State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian 116024, Liaoning, China
燃料电池汽车(FCEV)的燃料为氢气,具有排放无污染的特点,所以燃料电池汽车吸引了越来越多科研人员的关注。目前,燃料电池汽车具有燃料电池和动力电池两个动力源,整车能量控制策略的制定尤为重要[1-2]。通过制定合理的整车能量控制策略,从而进行最佳的能量流分配,以提高整车的动力性、经济性和安全性。随着运行时间的增加,燃料电池是不断老化的。如何保证燃料电池始终工作在高效区间,同时减缓燃料电池衰老是一个亟待解决的关键问题[3]。目前,已开展的研究工作多在不考虑燃料电池老化的前提下,实现燃料电池的最大效率跟踪[4]。为了保证燃料电池系统在负载工况变化的条件下仍能无扰动地运行在最大效率点,王天宏等[5]提出了一种基于遗忘因子递推最小二乘在线辨识和Super-Twisting滑膜算法的燃料电池系统实时最大效率跟踪方法,该方法能够实现最大效率点的实时估计。Zhong等[6]设计了一种采用极值寻求算法的自适应最大功率跟踪控制器,该控制器基于动态自适应控制原理,在MATLAB/Simulink环境下,通过仿真验证了所提出的燃料电池最大功率控制方案在大工作范围内的有效性。由于燃料电池的最大效率点会随着工况的变化而改变,这无疑会增加燃料电池电流的动态变载次数,增加燃料电池水、气的管理难度,从而缩短燃料电池的寿命[7-8]。为了减少燃料电池的变载次数,科研人员提出了模糊逻辑控制策略[9-10]和恒温器控制策略[11],这些控制策略基于已制定好的规则对燃料电池汽车的能量流进行分配。模糊自适应策略基于方程的权重值,这个权重值定义了参数的相对重要性。基于驾驶环境感知的自适应模糊规则控制器利用驾驶环境意识(包括车道类型、驾驶情况和传动系中的能量流等专家知识)[12-13],通过智能能量管理来进行能量流的分配。恒温器控制策略具有鲁棒性强、简单易于实现等特点,主要是依据动力电池的SOC来决策燃料电池的输出功率,有利于减少燃料电池的变载次数。但是在实际应用中,恒温器控制策略中制定的规则没有考虑到燃料电池老化后电池参数的变化,所以在燃料电池的整个生命周期内未能完全达到最佳的能量流分配。
为了提高燃料电池汽车氢气平均利用效率,本文提出了一种改进的恒温器控制策略。通过测量燃料电池的实时数据,利用最小二乘法实现燃料电池极化曲线的拟合,从而完成燃料电池的老化状态识别;然后通过遗传算法优化出燃料电池的高效率工作点;最后及时更新恒温器中制定的规则参数,从而实现了提高氢气平均利用效率目的。
1 燃料电池公交车模型本文研究的燃料电池公交车动力系统结构见图 1。整车的能量源有燃料电池和动力电池,其中燃料电池是整车的主要能量源。由于燃料电池的输出电压低,且输出特性偏软,所以燃料电池需要DC/DC变换器进行升压。为了满足整车快速变化的需求功率,及对整车的制动能量进行回收,在DC/DC变换器的输出侧并联了一个动力电池。

|
图 1 燃料电池汽车的动力系统结构 Fig. 1 Power system structure of fuel cell vehicle |
利用Matlab/Simulink建立了燃料电池汽车动力系统模型,具体参数见表 1。燃料电池的电压等于所有单体电压之和,而单体电压是一个与电流有关的函数:
| ${V_{{\rm{fc}}}} = {n_{{\rm{stack}}}}{V_{{\rm{cell}}}} = f({I_{{\rm{fc}}}})$ | (1) |
| 表 1 燃料电池公交车的相关参数 Tab. 1 Parameters of fuel cell bus |
式中:Vfc和Ifc分别是燃料电池电堆的电压和电流,nstack为燃料电池的单体数量。
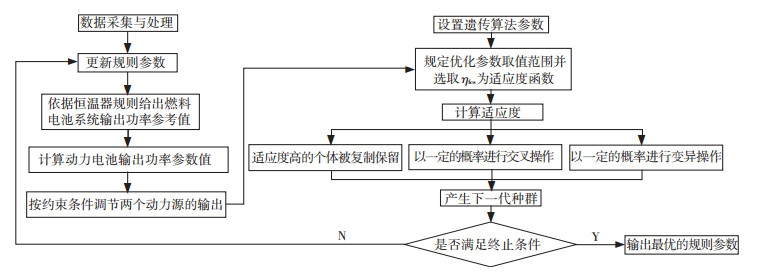
2 改进的恒温器控制策略图 2为一种能提高氢气平均利用效率的改进恒温器控制策略。随着燃料电池汽车的使用时间不断增加,燃料电池不断老化,其高效的工作区间也随之变化。该策略通过遗传算法不断地对规则参数进行优化,将优化后的规则参数应用到改进的恒温器中,其具体的流程如图 2所示。
|
图 2 改进的恒温器控制策略流程图 Fig. 2 low chart of improved thermostat control strategy |
燃料电池是一个非常复杂的系统,它涉及到电化学、热动力学、传热与传质等。因此本文对燃料电池的电压模型做以下的假设:
1) 氢气的纯度和利用率均为100%;空气中氧气的质量分数为21%;
2) 电堆内的温度均为一恒定值334 K;
3) 气体的温度和浓度在燃料电池的电堆内部是一致的。
燃料电池的单体电压可以由式(2)来表示[14]:
| ${V_{{\rm{cell}}}} = {E_{{\rm{thermo}}}} - {V_{{\rm{act}}}} - {V_{{\rm{ohm}}}} - {V_{{\rm{conc}}}}$ | (2) |
式中:Vcell是燃料电池的单体电压,Ethermo是能斯特电压(燃料电池单体的开路电压),Vact、Vohm和Vconc分别表示活化极化损失、欧姆极化损失和浓差极化损失。
| $\begin{array}{l} {E_{{\rm{thermo}}}} = {\rm{ }}1.229 - 0.85 \times {10^{ - 3}}\left( {T - 298.15} \right) + \\ \;\;\;\;\;\;\frac{{{\rm{R}}T}}{{2F}}(\ln\left( {p_{{{\rm{H}}_2}}^{i{\rm{nterface}}}} \right) + \frac{1}{2}\ln \left( {p_{{{\rm{O}}_2}}^{i{\rm{nterface}}}} \right)) \end{array}$ | (3) |
式中:T为电堆的温度,理想气体常数R=8.314,法拉第常数F=96 485,pO2interface为氧气在阴极催化剂层表面的压力,pH2interface为氢气在阳极催化剂层表面的压力。当燃料电池在稳态条件下工作时,氢气和氧气在催化剂层表面的压力分别与阳极和阴极侧入口的气体压力是相等的。根据燃料电池电堆的控制算法可知,阳极侧入口氢气压力pH2和阴极侧入口氧气压力pO2随着燃料电池电流的变化而变化。当燃料电池的电流变大时,空压机的转速就会提高,因此阴极侧的氧气压力就会变大;同理阳极侧的压力也随之增加。
| $\left\{ \begin{array}{l} p_{{{\rm{O}}_2}}^{i{\rm{nterface}}} = {p_{{{\rm{O}}_2}}} \approx \left( {\mu i + 1} \right){\eta _{{{\rm{O}}_2}}}\\ p_{{{\rm{H}}_2}}^{i{\rm{nterface}}} = {p_{{{\rm{H}}_2}}} \approx \mu i + 1 \end{array} \right.$ | (4) |
式中:ηO2为氧气在空气中所占的比例。为了使燃料电池能正常工作,阴极侧和阳极侧的最大压力均为200 kPa [16-17]。本文研究的燃料电池电流密度最大可达1 A·cm-2,因此,μ为100 kPa·cm2·A-1。
活化极化损失Vact主要是克服活化能垒而损失的电压量, 可以由塔菲尔经验公式来表达[18]:
| ${V_{{\rm{act}}}} = \frac{{{\rm{R}}T}}{{\alpha nF}}\ln (\frac{i}{{{i_0}}}) \Rightarrow {V_{{\rm{act}}}} = a + b\ln \left( i \right)$ | (5) |
式中:α为电荷转移系数,i0为交换电流密度,i为燃料电池的电流密度。随着电堆的不断老化,系数a和b是不断变化的,所以将系数a和b作为在线辨识的参数之一。
欧姆极化损失主要是因为离子在质子交换膜中移动所受的阻抗和电子通过电极时所受到的阻抗。通过欧姆定律来表示欧姆极化损失:
| ${V_{{\rm{ohm}}}} = i{R_{{\rm{ohm}}}}{A_{{\rm{cell}}}}$ | (6) |
式中:Rohm为燃料电池的欧姆内阻,随着质子交换膜的老化而变大;Acell为燃料电池的有效面积。在拟合极化曲线时,应不断地辨识燃料电池的内阻Rohm。
燃料电池连续工作时,需要将氢气和氧气不间断地送入燃料电池内部,同时将反应生成的水排除,
这个过程伴随着阻力,因此产生了浓差极化损失Vconc。电流密度越大时,浓差损失就越明显,其表达式为
| ${V_{{\rm{conc}}}} = - \frac{{RT}}{{nF}}\ln (1 - \frac{i}{{{i_{{\rm{max}}}}}})$ | (7) |
式中imax为燃料电池输出的最大电流值。随着电池的老化,质子交换膜和催化剂层的有效面积不断减小,燃料电池的电流最大值也不断减小。因此,imax也是需要辨识的参数之一。将Vconc进行泰勒展开,由于imax大于1,所以Vconc还可以表示为
| ${V_{{\rm{conc}}}} = \frac{{{\rm{R}}T}}{{nF}}\frac{i}{{{i_{{\rm{max}}}}}}$ | (8) |
将式(3)~(8)带入式(2)中,可得燃料电池的单体电压:
| $\begin{array}{l} {V_{{\rm{cell}}}} = 1.274 + \frac{{3{\rm{R}}T}}{{4F}}\ln(\left( {\mu i + 1} \right)\eta _{{{\rm{O}}_2}}^{\frac{1}{3}}) - a - \\ \;\;\;\;\;\;\;\;\;\;b\ln \left( i \right) - i{R_{{\rm{ohm}}}}{A_{{\rm{cell}}}} - \frac{{RT}}{{nF}}\frac{i}{{{i_{{\rm{max}}}}}} \end{array}$ | (9) |
由式(9)可知,只有a、b、Rohm和imax这4个参数需要在线辨识。
2.1.2 参数辨识通过车载数据采集终端,将燃料电池公交车的相关数据发送到信息采集平台。由于无线传输速率的限制,数据采集终端的传输数据频率为1 Hz。在采集的数据中,会出现启停、变载等工况导致的电压不稳定情况,所以对这一部分不稳定的数据进行滤波,对稳定状态下的数据求平均值。
目前,所监控的燃料电池公交车已累计运行800 h,每隔200 h为一个周期。将采集到的数据进行如下处理:1)剔除由于数据传输和数据存储导致错误数据;2)剔除错误的数据后,对同一电流密度ik(k=1, 2, …, 30)条件下的燃料电池单体电压取平均值。
在第j周期内,式(9)可以表示为:
| $\begin{array}{l} \mathit{\boldsymbol{V}}(j) = \left[ {\begin{array}{*{20}{l}} {{{\bar v}_{j, 1}} - 1.274 - \frac{{3{\rm{R}}T}}{{4F}}\ln \left[ {\left( {\mu {i_1} + 1} \right)\eta _{{{\rm{O}}_2}}^{\frac{1}{3}}} \right]}\\ \vdots \\ {{{\bar v}_{j, k}} - 1.274 - \frac{{3{\rm{R}}T}}{{4F}}\ln \left[ {\left( {\mu {i_k} + 1} \right)\eta _{{{\rm{O}}_2}}^{\frac{1}{3}}} \right]}\\ \vdots \\ {{{\bar v}_{j, n}} - 1.274 - \frac{{3{\rm{R}}T}}{{4F}}\ln \left[ {\left( {\mu {i_n} + 1} \right)\eta _{{{\rm{O}}_2}}^{\frac{1}{3}}} \right]} \end{array}} \right] = \\ \;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{G}}(i)\mathit{\boldsymbol{\beta }}(j);j = 0, 1, \cdots , 4 \end{array}$ | (10) |
式中:vj, 1为在第j周期内,电流密度为ik时的燃料电池单体实际电压。其中G(i)和β(j)可表达为:
| $\mathit{\boldsymbol{G}}\left( i \right) = \left[ \begin{array}{l} g\left( {{i_1}} \right)\\ \;\; \vdots \\ g\left( {{i_k}} \right)\\ \;\; \vdots \\ g\left( {{i_n}} \right) \end{array} \right];\mathit{\boldsymbol{g}}\left( \mathit{\boldsymbol{i}} \right) = \left[ {1, \ln \left( i \right), i} \right]$ | (11) |
| $\mathit{\boldsymbol{\beta }}(j) = \left[ {\begin{array}{*{20}{l}} {{\beta _1}(j)}\\ {{\beta _2}(j)}\\ {{\beta _3}(j)} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} { - a(j)}\\ { - b(j)}\\ { - {R_{{\rm{ohm}}}}(j){A_{{\rm{cell}}}}}{ - \frac{{{\rm{R}}T}}{{nF}}\frac{1}{{{i_{\max }}(j)}}} \end{array}} \right]$ | (12) |
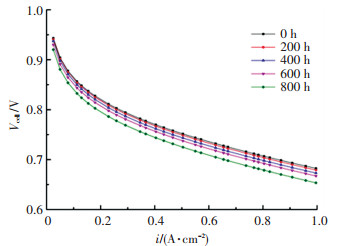
β(j)为待辨识参数的矩阵,这些参数值随着燃料电池运行周期的变化而变化。利用最小二乘法对式(12)进行拟合,不同周期内的燃料电池极化曲线相关参数如表 2所示。将拟合出的参数带入式(9)中,可以求出燃料电池在不同周期内的极化曲线,如图 3所示。随着燃料电池使用时间的增加,燃料电池的电压是不断下降的,当燃料电池运行800 h时,其电压衰减的速度明显加快。
| 表 2 拟合的燃料电池极化曲线相关参数 Tab. 2 Parameters of fuel cell polarization curve fitting |
|
图 3 不同周期内拟合的燃料电池极化曲线 Fig. 3 Polarization curve fitting of fuel cells in different cycles |
燃料电池电堆的能量转换效率可以通过单位时间内电堆输出的电能和消耗的氢能求得,所以燃料电池电堆的效率为
| ${\eta _{{\rm{fc}}}} = \frac{{{P_{{\rm{fc}}}}}}{{{P_{{{\rm{H}}_2}}}}} \times 100\% = \frac{{2F{V_{{\rm{cell}}}}{I_{{\rm{fc}}}}}}{{\Delta {H_{{{\rm{H}}_2}}}{I_{{\rm{fc}}}}}} \times 100\% = \frac{{{V_{{\rm{cell}}}}}}{{1.482}} \times 100\% $ | (13) |
式中:Vcell为燃料电池的单体电压,Ifc为燃料电池的输出电流,ΔHH2为1 mol氢气燃烧所释放的能量(286 kJ/mol)。
燃料电池系统的效率可以定义为
| ${\eta _{{\rm{fcs}}}} = \frac{{{V_{{\rm{cell}}}}}}{{1.482}}{\rm{ }} \times \frac{{{P_{{\rm{fc}}}} - {P_{{\rm{aux}}\_{\rm{fc}}}}}}{{{P_{{\rm{fc}}}}}} \times 100\% $ | (14) |
式中:Pfc为电堆的输出功率,Paux_fc为电堆辅助设备的损耗功率。
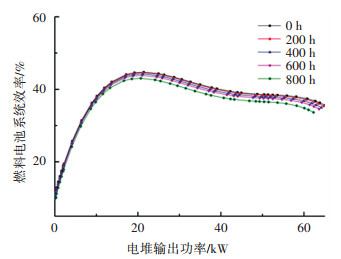
利用上一节拟合出的燃料电池极化曲线和实际采集的整车运行的相关数据,根据式(14)可以求出燃料电池不同老化阶段的系统效率,如图 4所示。随着燃料电池运行时间的增加,系统的最高效率是逐渐下降的,由45%下降至43%左右;系统效率在40%以上的区域逐渐减少,对应的电堆输出功率由12~40 kW变为13~32 kW;当电堆的输出功率在20 kW以内时,各个周期内的系统效率相差不大,但超过20 kW时,系统的效率相差明显。
|
图 4 燃料电池系统效率与电堆输出功率之间的关系 Fig. 4 Relationship between fuel cell system efficiency and stack output power |
原有的恒温器控制策略由于其具有简单且不需要路况信息等优点而用于实时控制。但是,其控制参数是固定的,故不能在FCEV的整个寿命周期内均能做出合理的控制决策。因此,本文提出了改进的恒温器控制策略,该策略综合了动力电池的SOC和燃料电池系统的高效工作区间两个因素,通过遗传算法对规则参数不断优化,在燃料电池的整个寿命周期内,使燃料电池尽可能长时间在高效区间内工作。
改进的恒温器控制策略规则如表 3所示,当SOC高于90%时,为了保护动力电池的安全,燃料电池是不工作的;当SOC降至65%时,应及时增加燃料电池输出功率,以减缓SOC下降速度;当SOC低于40%时,应以提高SOC为目标,否则会影响动力电池的寿命。燃料电池输出功率Pfc_1、Pfc_2和Pfc_3由遗传算法寻求最优值。而恒温器控制策略燃料电池的输出功率是定值,Pfc_1、Pfc_2和Pfc_3分别为22、36和57 kW。
| 表 3 改进的恒温器控制策略规则 Tab. 3 Rules of improved thermostat control strategy |
为了保证燃料电池不会过度的变载,该控制策略在SOC为40%、65%和90%处均加了5%的冗余,即ΔSOCfloat为5%。例如,当燃料电池的输出功率由Pfc_2增加到Pfc_1时,SOC的值有可能大于40%,若此时立即减少燃料电池的输出功率,可能会造成SOC立刻跌落到40%以下,又触发了升高燃料电池输出功率的规则。这样会增加燃料电池的变载次数,减小其使用寿命,故通过增加SOC的冗余,来达到稳定燃料电池输出功率的目的。
当改变燃料电池的输出功率时,燃料电池电流变化速率偏大,则会增加燃料电池电堆内部水和气体的调节难度,进而造成燃料电池寿命的缩短。所以,应限制燃料电池电流的变化速率,电流的变化速率应满足以下限制条件[2]:
| $\begin{array}{l} {I_{{\rm{fc}}}}\left( k \right) \le {I_{{\rm{fc}}}}\left( {k - 1} \right) + \Delta {I_{{\rm{fc\_add}}}}\\ {I_{{\rm{fc}}}}\left( k \right) \ge {I_{{\rm{fc}}}}\left( {k - 1} \right) - \Delta {I_{{\rm{fc\_minu}}}} \end{array}$ | (15) |
式中:ΔIfc_add和ΔIfc_minu分别是燃料电池最大的加载和减载速率,Ifc(k)是燃料电池的电流。
3 结果分析为了验证改进的恒温器控制策略在燃料电池的不同阶段均能做出合理的能量流分配,本节设置整车的状态参数SOC为90%,储氢瓶加满氢气,以相同的循环工况连续运行200 km。并且改变燃料电池不同运行阶段下的性能参数,以验证该控制方法的长效性。在本次仿真中,设置遗传算法的参数为:种群大小为50,迭代次数为40,交叉概率为0.6,变异为0.3。
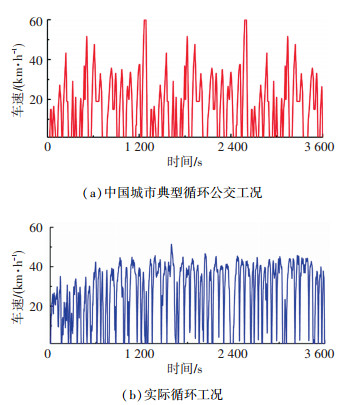
3.1 循环工况的选取本文选取了中国典型城市公交循环工况和实际采集的运行工况。图 5展示了这两种工况的信息。
|
图 5 两种循环工况 Fig. 5 Two cycle conditions |
以中国城市典型循环公交工况为基准,本节仿真分析了两种控制策略在燃料电池不同老化阶段的氢气平均利用效率,其结果如表 4所示。
| 表 4 不同燃料电池老化阶段条件下氢气平均利用效率 Tab. 4 Average utilization rate of hydrogen at different aging stages of fuel cells |
随着燃料电池的不断老化,其系统的效率是逐渐下降的,所以两种控制策略下氢气平均利用效率均是逐渐减小的。但是改进控制策略下的氢气平均利用效率始终要高于普通恒温器控制策略的。当燃料电池的运行周期j为1、2、3时,两种控制策略下的氢气平均利用效率逐渐接近,这是因为普通的恒温器控制策略在选择规则参数时重点考虑了燃料电池在此阶段的工作状态;当燃料电池的运行周期j为4时,改进的恒温器控制策略要比普通的恒温器控制策略氢气平均利用效率高1%,这是因为改进的恒温器控制策略是在整个燃料电池生命周期内不断寻求最优解。
3.3 不同循环工况下的氢气平均利用效率在仿真的过程中,对氢气的利用效率不断地取平均值,该值作为遗传算法的适应度函数。经过40次的不断迭代,得出了最优的燃料电池输出功率点。j为0的条件下,两种工况对应的燃料电池输出功率见表 5。
| 表 5 燃料电池输出功率 Tab. 5 Output power of fuel cell |
按照表 5中的参数进行仿真,得出两种工况条件下的燃料电池的输出功率变化情况,如图 6所示。当整车的平均需求功率不高时,燃料电池可以在高效率区域工作,且变载次数少。但是当整车的需求功率变高时,燃料电池就必须牺牲系统效率而提高输出功率,当SOC升高至规定值,燃料电池的输出功率又减小到高效率区间。

|
图 6 两种工况下燃料电池的输出功率 Fig. 6 Output power of fuel cell under two working conditions |
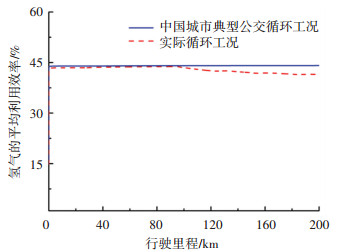
图 7为两种工况下氢气的平均利用效率与行驶里程之间的关系。在中国城市典型公交循环工况下,燃料电池系统的氢气平均利用效率一直保持在44%左右,这是由于其整车的需求平均功率为23.9 kW,燃料电池的输出功率Pfc_2和Pfc_3均在系统效率的最高区域,燃料电池不需要输出更高的功率。在实际的循环工况下,FCEV运行的前100 km内,氢气平均利用效率维持在43%左右,随后氢气的利用效率会逐渐的下降,直至降到最低值41%,这是因为实际循环工况下整车的需求功率偏高,燃料电池的大功率输出时间变长,拉低了整体的氢气平均利用效率。
|
图 7 两种工况下氢气平均利用效率 Fig. 7 Average utilization rate of hydrogen under two working conditions |
本文提出了一种提高氢气平均利用效率的改进恒温器控制策略,该策略的规则参数随着燃料电池的老化而不断变化。利用实时采集的燃料电池电压和电流数据,通过最小二乘法不断地识别燃料电池的老化程度,然后利用遗传算法不断地优化恒温器的规则参数,恒温器控制策略通过优化后的规则参数和SOC来控制燃料电池的功率。在不同的循环工况下连续运行200 km,分析200 km内的氢气平均利用效率。
1) 在中国城市典型循环公交工况条件下,随着燃料电池的老化,两种控制策略下的氢气平均利用效率均是下降的,但在燃料电池运行的任何周期内,改进的恒温器控制策略下的氢气平均利用效率均大于原恒温器控制策略,最多可提高1.1%。
2) 对比两种循环工况下的氢气平均利用效率发现,整车的需求功率越高,氢气平均利用效率就越低。所以应及时调整燃料电池的大功率工作点,兼顾大功率的运行时间和对应的效率。
3) 在不同的燃料电池老化阶段和不同的循环工况下,改进的恒温器控制均能做出合理的能量流分配,表明本文提出的控制策略具有很强的实用性。
| [1] |
ZHOU Y F, HUANG L J, SUN X X, et al. A long-term energy management strategy for fuel cell electric vehicles using reinforcement learning[J]. Fuel Cells, 2020, 20(6): 753. DOI:10.1002/fuce.202000095 |
| [2] |
XU Liangfei, LI Jianqiu, OUYANG Minggao, et al. Multi-mode control strategy for fuel cell electric vehicles regarding fuel economy and durability[J]. International Journal of Hydrogen Energy, 2014, 39(5): 2374. DOI:10.1016/j.ijhydene.2013.11.133 |
| [3] |
王骞, 李顶根, 苗华春. 基于模糊逻辑控制的燃料电池汽车能量管理控制策略研究[J]. 汽车工程, 2019, 41(12): 1347. WANG Qian, LI Dinggen, MIAO Huachun. Research on energy management strategy of fuel cell vehicle based on fuzzy logic control[J]. Automotive Engineering, 2019, 41(12): 1347. DOI:10.19562/j.chinasae.qcgc.2019.012.001 |
| [4] |
尹良震, 李奇, 洪志湖, 等. PEMFC发电系统FFRLS在线辨识和实时最优温度广义预测控制方法[J]. 中国电机工程学报, 2017, 37(11): 3223. YIN Liangzhen, LI Qi, HONG Zhihu, et al. FFRLS online identification and real-time optimal temperature generalized control method of PEMFC power generation system[J]. Proceedings of the CSEE, 2017, 37(11): 3223. DOI:10.13334/j.0258-8013.pcsee.160907 |
| [5] |
王天宏, 李奇, 尹良震, 等. 燃料电池系统在线辨识和实时最大效率滑模控制方法[J]. 中国电机工程学报, 2019, 39(17): 5118. WANG Tianhong, LI Qi, YIN Liangzhen, et al. Fuel cell system online identification and real-time maximum efficiency sliding mode control method[J]. Proceedings of the CSEE, 2019, 39(17): 5118. DOI:10.13334/j.0258-8013.pcsee.181559 |
| [6] |
ZHONG Zhidan, HUO Haibo, ZHU Xinjian, et al. Adaptive maximum power point tracking control of fuel cell power plants[J]. Journal of Power Sources, 2008, 176(1): 259. DOI:10.1016/j.jpowsour.2007.10.080 |
| [7] |
JOUIN M, GOURIVEAU R, HISSEL D, et al. Degradations analysis and aging modeling for health assessment and prognostics of PEMFC[J]. Reliability Engineering & System Safety, 2016, 148: 78. DOI:10.1016/j.ress.2015.12.003 |
| [8] |
WANG Guangjin, HUANG Fei, YU Yi, et al. Degradation behavior of a proton exchange membrane fuel cell stack under dynamic cycles between idling and rated condition[J]. International Journal of Hydrogen Energy, 2018, 43(9): 4471. DOI:10.1016/j.ijhydene.2018.01.020 |
| [9] |
AHMADI S, BATHAEE S M T, HOSSEINPOUR A H. Improving fuel economy and performance of a fuel-cell hybrid electric vehicle (fuel-cell, battery, and ultra-capacitor) using optimized energy management strategy[J]. Energy Conversion and Management, 2018, 160: 74. DOI:10.1016/j.enconman.2018.01.020 |
| [10] |
ALIASGHARY M. Control of PEM fuel cell systems using interval type-2 fuzzy PID approach[J]. Fuel Cells, 2018, 18(4): 449. DOI:10.1002/fuce.201700157 |
| [11] |
LI Dinggen, FENG Daiwei. Thermostatic control for series hydraulic hybrid vehicle (SHHV) energy management[J]. Advanced Materials Research, 2012, 512: 2676. DOI:10.4028/www.scientific.net/AMR.512-515.2676 |
| [12] |
WON J S, LANGARI R. Intelligent energy management agent for a parallel hybrid vehicle-part Ⅱ: torque distribution, charge sustenance strategies, and performance results[J]. IEEE Transactions on Vehicular Technology, 2005, 54(3): 935. DOI:10.1109/TVT.2005.844683 |
| [13] |
LANGARI R, WON J S. Intelligent energy management agent for a parallel hybrid vehicle-part Ⅰ: system architecture and design of the driving situation identification process[J]. IEEE Transactions on Vehicular Technology, 2005, 54(3): 925. DOI:10.1109/TVT.2005.844685 |
| [14] |
AMPHLETT J C, BAUMERT R M, MANN R F, et al. Parametric modelling of the performance of a 5 kW proton-exchange membrane fuel cell stack[J]. Journal of Power Sources, 1994, 49. DOI:10.1016/0378-7753(93)01835-6 |
| [15] |
ZHAO Yuehong, PISTIKOPOULOUS E. Dynamic modelling and parametric control for the polymer electrolyte membrane fuel cell system[J]. Journal of Power Sources, 2013, 232: 270. DOI:10.1016/j.jpowsour.2012.12.116 |
| [16] |
CHEN Ben, CAI Yonghua, TU Zhengkai, et al. Gas purging effect on the degradation characteristic of a proton exchange membrane fuel cell with dead-ended mode operation I. with different electrolytes[J]. Energy, 2017, 141: 40. DOI:10.1016/j.energy.2017.09.067 |
| [17] |
RESHETENKO T V, BENDER G, BETHUNE K, et al. Systematic study of back pressure and anode stoichiometry effects on spatial PEMFC performance distribution[J]. Electrochimica Acta, 2011, 56(24): 8700. DOI:10.1016/j.electacta.2011.07.058 |
| [18] |
ZHANG Xinfeng, RUI Yang, TONG Zhang, et al. The characteristics of voltage degradation of a proton exchange membrane fuel cell under a road operating environment[J]. International Journal of Hydrogen Energy, 2014, 39: 9420. DOI:10.1016/j.ijhydene.2014.03.239 |
 2022, Vol. 54
2022, Vol. 54


