2. 哈尔滨工业大学(威海)海洋工程学院,山东 威海 264209;
3. 山东船舶技术研究院,山东 威海 264209
2. School of Ocean Engineering, Harbin Institute of Technology, Weihai, Weihai 264209, Shandong, China;
3. Shandong Institute of Shipbuilding Technology, Weihai 264209, Shandong, China
海洋环境中由于盐度差导致流体分层。航行于分层流体中的潜艇,不仅会在自由液面上兴起波浪,同时也会在流体内部交界面上产生内波[1]。内波的周期和波长变化幅度均较大,研究分层流体中交界面处兴波尾迹,可为水下潜艇非声探测及运动反演提供重要的参考[2],具有十分重要的意义。
自19世纪末Kelvin提出“Kelvin”船行波以来,航行体自由面兴波问题一直是水动力学领域内的经典问题,国内外对于静水面上兴波尾迹的研究已经较为完善[3-5]。近年来以此为基础,运动物体在分层流体中激发内波的现象已成为国内外的研究热点。内波常被分为两类,一是体积效应内波(即Lee波[6]),另一类是湍流尾迹效应内波[7]。对于体积效应内波,Long等[8-10]的研究比较早,他们通过理论推导,建立了二维体积效应内波的理论解。随后,Lighthill等[11]对分层流体中移动源相关理论进行了系统的研究。近年来,Wei等[12]对有限水深条件下运动偶极子兴波问题进行了研究。Milder等[13]建立了具有速度和体积的等效质量源。尤云祥等[14]对Milder的等效质量源理论进行了发展。Hanazaki[15]和常煜等[16]则使用计算流体力学CFD方法对体积效应内波进行了数值研究。湍流尾迹内波指由运动潜体尾流产生的涡脱落、湍流尾迹等效应而发生的内波。20世纪中期便有学者对水下潜艇运动激发尾迹的形成及演化机理进行了研究[17-19]。Abdilghanie等[20]采用数值方法对尾流产生的随机内波进行了系统的分析。Gou[21]等采用时域高阶边界元法研究了有限水深两层流体中的波衍射问题。Yeung等[22]采用求解Green函数的方法,讨论了运动潜体产生的界面波模式。Posa等[23]研究了雷诺数对潜艇尾迹特征的影响。勾莹、赵先奇、Bonneton等[24-26]应用试验方法对内波问题进行了相关研究。
现有研究大多主要考虑分层流体中航行体运动激发的内波模式,但对多种参数影响下表面波、内波的尾迹研究较少。与此同时,多数研究均将潜艇置于浅水密度层即淡水中航行,而对潜艇在深水密度层即内波面以下航行时的尾迹特征研究较少。
针对上述问题,在刘双等[27]研究的基础上,本研究将利用计算流体力学(CFD)方法开展数值模拟,分析多种参数影响下表面波、内波的尾迹,并着重探讨位于深水密度层航行潜艇的尾迹特性。
基于RANS方程,采用综合Realizable k-ε湍流模型、欧拉多相流模型及用户自定义函数方法建立了深水密度层航行潜艇尾迹特性分析的数值模型。以SUBOFF潜艇为模型,研究了其在深水密度层不同位置处以不同航速航行时的兴波尾迹特性。全面地分析深水密度层航行潜艇在不同工况下的航行特征。
1 数值计算模型本数值模型基于雷诺平均的N-S方程、相关控制方程及理论可参考文献[3],此处不再赘述。
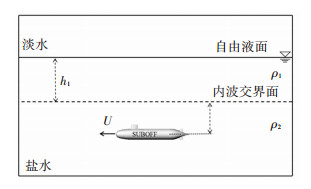
采用图 1所示的计算域进行仿真模拟,h1为淡水层深度;ρ1、ρ2分别为淡水层与盐水层流体的密度,分别取ρ1=997 kg / m3,ρ2=1 020 kg / m3。潜艇在内波交界面以下的深水密度层航行,通过改变潜艇重心与内波交界面距离d1以及航速U来研究不同参数下潜艇的兴波尾迹特性。因所研究的问题及几何结构是对称的,故采用半计算域和半潜艇模型来提高计算效率,潜艇模型为SUBOFF标模,其长度为3 m,最大半径0.174 m。
|
图 1 分层示意 Fig. 1 Diagram of density stratified fluid |
在边界条件处,采用用户自定义场函数的方式分别给定空气、淡水、盐水的密度、初始体积分数以及整个计算域的压力分布。本数值模型采用切割体网格及棱柱层网格进行计算域的网格划分,在潜艇附近及交界面处进行网格加密以更好地捕捉流场特性;经收敛性研究,确定最终总网格数为400万左右,潜艇周围网格如图 2所示。此外,考虑库朗数的要求,经过大量的数值实验,最终确定的时间步长为0.01 s,可实现计算精度和计算资源消耗的平衡。

|
图 2 潜艇周围网格分布 Fig. 2 Grid distribution around the submarine |
在真实航行过程中,潜艇与内波交界面的相对位置是变化的。文献[27]对潜艇航行于淡水层的兴波尾迹进行了研究,本文着重关注潜艇位于盐水层中航行时的尾迹特征。根据前述研究[3],为使兴波尾迹更加明显,设置两个典型工况A、B(见表 1)。
| 表 1 各工况参数设置 Tab. 1 Parameters of working conditions |
表 1中L为潜艇长度。工况A用以分析潜艇兴波尾迹随航速的变化情况,而工况B侧重于潜艇的下潜深度对交界面处兴波的影响。本研究在讨论潜艇在各交界面处的兴波尾迹随不同航行参数的变化规律时,不考虑海洋背景噪音及波浪的影响,将自由液面设置为静水面。
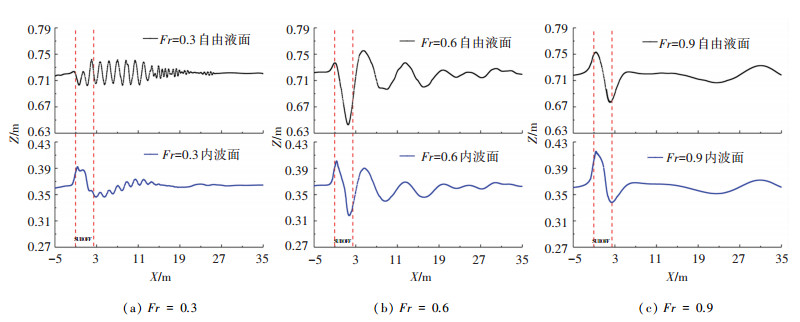
2.1 潜艇航速对兴波尾迹的影响 2.1.1 航速对波面抬升的影响针对工况A,选择Fr为0.3、0.6、0.9来分别讨论低、中、高速情况下交界面处的波面抬升结果。图 3为潜艇中纵剖面(Y=0)与上方自由液面、内波面相切得到的波切线;图中横坐标X代表计算域在长度方向的尺寸;纵坐标为潜艇运动引起的波面抬升Z,单位均为m,两条虚线之间表示潜艇的纵向位置,潜艇重心位置的Z坐标为0。
|
图 3 不同航速下兴波波面抬升(Y =0) Fig. 3 Wave profiles with different forward speeds (Y=0) |
由图 3可见,随着潜艇航速的增加,自由液面与内波面处兴波的波长均不断增加;自由液面与内波面处的波形几乎一致,艇首位置均出现了“伯努利丘”现象;但艇首在内波面激起的波峰要高于同航速下自由液面处峰值,分析原因是由于内波面与潜艇距离相对较近而导致;对于艇尾处的波面抬升,无论自由液面处还是内波面处的兴波,在Fr=0.6附近中速阶段的波面抬升绝对值均要高于Fr=0.3附近低速及Fr=0.9附近高速阶段的结果。这说明潜艇在Fr=0.6附近中速阶段的兴波现象最为明显,这与常规的水面舰船是一致的[28]。
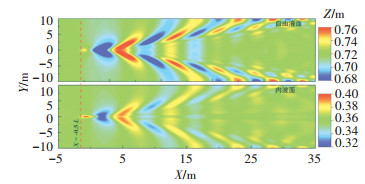
为进一步观察两交界面处兴波的波形特征,选择兴波较为剧烈的Fr=0.6工况;其兴波分布如图 4所示;在不同X位置处取得波切线,波切图如图 5所示,其中纵坐标为波面抬升Z;横坐标为Y方向(垂直于潜艇前进方向)的尺寸,单位均为m。从艇首(X=-0.5 L)处开始,每隔一个艇长得到一条波切线。
|
图 4 Fr=0.6时兴波云图(上:自由液面;下:内波面) Fig. 4 Wave distribution with Fr=0.6(Up: free surface; Down: internal surface) |

|
图 5 不同X位置处兴波波面抬升(Fr =0.6) Fig. 5 Wave profiles with different X (Fr=0.6) |
由图 5可见,当潜艇航行于内波交界面以下的盐水层中时,自由液面与内波面处的兴波波形几乎一致,即在艇首处为波峰、艇尾处为波谷,之后呈现峰谷交替向后传播。随着兴波向潜艇后方传播,波切线中间部分的峰、谷不断向两侧拓展。从波面抬升的数值来看,自由液面要略高于内波面,且此差别随着波切线向艇尾移动会逐渐加大。此外,当潜艇兴波传播到3.5 L以后,两个交界面波形的中间部分会有所不同。如图 5(b)中红点a、b所示,内波面处会出现幅值较小的波谷,且此波谷有逐渐分离的趋势,在图中表现为两红点间的距离逐渐增加。
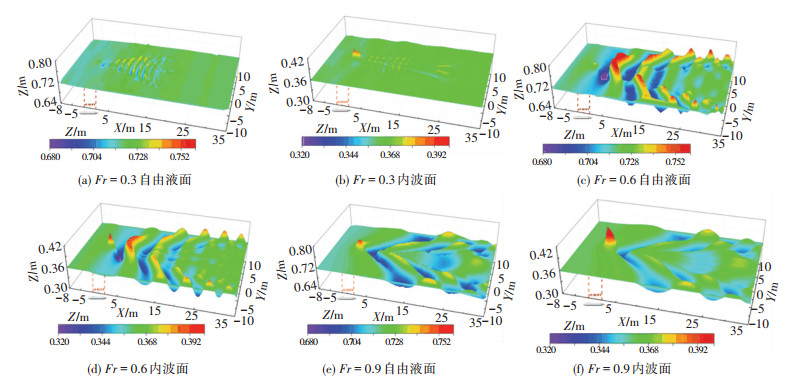
2.1.2 航速对兴波波系的影响潜艇的航行尾迹是非声探测的一种重要参考,图 6为潜艇以Fr分别为0.3、0.6、0.9航行时在自由液面及内波面处的波形图。图 6中X、Y为计算域在长度、宽度方向的尺寸,Z为波面抬升的数值,单位均为m,颜色代表波幅的大小,潜艇重心坐标位于原点,图中虚线之间给出了潜艇的位置示意。
|
图 6 不同航速下潜艇运动兴波特性 Fig. 6 Wave distribution generated by submarine with different forward speeds |
由图 6可见,自由液面与内波面波形具有一致性,两者均呈现出一定的“Kelvin”波特性,即艇首为峰、艇尾为谷,并以峰谷交替的形式向后方不断传播。随着航速的增加,潜艇在两个交界面处的兴波范围越来越大,兴波波长逐渐增加。
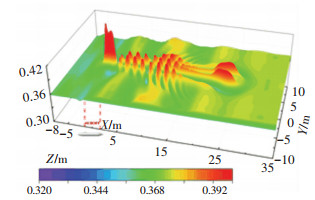
内波面处波形的前方同样为波峰,但峰值高于自由液面处结果,这与图 3中结果一致。此外,与自由液面不同的是,在内波面波形的尾部会出现狭长的‘V’字型“尾巴”。在之前的研究[27]中,曾经发现航行于浅水层中潜艇在内波面上的兴波后部存在一环形区域。现在本研究中也得到了类似的重现。图 7给出了波幅放大3倍后的Fr=0.3内波面波形图,可以看到,在X=15~25区域内存在明显的环形区域,这也证明了本文数值结果的正确性。
|
图 7 Fr =0.3内波面波形图(波幅放大3倍) Fig. 7 Wave distribution with Fr=0.3 (three times amplification of amplitude) |
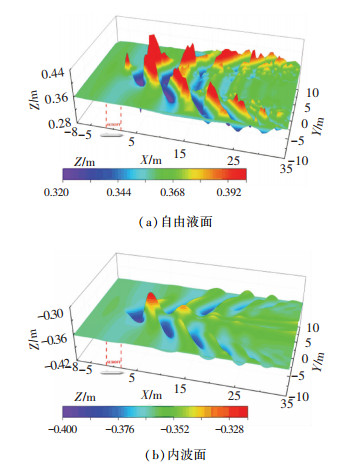
为了对比潜艇在深层和浅层中航行时自由面和内波面上的兴波情况,本文补充了潜艇在浅水密度层中以Fr=0.6航行时的波形图(图 8),具体的计算方法同文献[27],在此不再赘述,此时重心在原点处的潜艇距离自由液面及内波面均为0.12 L=0.36 m。对比图 6、8可知,从波形角度来看,无论潜艇航行于浅水密度层还是深水密度层,其在自由液面处激起的兴波波形几乎一致,即“Kelvin”波。但在浅水和深水密度层中航行潜艇所激起的内波波形有较大差异,最直观的差异在于:1)航行于深水密度层中的潜艇在内波面处兴波前方为波峰,而航行于浅水密度层中的潜艇在内波面处兴波前方为波谷;2)深水密度层航行潜艇内波面上兴波出现了类似于“Kelvin”波的波形,而浅水密度层中航行潜艇在内波面上的兴波并未有“Kelvin”模式,且横、散波分布特征不明显。3)位于深水密度层中航行潜艇的兴波在自由液面与内波面处的波幅整体相差不大,而浅水密度层中航行潜艇的自由面兴波波幅要明显高于内波面波幅。这些区别对潜艇非声探测具有重要的参考价值,可用于初步判断潜艇在海洋环境中相对于分层界面的位置。
|
图 8 浅水密度层潜艇运动兴波特性(Fr=0.6) Fig. 8 Wave distribution generated by submarine navigating in shallower density layer (Fr=0.6) |
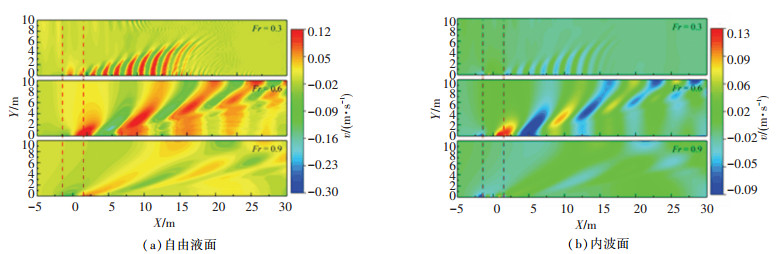
图 9、10分别为Fr=0.3、0.6、0.9时自由液面及内波面在X、Z方向上的水质点速度分布。其中各图横、纵坐标分别为X、Y方向的计算域尺寸,单位均为m,虚线间为潜艇所在的纵向位置。
|
图 9 不同航速下自由液面和内波面上水质点速度分布(X方向) Fig. 9 Velocity distribution of fluid particles on free and internal surfaces with different forward speeds (X direction) |
|
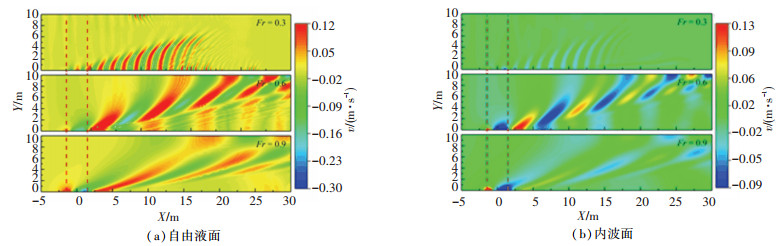
图 10 不同航速下自由液面和内波面上水质点速度分布(Z方向) Fig. 10 Velocity distribution of fluid particles on free and internal surfaces with different forward speeds (Z direction) |
由图 9可见,当潜艇航行于深水密度层时,自由液面与内波面处的水质点速度X方向分量分布基本一致,均表现为靠近艇首位置的水质点速度降低,而靠近尾部处速度提高。随着Fr的增加,两交界面处的水质点速度受影响范围均逐渐加大。由图 10可见,对于水质点速度Z方向的分量,在艇首处为正值,而艇尾处为负值,这与图 3中波面抬升现象一致,即波面上升、下降处水质点速度分别具有向上、向下的速度分量。此外,在Fr为0.6左右的中速阶段,自由液面与内波面的水质点速度值均大于Fr为0.3及0.9时的,与图 6中潜艇在各交界面处的兴波分布情况一致。说明当潜艇兴波较为剧烈时,各交界面处的水质点在X方、Z方向的速度值均较大。
2.2 潜艇下潜深度对兴波尾迹的影响 2.2.1 下潜深度对波面抬升的影响针对工况B,选择d1为0.12 L、0.15 L、0.18 L来分别研究浅、中、深3个下潜深度处潜艇运动在交界面处的波面抬升情况。图 11为波切线图。

|
图 11 不同下潜深度下潜艇兴波波面抬升(Y=0) Fig. 11 Wave profiles with different submerged depths (Y=0) |
由图 11可见,自由液面与内波面处波形的前方均为波峰,但自由液面处的第一个波峰峰值要低于内波面处,且自由液面处第二个波峰峰值最大。随着d1增加,潜艇在自由液面及内波面处的兴波波幅均略有下降,而兴波的波长几乎没有变化。
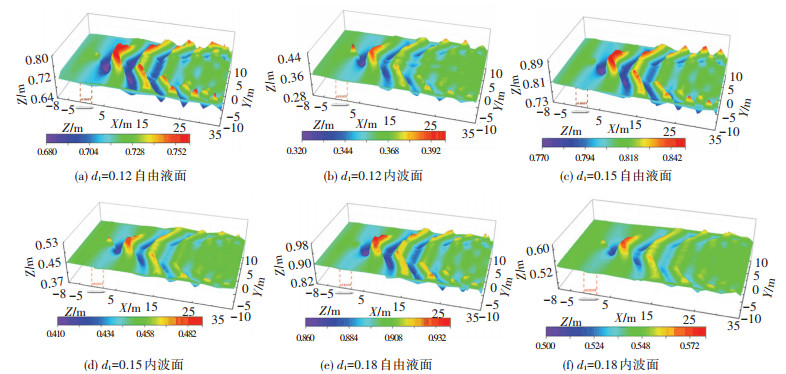
2.2.2 下潜深度对兴波波系的影响图 12为不同位置工况(0.12 L、0.15 L、0.18 L)下自由液面及内波面上的兴波云图。由图 12可知,随着下潜深度d1增加,自由液面及内波面处的兴波波幅均会略有下降,但波长几乎不变。对比整个波形的中后方区域处,自由液面上表现为明显横波、散波分离,并在散波包络线处相互叠加形成较大的波峰;而内波面兴波虽也出现了横、散波特征,但未展现出明显的分离。
|
图 12 不同位置处潜艇运动兴波特性 Fig. 12 Wave distribution generated by submarineat different positions |
由图 12(b)可见,在艇尾后方较远处,内波面波形中间部分出现分离现象,进而形成了狭长的‘V’字型尾迹,这与图 5中的分析一致,说明内波面上的兴波区域内存在复杂的波系相互叠加现象。此外,通过对比两交界面处的波形发现,自由液面处的兴波波幅略大于内波面处,但波长差别不大。
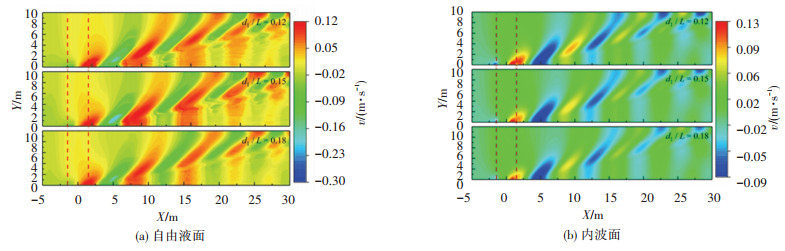
2.2.3 下潜深度对交界面处水质点速度分布的影响图 13、14分别为不同下潜深度(0.12 L、0.15 L、0.18 L)下自由液面及内波面上在X、Z方向上的水质点速度分布情况。由图 13、14可见,随着d1增加,自由液面及内波面处的水质点速度均略微降低。整体来看,下潜深度对各交界面处的水质点速度大小及分布形状几乎没有影响。同时由图 14可见,水质点速度在Z方向的分量变化与图 11中的波面抬升基本一致,这与2.1.3中的分析相同。
|
图 13 不同下潜深度下自由液面和内波面上水质点速度分布(X方向) Fig. 13 Velocity distribution of fluid particles on free and internal surfaces with different submerged depths (X direction) |

|
图 14 不同下潜深度下自由液面和内波面上水质点速度分布(Z方向) Fig. 14 Velocity distribution of fluid particles on free and internal surfaces with different submerged depths (Z direction) |
此外,两个交界面处的速度分布几乎一致,分析原因是由于其均位于潜艇上方,由于淡水层深度h1取得较小,故两个交界面处的速度差距不大。各交界面处速度分布的一致性也合理地解释了图 12中自由面和内波面上兴波波长差别不大的原因。
3 结论本研究基于黏流理论,结合UDF方法建立了一种可用于求解密度分层流中潜艇兴波尾迹特性的CFD数学模型,并着重针对深水密度层中航行潜艇的兴波尾迹特征进行了模拟分析,得到如下结论:
1) 航速对深水密度层航行潜艇的兴波特性影响较大。随着航速增加,潜艇在各交界面处的兴波波长不断增大。在Fr=0.6前后的中速阶段,自由面和内波面上的兴波情况均比Fr=0.3低速及Fr=0.9高速时的结果剧烈。
2) 相比于航速,潜艇与内波面的距离对兴波特性的影响较小。随着下潜深度的增加,潜艇在各交界面处的兴波波形中仅波幅略有下降,波长几乎没有变化。
3) 潜艇位于不同流体层中航行时,其在自由液面处的兴波差别不大,但内波面处兴波会有较大差别。潜艇在浅水密度层中航行时内波面波形前方为一波谷,波幅明显低于自由液面处,并且未出现“Kelvin”波特征;而深水密度层中航行潜艇在内波面处的波形前方为一较大的波峰,波幅与自由液面几乎一致,具有“Kelvin”波特征。
4) 潜艇航行时,航速及下潜深度会影响交界面上的水质点速度分布。x方向上水质点速度受影响的区域大小与兴波的波长的变化具有一致性。
5) 本研究方法具有较好的模拟精度,深水密度层航行潜艇的兴波尾迹分析对于潜艇航行及规避策略的选取具有一定的指导意义,同时可为潜艇的非声探测及其运动反演研究提供参考。
| [1] |
魏岗, 戴世强. 分层流体中运动源生成的内波研究进展[J]. 力学进展, 2006, 36(1): 111. WEI Gang, DAI Shiqiang. Advances in internal waves due to moving body in stratified fluid systems[J]. Advances in Mechanics, 2006, 36(1): 111. DOI:10.3321/j.issn:1000-0992.2006.01.016 |
| [2] |
SPEDDING G R. Wake signature detection[J]. Annual Review of Fluid Mechanics, 2014, 46: 273. DOI:10.1146/annurev-fluid-011212-140747 |
| [3] |
何广华, 刘双, 张志刚, 等. 附体对潜艇兴波尾迹的影响分析[J]. 华中科技大学学报(自然科学版), 2019, 47(10): 57. HE Guanghua, LIU Shuang, ZHANG Zhigang, et al. Analysis of influence of appendages on wake-making of submarine[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2019, 47(10): 57. DOI:10.13245/j.hust.191011 |
| [4] |
HE Guanghua, KASHIWAGI M. A time-domain higher-order boundary element method for 3D forward-speed radiation and diffraction problems[J]. Journal of Marine Science and Technology, 2014, 19(2): 228. DOI:10.1007/s00773-013-0242-1 |
| [5] |
BHUSHAN S, ALAM M F, WALTERS D K. Evaluation of hybrid RANS/LES models for prediction of flow around surface combatant and Suboff geometries[J]. Computers & Fluids, 2013, 88: 834. DOI:10.1016/j.compfluid.2013.07.020 |
| [6] |
HOPFINGER E J, FLOR J B, CHOMAZ J M, et al. Internal waves generated by a moving sphere and its wake in a stratified fluid[J]. Experiments in Fluids, 1991, 11(4): 255. |
| [7] |
王进, 尤云祥, 胡天群, 等. 密度分层流体中不同长径比拖曳潜体激发内波特性实验[J]. 科学通报, 2012, 57(8): 606. WANG Jin, YOU Yunxiang, HU Tianqun, et al. The characteristics of internal waves excited by towed bodies with different aspect ratios in a stratified fluid[J]. Chinese Science Bulletin, 2012, 57(8): 606. DOI:10.1360/972011-1361 |
| [8] |
LONG R R. Some aspects of the flow of stratified fluids: Ⅰ. A theoretical investigation[J]. Tellus, 1953, 5(1): 42. DOI:10.3402/tellusa.v5i1.8563 |
| [9] |
LONG R R. Some aspects of the flow of stratified fluids: Ⅱ. Experiments with a two-fluid system[J]. Tellus, 1954, 6(2): 97. DOI:10.3402/tellusa.v6i2.8731 |
| [10] |
LONG R R. Some aspects of the flow of stratified fluids: Ⅲ. Continuous density gradients[J]. Tellus, 1955, 7(3): 341. DOI:10.3402/tellusa.v7i3.8900 |
| [11] |
LIGHTHILL M J. On waves generated in dispersive systems by travelling forcing effects, with applications to the dynamics of rotating fluids[M]// FROISSART M. Hyperbolic Equations and Waves. Berlin: Springer, 1970: 124. DOI: 10.1007/978-3-642-87025-5_15
|
| [12] |
WEI Gang, LU Dongqiang, DAI Shiqiang. Waves induced by a submerged moving dipole in a two-layer fluid f finite depth[J]. Acta Mechanica Sinica, 2005, 21(1): 24. DOI:10.1007/s10409-004-0003-9 |
| [13] |
MILDER M. Internal waves radiated by a moving source. Vol. 1-Analytical Simulation, RDA-TR-2702-007 [R]. Santa Monica: R&D Associates, 1974.
|
| [14] |
尤云祥, 赵先奇, 陈科, 等. 有限深密度分层流体中运动物体生成内波的一种等效质量源方法[J]. 物理学报, 2009, 58(10): 6750. YOU Yunxiang, ZHAO Xianqi, CHEN Ke, et al. An equivalent mass source method for internal waves generated by a body moving in a stratified fluid of finite depth[J]. Acta Physica Sinica, 2009, 58(10): 6750. DOI:10.3321/j.issn:1000-3290.2009.10.014 |
| [15] |
HANAZAKI H. A numerical study of three-dimensional stratified flow past a sphere[J]. Journal of Fluid Mechanics, 1988, 192: 393. DOI:10.1017/S0022112088001910 |
| [16] |
常煜, 洪方文. 两层流体中潜艇水下运动尾迹的数值模拟[J]. 水动力学研究与进展, 2006, 21(1): 76. CHANG Yu, HONG Fangwen. Numerical simulation of wakes for moving submarine in a two-layer fluid[J]. Journal of Hydrodynamics, 2006, 21(1): 76. DOI:10.3969/j.issn.1000-4874.2006.01.012 |
| [17] |
CHOMAZ J M, BONNETON P, HOPFINGER E J. The structure of the near wake of a sphere moving horizontally in a stratified fluid[J]. Journal of Fluid Mechanics, 1993, 254: 1. DOI:10.1017/S0022112093002009 |
| [18] |
LIN J T, PAO Y H. Wakes in stratified fluids[J]. Annual Review of Fluid Mechanics, 1979, 11(1): 317. DOI:10.1146/annurev.fl.11.010179.001533 |
| [19] |
SPEDDING G R, BROWAND F K, FINCHAM A M. The long-time evolution of the initially turbulent wake of a sphere in a stable stratification[J]. Dynamics of Atmospheres and Oceans, 1996, 23(1/2/3/4): 171. DOI:10.1016/0377-0265(95)00414-9 |
| [20] |
ABDILGHANIE A M, DIAMESSIS P J. The internal gravity wave field emitted by a stably stratified turbulent wake[J]. Journal of Fluid Mechanics, 2013, 720: 104. DOI:10.1017/jfm.2012.640 |
| [21] |
GOU Ying, CHEN Xinjia, TENG Bin. A time-domain boundary element method for wave diffraction in a two-layer fluid[J]. Journal of Applied Mathematics, 2012, 2012(S2): 203. DOI:10.1155/2012/686824 |
| [22] |
YEUNG R W, NGUYEN T C. Waves generated by a moving source in a two-layer ocean of finite depth[J]. Journal of Engineering Mathematics, 1999, 35(1/2): 85. DOI:10.1023/a:1004399917692 |
| [23] |
POSA A, BALARAS E. A numerical investigation about the effects of Reynolds number on the flow around an appended axisymmetric body of revolution[J]. Journal of Fluid Mechanics, 2020, 884(A41): 1. DOI:10.1017/jfm.2019.961 |
| [24] |
勾莹, 张新未, 徐文彪, 等. 箱型结构在两层流中拖航阻力的实验研究[C]//第十八届中国海洋(岸) 工程学术讨论会论文集(上). 北京: 中国海洋学会, 2017: 471 GOU Ying, ZHANG Xinwei, XU Wenbiao, et al. Experimental study on towing resistance of box structure in two-layer flow[C]// Proceedings of the 18th China Ocean (Shore) Engineering Symposium. Beijing: Chinese Society for Oceanography, 2017: 471 |
| [25] |
赵先奇, 尤云祥, 陈科, 等. 分层流体中细长体生成内波的实验研究[J]. 上海交通大学学报, 2009, 43(8): 1298. ZHAO Xianqi, YOU Yunxiang, CHEN Ke, et al. Experimental study on the generation of internal waves by a slender body in stratified fluid[J]. Journal of Shanghai Jiaotong University, 2009, 43(8): 1298. |
| [26] |
BONNETON P, CHOMAZ J M, HOPFINGER E J. Internal waves produced by the turbulent wake of a sphere moving horizontally in a stratified fluid[J]. Journal of Fluid Mechanics, 1993, 254: 23. DOI:10.1017/S0022112093002010 |
| [27] |
刘双, 何广华, 王威, 等. 浅航艇在密度分层流中的兴波尾迹研究[J]. 哈尔滨工业大学学报, 2021, 53(7): 52. LIU Shuang, HE Guanghua, WANG Wei, et al. Analysis on the wake of a sallow navigation submarine in the density-stratified fluid[J]. Journal of Harbin Institute of Technology, 2021, 53(7): 52. DOI:10.119181/202005023 |
| [28] |
刘应中. 船舶兴波阻力理论[M]. 北京: 国防工业出版社, 2003. LIU Yingzhong. Theory of ship wave making resistance[M]. Beijing: National Defense Industry Press, 2003. |
 2022, Vol. 54
2022, Vol. 54


