行星滚柱丝杠(Planetary roller screw mechanism,PRSM)在航空、航天、船舶、石化、电力、医疗机械等领域中具有广阔的应用前景[1-3]。啮合特性研究方面,Jones、Fu等[4-5]建立了PRSM的啮合模型并计算了啮合点位置及啮合间隙。乔冠等[6]建立了法截面内零件的轮廓方程和滚道螺旋曲面方程,并讨论了结构参数对接触特性的影响规律。Ma等[7]基于有限元的方法对啮合特性进行了研究。在承载特性研究方面,Lisowski等[8]建立了PRSM中各构件间的载荷分布模型,并通过有限元方法对接触区刚度进行了分析。Aurégan等[9]利用有限元方法得出了丝杠-滚柱侧啮合的最大接触应力。Jones等[10]将丝杠等效成弹簧系统,利用直接刚度法,对PRSM的刚度及承载能力开展了研究。杨家军等[11]以Hertz弹性接触理论为基础,将滚柱作为整体并建立了刚度模型,得到了载荷分布曲线。刘柱等[12]建立了考虑装配误差的滚柱两侧螺纹牙载荷分布计算模型。
现有研究中,PRSM的丝杠和螺母螺纹牙截面轮廓通常为直线,滚柱的螺纹牙截面轮廓为凸圆弧,实际上牙型轮廓的设计对于PRSM的承载和寿命有着重要的影响。本文将丝杠和螺母的牙型轮廓设计为凹圆弧,滚柱牙型轮廓仍采用凸圆弧,形成凸-凹接触,建立凸凹接触式PRSM的啮合模型和承载模型,并系统分析结构参数对啮合点位置、轴向间隙和载荷分布的影响规律,将计算得出的接触应力分布与标准式进行了对比。
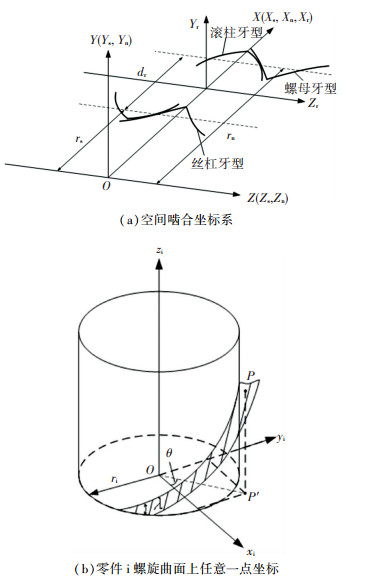
1 空间啮合模型的建立根据PRSM的结构特点,建立了如图 1所示的空间啮合坐标系及构件坐标系。
|
图 1 坐标系 Fig. 1 Coordinate system |
图 1(a)中,整体坐标系O-XYZ的Z轴与丝杠的轴线重合,X轴穿过滚柱的轴线;丝杠坐标系O-xsyszs、螺母坐标系O-xnynzn的z轴和x轴与整体坐标系O-XYZ的Z轴和X轴重合,滚柱坐标系的O-xryrzr的zr轴与滚柱轴线重合,xr与X轴重合。
图 1(b)为构件坐标系o-xiyizi(i=s, r, n分别表示丝杠、滚柱和螺母),点P为零件i螺旋曲面上的任意一点,则螺旋曲面的参数方程可以表示为
| ${Q_{\rm{i}}} = \left[ {{r_P}\cos {\theta _P}, {r_P}\sin {\theta _P}, {F_{\rm{i}}}\left( {{r_P}, {\theta _P}} \right)} \right]$ | (1) |
式中:rP、θP为曲面坐标,Fi(rP, θP)是由曲面坐标确定的螺旋曲面方程。
由图 1可得导程Li、螺旋角λi及中径ri的关系:
| ${L_{\rm{i}}} = 2{\rm{ \mathsf{ π} }}{r_{\rm{i}}}\tan {\lambda _{\rm{i}}} = {n_{\rm{i}}}{P_{\rm{i}}}$ | (2) |
式中:ni为头数,Pi为螺距。
1.1 曲面方程图 2为丝杠、滚柱及螺母的牙型轮廓图,凸凹接触式与标准式PRSM的丝杠、螺母有着不同的牙型轮廓,因此曲面方程也有所不同。

|
图 2 丝杠、滚柱及螺母的牙型轮廓图 Fig. 2 Thread profile of screw, roller, and nut |
图 2(a)为丝杠在丝杠坐标系xsoszs面中的牙型轮廓,设ose是丝杠圆弧的圆心,坐标ose(xso, zso)与牙型角αs、半牙厚cs和丝杠圆弧半径Rs的关系如下:
| $\left\{ \begin{array}{l} {x_{{\rm{so}}}} = {r_{\rm{s}}} + {R_{\rm{s}}}\sin {\alpha _{\rm{s}}}\\ {z_{{\rm{so}}}} = {c_{\rm{s}}} + {R_{\rm{s}}}\cos {\alpha _{\rm{s}}} \end{array} \right.$ | (3) |
接触线上任意一点(rPs, zs)满足
| ${z_{\rm{s}}} = {z_{{\rm{so}}}} - \sqrt {R_{\rm{s}}^2 - {{({r_{P{\rm{s}}}} - {x_{{\rm{so}}}})}^2}} $ | (4) |
最终得到丝杠螺旋曲面的曲面方程
| $\begin{array}{l} {F_{\rm{s}}}({r_{P{\rm{s}}}}, {\theta _{\rm{s}}}) = {\rho _{\rm{s}}}[{z_{{\rm{so}}}} - \sqrt {R_{\rm{s}}^2 - {{({r_{P{\rm{s}}}} - {x_{{\rm{so}}}})}^2}} ] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\theta _{\rm{s}}}{L_{\rm{s}}}/2{\rm{ \mathsf{ π} }} \end{array}$ | (5) |
式中:rPs、θs为丝杠螺旋曲面的参数坐标;ρs=1表示上螺旋曲面ΠSU;ρs=-1表示下螺旋曲面ΠSB。
1.1.2 滚柱的曲面方程图 2(b)是滚柱在滚柱坐标系xrorzr面中的牙型轮廓,设ore是滚柱圆弧的圆心,坐标ore(xro, zro)与牙型角αr、半牙厚cr和滚柱圆弧半径Rr的关系如下:
| $\left\{ \begin{array}{l} {x_{{\rm{ro}}}} = 0\\ {z_{{\rm{ro}}}} = - {R_{\rm{r}}}\cos {\alpha _{\rm{r}}} + {c_{\rm{r}}} \end{array} \right.$ | (6) |
接触线上任意一点(rPr, zr)满足
| ${z_{\rm{r}}} = {z_{{\rm{ro}}}} + \sqrt {R_{\rm{r}}^2 - {{({r_{P{\rm{r}}}} - {x_{{\rm{so}}}})}^2}} $ | (7) |
最终得到滚柱螺旋曲面的曲面方程
| ${F_{\rm{r}}}({r_{P{\rm{r}}}}, {\theta _{\rm{r}}}) = {\rho _{\rm{r}}}[{z_{{\rm{ro}}}} + \sqrt {R_{\rm{r}}^2 - {{({r_{P{{r}}}} - {x_{{\rm{ro}}}})}^2}} ] + {\theta _{\rm{r}}}{L_{\rm{r}}}/2{\rm{ \mathsf{ π} }}$ | (8) |
式中:rPr、θr是丝杠螺旋曲面的参数坐标;ρr=1表示上螺旋曲面ΠRU;ρr=-1表示下螺旋曲面ΠRB。
1.1.3 螺母的曲面方程图 2(c)为螺母在螺母坐标系xnonzn面中的牙型轮廓,设one是螺母圆弧的圆心,坐标one(xno, zno)与牙型角αn、半牙厚cn和丝杠圆弧半径Rn的关系如下:
| $\left\{ \begin{array}{l} {x_{{\rm{no}}}} = {r_{\rm{n}}} - {R_{\rm{n}}}\sin {\alpha _{\rm{n}}}\\ {z_{{\rm{no}}}} = - {R_{\rm{n}}}\cos {\alpha _{\rm{n}}} + {c_{\rm{n}}} \end{array} \right.$ | (9) |
接触线上任意一点(rPn, zn)满足
| ${z_{\rm{n}}} = {z_{{\rm{no}}}} + \sqrt {R_{\rm{n}}^2 - {{({r_{P{\rm{n}}}} - {x_{{\rm{no}}}})}^2}} $ | (10) |
最终得到螺母螺旋曲面的曲面方程
| ${F_{\rm{n}}}({r_{P{\rm{n}}}}, {\theta _{\rm{n}}}) = {\rho _{\rm{n}}}({z_{{\rm{no}}}} + \sqrt {R_{\rm{n}}^2 - {{({r_{P{\rm{n}}}} - {x_{{\rm{no}}}})}^2}} ) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\theta _{\rm{n}}}{L_{\rm{n}}}/2{\rm{ \mathsf{ π} }}$ | (11) |
式中:rPn、θn为螺母螺旋曲面的参数坐标,ρn=1表示上螺旋曲面ΠNU,ρn=-1表示下螺旋曲面ΠNB。
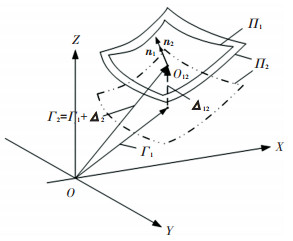
1.2 啮合方程PRSM要保持连续啮合,要求两啮合曲面在传动过程中时刻处于相切接触状态,同时为了保证行星滚柱丝杠的正常装配和运动的流畅性,各零件的螺纹之间通常具有一定的间隙[13]。图 3为PRSM在O-XYZ下两啮合曲面的相切接触关系,图中Π1和Π2为凸凹接触的PRSM中两个可能发生接触的螺旋曲面,曲面Π2沿着向量Δ12=[0, 0, e12]移动后与曲面Π1在点O12处相接触,e12即为两螺旋曲面的轴向间隙。根据齿轮啮合原理[14],可以得到凸凹接触式行星滚柱丝杠两螺旋曲面的相切接触条件:
| $\left\{ \begin{array}{l} {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_2}\left( {{u_2}, {\theta _2}} \right) = {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_1}\left( {{u_1}, {\theta _1}} \right) + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{_{12}}\\ \mathit{\boldsymbol{n}}{_2} = {\mu _{12}}{\mathit{\boldsymbol{n}}_1} \end{array} \right.$ | (12) |
|
图 3 PRSM两啮合曲面的相切接触关系 Fig. 3 Tangent relation between two meshing surfaces of PRSM |
式中μ12为常数。
由式(12)可得:
| $\left\{ \begin{array}{l} \mathit{\Gamma }_1^x = \mathit{\Gamma }_2^x\\ \mathit{\Gamma }_1^y = \mathit{\Gamma }_2^y\\ \mathit{\Gamma }_2^z = \mathit{\Gamma }_1^z + {e_{12}} \end{array} \right.$ | (13) |
由式(13)可得PRSM在丝杠-滚柱侧的啮合方程为:
| $\left\{ {\begin{array}{*{20}{l}} {r_{\rm{s}}^\prime \cos \theta _{\rm{s}}^\prime = - r_{\rm{r}}^\prime \cos \theta _{\rm{r}}^\prime }\\ {r_{\rm{s}}^\prime \sin \theta _{\rm{s}}^\prime = r_{\rm{r}}^\prime \sin \theta _{\rm{r}}^\prime }\\ {T_{\rm{s}}^z = T_{\rm{r}}^z + {e_{{\rm{sr}}}}}\\ {{\mathit{\boldsymbol{n}}_{\rm{s}}} = \frac{{\left| {{\mathit{\boldsymbol{n}}_{\rm{s}}}} \right|}}{{\left| {{\mathit{\boldsymbol{n}}_{\rm{r}}}} \right|}}{\mathit{\boldsymbol{n}}_{\rm{r}}}} \end{array}} \right.$ | (14) |
式中:rs′、θs′、rr′、θr′分别表示丝杠-滚柱啮合时,丝杠的啮合半径和啮合角,以及滚柱的啮合半径和啮合角;esr表示丝杠和滚柱啮合时的轴向间隙;ns、nr分别表示丝杠和滚柱的法向量;Tsz、Trsz分别表示丝杠和滚柱的啮合点在Z轴的分量:
| $\left\{ \begin{array}{l} T_{\rm{s}}^z = {\rho _{\rm{s}}}\left[ {{z_{{\rm{so}}}} - \sqrt {R_{\rm{s}}^2 - {{\left( {r_{\rm{s}}^\prime - {r_{\rm{s}}} - {x_{{\rm{so}}}}} \right)}^2}} } \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\theta _{\rm{s}}^\prime {L_{\rm{s}}}/2{\rm{ \mathsf{ π} }} + {P_{\rm{s}}}\left( {{t_{\rm{s}}} - 1} \right)\\ T_{\rm{r}}^z = - {\rho _{\rm{r}}}\left[ {{z_{{\rm{ro}}}} + \sqrt {R_{\rm{r}}^2 - {{\left( {r_{\rm{r}}^\prime - {r_{\rm{r}}} - {x_{{\rm{ro}}}}} \right)}^2}} } \right] + \\ \;\;\;\;\;\;\;\;\;\theta _{\rm{r}}^\prime {L_{\rm{r}}}/2{\rm{ \mathsf{ π} }} + {P_{\rm{r}}}\left( {{t_{{\rm{rs}}}} - 1} \right) \end{array} \right.$ | (15) |
当ρi=1时,表示丝杠上螺旋面和滚柱下螺旋面啮合;ρi=-1时,表示丝杠下螺旋面和滚柱上螺旋面啮合。由式(15)可得具有5个未知数rs′、θs′、rr′、θr′和esr的5个独立的非线性方程,可以利用牛顿-拉弗逊算法[15],通过MATLAB对其进行求解,最终获得单节丝杠和滚柱的啮合半径与轴向间隙。
同理可以得到PRSM在丝杠-滚柱侧的啮合方程为:
| $\left\{ {\begin{array}{*{20}{l}} {r_{\rm{n}}^\prime \cos \theta _{\rm{n}}^\prime = r_{\rm{r}}^\prime \cos \theta _{\rm{r}}^\prime }\\ {r_{\rm{n}}^\prime \sin \theta _{\rm{n}}^\prime = r_{\rm{r}}^\prime \sin \theta _{\rm{r}}^\prime }\\ {T_{\rm{n}}^z = T_{\rm{r}}^z + {e_{{\rm{nr}}}}}\\ {{\mathit{\boldsymbol{n}}_{\rm{n}}} = \frac{{\left| {{\mathit{\boldsymbol{n}}_{\rm{n}}}} \right|}}{{\left| {{\mathit{\boldsymbol{n}}_{\rm{r}}}} \right|}}{\mathit{\boldsymbol{n}}_{\rm{r}}}} \end{array}} \right.$ | (16) |
式中:rn′、θn′、rr′、θr′分别表示螺母-滚柱啮合时,螺母的啮合半径和啮合角以及滚柱的啮合半径和啮合角;enr表示丝杠和滚柱啮合时的轴向间隙;nn、nr表示螺母和滚柱的法向量;Tnz、Trnz分别表示螺母和滚柱的啮合点在Z轴的分量:
| $\left\{ \begin{array}{l} \mathit{\boldsymbol{T}}_{\rm{n}}^z = {\rho _{\rm{n}}}\left[ {{z_{{\rm{no}}}} - \sqrt {R_{\rm{n}}^2 - {{\left( {r_{\rm{n}}^\prime - {r_{\rm{n}}} - {x_{{\rm{no}}}}} \right)}^2}} } \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\theta _{\rm{n}}^\prime {L_{\rm{n}}}/2{\rm{ \mathsf{ π} }} + {P_{\rm{n}}}\left( {{t_{\rm{n}}} - 1} \right)\\ \mathit{\boldsymbol{T}}_{\rm{r}}^z = - {\rho _{\rm{r}}}\left[ {{z_{{\rm{ro}}}} + \sqrt {R_{\rm{r}}^2 - {{\left( {r_{\rm{r}}^\prime - {r_{\rm{r}}} - {x_{{\rm{ro}}}}} \right)}^2}} } \right] + \\ \;\;\;\;\;\;\;\;\;\theta _{\rm{r}}^\prime {L_{\rm{r}}}/2{\rm{ \mathsf{ π} }} + {P_{\rm{r}}}\left( {{t_{{\rm{rs}}}} - 1/2} \right) \end{array} \right.$ | (17) |
当ρi=1时,表示螺母下螺旋面和滚柱上螺旋面啮合;ρi=-1时,表示螺母下螺旋面和滚柱上螺旋面啮合。由式(17)可得具有5个未知数rn′、θn′、rr′、θr′和enr的5个独立的非线性方程,可以求得螺母和滚柱的啮合半径与轴向间隙。
2 行星滚柱丝杠承载模型 2.1 赫兹接触变形凸凹接触式PRSM的滚柱与丝杠和螺母之间仍为点接触,只是由原来的平面-曲面接触变为了曲面-曲面接触,可以利用赫兹接触理论进行接触分析和承载分析。对于凸凹接触的PRSM,主曲率在滚柱与丝杠接触侧为:
| $\left\{ \begin{array}{l} {\rho _{11}} = 1/{R_{\rm{r}}}\\ {\rho _{12}} = 1/{R_{\rm{r}}}\\ {\rho _{21}} = - 1/{R_{\rm{s}}}\\ {\rho _{22}} = \frac{{2\cos {\alpha _{\rm{s}}}\cos {\lambda _{\rm{s}}}}}{{{d_{\rm{m}}} - 2R\cos {\alpha _{\rm{s}}}}} \end{array} \right.$ | (18) |
主曲率在滚柱与螺母接触侧为:
| $\left\{ \begin{array}{l} {\rho _{11}} = 1/{R_{\rm{r}}}\\ {\rho _{12}} = 1/{R_{\rm{r}}}\\ {\rho _{21}} = - 1/{R_{\rm{n}}}\\ {\rho _{22}} = \frac{{-2\cos {\alpha _{\rm{n}}}\cos {\lambda _{\rm{n}}}}}{{{d_{\rm{m}}} + 2R\cos {\alpha _{\rm{n}}}}} \end{array} \right.$ | (19) |
式中:dm为PRSM滚柱公转直径,且dm=dr+ds。
以丝杆侧为例,当PRSM受负载作用后,滚柱与丝杠之间的点接触发生弹性变形,瞬时接触点会变成瞬时接触椭圆,丝杠与滚柱接触时的赫兹弹性变形量及啮合区域的接触应力可以表示为
| ${\delta _{\rm{s}}} = {C_{{\rm{s}}\;}}_{\rm{r}}{F_{\rm{n}}}^{2/3}$ | (20) |
| $\sigma = \frac{{3{F_{\rm{n}}}}}{{2{\rm{ \mathsf{ π} }}ab}}$ | (21) |
长短半轴a、b表示为[16]:
| $\left\{ \begin{array}{l} a = {m_{\rm{a}}}\sqrt[3]{{\frac{{3{F_{\rm{n}}}E}}{{2\sum \rho }}}}\\ b = {m_{\rm{b}}}\sqrt[3]{{\frac{{3{F_{\rm{n}}}E}}{{2\sum \rho }}}} \end{array} \right.$ | (22) |
式中:Csr为丝杠与滚柱的赫兹接触刚度,Fn为法向接触力,E为综合弹性模量,∑ρ为主曲率和且∑ρ=ρ11+ρ12+ρ21+ρ22。
2.2 变形协调关系PRSM受载后滚柱与丝杠之间产生的接触力沿螺旋曲面法线方向,可分解为3个方向的分力,如图 4所示,根据单根滚柱轴向力受力平衡可得从m-1到m节螺纹牙滚柱受丝杠传递的力为
| ${F_{{\rm{a}}, m}} = {F_{\rm{N}}} - \sum\limits_{i = 1}^m {{F_{{\rm{n}}, {\rm{i}}}}\sin \alpha \cos \lambda } $ | (23) |

|
图 4 滚柱接触点受力分解 Fig. 4 Force decomposition of roller contact point |
式中:Fa, m为单根滚柱在丝杠侧第m节螺纹牙所受轴向力,Fn, m为单根滚柱第m节螺纹牙所受法向力;λ为螺旋升角且λ=arctan(Ps/2πrs′);M为滚柱螺纹牙数,FN为单根滚柱所受总轴向力
| ${F_{\rm{N}}} = \sum\limits_{i = 1}^M {{F_{{\rm{n}}, {\rm{i}}}}\sin \alpha \cos \lambda } $ | (24) |
PRSM在载荷的作用下,除存在丝杠和螺母与滚柱之间产生赫兹接触变形、各轴段的轴向变形外,螺纹牙的变形也不可忽略。PRSM的螺纹牙变形主要包括螺纹牙弯曲变形σ1、螺纹牙剪切变形σ2、牙根倾斜导致的变形σ3、牙根剪切导致的变形σ4及螺纹牙径向分力导致的变形σ5。
螺纹牙5种变形分别为[17]:
| $\begin{array}{l} {\sigma _1} = \left( {1 - {\mu ^2}} \right)\frac{{3{F_{{\rm{a}}, i}}}}{{4E}}[1 - 2 - {\left( {b/a} \right)^2} + \\ \;\;\;\;\;\;\;\;2\ln \left( {a/b} \right)){\rm{co}}{{\rm{t}}^3}\alpha - 4\left( {h/a} \right)\tan \alpha ] \end{array}$ | (25) |
| ${\sigma _2} = (1 + \mu )\frac{{6{F_{{\rm{a}}, i}}}}{{5E}}{\rm{cot}}\alpha \ln \left( {a/b} \right)$ | (26) |
| ${\sigma _3} = \left( {1-{\mu ^2}} \right)\frac{{12{F_{{\rm{a}}, i}}h}}{{{\rm{ \mathsf{ π} }}E{a^2}}}\left( {h - \frac{{c\tan \alpha }}{2}} \right)$ | (27) |
| $\begin{array}{l} {\sigma _4} = \left( {1 - {\mu ^2}} \right)\frac{{2{F_{{\rm{a}},i}}}}{{{\rm{ \mathsf{ π} }}E}}\left[ {\frac{P}{a}\ln \left( {\frac{{P + 0.5a}}{{P - 0.5a}}} \right) + } \right.\\ \left. {\;\;\;\;\;\;0.5\ln \left( {\frac{{4{P^2} - {a^2}}}{{{a^2}}}} \right)} \right] \end{array}$ | (28) |
| ${\sigma _{{\rm{5n}}}} = \left( {\frac{{D_0^2 + d_{\rm{p}}^2}}{{D_0^2 - d_{\rm{p}}^2}} + \mu } \right)\frac{{{F_{{\rm{r}}, i}}{d_{\rm{p}}}\sin \alpha \tan \alpha }}{{2PE}}$ | (29) |
| ${\sigma _{{\rm{5s}} - {\rm{r}}}} = \left( {1 - \mu } \right)\frac{{{F_{{\rm{r}}, i}}{d_{\rm{p}}}\sin \alpha \tan \alpha }}{{2PE}}$ | (30) |
式中:μ为材料的泊松比,a为螺纹牙牙底宽,b为螺纹牙牙厚,h为螺纹牙牙底高,D0为螺母外径,dp为螺纹牙中径,Fr, i为第i节螺纹牙所受径向分力且Fr, i=Fa, itan α,σ5n为螺母螺纹牙的变形,σ5s-r为丝杠或滚柱螺纹牙的变形。
图 5为PRSM的变形协调关系,以丝杆侧为例,设τsm为产生于e、f两点间的丝杠的轴向变形量,τrm为产生于e、f两点间的滚柱的轴向变形量;σsm(σsm=σ1+σ2+σ3+σ4+σ5s)为丝杠在第m节螺纹牙的总螺纹牙变形,σs rm(σs rm=σ1+σ2+σ3+σ4+σ5r)为滚柱在第m节螺纹牙的总螺纹牙变形量,δs rm为第m节螺纹牙的接触变形。丝杆和滚柱的总变形量分别可表示为:
| $\Delta S = {\tau _{{\rm{sm}}}} + \sigma _s^{m - 1} + \sigma _{\rm{s}}^m + \delta _{{\rm{s}}\;{\rm{r}}}^{m - 1}$ | (31) |
| $\Delta R = {\tau _{{\rm{rm}}}} + \sigma _{{\rm{s}}\;{\rm{r}}}^{m - 1} + \sigma _{{\rm{s}}\;{\rm{r}}}^m + \delta _{{\rm{s}}\;{\rm{r}}}^m$ | (32) |

|
图 5 PRSM的变形协调关系 Fig. 5 Deformation coordinated relations of PRSM |
式中:
| $\left\{ \begin{array}{l} {\tau _{{\rm{sm}}}} = \frac{{P{F_{{\rm{a}}, m}}}}{{2{A_{\rm{s}}}{E_{\rm{s}}}}}, \\ {\tau _{{\rm{rm}}}} = \frac{{P{F_{{\rm{a}}, m}}}}{{2{A_{\rm{r}}}{E_{\rm{r}}}}} \end{array} \right.$ | (33) |
式中:Es和Er为丝杠和滚柱的弹性模量; As和Ar为丝杠和滚柱的有效接触面积,As=πds2/4,Ar=πdr2/4; ds为丝杠中径; dr为滚柱中径。
相邻螺纹对在丝杠侧形成的两个接触点e、f满足变形协调关系。根据赫兹接触变形、轴向变形与螺纹牙变形的变形协调关系可得
| ${P_{\rm{s}}} + \Delta S = {P_{\rm{r}}} + \Delta R$ | (34) |
由于Ps=Pr,因此式(36)可写为ΔS=ΔR,于是由式(22)~(34)可得PRSM丝杠侧螺纹牙载荷分布公式为
| $\begin{array}{l} \frac{{{F_{{\rm{a}}, m}} - {F_{{\rm{a}}, m - 1}}}}{{{C_{{\rm{RS}}}}}} + \frac{{{F_{\rm{N}}} - \sum\nolimits_{j = 1}^{m - 1} {{F_{{\rm{a}}, j}}} }}{{{K_{{\rm{SB}}}}}} + \frac{{{F_{{\rm{a}}, m}} - {F_{{\rm{a}}, m - 1}}}}{{{K_{{\rm{ST}}}}}} = \\ \;\;\;\;\frac{{\sum\nolimits_{j = 1}^{m - 1} {{F_{{\rm{a}}, j}}} - \sum\nolimits_{j = 1}^{m - 1} {{F_{{\rm{a - n}}, j}}} }}{{{K_{{\rm{RB}}}}}} + \frac{{{F_{{\rm{a}}, m}} - {F_{{\rm{a}}, m - 1}}}}{{{K_{{\rm{RST}}}}}} \end{array}$ | (35) |
式中:Fa-n.j为螺母第j节螺纹牙所受轴向力,KST为丝杠的螺纹牙变形刚度且KST=Fa/σs,KRST为滚柱的螺纹牙变形刚度且KRST=Fa/σsr,KSB为丝杠的轴向变形刚度,KRB为滚柱的轴向变形刚度。
3 行星滚柱丝杠啮合与承载分析 3.1 啮合分析利用MATLAB并使用本文的计算方法对凸凹接触的PRSM的接触点位置和轴向间隙进行计算,同时分析牙型半角、螺距、滚柱等效球半径及丝杠和螺母等效球半径对接触点位置和轴向间隙的影响。由于参数变化对滚柱-螺母侧接触点位置和轴向间隙影响很小,下面仅对丝杠-滚柱侧进行分析,分析使用的PRSM几何参数见表 1,其中滚柱数为10。
| 表 1 PRSM几何参数 Tab. 1 Geometric parameters of PRSM |
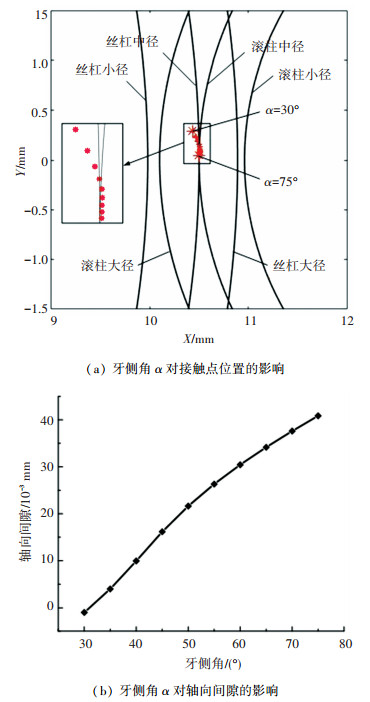
牙侧角是影响PRSM啮合特性的重要因素,为探究牙型角对凸凹接触的PRSM啮合性能的影响,牙侧角α在[30°,75°]内取值,其他参数保持不变,螺距P=2.0 mm, 滚柱凸圆弧半径rre=rr/sin α,丝杠和螺母凹圆弧半径rse=rne=1.10rre。牙侧角对接触点位置和轴向间隙的影响如图 6所示。
|
图 6 牙侧角α对接触点位置和轴向间隙的影响 Fig. 6 Influence of flank angle α on contact point position and axial clearance |
由图 6(a)可知,牙侧角从30°变化到75°,啮合点在滚柱螺纹曲面上的轨迹朝着小啮合半径以及小啮合偏角的趋势变化。牙侧角为30°时,啮合半径rs′=10.441 5 mm,啮合偏角φs=4.59°;牙侧角为75°时,啮合半径rs′=10.503 4 mm,啮合偏角φs=0.71°,随着牙侧角的增大,啮合半径增大了0.061 9 mm,啮合角减小了3.88°。随牙侧角的增大,啮合点位置逐渐靠近丝杠和滚柱中心的连接线,并偏向丝杠牙顶,滚柱的啮合半径比丝杠啮合半径对牙侧角的变化更敏感;啮合点逐渐趋向于丝杠和滚柱的理论啮合点,即丝杠中径与滚柱中径交点,从而使非啮合区域的干涉减少。从图 6(b)可以看出,随着牙侧角的增加,丝杠与滚柱之间的轴向间隙随之增大。α=75°时,轴向间隙为0.040 9 mm,较大的轴向间隙会导致PRSM运行不平稳且产生较大的噪音;牙侧角为30°时,轴向间隙为负表明此时存在干涉,因此要选择合理的牙侧角以保证PRSM的性能。
3.1.2 螺距P对啮合性能的影响螺距P在[0.5 mm,3.0 mm]内取值,其他参数保持不变,牙侧角α=45°, 滚柱凸圆弧半径rre=rr/sin α,丝杠和螺母凹圆弧半径rse=rne=1.10rre。螺距P对接触点位置的影响如图 7所示。

|
图 7 螺距P对接触点位置的影响 Fig. 7 Influence of pitch P on contact point position and axial clearance |
由图 7可知,螺距从0.5 mm变化到3.0 mm,啮合点在螺纹曲面上的轨迹朝着大啮合偏角的趋势变化。螺距为0.5 mm时,啮合半径rs′=10.500 0 mm,啮合偏角φs=0.65°;螺距为3.0 mm时,啮合半径rs′=10.501 5 mm,啮合偏角φs=3.92°。随着螺距的增大, 丝杠的啮合半径变化较小,啮合偏角增大了3.27°。随螺距增大,啮合点位置将远离丝杠和滚柱中心的连接线,啮合点均在丝杠和滚柱中径附近。
3.1.3 滚柱凸圆弧半径rre对啮合性能的影响滚柱凸圆弧半径rre分别取3.0000、9.8995、20.0000、30.0000、40.0000、50.0000 mm,其他参数保持不变,牙型半角α=45°, 螺距P=2.0 mm,丝杠和螺母凹圆弧半径rse=rne=1.10rre。滚柱凸圆弧半径rre对接触位置和轴向间隙的影响如图 8所示。

|
图 8 滚柱凸圆弧半径rre对接触点位置和轴向间隙的影响 Fig. 8 Influence of convex arc radius rre of roller on contact point position and axial clearance |
由图 8(a)可知,滚柱凸圆弧半径rre从3 mm变化到50 mm,啮合点位置始终在丝杠和滚柱中心的连接线附近,同时啮合点位置向丝杠牙根方向移动。当rre=3 mm时,啮合半径rs′=10.520 0 mm,啮合偏角φs=2.63°;rre=50 mm时,啮合半径rs′= 10.322 4 mm,啮合偏角φs=2.81°,随着rre的增大,丝杠的啮合半径减小了0.197 6 mm,啮合偏角变化较小。由图 8 (b)可以看出, 随着rre的增大,在其他参数不变的情况下,轴向间隙呈减小趋势,由0.016 1 mm减小到0.012 9 mm。
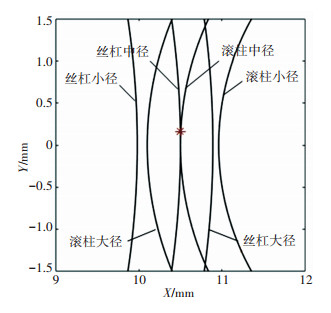
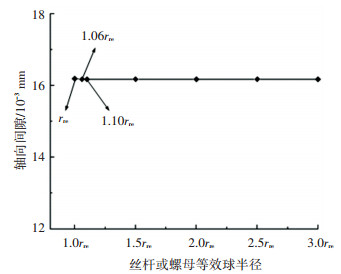
3.1.4 丝杠和螺母凹圆弧半径rse、rne对啮合性能的影响分别取丝杠和螺母凹圆弧半径rse=rne为rre、1.06rre、1.10rre、1.50rre、2.00rre、2.50rre、3.00rre,其他参数保持不变,牙侧角α=45°, 螺距P=2 mm,滚柱凸圆弧半径rre=9.899 5 mm。丝杠和螺母凹圆弧半径对接触位置和轴向间隙的影响见图 9和图 10。
|
图 9 丝杠和螺母凹圆弧半径对接触点位置的影响 Fig. 9 Influence of concave arc radius of screwand nut on contact point position |
|
图 10 丝杠和螺母凹圆弧半径对轴向间隙的影响 Fig. 10 Influence of concave arc radii of screw and nut on axial clearance |
由图 9和图 10可知,丝杠和螺母凹圆弧半径取值对接触点位置和轴向间隙几乎没有影响。
3.2 承载特性分析由于行星滚柱丝杠牙型轮廓发生变化,主曲率将会发生变化,从而引起接触应力的变化。施加30 kN的轴向力对接触应力进行计算,并讨论牙侧角、螺距和滚柱螺纹牙数对凸凹接触的PRSM接触应力的影响,并对标准式和凸凹接触的PRSM的接触应力进行对比。几何参数见表 1中的参数,且取螺距P=2 mm,牙侧角α=45°,滚柱等效球半径rre=rr/sin α,丝杠和螺母凹圆弧半径为rse=rne=1.10rre。
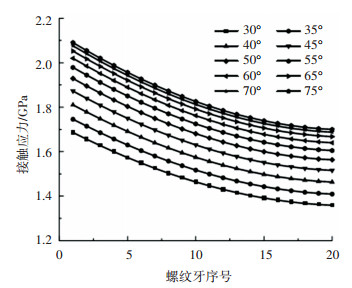
3.2.1 牙侧角α对承载性能的影响牙侧角是影响PRSM承载性能的重要因素之一,如图 11所示,随着螺纹牙序号的增加,PRSM的接触应力逐渐减小,不同牙侧角的接触应力的变化趋势基本一致,随着牙侧角的增大,PRSM的接触应力逐渐增加,且增大趋势越来越小。
|
图 11 牙侧角对接触应力的影响 Fig. 11 Influence of flank angle on contact stress |
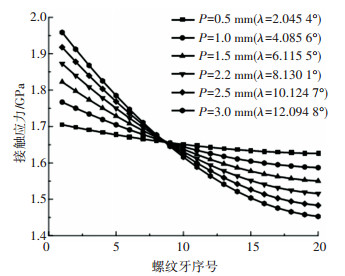
如图 12所示,随着螺纹牙序号的增加,螺纹牙上的接触应力仍然逐渐减小;但随着螺距的减小,前8颗螺纹牙上的接触应力逐渐减小,后12颗螺纹牙上的接触应力逐渐增大;螺距P=3.0 mm,λ=12.094 8°时,最大和最小应力差为505.63 Mpa;螺距P=0.5 mm,λ=2.054 5°时,最大和最小应力差为79.13 Mpa,可见螺距越小应力分布越均匀。
|
图 12 螺距P对接触应力的影响 Fig. 12 Influence of pitch P on contact stress |
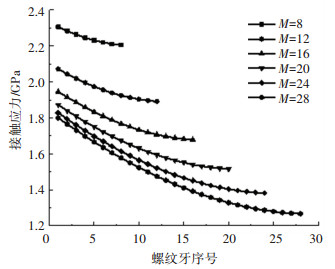
滚柱螺纹牙数直接影响着PRSM的接触应力分布,如图 13。
|
图 13 滚柱螺纹牙数对接触应力的影响 Fig. 13 Influence of thread tooth number on contact stress |
随着螺纹牙序号的增加,PRSM的接触应力逐渐减小,随总螺纹牙数一定程度地增加,每颗螺纹牙上的接触应力均会减小,但应力分布不均的现象加剧,接触应力整体变化趋势保持一致。
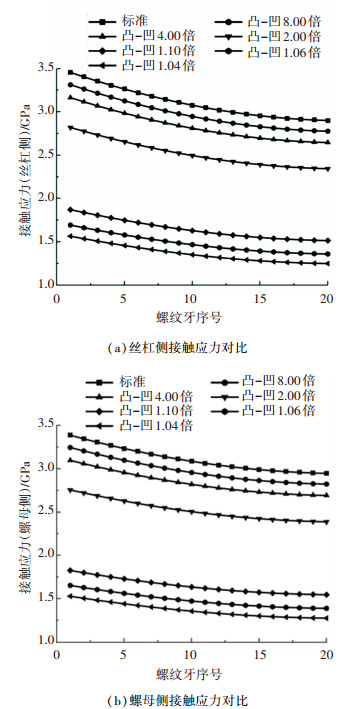
3.2.4 标准式和凸凹接触的PRSM的接触应力对比图 14为标准式和凸凹接触式PRSM在丝杠侧和螺母侧的接触应力对比。可以看出,标准式PRSM的接触应力在丝杠侧和螺母侧应力分布规律基本一致,但均大于凸凹接触式PRSM的,当丝杠和螺母牙型凹圆弧半径为滚柱凸圆弧半径的1.06倍时,凸凹接触的PRSM最大接触应力较标准式的减小了1/2左右。随着丝杠和螺母凹圆弧半径的增大,两侧的接触应力也逐渐增大,对承载能力的提高就越不明显,且圆弧半径的增大可能会引起滑动;丝杠和螺母圆弧半径越小,虽然两侧的接触应力有明显的降低,但丝杠和螺母圆弧半径的减小将增加啮合干涉和安装困难的风险,因此丝杠和螺母要选择合理的凹圆弧半径。
|
图 14 标准式和凸凹接触式PRSM的接触应力对比 Fig. 14 Comparison of contact stress between PRSM and PRSM with convex-concave contact |
1) 提出了一种凸凹接触的PRSM,将丝杠和螺母的牙型轮廓设计为凹圆弧,建立了凸凹接触式PRSM的空间啮合模型和承载模型,系统分析了牙侧角、螺距等结构参数对其啮合特性和承载特性的影响。
2) 随牙侧角增大,丝杠和滚柱的接触点将逐渐靠近丝杠和滚柱回转中心连接线,且轴向间隙逐渐增大;随螺距增大,其接触点位置将远离丝杠和滚柱回转中心连接线,且接触点均在丝杠中径附近;随滚柱凸圆弧半径增大,接触点位置往丝杠牙根方向变化,轴向间隙逐渐减小;丝杠和螺母的凹圆弧半径对接触点位置和轴向间隙几乎没有影响。
3) 凸凹接触的PRSM承载能力随牙侧角的增大而减小;随螺距减小,前8颗螺纹牙上的接触应力逐渐减小,后面螺纹牙上的接触应力逐渐增大,且整体接触应力分布逐渐均匀;随滚柱螺纹牙数一定程度地增加,每颗螺纹牙上的接触应力减小,但应力分布不均现象加剧。
4) 凸凹接触的PRSM与标准式PRSM在滚柱螺纹牙上的接触应力分布规律基本一致,凸凹接触式PRSM的滚柱在丝杠侧和螺母侧的接触应力都有明显降低,且随丝杠和螺母的凹圆弧半径的减小接触应力逐渐减小;但为保证PRSM的性能,丝杠和螺母要选择合理的凹圆弧半径。
| [1] |
刘更, 马尚君, 佟瑞庭, 等. 行星滚柱丝杠副的新发展及关键技术[J]. 机械传动, 2012, 36(5): 103. LIU Geng, MA Shangjun, TONG Ruiting, et al. New development and key technology of planetary roller screw[J]. Journal of Mechanical Transmission, 2012, 36(5): 103. DOI:10.3969/j.issn.1004-2539.2012.05.031 |
| [2] |
LIU Yanqiang, WANG Jianshen, CHENG Hongxun, et al. Kinematics analysis of the roller screw based on the accuracy of meshing point calculation[J]. Mathematical Problems in Engineering, 2015, 2015: 303972. DOI:10.1155/2015/303972 |
| [3] |
LI Zu, ZHOU Zhang, LIANG Gao. Design and bearing characteristics of planetary roller screws based on aerospace high-load conditions[J]. Advances in Mechanical Engineering, 2018, 10(11): 168781401881119. DOI:10.1177/1687814018811197 |
| [4] |
JONES M H, VELINSKY S A. Contact kinematics in the roller screw mechanism[J]. Journal of Mechanical Design, 2013, 135(5): 451. DOI:10.1115/DETC2012-70254 |
| [5] |
FU Xiaojun. Studies on meshing mechanism of helical surfaces in planetary roller screw mechanism[J]. Journal of Mechanical Engineering, 2016, 52(3): 26. |
| [6] |
乔冠, 刘更, 马尚君. 行星滚柱丝杠副主曲率计算与接触特性分析[J]. 机械工程学报, 2020, 56(21): 140. QIAO Guan, LIU Geng, MA Shangjun. Principal curvature calculation and contact characteristics analysis of the planetary roller screw mechanism[J]. Journal of Mechanical Engineering, 2020, 56(21): 140. |
| [7] |
MA Shangjun, DUAN Zhenhao, NIU Maodong, et al. Contact analysis of thread pairs in a planetary roller screw based on finite element method[J]. Journal of Physics: Conference Series, 2020, 1519: 012006. DOI:10.1088/1742-6596/1519/1/012006 |
| [8] |
LISOWSKI F. The analysis of displacements and the load distribution between elements in a planetary roller screw[J]. Applied Mechanics & Materials, 2014, 680: 326-329. |
| [9] |
AURÉGAN G, FRIDRICI V, KAPSA P, et al. Experimental simulation of rolling-sliding contact for application to planetary roller screw mechanism[J]. Wear, 2015, 332/333: 1176. DOI:10.1016/j.wear.2015.01.047 |
| [10] |
JONES M H, VELINSKY S A. Stiffness of the roller screw mechanism by the direct method[J]. Mechanics Based Design of Structures and Machines, 2014, 42(1): 17. DOI:10.1080/15397734.2013.839385 |
| [11] |
杨家军, 韦振兴, 朱继生, 等. 行星滚柱丝杠副载荷分布及刚度计算[J]. 华中科技大学学报, 2011, 39(4): 1. YANG Jiajun, WEI Zhenxing, ZHU Jisheng, et al. Calculation of load distribution of planetary roller screws and static rigidity[J]. Journal of Huazhong University of Science and Technology, 2011, 39(4): 1. |
| [12] |
刘柱, 范元勋. 考虑装配误差的行星滚柱丝杠副载荷分析与研究[J]. 机械制造与自动化, 2020, 49(6): 120. LIU Zhu, FAN Yuanxun. Analysis and research on pair load of planetary roller screw in consideration of assembly error[J]. Machine Building & Automation, 2020, 49(6): 120. DOI:10.19344/j.cnki.issn1671-5276.2020.06.031 |
| [13] |
FU Xiao, LIU Geng, MA Shangjun, et al. A comprehensive contact analysis of planetary roller screw mechanism[J]. Journal of Mechanical Design, 2016, 139(1): 012302. DOI:10.1115/1.4034580 |
| [14] |
LITVIN F L. Gear geometry and applied theory[M]. New Jersey: PTR Prentice Hall, 1994: 267.
|
| [15] |
陈宝林. 最优化理论与算法[M]. 北京: 清华大学出版社, 2005: 1. CHEN Baolin. Optimization theory and algorithm[M]. Beijing: Tsinghua University Press, 2005: 1. |
| [16] |
姚琴, 吴立言, 刘更, 等. 行星滚柱丝杠副弹塑性接触分析[J]. 机械传动, 2016, 40(11): 106. YAO Qin, WU Liyan, LIU Geng, et al. Elastic-plastic contact analysis of the planetary roller screw mechanism[J]. Journal of Mechanical Transmission, 2016, 40(11): 106. DOI:10.16578/j.issn.1004.2539.2016.11.031 |
| [17] |
ZHANG Wenjie, LIU Geng, TONG Ruiting, et al. Load distribution of planetary roller screw mechanism and its improvement approach[J]. Journal of Mechanical Engineering Science, 2016, 230(18): 3304. DOI:10.1177/0954406215610361 |
 2021, Vol. 54
2021, Vol. 54


