2. 河北工业大学 机械工程学院,天津 300000
2. School of Mechanical Engineering, Hebei University of Technology, Tianjin 300000, China
步态识别作为一种生物识别技术,有着远距离、非侵犯性和不易盗用的特点[1],在刑事侦查、医疗诊断、考勤门禁等方面已经取得了一定的研究成果[2-3]。步态识别方法主要分为基于模型的方法和基于运动的方法两大类,基于模型的方法是通过建立人体的物理结构模型,得到对应时刻的空间信息来表示人体步态运动状态,能够有效解决遮挡、负重以及随动物体对识别带来的影响。
较早的步态模型有Cunado等[4]提出的内链钟摆模型和Bouchrika等[5]提出的动态耦合钟摆模型,这两种模型只包括了下肢的摆动;Yoo等[6-7]先是提出了包含上身躯干的2D杆状人体模型,随后对该模型进行改进,提出了包含一侧手臂的七椭圆模型;Zhang[8]提出了五连杆双足人体模型,同样忽略了上肢的摆动;Lu等[9]提出了全身分层可变模型,该模型涵盖了人体步态运动中的四肢和躯干的步态运动。传统的步态模型以视觉特征作为出发点,但步态识别的整体系统应尽可能地整合更多的特征,触觉特征作为另一类主要的步态特征,常作为融合的对象。对于单一的触觉特征,Qian等[10]提取两只脚的1D压力中心曲线和2D位置轨迹形成3D压力中心曲线进行识别;Yamakawa等[11]将足底压力均分为4部分,提出了一种基于模糊推理的识别算法;Tekeda等[12]将足底压力分为8部分以此进行步态识别;Dai等[13]虽然融合触觉和视觉特征进行步态识别,但同样只涉及了下半身的步态运动。
针对目前建立的模型只依靠单一特征或者只涉及下半身运动状态的情况,本文建立包含上肢摆动并且融合视觉和触觉特征的全身步态运动模型,提取特征矩阵;同时将足底压力分区,通过增加特征识别点的方式减少鞋靴对于识别率的影响。为进一步提高识别率,采用参数寻优情况下的支持向量机进行分类识别,实验验证了本文模型的有效性。
本文所提算法主要包括全身步态模型的建立、视觉特征和触觉特征的提取与分类器的分类识别3部分,如图 1。
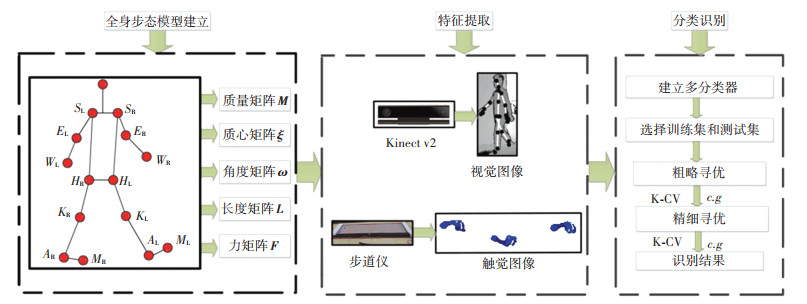
|
图 1 步态识别算法框图 Fig. 1 Block diagram of gait recognition algorithm |
人在行走过程中,左右腿作为支撑腿和摆动腿交替变化,并且同一条腿的同一骨骼在作为支撑腿和摆动腿时,对支持力的作用效果是不同的。在实际测量中,通过足底直接接触测量仪器获得触觉特征,测量结果更加准确,所以本文以支撑腿为基础进行建模,并且对支撑腿、摆动腿和上半身的运动参数进行了分类讨论。
1.1 建立地面支持力的动力学模型在步态运动中,人体所受的力主要来自于地面的反作用力N和自身重力Mg。根据牛顿力学第二定律,人体受力的动力学方程可表示为
| $ \boldsymbol{N}+\boldsymbol{M} g=\boldsymbol{M} a $ | (1) |
式中:a为人体质心加速度。地面反作用力包括摩擦力和支持力,本文通过地面支持力建立全身人体步态运动模型,所以只讨论人体步态运动过程中在竖直方向所受到的力,如图 2。将竖直向上的方向设为y轴的正方向,则人体的受力关系可表示为
| $ \left|\boldsymbol{N}_{y}\right|-|\boldsymbol{M} g|=\boldsymbol{M} a_{y} $ | (2) |

|
图 2 人体竖直方向受力示意图 Fig. 2 human body vertical direction |
人体的质心位置会随着行走状态变化而发生改变,仅根据质量分布和身高来判断质心的运动情况是不合理的。所以将式(2)中May分解为身体各个部分的质量与其质心位置在竖直方向的加速度乘积之和,则可得到人体步态运动的动力学模型为
| $ \left|\boldsymbol{N}_{y}\right|-|\boldsymbol{M} g|=m_{1} a_{1 y}+m_{2} a_{2 y}+\cdots+m_{n} a_{n y} $ | (3) |
式中:aiy(i=1, 2, …, n)为身体各个部分质心在竖直方向的加速度,加速度的获取一般通过视觉特征,以此引入视觉特征构建融合视觉和触觉特征的全身步态模型。
1.2 求解动力学模型的质心加速度为了更好地求取身体各部分的垂直方向加速度,作如下假设:
1) 将人体的运动关节看作铰链,人体骨架由铰链连接构成,如图 3。
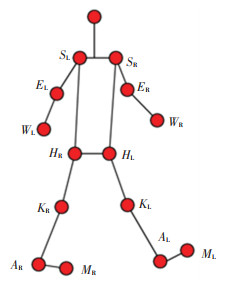
|
图 3 人体全身步态模型 Fig. 3 Full-body gait model |
2) 步态运动过程中支撑脚始终脚底接触地面,不滑动。
3) 身体结构质心等效在两关节连线上。
4) 模型简化为11个刚体,n=11。正常行走过程中除了四肢的摆动基本不发生大的自由度运动,所以将上身躯干和头部看做整体。
5) 在步态运动过程中,双髋关节做垂直于人体轴心的旋转运动,并且双髋关节连线在做绕连线中心的旋转运动时,在冠状面的转动角度小,在横断面转动角度大,因此认为双髋关节连线只做与横断面平行的竖直运动和旋转运动。
6) 当旋转角与行走方向一致时为正值。
以左腿作为支撑腿,右腿作为摆动腿为例,对全身11个部分在竖直方向上的加速度进行求解。W、E、S、H、K、A、M分别代表手腕、手肘、肩、髋、膝、踝、跖骨末端的骨骼关节点。
1.2.1 支撑腿加速度求解左脚做为支撑脚,跖骨末端与踝关节的连线与地面的夹角经历了一个由0°到接近90°的过程,到达最大夹角后,支撑腿变为摆动腿。以此运动过程为基础研究支撑腿摆动模型,如图 4。
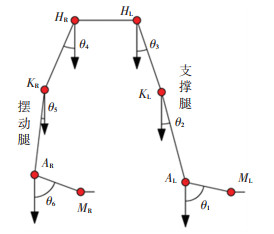
|
图 4 下半身运动状态示意图 Fig. 4 Schematic diagram of lower body movement status |
根据加速度与角加速度关系,将踝关节的加速度分解为水平和竖直两个方向,可得其在竖直方向上相对于跖骨末端的加速度为
| $ a_{A_{\mathrm{L}} \rightarrow M_{\mathrm{L}}}=\ddot{\theta}_{1} l_{A M} \sin \theta_{1} $ | (4) |
则足部质心相对于跖骨末端在竖直方向上的加速度为
| $ a_{\mathrm{C}_{A M-\mathrm{L}}}=\left(1-\varepsilon_{1}\right) \ddot{\theta}_{1} l_{A M} \sin \theta_{1} $ | (5) |
在求解小腿竖直方向加速度时,踝关节的速度是已知的,小腿的旋转范围为45°~-45°,膝关节相对于踝关节在竖直方向上的加速度为
| $ a_{K_{\mathrm{L}} \rightarrow A_{\mathrm{L}}}=\ddot{\theta}_{2} l_{K A} \sin \theta_{2} $ | (6) |
则小腿质心相对于踝关节在垂直方向上的线加速度为
| $ a_{\mathrm{C}_{KA-L}} \rightarrow A_{\mathrm{L}}=\left(1-\varepsilon_{2}\right) \ddot{\theta}_{2} l_{K A} \sin \theta_{2} $ | (7) |
根据加速度合成原理,小腿质心在竖直方向上的加速度为
| $ a_{\mathrm{C}_{K A-1}}=\ddot{\theta}_{1} l_{A M} \sin \theta_{1}+\left(1-\varepsilon_{2}\right) \ddot{\theta}_{2} l_{K A} \sin \theta_{2} $ | (8) |
同上可求得左大腿质心在垂直方向的加速度为
| $ \begin{aligned} a_{\mathrm{C}_{H K-\mathrm{L}}}=& \ddot{\theta}_{1} l_{A M} \sin \theta_{1}+\ddot{\theta}_{2} l_{K A} \sin \theta_{2}+\\ &\left(1-\varepsilon_{3}\right) \ddot{\theta}_{3} l_{H K} \sin \theta_{3} \end{aligned} $ | (9) |
人体在步态运动中,腹部、胸部和头部之间的相对运动小,所以在求取摆动腿和上半身各部分加速度时,将髋关节、腹部、胸部和头部看做整体,如图 5。
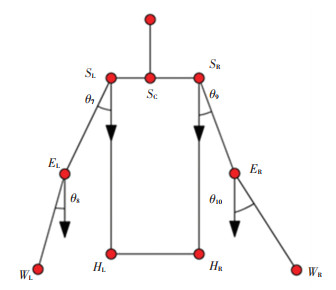
|
图 5 上半身运动状态示意图 Fig. 5 Schematic diagram ofbody movement status |
则左髋关节、右髋关节、左肩关节、右肩关节和脖颈根部在竖直方向的加速度相等,即
| $ \begin{aligned} a_{H_{\mathrm{L}}}=& a_{H_{\mathrm{R}}}=a_{S_{\mathrm{C}}}=a_{S_{\mathrm{L}}}=a_{S_{\mathrm{R}}}=\\ & \ddot{\theta}_{1} l_{A M} \sin \theta_{1}+\ddot{\theta}_{2} l_{K A} \sin \theta_{2}+\ddot{\theta}_{3} l_{H K} \sin \theta_{3} \end{aligned} $ | (10) |
将右髋关节作为求解摆动腿各部分质心加速度的起点,根据运动传递规律,可求得右大腿质心在竖直方向的加速度为
| $ a_{\mathrm{C}_{H K-\mathrm{R}}}=a_{H_{\mathrm{R}}}+\varepsilon_{4} \ddot{\theta}_{4} l_{H K} \sin \theta_{4} $ | (11) |
右小腿质心在竖直方向上的加速度为
| $ a_{\mathrm{C}_{K A-\mathrm{R}}}=a_{\mathrm{C}_{H K-\mathrm{R}}}+\varepsilon_{5} \ddot{\theta}_{5} l_{K A} \sin \theta_{5} $ | (12) |
右足部质心在竖直方向上的加速度为
| $ a_{\mathrm{C}_{A M-\mathrm{R}}}=a_{\mathrm{C}_{K A-\mathrm{R}}}+\varepsilon_{6} \ddot{\theta}_{6} l_{A M} \sin \theta_{6} $ | (13) |
将左右肩关节分别作为求解左右臂各部分质心加速度的起点,根据运动传递规律,可求得左大臂质心在竖直方向上的加速度为
| $ a_{\mathrm{C}_{S E-\mathrm{L}}}=a_{S \mathrm{~L}}+\varepsilon_{7} \ddot{\theta}_{7} l_{S E} \sin \theta_{7} $ | (14) |
左小臂质心在竖直方向上的加速度为
| $ a_{\mathrm{C}_{E W-\mathrm{L}}}=a_{\mathrm{C}_{S E-\mathrm{L}}}+\varepsilon_{8} \ddot{\theta}_{8} l_{E W} \sin \theta_{8} $ | (15) |
右大臂质心在竖直方向上的加速度为
| $ a_{\mathrm{C}_{S E-\mathrm{R}}}=a_{S_{\mathrm{R}}}+\varepsilon_{9} \ddot{\theta}_{9} l_{S E} \sin \theta_{9} $ | (16) |
右小臂质心在竖直方向上的加速度为
| $ a_{\mathrm{C}_{E W-\mathrm{R}}}=a_{\mathrm{C}_{S E-\mathrm{R}}}+\varepsilon_{10} \ddot{\theta}_{10} l_{E W} \sin \theta_{10} $ | (17) |
将求出的人体各个部分在竖直方向上的加速度代入式(3),得到任意时刻下的人体步态动力学关系式:
| $ \begin{aligned} \left|\boldsymbol{N}_{y}\right|-|\boldsymbol{M} g|=&\left[\left(1-\varepsilon_{1}\right) \ddot{\theta}_{1} l_{A M} \sin \theta_{1}\right] m_{1}+\left[\ddot{\theta}_{1} l_{A M} \sin \theta_{1}+\right.\\ &\left.\left(1-\varepsilon_{2}\right) \ddot{\theta}_{2} l_{K A} \sin \theta_{2}\right] m_{2}+\left[\ddot{\theta}_{1} l_{A M} \sin \theta_{1}+\ddot{\theta}_{2} l_{K A} \sin \theta_{2}+\right. \\ &\left.\left(1-\varepsilon_{3}\right) \ddot{\theta}_{3} l_{H K} \sin \theta_{3}\right] m_{3}+\left(\ddot{\theta}_{1} l_{A M} \sin \theta_{1}+\ddot{\theta}_{2} l_{K A} \sin \theta_{2}+\right. \\ &\left.\ddot{\theta}_{3} l_{H K} \sin \theta_{3}\right) m_{0}+\left(\ddot{\theta}_{1} l_{A M} \sin \theta_{1}+\ddot{\theta}_{2} l_{K A} \sin \theta_{2}+\ddot{\theta}_{3} l_{H K} \sin \theta_{3}+\right. \\ &\left.\varepsilon_{4} \ddot{\theta}_{4} l_{H K} \sin \theta_{4}\right) m_{4}+\left(\ddot{\theta}_{1} l_{A M} \sin \theta_{1}+\ddot{\theta}_{2} l_{K A} \sin \theta_{2}+\ddot{\theta}_{3} l_{H K} \sin \theta_{3}+\right. \\ &\left.\ddot{\theta}_{4} l_{H K} \sin \theta_{4}+\varepsilon_{5} \ddot{\theta}_{5} l_{K A} \sin \theta_{5}\right) m_{5}+\left(\ddot{\theta}_{1} l_{A M} \sin \theta_{1}+\ddot{\theta}_{2} l_{K A} \sin \theta_{2}+\right. \\ &\left.\ddot{\theta}_{3} l_{H K} \sin \theta_{3}+\ddot{\theta}_{4} l_{H K} \sin \theta_{4}+\ddot{\theta}_{5} l_{K A} \sin \theta_{5}+\varepsilon_{6} \ddot{\theta}_{6} l_{A M} \sin \theta_{6}\right) m_{6}+\\ &\left(\ddot{\theta}_{1} l_{A M} \sin \theta_{1}+\ddot{\theta}_{2} l_{K A} \sin \theta_{2}+\ddot{\theta}_{3} l_{H K} \sin \theta_{3}+\varepsilon_{7} \ddot{\theta}_{7} l_{S E} \sin \theta_{7}\right) m_{7}+ \\ &\left(\ddot{\theta}_{1} l_{A M} \sin \theta_{1}+\ddot{\theta}_{2} l_{K A} \sin \theta_{2}+\ddot{\theta}_{3} l_{H K} \sin \theta_{3}+\ddot{\theta}_{7} l_{S E} \sin \theta_{7}+\right. \\ &\left.\varepsilon_{8} \ddot{\theta}_{8} l_{E W} \sin \theta_{8}\right) m_{8}+\left(\ddot{\theta}_{1} l_{A M} \sin \theta_{1}+\ddot{\theta}_{2} l_{K A} \sin \theta_{2}+\right. \\ &\left.\ddot{\theta}_{3} l_{H K} \sin \theta_{3}+\varepsilon_{9} \ddot{\theta}_{9} l_{S E} \sin \theta_{9}\right) m_{9}+\left(\ddot{\theta}_{1} l_{A M} \sin \theta_{1}+\right. \\ &\ddot{\theta}_{2} l_{K A} \sin \theta_{2}+\ddot{\theta}_{3} l_{H K} \sin \theta_{3}+\ddot{\theta}_{9} l_{S E} \sin \theta_{9}+ \\ &\left.\varepsilon_{10} \ddot{\theta}_{10} l_{E W} \sin \theta_{10}\right) m_{10} \end{aligned} $ | (18) |
式中:l为对应四肢各部分长度,θ1~θ10为对应各关节点的连线并且指向近端关节点的向量与竖直方向的夹角,
为了提高步态特征提取的速度,简化特征提取方式,对式(18)进行矩阵化分离,得到矩阵式为
| $ \mathit{\boldsymbol{M\xi \omega L}} = \mathit{\boldsymbol{F}} $ | (19) |
式中:M为关于身体11个部分的质量矩阵,ξ为关于身体10个部分的质心矩阵,ω为关于某个时刻身体10个部分的运动角度和角加速度的矩阵,L为关于身体10个部分的长度矩阵,F为关于地面支反力和自身重力的力矩阵。其中, 矩阵ξ、ω、L为视觉特征,矩阵F为触觉特征,则各个矩阵式可以写为
| $ \boldsymbol{M}=\left[\begin{array}{lllllllllll} m_{1} & m_{2} & m_{3} & m_{0} & m_{4} & m_{5} & m_{6} & m_{7} & m_{8} & m_{9} & m_{10} \end{array}\right] $ |
| $ \boldsymbol{\xi}=\left[\begin{array}{ccccccccccc} 1-\varepsilon_{1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1-\varepsilon_{2} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 1-\varepsilon_{3} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 & \varepsilon_{4} & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 & 1 & \varepsilon_{5} & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 & 1 & 1 & \varepsilon_{6} & 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 & 0 & 0 & 0 & \varepsilon_{7} & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 & 0 & 0 & 0 & 1 & \varepsilon_{8} & 0 & 0 \\ 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & \varepsilon_{9} & 0 \\ 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & \varepsilon_{10} \end{array}\right] $ |
| $ \boldsymbol{L}^{\mathrm{T}}=\left[\begin{array}{lllllllllll} l_{1} & l_{2} & l_{3} & l_{3} & l_{4} & l_{5} & l_{6} & l_{7} & l_{8} & l_{9} & l_{10} \end{array}\right] $ |
| $ \boldsymbol{F}=\left[\left|\boldsymbol{N}_{y}\right|-|\boldsymbol{M g}|\right] $ |
| $ \boldsymbol{\omega}=\left[\begin{array}{ccccccccccccc} \ddot{\theta}_{1} \sin \theta_{1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & \ddot{\theta}_{2} \sin \theta_{2} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & \ddot{\theta}_{3} \sin \theta_{3} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & \ddot{\theta}_{3} \sin \theta_{3} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & \ddot{\theta}_{4} \sin \theta_{4} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \ddot{\theta}_{5} \sin \theta_{5} & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & \ddot{\theta}_{6} \sin \theta_{6} & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & \ddot{\theta}_{7} \sin \theta_{7} & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \ddot{\theta}_{8} \sin \theta_{8} & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \ddot{\theta}_{9} \sin \theta_{9} & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \ddot{\theta}_{10} \sin \theta_{10} \end{array}\right] $ |
Kinect能够为开发者提供原始深度数据流,用来进行骨骼追踪和关节坐标提取,而普通相机只能够通过坐标转换等方式来提取坐标,这使得Kinect具有更快的特征提取速度, 也被广泛用于步态识别的视觉特征提取中[14-15]。实验系统主要包括Walkway步道式足底压力测试设备和微软的Kinect For Windows v2。采样频率设置为25帧/s,通过足底压力仪获得某时刻的足底压力分布,通过Kinect获得人体25个关节的空间三维坐标和行走时的彩色图像序列,获得的足底压力和视觉图像每帧互相对应。实验系统具体位置摆放如图 6。
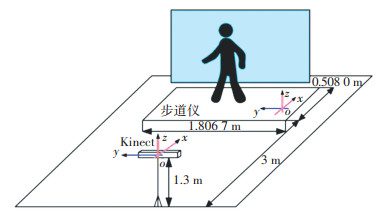
|
图 6 实验系统布局图 Fig. 6 Layout of experimental system |
实验时的具体步骤和条件为:
1) 室内光线柔和,没有其他杂物;
2) Kinect光轴与人体行走方向垂直;
3) 在实验开始前,实验人要先进入自然行走状态后进入实验区域;
4) 参与实验的人分别按正常、背包和穿大衣3种状态进行特征采集,并且在实验区域内走直线。
2.2 提取特征矩阵参数步态运动模型的建立可以很大程度提高步态识别精度,提高抗干扰性。但对于模型中各个特征的求取也非常关键,更准确的特征提取也意味着更好的识别精度。
2.2.1 质量矩阵M的选取根据中国国家标准化管理委员会发布的《成年人人体惯性参数》(GB/T 17245—2004)求取人体的各部分质量,得到m0~m10,如表 1。
| 表 1 成年人人体惯性参数 Tab. 1 Inertial parameters of adult human body |
在计算四肢质心时,认为大臂、小臂、大腿、小腿的质心在其关节连线上,将其看做均匀密度,且斜率很小的圆台,如图 7(a)。因为圆台关于轴线旋转对称,所以圆台上所有平行于上下底面的横截面的重心都在O1O2上,这样可以把圆台横截面的质量假设在自身的重心上,将求圆台重心的三维问题转化为求一维线性体O1O2的重心问题,如图 7(b)。设线性体的线密度为
| $ \rho(X)=\rho_{0} \pi\left(r_{1} / 2+X \tan \alpha\right)^{2} $ | (21) |
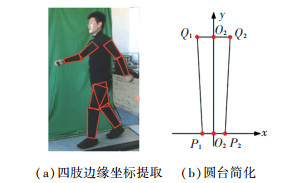
|
图 7 四肢重心示意图 Fig. 7 Schematic diagram of center of gravity |
式中:r1为圆台上底面直径,X为圆台高度,α为轴线与母线的夹角。
可得圆台质心到底面的距离LC和距离占圆台总高度的比例ε分别为:
| $ L_{\mathrm{C}}=\frac{\int X \mathrm{~d} m}{M}=\frac{\int_{0}^{L} X \pi \rho_{0}\left(r_{1} / 2+X \tan \alpha\right)^{2} \mathrm{~d} x}{\int_{0}^{L} \pi \rho_{0}\left(r_{1} / 2+X \tan \alpha\right)^{2} \mathrm{~d} x} $ | (22) |
| $ \varepsilon=\frac{L_{\mathrm{C}}}{L}=\frac{\frac{1}{2}+\frac{4}{3} \frac{L}{r_{1}} \tan \alpha+\left(\frac{L}{r_{1}} \tan \alpha\right)^{2}}{1+\frac{2 L}{r_{1}} \tan \alpha+\frac{4}{3}\left(\frac{L}{r_{1}} \tan \alpha\right)^{2}} $ | (23) |
式中:M为对应各部分质量,L为对应各部分关节连线长度。
2.2.3 速度及加速度矩阵ω的提取速度特征可以通过Kinect数据流中的关节空间坐标求得,每帧的时间差为0.04 s。选取任意连续变化的2帧图像可以求取角速度特征,选取任意的连续变化的3帧图像可以求取角加速度特征,即θ1~θ10和
身体长度特征可以由Kienct得到的关节三维空间坐标来计算,可得四肢和足部长度l1~l10。
2.2.5 力矩阵F的提取分析足底压力分布图像,通过将足底压力分区的方式,增多特征识别点,提高模型识别率,如图 8。以足底最大压力图像为例,取得非零行数r和非零列数p,每个区域的大小为一个r/4行、p/4列的矩阵,则此时的足底压力矩阵为
| $ \boldsymbol{N}_{y}=\boldsymbol{N}_{1}+\boldsymbol{N}_{2}+\boldsymbol{N}_{3}+\boldsymbol{N}_{4} $ | (24) |
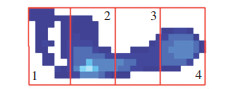
|
图 8 足底压力分区方法 Fig. 8 Plantar pressure partition method |
相对于其他的机器学习方法,因为支持向量机能够利用有限数量样本特征在复杂模型情况下进行折中学习,可以避免欠学习和过学习情况带来的问题,因此常用在步态识别中[16-17]。以支持向量机的C-SVC模型为基础,选用径向基核函数(RBF)构造多分类器,因为RBF能够实现非线性映射,并且计算速度快。
定义空间中任意一点x到某一个中心xc之间欧氏距离的单调函数为k(‖x-xc‖),则径向基函数对应的高斯核函数为
| $ k\left(\left\|x-x_{c}\right\|\right)=\exp \left\{-\left\|x-x_{c}\right\|^{2} /\left[(2 * \sigma)^{2}\right]\right\} $ | (25) |
| $ {\rm{g}}=1 /(2 \mathtt{σ})^{2} $ | (26) |
式中:xc为核函数中心;σ为函数的宽度参数;g为单个训练样本的影响,g越大单个训练样本的影响越小。
C-SVC模型的惩罚参数c和核函数的参数g对识别预测的准确率有很大的影响[18],仅凭经验选取的参数不能发挥模型的识别性能。本文使用交叉验证法中的K-CV法来寻找最优参数c和g。在寻找使步态模型达到最高分类准确率对应的参数时,选取c最小组对应的c和g作为最佳参数,因为过大的c会导致训练集分类准确率很高而测试集分类准确率很低。经过大范围的粗略寻优和小范围的精细寻优得到本模型最优的参数c为1,g为1,如图 9。图中x轴表示c取以2为底的对数值,y轴表示g取以2为底的对数值,方框中数值代表当前参数下的识别率。
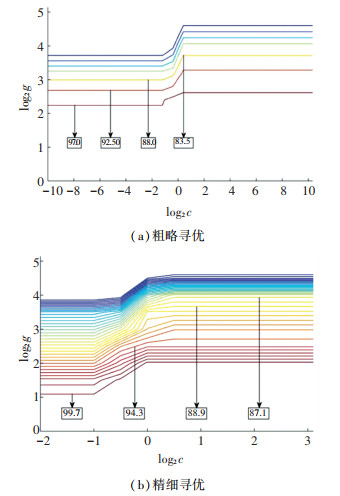
|
图 9 参数寻优 Fig. 9 Parameter optimization |
目前,国内外基于Kinect和足底压力的步态研究还在初级阶段,仍没有一个完整的Kinect和足底压力结合的数据库,因此对模型的验证都是在本文数据库下进行的。本文模型所需的视觉特征和触觉特征是同时提取的,每一帧的视觉图像、人体的关节三维坐标和足底压力图像相互对应,如图 10。
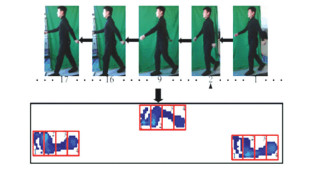
|
图 10 Kinect图像与足底压力图像 Fig. 10 Kinect image and plantar pressure image |
通过Kinect提取包括四肢长度和摆动角度在内的视觉特征是目前常用的步态特征提取方式。取一个步态周期中的某一帧视觉特征进行分析,通过Kinect提取关节坐标,分别计算人体两侧的四肢长度,如表 2。
| 表 2 四肢长度计算值与测量值 Tab. 2 Calculated and measured values of limb lengths |
由表 2可知,计算值与测量值的最大误差为足部的8.96%,最小误差为大腿的0.45%,说明Kinect在视觉特征提取上有着很好的精度。
取每名实验者在正常、背包和穿大衣3种情况下视觉特征和触觉特征100帧进行融合,其中50帧作为训练集,另外50帧作为测试集。根据参数寻优结果,将惩罚参数c设为1,核函数参数g设为1,同时将矩阵F中的足底压力分区。随机抽取训练集中的10帧特征和测试集中的10帧特征输入分类器,对模型的识别性能进行验证。通过对15名实验者在3种不同步态运动状态下的数据采集和特征处理,建立数据库。在MATLAB中运用支持向量机的多分类算法对全身步态模型的识别性能进行验证,平均运行时间为1.124 s。同时根据本文所建立的Kinect和足底压力数据库,提取了文献[8]提出的五连杆模型和文献[9]提出的全身分层可变模型所需的视觉特征,以及文献[11]和文献[12]所需的触觉特征,对4个不同模型在本数据库下的识别性能进行验证,结果见表 3。
| 表 3 本文数据库下不同模型的识别率 Tab. 3 Recognition rate of different models in the database of this paper |
由表 3可知,本文模型通过对足底压力分区增加特征识别点的方式,提高了步态识别的准确率,并且模型在背包负重和穿大衣遮挡情况下的识别性能下降更少,具有很好的鲁棒性。融合了视觉和触觉特征的全身步态模型与只使用视觉特征进行建模的方法相比识别率更高;对于只使用触觉特征进行识别的方法,由于自身重力的增大,在背包负重情况下识别性能下降很多,而本文由于引入视觉特征进行建模,在背包负重情况下的表现更好。
5 结论1) 本文提出一种融合视觉和触觉特征的全身步态运动模型,减少了背包负重和穿大衣遮挡情况下对步态识别结果的影响。采用足底压力分区的方式增多特征识别点,提高了步态识别率。
2) 为更加快速和方便地提取步态运动特征,将步态模型进行特征分离,得到代表不同人体步态运动特征的矩阵。并且通过Kinect和步道式足底压力仪搭建实验系统,建立了包括正常、背包负重和穿大衣3种情况下的数据库,方便特征提取和模型验证。
3) 为进一步提高识别率,在步态识别过程中采用支持向量机中的多分类器方法,对分类器中的主要参数先后进行了粗略寻优和精细寻优。在本文数据库范围内验证了算法的有效性,比较了4种模型在本文数据库下的表现,结果表明,本文提出的算法识别率最高。
| [1] |
YANG Gelan, TAN Wei, JIN Huixia, et al. Review wearable sensing system for gait recognition[J]. Cluster Computing, 2019, 22: 3021. DOI:10.1007/s10586-018-1830-y |
| [2] |
BOUCHRIKA I, GOFFREDP M, CARTER J, et al. On using gait in forensic biometrics[J]. Journal of Eorensic Sciences, 2011, 56(4): 882. DOI:10.1111/j.1556-4029.2011.01793.x |
| [3] |
JARCHI D, POPE J, LEE T K M, et al. A review on accelerometry-based gait analysis and emerging clinical applications[J]. IEEE Reviews in Biomedical Engineering, 2018, 11: 177. DOI:10.1109/REME.2018.2807182 |
| [4] |
CUNADO D, NIXON M S, CARTER J N. Using gait as a biometric, via phase-weighted magnitude spectra[J]. Lecture Notes in Computer Science, 1999, 1206: 93. DOI:10.1007/BFb0015984 |
| [5] |
BOUCHRIKA I, CARTER J N, NIXON M S. Towards automated visual surveillance using gait for identity recognition and tracking across multiple non-intersecting cameras[J]. Multimedia Tools & Applications, 2016, 75(2): 1201. DOI:10.1007/s11042-014-2364-9 |
| [6] |
YOO J H, NIXON M S, HARRIS C J. Extracting gait signatures based on anatomical knowledge[C]// Proceedings of BMVA Symposium on Advancing Biometric Technologies. London: Southampton Wireless Group Press, 2002: 596
|
| [7] |
YOO J H, NIXON M S, HARRIS C J. Model-driven statistical analysis of human gait motion[C]// Proceedings of International Conference on Image Processing. New York: IEEE, 2002: 285. DOI: 10.3390/s19112542
|
| [8] |
ZHANG Rong, VOGLER C, METAXAS D N. Human gait recognition at sagittal plane[J]. Image and Vision Computing, 2007, 25(3): 321. DOI:10.1016/j.imavis.2005.10.1007 |
| [9] |
LU Haiping, PLATANIOTIS K N, VENETSANOPOULOS A N. A full-body layered deformable model for automatic model-based gait recognition[J]. EURASIP Journal on Advances in Signal Processing, 2008, 8(1): 261. DOI:10.1155/2008/261317 |
| [10] |
QIAN Gang, ZHANG Jiqing, KIDANE A. People identification using floor pressure sensing and analysis[J]. IEEE Sensors Journal, 2010, 10(9): 1447. DOI:10.1109/JSEN.2010.2045158 |
| [11] |
YAMAKAWA T, TANIGUCHI K, ASARI K, et al. Biometric personal identification based on gait pattern using both feet pressure change[C]// Proceedings of 2008 World Automation Congress. Waikoloa: IEEE, 2010: 1
|
| [12] |
TAKEDA T, TANIGUCHI K, ASARIS K, et al. Biometric personal authentication by one step foot pressure distribution change by load distribution sensor[C]//Proceedings of 2009 International Conference on Fuzzy Systems. Barcelona: IEEE, 2010: 1. DOI: 10.1109/FUZZY.2009.5277149
|
| [13] |
DAI Shijie, WANG Rui, ZHANG Huibo. A gait skeleton model extraction method based on the fusion between vision and tactility[J]. Visual Computer, 2019, 35(12): 1713. DOI:10.1007/s00371-018-1601-z |
| [14] |
DENG Muqing, WANG Cong. Human gait recognition based on deterministic learning and data stream of Microsoft Kinect[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2018, 29(12): 3636. DOI:10.1109/TCSVT.2018.2883449 |
| [15] |
HUITZIL I, DRANCA L, BERNAD J, et al. Gait recognition using fuzzy ontologies and Kinect Sensor data[J]. International Journal of Approximate Reasoning, 2019, 113: 354. |
| [16] |
WANG Hao, FAN Yuanyuan, FANG Baofu, et al. Generalized linear discriminant analysis based on euclidean norm for gait recognition[J]. International Journal of Machine Learning and Cybernetics, 2018, 9(4): 569. DOI:10.1007/s13042-016-0540-0 |
| [17] |
ZHANG He, YE Cang. RGB-D camera based walking pattern recognition by support vector machines for a smart rollator[J]. International Journal of Intelligent Robotics & Applications, 2017, 1: 32. DOI:10.1007/s41315-016-0002-6 |
| [18] |
WANG Xiuhui, WANG Jun, YAN Ke. Gait recognition based on Gabor wavelets and (2D)2PCA[J]. Multimedia Tools and Applications, 2018, 77(3): 1. DOI:10.1007/s11042-017-4930-7 |
 2022, Vol. 54
2022, Vol. 54


