为简化控制系统、降低控制成本,导弹采用旋转体制来实现单通道控制[1],随着近几年舵机技术的发展,导弹舵系统小型化水平的不断提高,采用双通道控制的旋转导弹应运而生[2]。双通道控制的旋转导弹是将两对舵的指令进行正、余弦分解,使导弹在任意滚转位置上的控制力始终指向所要求的控制合力方向,通过调节指令的初始相位来控制导弹的机动方向。
目前,国内外已有很多学者对旋转导弹的气动特性和带有鸭舵控制的旋转导弹稳定性进行了相关研究。Yin和吴放等[3-5]对带有尾翼的旋转导弹进行了数值模拟,结果表明尾翼的前缘激波、背风区的分离涡和翼根流动是造成弹体在不同迎角下马格努斯效应出现非线性特征的主要原因,尾翼产生的周期平均侧向力方向与弹身相反。Yin等[6]研究了带有不控鸭舵的旋转导弹,结果表明鸭舵产生的周期平均侧向力方向与尾翼相同。鸭舵产生的洗流随迎角的增大先与弹身分离涡融合、而后远离弹身,这导致尾翼的侧向力先增大后减小。Gene[7-8]等对采用正弦控制方式导弹的稳定性进行了分析,发现鸭舵的偏转是导致飞行不稳定的潜在因素。Tobak等[9]研究发现:初始扰动、马格努斯力和力矩是导致锥形运动的主要因素。Nicolaides和卢天宇等[10-11]发现旋转诱导产生的面外力和力矩是产生锥形运动的重要因素。
目前,国内外关于正、余弦指令控制旋转导弹气动特性的研究相对较少,工程上也常采用不同滚转角、舵偏角下的静态试验结果与仿真数据来代替动态的过程。以俯仰控制为例,虽然通过正、余弦指令的分解使得两对鸭舵产生的侧向力相互抵消,但是由于弹体旋转耦合鸭舵的正、余弦偏转对全弹气动特性的影响需要进一步明确,对于锥进运动过程中鸭舵偏转耦合弹体锥进运动的气动特性尚不清楚。由于导弹旋转、鸭舵的正余弦偏转是动态的气动过程,通过风洞试验对其研究难度较大。因此,本文采用数值计算的方法,通过CFD软件ANSYS Fluent 2021 R1研究了正、余弦控制方式旋转导弹在不同马赫数、迎角和锥进运动条件下的气动特性。通过重叠网格来实现鸭舵的偏转运动,用旋转坐标系方法实现导弹的旋转,通过用户自定义函数来实现鸭舵的正、余弦偏转和导弹的锥进运动。
1 几何模型与数值仿真方法 1.1 几何模型本文采用的几何模型如图 1所示,头部装有四片鸭舵,鸭舵通过对正、余弦指令进行分解,可对导弹进行俯仰、偏航操纵。定义舵偏角为δ,滚转角为φ,迎角为α,由弹头向弹尾看去导弹顺时针旋转为正,φ=0°时导弹为十字状态、φ=45°时导弹为×字状态。参考长度为全弹长L,参考面积S=πD2/4,参考点取质心0.56L。

|
图 1 鸭式布局导弹模型 Fig. 1 Canard layout missile model |
图 2为正、余弦指令控制方式旋转导弹在一个自旋周期内的控制方式示意图。当导弹要进行法向控制时,如图 2(a)所示两片鸭舵产生向上的力。随着导弹的旋转,鸭舵的舵偏角会进行正、余弦分解(如图 2(b)、(c)所示),在舵面法向力是线性分布的前提下,通过正、余弦指令的分解使得两对鸭舵产生的侧向力相互抵消。当导弹要进行侧向或者其它方向的控制时,只需将合力的方向进行相应的偏转即可实现。

|
图 2 模拟工况示意图 Fig. 2 Simulated working condition |
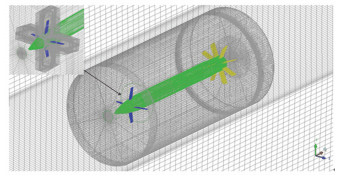
图 3展示了三维结构六面体网格,超声速条件下,扰动只能在马赫锥内部顺流传播,上游的流场不受扰动波的影响。为了节约计算资源,超声速远场网格向前延伸1倍弹长,向后延伸10倍弹长,径向约20倍弹径。亚声速条件下,扰动的影响域为全流场。因此,亚声速远场网格向前延伸10倍弹长,向后延伸10倍弹长,径向约20倍弹径。设置第一层网格高度为1.8×10-6以保证y+ < 1,将网格内边界设置为无滑移绝热壁。导弹的自旋是通过重叠网格区域的网格运动实现的,重叠网格技术是将一个背景网格与多个部件网格进行组合,每一套网格单独进行结构化网格划分。在CFD中采用插值法获得背景网格与部件网格中的数据,网格重叠区域采用最小二乘法进行插值,网格重叠的边界处采用三线性插值的方式传递数据。数值计算中,背景网格为亚声速和超声速压力远场,弹体和鸭舵均采用部件网格,外部边界条件设置为Overset。弹体的转动采用旋转坐标系方法,鸭舵偏转耦合弹体摆动通过UDF实现,当导弹只做自旋运动时鸭舵的运动方程为
| $ \left\{\begin{array}{l} \omega_{x}=\omega_{1} \\ \omega_{y}=\omega_{2} \sin \left(\omega_{1} t\right) \sin \left(\omega_{1} t\right) \\ \omega_{z}=-\omega_{2} \sin \left(\omega_{1} t\right) \cos \left(\omega_{1} t\right) \end{array}\right. $ | (1) |
|
图 3 流场网格示意图 Fig. 3 Flow field mesh |
当导弹做锥进运动时,弹体的运动方程为
| $ \left\{\begin{array}{l} \omega_{x}=\omega_{1} \cos (\alpha) \\ \omega_{y}=\left(\omega_{1}+\omega_{3}\right) \sin (\alpha) \cos \left(\omega_{3} t\right) \\ \omega_{z}=-\left(\omega_{1}+\omega_{3}\right) \sin (\alpha) \sin \left(\omega_{3} t\right) \end{array}\right. $ | (2) |
鸭舵相对于导弹的运动方程为(采用Relative Motion方法实现鸭舵相对于弹体的正、余弦偏转)
| $ \left\{\begin{array} { l } { \omega _ { x } = 0 } \\ { \omega _ { y } = 0 } \\ { \omega _ { z } = - \omega _ { 2 } \sin ( \omega _ { 1 } t ) } \end{array} \quad \left\{\begin{array}{l} \omega_{x}=0 \\ \omega_{y}=0 \\ \omega_{z}=-\omega_{2} \cos \left(\omega_{1} t\right) \end{array}\right.\right. $ | (3) |
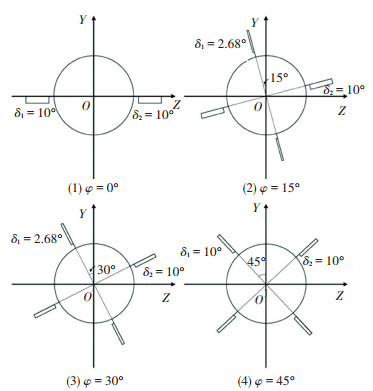
试验在南京理工大学采用HG-4号风洞进行。HG-4风洞为直流下吹暂冲式闭口亚、跨、超声速风洞,试验段截面尺寸为300 mm×300 mm,试验段长为0.6 m,试验马赫数范围为0.5~4.5,攻角变化范围为-4°~8°,本试验段中的阻塞度为0.665%,天平载荷能力与静校指标性能如表 1所示。试验为静态试验,采用图 1中的模型、图 4所示的4种舵偏与滚转状态组合来进行试验,从而实现正、余弦指令的模拟。
| 表 1 天平载荷能力与静校指标性能 Tab. 1 Balance load capacity and static calibration index performance |
|
图 4 试验工况图 Fig. 4 Experiment cases |
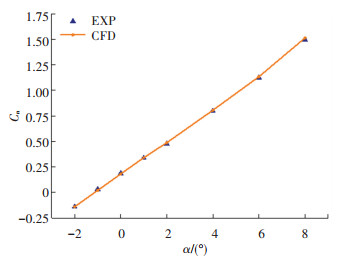
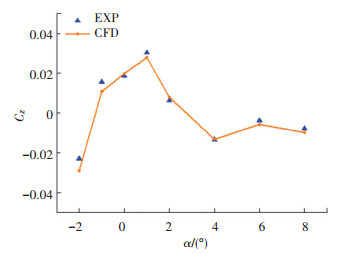
图 5和6分别为采用重叠网格计算的Ma=2、φ=30°时(即工况3)法向力系数和侧向力系数随迎角变化曲线。随着迎角的增加,侧向力系数先增大后减小。但是侧向力系数较小,这是由于两对鸭舵在各自的位置舵偏角不同,因此在侧向上的力相互抵消。图 7为Ma=2、α=4°时侧向力系数随滚转角变化曲线,由于鸭舵进行了正余弦指令的分解,因此侧向力相对较小。图 5~7中数值模拟的结果与试验值吻合较好,说明采用静态的重叠网格对该导弹进行数值模拟具有可信度。
|
图 5 Ma =2、φ =30°时升力系数随迎角变化曲线 Fig. 5 Lift coefficient changes with angle of attack at Ma=2, φ=45° |
|
图 6 Ma =2、φ =30°时侧向力系数随迎角变化曲线 Fig. 6 Lateral force coefficient changes with angle of attack at Ma=2, φ=30° |

|
图 7 Ma =2、α =4°时侧向力系数随滚转角变化曲线 Fig. 7 Lateral force coefficient changes with roll angle at Ma=2, α=4° |
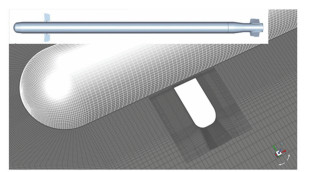
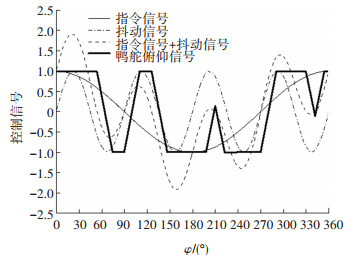
为了进一步验证采用动态的重叠网格对旋转导弹气动特性数值模拟的准确,采用FM-3导弹的试验结果进行验证。FM-3导弹有一个半球形头部,圆柱段弹身,四个尾翼和一对鸭舵,鸭舵部分的重叠网格如图 8所示。当导弹旋转时,鸭舵由一个具有恒定速率的执行器进行驱动。执行器信号在±1之间根据指令信号和抖动信号的两个正弦波和进行触发,指令信号用滚转速率调制,抖动信号用抖动频率调制。指令信号相对于抖动信号的振幅比称为指令水平,它反映了试图机动的强度。图 9为导弹滚转速率为8.75 Hz,鸭舵抖动速率为35 Hz,指令水平为100%时鸭舵俯仰指令示意图[12-13]。
|
图 8 FM-3嵌套网格示意图 Fig. 8 FM-3 overset mesh |
|
图 9 鸭舵俯仰指令示意图(导弹滚转速率8.75 Hz,鸭舵抖动速率35 Hz,指令水平100%) Fig. 9 Schematic diagram of canard pitching instruction(The missile roll rate is 8.75 Hz, the canard dither rate is 35 Hz, and the command level is 100%) |
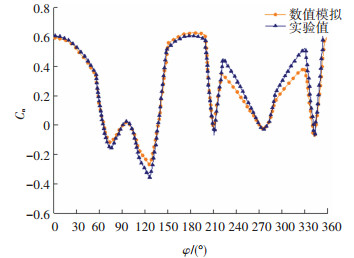
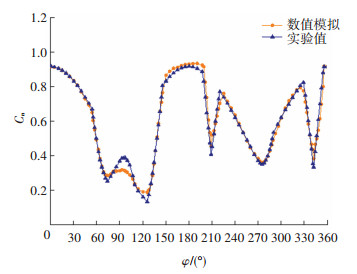
图 10和11为FM-3采用重叠网格方法得到的法向力系数与试验值的对比,导弹滚转速率为8.75 Hz,鸭舵抖动速率为35 Hz,鸭舵的最大舵偏角为15°,马赫数为1.6,迎角为0°和3°。采用k-ω SST模型得到的数值模拟结果与试验值吻合较好。由于鸭舵的抖动,这会导致法向力系数的突变,尤其是在迎角为0°时,导弹的周期平均法向力全部是由鸭舵的抖动所产生的。从图 10和11能够看出,采用数值模拟能够较好的模拟法向力系数的变化规律。因此,采用重叠网格方法模拟鸭舵和弹体的耦合运动具有一定的可信度。
|
图 10 FM-3法向力系数对比曲线(Ma =1.6, α =0°) Fig. 10 FM-3 coefficient of normal force(Ma=1.6, α=0°) |
|
图 11 FM-3法向力系数对比曲线(Ma =1.6, α =3°) Fig. 11 FM-3 coefficient of normal force(Ma=1.6, α=3°) |
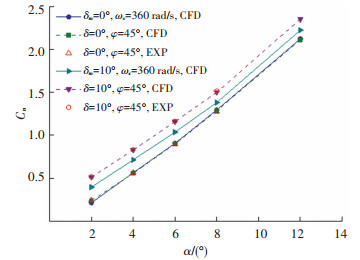
图 12为马赫数为2时法向力系数随迎角变化曲线,其中数值模拟是采用重叠网格进行正、余弦方式打舵计算得到的旋转导弹周期平均值,其最大舵偏值δm分别为0°和10°(δm=0°时即为导弹旋转而鸭舵没有进行摆动控制的状态,δm=10°时即为导弹旋转且鸭舵进行了正、余弦控制摆动的状态)。试验值是滚转角为45°时(即导弹×字状态)静态风洞试验结果。0°舵偏时,静态试验结果与动态数值模拟周期平均结果吻合较好,这是由于导弹的纵向气动特性受转速变化影响很小[14]。10°舵偏时,静态试验结果比动态数值模拟周期平均结果大,这是由于在正、余弦控制过程中鸭舵的舵效理论上为最大机械舵偏角舵效的50%。将舵偏0°和10°正、余弦控制法向力系数的差值除以静态试验中舵偏0°和10°法向力系数的差值,便得到了如表 2所示的舵效。随着迎角的增加,正、余弦控制的舵效逐渐降低。
|
图 12 Ma=2时法向力系数随迎角变化曲线 Fig. 12 Curve of normal force coefficient with attack angle at Ma=2 |
| 表 2 Ma=2时正、余弦控制鸭舵舵效 Tab. 2 Canard effect under sine and cosine control at Ma=2 |
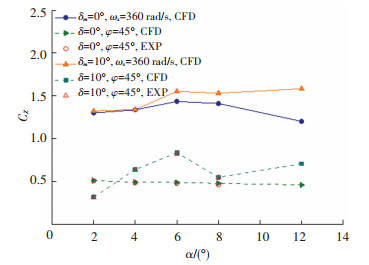
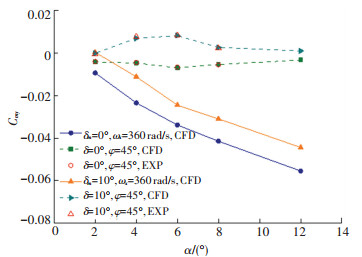
图 13和14分别为侧向力系数和偏航力矩系数随迎角的变化曲线。对于静态的风洞试验,其侧向力系数和偏航力矩系数较小。但是对于动态的数值模拟结果,其侧向力系数和偏航力矩系数数值较大,这是由于导弹的旋转导致了马格努斯效应的产生。对于侧向力系数,δm=0°时其随着迎角的增大先增大后减小,δm=10°时其随着迎角的增大而增大,偏航力矩系数均随着迎角的增大而减小。
|
图 13 Ma=2时侧向力系数随迎角变化曲线 Fig. 13 Curve of normal force coefficient with attack angle at Ma=2 |
|
图 14 Ma=2时偏航力矩系数随迎角变化曲线 Fig. 14 Curve of lateral moment coefficient with attack angle at Ma=2 |
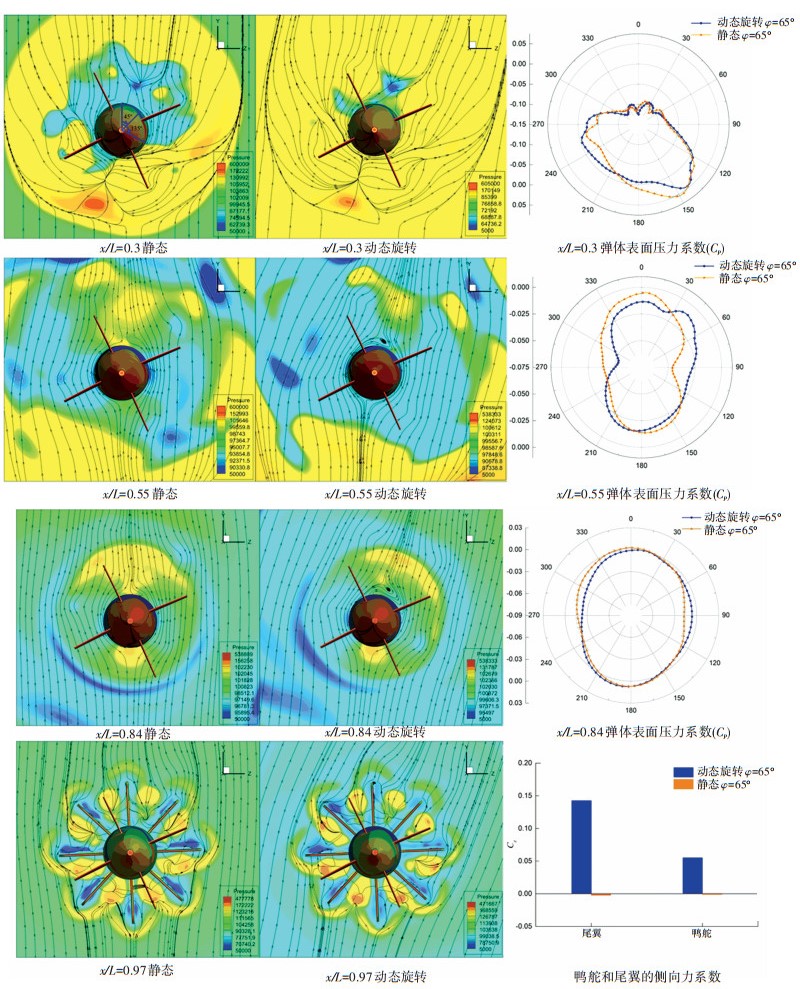
与静态试验相比,动态旋转时导弹的侧向力系数大幅增加。图 7中给出了不旋转时导弹侧向力系数随滚转角的变化曲线,数值模拟值与风洞试验值吻合较好,其侧向力系数均为较小的值,这说明由于鸭舵洗流的不对称对导弹的侧向力的影响较小,而旋转效应是引起导弹产生侧向力原因。为了进一步的说明旋转效应对导弹侧向力特性的影响,图 15给出了马赫数为2、迎角为6°、滚转角φ=25°时静态与动态旋转时导弹不同截面流线图与表面压力分布,其中静态条件下的鸭舵舵偏角与动态时导弹滚转至φ=25°时的鸭舵舵偏角相同。此时,静态条件下导弹的侧向力系数为-0.011 87,动态旋转条件下导弹的侧向力系数为0.135 91,这表明由于旋转耦合鸭舵偏转导致弹身压力分布不对称,从而导致侧向力的出现。
|
图 15 Ma=2、攻角α =6°、滚转角φ =25°时静态与动态旋转时导弹不同截面流线图与表面压力分布 Fig. 15 Flow diagram and surface pressure distribution of missile at different sections under static and dynamic rotation when Ma=2, α=6°, φ=25° |
表 3给出了此时两种状态下不同部件的侧向力系数。可以看出,由旋转引起的导弹侧向力中鸭舵和尾翼占到了绝大部分,并且弹身产生的侧向力方向与鸭舵、尾翼产生的侧向力方向相反。从流线图可以看出,静态条件下弹体周围的流场比较对称,而动态旋转条件下弹体周围流场向一侧偏移。x/L=0.3处位于鸭舵后较近的位置,此时静态条件下弹体表面压力系数分布要比动态旋转条件下的更不对称,这是由于鸭舵洗流的不对称导致的结果。但是随着x/L的增加,静态条件下弹体表面压力系数分布变得对称,而动态旋转条件下弹体表面压力系数分布始终是不对称的。动态旋转条件下尾翼和鸭舵产生的侧向力要比静态条件下大很多。因此,旋转效应是正、余弦控制方式旋转导弹产生侧向力的原因,并且鸭舵、尾翼产生的侧向力占主导地位。
| 表 3 部件侧向力系数 Tab. 3 Component lateral force coefficient |
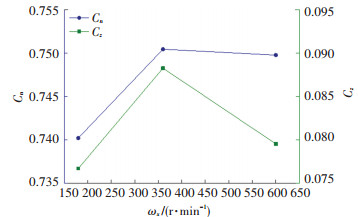
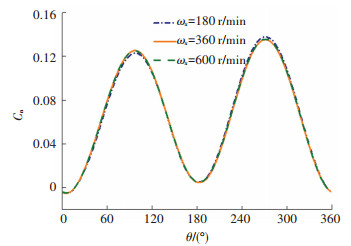
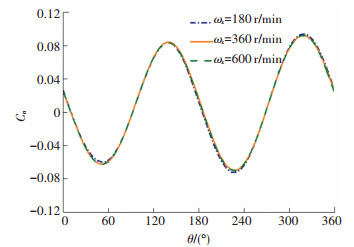
为了分析转速的变化对导弹气动特性的影响,图 16为不同转速下、最大舵偏角δm=10°、4°迎角时采用正、余弦指令打舵的旋转导弹法向力系数、侧向力系数随转速变化曲线。可以看出,转速的变化对全弹法向力、侧向力特性影响相对较小。对于旋转导弹来说,其法向力主要由尾翼和鸭舵提供,国内外研究表明转速的变化对不控时的旋转导弹法向力特性影响较小[3, 5-6, 14]。图 17为正余弦控制下不同转速导弹一个旋转周期内鸭舵提供的法向力变化曲线,转速的变化对鸭舵周期法向力系数影响很小,因此转速对全弹的法向力特性影响较小。图 18为正余弦控制下不同转速导弹一个旋转周期内鸭舵提供的侧向力系数变化曲线,对于导弹来说其转速相对较低,因此在这一范围内导弹的侧向力系数随转速变化较小。
|
图 16 Ma=2、α =4°时法向力系数、侧向力系数随转速变化曲线 Fig. 16 Curve of normal force coefficient and lateral force coefficient changing with rotational speed at Ma=2, α=4° |
|
图 17 不同转速下导弹一个旋转周期内鸭舵提供的法向力变化曲线 Fig. 17 Curve of normal force provided by the canard in one rotation period of the missile at different rotational speeds |
|
图 18 不同转速下导弹一个旋转周期内鸭舵提供的侧向力变化曲线 Fig. 18 Curve of lateral force provided by the canard in one rotation period of the missile at different rotational speeds |
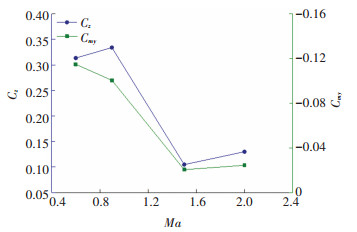
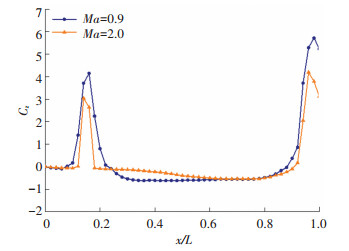
图 19是不同马赫数下转速ωx=360 rad/s时导弹侧向力系数、偏航力矩系数随马赫数变化曲线。在亚声速条件下,导弹的侧向力系数和偏航力矩系数数值较大,尤其是偏航力矩系数。图 20为侧向力系数沿弹轴分布曲线,可以看出亚声速条件下鸭舵和尾翼产生的侧向力要比超声速条件下的大。并且在亚声速条件下扰动的传播是全流场的,与超声速相比,亚声速条件下在鸭舵和尾翼之前即出现较大的侧向力分布。
|
图 19 侧向力系数、偏航力矩系数随马赫数变化曲线 Fig. 19 Curve of lateral force coefficient and yaw moment coefficient with Mach number |
|
图 20 侧向力系数沿弹轴分布曲线 Fig. 20 Distribution of lateral force coefficient along the elastic axis |
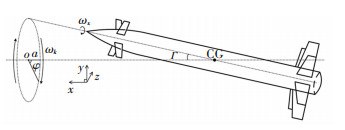
采用重叠网格方法,运用1.2节中介绍的部件网格运动技术,让导弹做如图 21所示的锥进运动,在锥进运动过程中鸭舵进行正、余弦指令打舵控制,最大舵偏角δm=10°。锥进运动过程中导弹自转速率ωx=360 r/min,导弹锥进速率ωk=120 r/min,合成迎角(锥进角)Г为5°和10°,oa为锥进运动起始位置,ϕ沿顺时针为正。在导弹进行锥进运动的过程中,鸭舵进行的正、余弦控制方向始终指向y轴正向。
|
图 21 锥进运动示意图 Fig. 21 Schematic diagram of coning motion |
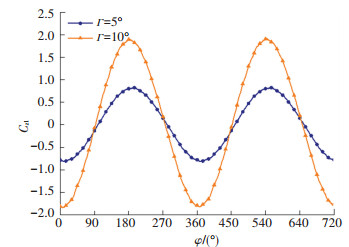
图 22~25为导弹做锥进运动时两个锥进运动周期内导弹的阻力系数、升力系数、侧向力系数和偏航力矩系数曲线。其阻力系数平均值分别为-0.823 19和-1.116 56。其升力系数平均值分别为0.219 18和0.215 55,侧向力系数平均值分别为0.008 13和0.005 11,偏航力系数平均值分别为-0.007 63和-0.017 87。合成迎角Г的变化对周期平均升力系数和侧向力系数影响较小,Г的变大会使周期平均偏航力系数数值变大,周期平均阻力系数数值变大。

|
图 22 锥进运动过程中导弹阻力系数曲线 Fig. 22 Curve of missile drag coefficient during coning motion |

|
图 23 锥进运动过程中导弹升力系数曲线 Fig. 23 Curve of missile lift coefficient during coning motion |
|
图 24 锥进运动过程中导弹侧向力系数曲线 Fig. 24 Curve of missile lateral force coefficient during coning motion |

|
图 25 锥进运动过程中导弹偏航力矩系数曲线 Fig. 25 Curve of missile yaw moment coefficient during coning motion |
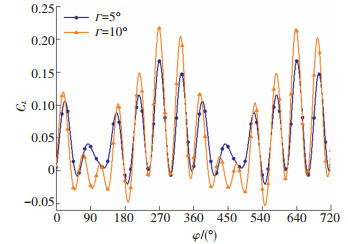
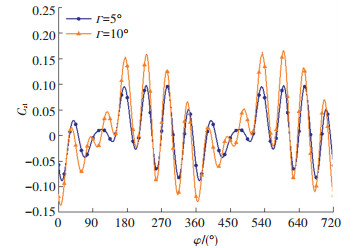
图 26和27分别为锥进运动过程中舵面升力系数和侧向力系数曲线,舵面产生的周期平均升力系数为0.050 77和0.049 87,周期平均侧向力系数为0.004 73和0.010 1。合成迎角Г的变化对鸭舵产生的周期平均升力影响较小,Г的变大会使周期平均侧向力系数变大,Г=10°时曲线的极值均要比Г=5°时大,鸭舵的侧向力变大会增加导弹的偏航力矩系数。
|
图 26 锥进运动过程中舵面升力系数曲线 Fig. 26 Curve of lift coefficient of canard surface during coning |
|
图 27 锥进运动过程中舵面侧向力系数曲线 Fig. 27 Curve of lateral force coefficient on canard surface during coning |
1) 当采用相同最大舵偏角时,导弹进行正、余弦控制时其法向力系数要比静态条件下小,其侧向力系数和偏航力矩系数要比静态条件下大。导弹进行正、余弦控制时的偏航力矩系数大小要比不控时小。
2) 旋转效应是正、余弦控制方式旋转导弹产生侧向力的原因,并且鸭舵、尾翼产生的侧向力占主导地位。转速的变化对全弹法向力、侧向力特性以及鸭舵提供的法向力、侧向力影响相对较小。
3) 导弹做锥进运动时,合成迎角Г的变化对周期平均升力系数和侧向力系数影响较小,Г的变大会使周期平均偏航力系数数值和周期平均阻力系数数值变大。
| [1] |
陈成, 赵良玉, 谢浩怡. 单通道控制旋转弹角运动的复分析方法[J]. 兵工学报, 2021, 42(02): 308. CHEN Cheng, ZHAO Liangyu, XIE Haoyi. Complex analysis for angular motion of a spinning projectile with one pair of canards[J]. Acta Armamentarii, 2021, 42(02): 308. DOI:10.3969/j.issn.1000-1093.2021.02.009 |
| [2] |
王波兰, 李克勇, 杨永强. 近程/末端防御旋转导弹发展及关键技术综述[J]. 上海航天, 2017, 34(S1): 1. WANG Polang, LI Keyong, YANG Yongqiang. Review of development and key techniques of rolling airframe missiles[J]. Shanghai Aerospace, 2017, 34(S1): 1. |
| [3] |
YIN Jintao, WU Xiaosheng, LEI Juanmian. Body-fin interference on the Magnus effect of spinning projectile in supersonic flows[J]. Engineering Applications of Computational Fluid Mechanics, 2017, 11(1): 496. DOI:10.1080/19942060.2017.1319878 |
| [4] |
吴放, 王学德, 常思江, 等. 旋转尾翼弹马格努斯效应数值模拟[J]. 弹道学报, 2018, 30(01): 12. WU Fang, WANG Xuede, CHANG Sijiang, et al. Numerical simulation of Magnus effect of rotating tail projectiles[J]. Journal of Theoretical and Applied Mechanics, 2018, 30(01): 12. |
| [5] |
张超, 王学德, 王勇, 等. 低速旋转尾翼式弹箭气动特性数值研究[J]. 弹道学报, 2017, 29(04): 40. ZHANG Chao, WANG Xuede, WANG Yong, et al. Numerical study on aerodynamic characteristics of low-speed rotating fin projectile[J]. Journal of Ballistic Science, 2017, 29(04): 40. DOI:10.3969/j.issn.1004-499X.2017.04.007 |
| [6] |
YIN Jintao, WU Xiaosheng, LEI Juanmian, et al. Canards interference on the Magnus effect of a fin-stabilized spinning missile[J]. Advances in Mechanical Engineering, 2018, 10(7): 2072048174. |
| [7] |
COOPER G, FRESCONI F, COSTELLO M. Flight stability of an asymmetric projectile with activating canards[J]. Journal of Spacecraft and Rockets, 2012, 49(01): 130. DOI:10.2514/1.A32022 |
| [8] |
FRESCONI F, GUIDOS B, CELMINS I, et al. Flight behavior of an asymmetric missile through advanced characterization techniques[J]. Journal of Spacecraft and Rockets, 2017, 54(1): 266. DOI:10.2514/1.A33593 |
| [9] |
TOBAK M, SCHIFF L B, PETERSON V L. Aerodynamics of bodies of revolution in coning motion[J]. AIAA Journal, 1969, 7(1): 95. DOI:10.2514/3.5040 |
| [10] |
NICOLAIDES J D, INGRAM C W, CLARE T A. Investigation of the non-linear flight dynamics of ordnance weapons[J]. Journal of Spacecraft and Rockets, 1970, 7(10): 1241. DOI:10.2514/3.30141 |
| [11] |
卢天宇. 超声速下尾翼式旋转弹箭面外力和面外力矩数值研究[D]. 北京: 北京理工大学, 2018 LU Tianyu. Numerical study on surface force and out-of-plane torque of tail rotor projectile at supersonic speed[D]. Beijing: Beijing Institute of Technology, 2018 |
| [12] |
NYGAARD T A, MEAKIN R L. Aerodynamic analysis of a spinning missile with dithering canards[J]. Journal of Spacecraft and Rockets, 2004, 1(3): 154. |
| [13] |
AUMAN L, WINN G, HALL J. Wind tunnel investigation of a spinning missile with active canard control[C]//32nd Aerospace Sciences Meeting and Exhibit. Reno: AIAA, 1994
|
| [14] |
张超. 低速旋转弹箭气动特性计算与研究[D]. 南京: 南京理工大学, 2018 ZHANG Chao. Calculation and research on aerodynamic characteristics of low-speed rotating projectile[D]. Nanjing: Nanjing University of Science and Technology, 2018 |
 2022, Vol. 54
2022, Vol. 54


