随着信息技术的快速发展,现代战争形式发生巨大演变,对常规弹药的打击精度提出了更高要求,基于传统弹药改装而来的弹道修正弹便由此应运而生,并先后基于阻力器、脉冲发动机和鸭舵等执行机构衍生出多种修正弹类型[1-2]。固定鸭舵双旋弹正是基于鸭舵机构发展起来的一种新型弹道修正弹,其由滚动轴承将装有固定鸭舵的前体和高旋后体联接起来,通过一对差动舵产生的反转力矩使前体在弹丸发射后快速减旋,从而消除了弹体转速过快给姿态测量和机构动作造成的不利影响[3-4]。
20世纪70年代,Regan等[5]率先提出了双旋弹的概念并就其气动特性和弹道特性作了初步研究。此后国外相关机构和学者从动力学建模和控制特性分析等角度出发对双旋弹开展了大量研究,其中Costello等[6]在考虑前体与后体相互作用的基础上建立了双旋弹的动力学模型;法德圣路易斯研究所[7-9]在双旋弹风洞试验、弹道特性分析和控制系统设计等方面开展了系统研究;Jaemin等[10]基于神经网络技术提出了一种双旋弹自适应控制方法,并对其有效性进行了仿真分析。国内对双旋弹的研究起步较晚,郝永平等[11]和纪秀玲等[12]提出了固定翼双旋弹的修正模型并进行了气动特性分析;许诺等[13-14]利用角运动方程对固定鸭舵双旋弹的动力学特性进行了分析,并基于周期平均原理研究了其弹道修正方法;常思江等[15-16]分析了鸭舵式双旋弹的飞行原理,对其强迫角运动和在重力及鸭舵控制力作用下的动态响应规律作了研究;张鑫等[17]基于对修正组件电气系统和机械系统的分析,建立了滚转通道控制模型。关于双旋弹的飞行稳定性问题,近年来相关学者主要围绕其动态稳定性展开研究。其中,Zhu等[18]利用Hurwitz方法研究了该类弹丸的动态稳定性条件;马国梁等[19-20]在考虑前体滚转角任意时变时,基于范数概念提出了固定鸭舵双旋弹的绝对稳定性判据,并对其控制效果作了分析。但是对于动态稳定的弹丸,攻角过大也会使其飞行特性变差,特别是对固定鸭舵双旋弹,在考虑鸭舵控制时,复攻角的幅值始终较大,且最大值不再仅由复动力平衡角决定,因此有必要在理解舵面控制力对弹丸角运动影响的基础上,就其控制稳定性作进一步研究。
本文沿袭常规旋转稳定弹的稳定性分析方法,拟对固定鸭舵双旋弹的角运动特性和控制稳定性展开研究。首先在增加舵面控制力和力矩的条件下,通过建立固定鸭舵双旋弹的复攻角运动方程并对其求解,从理论上直观阐述固定鸭舵双旋弹起控后复攻角运动的形成机理。据此,基于攻角的幅值有限性条件提出该类弹丸的控制稳定性条件,并给出复控制平衡角幅值允许限的确定方法,所得结果对该类弹丸的稳定性分析与设计具有工程实践参考意义。最后通过弹道数值计算对起控后复攻角运动形成机理和控制稳定性条件的合理性进行验证;通过讨论前体滚转角与复扰动攻角和复偏角运动的相位关系,分析固定鸭舵双旋弹弹道修正的力学本质,解释其在相同控制条件下沿不同方向的弹道修正能力并不完全相等的原因。
1 弹道建模 1.1 基本假设如图 1所示,固定鸭舵双旋弹的修正执行机构位于弹丸前体,由两对固定舵面组成。其中一对同向布置的固定舵为操纵舵面,提供弹道修正所需的控制力和力矩,舵偏角为δD;一对反向布置的差动舵为减旋舵面,用于产生反转力矩使前体在弹丸发射后转速下降,斜置角为δF。
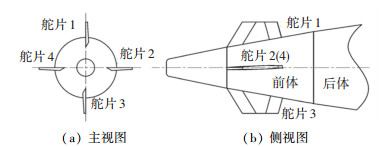
|
图 1 固定鸭舵结构示意图 Fig. 1 Configuration of fixed canard |
无控飞行时, 前体在反转力矩作用下会快速减旋到某一平衡转速[16],其值通常较小(为几转每秒),这样由前体产生的陀螺效应和马格努斯效应较弱,一般可以忽略。因此为简化问题,将舵偏角为零时由攻角产生的舵面力合并到弹体气动力中,固定鸭舵双旋弹在弹道飞行中所受的空气动力和力矩包括由高旋弹体产生的力和力矩以及由固定鸭舵产生的力和力矩两部分。
1.2 坐标系定义及转换为便于对作用在固定鸭舵双旋弹上的力和力矩进行分析,本文引入的正交直角坐标系包括:基准坐标系OxNyNzN(N)、弹道坐标系Ox2y2z2(V)、弹轴坐标系Oξηζ(A)、第二弹轴坐标系Oξη2ζ2(A2)、弹体坐标系Ox1y1z1(B)和前体坐标系OFxFyFzF(F)。其中前体坐标系由弹轴坐标系绕Oξ轴向右旋转γD角而来,二者间的转换矩阵为
| $ {\mathit{\boldsymbol{L}}_{{\rm{FA}}}} = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&{\cos {\gamma _{\rm{D}}}}&{\sin {\gamma _{\rm{D}}}}\\ 0&{ - \sin {\gamma _{\rm{D}}}}&{\cos {\gamma _{\rm{D}}}} \end{array}} \right] $ | (1) |
其它坐标系的定义和转换关系详见文献[21]。
1.3 弹体空气动力和力矩考虑到弹丸所受空气动力和力矩依据弹丸相对空气的速度进行计算,在此给出考虑风速w时相对速度的表达式为
| $ \boldsymbol{v}_{r}=\boldsymbol{v}-\boldsymbol{w} $ | (2) |
为便于确定空气动力和力矩矢量的方向,在此引入相对攻角平面和相对攻角的概念[21]。旋转稳定弹的相对攻角一般为一小量,其计算方法为
| $ \alpha_{r}=\arccos \left(\boldsymbol{v}_{r} \cdot \boldsymbol{\xi} / v_{r}\right) $ | (3) |
式中:vr= |vr|,ξ为Oξ轴上的单位向量。
1.3.1 弹体空气动力忽略较小的马格努斯力对质心运动的影响,可以将作用在弹体上的空气动力在相对攻角平面内分解为沿速度反方向的阻力和垂直于速度且在弹轴一侧的升力,得到弹体空气动力的矢量表达式为
| $ \left\{\begin{array}{l} \boldsymbol{F}_{x}=\frac{1}{2} \rho S c_{x} v_{r}\left(-\boldsymbol{v}_{r}\right) \\ \boldsymbol{F}_{y}=\frac{1}{2} \rho S c_{y} \boldsymbol{v}_{r} \times\left(\boldsymbol{\xi} \times \boldsymbol{v}_{r}\right) / \sin \alpha_{r} \end{array}\right. $ | (4) |
式中:ρ为空气密度,取炮兵标准气象条件;S=πd2/4为特征面积,d为弹径;cx=cx0 1+k1αr2为弹体阻力系数,cx0和k1分别是弹体零升阻力系数和诱导阻力系数;cy为弹体升力系数,小攻角下取c′yδr,c′y为弹体升力系数对攻角的导数。
1.3.2 弹体空气动力矩忽略气动偏心和动不平衡,旋转稳定弹在飞行过程中受到的空气动力矩主要包括:翻转力矩、赤道阻尼力矩、极阻尼力矩和马格努斯力矩,其表达式分别为
| $ \left\{\begin{array}{l} \boldsymbol{M}_{z}=\frac{1}{2} \rho v_{r} {Slm}^{\prime}{}_{z}\left(\boldsymbol{v}_{r} \times \boldsymbol{\xi}\right) / \sin \alpha_{r} \\ \boldsymbol{M}_{z z}=-\frac{1}{2} \rho v_{r} {Sldm}^{\prime}{}_{zz} \boldsymbol{\omega}_{1} \\ \boldsymbol{M}_{x z}=-\frac{1}{2} \rho v_{r} {Sldm}^{\prime}{}_{x z} \omega_{\xi} \boldsymbol{\xi} \\ \boldsymbol{M}_{y}=\frac{1}{2} \rho {Sld} \omega_{\xi} m_{y}^{\prime \prime} \delta_{r} \boldsymbol{\xi} \times\left(\boldsymbol{\xi} \times \boldsymbol{v}_{r}\right) / \sin \alpha_{r} \end{array}\right. $ | (5) |
式中:l为弹长;ω1为弹轴摆动角速度;ωξ≈
将舵偏角为零时由攻角产生的舵面力合并到弹体气动力中,一对操纵舵由舵偏角引起的舵面升力指向OFyF轴,其表达式为
| $ F_{\delta_{\mathrm{D}} y_{\mathrm{F}}}=\frac{1}{2} \rho v_{r}^{2} S c^{\prime}{}_{y \delta} \delta_{\mathrm{D}} $ | (6) |
式中c′yδ为一对操纵舵升力系数导数。
考虑弹丸质心运动是在弹道坐标系下进行分析的,利用前体坐标系到弹道坐标系的转换矩阵LVF将一对操纵舵由舵偏角引起的舵面升力投影到弹道坐标系下,其矩阵形式为
| $ \left[\begin{array}{lll} F_{\delta_{\mathrm{D}} x_2} & F_{\delta_{\mathrm{D}} y_2} & F_{\delta_{\mathrm{D}} z_2} \end{array}\right]^{\mathrm{T}}=\boldsymbol{L}_{\mathrm{VF}}\left[\begin{array}{lll} 0 & F_{\delta_{\mathrm{D}} y_{\mathrm{F}}} & 0 \end{array}\right]^{\mathrm{T}} $ | (7) |
将上式展开,等号左边各参数的表达式分别为
| $ \begin{gathered} F_{\delta_{\mathrm{D}} x_{2}}=F_{\delta_{\mathrm{D}} y_{\mathrm{F}}} \cos \gamma_{\mathrm{D}}\left(-\sin \alpha \cos \gamma_{\mathrm{A}}+\sin \beta \cos \alpha \sin \gamma_{\mathrm{A}}\right)+ \\ F_{\delta_{\mathrm{D}} y_{\mathrm{F}}} \sin \gamma_{\mathrm{D}}\left(-\sin \alpha \sin \gamma_{\mathrm{A}}-\sin \beta \cos \alpha \cos \gamma_{\mathrm{A}}\right) \\ F_{\delta_{\mathrm{D}} y_{2}}=F_{\delta_{\mathrm{D}} y_{\mathrm{F}}} \cos \gamma_{\mathrm{D}}\left(\cos \alpha \cos \gamma_{\mathrm{A}}+\sin \beta \sin \alpha \sin \gamma_{\mathrm{A}}\right)+ \\ F_{\delta_{\mathrm{D}} y_{\mathrm{F}}} \sin \gamma_{\mathrm{D}}\left(\cos \alpha \sin \gamma_{\mathrm{A}}-\sin \beta \sin \alpha \cos \gamma_{\mathrm{A}}\right) \\ F_{\delta_{\mathrm{D}} z_{2}} =F_{\delta_{\mathrm{D}} y_{\mathrm{F}}} \left(\sin \gamma_{\mathrm{D}} \cos \beta \cos \gamma_{\mathrm{A}}-\cos \gamma_{\mathrm{D}} \cos \beta \sin \gamma_{\mathrm{A}}\right) \end{gathered} $ |
式中α、β和γA均为小量,分别表示高低攻角、方向攻角和弹轴坐标系相对第二弹轴坐标系的滚转角。忽略其中小量影响,化简得到
| $ F_{\delta_{\mathrm{D}} x_{2}}=0, F_{\delta_{\mathrm{D}} y_{2}}=F_{\delta_{\mathrm{D}} y_{\mathrm{F}}} \cos \gamma_{\mathrm{D}}, F_{\delta_{\mathrm{D}} z_2}=F_{\delta_{\mathrm{D}} y_{\mathrm{F}}} \sin \gamma_{\mathrm{D}} $ | (8) |
式中:FδDy2和FδDz2合力等于FδDyF,记为舵面控制力;γD为控制方向。
设舵面压心到弹丸质心的距离为LD,一对操纵舵产生的控制力矩指向OFzF轴,其在弹轴坐标系下的分量形式为
| $ \left[ {\begin{array}{*{20}{c}} {{M_{{\delta _{\rm{D}}}\xi }}}\\ {{M_{{\delta _{\rm{D}}}\eta }}}\\ {{M_{{\delta _{\rm{D}}}\zeta }}} \end{array}} \right] = \mathit{\boldsymbol{L}}_{{\rm{FA}}}^{ - 1}\left[ {\begin{array}{*{20}{c}} 0\\ 0\\ {{F_{{\delta _{\rm{D}}}{y_{\rm{F}}}}}{L_{\rm{D}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0\\ { - {F_{{\delta _{\rm{D}}}{y_{\rm{F}}}}}{L_{\rm{D}}}\sin {\gamma _{\rm{D}}}}\\ {{F_{{\delta _{\rm{D}}}{y_{\rm{F}}}}}{L_{\rm{D}}}\cos {\gamma _{\rm{D}}}} \end{array}} \right] $ | (9) |
一对差动舵以斜置角δF反向安装,由其产生的舵面升力合力为零,但是会形成沿弹轴方向的反转力矩,其表达式为
| $ M_{x \delta_{\mathrm{F}} \xi}=\frac{1}{2} \rho v_{r}^{2} {Slm}^{\prime}{}_{x \delta_{\mathrm{F}}} \delta_{\mathrm{F}} $ | (10) |
式中,m′xδ为一对差动舵的反转力矩系数导数。
在一对差动舵作用下,弹丸前体减旋后与后体发生相对转动,使弹体受到沿弹轴方向的滚转阻尼力矩作用,其表达式为
| $ M_{xz \delta _{\mathrm{F}} \xi}=C_{\mathrm{FA}}\left(\omega_{\xi \delta_{\mathrm{F}}}-\omega_{\xi}\right) $ | (11) |
式中:CFA为折算了前体与后体相对滚转角运动摩擦影响的阻尼力矩系数;ωξδF为前体滚转角速度。
1.5 七自由度刚体弹道方程为了能够对固定鸭舵双旋弹起控后的弹道特性和角运动特性进行准确描述,根据牛顿第二定律和动量矩定理,分别在弹道坐标系和弹轴坐标系下对弹丸的质心运动和绕质心运动进行分析,并补充前体滚转角运动方程,建立固定鸭舵双旋弹的七自由度刚体弹道方程为
| $ \left\{\begin{array}{l} \dot{v}=\left(F_{x_{2}}+F_{\delta_{\mathrm{D}} x_{2}}-m g \sin \theta_{\mathrm{a}} \cos \psi_{2}\right) / m \\ \dot{\theta}_{\mathrm{a}}=\frac{1}{m v \cos \psi_{2}}\left(F_{y_{2}}+F_{\delta_{\mathrm{D}} y_{2}}-m g \cos \theta_{\mathrm{a}}\right) \\ \dot{\psi}_{2}=\frac{1}{m v}\left(F_{z_{2}}+F_{\delta_{\mathrm{D}} z_{2}}+m g \sin \theta_{\mathrm{a}} \sin \psi_{2}\right) \\ \dot{x}=v \cos \psi_{2} \cos \theta_{\mathrm{a}}, \dot{y}=v \cos \psi_{2} \sin \theta_{\mathrm{a}}, \dot{z}=v \sin \psi_{2} \\ \dot{\omega}_{\xi}=\left(M_{\xi}+M_{x z \delta_{\mathrm{F}} \xi}\right) / C\\ \dot{\omega}_{\eta}=\left(M_{\eta}+M_{\delta_{\mathrm{D}} \eta}\right) / A-\frac{C}{A} \omega_{\xi} \omega_{\zeta}+\omega_{\zeta}^{2} \tan \varphi_{2} \\ \dot{\omega}_{\zeta}=\left(M_{\zeta}+M_{\delta_{\mathrm{D} }\zeta}\right) / A-\frac{C}{A} \omega_{\eta} \omega_{\xi}-\omega_{\eta} \omega_{\zeta} \tan \varphi_{2} \\ \dot{\varphi}_{\mathrm{a}}=\omega_{\zeta} / \cos \varphi_{2}, \dot{\varphi}_{2}=-\omega_{\eta}, \dot{\gamma}=\omega_{\xi}-\omega_{\zeta} \tan \varphi_{2} \\ \dot{\omega}_{\xi\delta_{\mathrm{F}}}=\left(M_{x \delta_{\mathrm{F} }\xi}-M_{xz \delta_{\mathrm{F}} \xi}\right) / C_{\mathrm{F}}, \dot{\gamma}_{\mathrm{D}}=\omega_{\xi \delta_{\mathrm{F}}} \end{array}\right. $ | (12) |
式中:g为重力加速度;C和A分别为弹体极转动惯量和赤道转动惯量;CF为前体极转动惯量。
2 角运动分析与控制稳定性条件 2.1 角运动几何描述基于外弹道基本假设,用下标i表示理想弹道参数,得到理想弹道方程组为
| $ \left\{\begin{array}{l} \dot{v}_{i}=-0.5 \rho v_{i}^{2} S c_{x} / m-g \sin \theta_{i} \\ \dot{\theta}_{i}=-g \cos \theta_{i} / v_{i} \\ \dot{x}_{i}=v_{i} \cos \theta_{i}, \dot{y}_{i}=v_{i} \sin \theta_{i} \end{array}\right. $ | (13) |
式中,θi为理想弹道倾角,后文简写为θ。
假设固定鸭舵双旋弹的七自由度刚体弹道与理想弹道偏差较小,即认为其角运动也在理想弹道附近进行。引入复数平面对其角运动进行描述,可以定义以下复数:
| $ \boldsymbol{\varPhi}=\varphi_{1}+i \varphi_{2}, \boldsymbol{\varPsi}=\psi_{1}+i \psi_{2}, \boldsymbol{\varDelta}=\alpha+i \beta $ | (14) |
式中:Φ为复摆动角,Ψ为复偏角,分别描述七自由度刚体弹道中弹轴和速度矢量相对于理想弹道切线的空间方位;Δ为复攻角,描述弹轴相对于速度矢量的空间方位;φ1, φ2, ψ1, ψ2, α, β均为小量。
2.2 复攻角运动方程旋转稳定弹的角运动变化非常迅速,在一段弹道上忽略其它量变化,基于小量假设可取近似关系:
| $ \left\{\begin{array}{l} v_{i}=v_{r}=v_{r \xi}=v_{r x_{2}} \approx v, \\ \alpha_{r} / \sin \alpha_{r}=1, \theta_{\mathrm{a}}=\theta, \\ \dot{\varphi}_{\mathrm{a}}=\omega_{\zeta}, \dot{\varphi}_{2}=-\omega_{\eta}, \dot{\gamma}=\omega_{\xi} \end{array}\right. $ | (15) |
将上式代入方程(12)中2~3式和7~9式,再利用方程(13)消去其中
| $ \dot{\boldsymbol{\varPsi}}=\left(b_{x}+b_{y}\right) \boldsymbol{w}_{\perp}+b_{y} v \boldsymbol{\varDelta}+\frac{g}{v} \sin \theta \boldsymbol{\varPsi}+\frac{F_{\delta_{\mathrm{D}} y_{\mathrm{F}}}}{m v} e^{i \gamma_{\mathrm{D}}} $ | (16) |
| $ \begin{aligned} \ddot{\boldsymbol{\varPhi}}+&\left(k_{z z} v-i \frac{C}{A} \dot{\gamma}\right) \boldsymbol{\varPhi}-\left(k_{z} v^{2}-i k_{y} v \dot{\gamma}\right)\left(\boldsymbol{\varDelta}+\frac{\boldsymbol{w}_{\perp}}{v}\right)=\\ &-\ddot{\theta}+\left(i \frac{C}{A} \dot{\gamma}-k_{z z} v\right) \dot{\theta}+\frac{1}{A} F_{\delta_{\mathrm{D}} y_{\mathrm{F}}} L_{\mathrm{D}} e^{i \gamma_{\mathrm{D}}} \end{aligned} $ | (17) |
式中:w⊥=wy2+iwz2,bx=0.5ρScx/m,by=0.5ρSc′y/m,kzz=0.5ρSldm′zz/A,kz=0.5ρSlm′z/A,ky=0.5ρSldm′y/A。
根据定义Δ=Φ-Ψ,利用常规旋转稳定弹复攻角方程的建立方法[21],忽略高阶小量,化简得到固定鸭舵双旋弹以时间t为自变量的复攻角方程为
| $ \begin{aligned} &\ddot{\boldsymbol{\varDelta}}+\left(b_{y} v+k_{zz} v-i \frac{C}{A} \dot{\gamma}\right) \dot{\boldsymbol{\varDelta}}-\left[k_{z} v^{2}+i\left(\frac{C}{A} \dot{\gamma} b_{y} v-\dot{\gamma} k_{y} v\right)\right] \boldsymbol{\varDelta}= \\ &\quad-\ddot{\theta}+\left(i \frac{C}{A} \dot{\gamma}-k_{z z} v\right) \dot{\theta}+\\ &\quad{\left[\left(k_{z} v-i k_{y} \dot{\gamma}\right)+i \frac{C}{A} \dot{\gamma}\left(b_{x}+b_{y}\right)\right] \boldsymbol{w}_{\perp}+} \\ &\quad\left(\frac{m v L_{\mathrm{D}}}{A}-k_{zz} v-b_{x} v-\frac{g \sin \theta}{v}+i \frac{C \dot{\gamma}}{A}\right) \frac{F_{\delta_{\mathrm{D}} y_{\mathrm{F}}}}{m v} e^{i \gamma_{\mathrm{D}}} \end{aligned} $ | (18) |
利用
| $ \boldsymbol{\varDelta}^{\prime \prime}+(H-i P) \boldsymbol{\varDelta}^{\prime}-(M+i P T) \boldsymbol{\varDelta}=\boldsymbol{G}+\boldsymbol{F}+\boldsymbol{W} $ | (19) |
式中,G, F, W项分别表示重力、舵面控制力和横风对复攻角运动的影响,其余各项与常规旋转稳定弹复攻角方程含义一致。推导得到各项表达式分别为
| $ \begin{gathered} H=k_{z z}+b_{y}-b_{x}-\frac{g \sin \theta}{v^{2}}, P=\frac{C \dot{\gamma}}{A v}, M=k_{z} \\ T=b_{y}-\frac{A}{C} k_{y}, \boldsymbol{G}=-\frac{\ddot{\theta}}{v^{2}}-\left(k_{z z}-i P\right) \frac{\dot{\theta}}{v} \\ \boldsymbol{W}=\left[k_{z}+i\left(b_{x}+b_{y}-\frac{A}{C} k_{y}\right) P\right] \frac{\boldsymbol{w}_{\perp}}{v} \\ \boldsymbol{F}=\left(\frac{m L_{\mathrm{D}}}{A}-k_{z z}-b_{x}-\frac{g \sin \theta}{v^{2}}+i \frac{C \dot{\gamma}}{A v}\right) \frac{F_{\delta_{\mathrm{D}} y_{\mathrm{F}}}}{m v^{2}} e^{i \gamma_{\mathrm{D}}} \end{gathered} $ |
假设在某一小段弹道上,上述系数变化较小可近似为常数,则方程(19)变为线性常系数非齐次方程。
2.3 固定鸭舵控制下复攻角方程的解固定鸭舵双旋弹进行弹道修正时,通过控制前体滚转角来改变舵面控制力和力矩的方向。不考虑横风影响,根据方程(19)可知包含重力项和舵面控制力项的线性非齐次复攻角方程为
| $ \boldsymbol{\varDelta}^{\prime \prime}+(H-i P) \boldsymbol{\varDelta}^{\prime}-(M+i P T) \boldsymbol{\varDelta}=\boldsymbol{F}+\boldsymbol{G} $ | (20) |
方程的解为
| $ \boldsymbol{\varDelta}=C_{1} e^{l_{1^{s}}}+C_{2} e^{l_{2^{s}}}+\boldsymbol{\varDelta}_{\mathrm{F}}+\boldsymbol{\varDelta}_{\mathrm{G}} $ | (21) |
式中:前两项为齐次方程的通解,描述了复攻角的自由角运动,l1, 2=λ1, 2+iϕ1, 2是特征方程的根,C1, 2是由起始条件决定的待定常数;后两项分别为舵面控制力和重力引起的非齐次方程的特解,描述了复攻角的强迫角运动,即复平衡攻角的变化规律。
依据弹箭飞行稳定性基本原理,对于动态稳定的弹丸,由起始条件决定的自由角运动会逐渐衰减为零。因此在起控前,固定鸭舵双旋弹的复攻角运动主要由重力引起的强迫角运动决定,数值上约为ΔG;起控后,复平衡攻角在舵面控制力和重力综合作用下变为(ΔF+ΔG)。易见,在开始控制的瞬间,复攻角与复平衡攻角之间出现差值
| $ \boldsymbol{\varDelta}_{\tau}=-\boldsymbol{\varDelta}_{\mathrm{F}} $ | (22) |
将Δτ记为由ΔF引起的起始扰动,起控后固定鸭舵双旋弹的复攻角运动是由起始扰动产生的自由角运动和复平衡攻角综合作用的结果。
现将起控时的弹道点记为s=0,分别对固定鸭舵双旋弹起控后复攻角运动的自由角运动和强迫角运动进行求解。
2.3.1 自由角运动由于舵面控制力仅作用于复攻角方程的非齐次项,因此可以直接给出式(20)齐次方程的特征根为
| $ l_{1,2}=\left[-H+i P \pm \sqrt{4 M+H^{2}-P^{2}+2 i P(2 T-H)}\right] / 2 $ | (23) |
整理得到分离实部和虚部后的形式为
| $ \left\{\begin{array}{l} \lambda_{1,2}=\frac{1}{2}\left(-H \pm \sqrt{\left.\left(\alpha^{*}+\sqrt{\alpha^{* 2}+\beta^{* 2}}\right) / 2\right)}\right. \\ \phi_{1,2}=\frac{1}{2}\left(P \pm \sqrt{\left.\left(\alpha^{*}+\sqrt{\alpha^{* 2}+\beta^{* 2}}\right) / 2\right)}\right. \end{array}\right. $ | (24) |
式中:α*=4M+H2-P2,β*=2P(2T-H)。
将l1, 2代入式(21)的前两项,由起始条件Δτ=-ΔF和Δ′τ=0可以确定
| $ C_{1,2}=-\frac{\lambda_{2,1}+i \omega_{2,1}}{\left(\lambda_{1,2}-\lambda_{2,1}\right)+i\left(\omega_{1,2}-\omega_{2,1}\right)} \boldsymbol{\varDelta}_{\tau} $ | (25) |
因此由Δτ引起的自由角运动的解为
| $ \boldsymbol{\varDelta}_{0}=C_{1} e^{l_{1} s}+C_{2} e^{l_{2} s} $ | (26) |
利用常数变易法对固定鸭舵双旋弹的强迫角运动进行求解,可以假设特解ΔG和ΔF仍有式(26)的形式,其中C1, 2变为弧长s的待定函数。
首先将ΔG代入包含重力项的非齐次复攻角方程,并补充限定条件C′1el1s+C′2el2s=0,在零起始条件下求得
| $ C_{1,2}(s)=\pm \frac{1}{l_{1}-l_{2}}\left[\frac{\ddot{\theta}}{l_{1,2} v^{2}}+\frac{\left(k_{z z}-i P\right)}{l_{1,2} v}\left(\dot{\theta}+\frac{\ddot{\theta}}{l_{1,2} v}\right)\right] e^{-l_{{1,2}}s} $ | (27) |
式中,
| $ \begin{array}{r} -(M+i P T) \boldsymbol{\varDelta}_{\mathrm{G}}=-\frac{\ddot{\theta}}{v^{2}}-\frac{\left(k_{z z}-i P\right)}{v} \times \\ \left(\dot{\theta}+\frac{H-i P}{M+i P T} \frac{\ddot{\theta}}{v}\right) \end{array} $ | (28) |
此式表明,由攻角ΔG产生的翻转力矩与
由于P2T2
| $ \boldsymbol{\varDelta}_{\mathrm{G}}=\frac{a+i b}{M+i P T} $ | (29) |
式中:
对式(29)进行变换,使分母实数化,得到由重力引起的强迫角运动的解为
| $ \boldsymbol{\varDelta}_{\mathrm{G}}=\frac{\sqrt{(a M+b P T)^{2}+(b M-a P T)^{2}}}{M^{2}} \mathrm{e}^{i \varphi_{\mathrm{G}}} $ | (30) |
式中
由于bM-aPT
同理,利用常数变易法对舵面控制力引起的强迫角运动进行求解,得到ΔF满足关系式
| $ \begin{aligned} &-(M+i P T) \boldsymbol{\varDelta}_{\mathrm{F}}=\frac{F_{\delta_{\mathrm{D} }y_{\mathrm{F}}}}{m v^{2}} \mathrm{e}^{i \gamma_{\mathrm{D}}} \times\left[\frac{m L_{\mathrm{D}}}{A}-k_{z z}-b_{x}-\right. \\ &\left.\frac{g}{v^{2}}\left(\sin \theta+\frac{H-i P}{M+i P T} \frac{\cos \theta \dot{\theta}}{v}\right)+i \frac{C \dot{\gamma}}{A v}\right] \end{aligned} $ | (31) |
此式表明,由攻角ΔF产生的翻转力矩与FδDyF产生的控制力矩相平衡,故称ΔF为复控制平衡角。
为书写方便,引入符号
| $ \begin{gathered} c=\frac{m L_{\mathrm{D}}}{A}-k_{z z}-b_{x}-\frac{g \sin \theta}{v^{2}}-\frac{P^{2} T g \cos \theta \dot{\theta}}{M^{2} v^{3}}, \\ d=\frac{C {\dot{\gamma}}}{A v}+\frac{P g \cos \theta \dot{\theta}}{M v^{3}}, K_{\delta_{\mathrm{D}}}=\frac{F_{\delta_{\mathrm{D}} y_{\mathrm{F}}}}{m v^{2}} \end{gathered} $ |
式(31)进行变换,使分母实数化,得到由舵面控制力引起的强迫角运动的解为
| $ \boldsymbol{\varDelta}_{\mathrm{F}}=\frac{\sqrt{(c M+d P T)^{2}+(d M-c P T)^{2}}}{M^{2}} K_{\delta_{\mathrm{D}}} \mathrm{e}^{i\left(\gamma_{\mathrm{D}}+{\rm{ \mathsf{ π} }}+\varphi_{\mathrm{F}}\right)} $ | (32) |
式中
由于d
至此,得到重力和控制力引起的非齐次方程的特解ΔG和ΔF。将Δτ=-ΔF代入式(25)~(26),可以求得固定鸭舵双旋弹起控后的自由角运动Δ0,其为典型的二圆运动,对于动态稳定的弹丸随弧长逐渐衰减;ΔG和ΔF叠加组成固定鸭舵双旋弹起控后的强迫角运动,反映了复平衡攻角,即自由角运动的中心在复数平面上的变化规律;将自由角运动与强迫角运动叠加即为起控后复攻角运动的完整解析解。
2.4 控制稳定性条件根据对固定鸭舵双旋弹起控后复攻角运动形成机理的分析可知,要使固定鸭舵双旋弹满足动态稳定性条件,必须使起始扰动产生的自由角运动收敛,即要求特征根的实部均小于0。根据式(23)和(24)可知,起控前动态稳定的双旋弹满足λ1, 2 < 0,表明固定鸭舵引起的M项和T项增量均不超过某一界限值。同时,为保证起控后固定鸭舵双旋弹在飞行过程中攻角较小,还须满足攻角的幅值有限性条件,根据式(25)和(26)可知,即保证起始攻角不宜过大,这就要求对Δτ的幅值进行限制。
由于Δτ=-ΔF,且根据式(31)可知,舵面控制力幅值越大,同一弹道点上对应的控制力矩就越大,在弹体气动特性一定的条件下控制平衡角就越大。因此,为了使固定鸭舵双旋弹起控后具有良好的控制稳定性,必须限制复控制平衡角的幅值。根据式(32),复控制平衡角的幅值为
| $ \left|\boldsymbol{\varDelta}_{\mathrm{F}}\right|=\frac{\sqrt{(c M+d P T)^{2}+(d M-c P T)^{2}}}{M^{2}} K_{\delta_{\mathrm{D}}} $ | (33) |
定义αDm为复控制平衡角的幅值允许限,固定鸭舵双旋弹的控制稳定性条件可以写为
| $ \left|\boldsymbol{\varDelta}_{\mathrm{F}}\right|_{\max }<\alpha_{\mathrm{Dm}} $ | (34) |
由于复动力平衡角在弹道顶点附近达到最大,故在弹道顶点附近起控时,αDm的取值应满足关系式
| $ \alpha_{\mathrm{Dm}}+\alpha_{\mathrm{Pm}}<\alpha_{\max } $ | (35) |
式中: αPm为弹道顶点处复动力平衡角的幅值;αmax为复攻角幅值的允许限,一般取12°~15°。
3 弹道数值计算分析 3.1 计算条件本文以某155 mm固定鸭舵双旋弹作为研究对象,在炮兵标准气象条件下进行弹道数值计算分析,弹丸主要物理参数如表 1所示。仿真条件设为:初速v0=930 m/s,初始转速
| 表 1 弹丸物理参数 Tab. 1 Physical parameters of projectile |
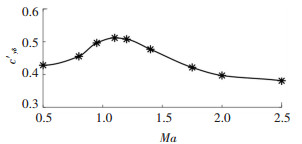
|
图 2 固定鸭舵升力系数导数 Fig. 2 Lift coefficient derivative of fixed canard |
基于上述计算条件,利用建立的七自由度刚体弹道方程对全弹道无控飞行时的某155 mm固定鸭舵双旋弹进行弹道仿真,并与利用经典六自由度刚体弹道方程对常规旋转稳定弹的弹道仿真结果进行比较,图 3给出了二者的复攻角运动曲线。
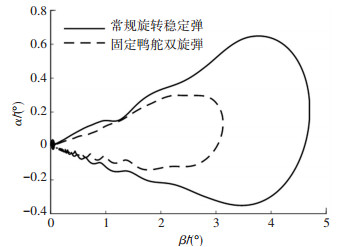
|
图 3 无控飞行时复攻角运动曲线 Fig. 3 Curves of complex attack angle motion in uncontrolled flight |
对于动态稳定的弹丸,自由角运动在弹道初始段已经逐渐衰减为零,因此图 3中曲线近似为复动力平衡角运动曲线。结果表明:无控飞行时固定鸭舵双旋弹复攻角的幅值小于常规旋转稳定弹。分析式(30)可知,这主要与合并到弹体上的舵面力使翻转力矩显著增大有关,图 4给出的翻转力矩项M随弹道弧长的变化曲线验证了这一结论。

|
图 4 翻转力矩项变化曲线 Fig. 4 Curves of overturning moment term |
根据式(23)可知,翻转力矩增大必然使弹丸动态稳定性降低,这为前文基于动态稳定性条件提出固定鸭舵双旋弹的控制稳定性条件提供了依据。
3.2.2 起控后固定鸭舵对复攻角运动的影响根据前文分析,起控后固定鸭舵对复攻角运动的影响主要体现在复控制平衡角运动及其引起的自由角运动两个方面。考虑到弹丸在42 s时到达弹道顶点附近,图 5和图 6给出了T0=42 s,前体滚转角分别取0°, 90°, 180°和270°时,固定鸭舵双旋弹从开始控制到弹道结束时复攻角运动的解析解。

|
图 5 起控后复控制平衡角运动曲线 Fig. 5 Curves of complex control equilibrium attack angle motion after the control starts |
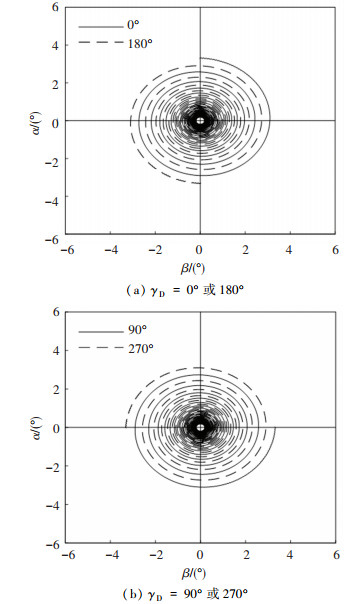
|
图 6 起控后自由角运动曲线 Fig. 6 Curves of free attack angle motion after the control starts |
图 5为起控后复控制平衡角运动曲线,结果表明:1)复控制平衡角的相位与前体滚转角相差约180°,偏差值较小;2)相较于复动力平衡角的变化量来说,复控制平衡角的幅值和相位基本保持不变,故可以近似为一常量。
图 6为复控制平衡角引起的自由角运动曲线。当前体滚转角取不同值时,自由角运动随弹道弧长逐渐衰减的趋势和频率基本保持一致,在复数平面内的起始位置由复控制平衡角决定,值为-ΔF。
由于舵面控制力对复动力平衡角不产生影响,因此可以认为起控后固定鸭舵对复攻角运动的影响是复控制平衡角和自由角运动的叠加,定义为复扰动攻角。图 7给出了前体滚转角分别取0°, 90°, 180°和270°时的复扰动攻角运动曲线,其在复数平面上是以复控制平衡角为中心的二圆运动,其中快圆运动很快衰减为零,慢圆运动逐渐收敛于ΔF,幅值最大值约为2|ΔF|。

|
图 7 起控后复扰动攻角运动曲线 Fig. 7 Curves of complex disturbance attack angle motion after the control starts |
将复扰动攻角与复动力平衡角叠加,图 8给出了前体滚转角分别取0°, 90°, 180°和270°时固定鸭舵双旋弹起控制后完整的复攻角运动曲线。可以看到,通过解析法求得的复攻角运动与数值计算结果在频率和幅值上基本吻合,表明前文对固定鸭舵双旋弹起控后复攻角运动形成机理的分析具有一定合理性,为建立固定鸭舵双旋弹的控制稳定性条件提供了理论依据。
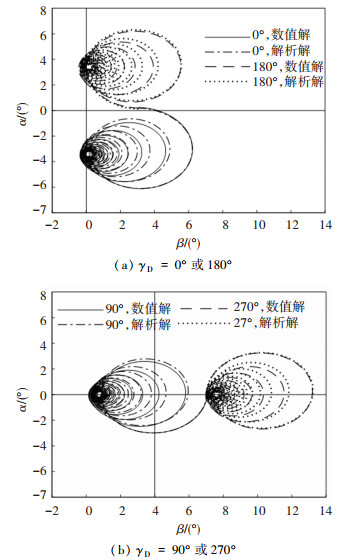
|
图 8 起控后复攻角运动曲线 Fig. 8 Curves of complex attack angle motion after the control starts |
为了分析固定鸭舵双旋弹弹道修正的力学本质,对复偏角方程(16)进行求解,当仅考虑舵面控制力和最大的升力项时,简化得到由舵面控制力和复扰动攻角产生的复偏角方程为
| $ \Delta \varPsi^{\prime}=\frac{F_{\delta_{\mathrm{D}} y_{\mathrm{F}}}}{m v^{2}} e^{i \gamma_{\mathrm{D}}}+b_{y}\left(\boldsymbol{\varDelta}_{\mathrm{F}}+\boldsymbol{\varDelta}_{0}\right) $ | (36) |
基于周期平均原理忽略Δ0的影响,再根据φF≈0可以在小扰动假设下对上式积分得到
| $ \Delta \varPsi=s \cdot(K-1) K_{\delta_{\mathrm{D}}} e^{i\left(\gamma_{\mathrm{D}}+{\rm{ \mathsf{ π} }}\right)} $ | (37) |
式中,
将ΔΨ代入方程(12)的4~6式,得到由ΔΨ引起的惯性空间内各速度分量的增量形式为
| $ \left\{\begin{array}{l} \varDelta \dot{x}=\cos \left(\psi_{2}+\varDelta \psi_{2}\right) \cos \left(\theta_{\mathrm{a}}+\varDelta \psi_{1}\right)-\cos \psi_{2} \cos \theta_{\mathrm{a}} \\ \varDelta \dot{y}=\cos \left(\psi_{2}+\varDelta \psi_{2}\right) \sin \left(\theta_{\mathrm{a}}+\varDelta \psi_{1}\right)-\cos \psi_{2} \sin \theta_{\mathrm{a}} \\ \varDelta \dot{z}=\sin \left(\psi_{2}+\varDelta \psi_{2}\right)-\sin \psi_{2} \end{array}\right. $ | (38) |
式(37)~(38)表明:当前体滚转角固定不变时,复偏角会向与前体滚转角近似相反的方向发生偏转,使弹丸质心运动受到影响,从而实现弹道修正。
根据ψ1=θa-θ,图 9给出了γD分别取0°, 90°, 180°和270°时固定鸭舵双旋弹复偏角运动曲线,图 10为对应的末端弹道曲线。数值计算结果表明:在固定方位的舵面控制力长时间作用下,复扰动攻角的平衡相位与舵面控制力方向近似差180°,复偏角与弹丸质心位置会向与复扰动攻角近似相同的方向发生偏转,这与式(37)和式(38)反映的规律一致。

|
图 9 起控后复偏角运动曲线 Fig. 9 Curves of complex velocity deflection angle motion after the control starts |

|
图 10 有控飞行时末端弹道曲线 Fig. 10 Curves of terminal trajectory in controlled flight |
此外,图 10还给出了γD以30°为间隔时的弹丸落点散布,结果表明:在不同控制方位下,固定鸭舵双旋弹的弹道修正能力不完全相同,修正方向也与复偏角的偏转方向存在一定偏差。这主要是由于弹体自旋会产生陀螺效应和马格努斯效应,从而发生惯性交联和气动交联,使弹丸纵向和侧向运动产生耦合,这些耦合效应在不同控制方位下并不相同。
4 结论本文通过建立七自由度刚体弹道方程,推导了固定鸭舵双旋弹的复攻角运动方程及其解析解,研究了固定鸭舵双旋弹起控后的角运动特性,所得主要结论如下:
1) 固定鸭舵双旋弹起控后的复攻角运动由复动力平衡角、复控制平衡角的强迫角运动和舵控起始扰动产生的自由角运动综合构成。
2) 固定鸭舵双旋弹起控后复控制平衡角的相位与固定鸭舵的控制方位近似成180°,两者相差一个较小的角度φF。
3) 受动态稳定性条件的约束,在舵面控制力和起始攻角幅值均不能过大的条件下,为使固定鸭舵双旋弹具有良好的控制稳定性,必须限制控制平衡角的幅值,即令|ΔF|max < αDm,且αDm+αPm < αmax。
4) 固定鸭舵通过产生固定方向的舵面控制力和复扰动攻角,使复偏角运动近似向与复扰动攻角平衡相位相同的方向发生偏转,从而实现弹道修正。弹道数值计算分析表明,其在相同控制条件下沿不同方向的弹道修正能力不完全相等。
| [1] |
赵金强, 龙飞, 孙航. 弹道修正弹综述[J]. 制导与引信, 2005, 26(4): 16. ZHAO Jinjiang, LONG Fei, SUN Hang. The summary of trajectory correction projectiles[J]. Guidance & Fuze, 2005, 26(4): 16. DOI:10.3969/j.issn.1671-0576.2005.04.004 |
| [2] |
张民权, 刘东方, 王冬梅, 等. 弹道修正弹发展综述[J]. 兵工学报, 2010(Z2): 127. ZHANG Minquan, LIU Dongfang, WANG Dongmei, et al. A summary for trajcectory correction projectiles[J]. Acta Armamentarii, 2010(Z2): 127. |
| [3] |
STOCKENSTROM A. A simplified approach to range dispersion reduction[C]// 20th International Symposium on Ballistics. Orlando: IBC, 2002: 179
|
| [4] |
PETTERSSON T, BURETTA R, COOK D. Aerodynamics and flight stability for a course corrected artillery round[C]//23rd International Symposium on Ballistics. Tarragona: IBC, 2007: 647
|
| [5] |
REG F J, SMITH J. Aeroballistics of a terminally corrected spinning projectile(TCSP)[J]. Journal of Spacecraft & Rockets, 1975, 12(12): 733. |
| [6] |
COSTELLO M, PETERSON A. Linear theory of a dual-spin projectile in atmospheric flight[J]. Journal of Guidance Control & Dynamics, 2012, 23(5): 62. |
| [7] |
WERNERT P, LEOPOLD F, LEHMANN L, et al. Wind tunnel tests and open-loop trajectory simulations for a 155 mm canards guided spin stabilized projectile[C]// AIAA Atmospheric Flight Mechanics Conference and Exhibit. Honolulu: AIAA, 2008
|
| [8] |
THEODOULIS S, GASSMANN V, WERNERT P, et al. Guidance and control design for a class of spin-stabilized fin-controlled projectiles[J]. Journal of Guidance Control & Dynamics, 2013, 36(2): 517. |
| [9] |
SÈVE F, THEODOULIS S, WERNERT P, et al. Flight dynamics modeling of dual-spin guided projectiles[J]. IEEE Transactions on Aerospace & Electronic Systems, 2017, 53(4): 1625. |
| [10] |
SUNG J, KIM B S, SONG M S. Neural network-based adaptive control design of dual-spin projectile with rotating canards[J]. International Journal of Aeronautical and Space Sciences, 2019, 20: 806. DOI:10.1007/s42405-019-00162-9 |
| [11] |
郝永平, 孟庆宇, 张嘉易. 固定翼二维弹道修正弹气动特性分析[J]. 弹箭与制导学报, 2012, 32(3): 171. HAO Yongping, MENG Qingyu, ZHANG Jiayi. Aerodynamic characteristic analysis on two-dimensional trajectory corrector shell with fixed-wing[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2012, 32(3): 171. DOI:10.3969/j.issn.1673-9728.2012.03.047 |
| [12] |
纪秀玲, 王海鹏, 曾时明, 等. 可旋转鸭舵对旋转弹丸纵向气动特性的影响[J]. 北京理工大学学报, 2011, 31(3): 265. JI Xiuling, WANG Haipeng, ZENG Shiming, et al. CFD prediction of longitudinal aerodynamics for a spinning projectile with fixed canard[J]. Transactions of Beijing Institute of Technology, 2011, 31(3): 265. |
| [13] |
许诺, 于剑桥, 王亚飞, 等. 固定翼双旋弹动力学特性分析[J]. 兵工学报, 2015, 36(4): 602. XU Nuo, YU Jianqiao, WANG Yafei, et al. Analysis of dynamic characteristics of fixed-wing dual-spin projectiles[J]. Acta Armamentarii, 2015, 36(4): 602. DOI:10.3969/j.issn.1000-1093.2015.04.005 |
| [14] |
许诺, 于剑桥, 王亚飞. 基于周期平均的固定翼双旋弹弹道修正方法[J]. 航空学报, 2015, 36(9): 2892. XU Nuo, YU Jianqiao, WANG Yafei. Trajectory correcting method of fixed-canard of dual-spin projectiles based on period average[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(9): 2892. |
| [15] |
常思江, 王中原, 刘铁铮. 鸭式布局双旋弹飞行动力学建模与仿真[J]. 弹道学报, 2014, 26(3): 1. CHANG Sijiang, WANG Zhongyuan, LIU Tiezheng. Modeling and simulation of flight dynamic for dual-spin stabilized projectile equipped with canards[J]. Journal of Ballistics, 2014, 26(3): 1. DOI:10.3969/j.issn.1004-499X.2014.03.001 |
| [16] |
常思江, 王中原, 刘铁铮. 鸭式布局双旋稳定弹强迫运动理论研究[J]. 兵工学报, 2016, 37(5): 829. CHANG Sijiang, WANG Zhongyuan, LIU Tiezheng. A theoretical study of forced motion for dual-spin-stabilized projectiles with canards[J]. Acta Armamentarii, 2016, 37(5): 829. DOI:10.3969/j.issn.1000-1093.2016.05.009 |
| [17] |
张鑫, 姚晓先. 固定翼双旋弹修正组件滚转控制研究[J]. 北京理工大学学报, 2020, 40(4): 386. ZHANG Xin, YAO Xiaoxian. Roll control of course correction fuze for dual-spin projectile with fixed-canards[J]. Transactions of Beijing Institute of Technology, 2020, 40(4): 386. |
| [18] |
ZHU Dalin, TANG Shengjing, GUO Jie, et al. Flight stability of a dual-spin projectile with canards[J]. Proceedings of the Institution of Mechanical Engineers, 2015, 229(4): 703. DOI:10.1177/0954410014539293 |
| [19] |
马国梁, 蔡红明, 常思江. 固定鸭舵双旋弹动态稳定性分析[J]. 兵工学报, 2019, 40(10): 1987. MA Guoliang, CAI Hongming, CHANG Sijiang. Analysis of dynamic stability of fixed canard dual-spin Projectile[J]. Acta Armamentarii, 2019, 40(10): 1987. |
| [20] |
马国梁. 基于修正质点弹道模型的双旋弹控制效果分析[J]. 北京理工大学学报, 2019, 39(8): 777. MA Guoliang. Control effect analysis of dual-spin projectile based on modified mass point trajectory model[J]. Transactions of Beijing Institute of Technology, 2019, 39(8): 777. |
| [21] |
韩子鹏. 弹箭外弹道学[M]. 北京: 北京理工大学出版社, 2008. HAN Zipeng. Rocket exterior ballistics[M]. Beijing: Beijing Institute of Technology Press, 2008. |
 2022, Vol. 54
2022, Vol. 54


