近年来，用于核电站或大型装配式建筑综合施工平台上的吊装用起重机，由于其特殊的使用环境，起重机运行过程中的稳定性与定位准确性是起重吊装作业的首要考虑因素^[1-2]。传统的定位方法是在起重机传动轴上安装一个绝对值编码器^[3]。绝对值编码器将轴的转动转换为移动距离，进行定位控制。但是，当起重机车轮与轨道发生滑动的时候，偏差是不可避免的。此外，射频技术^[4]也在这一领域得到了应用，但由于信号的屏蔽和干扰，其性能大打折扣。文献[5]建立了包括扰动因素在内的吊装动力学模型，但是，其并未将视觉信息模型用于自主精确定位。文献[6]实现了基于PLC控制的起重机吊装精确定位，但是该方法并未考虑起重机运行过程中的扰动工况及其对控制系统带来的影响。文献[7]提出了一种基于李雅普诺夫的未标定算法来估计视觉伺服定位系统中的雅可比矩阵。文献[8]重点研究基于光度矩的视觉伺服技术。但上述两种方法稳定性难以保证。文献[9]提出了一种基于神经网络的视觉伺服方案，但对神经网络的构建提出了更高的要求。文献[10]提出了一种基于嵌入式概念的视觉伺服定位方法，但多摄像头系统的精度受到限制，增加了系统的处理负荷。

在起重机视觉伺服定位过程中，存在外部环境扰动和视觉雅可比矩阵参数难以获得等问题。本文通过构建自抗扰控制器进行扰动抑制，设计自适应更新算法对雅可比矩阵参数值进行自适应估计，提高起重机视觉伺服系统定位精度和鲁棒性。

1 模型建立 1.1 吊装动力学模型

四自由度吊装简化模型如图 1所示，G表示世界坐标系，v_x表示大车行走装置沿X轴的运动速度，v_y表示小车行走装置沿Y轴的运动速度，v_z表示重物沿Z轴的运动速度，ω_φ表示重物绕Z轴的旋转角速度。

理想状态下，吊装动力学模型可以表示为

$ \boldsymbol{M}(\boldsymbol{\eta}) \dot{\boldsymbol{v}}+\boldsymbol{C}(\boldsymbol{\eta}, \boldsymbol{v}) \boldsymbol{v}+\boldsymbol{G}(\boldsymbol{\eta})=\boldsymbol{Q} $

(1)

式中：η=[x, y, z, φ, 0, 0]^T∈${{\mathbb{R}}^{6}}$表示重物的位置状态向量，包括位移向量η_a=[x, y, z]^T和角度向量η_b=[φ, 0, 0]^T，v=[v_x, v_y, v_z, ω_φ, 0, 0]^T∈${{\mathbb{R}}^{6}}$表示运动速度向量，包括线速度向量v_a=[v_x, v_y, v_z]^T和角速度向量v_b=[ω_φ, 0, 0]^T。M(·)>0表示系统的正定惯性矩阵，C(·)是科里奥利向心矩阵，G(·)表示重力矢量，Q表示控制矢量^[11]。

但在实际吊装定位工程中，考虑吊装设备自身因素而存在的不确定性和外界干扰，本文引入扰动项，将吊装动力学方程描述如下：

$ \boldsymbol{M}(\boldsymbol{\eta}) \dot{\boldsymbol{v}}+\boldsymbol{C}(\boldsymbol{\eta}, \boldsymbol{v}) \boldsymbol{v}+\boldsymbol{G}(\boldsymbol{\eta})+\boldsymbol{D}(\boldsymbol{v})=\boldsymbol{Q}+\boldsymbol{\tau} $

(2)

式中：D(v)表示阻尼项，τ表示扰动项。

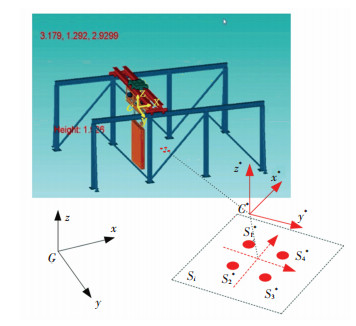
1.2 视觉投影模型

将摄像机以“手在眼”的形式固定在吊装末端执行器上，如图 2所示。我们假定相机坐标系C与末端执行器中心重合，则相机与末端执行器位置与运动速度一致。G表示世界坐标系，C^*表示期望位置相机坐标系。

S_i=(X_i, Y_i, Z_i)^T和S_i^*=(X_i^*, Y_i^*, Z_i^*)^T分别表示相机坐标系C和期望位置相机坐标系C^*中的特征点坐标，对S_i进行微分计算可得

$ {\mathit{\boldsymbol{\dot S}}_i} = {\mathit{\boldsymbol{v}}_a} + {\mathit{\boldsymbol{v}}_b} \times {\mathit{\boldsymbol{S}}_i} $

(3)

根据焦距与成像关系^[12]，可得

$ \left\{\begin{array}{c} x_{i}=\frac{l}{Z_{i}} X_{i} \\ y_{i}=\frac{l}{Z_{i}} Y_{i} \end{array}\right. $

(4)

式中：l表示焦距，x和y表示图像物理坐标。然后我们进行图像坐标系与像素坐标系转换:

$ \left\{\begin{array}{l} u=\frac{x_{i}}{\mathrm{~d} x}+u_{0}=\alpha_{1} x_{i}+u_{0} \\ v=\frac{y_{i}}{\mathrm{~d} y}+v_{0}=\alpha_{2} y_{i}+v_{0} \end{array}\right. $

(5)

式中：α₁表示x方向上单位距离内像素的个数，而α₂则表示y方向上内像素的个数，u₀, v₀表示图像平面的原点。根据透视投影原理^[13], 计算图像坐标系和期望坐标系中特征点的坐标:

$ \boldsymbol{s}_{i}=\left[u_{i}, v_{i}\right]^{\mathrm{T}}=\frac{\boldsymbol{F}}{Z_{i}}\left[x_{i}, y_{i}\right]^{\mathrm{T}} $

(6)

$ \boldsymbol{s}_{i}^{*}=\left[u_{i}^{*}, v_{i}^{*}\right]^{\mathrm{T}}=\frac{F}{Z_{i}}\left[x_{i}^{*}, y_{i}^{*}\right]^{\mathrm{T}} $

(7)

式中：$\boldsymbol{F}=\left[\begin{array}{cc}\alpha_{1} l & 0 \\ 0 & \alpha_{2} l\end{array}\right]$而u_i, v_i表示特征点在像素坐标系中的坐标。

根据目标特征微分方程，我们可以这样定义图像特征，视觉雅可比矩阵与运动速度之间的关系：

$ {\mathit{\boldsymbol{\dot s}}_i} = {\mathit{\boldsymbol{J}}_c}\mathit{\boldsymbol{v}} $

(8)

式中：v表示运动速度，J_c是依赖于相机参数和图像深度的雅可比矩阵。

根据实时目标特征s和期望目标特征s^*，则图像特征误差可表示如下：

$ \mathit{\boldsymbol{\dot e}} = \mathit{\boldsymbol{s}} - {\mathit{\boldsymbol{s}}^*} $

(9)

在s^*为常数的情况下，对上式进行微分可得

$ \dot{\boldsymbol{e}}=\boldsymbol{J}_{c} \boldsymbol{v} $

(10)

2 基于图像的视觉伺服 2.1 自抗扰控制器设计

利用视觉信息进行四自由度吊装定位反馈，将目标特征点个数设为4，精确定位的目的是使特征点在图像平面中的投影趋于期望位置，即视觉误差逐渐趋于零。我们利用雅可比矩阵将视觉误差定义为

$ \mathit{\boldsymbol{\sigma }} = {\mathit{\boldsymbol{\hat J}}_c} + \mathit{\boldsymbol{e}} $

(11)

式中${{\widehat{\boldsymbol{J}}}_{c}}^{+}$是估计雅可比矩阵的伪逆^[14]，e是图像特征误差。

扰动工况下，末端执行器的位姿公式可以表示如下：

$ \eta=\eta_{b}+\eta_{\tau} $

(12)

式中，η_b表示控制系统位姿反馈信号，η_τ表示扰动位姿信号。

由于线性自抗扰具有广泛的通用性和较好的抗扰动性能，将比例积分控制转化为二阶自抗扰控制算法，建立位姿数学模型

$ \ddot{\eta}(t)=B_{o} e(t)+y(\eta(t), e(t), \tau(t)) $

(13)

式中：B_o表示高频增益，y(η(t), e(t), τ(t))代表观测总扰动项。

设f=[f₁, f₂, f₃]，其中f₁=v，f₂=$\dot{v}$，f₃=y，则式(13)可以写为

$ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot f}} = {\mathit{\boldsymbol{M}}_a}\mathit{\boldsymbol{f}} + {\mathit{\boldsymbol{N}}_a}\mathit{\boldsymbol{\sigma }} + {\mathit{\boldsymbol{P}}_a}\mathit{\boldsymbol{\dot y}}}\\ {\mathit{\boldsymbol{\eta }} = {\mathit{\boldsymbol{H}}_a}\mathit{\boldsymbol{f}}} \end{array}} \right. $

(14)

式中：$\boldsymbol{M}_{a}=\left[\begin{array}{ccc}0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0\end{array}\right], \boldsymbol{N}_{a}=\left[\begin{array}{c}0 \\ B_{o} \\ 0\end{array}\right], \boldsymbol{P}_{a}=\left[\begin{array}{l}0 \\ 0 \\ 1\end{array}\right]$，$\boldsymbol{H}_{a}=\left[\begin{array}{lll}1 & 0 & 0\end{array}\right]$.

由此设计的线性扩张状态观测器可以表示为

$ \mathit{\boldsymbol{\dot {\hat f}}}(t) = {\mathit{\boldsymbol{M}}_\sigma }\mathit{\boldsymbol{\hat f}} + {\mathit{\boldsymbol{N}}_a}\mathit{\boldsymbol{\sigma }} + {\mathit{\boldsymbol{L}}_o}\left( {\mathit{\boldsymbol{v}} - {\mathit{\boldsymbol{H}}_\omega }\mathit{\boldsymbol{\hat f}}} \right) $

(15)

式中：$\widehat{\boldsymbol{f}}$表示f的估计值，L_o表示观测器增益。

为了得到渐进稳定项，对式(15)相关项进行合并，可得

$ \dot{\hat{\boldsymbol{f}}}(t)=\left(\boldsymbol{M}_{a}-\boldsymbol{L}_{o} \boldsymbol{H}_{a}\right) \hat{\boldsymbol{f}}+\boldsymbol{N}_{a} \boldsymbol{\sigma}+\boldsymbol{L}_{o} \boldsymbol{v} $

(16)

式中：当M_a－L_oH_a逐渐趋于0时，${{\widehat{f}}_{1}}$趋近于v，${{\widehat{f}}_{2}}$趋近于${\dot{v}}$，${{\widehat{f}}_{3}}$趋近于y.

为了消除系统扰动，设定

$ \begin{aligned} \boldsymbol{\eta}(t)=& \frac{\lambda_{p}\left(r(t)-\hat{f}_{1}(t)+\lambda_{d}\left(\dot{r}(t)-\hat{f}_{2}(t)\right)-\hat{f}_{3}(t)\right.}{B_{o}}=\\ & \boldsymbol{\lambda}_{o}(\hat{r}(t)-\hat{f}(t)) \end{aligned} $

(17)

式中：$\widehat{r}\left(t \right)$为扩张状态信号，λ_o是反馈增益，且λ_o=[λ_p/B_o  λ_d/B_o  1/B_o].

2.2 自适应算法设计

根据图像投影特性，可以将雅可比矩阵与图像特征微分关系表示如下：

$ \mathit{\boldsymbol{\dot s}} = {\mathit{\boldsymbol{\hat J}}_c}\mathit{\boldsymbol{v}} = \mathit{\boldsymbol{\psi }}(\mathit{\boldsymbol{\dot \eta }}){\widehat {\mathit{\boldsymbol{ {\vartheta}}}} _c} $

(18)

式中ψ(${\mathit{\boldsymbol{\dot \eta }}}$)是不依赖于相机内外参数的位姿映射矩阵^[15]。${\widehat {\boldsymbol{\vartheta}} _c}$ 表示估计雅可比矩阵${\mathit{\boldsymbol{\widehat J}}_c}$中的参数向量。

根据动力学方程(2)，位姿模型(13)以及图像特征微分方程(18)，将视觉伺服系统控制方程定义如下：

$ \left\{\begin{array}{l} \boldsymbol{Q}+\boldsymbol{\tau}=\boldsymbol{G}(\boldsymbol{\eta})+\|\dot{\boldsymbol{\eta}}\| \boldsymbol{K}_{1} \boldsymbol{\psi}(\dot{\boldsymbol{\eta}}) \hat{\boldsymbol{\vartheta}}_{c}-\boldsymbol{K}_{2} \dot{\boldsymbol{\eta}} \\ \dot{\boldsymbol{\eta}}=-\boldsymbol{K}_{3} \hat{\boldsymbol{J}}_{c}^{+} \boldsymbol{e} \end{array}\right. $

(19)

式中：K₁，K₂，K₃均为正定增益矩阵。

根据方程(2)和方程(19), 得闭环动力学方程

$ \boldsymbol{M}(\boldsymbol{\eta}) \dot{\boldsymbol{v}}+\boldsymbol{C}(\boldsymbol{\eta}, \boldsymbol{v}) \boldsymbol{v}+\boldsymbol{D}(\boldsymbol{v})=\|\dot{\boldsymbol{\eta}}\| \boldsymbol{K}_{1} \boldsymbol{\psi}(\dot{\boldsymbol{\eta}}) \hat{\boldsymbol{\vartheta}}_{c}-\boldsymbol{K}_{2} \dot{\boldsymbol{\eta}} $

(20)

雅可比矩阵参数估计值的更新率定义为

$ \dot{\hat{\boldsymbol{\vartheta}}}_{c}=-\|\dot{\boldsymbol{\eta}}\| \boldsymbol{B}_{o}{ }^{-\mathrm{T}} \boldsymbol{K}_{1} \dot{\boldsymbol{\eta}} $

(21)

根据图像特征误差，构建李雅普诺夫函数

$ \mathit{\boldsymbol{V}}(t) = \frac{1}{2}{\left\| {\mathit{\boldsymbol{e}}(t)} \right\|^2} = \frac{1}{2}\mathit{\boldsymbol{e}}{(t)^{\rm{T}}}\mathit{\boldsymbol{e}}(t) $

(22)

对李雅普诺夫函数进行求导

$ \dot{\boldsymbol{V}}(t)=\frac{d}{\mathrm{~d} t} \frac{1}{2} \boldsymbol{e}(t)^{\mathrm{T}} \boldsymbol{e}(t)=\boldsymbol{e}(t)^{\mathrm{T}} \dot{\boldsymbol{e}}(t) $

(23)

将图像特征误差微分方程(9)和视觉伺服系统控制方程(31)代入(35)，可得

$ \dot{\boldsymbol{V}}(t)=\boldsymbol{e}(t)^{\mathrm{T}} \dot{\boldsymbol{e}}(t)=-\boldsymbol{e}(t)^{\mathrm{T}} \boldsymbol{J}_{c} \boldsymbol{K}_{3} \hat{\boldsymbol{J}}_{c}^{+} \boldsymbol{e}(t) $

(24)

由于K₃正定，$\boldsymbol{J}_{c} \boldsymbol{K}_{3} \hat{\boldsymbol{J}}_{c}^{+}$半正定，有$\boldsymbol{e}(t)^{\mathrm{T}} \boldsymbol{J}_{c} \boldsymbol{K}_{3} \hat{\boldsymbol{J}}_{c}^{+} \boldsymbol{e}(t) \geqslant 0$，则$\mathit{\boldsymbol{\dot V}}\left(t \right)$≤0。根据李雅普诺夫稳定性原理可知该控制系统是稳定的。

视觉伺服控制架构如图 3所示，系统获得参考视觉特征s与期望视觉特征s^*，图像特征误差e可以表示为(9)。视觉与控制信号处理框架中包含雅可比矩阵估计和系统控制方程。雅可比矩阵参数估计值的更新率定义为式(21)，系统控制方程表示为(19)。自抗扰控制框架中，P表示被控对象，ESO表示线性扩张状态观测器，λ_o表示反馈控制增益。位姿数学模型表示为式(13)。

3 仿真 3.1 仿真结果分析

本节将所提出的视觉伺服定位方法应用于仿真平台。仿真研究了该控制器在外部扰动工况下的控制性能。该仿真研究的目标是在提出算法的控制下，使吊装执行器到达期望位姿。与实际情况一致，采用了“手在眼”的相机固定方式。在精确定位过程中，认为目标点在视域范围内。为了模拟真实摄像机投影模型，使用了一个可视化工具箱，基本参数: 焦距8 mm，成像像素帧1 024×1 024。施加于控制量中的恒定扰动项设置为[1, 1, 1, 0.5, 0, 0]^T，系统采样时间10 ms, 系统参数设置：

$ \boldsymbol{K}_{1}=\operatorname{diag}\{0.9,0.65,0.4,0.25,0,0\} $

$ \boldsymbol{K}_{2}=\operatorname{diag}\{0.8,0.65,0.65,0.6,0,0\} $

$ \boldsymbol{K}_{3}=\operatorname{diag}\{0.6,0.6,0.4,0.2,0,0\} $

该仿真研究使用的电脑配置为Intel Corei5 2.67 GHz CPU, 4 GB RAM。在仿真中不考虑延迟，即在理想状态下不计算视觉特征提取和处理的时间，且视觉误差曲线平滑。我们将采样的数据作为后续分析和计算的更新数据。

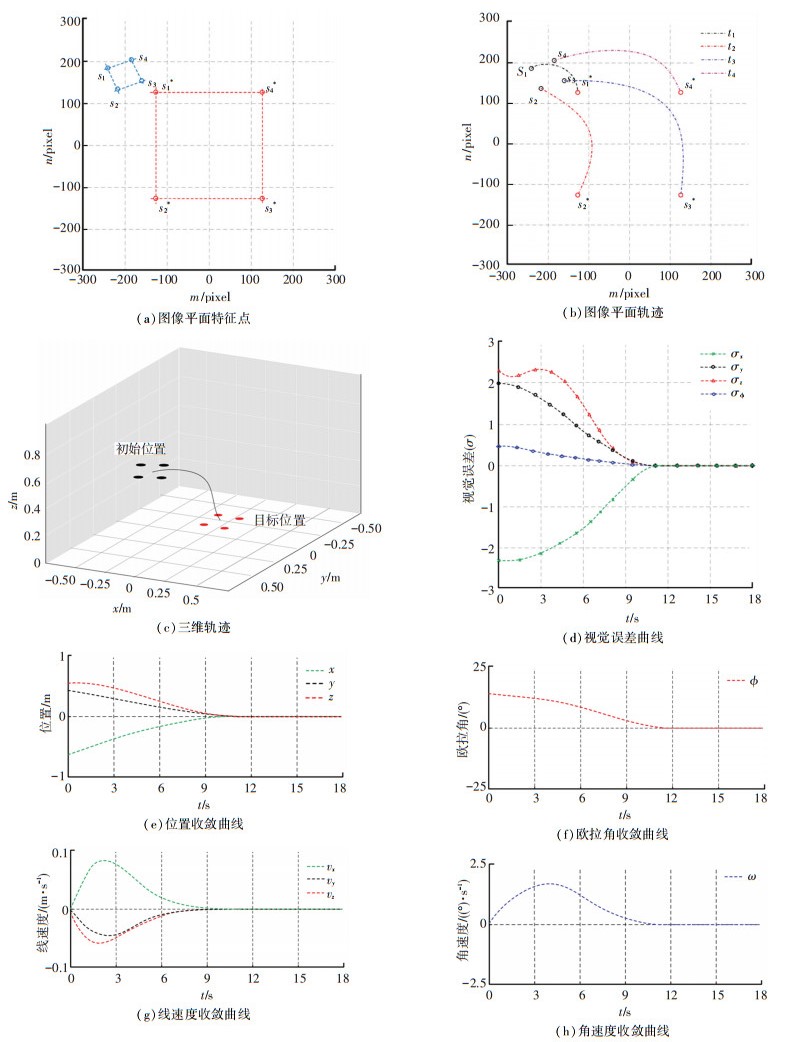
图像平面上的初始特征点和期望特征点如图 4(a)所示。s₁, s₂, s₃, s₄表示初始特征点，s₁^*, s₂^*, s₃^*, s₄^*表示期望特征点。在图 4(b)中，t₁, t₂, t₃, t₄表示4个特征点的移动轨迹。可以看到，虽然在初始位置和期望位置之间有较大的位移，但是最终仍然可以被驱动到准确的位置。在整个运动过程中，我们以特征中心点作为记录点，在三维空间中显示其轨迹，如图 4(c)所示。从仿真曲线中可以看出，在视觉误差收敛后，位置与速度均在零点处保持稳定，说明存在视觉不确定性和恒定扰动的情况下，本文方法仍然具有令人满意的定位精度。本文方法采用自抗扰控制算法来减小外部干扰的影响，基于自适应算法实现雅可比矩阵参数估计，并建立闭环动力学方程实现精确定位控制。仿真结果表明，控制算法可以平稳地将对象驱动到目标位置，且具有较好的定位精度与收敛性。

3.2 对比分析

为了进一步验证本文方法的性能，将其与其他几种控制方法进行对比研究，包括：比例积分控制(PI)视觉伺服系统，滑模控制(SMC)视觉伺服系统，比例滑模控制(PSMC)视觉伺服系统。采用同样初始条件进行对比仿真，将视觉累积误差作为评价指标，对比结果如图 5所示。视觉累积误差公式表示如下：

$ \xi=\left|\sigma_{x}\right|+\left|\sigma_{y}\right|+\left|\sigma_{z}\right|+\left|\sigma_{\varphi}\right| $

(25)

具体定量比较的结果见表 1。由收敛时间可以看出相比其他方法本文方法在收敛速度方面提高了17%左右。由图 5可以看出，在初始视觉累积误差相同的情况下，采用本文方法的视觉累积误差比其他方法更早收敛，虽然本文提出方法比其他视觉伺服的单次循环计算时间长，但本文提出方法的迭代循环次数更少，总收敛时间最短，说明它可以更快地到达目标点。此外，视觉累积误差最终可以准确地收敛到零值，说明目标点定位精度高。本文方法通过将比例积分控制转化为二阶自抗扰控制算法，建立位姿数学模型，在高频增益与图像误差乘积的基础上增加了位姿观测扰动项，大大提高了位姿数学模型的表达精度，并可以更好的消除扰动。由于自抗扰控制较好的抗扰动性能以及基于自适应算法实现雅可比矩阵参数估计，并建立闭环动力学方程实现精确定位控制，使得本文方法在扰动工况下相比其他方法具有更好的收敛性能。

4 实验

在上述仿真中采用在控制量中施加恒定扰动的方式，分析了恒定扰动工况下本文方法与比例积分控制(PI)视觉伺服系统，滑模控制(SMC)视觉伺服系统和比例滑模控制(PSMC)视觉伺服系统的收敛性能与定位精度。本节中，进行实验对比分析上述几种方法对随机瞬时扰动的抑制能力及收敛性能。本实验在实验室门式起重机平台上进行，实验台如图 6所示。吊装重物固定在起重机电磁挂钩上，电磁挂钩由固定在小车上的末端控制器驱动。将OMRON编码器同轴固定在旋转电机轴端，将MiniAHRS (3Dsuit)固定在电磁挂钩上，可以通过速比来测量各个方向的运动速度。将相机固定在吊装重物底部位置，通过手动操作系统将起重机初始定位到某一位置，然后启动视觉伺服控制系统，将吊装重物驱动到目标点位置。

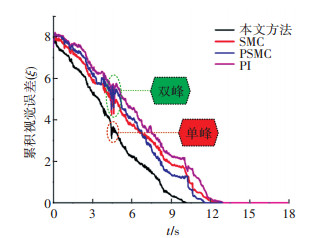
在实验过程中，通过在吊装重物上施加瞬时敲击模拟吊装过程中受到的外部瞬时扰动。实验对比结果如图 7所示。从实验结果中可以看出，在4.5 s左右施加于吊装重物上的瞬时敲击对视觉伺服控制系统产生影响，累积视觉误差曲线发生了突变，其中采用本文方法的累积视觉误差曲线在突变处具有单峰特性，而其他几种对比方法的累积视觉误差曲线在突变处具有双峰特性。这说明本文方法具有较好的扰动抑制能力，受到外部瞬时扰动的情况下，仍然可以快速收敛，并且最终成功收敛到零值。且实验结果与仿真结果基本相符，验证了仿真结果的正确性。

5 结论

本文提出了一种吊装用起重机自动定位视觉伺服控制方法。首先，建立了吊装动力学模型和视觉投影模型。针对外部扰动影响视觉伺服定位精度和稳定性的问题，将扰动工况下，末端执行器的位姿表示为系统反馈信号和扰动位姿信号。基于二阶自抗扰控制算法，建立位姿数学模型，设计了自抗扰控制器进行扰动抑制。而后，构建雅可比矩阵参数与图像特征微分关系。根据动力学方程, 位姿模型以及视觉特征微分方程定义视觉伺服系统控制方程。并设计雅可比矩阵参数估计值的自适应更新率，实现了雅可比矩阵参数值的估计。通过仿真与实验分析验证了本文提出方法的有效性，通过仿真与实验对比结果可知，本文方法在保证视觉伺服系统定位精度的同时，有效提高了视觉误差的收敛速度，具有视觉伺服控制的高精度与强鲁棒性。