圆柱绕流的研究受到国内外学者的广泛关注,大部分学者研究目的是减阻减振,而对于某些工程领域,如涡激振动发电[1],减阻增振研究就显得尤为重要。
对于单圆柱研究,国内外许多学者围绕改变圆柱外形来控制圆柱周围的流动结构,来达到减阻或增振的目的。LAM等[2]和ZHANG Zhihao等[3]通过改变波浪形圆柱波长比和波幅比,发现波浪形圆柱的阻力系数相对于直圆柱能显著降低。而存在自由端的圆柱,ZHANG Hui等[4]发现有限长圆柱时均阻力系数以及脉动升力系数远小于无限长圆柱。赵桂欣等[5]对12种不同波长的单自由端圆柱进行了研究,发现对于有限长圆柱,波浪外形也能有很好的减阻效果,最大可达5.36%。杨耀宗[6]则通过在波浪形圆柱中引入锥度得到波浪锥形圆柱,发现波长比为1.75,波幅比为0.1,斜率为0.05的波浪锥形圆柱脉动升力系数相对于直圆柱增加约20%。
双圆柱之间的流动模式十分复杂,ALAM等[7-8]通过实验观察不同交错角和间距比下的流动特性,将两个圆柱之间的流动状态进行分类,同时发现在交错角为10°时,间隙流作用于下游柱最强烈,下游柱脉动阻力达到最大。SUMNER等[9]通过实验重点研究了错列圆柱近尾涡的流动模式,发现下游柱阻力系数较单圆柱低。LAM等[10]研究发现,间距比为3.5左右为串列波浪锥形圆柱临界间距比,其他间距比减阻效果仍然存在。杜晓庆等[11]通过数值模拟研究错列双圆柱的脉动升力系数,发现在较大间距比及较小的交错角下,下游柱的脉动升力系数较单圆柱能够显著提升。汪洋等[12]研究的错列双圆柱,发现在交错角约为8°时,下游柱的脉动升力系数达到最大值。
综上所述,在小交错角以及中等间距比时,下游柱有很好的减阻增振效果。因此,本文采用商用软件Fluent中的大涡模拟,在亚临界雷诺数(Re=3 900)下,探究错列波浪锥柱在间距比L/Dm = 4、5下(L为两个波浪锥柱的中心距离,Dm为波浪锥柱的平均直径),随交错角α(α = 0~15°)变化的上下游柱之间流场机理,分析其升阻力变化原因,以达到减阻增振目的,为风力俘能结构列阵布局提供理论支持。
1 控制方程本文采用大涡模拟进行求解,大涡模拟通过滤波函数和截止尺度Δ将涡分为大尺度旋涡和小尺度旋涡两种,大尺度旋涡通过Navier-Stokes方程直接求解,小尺度涡则通过SGS(Sub-gird-scale Stress, SGS)模型进行求解[11]。
对于不可压缩粘性流体,其Navier-Stokes运动方程
| $ \frac{{\partial {{\bar u}_i}}}{{\partial {x_i}}} = 0 $ | (1) |
| $ \frac{{\partial {{\bar u}_i}}}{{\partial t}} + \frac{{\partial {{\bar u}_i}{{\bar u}_j}}}{{\partial {x_j}}} = - \frac{1}{\rho }\frac{{\partial \bar p}}{{\partial {x_i}}} + \nu \frac{{{\partial ^2}{{\bar u}_i}}}{{\partial {x_j}\partial {x_j}}} - \frac{{\partial {\tau _{ij}}}}{{\partial {x_j}}} $ | (2) |
式中:i, j∈[1,2,3],对应于笛卡尔坐标系中的x, y和z轴;
亚格子应力τij计算采用Smagorinsky-Lilly的亚格子模型:
| $ \begin{gathered} \tau_{i j}-\frac{1}{3} \tau_{k k} \delta_{i j}=-2 \nu_{\mathrm{sgs}} \bar{S}_{i j} \end{gathered} $ | (3) |
| $ \begin{gathered} \bar{S}_{i j}=\frac{1}{2}\left(\frac{\partial \bar{u}_{i}}{\partial x_{j}}+\frac{\partial \bar{u}_{i}}{\partial x_{i}}\right) \end{gathered} $ | (4) |
式中:δij其中表示Kronecker增量,νsgs表示SGS涡流粘度,
| $ {\nu _{{\rm{sgs}}}} = {\left( {{C_s}\Delta } \right)^2}|\bar S| $ | (5) |
| $ |\bar S| = \sqrt {2{{\bar S}_{ij}}{{\bar S}_{ij}}} $ | (6) |
| $ \Delta = {V^{\frac{1}{3}}} $ | (7) |
式中:Δ表示过滤的网格尺度,Cs为Smagorinsky常数,本文取0.2。
2 模型验证计算域大小为30D×10D×10D,D为圆柱直径,D=0.01 m,圆柱总长为H0,长径比H0/D=7,笛卡尔坐标系的原点位于圆柱中心,圆柱中心距入口为10D,距离出口为20D,x轴正方向为顺流向,z轴正方向沿圆柱轴心向上,如图 1所示。

|
图 1 网格验证及计算域示意图 Fig. 1 Grid model and calculation domain |
用结构化网格对整个流场进行网格划分,其中圆柱周围有0.1D的O形块区域来控制近壁面网格的高度,本次验证采用近壁面网格高度为0.001D,使圆柱壁面y+最大值小于1。流体为空气,密度ρ=1.225 kg/m3,动力粘度μ=1.813 Pa·s,入口采用速度入口(Velocity-inlet),大小为5.772 m/s,出口采用压力出口(Pressure-outlet),大小设置为0,侧面以及底面采用对称边界(Symmetry),圆柱表面采用无滑移壁面(No slip wall)。无量纲时间步长Δt* = U∞Δt/D,U∞为来流速度,Δt为时间步长, 大涡模拟在计算中,要求时间步长Δt满足库朗数C(Courant number)在0.5~1.0之间,C = uΔt/Δx,Δx为最小网格尺寸。当取Δt* = 0.001时,相应库朗数约为0.981,满足计算条件。
本文计算压力速度耦合采用PISO算法,离散化采取二阶迎风格式[4]。表 1为计算模型网格独立性及时间步长无关性验证结果,本文计算结果与实验以及数值仿真结果基本一致,可以认为case2网格密度、无量纲时间步长Δt*=0.001以及本次仿真所用的算法正确,可以运用于错列双波浪锥柱仿真实验。
| 表 1 仿真结果与已有文献对比 Tab. 1 Simulation results compared with previous literature |
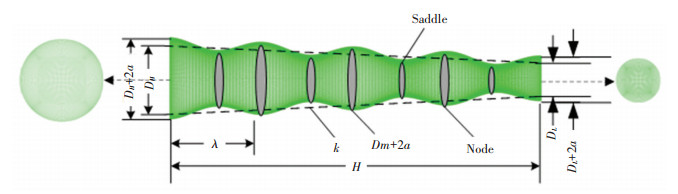
波浪锥柱如图 2所示,其几何表达式为
| $ D_{z}=D_{m}+2 a \times \cos \frac{2 \pi z}{\lambda}+2 k \times\left(z-\frac{H}{2}\right) $ | (8) |
|
图 2 波浪锥柱几何模型示意图 Fig. 2 Geometric model of wavy conical cylinder |
式中:Dz表示波浪锥柱对应高度Z处的直径,Dm表示波浪锥柱的平均直径,DH和DL分别表示波浪锥柱对应斜率为k的直锥柱最大直径和最小直径,H为波浪锥柱总长,H = 7Dm;a、λ分别表示波浪锥柱表面的波幅与波长。根据杨耀宗[6]的研究,选取振动性能最佳的一组参数,即k = 0.05,a/Dm = 0.1,λ/Dm = 1.75。
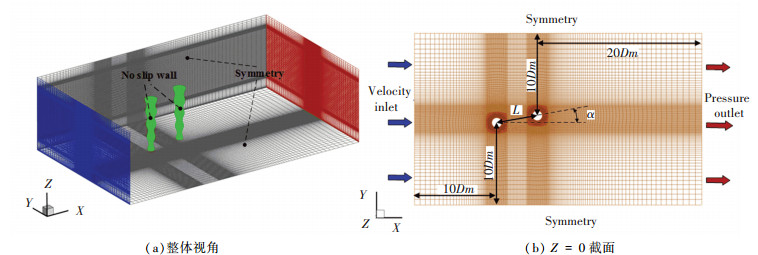
本次仿真计算域为(30Dm+Lcos α)×(20Dm+ Lsin α) ×10Dm。原点位于上游波浪锥柱的中心,两个波浪锥柱中心距为L,中心线与入流向夹角为α,即交错角,波浪锥柱长径比H/Dm=7。
入口采用速度入口(Velocity-inlet),大小为5.772 m/s,出口采用压力出口(Pressure-outlet),背压设置为零,波浪锥柱壁面采用无滑移边界条件,计算域顶面、底面和侧面均采用Symmetry壁面,如图 3所示。为了探究小交错角下和中等间距下波浪锥柱的升、阻力系数特性,本次研究的间距比L/Dm为4和5,交错角α为0°、5°、7.5°、10°、12.5°和15°。网格划分方法和数值算法均参照验证中的Case2,网格模型如图 3所示。
|
图 3 错列波浪锥柱计算域及网格模型示意图 Fig. 3 Schematic diagram of calculation domain and grid model of two staggered wavy conical cylinders |
升力系数Cd和阻力系数Cl的计算公式如下:
| $ \begin{aligned} \mathrm{Cd}=2 F_{\mathrm{d}} /\left(\rho U_{\infty}^{2} D m \cdot H\right) \end{aligned} $ | (9) |
| $ \mathrm{Cl}=2 F_{\mathrm{l}} /\left(\rho U_{\infty}^{2} D m \cdot H\right) $ | (10) |
式中Fd、Fl分别为顺流向受到的阻力和横流向受到的升力。
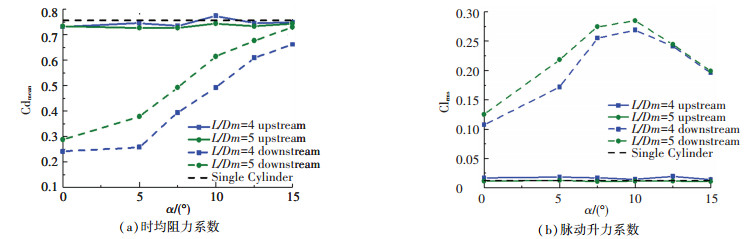
图 4 (a)为上游波浪锥柱和下游波浪锥柱(下文分别简称为上游柱和下游柱)的时均阻力系数随交错角变化曲线。当交错角为α=0°时,下游柱时均阻力系数远小于上游柱,随交错角增加,下游柱时均阻力系数急剧上升,逐渐逼近上游柱时均阻力系数;除间距比L/Dm=4,交错角α=15°工况外,两种间距比的上游柱阻力系数均略小于单直圆柱;对于下游柱,间距比L/Dm=5的时均阻力系数大于间距比L/Dm=4工况,最大可达24.7%。图 4(b)是升力系数的均方根值Clrms曲线。两种工况下下游柱的Clrms均远大于上游柱,且随交错角的变化趋势基本相同,均在交错角α=10°时取得最大值,间距比L/Dm=4和L/Dm=5取得脉动升力系数最大值时相对单直圆柱分别提高约20.1倍和21.4倍。在α=10°时脉动升力系数取得最大值,这与ALAM等[8]和汪洋等[12]的研究基本一致。时均阻力系数的降低和脉动升力系数的显著提高将有利于风力俘能结构的能量获取[6]。
|
图 4 时均阻力系数和脉动升力系数(upstream: 上游波浪锥柱;downstream: 下游波浪锥柱) Fig. 4 Time-average drag coefficient and fluctuating lift coefficient(upstream: upstream wavy conical cylinder; down steam: downstream wavy conical cylinder) |
圆柱表面的时均压力系数能够清晰展示表面的压力分布规律,为方便观察其分布形式,将圆柱表面以角度展开成二维平面,如图 5(a)所示,展开后的压力系数分布如图 5(b)所示。

|
图 5 波浪锥柱表面时均压力系数分布 Fig. 5 Time-average pressure coefficient on the surface of the wavy conical cylinder |
时均压力系数<Cp>计算公式为
| $ \langle\mathrm{Cp}\rangle=\frac{\bar{p}-\bar{p}_{\infty}}{0.5 \rho U_{\infty}^{2}} $ | (11) |
式中
对于上游柱,其压力系数分布随间距比和交错角变化,基本保持对称,高压区(<Cp> >0.8)约在在0~25°和335~360°之间,由于波浪锥柱形状的影响,沿z方向变化时区域有一定波动,低压区中心(<Cp> < 0.6)约在75°和285°,受到波浪锥柱锥度和表面的影响,其分布形式类似三角形,同时也沿z方向区域存在波动,两种间距比下高压区和低压区分布范围基本相同,这可能是阻力系数随交错角变化时,两种间距比相差不大的原因。对于下游柱,其时均压力系数随交错角α的变化存在较大变化,当α=0°时,两种间距比下,圆柱表面正压和负压区域能保持对称,但高压范围和低压范围都很小,这可能导致下游柱时均阻力系数较小;随着α的增加,高压区和低压区范围逐渐扩大,当达到α=15°时,其分布形式已经接近上游柱,这是时均阻力系数随着交错角增加而增加最终接近上游柱时均阻力系数的主要原因;同时可以观察到当间距比为L /Dm=5时,正压区间和负压区间面积略大于间距比L/Dm=4,这可能是导致时均阻力系数随交错角α变化时,L/Dm=5略大于L/Dm=4的原因。
4.3 流动结构如图 6给出了间距比L/Dm=4和5,交错角α=0°,5°,10°和15°的三维时均流线图和对应的Node1、Saddle1和Node2截面的时均流线图。

|
图 6 错列波浪锥柱绕流时均流线图 Fig. 6 Time-average streamline of two staggered wavy conical cylinders |
两种间距比下错列双波浪锥柱的流动模式,按照下洗(流经上自由端部的流体在柱体后方向下运动)和上洗(流经下自由端部的流体在柱体后方向上运动)在两个圆柱中间形成的流动状态可分为两类:
第一类为上游柱上自由端的下洗作用占主导,一部分流线在上游柱的后上方形成X-Z方向的回流区,一部分则继续向波浪锥柱下端流动在下游柱迎风面的底部与上游柱下自由端的射流相互作用形成一个X-Z方向回流区,这两个回流区中心向两侧发展出的流体与上游柱侧面来流相互作用形成“拱形”涡。如图 6(a),(g)所示,三维图中的“拱形”涡对应右侧Node和Saddle截面波浪锥柱之间形成的回流区。
第二类为上游柱下自由端的上洗作用占主导,一部分流线在上游柱的背风面底部形成Y方向的回流区,一部分则继续向上端发展与来自上游柱顶部自由端的射流相互作用在下游柱上端迎风面形成一个X-Z方向回流区,同样,两个回流区中心也会向两侧发展出流体与来自上游柱侧面的流体相互作用形成“拱形”涡,如图 6(b),(c),(d),(e),(f)和(h)所示。第一类流动中,上游柱上侧形成的回流区和下游柱的迎风面下侧的回流区使这两个区域压力降低,这与图 5(b)中L/Dm=4,α=0°,15°压力系数分布区域相符。同样的,第二类流动中,上游柱的背风面下端和下游柱迎风面的上端能形成的两个回流区使这两个区域的压力降低,这可能是图 5(b)中对应区域压力系数低的原因。
4.4 涡量图 4.4.1 三维涡量图上游柱的尾流对下游柱表面及其尾涡有很大的影响,使得下游柱相对于上游柱有更大的脉动升力系数值,并且在不同间距比和交错角下尾流作用形式各有不同,下面通过分析不同间距比下取得脉动升力系数峰值的两组参数(L/Dm=4,α=10°,L/Dm=5,α=10°)的涡量图,来分析下游柱取得脉动升力最大值的原因,Q定义[16]为
| $ Q = \frac{1}{2}\left( {\left\| {{\mathit{\Omega }^2}} \right\| - \left\| {{S^2}} \right\|} \right) $ |
式中:Ω表示涡量,S表示应变率张量,‖ ‖为取范数运算符。
图 7中显示的是Q=1×106时错列波浪锥柱周围的涡量图,可以观察到,锥柱之间的涡主要集中在波浪锥柱的中上部,由于波浪锥柱表面为波浪型,使得流过波浪锥柱表面的流体同时具有波浪型的特征,波浪锥柱后方涡出现按圆柱波长周期性分层现象。上游柱在后上方形成的大量涡团,由于下游柱的存在,阻碍了其向正后方继续发展,而是偏向一侧,如图 7中View1,在下游柱迎风面和侧面均有大量涡聚集,这些涡部分形成于流体与下游柱表面的撞击,部分来自上游柱向下发展的涡,因此在下游柱表面形成周期性的力,同时可以观察到下游柱另一侧面,如图 7中View2,也能观察到周期性脱落的涡,同样也能对下游柱表面产生周期性的力,两种周期性的力相互耦合作用,极易产生大的脉动升力值。

|
图 7 α=10°时的Q准则瞬时涡量图(Q=1×106) Fig. 7 Instantaneous vorticity of Q criterion at α=10°(Q=1×106) |
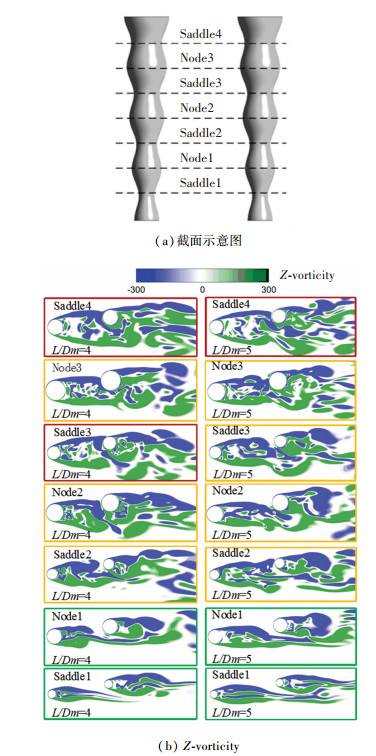
上游柱的尾流对下游柱作用非常复杂,为了更好观察两种间距比下的流动模式,选用图 8(a)中各个截面观察流动情况。
|
图 8 α=10°时Z方向瞬时涡量图 Fig. 8 Instantaneous Z-vorticity at α=10° |
由于波浪锥柱表面形状的影响,流动结构存在明显分层,上游柱尾流对下游柱的作用展现为完全撞击状态,侧面撞击状态和尾流干扰状态。如图 8(b)所示(红色线框表示完全撞击状态,橙色线框表示侧面撞击状态,绿色线框表示尾流干扰状态)。完全撞击状态下,上游柱上侧剪切层将下游柱迎风面完全包裹,使下游柱表面阻力系数(前端压力降低)和脉动升力系数(侧面压力降低)均有影响。而侧面撞击状态下,上游柱尾流作用下游柱时,下游柱的侧面受到上游柱的影响增强(侧面压力降低大),而正面受到的影响则变弱(正面压力降低小)。侧面压力更大的增幅导致下游柱的脉动升力系数更大,如图 8(b)所示,间距比L/Dm=5相对于L/Dm=4拥有更多的侧面撞击状态,这也表明该交错角下的L/Dm=5的下游柱有更大的脉动升力系数。同时,间距比L/Dm=4相对于间距比L/Dm=5拥有更多的尾流包裹状态,因此下游柱的时均阻力系数更低。
5 结论本文采用大涡模拟数值研究了亚临界雷诺数(Re=3 900)下对间距比L/Dm=4和5,交错角α= 0°,5°,7.5°,10°,12.5°和15°错列双波浪锥柱绕流流动机理,探究了波浪锥柱平均阻力系数和脉动升力系数的变化规律,并对圆柱表面的时均压力系数和流场结构进行了分析。主要结论如下:
1) 由于上游柱的影响,下游柱时均阻力系数存在较大降幅,但随着交错角的增加,下游柱时均阻力系数也逐渐增大,趋近于上游柱。下游柱脉动升力系数较单圆柱均有大幅提升,且在交错角α= 10°时,两种间距比下均能取得最大值,分别提升约20.1倍和21.4倍。
2) 上游柱尾迹对下游柱的迎风面和背风面均有影响,当交错角较小时,正压区和负压区主要集中在柱体底部和受上游柱影响小的一侧;当交错角逐渐增大时,正压区和负压区的范围逐渐向圆柱上端扩散,强度也有所增加。
3) 波浪锥柱之间在Y截面存在两个回流区,回流区中心向两边发展的涡与侧面的涡相互作用形成“拱形”涡,存在回流区的波浪锥柱区域有较大的压力系数变化。
4) 在交错角α=10°时,上游柱的下自由端上洗作用较上自由端下洗作用强,使得下游柱迎风面上端有大量涡聚集;间距比L/Dm=5相对于L/Dm=4的下游柱有更多的侧面撞击状态,脉动升力系数更大。本文的研究结果将对风力俘能结构布局提供有益理论支持。
| [1] |
白旭, 仇北平, 乐智斌. 圆柱体涡激振动海流能捕获效率影响参数分析[J]. 可再生能源, 2017, 35(05): 784. BAI Xu, QIU Beiping, LE Zhibin. Analysis of the parameters influencing the ocean current energy harvesting efficiency of circular cylinder VIV[J]. Renewable Energy Resources, 2017, 35(05): 784. DOI:10.13941/j.cnki.21-1469/tk.2017.05.024 |
| [2] |
LAM K, LIN Y F. Effects of wavelength and amplitude of a wavy cylinder in cross-flow at low Reynolds numbers[J]. Journal of Fluid Mechanics, 2009, 620: 195. DOI:10.1017/S0022112008004217 |
| [3] |
ZHANG Zhihao, TU Jiahuang, ZHANG Kai, et al. Vortex characteristics and flow-induced forces of the wavy cylinder at a subcritical Reynolds number[J]. Ocean Engineering, 2021, 222(2): 1085593. DOI:10.1016/J.OCEANENG.2021.108593 |
| [4] |
ZHANG Hui, YANG Jianmin, XIAO Longfei. Large-eddy simulation of the flow past both finite and infinite circular cylinders at Re=3900[J]. Journal of Hydrodynamics, Ser.B, 2015, 27(2): 195. DOI:10.1016/S1001-6058(15)60472-3 |
| [5] |
赵桂欣, 桂洪斌, 王晓聪. 有限长波浪形圆柱绕流数值模拟[J]. 哈尔滨工业大学学报, 2021, 53(06): 163. ZHAO Guixin, GUI Hongbin, WANG Xiaochong. Numerical simulation of flow around finite-length wavy cylinders[J]. Journal of Harbin Institute of Technology, 2021, 53(06): 163. DOI:10.11918/201909017 |
| [6] |
杨耀宗. 波浪锥型圆柱流固耦合振动机理的研究[D]. 武汉: 武汉理工大学, 2020. DOI: 10.27381/d.cnki.gwlgu.2020.001919 YANG Yaozong. Study on the fluid-solid coupling vibration mechanism of wavy conical cylinder[D]. Wuhan: Wuhan University of Technology, 2020. DOI: 10.27381/d.cnki.gwlgu.2020.001919 |
| [7] |
ALAM M M, SAKAMOTO H, ZHOU Y. Determination of flow configurations and fluid forces acting on two staggered circular cylinders of equal diameter in cross-flow[J]. Journal of Fluids and Structures, 2005, 21(4): 363. DOI:10.1016/j.jfluidstructs.2005.07.009 |
| [8] |
ALAM M M, MEYER J P. Two interacting cylinders in cross flow[J]. Physical Review. E, Statistical, Nonlinear, and Soft Matter Physics, 2011, 84(5 Pt 2). |
| [9] |
SUMNER D. Two circular cylinders in cross-flow: a review[J]. Journal of Fluids and Structures, 2010, 26(6): 849. |
| [10] |
LAM K, LIN Y F, ZOU L, et al. Numerical simulation of flows around two unyawed and yawed wavy cylinders in tandem arrangement[J]. Journal of Fluids and Structures, 2011, 28: 135. DOI:10.1016/j.jfluidstructs.2011.08.012 |
| [11] |
杜晓庆, 顾李敏, 吴葛菲, 等. 错列双圆柱的脉动升力特性及其流场机理[J]. 哈尔滨工业大学学报, 2020, 52(08): 62. DU Xiaoqing, GU Limin, WU Gefei, et al. Fluctuating lift and flow field mechanisms of two staggered circular cylinders[J]. Journal of Harbin Institute of Technology, 2020, 52(08): 62. DOI:10.11918/201904102 |
| [12] |
汪洋, 陈立. 错列圆柱的三维大涡模拟[J]. 四川建筑, 2020, 40(04): 213. WANG Yang, CHEN Li. Large eddy simulation of three-dimensional staggered cylinders[J]. Sichuan Architectural, 2020, 40(4): 213. |
| [13] |
SUMNER D. Flow above the free end of a surface-mounted finite-height circular cylinder: a review[J]. Journal of Fluids and Structures, 2013, 43: 41. DOI:10.1016/j.jfluidstructs.2013.08.007 |
| [14] |
GAO Wenjun, NELIAS D, LIU Zhenxia, et al. Numerical investigation of flow around one finite circular cylinder with two free ends[J]. Ocean Engineering, 2018, 156: 373. DOI:10.1016/j.oceaneng.2018.03.020 |
| [15] |
ZDRAVKOVICH M, BRAND V, MATHEW G, et al. Flow past short circular cylinders with two free ends[J]. Journal of Fluid Mechanics, 2006, 203(203): 557. DOI:10.1017/S002211208900159X |
| [16] |
王义乾, 桂南. 第三代涡识别方法及其应用综述[J]. 水动力学研究与进展(A辑), 2019, 34(4): 413. WANG Yiqian, GUI Nan. A review of the third-generation vortex identification method and its applications[J]. Chinese Journal of Hydrodynamics, 2019, 34(4): 413. DOI:10.16076/j.cnki.cjhd.2019.04.001 |
 2022, Vol. 54
2022, Vol. 54


