2. 土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学),哈尔滨 150090
2. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China
混凝土板-柱结构是指板和柱利用节点连接组成的结构。板-柱结构具有可降低层高,管道布置灵活,方便施工等突出优点。板-柱结构除在地上工程应用外,在地下工程也得到大量应用。文献[1-10]在板-柱结构计算理论、设计方法及工程应用等方面开展了一些工作。近年来板-柱结构(无梁楼盖)坍塌事故频发,有必要关注这一领域。
板柱节点在板和柱之间传递荷载效应,在板-柱结构中至关重要。近年来,在国内坍塌的板-柱结构(无梁楼盖)工程有:2014年济南市长清区名流华第项目在建车库无梁楼盖因板柱节点破坏而坍塌,2016年12月广东省河源市雅居乐花园二期工程平板-柱结构地下室坍塌,2017年北京市石景山区西黄村A-E地块的地下车库无梁楼盖坍塌,2018年11月广东省中山市古镇东岸西路的昇海豪庭一期工程的地下室无梁楼盖坍塌,2019年8月1日凌晨江西省南昌市中骏雍景湾5号楼和10号楼之间地下车库无梁楼盖坍塌,2019年8月31日山东省烟台市富力湾地下车库无梁楼盖坍塌。在济南、合肥、河源、秦皇岛、佛山、深圳、鄂尔多斯、天津、北京、沧州、中山、南昌、烟台等地,均发生了无梁楼盖坍塌的事故。在国外坍塌的板-柱结构(无梁楼盖)工程有:1995年韩国三丰百货大楼无梁楼盖坍塌,1997年英国Pipers Row停车场无梁楼盖因板柱节点破坏而坍塌。
当板柱节点及相关区域的板中负弯矩纵筋偏少,板柱节点承受的板传来的弯矩和剪力又较大时,可能发生秃柱头破坏[11]。发生秃柱头破坏是由于板柱节点处剪压区高度较小,节点及其附近板顶纵筋拉应变大,使得柱周边板底区域剪压应变达到极限剪压应变。另一种板柱节点破坏形式是弯冲破坏或冲切破坏。弯冲破坏是柱边高度集中的冲切和弯曲效应共同作用的结果[12-14]。相对剪压区高度是影响节点承载力的因素,相对剪压区高度越小,板柱节点承载力越低。而冲切破坏可近似视为理想刚塑性破坏。破坏前板面的变形很小,破坏时呈脆性[15-30]。
白生翔[31]指出,如果设计中受冲切承载力为满足设计要求的下限值或略低于规范[32-33]的规定,为什么在荷载和材料分项系数以及薄膜效应等提供承载力储备后,无梁楼盖仍在板面荷载处于标准值水平时就发生了坍塌?按照规范[32-33]进行设计,理论上在发生事故的荷载水平下,无梁楼盖不应该发生坍塌。屡见不鲜的无梁楼盖坍塌事故,表明我们对板柱节点和板-柱结构力学行为的一些深层次问题的认识还不清楚。
1 板柱节点冲切或弯冲破坏面的倾角板柱节点的破坏面是指节点发生破坏时的冲切面或弯冲面。板柱节点破坏面的倾角是指破坏面的倾斜区段上下两点的连线与水平面的夹角。板柱节点破坏面的倾角一般介于18.6°~60.0°。表 1汇总了部分文献中的板柱节点冲切或弯冲破坏面倾角试验值。从表 1可看到,冲切或弯冲破坏面倾角试验值离散性较大,广泛分布在18.6°~50.0°。GB 50010—2010《混凝土结构设计规范》(简称《规范》)[32]认为节点破坏面倾角是45°,是为了简化节点承载力计算,也有进一步完善的空间。
| 表 1 冲切或弯冲破坏面倾角试验值 Tab. 1 Test values of inclination angle of punching or bending-punching failure surface |
曹声远等[38]开展了混凝土强度不同的12个板柱节点承载力试验。结合试验结果和相关文献,认为影响冲切或弯冲破坏面倾角的主要因素是板的冲跨比,并通过数据拟合,得到了冲切或弯冲破坏面倾角的计算公式:
| $ \cot \theta=2.1-1.6 / \lambda $ | (1) |
式中θ为冲切或弯冲破坏面倾角,λ为冲跨比。
需指出,板柱节点的冲跨比λ=(∑Mi)/[∑(Vih0i)],Mi为一侧冲切面或弯冲面所辖板宽范围内的负弯矩,Vi为一侧冲切面或弯冲面所承担的剪力,h0i为板截面有效高度;对于梁,λ为计算截面剪跨比,可取λ等于a/h0或M/(Vh0),a为剪跨,M、V分别为所考察截面弯矩计算值和剪力计算值,h0为截面有效高度。可以看到,板柱节点冲跨比计算公式中弯矩和剪力的计算截面的宽度与梁中剪跨比的计算不同。
Bompa等[34]认为冲切或弯冲破坏面倾角与纵筋配筋率、板厚、混凝土和钢筋强度有关。根据试验数据[39-42]拟合了冲切或弯冲破坏面倾角计算公式:
| $ \tan \theta=0.6+\rho f_{\mathrm{y}} / f_{\mathrm{c}}^{\prime}\left(\frac{h_0}{265}\right)^{1 / 2} $ | (2) |
式中:ρ为受拉纵筋配筋率,fy为受拉纵筋抗拉强度,f′c为混凝土圆柱体抗压强度,h0为板有效厚度。
夏成亮等[43]认为冲切或弯冲破坏面倾角主要和柱截面周长与板有效厚度之比以及ρfy/fc有关。根据试验数据拟合了冲切或弯冲破坏面倾角计算公式:
| $ \theta=32\left(C_{\mathrm{c}} / h_0\right)^{-0.12}\left(\rho f_{\mathrm{y}} / f_{\mathrm{c}}\right)^{-0.08} $ | (3) |
式中Cc为柱截面周长,fc为混凝土轴心抗压强度。
林旭健等[44]根据塑性理论,推导了冲切或弯冲破坏面倾角计算公式:
| $ \tan \theta=\frac{2(m-1)}{\sqrt{12 m-3}} $ | (4) |
式中:m=fcm/ftm,其中ftm=vt ft、fcm=vc fc分别是混凝土的塑性有效抗拉、抗压强度,ft为混凝土轴心抗拉强度,vt、vc分别是ft、fc的折减系数。参考Jiang等[45]的研究,取m=10~30,vc=0.35。
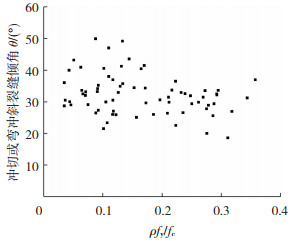
邓清[14]开展了9个不同混凝土强度和纵筋配筋率的板柱节点试件冲切试验。其中发生冲切破坏的试件倾角范围为31.6°~39.8°,平均值35.0°;发生弯冲破坏的试件破坏面倾角范围为26.0°~50.0°,平均值为40.8°。随后,统计了相关文献中的破坏面倾角数据,发现倾角分布范围为18.6°~50.0°,主要分布在25°~35°区间内,见图 1。根据试验数据拟合了冲切或弯冲破坏面倾角计算公式[14]:
| $ \theta=35-20 \rho f_{\mathrm{y}} / f_{\mathrm{c}} $ | (5) |
|
图 1 斜截面倾角统计分析 Fig. 1 Statistical analysis of inclination angle of inclined section |
国内外学者对板柱节点的冲切或弯冲破坏面的倾角认识尚不一致,本文认为应将相应的数据点汇集于以冲切或弯冲破坏面的倾角为纵坐标、分别以纵筋配置特征值ρfy/fc和冲跨比λ= (∑Mi)/[∑(Vih0i)]为两个横坐标的三维坐标系中拟合获得计算结果与试验结果吻合程度相对较好的拟合面方程,对完善板柱节点承载力的计算是必要的。
2 对板柱节点承载力计算公式的分析 2.1 对GB 50010—2010中板柱节点承载力计算公式的分析中国GB 50010—2010《规范》[32]中不配置抗冲切钢筋的板柱节点冲切承载力:
| $ F_1 \leqslant\left(0.7 \beta_{\mathrm{h}} f_{\mathrm{t}}+0.25 \sigma_{\mathrm{pc}, \mathrm{m}}\right) \eta u_{\mathrm{m}} h_0 $ | (6) |
配置抗冲切钢筋时:
| $ \begin{aligned} F_1 \leqslant &\left(0.5 f_{\mathrm{t}}+0.25 \sigma_{\mathrm{pc}, \mathrm{m}}\right) \eta u_{\mathrm{m}} h_0+0.8 f_{\mathrm{yv}} A_{\mathrm{svu}}+\\ & 0.8 f_{\mathrm{y}} A_{\mathrm{sbu}} \sin \alpha \end{aligned} $ | (7) |
式中:F1为冲切荷载,βh为板截面高度影响系数,σpc, m为计算截面周长上两个方向混凝土有效预压应力按长度的加权平均值,η为用来考虑柱截面形状和位置(中柱、边柱和角柱)的影响系数,um为计算冲切截面周长,fyv为箍筋的抗拉强度,Asvu、Asbu分别为与冲切破坏锥体斜截面相交的全部箍筋、弯起钢筋截面面积,α为弯起钢筋在水平方向的倾角。
对于设置柱帽和托板的板-柱结构,柱与柱帽、托板交接处的板截面应满足受冲切承载力的要求。式(6)中,0.7βhftumh0是混凝土剪压区对受冲切承载力的贡献,是由单向受力构件剪压区对斜截面受剪承载力的贡献类推过来的。梁板中混凝土剪压区对斜截面受剪承载力的贡献为0.7βh ftbh0(这里b为梁宽或板宽)。但该项中隐含纵筋销栓作用及其间接影响的贡献,这是因为一般简支构件在支座附近发生斜截面受剪破坏时截面弯矩较小,纵筋远未屈服,销栓作用及纵筋间接影响较大。而实际无梁楼盖中受拉纵筋屈服先于板柱节点破坏,几乎没有销栓作用。这里需要指出,纵筋销栓作用主要是指受拉纵筋,受压纵筋的销栓作用是极其有限的。以C25的混凝土梁板为例,剪压区的纵筋的销栓作用引起的剪应力也就22 N/mm2左右。所以,纵筋销栓作用主要是考虑受拉纵筋的销栓作用。纵筋的销栓作用受到冲跨比、纵筋配置和箍筋配置等的影响。对于无梁楼盖内支座附近斜截面,受拉纵筋屈服前,混凝土剪切变形小,纵筋销栓作用较弱。受拉纵筋屈服后,纵筋应力基本不再增长,抗剪能力不再增加,销栓作用也不再增加。因此,无梁楼盖内支座附近受拉纵筋基本没有销栓作用。
冲跨比λ=(∑Mi)/[∑(Vih0i)],Mi为一侧冲切面或弯冲面所辖板宽范围内的负弯矩,该负弯矩明显小于柱上板带负弯矩,更小于柱上板带的负弯矩加跨中板带的负弯矩。冲跨比较大时,可能会发生板柱节点弯冲破坏。目前《规范》[32]只规定了板柱节点的冲切承载力计算方法,没有给出冲切破坏和弯冲破坏的判据,没有给出弯冲破坏承载力计算公式。受力筋配置不同,剪压区高度也不同,《规范》[32]中相对剪压区高度和剪压区压-剪相关作用对板柱节点承载力的影响尚欠考虑。
2.2 对美国规范ACI 318-19板柱节点承载力计算公式的分析美国规范ACI 318-19[46]不配置抗冲切钢筋的板柱节点承载力计算公式:
| $ F_1 \leqslant V_\rm c $ | (8) |
| $ V_{\mathrm{c}}=\min \left\{\begin{array}{l} 0.17 \beta_{\mathrm{h}}\left(1+\frac{2}{\beta_{\mathrm{c}}}\right) \sqrt{f_{\mathrm{c}}^{\prime}} u_{\mathrm{m}} h_0 \\ 0.083 \beta_{\mathrm{h}}\left(2+\frac{\alpha_{\mathrm{s}} h_0}{u_{\mathrm{m}}}\right) \sqrt{f_{\mathrm{c}}^{\prime}} u_{\mathrm{m}} h_0 \\ 0.33 \beta_{\mathrm{h}} \sqrt{f_{\mathrm{c}}^{\prime}} u_{\mathrm{m}} h_0 \end{array}\right. $ | (9) |
| $ \beta_{\mathrm{h}}=\sqrt{\frac{2}{1+0.004 h_0}} \leqslant 1.0 $ | (10) |
配置抗冲切钢筋时:
| $ V_{\mathrm{T}}=0.5 V_{\mathrm{c}}+f_{\mathrm{y}} A_{\mathrm{sp}}\left(\leqslant 0.5 \sqrt{f_{\mathrm{c}}^{\prime}} u_{\mathrm{m}} h_0\right) $ | (11) |
式中:Vc、VT分别为不配置、配置抗冲切钢筋的板柱节点承载力,βc为柱的长短边之比,αs为柱位置影响系数,Asp为抗冲切钢筋截面面积。该公式未考虑相对剪压区高度的影响,也未考虑压-剪相关作用的影响。
2.3 对欧洲规范EN 1992-1-1:2004板柱节点承载力计算公式的分析欧洲规范EN 1992-1-1:2004[47]中不配置抗冲切钢筋的板柱节点承载力计算公式:
| $ V_{\mathrm{c}}=0.18 k\left(100 \rho_1 f_{\mathrm{c}}^{\prime}\right)^{1 / 3} u_{\mathrm{m}} h_0 $ | (12) |
| $ \rho_1=\sqrt{\rho_x \rho_y} $ | (13) |
| $ k=\left[1+\left(\frac{200}{h_0}\right)^{1 / 2}\right] \leqslant 2 $ | (14) |
配置抗冲切钢筋时:
| $ V_{\mathrm{T}}=0.75 V_{\mathrm{c}}+1.5\left(h_0 / s_{\mathrm{r}}\right) A_{\mathrm{sp}} f_{\mathrm{y}} \sin \alpha $ | (15) |
式中: ρx和ρy分别为板的x和y方向的抗弯钢筋配筋率,sr为抗冲切钢筋间距。该公式考虑了贯穿板柱节点冲切面纵筋配筋率对板柱节点承载力的影响,但未考虑剪压区压-剪相关作用和冲跨比的影响。
2.4 对英国规范BS 8110-1:1997板柱节点承载力计算公式的分析英国规范BS 8110-1:1997[48]不配置抗冲切钢筋的板柱节点冲切承载力计算公式:
| $ V_{\mathrm{c}}=0.79\left(\frac{100 A_{\mathrm{s}}}{u_{\mathrm{m}} h_0}\right)^{\frac{1}{3}}\left(\frac{400}{h_0}\right)^{\frac{1}{4}}\left(\frac{f_{\mathrm{cu}}}{25}\right)^{\frac{1}{3}} u_{\mathrm{m}} h_0 $ | (16) |
配置抗冲切钢筋时:
| $ V_{\mathrm{T}}=V_{\mathrm{cp}}+V_{\mathrm{p}} $ | (17) |
F1≤1.6Vc时:
| $ V_{\mathrm{cp}}=V_{\mathrm{c}} $ | (18) |
| $ V_{\mathrm{p}}=0.95 \sum A_{\mathrm{sp}} f_{\mathrm{y}} \sin \alpha $ | (19) |
1.6Vc≤F1≤2.0Vc时:
| $ V_{\mathrm{cp}}=1.42 V_{\mathrm{c}} $ | (20) |
| $ V_{\mathrm{p}}=0.27 \sum A_{\mathrm{sp}} f_{\mathrm{y}} \sin \alpha $ | (21) |
式中:As为受拉纵筋面积,fcu为混凝土立方体抗压强度。英国规范公式包含了纵筋用量、板厚和混凝土强度等因素,但未考虑剪压区压-剪相关作用和冲跨比的影响。
2.5 对欧洲模式规范MC 2010板柱节点承载力计算公式的分析欧洲模式规范MC 2010[49]不配置抗冲切钢筋的板柱节点承载力计算公式:
| $ V_{\mathrm{c}}=k_\psi \sqrt{f_{\mathrm{c}}^{\prime}} u_{\mathrm{m}} d_{\mathrm{v}} $ | (22) |
| $ k_\psi=\frac{1}{1.5+0.9 k_{\mathrm{dg}} \psi h_0} \leqslant 0.6 $ | (23) |
不考虑内力重分布时:
| $ \psi=1.5 \frac{r_{\mathrm{s}}}{h_0} \frac{f_{\mathrm{y}}}{E_{\mathrm{s}}} $ | (24) |
考虑内力重分布及弯矩影响时:
| $ \psi=1.5 \frac{r_{\mathrm{s}}}{h_0} \frac{f_{\mathrm{y}}}{E_{\mathrm{s}}}\left(\frac{m_{\mathrm{E}}}{m_{\mathrm{R}}}\right)^{1.5} $ | (25) |
配置抗冲切钢筋时板柱节点承载力:
| $ V_{\mathrm{T}}=V_{\mathrm{cp}}+V_{\mathrm{p}} $ | (26) |
| $ V_{\mathrm{cp}}=k_\psi \sqrt{f_{\mathrm{c}}^{\prime}} u_{\mathrm{m}} h_0 $ | (27) |
| $ V_{\mathrm{p}}=\frac{A_{\mathrm{sp}}}{s_{\mathrm{r}}} h_0 f_{\mathrm{y}} \cot \alpha $ | (28) |
式中:ψ为板破坏时的转角;dv为截面的抗剪有效高度;kdg为考虑最大骨料粒径影响的系数,取kdg≥1.15;rs为反弯点到柱轴线距离;Es为抗弯钢筋的弹性模量;mE为荷载作用下单位长度的弯矩值;mR为单位长度的抵抗弯矩。该公式考虑了作用弯矩与抵抗弯矩的比值和反弯点到柱的距离等关键因素对板柱节点承载力的影响,但未考虑剪压区高度对板柱节点承载力的影响。
3 对于板柱节点承载力计算公式中板的截面高度影响分析 3.1 各个规范关于截面高度对板柱节点承载力的考虑由2节可知,各个规范中板厚对板柱节点承载力是有影响的。中国《规范》[32]考虑截面高度对板柱节点承载力中的混凝土项贡献的影响或梁高对梁斜截面受剪承载力中混凝土项贡献的影响。在板柱节点承载力或梁斜截面受剪承载力计算公式中引入了截面高度影响系数βh。对板柱节点承载力计算,当板厚d≤800 mm时,取βh=1.0;当板厚d≥2 000 mm时,取βh=0.9;其间线性插值。对于梁斜截面受剪承载力计算,βh=(800/h0)1/4,当h0 < 800 mm时,取800 mm;当h0>2 000 mm,取2 000 mm。
美国规范ACI 318-19[46]也在不配置抗剪或抗冲切钢筋的计算公式中引入了系数βh考虑截面高度的影响,$\beta_{\mathrm{h}}=\sqrt{\frac{2}{1+0.004 h_0}} \leqslant 1$。
欧洲规范EN 1992-1-1:2004[47]在不配置增强节点斜截面受剪承载力的钢筋的计算公式中引入了系数k以考虑尺寸效应,$k=\left[1+\left(\frac{200}{h_0}\right)^{1 / 2}\right] \leqslant 2$。
英国规范BS 8110-1:1997[48]在不配置增强节点斜截面受剪承载力的钢筋的计算公式中引入了系数$\left(\frac{400}{h_0}\right)^{1 / 4}$,以考虑截面高度的影响。
欧洲模式规范MC 2010[49]在不配置增强节点斜截面受剪承载力的钢筋的计算公式中引入了系数kψ,$k_\psi=\frac{1}{1.5+0.9 k_{\mathrm{dg}} \psi h_0} \leqslant 0.6$,该系数反映了多个因素的影响,包括h0对受剪承载力的影响。
3.2 关于各个规范中板厚对板柱节点承载力影响考虑方法的分析各国规范关于板厚对板柱节点承载力的考量各不相同,有必要具体分析一下板厚或梁高对板柱节点承载力或梁斜截面受剪承载力的影响规律。
本文收集了以截面高度为变量的板或梁斜截面受剪承载力试验数据,见图 2。两组试验均未配置增强节点斜截面受剪承载力的钢筋。

|
图 2 截面高度对Vc/(0.7ftbh0)的影响 Fig. 2 Effect of section height h0 on Vc/(0.7ftbh0) |
从图 2可看出,第一组试件截面有效高度h0>125 mm时、第二组试件截面有效高度h0>203 mm时,$\frac{V_\rm c}{0.7 f_\rm t b h_0} < 1$。随着截面有效高度h0的增加,$\frac{V_\rm c}{0.7 f_{\mathrm{t}} b h_0}$逐渐减小。
两组试验中,$\frac{V_\rm c}{0.7 f_{\mathrm{t}} b h_0}$随截面有效高度增加而减小的速度略有不同。截面有效高度在1 000 mm以内时,第一组试验$\frac{V_{\mathrm{c}}}{0.7 f_{\mathrm{t}} b h_0}$下降速度相对较慢,第二组试验$\frac{V_{\mathrm{c}}}{0.7 f_{\mathrm{t}} b h_0}$下降速度相对较快。这是由于两组试件斜裂缝两侧骨料咬合不一样。骨料粒径、配合比不同会引起骨料咬合作用的不同。试件的混凝土强度等级越高,内部骨料用量越小,咬合作用越弱。
将收集到的试验数据置于同一坐标系内,拟合了$\frac{V_{\mathrm{c}}}{0.7 f_{\mathrm{t}} b h_0}$与截面有效高度h0的关系式,并与规范公式进行了对比,见图 3。拟合得到关系式:
| $ \frac{V_{\mathrm{c}}}{0.7 f_{\mathrm{t}} b h_0}=\left(\frac{150}{h_0}\right)^{4 / 9} $ | (29) |

|
图 3 截面高度影响系数的比较 Fig. 3 Comparison of influence coefficients of section height |
从图 3可看出,随着板或梁截面有效高度逐渐增大,尤其是高度在1 000 mm以内时,$\frac{V_\rm c}{0.7 f_{\mathrm{t}} b h_0}$下降速度较快,而《规范》[32]在板厚h0>800 mm时才开始考虑截面高度增加对斜截面受剪承载力的削弱作用,不能较好地反映这种影响。相比之下,式(29)能更好地表示这种不利作用,且结果偏于安全。因此建议取$\beta_{\mathrm{h}}=\left(\frac{150}{h_0}\right)^{4 / 9}$,h0≤150 mm时,取h0=150 mm。
4 结论1) 板柱节点发生冲切或弯冲破坏时破坏面的倾角目前还没有统一的计算方法,应综合考虑纵筋配置特征值ρfy/fc和冲跨比λ=(∑Mi)/[∑(Vih0i)]对破坏面与水平面所夹倾角的影响。
2) 冲跨比相对较小时,无梁楼盖板柱节点发生冲切破坏;冲跨比相对较大时,无梁楼盖板柱节点发生弯冲破坏。中国《规范》给出了小冲跨比的板柱节点受冲切承载力公式,没有给出发生冲切破坏和弯冲破坏的判据,没有给出弯冲破坏承载力计算公式。
3) 中国《规范》中板柱节点承载力计算公式是基于板中纵筋高量配置下的试验结果建立的,包括纵筋销栓作用及其间接影响对承载力的贡献。实际无梁楼盖板柱节点纵筋屈服是先于板柱节点破坏的,纵筋的销栓作用并不明显。板与柱相交处既是冲切或弯冲控制截面,也是负弯矩控制截面,应考虑混凝土的压-剪相关性。
| [1] |
郑文忠. 后张预应力混凝土平板-柱结构计算理论及设计方法的研究[D]. 南京: 东南大学, 1994 ZHENG Wenzhong. Research on calculation theory and design method for post-tensioned prestressed concrete slab-column structures[D]. Nanjing: Southeast University, 1994 |
| [2] |
郑文忠. 后张预应力混凝土平板-柱结构设计与工程实例[M]. 哈尔滨: 黑龙江科学技术出版社, 1999.
|
| [3] |
郑文忠, 俞伟根, 吕志涛. 后张无粘结预应力平板-柱结构合理计算模式和方法的研究[J]. 工程力学, 1995, 2(3): 39. ZHENG Wenzhong, YU Weigen, LÜ Zhitao. Research on reasonable calculation scheme for unbonded post-tensioned flat-column structures[J]. Engineering Mechanics, 1995, 2(3): 39. |
| [4] |
郑文忠, 俞伟根, 吕志涛. 后张预应力平板-柱结构实用设计方法的研究[J]. 东南大学学报(自然科学版), 1994, 24(6): 32. ZHENG Wenzhong, YU Weigen, LÜ Zhitao. Research on practical method for design of post-tensioned flat slab-column structures[J]. Journal of Southeast University, 1994, 24(6): 32. |
| [5] |
郑文忠, 吕志涛. 后张预应力平板-柱结构设计软件编制方法的研究[J]. 工业建筑, 1995, 25(6): 17. ZHENG Wenzhong, LÜ Zhitao. Research on computer programming method in design of post-tensioned flat slab-column structures[J]. Industrial Construction, 1995, 25(6): 17. |
| [6] |
郭楠, 郑文忠. 板-柱结构在竖向荷载作用下的弯矩分布规律研究[J]. 工业建筑, 2008, 38(增刊1): 174. GUO Nan, ZHENG Wenzhong. Research on moment distribution law of plate-column structure subjected to vertical loads[J]. Industrial Construction, 2008, 38(S1): 174. |
| [7] |
郭楠, 郑文忠. 板-柱结构设计相关问题[J]. 哈尔滨工业大学学报, 2007, 39(6): 1206. GUO Nan, ZHENG Wenzhong. Correlative problems in design of plate-column structures[J]. Journal of Harbin Institute of Technology, 2007, 39(6): 1206. |
| [8] |
郑文忠, 张格明, 王英. 柱支承板变形计算的双向板带叠加法及裂缝验算建议方法[J]. 工业建筑, 2006, 36(11): 52. ZHENG Wenzhong, ZHANG Geming, WANG Ying. Two-way slab strip superposition method for calculation of plate center deflection and recommendatory method on crack check in flat plate supported by column[J]. Industrial Construction, 2006, 36(11): 52. DOI:10.3321/j.issn:1000-8993.2006.11.013 |
| [9] |
郑文忠, 周威. 后张预应力混凝土平板-柱工程平板塌陷与复位[J]. 哈尔滨工业大学学报, 2004, 36(4): 463. ZHENG Wenzhong, ZHOU Wei. Reposition and reinforcement of subsidence for flat slabs of a post-prestressed concrete flat slab-column construction[J]. Journal of Harbin Institute of Technology, 2004, 36(4): 463. DOI:10.3321/j.issn:0367-6234.2004.04.014 |
| [10] |
王晓东, 郑文忠, 王英. 柱支承无粘结预应力混凝土双向板内力重分布[J]. 哈尔滨工业大学学报, 2014, 46(12): 1. WANG Xiaodong, ZHENG Wenzhong, WANG Ying. Internal force redistribution of unbonded prestressed concrete flat plates[J]. Journal of Harbin Institute of Technology, 2014, 46(12): 1. |
| [11] |
高文皂, 焦亚洲, 赵婉君. 对无梁楼盖地库坍塌问题的思索[J]. 建筑结构, 2019, 49(增刊2): 199. GAO Wenzao, JIAO Yazhou, ZHAO Wanjun. Thoughts on the collapse of the basements of the beamless floor[J]. Building Structure, 2019, 49(S2): 199. DOI:10.19701/j.jzjg.2019.S2.037 |
| [12] |
余志武. 钢筋砼板和基础的极限承载力计算及破坏类型判别方法[J]. 建筑结构学报, 1990, 11(4): 46. YU Zhiwu. Ultimate strength and criterion of failure types of reinforced concrete slabs and footings[J]. Journal of Building Structures, 1990, 11(4): 46. DOI:10.14006/j.jzjgxb.1990.04.006 |
| [13] |
林旭健, 郑作樵, 钱在兹. 混凝土弯冲板的破坏机构与极限强度[J]. 工程力学, 2003(1): 60. LIN Xujian, ZHENG Zuoqiao, QIAN Zaizi. New collapse mechanism and ultimate punching shear strength of reinforced concrete slabs[J]. Engineering Mechanics, 2003(1): 60. DOI:10.3969/j.issn.1000-4750.2003.01.011 |
| [14] |
邓清. 板柱节点冲切受力性能及承载力计算方法研究[D]. 长沙: 湖南大学, 2018 DENG Qing. Study on punching shear behavior and capacity of reinforced concrete slab-column connections[D]. Changsha: Hunan University, 2018 |
| [15] |
张正雨. 混凝土板抗冲切性能的研究与分析[D]. 杭州: 浙江大学, 2006 ZHANG Zhengyu. Study on punching shear performance of reinforced concrete slabs[D]. Hangzhou: Zhejiang University, 2006 |
| [16] |
舒兆发. 板柱结构边柱节点的受冲切承载力[J]. 湖南大学学报(自然科学版), 2007(1): 19. SHU Zhaofa. Punching capacity of slab-column edge connections[J]. Journal of Hunan University (Natural Sciences), 2007(1): 19. DOI:10.3321/j.issn:1000-2472.2007.01.005 |
| [17] |
许清风, 蒋永生, 梁书亭, 等. 板柱节点的破坏形式及改进方法[J]. 建筑科学, 1999(6): 21. XU Qingfeng, JIANG Yongsheng, LIANG Shuting, et al. Failure types and improvement methods of slab-column connections[J]. Building Science, 1999(6): 21. DOI:10.3969/j.issn.1002-8528.1999.06.005 |
| [18] |
王必刚. 板柱结构静力弹塑性分析与试验研究[D]. 杭州: 浙江大学, 2007 WANG Bigang. Nonlinear static analysis and test research on slab-column structure[D]. Hangzhou: Zhejiang University, 2007 |
| [19] |
易伟建, 洪枫, 彭检. 钢筋混凝土板柱节点抗冲切试验研究[J]. 建筑结构, 2016, 46(15): 11. YI Weijian, HONG Feng, PENG Jian. Experimental investigation of punching shear failure of reinforced concrete slab-column connections[J]. Building Structure, 2016, 46(15): 11. DOI:10.19701/j.jzjg.2016.15.003 |
| [20] |
梁书亭, 蒋永生, 刘美景, 等. 关于板柱节点受冲切承载力的讨论[J]. 工业建筑, 2003(3): 68. LIANG Shuting, JIANG Yongsheng, LIU Meijing, et al. Discussion on punching shear resistance capacity of slab-column connections[J]. Industrial Construction, 2003(3): 68. DOI:10.3321/j.issn:1000-8993.2003.03.023 |
| [21] |
曹明, 龚绍熙. 钢筋混凝土板柱节点弯冲界限破坏的分析[J]. 福州大学学报(自然科学版), 1996(增刊1): 186. CAO Ming, GONG Shaoxi. Analysis of flexural impact limit failure of reinforced concrete slab-column connections[J]. Journal of Fuzhou University (Natural Science), 1996(S1): 186. |
| [22] |
田文秀. 钢筋混凝土板及钢筋钢纤维混凝土板的抗冲切性能研究[D]. 西安: 长安大学, 2008 TIAN Wenxiu. Study on reinforced concrete slabs and steel fiber reinforced concrete slabs subjected to punching shear[D]. Xi'an: Chang'an University, 2008 |
| [23] |
洪枫. 钢筋混凝土板柱节点冲切破坏试验研究[D]. 长沙: 湖南大学, 2015. HONG Feng. Experimental study on punching shear failure of reinforced concrete slabs-column connection[D]. Changsha: Hunan University, 2015 |
| [24] |
吴强, 程文瀼, 杜新年. 混凝土板柱结构中柱节点承载力及破坏形态的研究[J]. 工业建筑, 2004(4): 43. WU Qiang, CHENG Wenrang, DU Xinnian. The bearing capacity and failure modes study of interior connections in RC slab-column structures[J]. Industrial Construction, 2004(4): 43. DOI:10.3321/j.issn:1000-8993.2004.04.013 |
| [25] |
何芳. 钢筋混凝土板冲切性能试验研究[D]. 银川: 宁夏大学, 2017 HE Fang. Experimental study on punching shear performance of reinforced concrete slabs[D]. Yinchuan: Ningxia University, 2017 |
| [26] |
吴丽丽, 王芮. 板柱结构节点破坏形态及受力性能研究[J]. 建筑技术, 2015, 46(8): 733. WU Lili, WANG Rui. Progress of research on failure modes and mechanical behavior of joints of slab-column structures[J]. Architecture Technology, 2015, 46(8): 733. DOI:10.13731/j.issn.1000-4726.2015.08.017 |
| [27] |
隆发权. 钢筋混凝土板柱结构节点区域板的抗冲切性能研究[D]. 重庆: 重庆大学, 2014 LONG Faquan. Study on punching shear performance of slab around the joint area of reinforced concrete slab-column structure[D]. Chongqing: Chongqing University, 2014 |
| [28] |
邱鹏. 竖向荷载下板柱内节点冲切承载力与变形研究[D]. 重庆: 重庆大学, 2015 QIU Peng. Study on punching capacity and deformation of interior slab-column connections under vertical load[D]. Chongqing: Chongqing University, 2015 |
| [29] |
韦锋, 任子华, 张俊华. 钢筋混凝土板柱节点抗冲切性能研究综述[J]. 建筑结构, 2020, 50. WEI Feng, REN Zihua, ZHANG Junhua. State of the art of research on punching shear behavior of reinforced concrete slab-column connections[J]. Building Structure, 2020, 50(S2): 499. |
| [30] |
郑愚, 李春红, 于国友. 基于压缩薄膜效应对无梁楼盖中钢筋混凝土板柱节点极限冲切承载力的计算方法[J]. 东莞理工学院学报, 2010, 17(5): 99. ZHENG Yu, LI Chunhong, YU Guoyou. Predicting ultimate punching strength of slab-column connections in flat slabs based on compressive membrane action[J]. Journal of Dongguan University of Technology, 2010, 17(5): 99. DOI:10.3969/j.issn.1009-0312.2010.05.023 |
| [31] |
白生翔. 无梁楼盖倒塌的原因[Z/OL]. (2019-08-05). http://www.360doc.com/content/19/0805/07/3887277_853042825.shtml
|
| [32] |
混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2010 Code for design of concrete structures: GB 50010—2010[S]. Beijing: China Architecture & Building Press, 2010 |
| [33] |
建筑结构荷载规范: GB 50009—2012[S]. 北京: 中国建筑工业出版社, 2012 Load code for the design of building structures: GB 50009—2012[S]. Beijing: China Architecture & Building Press, 2012 |
| [34] |
BOMPA D V, ONET T. Punching shear strength of RC flat slabs at interior connections to columns[J]. Magazine of Concrete Research, 2016, 68(1): 24. DOI:10.1680/macr.14.00402 |
| [35] |
邹品增. 柱截面形状对板柱节点受冲切性能影响的试验研究[D]. 长沙: 湖南大学, 2015 ZOU Pinzeng. Experimental study on column section shape role in punching shear performance of slab-column connection[D]. Changsha: Hunan University, 2015 |
| [36] |
彭检. 钢筋混凝土板柱节点抗冲切试验研究[D]. 长沙: 湖南大学, 2013 PENG Jian. Experimental study on punching shear failure of reinforced concrete slabs-column connections[D]. Changsha: Hunan University, 2013 |
| [37] |
林旭健. 钢纤维高强混凝土板抗冲切受力性能研究[D]. 杭州: 浙江大学, 1999 LIN Xujian. Research on the mechanical behavior of steel fiber reinforced high strength concrete slabs subjected to punching shear[D]. Hangzhou: Zhejiang University, 1999 |
| [38] |
曹声远, 郭晓林. 钢筋砼冲切破坏机理及冲切强度理论[C]//混凝土结构基本理论及应用第二届学术讨论会论文集(第二卷). 北京: [s. n. ], 1990: 283
|
| [39] |
GUANDALINI S, BURDET O, MUTTONI A. Punching tests of slabs with low reinforcement ratios[J]. ACI Structural Journal, 2009, 106(1): 87. DOI:10.14359/56287 |
| [40] |
HALLGREN M. Punching shear capacity of reinforced high strength concrete slabs[D]. Stockholm: KTH Royal Institute of Technology, 1996
|
| [41] |
HEGGER J, RICKER M, SHERIF A G. Punching strength of reinforced concrete footings[J]. ACI Structural Journal, 2009, 106(5): 706. DOI:10.14359/51663111 |
| [42] |
HEINZMANN D, ETTER S, VILLIGER S, et al. Punching tests on reinforced concrete slabs without shear reinforcement[J]. ACI Structural Journal, 2012, 109(6): 787. DOI:10.14359/51684122 |
| [43] |
夏成亮, 史庆轩, 王震. 无抗冲切钢筋的RC板柱节点受冲切承载力计算[J]. 哈尔滨工业大学学报, 2022, 54(4): 18. XIA Chengliang, SHI Qingxuan, WANG Zhen. Calculation of punching shear capacity of RC slab-column connections without shear reinforcement[J]. Journal of Harbin Institute of Technology, 2022, 54(4): 18. DOI:10.11918/202106064 |
| [44] |
林旭健, 郑作樵, 钱在兹. 钢纤维高强混凝土冲切板的试验研究[J]. 建筑结构学报, 2003(5): 77. LIN Xujian, ZHENG Zuoqiao, QIAN Zaizi. Research on steel fiber high-strength concrete slab subjected to punching shear[J]. Journal of Building Structures, 2003(5): 77. DOI:10.3321/j.issn:1000-6869.2003.05.010 |
| [45] |
JIANG D H, SHEN J H. Strength of concrete slabs in punching shear[J]. Journal of Structural Engineering, 1986, 112(12): 2578. DOI:10.1061/(ASCE)0733-9445(1986)112:12(2578) |
| [46] |
Building code requirements for structural concrete: ACI 318-19[S]. Farming Hills: American Concrete Institute, 2019
|
| [47] |
Eurocode 2: design of concrete structures—part 1-1: general rules and rules for buildings: EN 1992-1-1: 2004[S]. Brussels: European Committee for Standardization, 2004
|
| [48] |
Structural use of concrete: partⅠ: code of practice for design and construction: BS 8110-1: 1997[S]. London: British Standards Institution, 1997
|
| [49] |
CEB-FIP fib model code for concrete structures 2010: MC 2010[S]. Berlin: International Federation for Structural Concrete, 2013
|
 2022, Vol. 54
2022, Vol. 54


