2. 土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学),哈尔滨 150090
2. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China
网格箍筋约束混凝土方柱在实际工程中大量存在,合理配置网格箍筋约束高强混凝土可明显提高柱的承载能力和变形能力[1],然而GB 50010—2010《混凝土结构设计规范》[2]中没有给出其轴心受压承载力计算公式。约束高强混凝土方柱达到轴压承载力时,网格箍筋不一定屈服[3-6]。若按网格箍筋屈服计算其提供的侧向约束,网格箍筋的约束作用和网格箍筋约束混凝土柱的受压承载力可能会被高估。规范[2]中一、二、三级框架柱的箍筋配置一般为中、低约束水平,为判断约束混凝土峰值压应力下网格箍筋屈服与否,需研究确定不同强度的网格箍筋能够屈服的体积配箍率下限值。国内外学者对约束混凝土峰值压应力下箍筋拉应力的计算方法有回归分析法[3-4, 7-8]和迭代法[9],迭代法步骤繁琐,不便于实际工程应用。文献[3-4, 7-8]均提出了峰值荷载下的箍筋拉应变预测公式,但文献[3-4, 7]提出的公式在不配置箍筋时所算得的箍筋拉应变为正值,不够准确;文献[8]提出的公式将箍筋屈服强度作为影响因素,不够准确。本文基于峰值荷载下箍筋未屈服的试验数据,得到了约束混凝土柱峰值受压荷载下的箍筋拉应变计算公式,该公式考虑了体积配箍率、有效约束系数、箍筋弹性模量和混凝土轴心抗压强度的影响。已有的约束混凝土受压应力-应变关系曲线大多是用箍筋屈服强度代替箍筋的真实拉应力来考虑箍筋的约束效果[10-11],不够准确。因此,基于峰值压应力下箍筋的实际拉应力,提出网格箍筋约束高强混凝土峰值压应力、峰值压应变的计算公式,建立其轴心受压应力-应变关系模型,具有重要意义。
1 试验概况 1.1 试件设计与制作42根网格箍筋约束高强混凝方柱的试件设计见图 1和表 1。试件截面为400 mm×400 mm,高度为1 300 mm。非约束混凝土轴心抗压强度为50.0、57.2、63.6、68.0 MPa。箍筋采用HRB400、HRB500、HRB600、PC800、PC1 270和1 570 MPa钢丝,体积配箍率为1.0%~1.6%,试验段箍筋间距s为40~100 mm,加密区箍筋间距为40 mm。采用了A、B两种形式的箍筋,见图 1(a)和1(b),箍筋保护层厚度为10 mm。纵筋采用直径为10 mm的HRB400钢筋。混凝土的基本力学性能指标见表 2,钢筋的基本力学性能指标见表 3、4。

|
图 1 试件设计(mm) Fig. 1 Specimen design(mm) |
| 表 1 试件设计参数 Tab. 1 Specimen design parameters |
| 表 2 混凝土基本力学性能指标 Tab. 2 Basic mechanical properties of concrete |
| 表 3 热轧钢筋基本力学性能指标 Tab. 3 Basic mechanical properties of hot rolled steel bars |
| 表 4 高强预应力筋基本力学性能指标 Tab. 4 Basic mechanical properties of high-strength prestressed reinforcement |
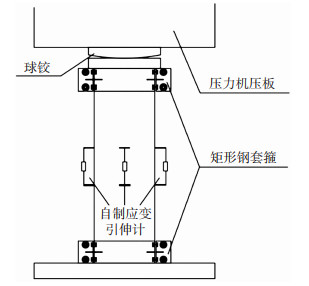
用自制的应变引伸计测量约束混凝土的纵向应变,自制应变引伸计由电阻式位移计、固定板、承托板和金属接长杆组成,在柱每个侧面中部各布置一个标距为250 mm的应变引伸计,金属接长杆插入柱子内部50 mm,应变引伸计布置见图 2。
|
图 2 应变引伸计布置和加载装置 Fig. 2 Strain extensometer layout and loading device |
加载前,在试件中部相对的两个侧面分别粘贴1个混凝土应变片,在外圈箍筋角部粘贴4圈共8个应变片,在内圈箍筋端部粘贴4圈共8个应变片,任选2根纵筋在其中部粘贴应变片。试验在3 000 t压力试验机上完成,加载装置见图 2、3。

|
图 3 3 000 t试验机加载装置 Fig. 3 Loading device of 3 000 t testing machine |
为防止加载时试件端部先于试件中部区段发生破坏,在方柱上下端各放置高度为125 mm的方形钢板套箍进行局部加固,钢套箍设计见图 4。试验采用力-位移双控制度,在70%预估峰值荷载前用力控制加载,之后用位移控制加载。

|
图 4 套箍设计(mm) Fig. 4 Hoop design(mm) |
加载初期,试件处于弹性阶段,表面未出现明显现象,箍筋拉应变增长缓慢。荷载达到峰值荷载的65%~85%时,柱中出现第一条竖向裂缝。此时外围混凝土压应变为1.7×10-3~2.3×10-3,约为非约束混凝土峰值压应变的0.6~0.8倍。随着荷载的继续增加,伴随着噼里啪啦的开裂声,竖向裂缝不断增多、扩展和延伸,混凝土保护层开始剥落。裂缝出现后,箍筋拉应变增长加快,约束混凝土压应力的提高主要依靠箍筋提供的侧向约束应力,约束混凝土的受压应力-应变曲线上升段开始变缓。
峰值荷载时刻,混凝土保护层已开始成块大面积脱落。此时用高强预应力筋制作的约束箍筋均未屈服,热轧钢筋制作的约束箍筋部分屈服,具体的箍筋屈服与否情况见表 5。峰值荷载后,约束混凝土横向膨胀加快,箍筋拉应变继续增大,未屈服的箍筋可以为核心区混凝土提供更大的侧向约束应力,试件表现出较好的变形性能。试验发现,用高强预应力筋制作的箍筋在荷载降至峰值荷载的75%~90%左右时才屈服,峰值荷载时的试件损伤情况见图 5。
| 表 5 试验结果 Tab. 5 Test results |

|
图 5 峰值荷载时的损伤状况 Fig. 5 Damage condition under peak load |
荷载降至峰值荷载的40%~45%时,C-17、C-18、C-27、C-42的箍筋破断,破断位置仅有一处且位于试件中部,箍筋破断形态见图 6。荷载降至峰值荷载的40%以下时停止加载,此时纵筋屈曲。试件最终破损形态见图 7。

|
图 6 箍筋破断状态 Fig. 6 State of stirrup breaking |

|
图 7 试验结束后试件破损状态 Fig. 7 Damaged state of specimen after test |
试验测得的荷载由试件的3部分来承担:核心区外非约束混凝土、纵筋和箍筋所约束的核心区混凝土。核心区混凝土承担的荷载为实测荷载减去纵筋和保护层承担的荷载。试验数据结果见表 5。
C-1~C-42的约束混凝土轴压应力-应变关系实测曲线见图 8,其中σc为约束混凝土压应力,εc为约束混凝土压应变,黑色圆点为箍筋破断时约束混凝土的应力-应变点。体积配箍率相同,且约束混凝土峰值压应力下箍筋未屈服时,箍筋的强度等级对约束混凝土峰值压应力的影响不大,但对其变形性能影响较大。箍筋屈服强度越高,体积配箍率越大,下降段越缓,网格箍筋约束高强混凝土的变形能力越好。

|
图 8 约束混凝土轴压应力-应变关系实测曲线 Fig. 8 Measured curves of compressive stress and strain of confined concrete |
C-1~C-42的约束混凝土压应力与箍筋拉应变关系实测曲线见图 9,其中σc为约束混凝土压应力,εs为箍筋拉应变,黑色圆点表示箍筋拉应变达到屈服应变。

|
图 9 约束混凝土压应力与箍筋拉应变关系实测曲线 Fig. 9 Measured curves of confined concrete compressive stress and stirrup tensile strain |
基于试验结果,约束混凝土峰值压应力下,33个试件的箍筋未屈服,峰值压应力下箍筋的拉应变与混凝土轴心抗压强度、体积配箍率和箍筋间距有关。
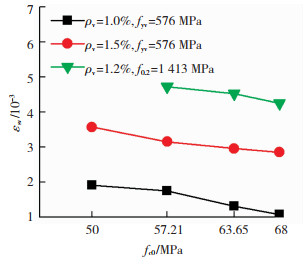
3.1 非约束混凝土轴心抗压强度对箍筋应力水平发挥的影响约束混凝土峰值压应力下的箍筋拉应变与非约束混凝土轴心抗压强度的关系见图 10。可以看出两者呈负相关,这是因为箍筋对混凝土的约束为被动约束,箍筋拉应力水平的发挥依赖于混凝土的侧向膨胀,非约束混凝土轴心抗压强度越高,其脆性越大,变形能力越差,不利于箍筋拉应力的发挥。
|
图 10 混凝土轴心抗压强度的影响 Fig. 10 Influence of axial compressive strength of concrete |
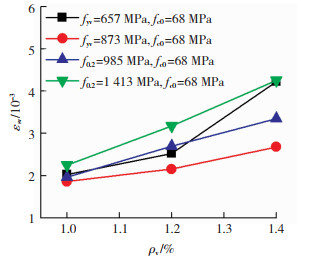
约束混凝土峰值压应力下的箍筋拉应变与体积配箍率的关系见图 11。约束箍筋抗拉强度相同时,体积配箍率越高,峰值荷载下箍筋拉应变越大。
|
图 11 体积配箍率的影响 Fig. 11 Influence of volume stirrup ratio |
约束混凝土峰值荷载下的箍筋拉应变与箍筋屈服强度的关系见图 12。箍筋未屈服时,箍筋的屈服强度对于箍筋拉应力水平的发挥影响不大。原因是箍筋弹性模量相同,屈服前箍筋始终处于弹性变形阶段。

|
图 12 约束箍筋屈服强度的影响 Fig. 12 Influence of yield strength of stirrups |
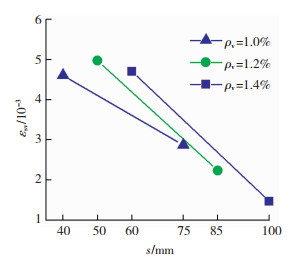
约束混凝土峰值荷载下的箍筋拉应变与箍筋间距的关系见图 13。体积配箍率和箍筋屈服强度相同时,峰值荷载下约束箍筋的拉应变随约束箍筋间距的减小而增大。
|
图 13 约束箍筋间距的影响 Fig. 13 Influence of stirrup spacing |
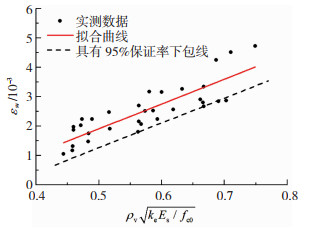
为考虑箍筋间距、形式以及纵筋布置对箍筋拉应力水平的影响,引入有效约束系数ke。约束混凝土峰值压应力下的箍筋应变与体积配箍率和有效约束系数呈正相关,与非约束混凝土轴心抗压强度呈负相关。将约束混凝土峰值压应力下箍筋的实际拉应变与
|
图 14 箍筋拉应变拟合曲线和具有95%保证率下包线 Fig. 14 Stirrup tensile strain fitting curve and envelope with 95% guarantee rate |
| $ \varepsilon_{\mathrm{sv}, \mathrm{f}}=0.0084 \rho_{\mathrm{v}} \sqrt{k_{\mathrm{e}} E_{\mathrm{s}} / f_{\mathrm{c} 0}}-0.0023 $ | (1) |
| $ \varepsilon_{\mathrm{sv}, \mathrm{n}}=0.0084 \rho_{\mathrm{v}} \sqrt{k_{\mathrm{e}} E_{\mathrm{s}} / f_{\mathrm{c} 0}}-0.00295 $ | (2) |
式中:εsv, f表示约束混凝土峰值压应力下箍筋拉应变的预测值;ρv为体积配箍率;ke为网格式箍筋约束混凝土方柱的有效约束系数,ke=[(1-∑ωi2/6Acor)(1-s/2bcor)2]/(1-ρs),其中ωi为相邻纵筋间的水平距离,Acor为约束混凝土核心区面积,s为箍筋间距,bcor为约束混凝土核心区边长,ρs为纵筋配筋率;Es为钢材弹性模量;fc0为非约束混凝土轴心抗压强度;εsv, n为具有95%保证率的箍筋拉应变预测值[11]。
文献[3-4, 7-8]给出的峰值压应力下箍筋不屈服时的拉应变计算公式见表 6,图 15将表中各式箍筋拉应力预测值与本文试验值进行了比较,结果表明本文的计算公式拟合效果相对较好。
| 表 6 约束混凝土峰值压应力下箍筋不屈服时的拉应变预测公式 Tab. 6 Prediction formula of tensile strain of stirrups under peak compressive stress of confined concrete |

|
图 15 预测公式计算值与试验值比较 Fig. 15 Comparison of calculated and experimental values of prediction formula |
当体积配箍率低于一定值时,算得的峰值荷载下箍筋拉应变为零甚至负值,这是因为当配箍率较低、箍筋间距较大时,箍筋基本上不再发挥约束作用。规范[2]中对一级、二级、三四级抗震设计区箍筋加密区最小体积配箍率的规定分别为0.8%、0.6%和0.4%。取ke=0.7,Es=2.05×105 MPa,ρv=0.4%,混凝土强度等级为C30~C80,用式(1)算得的峰值荷载下箍筋拉应变见表 7。说明若加密区体积配箍率刚好满足规范的最低要求,该公式认为当混凝土强度高于C70时,箍筋不再对混凝土发挥约束作用。
| 表 7 按规范最低要求算得的峰值荷载下箍筋拉应变 Tab. 7 Tensile strain of stirrups under peak load calculated according to the minimum requirements of the code |
对于有明显屈服点的热轧钢筋,将箍筋拉应变预测公式(1)与式(3)联立,得到热轧箍筋能够屈服的体积配箍率下限值计算公式,见式(4)。
| $ f_{\mathrm{yv}}=E_{\mathrm{s}} \varepsilon_{\mathrm{yv}} $ | (3) |
| $ \rho_{\mathrm{v}, \min }=\frac{\left(0.0023 E_{\mathrm{s}}+f_{\mathrm{yv}}\right) \sqrt{f_{\mathrm{c} 0}}}{0.0084 \sqrt{E_{\mathrm{s}}^3 k_{\mathrm{e}}}} $ | (4) |
对于无明显屈服点的高强预应力筋,将箍筋拉应变预测公式(1)与式(5)联立,得到PC钢棒箍筋能够屈服的体积配箍率下限值计算公式,见式(6)。低于此体积配箍率下限值时,就要按箍筋不屈服来考虑,用式(1)来计算约束混凝土峰值压应力下箍筋的实际拉应力。
| $ f_{0.2}=E_{\mathrm{s}}\left(\varepsilon_{\mathrm{yv}}-0.002\right) $ | (5) |
| $ \rho_{\mathrm{v}, \min }=\frac{\left(0.0043 E_{\mathrm{s}}+f_{0.2}\right) \sqrt{f_{\mathrm{c} 0}}}{0.0084 \sqrt{E_{\mathrm{s}}^3 k_{\mathrm{e}}}} $ | (6) |
箍筋提供的侧向约束应力使约束混凝土抗压强度得以提高,试验发现约束混凝土峰值压应力和峰值压应变的提高倍数与约束程度(有效约束应力/非约束混凝土轴心抗压强度)近似呈线性关系。以箍筋的实际拉应力水平下的约束程度为横坐标,峰值压应力和峰值压应变提高倍数为纵坐标,拟合关系曲线见图 16、17,线性拟合公式见式(7)、(8)。
| $ {f_{{\rm{cc}}}} = {f_{{\rm{c}}0}}\left( {1 + 4.58{\sigma _{l{\rm{e}}}}/{f_{{\rm{c}}0}}} \right) $ | (7) |
| $ {\varepsilon _{{\rm{cc}}}} = {\varepsilon _{{\rm{c}}0}}\left( {1 + 7.9{\sigma _{l{\rm{e}}}}/{f_{{\rm{c}}0}}} \right)n $ | (8) |

|
图 16 峰值压应力拟合曲线 Fig. 16 Fitting curve of peak compressive stress |

|
图 17 峰值压应变拟合曲线 Fig. 17 Fitting curve of peak compressive strain |
式中:σle为箍筋提供的有效约束应力, σle=0.5keρvσsv[11],当约束混凝土峰值压应力下箍筋不能屈服时,取σsv=Esεsv,箍筋能够屈服时,取σsv=fyv。
4.2 下降段参数根据试验结果,约束混凝土应力下降至峰值荷载的85%和50%时,箍筋基本达到其屈服强度,此时取σle=0.5keρv fyv。用回归分析法拟合得到85%峰值应力时的应变和50%峰值应力时的应变计算公式见式(9)、(10)。
| $ \varepsilon_{\mathrm{cc} 85}=\varepsilon_{\mathrm{c} 0}\left(1+21 \sigma_{l \mathrm{e}} / f_{c 0}\right) $ | (9) |
| $ \varepsilon_{\mathrm{cc} 50}=\varepsilon_{\mathrm{c} 0}\left(1+40.8 \sigma_{l \mathrm{e}} / f_{\mathrm{c} 0}\right) $ | (10) |
文献[8-13]基于试验提出了约束高强混凝土受压应力-应变模型,这些模型中曲线的上升段差异不大,主要区别在曲线的下降段,箍筋的约束程度越强,曲线下降段越平缓。结合试验曲线特点,上升段采用文献[12]提出的模型,见式(11)。下降段采用文献[13]提出的模型,见式(12)。
| $ \sigma_{\mathrm{c}}=f_{\mathrm{cc}} \frac{\gamma x}{\gamma-1+x^\gamma}, x \leqslant 1 $ | (11) |
| $ \sigma_{\mathrm{c}}=f_{\mathrm{cc}} \frac{x}{k_1(x-1)^{k_2}+x}, x>1 $ | (12) |
式中:x=εc/εcc;
约束高强混凝土受压应力-应变模型下降段经过点(εcc85, 0.85fcc)和(εcc50, 0.5fcc),将这两点代入式(12),解得k1和k2:
| $ k_1=\frac{\varepsilon_{\mathrm{cc} 50} / \varepsilon_{\mathrm{cc}}}{\left(\varepsilon_{\mathrm{cc} 50} / \varepsilon_{\mathrm{cc}}-1\right)^{k_2}} $ | (13) |
| $ k_2=\frac{\ln \left(0.176 \varepsilon_{\mathrm{cc} 85} / \varepsilon_{\mathrm{cc} 50}\right)}{\ln \left(\left(\varepsilon_{\mathrm{cc} 85} / \varepsilon_{\mathrm{cc}}\right) /\left(\varepsilon_{\mathrm{cc} 50}-\varepsilon_{\mathrm{cc}}\right)\right)} $ | (14) |
部分网格箍筋约束高强混凝土轴心受压应力-应变关系拟合曲线与试验实测曲线的对比见图 18。

|
图 18 预测模型与试验曲线对比 Fig. 18 Comparison of prediction model and test curve |
1) 42根网格箍筋约束高强混凝土柱轴压试验表明,约束混凝土达到峰值压应力时存在箍筋不屈服的现象,此时应该用箍筋的实际拉应力计算箍筋的侧向约束应力。
2) 约束混凝土峰值压应力下的箍筋拉应变随混凝土轴心抗压强度的增大而减小,随体积配箍率的增大而增大。体积配箍率相同时,箍筋间距越小,约束混凝土峰值压应力下箍筋拉应变越大。
3) 用回归分析法给出了约束混凝土峰值压应力下箍筋实际拉应变计算公式,提出了在约束混凝土峰值压应力下网格箍筋约束高强混凝土柱的箍筋能够屈服的体积配箍率下限值计算公式。
4) 基于峰值压应力下箍筋的实际拉应力及试验结果,给出了约束混凝土峰值压应力、峰值压应变和下降段参数计算公式,提出了网格箍筋约束高强混凝土受压应力-应变关系全曲线方程。
| [1] |
史庆轩, 王南, 田建勃, 等. 高强箍筋约束混凝土实用本构关系模型[J]. 建筑材料学报, 2014, 17(2): 217. SHI Qingxuan, WANG Nan, TIAN Jianbo, et al. A practical stress-strain model for high-strength stirrups confined concrete[J]. Journal of Building Materials, 2014, 17(2): 217. |
| [2] |
混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2010 Code for design of concrete structures: GB 50010—2010[S]. Beijing: China Architecture & Building Press, 2010 |
| [3] |
RAZVI S, SAATCIOGLU M. Confinement model for high-strength concrete[J]. Journal of Structural Engineering, 1999, 125(3): 284. DOI:10.1061/(ASCE)0733-9445(1999)125:3(281) |
| [4] |
MITSUYOSHI A, SUZUKI M, FRANGOPOL D M. Stress-averaged strain model for confined high-strength concrete[J]. ACI Structual Journal, 2010, 107(2): 179. DOI:10.1061/(ASCE)ST.1943-541X.0000348 |
| [5] |
史庆轩, 王南, 田园, 等. 高强箍筋约束高强混凝土轴心受压应力-应变全曲线研究[J]. 建筑结构学报, 2013, 34(4): 149. SHI Qingxuan, WANG Nan, TIAN Yuan, et al. Study on stress-strain relationship of high-strength concrete confined with high-strength stirrups under axial compression[J]. Journal of Building Structures, 2013, 34(4): 149. |
| [6] |
RAZVI S. Confinement of normal and high-strength concrete columns[D]. Ottawa: University of Ottawa, 1995
|
| [7] |
王南. 高强箍筋约束混凝土柱及节点受力性能与抗震设计研究[D]. 西安: 西安建筑科技大学, 2015 WANG Nan. Mechanical behavior and seismic design of rc columns-joints confined with high-strength stirrups[D]. Xi'an: Xi'an University of Architecture and Technology, 2015 |
| [8] |
史庆轩, 王南, 王秋维, 等. 高强箍筋约束高强混凝土轴心受压本构关系研究[J]. 工程力学, 2013, 30(5): 135. SHI Qingxuan, WANG Nan, WANG Qiuwei, et al. Uniaxial compressive stress-strain model for high-strength concrete with high-strength lateral ties[J]. Engineering Mechanics, 2013, 30(5): 135. DOI:10.6052/j.issn.1000-4750.2011.12.0894 |
| [9] |
CUSSON D, PAULTRE P. Stress-strain model for confined high-strength concrete[J]. Journal of Structural Engineering, 1995, 121(3): 472. DOI:10.1061/(ASCE)0733-9445(1995)121:3(468) |
| [10] |
MANDER J B, PRIESTLEY M J N. Observed stress-strain behavior of confined concrete[J]. Journal of Structural Engineering, 1988, 114(8): 1848. DOI:10.1061/(ASCE)0733-9445(1988)114:8(1827) |
| [11] |
MANDER J A B, PRIESTLEY M J N. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering, 1988, 114(8): 1812. DOI:10.1061/(ASCE)0733-9445(1988)114:8(1804) |
| [12] |
POPOVICS S. A numerical approach to the complete stress-strain curve of concrete[J]. Cement and Concrete Research, 1973, 3(5): 583. DOI:10.1016/0008-8846(73)90096-3 |
| [13] |
张秀琴, 过镇海, 王传志. 反复荷载下箍筋约束混凝土的应力-应变全曲线方程[J]. 工业建筑, 1985(12): 18. ZHANG Xiuqin, GUO Zhenhai, WANG Chuanzhi. Stress-strain full curve equation of stirrup confined concrete under repeated loads[J]. Industrial Construction, 1985(12): 18. |
| [14] |
混凝土结构试验方法标准: GB/T 50152—2012[S]. 北京: 中国建筑工业出版社, 2012 Standard for test method of concrete structures: GB/T 50152—2012[S]. Beijing: China Architecture & Building Press, 2012 |
 2022, Vol. 54
2022, Vol. 54


