2. 中国电力科学研究院有限公司,北京 100192
2. China Electric Power Research Institute, Beijing 100192, China
框架梁柱节点的受力形态复杂,承受的力包括梁柱传递的弯矩、剪力和轴力,当梁轴线相对于柱轴线存在偏心时还可能会受扭矩作用[1]。梁柱边节点与内节点相比少了一侧梁的约束,而且梁中纵筋需要锚固在节点核心区内,使得节点受力更加复杂。为了防止边节点因承载能力不足或变形过大而破坏,应确保节点核心区具备足够的抗剪能力。
国内外学者对梁柱边节点进行了大量的试验,提出了多种节点受剪理论。Vollum[2]通过对现有试验数据的分析,指出节点抗剪强度随长径比的增加而降低,并在此结论的基础上提出新的梁柱边节点设计方法;Hwang等[3]基于软化拉压杆方法,提出了适用于不同节点破坏模式的节点抗剪强度模型;Russo等[4]提出强震作用下,梁柱边节点的抗剪强度主要考虑了混凝土强度、梁纵向配筋和箍筋的贡献;Kim等[5]建立了发生节点剪切破坏的梁柱节点试件数据库,研究了混凝土强度、节点几何形状、柱轴向荷载、钢筋黏结情况对节点关键点处剪应力和剪应变的影响,结果表明混凝土强度是最主要的影响因素;Shiohara[6]基于考虑裂缝扩展模式的九参数模型,定义了梁柱节点极限承载力和平衡破坏弯矩,该模型可有效识别节点破坏模式;Park等[7]基于斜压杆机构传力原理,提出了适用于无横向钢筋加固的梁柱边节点剪切强度模型;De Risi等[8]通过试验对现有RC建筑中无横向加固的梁柱边节点的抗剪性能进行了评估,结果表明节点是否出现梁筋的屈服,基本上取决于梁纵向配筋率的大小。游渊等[9]、傅剑平等[10]根据国内外抗震框架节点的试验结果,着重论证了在梁端和柱端先行屈服的梁柱组合体中,节点的抗剪承载力主要由梁柱纵筋配置数量来控制;张莹心等[11]证明了节点剪切变形计算模型所依据的平行四边形假定的合理性,同时指出对角线不转动假定将导致明显误差。
从以往文献调研可见,节点抗剪性能的影响因素主要有混凝土强度、节点几何形状、柱轴向荷载、梁纵筋配筋率、钢筋黏结情况等,但多数研究的侧重点为节点宏观抗剪受力特征或计算模型的提出,关于各因素的影响程度分析尚且稀缺,因此本文采用正交试验设计方法,探究混凝土强度、水平纵筋锚固方式、梁纵筋配筋率对HRB400E钢筋混凝土梁柱边节点抗剪性能的影响,通过极差和方差分析梳理出各因素主次关系和变化趋势,为复杂的节点设计提供优化的参数组合。
1 试验概况 1.1 试验材料试验使用P.O42.5普通硅酸盐水泥、普通I级粉煤灰、S95级矿粉作为胶凝材料,采用细度模数2.58的河砂、10~20 mm连续级配碎石作为骨料,减水剂为标准型聚羧酸减水剂。混凝土配合比设计见表 1。钢筋力学性能指标见表 2。
| 表 1 混凝土配合比设计 Tab. 1 Mix proportion design of concrete |
| 表 2 钢筋力学性能指标 Tab. 2 Mechanical property indexes of steel bar |
试验设计的3个变化因素为A混凝土强度、B水平纵筋锚固方式和C梁纵筋配筋率,各因素有3个变化水平。混凝土强度等级分别为C50、C60、C70;水平纵筋锚固方式分别为90°弯折锚固、螺栓锚固、两侧贴焊锚固,锚固方式符合GB 50010—2010《混凝土结构设计规范》[12]要求,如图 1所示;梁纵筋配筋率分别为1.63%、2.08%、2.58%。各因素间不存在相互作用,选用L9(34)正交表,正交参数水平见表 3,由于因素只有3个,因此令正交表第4列为空白列,以此来确定试验误差。

|
图 1 锚固方式示意 Fig. 1 Schematic diagram of anchorage |
| 表 3 正交参数水平 Tab. 3 Orthogonal factor levels |
共制作9个钢筋混凝土梁柱边节点试件,按正交表设计的各试件基本参数见表 4。试件的几何尺寸及配筋见图 2。
| 表 4 试件基本参数 Tab. 4 Basic parameters of specimens |

|
图 2 试件J5AL几何尺寸及配筋(mm) Fig. 2 Size and reinforcement details of J5AL (mm) |
试验在多通道电压伺服控制系统上完成。装置有2个液压伺服作动器,如图 3(a)所示,作动器①可实现500 kN加载,作动器行进距离为±20 cm,作动器②可施加1 000 kN压力,行进距离为10 cm。所有作动器端部装有力和位移传感器。加载全过程采用位移控制加载方法,首先由作动器②对柱施加指定竖向荷载,使其达到预定的轴压比。然后对梁端采用位移大小相等、方向相反方式加载,以试件J5AL为例,其加载制度见图 3(b)。在梁端表面开裂前,每级位移增量为1 mm,开裂之后每级位移增量为2 mm,控制位移循环1次。在纵筋达到屈服位移之后,以10 mm为步长,每级位移控制循环3次。在试件达到极限荷载之后,以5 mm为步长继续加载,每级位移控制循环3次,直到荷载下降至极限荷载的85%后结束加载。

|
图 3 试验加载装置和加载制度 Fig. 3 Test setup and loading system |
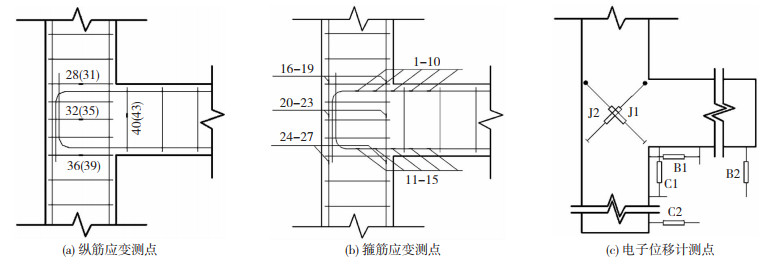
试验中量测的数据包括:1)梁端的竖向荷载值和相应的竖向位移值;2)采用电子位移计测量试件节点附近的梁、柱位移和节点核心区的变形;3)用电阻应变片测量试件关键受力区域纵向钢筋及箍筋的应变;4)采用裂缝测量仪测量实验过程中裂缝的宽度。位移计与应变片测点布置见图 4。
|
图 4 应变测点及位移计布置 Fig. 4 Strain measuring points and displacement meters layout |
节点的破坏类型主要有3种:1)梁端弯曲破坏;2)节点核心区剪切破坏;3)梁端弯曲-节点核心区剪切破坏。本次试验试件的破坏模式主要为梁端弯曲破坏和梁端弯曲-节点核心区剪切破坏。
试件J5AL的最终破坏形态为梁端弯曲破坏,见图 5(a)。当达到混凝土开裂应变时,靠近柱边的梁上方位置出现了第一条裂缝,随着荷载的增大,梁塑性铰区出现新裂缝,梁内纵筋应变达到屈服应变,荷载继续增大,节点核心区出现轻微裂缝,梁端裂缝开展严重,梁柱相交截面裂开,混凝土被压碎。

|
图 5 试件典型破坏形态 Fig. 5 Typical failure modes of specimens |
其他试件的最终破坏形态均为梁端弯曲-节点核心区剪切破坏,破坏过程相似:当梁筋应变达到屈服应变时,节点核心区并未表现出明显的剪切破坏形态,梁筋屈服后,随着加载位移的增大,节点核心区斜裂缝数量和宽度都不断增加,最终发生节点核心区的剪切破坏。但是这些试件的最终破坏形态又因为锚固方式的不同而表现出一些差异,见图 5(b)、(c)。相对于采用90°弯折锚固方式的试件J6AM、J7AH,采用螺栓锚固和两侧贴焊锚固方式的试件J5BM、J5CH、J6BH、J6CL、J7BL、J7CM节点核心区的裂缝数量更多,裂缝倾角更大,裂缝的位置也更偏向于梁端,由此可见弯折锚固方式可以有效减少核心区裂缝数量,抑制裂缝发展。
2.2 梁上部纵筋应变图 6为骨架曲线简化模型,特征位移取值参考文献[13]中的定义:开裂位移Δcr根据试件发生第一条裂缝时的试验现象确定;屈服位移Δy根据等效弹塑性屈服法[14]确定;峰值位移Δm为峰值荷载Pm所对应的位移;极限位移Δu为峰值荷载Pm下降至85%时对应的位移值。

|
图 6 骨架曲线简化模型 Fig. 6 Simplified model of skeleton curve |
由于梁上部与下部钢筋对称布置且施加的荷载对称,因此仅对上部纵筋的应变进行分析。图 7为正向加载中首次达到开裂位移Δcr、屈服位移Δy、峰值位移Δm、极限位移Δu时上部纵向钢筋的应变分布情况。随着位移荷载的增加,所有试件中上部纵筋最大应变值均超过εy,表明工程中常用的3种锚固方式均可提供可靠的黏结锚固力;开裂后梁根部纵筋应变增长幅度相较节点内水平锚固段有明显的提升,与试件梁根部多而密集的裂缝分布模式对应。应当指出,锚固方式对上部纵筋应变分布有显著的影响:采用90°弯折锚固的试件(图 7(a)、(d)、(g))上部纵筋在节点边缘达到屈服后,后续加载过程中纵筋屈服范围几乎未向节点区域延伸;螺栓锚固和两侧贴焊锚固的试件(图 7(b)、(c)、(e)、(f)、(h)、(i))在后续加载中纵筋屈服范围明显有向节点区域延伸的趋势。

|
图 7 正向加载时上部纵筋应变分布 Fig. 7 Strain distribution of upper longitudinal reinforcement under positive loading |
表 5为加载过程中各试件的特征值。螺栓锚固和两侧贴焊锚固试件的屈服位移相对90°弯折锚固试件较大,结合图 7中上部水平纵筋的应变分析可知,当采用这两种锚固方式时,上部纵筋屈服范围向节点的延伸会加大节点边缘处梁、柱裂缝的宽度,致使梁端加载点处的竖向位移增大。
| 表 5 加载过程特征值 Tab. 5 Characteristic values of loading process |
图 8为正向加载中首次达到Δcr、Δy、Δm、Δu时的箍筋应变分布,试件量测的箍筋应变包括两类:梁端箍筋应变和核心区箍筋应变。图 8(a)为梁端箍筋应变,由图可知各试件的梁箍筋应变值都较小,结束加载时均小于屈服应变,表明梁未发生剪切破坏;其中试件J5AL的梁箍筋应变比其他试件增长较快,因为试件J5AL的裂缝集中在梁端,裂缝开展到一定程度,剪力将会由梁端箍筋来承担。图 8(b)为核心区箍筋应变,发生梁端弯曲破坏的试件(J5AL)核心区裂缝较少,核心区箍筋应变比较小并且始终未达到屈服应变;发生梁端弯曲-节点核心区剪切破坏的试件(除J5AL以外的试件)在核心区混凝土开裂之前箍筋应变增长比较缓慢,混凝土开裂以后箍筋应变增长速度加快,当正向加载第一次达到峰值位移时箍筋应变超过屈服应变值,表明核心区混凝土已发生了剪切破坏。

|
图 8 正向加载时箍筋应变分布 Fig. 8 Strain distribution of stirrups under positive loading |
当梁端施加正向位移(向下)时,梁上部纵筋受拉,柱内侧纵筋受拉,核心区上、下部混凝土出现方向相反剪力且上外角混凝土和下内角混凝土均受压,呈现出对角压力趋势,见图 9(a)。根据图 9(b)节点剪切变形示意,节点剪切变形角为[15]
| $ \gamma_{\mathrm{j}}=\gamma_1+\gamma_2=\frac{\sqrt{h_{\mathrm{b}}^2+h_{\mathrm{c}}^2}}{h_{\mathrm{b}} h_{\mathrm{c}}} \frac{\Delta_1+\Delta_2}{2} $ | (1) |

|
图 9 节点受力简图和剪切变形 Fig. 9 Joint force diagram and shearing deformation |
式中:hb为梁截面高度,hc为柱截面高度,Δ1、Δ2为节点位移计读数,γ1、γ2为节点变形产生的角度。
节点核心区的破坏包括初裂、通裂、极限和破坏4个阶段。初裂状态和极限状态下节点的剪切变形角见表 6,初裂状态下节点的剪切变形角均较小,达到极限状态时节点剪切变形明显增大;当采用90°弯折锚固时,节点极限状态剪切变形角明显小于其他两种锚固方式,结合图 7中纵筋应变分析可知,纵筋屈服范围未向节点内部延伸是极限状态下剪切变形角减小的主要原因,表明采用90°弯折锚固对节点的剪切变形最有利。
| 表 6 节点剪切变形角 Tab. 6 Shearing angle of joints |
以Ki(i=1, 2, 3)表示各因素第i水平对应的试验结果之和,以Ki(i=1, 2, 3)表示各因素第i水平对应的试验结果平均值,各因素的极差值R=max{Ki}-min{Ki},R值越大表示该因素对评价指标的影响越大,根据R值的大小可以得到各因素对评价指标的主次影响顺序。
初裂状态节点剪切变形角极差分析的结果见表 7,极差值由大到小为:RA>RB>RC,即研究参数对初裂状态节点剪切变形角的影响从大到小为:混凝土强度>水平纵筋锚固方式>梁纵筋配筋率。
| 表 7 初裂状态下节点剪切变形角极差分析 Tab. 7 Range analysis of shearing deformation angle of joints at initial crack |
极限状态下节点剪切变形角极差分析的结果见表 8,极差值由大到小为:RB>RC>RA,即研究参数对极限状态下节点剪切变形角的影响规律为:水平纵筋锚固方式>梁纵筋配筋率>混凝土强度。
| 表 8 极限状态下节点剪切变形角极差分析 Tab. 8 Range analysis of shearing deformation angle of joints at ultimate state |
极差值只能反映各因素影响试验指标的主次关系,而方差值可以指明各因素对试验评价指标影响的程度并考察各因素的作用是否显著。根据方差分析理论[16],方差分析过程见图 10。

|
图 10 方差分析流程 Fig. 10 Flow chart of variance analysis |
初裂状态下节点剪切变形角方差分析的结果见表 9,查F分布表可以知道,F0.10(2, 2)=9.00,F0.05(2, 2)=19.00,F0.01(2, 2)=99.00。F0.05(2, 2)=19.00 < FA < F0.01(2, 2)=99.00,说明因素A(混凝土强度)的改变对初裂状态节点剪切变形角有显著的影响,记作*;FB < F0.10(2, 2)=9.00,FC < F0.10(2, 2)=9.00,说明因素B(水平纵筋锚固方式)和因素C(梁纵筋配筋率)改变对试验结果影响不显著。
| 表 9 初裂状态下节点剪切变形角方差分析 Tab. 9 Variance analysis of shearing deformation angle of joints at initial crack |
极限状态下节点剪切变形角方差分析的结果见表 10,F0.05(2, 2)=19.00 < FB < F0.01(2, 2)=99.00,说明因素B(水平纵筋锚固方式)的改变对初裂状态节点剪切变形角有显著的影响,记作*;F0.10(2, 2)=9.00 < FA < F0.05(2, 2)= 19.00,F0.10(2, 2)=9.00 < FC < F0.05(2, 2)=19.00,说明因素A(混凝土强度)和C(梁纵筋配筋率)的改变对试验结果的影响不显著。
| 表 10 极限状态下节点剪切变形角方差分析 Tab. 10 Variance analysis of shearing deformation angle of joints at ultimate state |
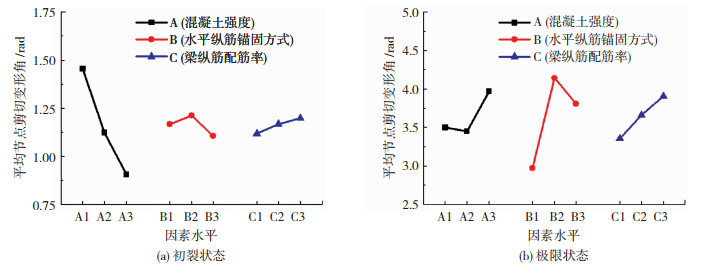
图 11(a)为初裂状态下平均节点剪切变形角随各因素水平的变化趋势。影响初裂状态下平均节点剪切变形角的最显著因素为A(混凝土强度),当混凝土强度等级从C50增大到C70时,平均节点剪切变形角减小了37.7%,这是因为在裂缝开展之前,节点剪力主要由混凝土来承担,混凝土强度等级越高,初裂状态的节点剪切变形角越小。因素B(水平纵筋锚固方式)和因素C(梁纵筋配筋率)对初裂状态节点剪切变形角的影响很小。图 11(b)为极限状态下平均节点剪切变形角随各因素水平的变化趋势。影响极限状态下平均节点剪切变形角的最显著因素为B(水平纵筋锚固方式),当采用B2(90°弯折锚固)方式时,节点的剪切变形角最小,相比采用螺栓锚固和两侧贴焊锚固方式的节点剪切变形角分别减小了28.3%和22.1%,原因是当节点核心区受力时,斜压杆受压,垂直于受压方向的混凝土会发生图 9(b)所示的侧向膨胀,这会导致节点剪切变形增大。
|
图 11 平均节点剪切变形角 Fig. 11 Average joint shearing deformation angle |
图 12为不同锚固方式下钢筋的受力机制,90°弯折锚固钢筋在受拉时对弯弧段内侧的混凝土产生压力,钢筋产生的压力可以对发生侧向膨胀的斜压杆混凝土产生约束作用,限制混凝土侧向膨胀程度,从而有效减小核心区的剪切变形,尤其在加载中后期,核心区混凝土裂缝增多以后侧向膨胀增大,90°弯折锚固钢筋的约束作用就越发明显(图 12(a))。而螺栓锚固方式(图 12(b))和贴焊锚固方式(图 12(c))没有这种对斜压杆混凝土侧向膨胀的约束作用,因此采用这两种方式的节点剪切变形要大于采用90°弯折锚固方式的节点剪切变形。

|
图 12 不同锚固方式钢筋的传力机理 Fig. 12 Stress transfer mechanism of steel bars with different anchorage methods |
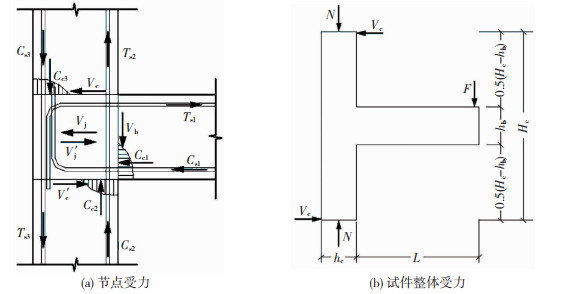
图 13为边节点的受力示意图,框架边节点核心区受到梁柱传递的弯矩、剪力和轴力等共同作用。
|
图 13 节点受力示意 Fig. 13 Diagram of joint force |
由图 13(a)梁上部钢筋力的平衡条件可得节点力计算公式为
| $ V_{\mathrm{j}}=T_{\mathrm{s} 1}-V_{\mathrm{c}}=C_{\mathrm{cl}}+C_{\mathrm{s} 1}-V_{\mathrm{c}}^{\prime} $ | (2) |
式中:Ts1为梁上部纵筋所受拉力,Vc、V′c分别为柱子上端、下端剪力,Cs1为梁下部纵筋传入节点的压力,Cc1为梁受压区混凝土压力。
由梁的弯矩平衡条件可得
| $ F L=T_{\mathrm{s} 1}\left(h_{\mathrm{b} 0}-a_{\mathrm{s}}^{\prime}\right) $ | (3) |
式中:F为梁端施加的荷载值,L为梁有效长度,hb0为梁有效截面高度,a′s为纵筋受压合力点到梁边缘的距离。
由力矩平衡条件可得
| $ V_{\mathrm{c}}\left(H_{\mathrm{c}}-h_{\mathrm{b}}\right)=F L $ | (4) |
式中:Hc为节点上柱和下柱反弯点之间的距离,hb为梁截面高度。
将公式(3)和公式(4)代入公式(2)中,得到Vj的计算公式为
| $ V_{\mathrm{j}}=\frac{F L}{h_{\mathrm{b} 0}-a_{\mathrm{s}}^{\prime}} \times\left(1-\frac{h_{\mathrm{b} 0}-a_{\mathrm{s}}^{\prime}}{H_{\mathrm{c}}-h_{\mathrm{b}}}\right) $ | (5) |
节点水平剪力计算结果见表 11。
| 表 11 节点水平剪力计算值 Tab. 11 Calculated joint horizontal shearing force |
节点水平剪力极差分析结果见表 12,极差值由大到小为:RC>RA>RB,即对节点水平剪力的影响从大到小为:梁纵筋配筋率>混凝土强度>水平纵筋锚固方式。
| 表 12 节点水平剪力极差分析 Tab. 12 Range analysis of horizontal shearing force of joints |
表 13为节点水平剪力方差分析的结果。F0.05(2, 2)=19.00 < FA < F0.01(2, 2)=99.00,说明因素A(混凝土强度)的改变对节点水平剪力有显著的影响,记作*;F0.10(2, 2)=9.00 < FB < F0.05(2, 2)=19.00,说明因素B(水平纵筋锚固方式)水平的改变对节点水平剪影响不显著;FC>F0.01(2, 2)=99.00,说明因素C(梁纵筋配筋率)水平的改变对节点水平剪力有非常显著的影响,记作**。
| 表 13 节点水平剪力方差分析 Tab. 13 Variance analysis of horizontal shearing force of joints |
图 14为平均节点水平剪力随各因素水平的变化趋势。影响平均节点水平剪力的最显著因素为C(梁纵筋配筋率),当梁纵筋配筋率从1.63%增加到2.58%时,节点水平剪力增大了40.6%,这是因为配筋率是影响带裂缝工作的钢筋混凝土结构剪力传递的重要因素[17],试件水平剪力随配筋率的增大而提高,因此因素C优选为第一水平C1(ρ=1.63%)。

|
图 14 平均节点水平剪力随各因素水平的变化趋势 Fig. 14 Variation trends of average joint horizontal shearing force at each factor level |
平均节点水平剪力同样随因素A(混凝土强度)的提高而增大,但其增长水平明显低于梁纵筋配筋率的影响,混凝土强度越高传入节点的剪力越大,节点延性也会越差,因此因素A优选为第一水平A1(C50)。
因素B(水平纵筋锚固方式)的方差分析结果表明水平纵筋锚固方式对节点水平剪力影响不显著,经计算螺栓锚固方式下的平均节点水平剪力值最小,理应优先采用螺栓锚固方式,但水平纵筋应变分析已表明3种锚固方式均可提供较好的黏结锚固力,而且90°弯折锚固对节点核心区剪切变形也有最佳的限制作用,因此综合评价认为这3种锚固方式均对节点抗剪有利。
5 结论以混凝土强度、水平纵筋锚固方式和梁纵筋配筋率为主要研究参数,基于正交试验原理设计并完成了9个HRB400E钢筋混凝土梁柱边节点的抗剪试验,得出以下结论:
1) 试件的破坏模式包括梁端弯曲破坏和梁端弯曲-节点核心区剪切破坏两种形式,采用90°弯折锚固方式与采用螺栓和贴焊锚固方式相比,可有效减少节点区裂缝数量,抑制裂缝的发展。
2) 初裂状态下节点剪切变形角的主要影响因素为混凝土强度,节点剪切变形角随混凝土强度的增加急剧减小;极限状态下节点剪切变形角的主要影响因素为纵筋锚固方式,采用90°弯折锚固时节点的剪切变形角最小,说明90°弯折锚固钢筋可有效减小节点的剪切变形。
3) 极差和方差分析均表明梁内纵筋配筋率对节点水平剪力影响最为显著,3种锚固方式均可提供可靠的锚固力,锚固方式对节点水平剪力的影响不显著。
4) 基于正交试验原理并结合极差、方差数理统计理论对梁柱边节点抗剪性能影响参数进行分析可梳理出各因素的主次关系和变化趋势。
| [1] |
MEGGET L M, PARK R. Reinforced concrete exterior beam-column joints under seismic loading[J]. New Zealand Engineering, 1971, 26(11): 341. |
| [2] |
VOLLUM R L. The design of external reinforced concrete beam-column joints[J]. Structural Engineer, 1999, 77(23/24): 21. |
| [3] |
HWANG S J, LEE H J. Analytical model for predicting shear strengths of exterior reinforced concrete beam-column joints for seismic resistance[J]. ACI Structural Journal, 1999, 96: 846. |
| [4] |
RUSSO G, SOMMA G. Shear strength of exterior beam-column joints under seismic loading[C]//Proceedings of the 2nd Fib Congress. Naples: [s. n. ], 2006: 9
|
| [5] |
KIM J, LAFAVE J M. Key influence parameters for the joint shear behaviour of reinforced concrete (RC) beam-column connections[J]. Engineering Structures, 2006, 29(10): 2523. DOI:10.1016/j.engstruct.2006.12.012 |
| [6] |
SHIOHARA H. Reinforced concrete beam-column joints: an overlooked failure mechanism[J]. ACI Structural Journal, 2012, 109(1): 65. DOI:10.1061/(ASCE)ST.1943-541X.0000413 |
| [7] |
PARK S, MOSALAM K M. Analytical model for predicting shear strength of unreinforced exterior beam-column joints[J]. ACI Structural Journal, 2012, 109(2): 149. DOI:10.1306/06021111020 |
| [8] |
DE RISI M T, RICCI P, VERSERAME G M. Experimental assessment of RC exterior beam-column joints without transverse reinforcement[J]. Analytical Chemistry, 2015, 245. DOI:10.2495/ERES150201 |
| [9] |
游渊, 傅剑平, 白绍良, 等. 对抗震钢筋混凝土框架节点抗剪承载力计算公式的重新识别[J]. 重庆建筑大学学报, 1997(1): 18. YOU Yuan, FU Jianping, BAI Shaoliang, et al. A new recognition of the calculation formula of shear capacity of seismic reinforced concrete frame joints[J]. Journal of Chongqing Jianzhu University, 1997(1): 18. |
| [10] |
傅剑平, 张川, 白绍良. 钢筋混凝土抗震框架节点各机构传递剪力的定量分析[J]. 建筑结构学报, 2005(1): 91. FU Jianping, ZHANG Chuan, BAI Shaoliang. Quantitative evaluation of two shear transfer mechanisms in earthquake-resistant beam-column joints[J]. Journal of Building Structures, 2005(1): 91. DOI:10.14006/j.jzjgxb.2005.01.014 |
| [11] |
张莹心, 杨红, 赵雯桐, 等. 梁柱节点剪切变形计算模型基本假定的校核[J]. 四川建筑科学研究, 2018, 44(2): 34. ZHANG Yingxin, YANG Hong, ZHAO Wentong, et al. Calibration of calculation assumption for beam-column joint shear deformation[J]. Sichuan Building Science, 2018, 44(2): 34. DOI:10.19794/j.cnki.1008-1933.2018.02.007 |
| [12] |
混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2010 Code for design of concrete structures: GB 50010—2010[S]. Beijing: China Architecture & Building Press, 2010 |
| [13] |
孟二从, 余亚琳, 张旭, 等. 钢管再生混凝土柱-再生混凝土短梁框架抗震性能及损伤演变[J]. 振动与冲击, 2019, 38(20): 192. MENG Ercong, YU Yalin, ZHANG Xu, et al. Seismic behavior and damage evolution of RAC filled steel tube column versus RAC short beam frame[J]. Journal of Vibration and Shock, 2019, 38(20): 192. DOI:10.13465/j.cnki.jvs.2019.20.027 |
| [14] |
陈惠发, 萨里普著. 弹性与塑性力学[M]. 余天庆, 译. 北京: 中国建筑工业出版社, 2004: 198 CHEN W F, SALIPU A F. Elasticity and plasticity[M]. YU Tianqing, translate. Beijing: China Architecture & Building Press, 2004: 198 |
| [15] |
BECKINGSALE C W. Post elastic behaviour of reinforced concrete beam-column joints[D]. Christchurch: University of Canterbury, 1980: 57
|
| [16] |
唐湘晋, 陈家清, 毛树华. 应用数理统计[M]. 武汉: 武汉理工大学出版社, 2013: 177. TANG Xiangjin, CHEN Jiaqing, MAO Shuhua. Applied mathematical statistics[M]. Wuhan: Wuhan University of Technology Press, 2013: 177. |
| [17] |
张申, 车轶, 谢庆红, 等. 钢筋混凝土开裂面剪力传递性能试验研究[J]. 建筑结构学报, 2011, 32(2): 48. ZHANG Shen, CHE Yi, XIE Qinghong, et al. Experimental research on shear transfer behavior in cracked reinforced concrete[J]. Journal of Building Structures, 2011, 32(2): 48. DOI:10.14006/j.jzjgxb.2011.02.008 |
 2022, Vol. 54
2022, Vol. 54



 16
16 8
8