2. 结构工程灾变与控制教育部重点实验室(哈尔滨工业大学), 哈尔滨 150090;
3. 土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学), 哈尔滨 150090
2. Key Lab of Structures Dynamic Behavior and Control (Harbin Institute of Technology), Ministry of Education, Harbin 150090, China;
3. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China
后张预应力摇摆墙作为一种可恢复功能结构,通过墙-基界面接缝的交替开合消耗地震动激励过程中输入的能量,在后张预应力筋等恢复力作用下,实现震后结构自复位,并可有效控制结构残余变形等损伤,不需修复或仅需少量修复就能快速恢复建筑物使用功能。
以往针对摇摆结构已开展了一定的前期研究,Housner[1]发现摇摆机制作为结构的一种独特的动力学运动模式,基于刚性质量块假设提出了用于描述摇摆刚体自由振动和在地震作用下自由摇摆的动力学公式。Pena等[2]对4种不同几何特征的刚性摇摆块进行了自由振动、基座简谐波激励振动和任意激励下的振动响应的振动台试验,并采用复杂耦合摇摆旋转法(CCRR)和离散元法(DEM)两种方法对刚性块体的摇摆运动进行数值模拟,模拟结果能够以良好的精度还原试验结果。Ma[3]针对配置无黏结预应力筋的受控摇摆墙摇摆运动,采用试验与模拟相结合的方法系统性分析了受控摇摆墙的自由衰减振动响应,在试验中发现了摇摆墙旋转中心的迁移行为,采用Dirac-δ公式进行了量化分析,准确地预测了摇摆过程中墙趾抬升和后张无黏结预应力筋伸长量。
事实上,后张预应力摇摆墙对地震动下能量耗散的来源包括:一是系统固有黏性阻尼, 二是在墙体发生较大横向侧移条件下受压侧墙趾混凝土非线性和强震下预应力筋屈服发生非弹性变形而产生的滞回阻尼,三是摇摆墙墙体与基础碰撞而产生的冲击阻尼。由于以往对摇摆墙多采用拟静力试验与理论分析相结合的方法,基于定性研究前两类阻尼成分的作用机理及其耗能贡献,并量化摇摆墙的耗能需求。而对冲击阻尼,国内外学者仅在少数自由衰减振动和振动台试验[4-8]中观察到拟静力试验中所忽视的墙-基础摇摆碰撞的现象,而尚未系统评价和分析对其在摇摆墙总耗能中的贡献,也未提出其耗能机理及影响因素。
为此,建立了自复位摇摆墙精细化分析模型,通过模拟墙体在大侧移条件下被释放使其发生自由衰减振动响应,基于恢复系数作为冲击阻尼的主要评估手段对摇摆墙的碰撞耗能进行量化分析,以高宽比和预应力水平为基本参数,对预应力摇摆墙进行了动力时程分析,并将各组分阻尼贡献进行对比,确定其综合耗能机制,为深化摇摆墙抗震结构设计和实际工程应用创造条件。
1 摇摆墙自由衰减振动模拟试验验证 1.1 试验概况为研究无黏结预应力摇摆墙的摇摆振动特性及动力响应,Twigden[8]对4片缩尺为1/5的预制后张自复位剪力墙试件进行了自由衰减振动试验和振动台模拟地震动试验。本文选用对其中的摇摆墙试件SRW-FA-A开展的自由衰减振动试验建立有限元模型,以验证模拟的准确性和可靠性,并结合模型进一步探究该类剪力墙的动力耗能特性。
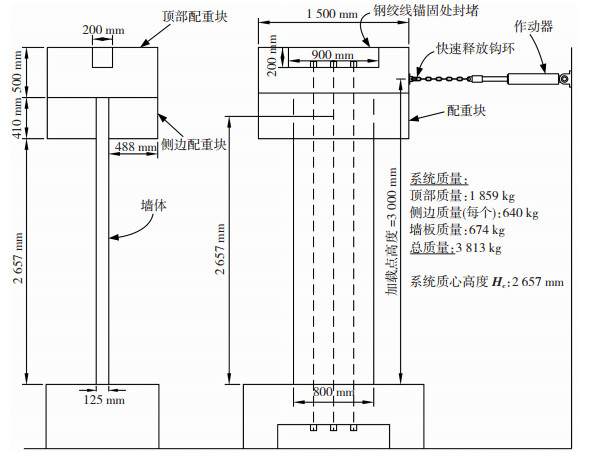
如图 1所示,摇摆墙主体高2 860 mm、宽800 mm、厚125 mm,为模拟原型结构上部楼板及作用于楼板的竖向荷载,通过相似关系确定了上部惯性质量相似比为1/25,在墙顶面固定一个高500 mm、长1 500 mm、宽1 100 mm并在墙的两侧各布置一个高410 mm、长1 500 mm、宽488 mm的质量块,模型总惯性质量为3 139 kg。预留于墙体中心线位置的孔道采用无黏结后张预应力筋贯穿质量块与摇摆墙。预应力筋选用ϕs15.2预应力钢绞线,初始张拉应力696 MPa(0.45fpy)。混凝土及预应力筋的材料特性见表 1。
| 表 1 试件材料特性 Tab. 1 Material properties of specimens |
自由衰减振动试验采用快速回弹的方式实现,通过作动器对墙体进行伪静态推覆,当墙体达到目标控制位移时,激活与作动器相连的快速释放装置释放墙体位移约束,摇摆墙在预应力筋和重力荷载提供的恢复力作用下发生摇摆,体现为自由振动衰减直到静止。
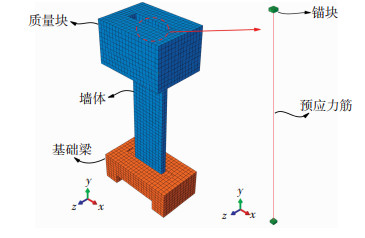
1.2 试验墙片的有限元模拟验证考虑到摇摆墙墙-基水平接缝界面的复杂接触问题,采用ABAQUS的动力隐式算法[9]可以精确并直观地反映墙趾界面的摇摆碰撞及其受力特性。所建立的摇摆墙有限元模型见图 2,上部墙体与质量块和下部基础梁的混凝土采用八节点线性六面体C3D8R三维实体单元分别建模,混凝土本构关系采用塑性损伤模型(CDP)。预应力筋采用两节点T3D2三维线性桁架单元,选用弹性强化模型本构,根据GB 50017—2017《钢结构设计标准》[10],线膨胀系数取1.2×10-5/℃。建模时,将预应力筋上下端嵌固在两端锚具内,孔道内预应力筋不设置与混凝土接触,即孔道内预应力筋可发生自由滑动。为防止墙体与基础之间发生相对滑动,将墙-基接触面的切向采用粗糙定义,法向采用“硬接触”定义以模拟接缝处墙趾开合。
|
图 2 摇摆墙有限元模型 Fig. 2 Finite element model of rocking wall |
设置3个分析步:1)在初始分析步中采用“降温法”对预应力筋施加初始预应力;2)在第二个分析步,对上部墙体施加与试验中相同的水平初始侧移,并限制其余两个方向的位移;3)第三个分析步,释放初始位移约束,使得摇摆墙发生自由摇摆振动。
数值模拟结果与试验结果的对比见图 3。模拟结果在振动周期上与试验结果同步较好,且振幅在前期基本吻合。而随振动时间增加,模拟与试验结果之间出现一定相位差,同时模拟振幅与试验值间的差值逐渐增大。这可能是因为在摇摆过程中,墙体内预应力筋与管道间不可避免地存在摩擦造成的能量损失,使振幅少许降低,而有限元模拟是在较为理想的条件下建立的,不能充分考虑各种情况导致的能量损耗。总体上,所建立的模型能较真实地反映摇摆墙自由振动衰减响应。

|
图 3 自由衰减振动动力时程对比 Fig. 3 Dynamic time history curves of free damping vibration |
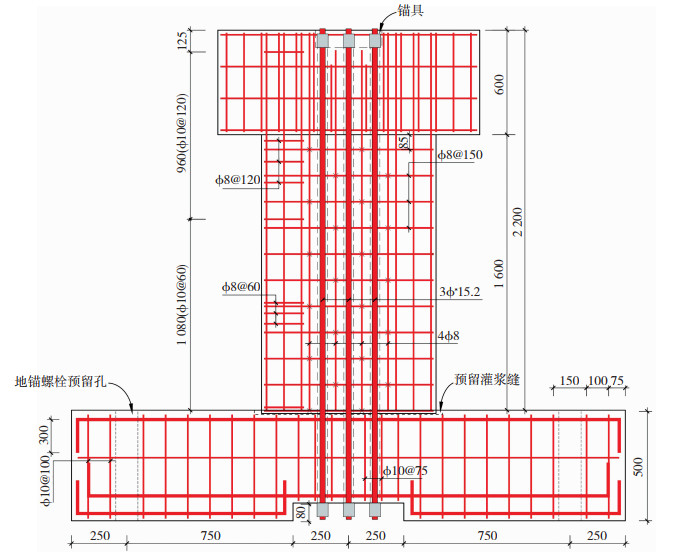
为了分析不同高宽比和初始预应力对摇摆墙动力响应及耗能的影响,以文献[11]中的后张预应力混凝土剪力墙作为参考,设计了9片对应不同高宽比和预应力水平的摇摆墙模型。以RW1为例,墙体主体高2 200 mm,长1 100 mm(上部加载梁为1 500 mm)、厚140 mm(上部为200 mm),预应力筋布置在墙体对称轴及两侧150 mm的位置,见图 4。同时,考虑上部楼板提供的荷载和惯性作用,因此在摇摆墙顶部加载梁的两侧分别附加了高600 mm、宽1 500 mm、厚450 mm的质量为972 kg的质量块。
|
图 4 分析模型配筋图(mm) Fig. 4 Reinforcement diagram of analysis model (mm) |
试件的混凝土设计强度等级为C40,弹性模量为3.20×104 MPa,预应力筋选用直径为ϕs15.2的1860级高强钢绞线,弹性模量为1.95×105 MPa。以墙高宽比(2.0、2.5、3.0),预应力筋张拉应力水平(0.4fptk、0.5fptk、0.6fptk)为基本设计参数,见表 2。
| 表 2 自由衰减振动试验试件设计参数 Tab. 2 Design parameters of specimens for free damping vibration test |
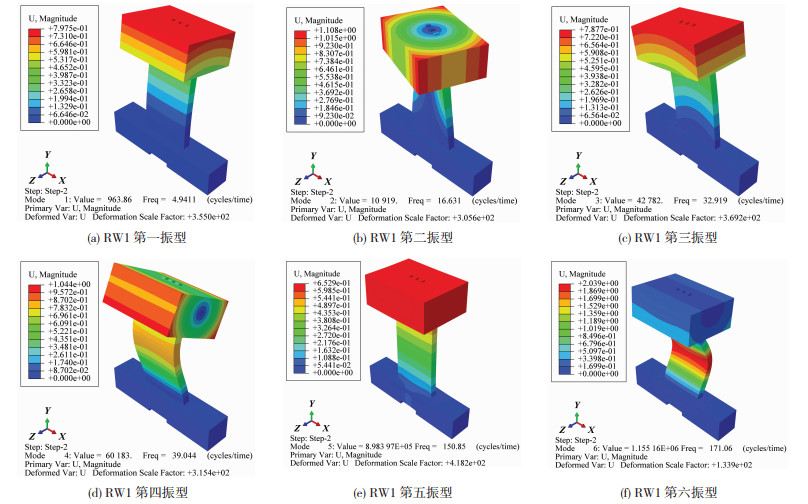
按1.2节中方法建立RW1~RW9的有限元模型。针对初始预应力水平和高宽比的两方面参数的影响,对摇摆墙开展了模态分析,获取了9片摇摆墙模型的主要振型及自振频率,见图 5、6。以试件RW1为例,获取模型的前24阶振型频率,见表 3。
|
图 5 结构主要振型 Fig. 5 Main vibration modes of structure |

|
图 6 模型前四阶振型对比 Fig. 6 Comparison of first four-order vibration modes of model |
| 表 3 模型RW1前24阶自振频率 Tab. 3 First 24 natural frequencies of model RW1 |
分析可知,9片摇摆墙第1阶振型均以平面外的自由振动为主,说明摇摆墙本身平面外刚度较小,振动过程中发生面外失稳的可能性较大,在设计中应尽量避免使其作为主要竖向传力构件。第2阶振型为模型绕中心垂线的扭转,第3阶振型则为平面内的绕墙底处转动,该振型为摇摆墙作为新型减震构件的主要作用机理:当地震动输入时,墙-基接缝处张开,并在后张预应力筋和重力联合提供的恢复力作用下,墙体绕墙趾发生交替开合转动,从而实现震后结构的自复位和低震损。第4阶及更高阶振型后,扭转效应增强,模型表现为扭转和平动的结合,振动频率提升明显。
对比9片摇摆墙前4阶振型可知,高宽比对摇摆墙的动力特性影响显著,随高宽比提高,摇摆墙的自振频率逐渐降低,响应周期逐渐延长。摇摆墙的振动特性对初始预应力水平并不敏感,在前4阶振型中,模型RW1~RW3的振动频率最大偏差仅0.2%,模型RW4~RW6的振动频率最大偏差仅0.2%,模型RW7~RW9的振动频率最大偏差仅0.4%。
2.3 动力响应参数敏感性分析通过9片摇摆墙的固有频率和振型分析发现了高宽比和初始预应力水平对摇摆墙的动力特性重要影响。因此,基于摇摆墙模态分析,对RW1~RW9开展自由衰减振动分析,采用与Twigden[8]相同的加载方式,对墙体首先施加初始位移,待其达到目标控制位移后,释放约束,使墙体自由地衰减摇摆直到静止。
在对墙体施加初始位移时,应避免由于墙顶水平位移过大造成预应力筋的屈服甚至破裂。为此按照ACI ITG-5.1-07[12]规定,自由衰减振动试验的初始位移角不得超过采用下述公式中计算得到的位移角限值θlim:
| $ \theta_{\mathrm{lim}}=0.8 \frac{h_{\mathrm{w}}}{l_{\mathrm{w}}}+0.5 $ | (1) |
式中hw和lw分别为摇摆墙墙高和墙长。
可得RW1的位移角限值为2.3%,本次加载的初始位移角偏保守地取2%。
2.3.1 高宽比的影响高宽比作为影响剪力墙抗侧向力的重要因素,在ACI 318-19[13]中规定,剪力墙的高宽比限值应大于1.0,以便当结构进入塑性阶段时,其承载能力和延性以墙-基临界截面的弯曲作用为主。相似地,为避免侧向加载时发生剪切滑移,其高宽比同样受到限制,ACI ITG-5.2-09[14]规定摇摆墙的高宽比应大于0.5,在本次模拟,摇摆墙高宽比为2.0、2.5、3.0。选取初始预应力相同(0.5fptk)的RW2、RW5、RW8的摇摆墙,对比高宽比对摇摆墙自由衰减振动响应的影响,见图 7。

|
图 7 不同高宽比下自复位摇摆墙动力响应对比 Fig. 7 Comparison of dynamic response of self-centering rocking wall under different aspect ratios |
由图 7可分析高宽比的影响:1)摇摆墙的摇摆周期随高宽比增大而逐渐增大,这与摇摆墙的模态分析结果一致。随着墙体发生摇摆,其振幅和振动周期逐渐衰减,高宽比较小的试件RW2衰减较快,RW8衰减相对较慢,说明摇摆墙的阻尼随高宽比增大而减小;2)当墙体在摇摆振动过程中与基础发生碰撞时,即摇摆墙在达到峰值位移后经历四分之一振动周期返回位移零点的瞬时,对应速度时程曲线上便出现一个“尖点”。通过对比尖点数目可发现,在相同时间内,高宽比较小的摇摆墙碰撞次数较多,墙体由于碰撞所造成的能量耗散越多,因此,最早恢复静止状态;3)3片摇摆墙(RW2、RW5、RW8)在自由摇摆运动过程中的峰值加速度分别为3.66g、2.79g、2.28g。由于高宽比较小的摇摆墙RW2刚度最大,抗弯能力最强,因此,在相同初始位移角的条件下,预应力筋和重力荷载提供的恢复能力最强,峰值加速度最大。
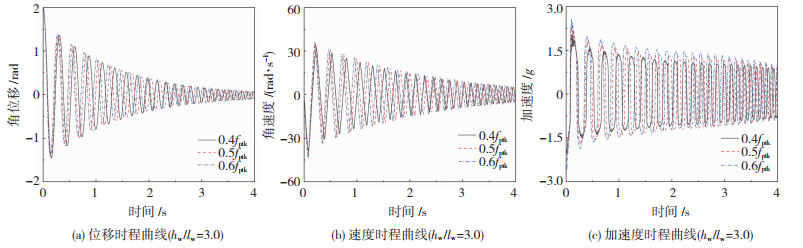
2.3.2 初始预应力水平的影响初始预应力作为设计自复位摇摆墙时的一个非常重要的参数,对墙体摇摆振动特性的影响较大。不同初始预应力水平(0.4fptk、0.5fptk、0.6fptk)的试件RW7、RW8、RW9的动力时程响应见图 8。
|
图 8 不同预应力水平下自复位摇摆墙动力响应对比 Fig. 8 Comparison of dynamic response of self-centering rocking wall under different prestress levels |
由图 8可分析初始预应力水平的影响:1)相同高宽比(hw/lw=3.0)下,摇摆墙墙体RW7、RW8、RW9在释放后的第一个半周期的位移峰值响应基本一致,分别为1.448%、1.446%、1.407%,相位最大仅相差0.02 s。当墙体经过第一次碰撞后到达峰值位移时,由于不同初始预应力,墙体储存不同的弹性势能,墙体在运动到下一个峰值位移过程中,初始预应力水平较高的RW9将内部更多的弹性势能储能转化为动能,墙体的摇摆速度更大,摇摆周期也更短,墙体的往复摇摆运动的相位差逐渐增大;2)高宽比相同的3片摇摆墙,其在自由摇摆振动过程中的峰值加速度分别为2.03g、2.28g、2.57g,数值较为接近,即虽然3片摇摆墙的动力响应存在较大的相位差异,同一周期内摇摆墙的位移和速度峰值相差最大仅为9.8%和13.3%,说明与高宽比不同,初始预应力水平对摇摆墙发生墙-基碰撞时的峰值速度影响较小,根据Housner[1]的研究,墙体碰撞时的瞬时速度峰值将直接影响到摇摆墙碰撞耗能能力。
3 动力耗能分析 3.1 恢复系数通过图 9所示简化刚体摇摆模型(SRM)来描述刚体结构围绕基底旋转中心的摇摆转动。

|
图 9 刚性摇摆块模型 Fig. 9 Rigid rocking block model |
基于刚体在运动过程中角动量守恒的假设,这种自由摇摆运动的公式可表示为:
| $ \begin{gathered} I_0 \ddot{\theta}+M g R \sin [\operatorname{sgn}(\theta) \alpha-\theta]= \\ -M \ddot{u}_{\mathrm{g}} R \cos [\operatorname{sgn}(\theta) \alpha-\theta] \end{gathered} $ | (2) |
式中:Io为刚体绕旋转中心的转动惯量,R为转动半径,α为刚体的长细比,
在刚性块自由摇摆运动过程中,块体与基础之间发生频繁碰撞,系统内的能量因此被耗散掉,块体的峰值速度逐渐减小直至块体停止摇摆。块体在撞击过程中的动能损失便可以近似用一个恢复系数r表示:
| $ r=\left(\frac{\dot{\theta}_2}{\dot{\theta}_1}\right)^2=\left[1-\frac{m R^2}{I_{\mathrm{o}}}(1-\cos 2 \alpha)\right] $ | (3) |
为验证这一理论,文献[15-17]采用不同的摇摆界面材料开展了一系列试验研究,发现式(3)高估了碰撞耗能造成的能量损耗,同时,由于采用的摇摆界面材料的不同,碰撞耗能能力也有所不同。因此,Kalliontzi等[6]通过引入以接触长度为基础定义的参数k提出了修正后的摇摆模型(MSRM)恢复系数:
| $ r=\left[\frac{4-3(\sin \alpha)^2\left(1+k^2\right)}{4-3(\sin \alpha)^2\left(1-k^2\right)}\right]^2 $ | (4) |
Kalliontzi等[5]通过试验确定了k的取值为0.72,Nazari等[4]通过对4片缩尺比为5/18的混凝土摇摆墙开展的振动台试验研究中得到该类剪力墙的恢复系数试验平均值r为0.82,这与通过式(4)计算得到r值为0.8吻合较好,证明该恢复系数计算值能够对摇摆构件在碰撞过程中的能量损耗提供准确的估计。
为分析恢复系数r的MSRM计算值对不同设计参数的敏感程度,基于9片后张预应力摇摆墙的自由衰减振动模拟(FEA)得到了恢复系数随碰撞次数n的变化,见图 10。并将其平均值与理论值进行比较,见表 4。

|
图 10 恢复系数的参数敏感度 Fig. 10 Parameter sensitivity of restitution coefficient |
| 表 4 恢复系数试验值与计算值对比 Tab. 4 Comparison between experimental value and calculated value of restitution coefficient |
结合图 10和表 4可知:1)9片摇摆墙摇摆振动试验的恢复系数平均值均略大于MSRM计算值,但最大误差仅为4.39%,说明MSRM能够为摇摆墙提供精确的耗能能力评估;2)摇摆墙的恢复系数对高宽比和初始预应力水平的敏感程度有所不同,高宽比对r值的影响较大,随高宽比提高,恢复系数逐渐增大,说明高宽比较大的摇摆墙的碰撞耗能损失较少,从MSRM的计算公式中可以得到一致的结论,因此高宽比较大的摇摆墙不宜用于地震高烈度区。初始预应力水平对r值的影响不大,预应力较小的摇摆墙r值仅有微弱的降低,RW1与RW3的试验平均值相差1.71%,RW4与RW6相差0.72%,RW7与RW9相差0.51%。
3.2 动力耗能能力摇摆墙在墙体摇摆往复运动过程中系统通过多种机制耗散输入的能量。为了衡量不同设计参数下摇摆墙的动力耗能能力,对数值模拟中9片摇摆墙的总能量耗散进行了对比,见图 11。可看出,该类剪力墙在动态响应过程中的耗能形式是渐进式的,随墙-基接缝的交替开合其总能量呈阶梯式下降,同时结合图 7、8的位移时程曲线可发现,在摇摆墙从峰值位置运动到静止位置的阶段,系统的总能量并未出现明显的损失,在墙-基界面闭合的前后很短的时间内,系统内能有显著的下降,说明由墙趾碰撞造成的能量损失较多。

|
图 11 摇摆墙动力耗能能力对比 Fig. 11 Comparison of dynamic energy dissipation capacity of rocking wall |
对比9个试验模型的总耗能可知,高宽比最小的试件RW1系统能量损耗最多,一方面,高宽比较小的摇摆墙振动周期小,因此相同时间内碰撞次数多,由碰撞所消耗的能量多;另一方面,高宽比较小的试件,固有黏性阻尼较高,滞回耗能能力强。初始预应力较大的试件由于其储存的弹性势能较多,系统总内能大,但是其对摇摆墙的耗能能力贡献并没有明显的提升。
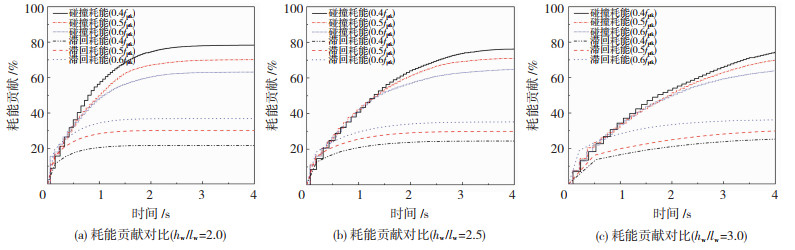
3.3 耗能成分分析为了量化不同阻尼成分在摇摆墙摇摆振动过程中的能量耗散贡献,通过记录墙体在运动到原点位置前后的瞬时速度变化,可计算该过程中的动能变化量,这部分能量损失主要是由于碰撞造成的。通过将系统的位移和惯性力的关系绘制在一起并计算出该滞回环的面积,可得到摇摆墙的滞回耗能。将两部分耗能在总能量损耗中所占的百分比随时间的变化进行对比,见图 12。可看出:1)滞回阻尼在前几个振动周期内作为主要耗能手段而在系统耗能中占据主要地位,此时摇摆墙的横向侧移较大,能量损耗来源于墙趾处受压区混凝土的塑性变形,随着振幅逐渐衰减,碰撞次数增大,由碰撞造成的能量损失逐渐增加并超过滞回耗能;2)通过对比最终的耗能贡献可发现,高宽比较小的试件,其由碰撞造成耗能损失更多,最终,RW1滞回耗能占系统总耗能的21.7%,碰撞耗能为78.3%,相比高宽比为3.0的试件RW7,碰撞耗能占比提升了4.7%。初始预应力对碰撞耗能占比的影响同样明显,随初始预应力增大,滞回阻尼的影响更加明显,RW3的滞回耗能占比为36.8%,碰撞耗能为63.2%。
|
图 12 不同耗能成分贡献对比 Fig. 12 Comparison of contributions of different energy dissipation components |
1) 采用的数值模型能够较好地模拟摇摆墙的动力特性,虽然位移时程曲线的模拟结果在衰减振动后期与试验结果存在相位差,但能够从整体上把握摇摆墙的动力响应。
2) 模型的动力特性对不同参数的敏感度有所不同。降低高宽比可显著降低摇摆墙振动周期和增大振动衰减速率,增大初始预应力对墙体振动特性影响并不明显,仅使振动周期最大降低0.4%。
3) 摇摆墙的动力耗能能力由多种耗能机制组成,高宽比较大的摇摆墙由于其恢复系数较高,碰撞所造成的能量损耗较少,而碰撞耗能作为摇摆墙系统中主要的能量耗散来源;高宽比较大的构件不适合用于高烈度区抗震耗能构件使用;预应力水平对滞回耗能的影响较大,增大初始预应力,可显著提高摇摆墙内滞回耗能能力。
| [1] |
HOUSNER G W. The behavior of inverted pendulum structures during earthquakes[J]. Bulletin of the Seismological Society of America, 1963, 53(2): 403. DOI:10.1785/BSSA0530020403 |
| [2] |
PENA F, PRIETO F, LOURENCO P B, et al. On the dynamics of rocking motion of single rigid-block structures[J]. Earthquake Engineering & Structural Dynamics, 2010, 36(15): 2383. DOI:10.1002/eqe.739 |
| [3] |
MA Q T. The mechanics of rocking structures subjected to ground motion[D]. Auckland: The University of Auckland, 2010
|
| [4] |
NAZARI M, SRITHARAN S, AALETI S. Single precast concrete rocking walls as earthquake force-resisting elements[J]. Earthquake Engineering & Structural Dynamics, 2017, 46(5): 753. DOI:10.1002/eqe.2829 |
| [5] |
KALLIONTZI S D, SRITHARAN S. Dynamic response and impact energy loss in controlled rocking members[J]. Earthquake Engineering & Structural Dynamics, 2020, 49(4): 319. DOI:10.1002/eqe.3240 |
| [6] |
KALLIONTZIS D, SRITHARAN S. Improved coefficient of restitution estimation for free rocking members[J]. Journal of Structural Engineering, 2016, 142(12): 06016002-1. DOI:10.1061/(ASCE)ST.1943-541X.0001598 |
| [7] |
NAZARI M, SRITHARAN S. Influence of different damping components on dynamic response of concrete rocking walls[J]. Engineering Structures, 2020, 212: 1. DOI:10.1016/j.engstruct.2020.110468 |
| [8] |
TWIGDEN K M. Dynamic response of unbonded post-tensioned concrete walls for seismic resilient structures[D]. Auckland: The University of Auckland, 2016
|
| [9] |
SMITH B. ABAQUS/Standard user's manual, version 2021[Z]. Pawtucket: ABAQUS Inc, 2021
|
| [10] |
钢结构设计标准: GB 50017—2017[S]. 北京: 中国建筑工业出版社, 2017
|
| [11] |
赵星. 后张预应力混凝土摇摆墙抗震性能试验研究[D]. 哈尔滨: 哈尔滨工业大学, 2019
|
| [12] |
ACI Innovation Task Group 5. Acceptance criteria for special unbonded post-tensioned precast structural walls based on validation testing and commentary: ACI ITG-5.1-07[S]. Farmington Hills: American Concrete Institute, 2007
|
| [13] |
ACI Committee 318. Building code requirements for structural concrete (ACI 318-19) commentary on building code requirements for structural concrete (ACI 318R-19)[S]. Farmington Hills: American Concrete Institute, 2019
|
| [14] |
ACI Innovation Task Group 5. Requirements for design of a special unbonded post-tensioned precast shear wall satisfying ACI ITG-5.1 (ACI ITG-5.2-09) and commentary: ACI ITG-5.2-2009[S]. Farmington Hills: American Concrete Institute, 2009
|
| [15] |
PRIESTLEY M, EVISON R J, CARR A J. Seismic response of structures free to rock on their foundation[J]. Bulletin of the New Zealand National Society for Earthquake Engineering, 1978, 11(3): 141. DOI:10.5459/bnzsee.11.3.141-150 |
| [16] |
ASLAM M, FODDEN W G, SCALISE D T. Earthquake rocking response of rigid bodies[J]. Journal of the Structural Division, 1980, 106(2): 377. DOI:10.1016/0022-1694(80)90029-3 |
| [17] |
FIELDER W T, VIRGIN L N, PLAUT R H. Experiments and simulation of overturning of an asymmetric rocking block on an oscillating foundation[J]. European Journal of Mechanics-A/Solids, 1997, 16(5): 905. |
 2022, Vol. 54
2022, Vol. 54