2. 深圳市建筑设计研究总院有限公司北京分院, 北京 100195;
3. 宁晋县住房和城乡建设局, 河北 邢台 055550
2. Beijing Branch Institute, Shenzhen Central Institute of Architectural Design and Research Co. Ltd., Beijing 100195, China;
3. Ningjin County Housing and Urban-Rural Development Bureau, Xingtai 055550, Hebei, China
某体育馆(图 1(a))由地上结构和地下结构两部分组成,地上部分为圆钢管大跨度桁架结构,地下部分主要为钢筋混凝土框架结构,上部桁架结构弦杆按一定角度热弯成型竖直插入下部结构框架柱内,并且在地下部分结构底面至地面以上1 m高度范围的钢管内填充混凝土,形成一种采用热弯圆钢管的钢管混凝土(CFST)-外包钢筋混凝土(RC)的复合柱节点(图 1(b)),在同类工程中罕有使用,其节点在弦杆、腹杆等复杂内力作用下的受力性能亟待确认。

|
图 1 体育馆及节点构造 Fig. 1 Gymnasium and joint structure |
Packer[1]通过对T型、X型和K型矩形钢管混凝土桁架节点进行试验研究,给出了支管受轴向压力作用下核心混凝土局部承压强度的承载力计算公式;李自林等[2]通过对主管受轴力的N型圆钢管相贯节点和在其主管填充混凝土的节点的静力试验,表明加强节点能显著提高节点的极限承载力;刘永健等[3-5]对桁架中X、T、Y、K型钢管混凝土强化节点的失效模式及承载力等进行试验研究,表明强化节点有较好的受力性能;Hou等[6-7]进行了圆形钢管混凝土受压节点横向局部承压试验和有限元分析;Yang等[8]进行了方形钢管混凝土受压节点横向局部承压试验,表明内填混凝土对圆形和方形节点主管局部承压能力均有较大提高;Han等[9]通过试验与有限元模拟相结合的办法对钢管热弯后残余应力进行对比分析,得到了数值模拟预测的残余应力与试验结果基本一致。
钢管混凝土应用在桁架结构中不同形式的节点都表现出了良好的受力性能,但工程中采用的热弯圆钢管CFST-外包RC组合节点中钢管经历了热弯曲成型,累积的残余应力对节点受力性能的影响尚未可知。基于此,本文以工程中弦杆钢管弯曲后直接插入地下钢筋混凝土框架柱的拱脚为原型,设计了3个采用热弯圆钢管的CFST-外包RC组合节点,进行节点在弦杆受压、腹杆受拉的复杂受力下加载试验与有限元数值模拟,研究热弯钢管残余应力、不同弯曲角度以及弦杆根部钢管内是否填充混凝土等对节点破坏形态、承载能力等受力性能的影响。
1 试验概况 1.1 试件设计节点试件选取地上、地下结构交界面附近区域,考虑弦杆、腹杆尺寸以及加载需要取弦杆长度1 000 mm或750 mm,下部结构的梁、柱长度取节点域外各自1倍截面高度,以便于传递压力。试件构造及配筋与原型结构一致,钢管弯曲处设置加劲肋,钢管外壁前后左右4个方向设置上下间距为100 mm的D19×80栓钉,由于钢管阻断无法锚固的梁内钢筋采用焊接板焊接锚固。
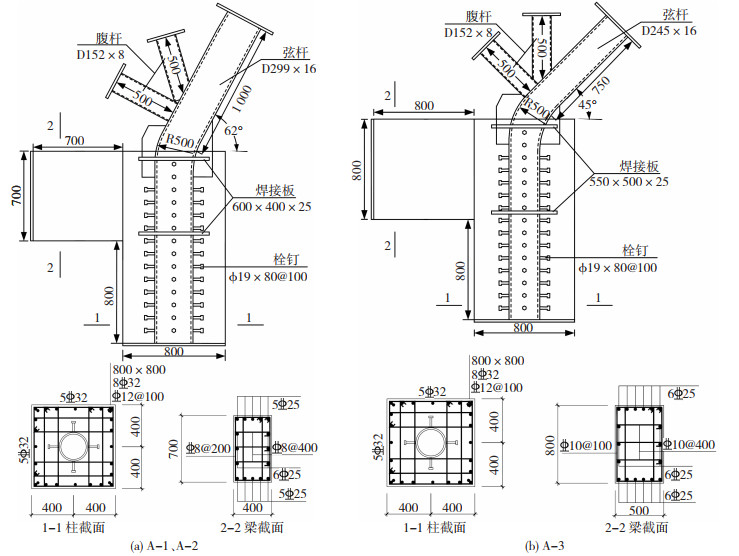
根据弦杆对地面的插入角度不同选取2种角度和管径共设计了3个足尺节点试件。体育馆高区拱脚节点试件A-1和弦杆地上部分不填充混凝土的试件A-2,确认内填混凝土对节点受力性能影响;体育馆低区拱脚节点试件A-3,管径较小但弯曲角度更大。各试件的主要参数见表 1,具体尺寸以及梁柱配筋等详细信息见图 2。
| 表 1 试件主要参数 Tab. 1 Main parameters of specimen |
|
图 2 试件详图(mm) Fig. 2 Detailed drawing of specimen (mm) |
试件外包柱和梁采用C40商用混凝土,弦杆包括插入下部结构部分钢管内填充混凝土采用C60微膨胀自密实混凝土,试验测得的混凝土的立方体抗压强度以及棱柱体抗压强度见表 2。
| 表 2 混凝土力学性能 Tab. 2 Mechanical properties of concrete |
试件钢结构部分采用的钢材均为Q345,主弦杆钢管壁厚均为16 mm,钢筋为HRB400,钢材的力学性能见表 3。
| 表 3 钢材力学性能 Tab. 3 Mechanical properties of steel |
试验利用40 MN多功能电液伺服加载系统进行,试件通过底部设置三角形或梯形钢墩承担支座反力并且钢墩使试件旋转一定的角度让弦杆处于竖直位置以方便对试件弦杆施加轴向压力荷载。腹杆上的拉力较小且在试验过程中固定不变,通过在试件底座上安装反力架进行施加,各试件腹杆的拉力值见表 4。以试件A-3为例,腹杆反力架加载图及试件加载图见图 3。
| 表 4 各腹杆设计拉力 Tab. 4 Designed tension of each web |

|
图 3 试件加载详图 Fig. 3 Details of loading specimen |
试验首先施加腹杆拉力并固定后,对弦杆采取力-位移混合控制的荷载分级加载,在试验荷载低于屈服荷载之前,每级荷载增量取预计承载力的1/10~1/15,持荷时间1 min,观察并记录试验现象,试验荷载达到或超过屈服荷载刚度明显降低时,改为位移控制加载,加载速率为0.5 mm/min,加载到承载力基本不再上升时结束试验。
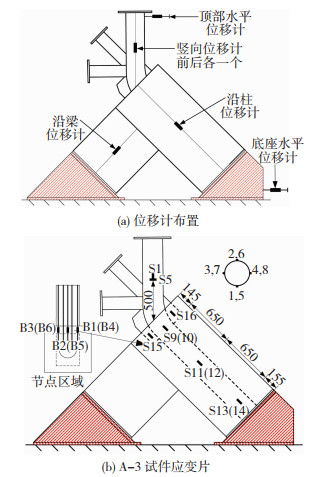
1.4 测量方案弦杆沿高度方向前后各布置一个YHD型位移传感器测量在加载过程中弦杆的轴向变形,A-1、A-2试件标距为1 000 mm,A-3试件为750 mm,在弦杆顶端布置一个横向位移计监测加载过程中是否出现明显的压偏现象。沿下部柱、梁各设置一个位移计测量加载过程中梁柱沿轴向的变形,在底部支墩处设置一个水平位移计,监测支座是否滑动。具体布置见图 4(a)。
|
图 4 测点布置示意 Fig. 4 Layout of measuring points |
在上部弦杆沿周长的四等分点处成对布置纵向应变片(S1~S4)和环向应变片(S5~S8),在外包RC柱内钢管外壁沿高度布置3组纵向应变片(S9~S14),测试不同位置钢管的受力状态;在钢管弯曲处的加劲肋上沿钢管受力方向布置应变片(S15、S16),测试加劲肋受力情况;在节点梁上下纵筋上设置了应变片(B1~B6)。具体贴片位置见图 4(b)。
2 试验现象及结果 2.1 试验现象 2.1.1 试件A-1加载初期试件处于弹性阶段,上部弦杆轴向变形随荷载增大呈线性增加,试件并无明显变形现象;加载至5 000 kN时试件进入弹塑性阶段,加载到6 250 kN时节点外包框架柱和梁开始出现裂缝,并随着荷载的增加裂缝发展延伸,加载到7 000 kN时距弦杆根部100 mm处钢管出现较明显的向外屈曲,随荷载增加钢管鼓曲加重,柱和梁最终裂缝宽度在0.1 mm以内,最终破坏状态见图 5(a)。

|
图 5 试件破坏状态 Fig. 5 Failure state of specimens |
上部弦杆内不填充混凝土的试件A-2与A-1现象相似,加载初期试件处于弹性阶段,加载到4 000 kN时试件进入明显弹塑性阶段,加载到5 000 kN时距弦杆根部100 mm处钢管出现较明显的向内屈曲,随荷载增加钢管向内屈曲加重,外包柱和梁基本无裂缝,最终破坏状态见图 5(b)。
2.1.3 试件A-3A-3加载初期试件处于弹性阶段,上部弦杆轴向变形随荷载增大呈线性增加,试件并无明显变形现象,加载至3 000 kN时试件弦杆根部出现轻微鼓曲,外包框架梁出现较明显的弯剪斜裂缝,随着荷载的增加裂缝发展延伸,加载到4 000 kN时试件进入明显的弹塑性阶段,随荷载增加弦杆根部鼓曲加重,框架梁裂缝宽度最大发展到0.2 mm左右,最终破坏状态见图 5(c)。
试件最终破坏均为弦杆钢管根部区域的屈曲破坏,A-1和A-2两者屈曲位置基本相同,但A-1为外凸屈曲A-2为内凹屈曲,说明钢管内填混凝土对钢管破坏模式的影响较大;A-3比A-1的钢管弯曲角度大,框架梁受力明显增大。
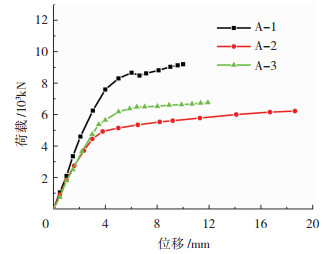
2.2 荷载-位移曲线3个试件的弦杆轴向荷载和位移关系曲线见图 6。可以看出进入塑性后荷载增长缓慢,但由于钢管壁较厚荷载未有下降,均表现出较高的承载能力和良好的变形能力。A-1与A-2在位移达到10 mm时,A-1的荷载比A-2提高了60.7%,A-1的刚度也明显高于A-2,说明钢管内填充混凝土可以明显提高构件的刚度与承载力;在A-1与A-3弦杆平均应变为1×10-2(A-1位移10 mm、A-3位移7.5 mm)时A-1的承载力比A-3提高了41.4%,A-1的刚度也高于A-3,说明试件的承载力与刚度随上部钢管的管径增大而增大。
|
图 6 荷载-位移曲线 Fig. 6 Load-displacement curve |
各试件弦杆荷载-弦杆中部位置纵向应变、环向应变关系见图 7,纵向应变和环向应变分别为纵向应变片(S1~S4)及环向应变片(S5~S8)测值的平均值。可以看出,试件纵向应变在到达钢管材料屈服应变之前曲线基本处于线性,纵向应变超过钢管材料屈服应变以后进入较明显的弹塑性阶段,试件的纵向变形明显加快。环向应变达到钢管材料屈服应变明显晚于纵向应变。A-1的钢管材料屈服时荷载明显高于A-2。

|
图 7 上部弦杆荷载-应变曲线 Fig. 7 Load-strain curve of upper chord |
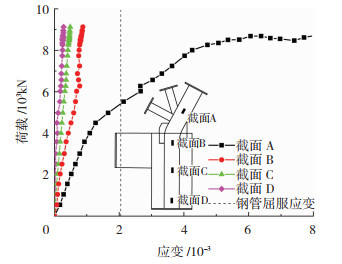
A-1弦杆荷载-不同截面处的钢管纵向应变关系曲线见图 8,钢管纵向应变为截面测点的钢管纵向应变平均值。上部弦杆应变较大,但在外包RC柱内的钢管纵向应变随截面位置向下而减小,最终也未达到钢管材料屈服应变,说明在外包段试件受力从钢管传递到外包RC柱承担。
|
图 8 不同截面钢管纵向应变 Fig. 8 Longitudinal strain of steel pipes at different sections |
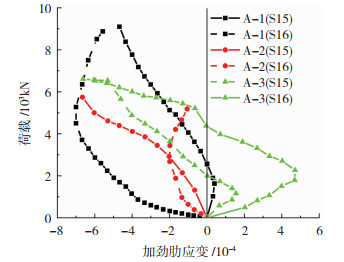
各试件弦杆荷载-钢管加劲肋应变关系曲线见图 9。A-1和A-2加劲肋应变变化趋势基本相同,其中测点S15随着荷载的增加应变一直上升,测点S16在达到峰值压应变后转为减小趋势,这是因为随着荷载的增加钢管有从弯管复原到直管的趋势;A-3加劲肋初始应变为受拉应变,原因是A-3钢管弯折角度较大,水平分力较大,使加劲肋受的拉力大于轴向力的压力而产生的结果。各试件加劲肋最终应变都小于8×10-4,还处于弹性范围内,结合试验过程并没有破坏现象,说明加劲肋的构造设置较为可靠,加劲肋可以对热弯钢管部分提供足够的支反力来防止热弯处过早发生应力集中而破坏。
|
图 9 弦杆荷载-加劲肋应变曲线 Fig. 9 Strain curve of stiffener with load |
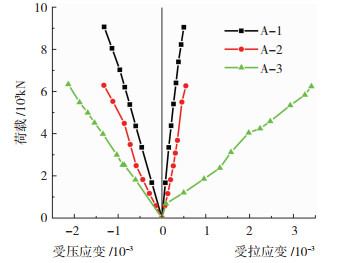
各试件弦杆荷载-梁端钢筋应变关系曲线见图 10,应变为梁端上排受压和下排受拉钢筋的纵向应变平均值。可看出各试件节点内梁钢筋应变增长和荷载增长基本为线性关系,应变基本保持在弹性范围内,A-3由于钢管的弯曲角度较大,梁下排钢筋受拉达到屈服。
|
图 10 弦杆荷载-钢筋应变曲线 Fig. 10 Strain curve of rebar with load |
钢管弯曲成型的中频热弯工艺见图 11,热弯设备由支承轮、转臂和感应加热系统组成。首先通过感应线圈对钢管进行加热,当温度达到800~1 200 ℃(模拟中加热温度为800 ℃)时,由油压动力系统推动圆钢管连续移动穿过加热线圈,在推力F、支承轮以及转臂夹具的共同作用下,圆钢管会在加热区域产生弯曲,并在通过加热线圈之后受热部分立即被冷却器喷水冷却以保持弯曲形状。钢管自身有两端冷却的支撑轮做支撑,使其弯曲部分始终在一个窄小宽度里进行,从而达到钢管弯曲成形后圆度不变或很少变形的效果。

|
图 11 中频热弯装置 Fig. 11 Intermediate frequency hot bending device |
Han等[9]通过对不同直径与厚度的热弯钢管进行残余应力试验测试并与有限元模拟结果进行对比,得到有限元模拟结果与试验测试结果基本一致的结论。本文采用同样的有限元模拟方法对Han等[9]的试验测试结果进行模拟,得到了相同的结果,限于篇幅原因,图 12给出了1根试验测点残余应力和有限元测点残余应力的对比结果。

|
图 12 残余应力有限元模拟与试验实测对比验证 Fig. 12 Comparison and verification of finite element simulation and experimental measurement of residual stress |
数值模拟中钢管采用实体单元,支撑轮和转臂简化为刚体且不考虑支撑轮与钢管之间的摩擦。图 13为划分完网格后的简化模型,约束条件为固定支撑轮,转臂只能绕Z轴进行转动,圆钢管只能沿X方向移动。

|
图 13 中频热弯有限元模型 Fig. 13 Finite element model of intermediate frequency hot bending |
钢材的应力-应变关系采用二折线模型,在热弯经历的加热和冷却过程中,室温下钢材的应力-应变关系由标准拉伸试验获得,其他温度范围内的应力-应变关系根据李国强等[10]所给温度与屈服强度的关系以及标准拉伸试验所得钢材屈服强度确定。表 5给出了不同温度下A-1的钢材屈服强度,其他温度相关材料参数如热膨胀系数αs、导热系数λs、比热Cs等均基于欧洲规范4[11]获得,具体取值见表 6。
| 表 5 不同温度下钢材屈服强度 Tab. 5 Yield strength of steel at different temperatures |
| 表 6 钢材温度参数 Tab. 6 Steel temperature parameters |
钢管热弯过程的数值模拟主要包括:钢管的初始温度设定为室温20 ℃,Step1将圆钢管加热至800 ℃模拟实际热弯工艺中的加热作用,Step2对模型施加位移荷载来模拟实际的弯曲过程,Step3将钢管冷却至室温20 ℃模拟冷却器对于钢管的冷却作用,Step4将所有约束释放得到钢管内无外荷载引起的应力即残余应力。计算得出A-1与A-3的残余应力(Mises应力)分布情况见图 14。

|
图 14 热弯残余应力分布 Fig. 14 Residual stress distribution of hot bending |
由图 14可以看出,在热弯圆钢管的长度方向上,残余应力主要分布在转弯处且最大值出现在转臂限制处,在热弯圆钢管转弯处的各个截面上,截面前后是完全对称分布,在中性轴附近残余应力较大,拱背和拱腹残余应力相对较小。A-1热弯部位的残余应力最大为453.93 MPa,A-3热弯部位的残余应力最大为500 MPa,说明了随着弯曲角度增大,热弯残余应力增大。
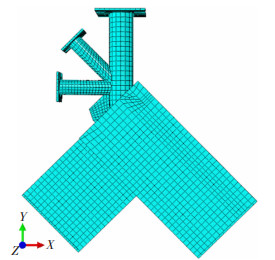
3.2 考虑钢管残余应力的节点模型数值模拟试验节点主要由钢管混凝土和外包混凝土以及加劲肋等组成,钢材和混凝土采用三维实体单元、钢筋采用三维桁架线性单元模拟。网格采用结构化和扫掠化网格划分技术[12],划分完网格后的试件见图 15。约束条件为顶部限制UX和UZ方向的自由度,梁端和柱端钢板完全固定,即限制3个方向的平动和转动。
|
图 15 划分完网格的节点有限元模型(A-3) Fig. 15 Finite element model of joint after meshing(A-3) |
节点梁柱混凝土材料本构关系由规范[13]给出;钢管内约束混凝土中混凝土的参数膨胀角ψ和不变量应力比Kc等取值采用Tao等[14]建议的公式进行计算,单轴受压本构采用《钢管混凝土结构》[15]中圆钢管混凝土的本构关系。
将3.1中热弯模型中钢管与节点模型中钢管网格划分一致,基于ABAQUS软件中应力文件处理模式将热弯钢管的残余应力通过写入inp文件的方式导入到节点模型的钢管单元上,即节点模型中钢管热弯部位在初始状态下就存在了由于热弯产生的残余应力,见图 16。

|
图 16 引入热弯残余应力的节点模型(A-3) Fig. 16 Joint chords with thermal bending residual stress introduced(A-3) |
然后在一个分析步中同时施加腹杆荷载和弦杆荷载,为了让计算更容易收敛,弦杆采用位移控制加载,腹杆采用力控制加载。
有限元数值模拟得到有无热弯残余应力的试件弦杆荷载-位移曲线与试验得到的荷载-位移曲线对比见图 17。可以看出,模拟值与试验值趋势较为一致,说明数值模拟较为可靠;节点中考虑钢管热弯残余应力后,试件的刚度有一定的下降,并且与试验值更为接近,但加载后期承载力基本没有差异,说明钢管热弯后的残余应力降低了试件的刚度,对承载力基本没有影响。由图 16(c)可看出,考虑热弯钢管残余应力后,弯曲角度更大的A-3刚度相比A-1降低更大。

|
图 17 荷载-位移曲线对比 Fig. 17 Comparison of load-displacement curves |
热弯钢管CFST-外包RC节点受压承载力基本取决于上部弦杆的受压承载力,采用《钢管混凝土结构技术规范》[16]计算公式对弦杆承载力进行计算(A-2上部弦杆无内填混凝土,承载力为钢管承载力),得到理论计算承载力。理论计算值(Nt)、有限元模拟值(Nf)与试验值(Nc)的对比见表 7,试验值和模拟值取各个试件上部弦杆平均应变为1×10-2时的节点轴压荷载。从表 7可以看出,各个试件的理论计算值、有限元模拟值与试验值之间误差都在10%以内,说明计算值和模拟值有较好的精度。
| 表 7 承载力比较 Tab. 7 Comparison of bearing capacity |
1) 热弯钢管CFST-外包RC组合节点在弦杆受压、腹杆受拉的复杂受力下的破坏形态主要为弦杆根部钢管的屈曲破坏,节点承载力取决于弦杆根部受压承载力。
2) 钢管热弯产生的残余应力降低了节点刚度且钢管弯曲角度越大节点刚度降低越大,但对承载力基本没有影响。
3) 钢管内填混凝土可以显著提高节点刚度和承载力,节点刚度和承载力随钢管直径增大而增大。
4) 采用钢管混凝土结构技术规范公式计算得到的热弯钢管CFST弦杆轴压承载力与试验值以及有限元数值模拟值三者吻合较好。
| [1] |
PACKER J A. Concrete-filled HSS connections[J]. Journal of Structural Engineering, 1995, 121(3): 458. DOI:10.1061/(ASCE)0733-9445(1995)121:3(458) |
| [2] |
李自林, 吴亮秦, 朱斌, 等. 不同加强措施下N型圆钢管相贯节点力学性能的试验比较[J]. 工程力学, 2008, 25(11): 179. LI Zilin, WU Liangqin, ZHU Bin, et al. Experimental comparison of static behavior of tubular N-joints reinforced in different ways[J]. Engineering Mechanics, 2008, 25(11): 179. |
| [3] |
狄谨, 周绪红, 刘永健. 矩形钢管混凝土桁架节点极限承载力研究[J]. 中国公路学报, 2004, 17(3): 62. DI Jin, ZHOU Xuhong, LIU Yongjian. Research on the ultimate bearing capacity of joint in the concrete filled rectangular steel tube truss[J]. China Journal of Highway and Transport, 2004, 17(3): 62. DOI:10.3321/j.issn:1001-7372.2004.03.013 |
| [4] |
刘永健, 周绪红, 刘君平. 主管内填混凝土的矩形钢管X型节点受拉和受弯性能试验研究[J]. 建筑结构学报, 2009, 30(1): 82. LIU Yongjian, ZHOU Xuhong, LIU Junping. Experimental research on rectangular steel tube X-joints with chord concrete-inside subjected to tension and bending[J]. Journal of Building Structures, 2009, 30(1): 82. DOI:10.3321/j.issn:1000-6869.2009.01.012 |
| [5] |
刘永健, 刘君平, 张俊光. 主管内填混凝土矩形和圆形钢管桁架受弯性能对比试验研究[J]. 建筑结构学报, 2010, 31(4): 86. LIU Yongjian, LIU Junping, ZHANG Junguang. Experimental research on RHS and CHS truss with concrete filled chord[J]. Journal of Building Structures, 2010, 31(4): 86. |
| [6] |
HOU C, HAN L H, ZHAO X L. Concrete-filled circular steel tubes subjected to local bearing force: experiments[J]. Journal of Constructional Steel Research, 2013, 83: 90. DOI:10.1016/j.jcsr.2013.01.008 |
| [7] |
HOU C, HAN L H, ZHAO X L. Concrete-filled circular steel tubes subjected to local bearing force: finite element analysis[J]. Thin-Walled Structures, 2014, 77: 109. DOI:10.1016/j.tws.2013.12.006 |
| [8] |
YANG Y F, HOU C, WEN Z, et al. Experimental behaviour of square CFST under local bearing forces[J]. Thin-Walled Structures, 2014, 74: 166. DOI:10.1016/j.tws.2013.09.022 |
| [9] |
HAN Q, HAN Z, LU Y. Experimental and numerical investigations on residual stresses in hot-bent circular steel tube[J]. Journal of Constructional Steel Research, 2019, 161(10): 31. DOI:10.1016/j.jcsr.2019.06.008 |
| [10] |
李国强, 韩林海, 楼国彪, 等. 钢结构及钢-混凝土组合结构抗火设计[M]. 北京: 中国建筑工业出版社, 2006: 97. LI Guoqiang, HAN Linhai, LOU Guobiao, et al. Fire resistance design of steel structure and steel-concrete composite structure[M]. Beijing: China Building Industry Press, 2006: 97. |
| [11] |
Eurocode 4. Design of composite and concrete structures, part 1.2: structural fire design [S]. Brussels: European Committee for Standardization, 1994
|
| [12] |
石亦平, 周玉蓉. ABAQUS有限元分析实例详解[M]. 北京: 机械工业出版社, 2006. SHI Yiping, ZHOU Yurong. Detailed explanation of ABAQUS finite element analysis examples[M]. Beijing: Machinery Industry Press, 2006. |
| [13] |
混凝土结构设计规范: GB 50010—2010 [S]. 北京: 中国标准出版社, 2010 Code for design of concrete structures: GB 50010—2010 [S]. Beijing: China Standards Press, 2010 |
| [14] |
TAO Z, WANG Z B, YU Q. Finite element modelling of concrete-filled steel stub columns under axial compression[J]. Journal of Constructional Steel Research, 2013, 121. DOI:10.1016/j.jcsr.2013.07.001 |
| [15] |
韩林海. 钢管混凝土结构: 理论与实践[M]. 北京: 科学出版社, 2007: 69. HAN Linhai. Concrete-filled steel tube structures: theory and practice[M]. Beijing: Science Press, 2007: 69. |
| [16] |
钢管混凝土结构技术规范: GB 50936—2014 [S]. 北京: 中国标准出版社, 2014 Technical code for concrete-filled steel tubular structures: GB 50936—2014 [S]. Beijing: China Standards Press, 2014 |
 2022, Vol. 54
2022, Vol. 54


