2. 上海大学 风工程和气动控制研究中心, 上海 200444
2. Wind Engineering and Aerodynamic Flow Control Research Center, Shanghai University, Shanghai 200444, China
圆柱型结构在土木工程中应用广泛,且常常以柱群的形式出现,如缆索承重桥并列索、烟囱群、冷却塔群、海洋立管、多分裂导线等[1-2]。当流体流经钝体时,出现剪切层分离、失稳及转捩等现象,并在尾流中形成交替脱落的旋涡[3]。为了进一步了解复杂的流动结构及潜在的流态转变机制,从高维非线性流场数据中提取低维空间下的流动特征,是当前研究的热点[4]。
近些年来,随着高精度数值模拟技术的迅猛发展,低维降阶技术在复杂流动分析中的应用日益广泛[4-5]。其中,本征正交分解(POD)、动力学模态分解(DMD)是较典型的两种方法。POD将流场分解为1组完全正交的模态,并根据其模态能量大小进行排序。该方法由Berkooz等[6]首先提出,用来识别湍流中的相干结构,捕捉流场中的主导模态。DMD方法是库普曼算子的一种近似,Schmid[7]首先提出DMD,用来分析试验或数值模拟得到的高维、大规模的流场数据,提取的低维子空间的特征值和特征向量包含流场的主要动力学特征,相比于POD,DMD得到的模态对应单一的频率与增长率。寇家庆等[8]对DMD的研究进展进行总结,提出DMD未来的发展方向。Sakai等[9]、叶坤等[10]、Bai等[11]将POD与DMD分别应用于单圆柱与并列双圆柱,分析其稳定性以及尾流流态的流动特性。
目前,对串列双圆柱绕流的研究主要集中在不同雷诺数下气动性能分析及临界间距比的确定[12-14]。Zdravkovich[1]对串列双圆柱的绕流场特性进行试验研究,并根据间距比将柱间流态分成:单一钝体、交替再附、定常再附、间歇性再附和双涡脱流态。Sumner[2]则将串列双圆柱流态分成3类:单一钝体流态、剪切层再附流态、双涡脱流态。然而,目前的研究仅通过试验或CFD对流场的流动特性进行分析,这意味着得到的数据通常包含多种信息成分,并且很难确定主导流态变化的流场特征。
为了澄清串列双圆柱的流态转变机制,分析各流态的模态特征,探究DMD流场重构的精度及误差。本文在雷诺数Re=100下,通过数值模拟对间距为1.1D~5D的串列双圆柱进行了研究,将数值模拟得到的气动力系数与文献结果进行了比较;并采用DMD方法对不同间距比下的串列双圆柱绕流场的动力学特性进行分析,通过对比分析3种流态下的各个主导模态,阐明3种流态的变化规律;最后根据DMD的主导模态建立降阶模型,从而对双圆柱绕流场进行了流场重构,并对其重构的精度与误差进行了分析。
1 数值方法 1.1 基本控制方程本文采用Fluent中的层流模型,在雷诺数Re=100下,对串列双圆柱绕流进行了模拟。对于此二维流动问题,流体视为黏性不可压流体,其在直角坐标系oxy下的连续方程和动量方程(N-S方程)分别为:
| $ \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0 $ | (1) |
| $ \rho \frac{\mathrm{D} u}{\mathrm{D} t}=\rho F_x-\frac{\partial p}{\partial x}+\mu\left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}\right) $ | (2) |
| $ \rho \frac{\mathrm{D} v}{\mathrm{D} t}=\rho F_y-\frac{\partial p}{\partial y}+\mu\left(\frac{\partial^2 v}{\partial x^2}+\frac{\partial^2 v}{\partial y^2}\right) $ | (3) |
式中:ρ为流体密度,p为流体压力,μ为黏性系数,u和v分别x、y方向的速度分量,Fx和Fy分别为流体在x、y方向的体力。
1.2 计算模型图 1为串列双圆柱的计算模型。两圆柱的直径均为D,中心间距为P,来流风速为U0,雷诺数为Re=100。图中的CD1和CL1分别表示上游圆柱的平均阻力系数和平均升力系数,C′D1和C′L1分别代表上游圆柱的脉动阻力系数与脉动升力系数。其中,阻力系数以顺流方向为正,升力系数以向上为正,下游圆柱同理。本文共计算了6种不同的中心间距:P/D=1.1、1.5、2、3、4、5。

|
图 1 双圆柱计算模型 Fig. 1 Computational model of two tandem circular cylinders |
数值模拟采用O型计算域,计算域直径为46D,阻塞率为2%,入流面采用速度入口边界条件;出流面采用自由出流边界条件,圆柱壁面为无滑移圆柱表面采用无滑移壁面条件。计算模型采用结构化网格,圆柱周向400个单元,径向180层单元;近壁面最小网格为0.000 1D,近壁面y+≈1;无量纲时间步Δt*为0.01(Δt*=ΔtU0/D,其中Δt为计算时间步,U0为来流风速)。计算模型网格总单元数从17万至20万不等,网格方案见图 2。

|
图 2 计算域网格方案 Fig. 2 Plane computation grid scheme |
动力学模态分解是将试验或数值仿真得到的N个时刻快照,从1到N时刻以快照序列的方式呈现,即X1N={x1, x2, x3, …, xm},且任意两个快照之间的时间间隔均为Δt。
假设1个线性动力系统来映射当前流场到后续流场,即假设流场xi+1可以通过流场xi的线性映射表示为
| $ x_{i+1}=\boldsymbol{A} x_i $ | (4) |
利用1到m时刻的流场快照,构建快照矩阵:
| $ \begin{aligned} \boldsymbol{X}_1^{m-1} &=\left[\boldsymbol{x}_1, \boldsymbol{x}_2, \boldsymbol{x}_3, \cdots, \boldsymbol{x}_{m-1}\right] \\ \boldsymbol{X}_2^m &=\left[\boldsymbol{x}_2, \boldsymbol{x}_3, \boldsymbol{x}_4, \cdots, \boldsymbol{x}_m\right] \end{aligned} $ | (5) |
根据(4)式的假设,可得:
| $ \begin{gathered} \boldsymbol{X}_2^m=\left[\boldsymbol{x}_2, \boldsymbol{x}_3, \boldsymbol{x}_4, \cdots, \boldsymbol{x}_m\right]= \\ {\left[\boldsymbol{A} \boldsymbol{x}_1, \boldsymbol{A} \boldsymbol{x}_2, \boldsymbol{A \boldsymbol { x } _ { 3 }}, \cdots, \boldsymbol{A} \boldsymbol{x}_{m-1}\right]=\boldsymbol{A} \boldsymbol{X}_1^{m-1}} \end{gathered} $ | (6) |
矩阵A可以使快照矩阵在时间上平移Δt,因此A可以反映系统的动力学特性。由于矩阵A的维度很高,直接计算难度很大。因此需要寻找一个与A相似的低维矩阵$\mathit{\boldsymbol{\tilde A}}$来代替A,用$\mathit{\boldsymbol{\tilde A}}$的特征值来近似估计A的特征值。
首先,对快照矩阵Xm-11进行奇异值分解:Xm-11=UΣV*。得到的3个矩阵中,U*,V*分别为U,V的复共轭转置矩阵,Σ是1个r×r阶对角矩阵,U*U=I,V*V=I。
$\mathit{\boldsymbol{\tilde A}}$是A矩阵在低阶子空间上的投影,定义为:$\mathit{\boldsymbol{\tilde A}}$=U*AU=U*Xm2VΣ-1。
因此,对矩阵$\mathit{\boldsymbol{\tilde A}}$(r×r)的特征分解可表示为: $\mathit{\boldsymbol{\tilde A}}$W=WΛ,Λ为对角矩阵包含着对应的特征向量,$\mathit{\boldsymbol{\tilde A}}$的第j个特征值为λj,特征向量为wj。则第j个DMD模态为:ϕj=Uwj。并且,该模态的频率与增长率(衰减率)分别为: fj=Im{lg(λj)}/Δt,gj=Re{lg(λj)}/Δt。
对于标准DMD方法,动力学模态分解所得到的模态是依据模态振幅来对各个模态的重要性排序[11]。近些年来,针对DMD模态重要性的排序准则,许多学者进行了研究。本文采用文献[15]的模态选择准则对模态进行排序:$\boldsymbol{I}_j=\sum\limits_{i=1}^N\left|\boldsymbol{\alpha}_j\left(\lambda_j\right)^{i-1}\right|\left\|\mathit{\pmb{\Phi}}_j\right\|_F^2 \times \Delta t$,其中αj=Wj-1U*x1, αj为第j个模态的振幅。
任意时刻流场可进行重构或预测:
| $\boldsymbol{x}_i=\mathit{\pmb{\Phi {\Lambda}}} ^{i-1} \boldsymbol{\alpha}=\sum\limits_{j=1}^r \mathit{\pmb{\Phi}}_j\left(\boldsymbol{\lambda}_j\right)^{i-1} \boldsymbol{\alpha}_{j }。$ |
为了验证本文所采用的计算方法和计算参数的合理性,本文首先以雷诺数为Re=100的固定单圆柱为研究对象进行计算模型的结果验证。表 1总结了本文固定单圆柱的网格验证结果以及文献[13, 16-18]已发表的试验和数值模拟结果,考虑周向网格数量、无量纲时间步长、阻塞率(B=D/H,H为计算域横向宽度)对计算结果的影响。可以发现,周向网格数量从256增加至400,模拟结果基本一致。考虑到双圆柱周围流场的复杂性,选择周向网格数量为400的工况进一步确认无量纲时间步长与阻塞率对模拟结果的影响。可以看出,在无量纲时间步长为0.01、阻塞率为2%时,模拟结果更接近文献结果,因此最终采用A3工况的网格参数进行后续模拟计算。
| 表 1 固定单圆柱模型的网格方案和结果验证(Re=100) Tab. 1 Grid scheme and results verification of fixed single circular cylinder model (Re=100) |
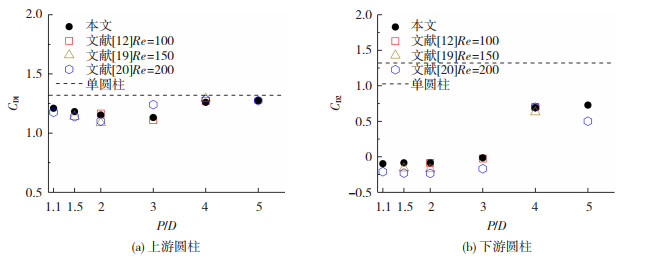
为了进一步验证本文计算模型的可靠性,图 3~图 5给出了间距比P/D=1.1~5串列双圆柱的平均阻力系数,脉动升力系数以及下游圆柱的St数,并与文献的结果进行对比。通过与文献[12]中相同雷诺数的结果比较可知,本文上、下游圆柱的平均阻力系数、脉动升力系数以及St数与文献[12]的误差均在5%以内。对比文献[19-20]相近雷诺数的结果可发现,随着间距比的变化,本文的气动力系数与St数的变化趋势与文献结果一致。
|
图 3 串列双圆柱平均阻力系数 Fig. 3 Mean drag coefficient of two tandem circular cylinders |

|
图 4 串列双圆柱脉动升力系数 Fig. 4 Fluctuating lift coefficient of two tandem circular cylinders |

|
图 5 下游圆柱升力的斯托罗哈数 Fig. 5 Strouhal number of lift force of downstream cylinder |
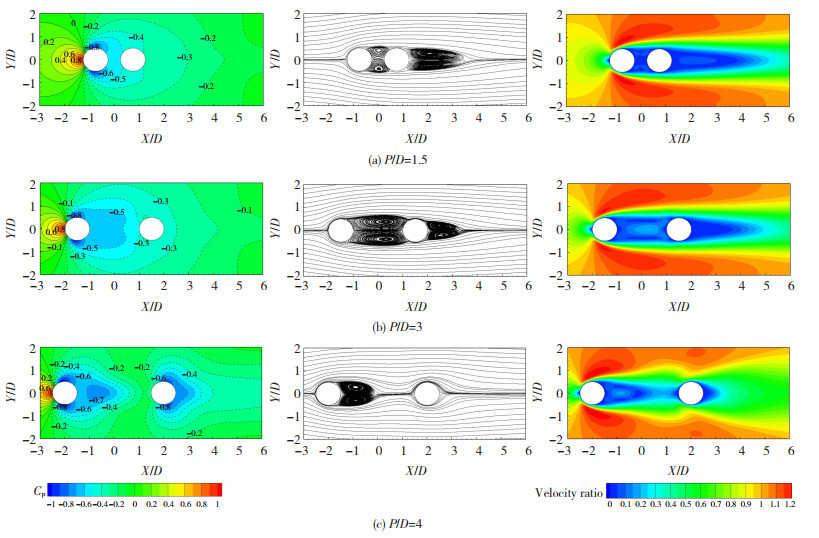
图 6为P/D=1.5、3、4时串列双圆柱的平均风压系数、平均流线、平均风速比图,其中平均风速比为流场内局部平均风速U与来流风速U0的比。由图 6可见,在P/D=1.5、3时,上游圆柱的尾流区没有完整的涡脱落产生;而在P/D=4时,上游圆柱尾流区产生了稳定的涡脱落。结合图 3、4可知,气动力在P/D=3~4之间发生了突变,说明该现象与上下游圆柱尾流发生变化直接相关。
|
图 6 串列双圆柱的平均风压系数、流线、风速比 Fig. 6 Contour of mean pressure coefficient, mean streamline, and mean velocity ratio of two tandem circular cylinders |
由图 6(a)可见,两圆柱间距较近时,上游圆柱的剪切层包住下游圆柱,两圆柱间隙存在两个回流区,回流区会经流下游圆柱的迎风面,从而导致下游圆柱迎风面的风压为负值,由上文分析可知,此时下游圆柱的平均阻力为负值;图 6(b)与图 6(a)类似,此时两圆柱间距比增大,两圆柱间的回流区进一步发展,回流的规律性逐渐被打破,导致间隙间的负压绝对值不断减小,从而使下游圆柱受到的负阻力绝对值相应减小;当P/D=4时,由图 6(c)可见,此时两圆柱间不存在回流区,上游圆柱的剪切层不再再附到下游圆柱表面,而是在上游圆柱的尾流中形成充分发展的漩涡,导致上游圆柱的背风面受到一定的负压,而迎风面存在较强的正压,这就使得上游圆柱所受阻力更大,也就导致气动力在P/D=3~4发生了明显的突变。
因此,通过如上分析可知,本文成功捕捉了串列双圆柱的3种流态,即当P/D≤2时为单一钝体流态,剪切层在下游圆柱后方形成充分发展的漩涡;当P/D=3时为剪切层再附流态,此时上游圆柱分离的剪切层再附到下游圆柱表面;当P/D=4、5时为双涡脱流态,此时上游圆柱尾流区产生旋涡脱落。
3.2 模态分解特征值为了进一步阐明3种流态的变化机制,本文采用DMD对3种流态的涡量场进行分析。分别对P/D=1.5、3、4时的串列双圆柱稳定阶段提取了6个周期的非定常涡量场数据,每个周期采样32次,选取前4阶主要模态进行分析。这3个间距比分别代表单一钝体流态、剪切层再附流态以及双涡脱流态。
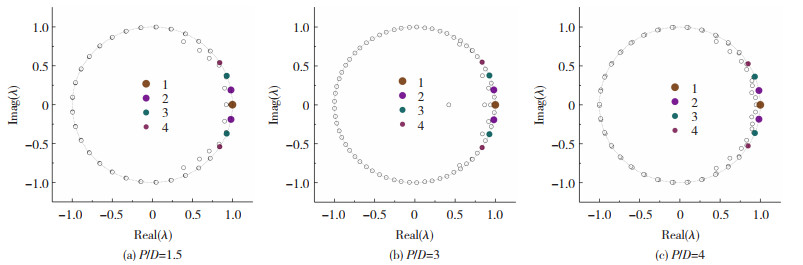
图 7为3个间距比下DMD特征值的实部与虚部在单位圆上的分布。横坐标为特征值的实部,对应模态的增长率。横坐标为正,表明该模态系数发散;横坐标为负,表明该模态系数收敛。纵坐标为特征值的虚部,对应模态的频率。由于本文所考虑的阶段为稳定极限阶段,因此3个间距比下串列双圆柱模态特征值均在单位圆内或单位圆上,对应周期性模态或稳定模态[10]。图 7给出了所选取的前4阶模态,模态特征值均处于单位圆上,表明本文所有模态均为周期性模态或稳定模态。同时,表 2给出了提取的前4阶模态所对应的频率与增长率,可见,前4阶模态增长率都为0或接近于0,说明选取的前4阶模态均属于稳定模态。
|
图 7 串列双圆柱的模态特征值 Fig. 7 Eigenvalues of each mode for wake flow of two tandem circular cylinders |
| 表 2 DMD主模态的增长率和频率 Tab. 2 Growth rate and frequency of dominant DMD modes |
图 8为3个间距比下DMD模态振幅与频率的关系,其中纵坐标振幅的大小即为标准DMD的排序标准。图 8中每个点都代表流场的1个空间模态。本文通过对涡量场快照使用动力学模态分解,采用了文献[15]发展的排序准则,依据模态对流场的贡献进行排序,并且提取了前4阶模态进行分析,这些模态包含大多数的动态信息。在P/D=1.5和3时,提取的模态没有完全按照振幅的大小进行排序,而是按照该模态对流场的贡献进行排序。模态1与模态2对流场的贡献最大,处于主导地位,而其他大部分模态对流场贡献相对较小。

|
图 8 DMD模态振幅与频率的关系 Fig. 8 DMD amplitude versus frequency |
图 9为P/D=1.5、3、4时DMD捕捉到的前4阶动力学模态。可见,随着模态阶数的增加,涡的尺度逐渐减小。当P/D=1.5时,模态分解的结果与单圆柱类似,区别在于模态1的剪切层相对于单圆柱延伸的更长且尺度更大,而对于模态2~4来说,单圆柱的模态中涡结构更接近圆柱表面;P/D=3时,其各阶模态沿流向的尾流长度均长于P/D=1.5时的串列双圆柱以及单圆柱;而在P/D=4时,其各阶模态上游圆柱的尾流与P/D=1.5、2以及单圆柱类似,而下游圆柱后方的近尾流区则有很大的不同。

|
图 9 涡量场的DMD前4阶主导模态 Fig. 9 First four-order dominant DMD modes of vorticity field |
进一步分析可知,模态1所对应的频率为0,近似于平均流场,对应于采样段内流场的平均值。当P/D=1.5、3时,上游圆柱的剪切层在下游圆柱后方分离;当P/D=4时,上游圆柱的剪切层在上游圆柱后方分离,这表明模态1体现了串列双圆柱流动剪切层的分离在3种流态间的转变过程。模态2所对应的频率与圆柱的涡脱主频相同,表明该模态与圆柱漩涡脱落的动力学特性有关;此外,3个间距比下串列双圆柱尾流中存在相似的涡结构,如图 9中红色虚线框所示,该涡结构由下游圆柱尾流逐渐平移至上游圆柱尾流中,表征了3种流态下旋涡脱落的内在演变机制。模态3则为2倍频模态,对应的频率为圆柱漩涡脱落频率的2倍,且呈反对称结构,该模态表明了圆柱后方交替脱落的旋涡在尾流中的发展。模态4所对应的频率为圆柱旋涡脱落频率的3倍,且呈正对称结构,为流场的高阶谐波模态,表征了流场中的高频行为,是对尾流沿流向延伸这一特征的补充。
3.4 流场重构与误差分析为了进一步评估DMD对串列双圆柱涡量场特征的提取效果,利用得到的DMD模态进行涡量场重构,选择圆柱采样段内升力峰值时刻的涡量场进行重构。同时,采用均方根误差对DMD模态重构的涡量场误差进行全面评估,均方根误差定义为
| $ x_{\mathrm{RMSE}}=\sqrt{\frac{1}{N} \sum\limits_{i=1}^{N_{\mathrm{p}}}\left|x_{\mathrm{CFD}}(i)-x_{\mathrm{DMD}}(i)\right|^2} $ |
式中Np为重构快照的数目,xCFD(i)和xDMD(i)分别为CFD计算与DMD模态重构的第i个涡量场快照。
图 10为实际涡量场与DMD重构涡量场的对比以及均方根误差云图。首先,将本文的3种流态与文献[2]中Re=1.2×104的流态对比可知,均依次呈现单一钝体流态、剪切层再附流态、双涡脱流态。对于DMD重构涡量场,单圆柱与P/D=1.5、3的串列双圆柱使用前4阶模态,P/D=4时的串列双圆柱使用前6阶模态进行流场重构,从而使均方根误差达到相同量级。

|
图 10 重构涡量场与真实涡量场的对比及均方根误差云图 Fig. 10 Comparison of reconstructed vorticity field with real vorticity field and root mean square error contour |
由图 10可见,4种工况的重构涡量场均能捕捉到主要结构,达到准确的重构效果。P/D=4的涡量场重构需要更多的模态来达到与其他工况相同的误差,原因在于其上下游圆柱尾流均发生旋涡脱落,仅用前4阶模态重构的涡量场误差较大。重构误差均集中在圆柱尾流处,也就是漩涡脱落发展的区域,这说明没有参与重构的高阶模态主要对圆柱尾流中旋涡发展的区域有贡献。同时可以发现,DMD可以较精确的捕捉低频大尺度的旋涡,但在捕捉高频小尺度涡上存在一定误差。
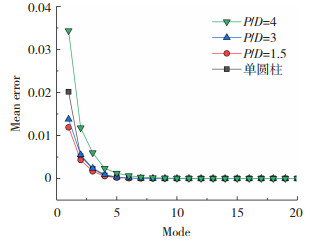
为进一步分析所用模态数对重构误差的影响,本文对单圆柱与串列双圆柱3种流态的重构涡量场的平均误差进行分析,如图 11所示。可见,随着重构涡量场所用模态数的增加,各工况平均误差均大幅减小,当所用模态数达到6~7时,平均误差基本接近于0。
|
图 11 重构涡量场的平均误差 Fig. 11 Mean error of reconstructed vorticity field |
本文利用动力学模态分解(DMD)方法,对串列双圆柱的涡量场进行模态分解,在低维空间分析了不同模态的流场特征; 并探讨了不同间距串列双圆柱流态转变的内在机制; 最后基于分解的主模态建立了降阶模型,并对串列双圆柱流场重构精度以及误差进行分析,主要结论如下:
1) 各阶模态的流场特征存在显著差异。第1阶模态表示平均流场,频率为0;第2阶模态所对应的频率与圆柱的涡脱主频相等,该模态与圆柱旋涡脱落的动力学特性有关;第3阶模态则为2倍频模态,该模态表明了圆柱后方交替脱落的旋涡在尾流中的发展。第4阶模态为3倍频模态,是流场的高阶谐波模态,反应了尾流中更小尺度的旋涡在尾流中沿横流向的延伸。此外,随着模态阶数的增加,涡的尺度逐渐减小。
2) 3种流态的模态特征也有显著区别。单一钝体流态(P/D=1.1~2)时,各阶模态特征与单圆柱类似;剪切层再附流态(P/D=3)时,各阶模态沿流向的尾流长度均长于单一钝体流态以及单圆柱;而在双涡脱流态(P/D=4~5)时,各阶模态上游圆柱的尾流与前2种流态以及单圆柱类似,而下游圆柱后方的近尾流区则有很大的不同。
3) 主导模态均具有明确的物理意义。频率为0的模态体现了串列双圆柱流动剪切层的分离在3种流态间的转变过程;与圆柱涡脱主频相对应的模态中存在相似的涡结构,该涡结构由下游圆柱尾流逐渐平移至上游圆柱尾流中,表征了3种流态的内在演变机制。
4) 流场重构结果表明,基于DMD的降阶模型可以较好地重构串列双圆柱涡量场。当子模态数量相同时,单一钝体与剪切层再附流态的重构精度高于单圆柱,而双涡脱流态的重构精度则低于单圆柱; 流场重构的误差主要集中在尾流区,由旋涡的交替脱落导致,具有较强非线性。
| [1] |
ZDRAVKOVICH M M. The effects of interference between circular cylinders in cross flow[J]. Journal of Fluids and Structures, 1987, 1(2): 239. DOI:10.1016/s0889-9746(87)90355-0 |
| [2] |
SUMNER D. Two circular cylinders in cross-flow: a review[J]. Journal of Fluids and Structures, 2010, 26(6): 849. DOI:10.1016/j.jfluidstructs.2010.07.001 |
| [3] |
WILLIAMSON C H K. Vortex dynamics in the cylinder wake[J]. Annual Review of Fluid Mechanics, 1996, 28(1): 477. DOI:10.1007/978-94-011-0249-0_5 |
| [4] |
TAIRA K, HEMATI M S, BRUNTON S L, et al. Modal analysis of fluid flows: applications and outlook[J]. American Institute of Aeronautics and Astronautics Journal, 2020, 58(3): 998. DOI:10.2514/1.j058462 |
| [5] |
ZHANG Qingshan, LIU Yingzheng, WANG Shaofei. The identification of coherent structures using proper orthogonal decomposition and dynamic mode decomposition[J]. Journal of Fluids and Structures, 2014, 49: 53. DOI:10.1016/j.jfluidstructs.2014.04.002 |
| [6] |
BERKOOZ G, HOLMES P, LUMLEY J L. The proper orthogonal decomposition in the analysis of turbulent flows[J]. Annual Review of Fluid Mechanics, 1993, 25(1): 539. DOI:10.1146/annurev.fl.25.010193.002543 |
| [7] |
SCHMID P J. Dynamic mode decomposition of numerical and experimental data[J]. Journal of Fluid Mechanics, 2010, 656: 5. DOI:10.1017/s0022112010001217 |
| [8] |
寇家庆, 张伟伟. 动力学模态分解及其在流体力学中的应用[J]. 空气动力学学报, 2018, 36(2): 163. KOU Jiaqing, ZHANG Weiwei. Dynamic mode decomposition and its applications in fluid dynamics[J]. Acta Aerodynamica Sinica, 2018, 36(2): 163. |
| [9] |
SAKAI M, SUNADA Y, IMAMURA T, et al. Experimental and numerical studies on flow behind a circular cylinder based on POD and DMD[J]. Transactions of the Japan Society for Aeronautical and Space Sciences, 2015, 58(2): 100. DOI:10.2322/tjsass.58.100 |
| [10] |
叶坤, 武洁, 叶正寅, 等. 动力学模态分解和本征正交分解对圆柱绕流稳定性的分析[J]. 西北工业大学学报, 2017, 35(4): 599. YE Kun, WU Jie, YE Zhengyin, et al. Analysis circular cylinder flow using dynamic mode and proper orthogonal decomposition[J]. Chinese Journal of Northwestern Polytechnical University, 2017, 35(4): 599. DOI:10.3969/j.issn.1000-2758.2017.04.007 |
| [11] |
BAI Xiaodong, ZHANG Wei, WANG Yong. Deflected oscillatory wake pattern behind two side-by-side circular cylinders[J]. Ocean Engineering, 2020, 197: 106847. DOI:10.1016/j.oceaneng.2019.106847 |
| [12] |
SHARMAN B, LIEN F S, DAVIDSON L, et al. Numerical predictions of low Reynolds number flows over two tandem circular cylinders[J]. International Journal for Numerical Methods in Fluids, 2005, 47(5): 423. |
| [13] |
SINGHA S, SINHAMAHAPATRA K P. High-resolution numerical simulation of low Reynolds number incompressible flow about two cylinders in tandem[J]. Journal of fluids engineering, 2010, 132(1): 011101. DOI:10.1115/1.4000649 |
| [14] |
CARMO B S, MENEGHINI J R. Numerical investigation of the flow around two circular cylinders in tandem[J]. Journal of Fluids and Structures, 2006, 22(6/7): 979. DOI:10.1016/j.jfluidstructs.2006.04.016 |
| [15] |
KOU Jiaqing, ZHANG Weiwei. An improved criterion to select dominant modes from dynamic mode decomposition[J]. European Journal of Mechanics-B/Fluids, 2017, 62: 109. DOI:10.1016/j.euromechflu.2016.11.015 |
| [16] |
WILLIAMSON C H K. Oblique and parallel modes of vortex shedding in the wake of a circular cylinder at low Reynolds numbers[J]. Journal of Fluid Mechanics, 1989, 206: 579. DOI:10.1017/s0022112089002429 |
| [17] |
SINGH S P, MITTAL S. Flow past a cylinder: shear layer instability and drag crisis[J]. International Journal for Numerical Methods in Fluids, 2005, 47(1): 75. DOI:10.1002/fld.807 |
| [18] |
QU Lixia, NORBERG C, DAVIDSON L, et al. Quantitative numerical analysis of flow past a circular cylinder at Reynolds number between 50 and 200[J]. Journal of Fluids and Structures, 2013, 39: 347. DOI:10.1016/j.jfluidstructs.2013.02.007 |
| [19] |
ZHAO Ming. Flow induced vibration of two rigidly coupled circular cylinders in tandem and side-by-side arrangements at a low Reynolds number of 150[J]. Physics of Fluids, 2013, 25(12): 123601. DOI:10.1063/1.4832956 |
| [20] |
ZHENG Tinghui, TANG S K, FEI Baoling. On the forces and Strouhal numbers in the low Reynolds number wakes of two cylinders in tandem[J]. Transactions of the Canadian Society for Mechanical Engineering, 2009, 33(3): 349. DOI:10.1139/tcsme-2009-0025 |
 2022, Vol. 54
2022, Vol. 54


