近年来,由于城市的快速发展与土地的稀缺性,群体排列的超高层建筑成为一种发展趋势。其中,双子塔因为其卓越的美学效果和建筑功能而受到青睐,例如昆明西山双子塔(典型的面对面双子塔)和贵阳花果园双子塔(典型的角对角双子塔)都已成为当地地标,见图 1。

|
图 1 代表性的双子塔建筑 Fig. 1 Typical twin towers |
已有研究大多针对面对面布置双子塔。文献[1-4]研究了不同布置方式双方柱的气动干扰效应,发现双柱串列时的“遮挡效应”会降低下游受扰建筑的平均气动力,而双柱并列时所引起的“峡谷效应”又会增大平均气动力;文献[5]提出串列双塔的气动力相关性和立面风压的非高斯区域对双塔间距的变化十分敏感;文献[6]提出连体结构会导致双塔的风荷载重新分布,串列的面对面双塔主要呈反相位运动;文献[7]从时域和频域的角度研究了不同间距下面对面双塔气动力的相关性,发现主要呈负相关;文献[8]发现双子塔气动力中包含可观的反相分量,以相反的方向作用在双塔上;文献[9-10]研究了面对面双塔层间风力系数的相关性以及双塔基底荷载的相关性;文献[11-12]使用本征正交分解(POD)方法对双子塔进行分析,发现双塔的2阶模态和3阶模态呈负相关;文献[13]提出面对面双塔结构风效应的最不利风向角为0°和90°,分别对应于方形截面最敏感的气动力方向, 也就是双塔并列和串列的情况。
双子塔设计中采用角对角的布局方式也很常见。角对角布局具有建筑上的特点与优点,但是上述0°和90°风向角将不再是最不利风向角,因为双子塔的最不利风向角受制于单体的气动特性,而0°和90°将对应于方形截面中最不敏感的气动力方向(即对角线方向)。文献[14]比较了角对角双塔与面对面双塔的的平均阻力系数;文献[15]研究了不同布置方式双子塔的体型系数与基底合力,发现双塔角对角排布时局部体型系数最小。目前国内外关于角对角双塔的抗风研究相对较少,且主要集中在平均气动力方面,而超高层双子塔的抗风设计一般由风振响应控制(如横风向响应),在结构设计风荷载中动力分量的占比可能大大超过平均分量。因此有必要对角对角双子塔的气动特性与风振特点进行详细研究,并形成可用于其抗风设计的建议。
为此,本文对不同间距的角对角双子塔进行了风洞试验,从结构风荷载与风振加速度的角度研究角对角双塔的气动特性,探讨了角对角双塔抗风设计的最不利风向角和最佳间距,为其抗风设计提供参考。
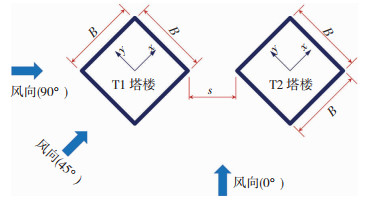
1 风洞试验简介 1.1 试验模型与测试工况角对角双子塔的同步测压试验在浙江大学ZD-1边界层风洞中进行。设计了两个尺寸相同的方柱进行风洞试验,模型缩尺比1∶300,足尺模型高300 m,长45 m,宽45 m。风洞试验的坐标系与风向角的定义见图 2,其中左边的是T1塔楼,右边的是T2塔楼。测试风向角为0°至90°,每10°一个间隔,以及45°风向角,共11个风向角。
|
图 2 坐标系与风向角的定义 Fig. 2 Definition of coordinate and wind direction |
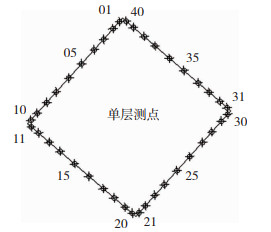
在每个方柱模型的表面布置6层测点,每层40个测点,双方柱一共布有480个测点同步测压,测点布置情况见图 3。试验采样频率为312.5 Hz,采样时长90 s。换算成足尺,这代表 3 Hz的采样频率和2.5 h的采样时长。
|
图 3 测点布置情况 Fig. 3 Distribution of pressure taps |
为方便表达,采用符号S/B(S为双塔间距,B为单塔的建筑宽度)表示双塔相对间距。根据实际超高层双子塔常见的间距范围,设置了S/B取值为0.25、0.5、0.75、1.0、1.25、1.5、1.75、2.0一共8个不同的相对间距。作为比较,同时对其中一栋塔楼进行单塔试验。图 4为间距S/B=0.5工况下的双子塔测压模型。

|
图 4 双子塔的测压模型(S/B=0.5) Fig. 4 Pressure model of twin towers (S/B=0.5) |
采用指数率风剖面,利用尖劈、粗糙元等模拟了地貌粗糙度指数为0.15、缩尺比1∶300的B类地貌风场,参考点高度为1 m,参考点风速约为10.8 m/s,湍流度约为9%。平均风速剖面与湍流度剖面见图 5。

|
图 5 平均风速剖面与湍流度剖面 Fig. 5 Mean wind speed profile and turbulence profile |
通过压力积分,计算出结构的整体荷载,即基底剪力和基底倾覆力矩。将基底荷载以无量纲的形式表达:
基底剪力系数:
| $ C_{F x}=\frac{F_x}{0.5 \rho U_H^2 B H}, C_{F y}=\frac{F_y}{0.5 \rho U_H^2 B H} $ | (1) |
基底倾覆力矩系数:
| $ C_{M x}=\frac{M_x}{0.5 \rho U_H^2 B H^2}, C_{M_y}=\frac{M_y}{0.5 \rho U_H^2 B H^2} $ | (2) |
式中:Fx和Fy是x方向和y方向的基底剪力,My和Mx是绕y轴和x轴的基底倾覆力矩,ρ是空气密度,UH是楼顶高度的参考风速,B和H分别为建筑的宽度和高度。
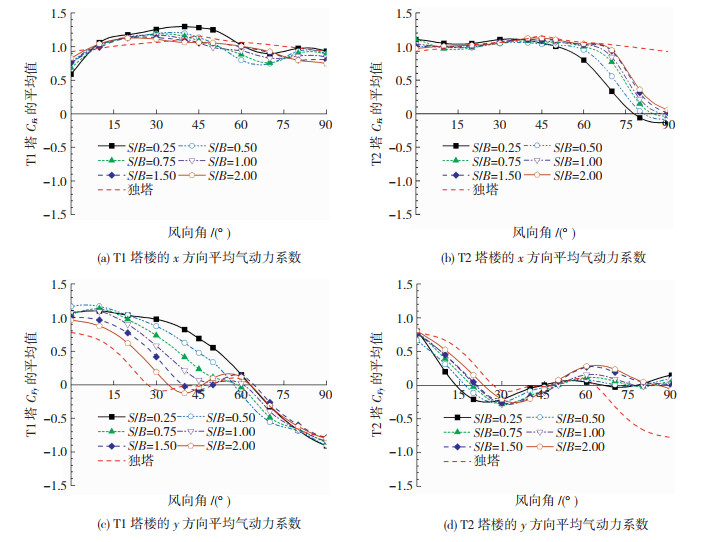
2 角对角双子塔的气动特性 2.1 平均气动力特性为考察双塔气动干扰对平均气动力的影响,以独塔的平均气动力系数作为对照,分别与T1塔和T2塔的结果进行比较,见图 6。气动力的方向按图 2坐标系定义。
|
图 6 平均气动力系数 Fig. 6 Mean aerodynamic force coefficients |
由图 6可得,对上游的T1塔,x方向的平均气动力受双塔影响较小,仅在约50°风向角以内略有升高,但y方向的平均气动力则会极大地受到双塔影响,特别是在45°左右风向角下会出现可观的横风向平均气动力。且双塔间距越小,横风向平均气动力越大。在独塔情况下,塔楼两侧受到大小相近的平均负风压,所以总的横风向平均气动力为零。而在角对角双塔情况下,靠近T2塔一侧的平均负风压有所减少,造成总的横风向平均气动力不为零。
对下游的T2塔,除了风向角大于60°,其余风向角下的平均气动力与独塔较为接近。y方向的平均气动力会随着双塔间距的减小而减弱。当风向角超过70°时,由于上游T1塔的遮挡效应,x方向和y方向的平均气动力都大为减小。
从结构设计角度考虑,最能表征角对角双塔平均气动力特性的是平均气动力的合力及其方向,见图 7。

|
图 7 平均气动力合力及其方向 Fig. 7 Resultant mean aerodynamic force and its direction |
由图 7可得,在角对角布局下,上游塔的合平均气动力明显高于独塔,且主要发生在0°到50°风向角之内。在大于50°风向角后,上游塔的合平均气动力会略低于独塔情况。而对下游塔而言,0°到50°风向角内合平均气动力与独塔情况类似。当大于50°风向角时,受遮挡效应影响,下游塔的合平均气动力将大幅低于独塔情况。
图 8为双塔间距S/B=0.5时在45°风向角下的合气动力相对大小与作用方向示意图。由于相互干扰的影响,在平均气动力较大的0°到50°风向角内,合平均气动力的作用方向与独塔区别很大。以风向为参照,上游塔的合平均气动力会向左偏转(定义为正偏转角),而下游塔的合平均气动力则向右偏转(定义为负偏转角),即两塔上的平均气动力在横风向具有相向作用的分量,而且这一气动力偏转特性随间距减小而更趋明显。

|
图 8 平均气动力合力的相对大小与作用方向 Fig. 8 Relative magnitude and direction of resultant mean aerodynamic force |
图 9给出不同风向角下脉动气动力系数的标准差。同样,以独塔的脉动气动力的标准差作为参照,分别与T1塔和T2塔的结果比较。

|
图 9 脉动气动力系数的标准差 Fig. 9 Standard deviations of fluctuating force coefficients |
由图 9可知,上游塔(T1)的x方向脉动气动力与独塔基本接近,但当双塔间距很小时,45°风向角下的x方向脉动气动力会有所增大。下游塔(T2)的x方向脉动气动力与独塔基本接近,但在风向角达到70°以上时,下游塔将受到上游塔的尾流影响,使得x方向脉动气动力明显增大。
受双塔效应影响,上游塔(T1)在风向正对建筑立面(45°风向角左右)时的横风向脉动气动力明显小于独塔情况。而且这一有利的双塔效应随着间距的减小而得到进一步增强。这是因为上游塔的尾流干扰了下游塔的周期性涡脱,以及下游塔对上游塔涡漩发育的干扰。因此在45°风向角下,双塔的涡激振动受到显著抑制,且双塔间距越小尾流效应对周期性涡脱的抑制越强。该现象与文献[16]的研究结果基本一致,45°风向角下角对角布置双塔的脉动升力系数小于独塔。
然而双塔效应对下游塔(T2)的横风向脉动气动力降低作用不如上游塔明显。特别是当双塔间距达到2左右时,横风向脉动气动力的数值基本接近独塔情况。值得注意的是在80°风向角左右,T2塔受到上游T1塔的尾流影响,出现较大的脉动气动力。
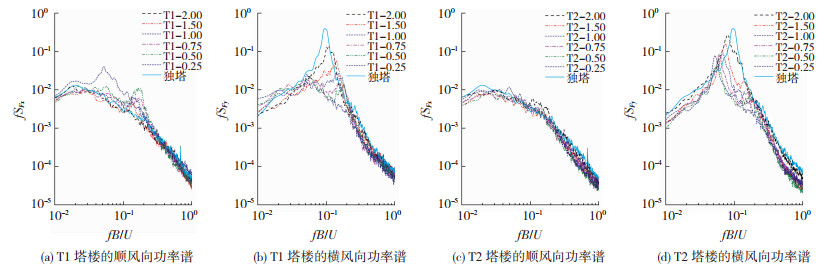
2.2.2 脉动气动力的频谱特性图 10为45°风向角下不同间距的双塔的整体气动力功率谱。方形截面独塔在不同风向角下的Strouhal数变化不大,都在0.1附近。当宽度为45 m的独塔自振周期为8 s时,相应涡激临界风速是56.25 m/s。
|
图 10 45°风向角下的气动力功率谱 Fig. 10 Spectra of force coefficients in wind direction of 45° |
由图 10可知,双子塔的顺风向功率谱与独塔情况基本类似。只有当双塔间距较小时(小于0.75),上游塔背风面的负压会有所增强,使得顺风向气动力谱略有增大。而双子塔的横风向功率谱则均小于独塔的情况,而且间距越小,横风向谱的峰值降低越多。最值得关注的是双子塔气动力在频谱分布上发生的变化。上游塔的气动力降低主要出现在较低的频段,而下游塔的气动力降低则出现在较高的频段,从而使得上游塔气动力功率谱峰值对应的约化频率随间距减小而变大,而下游塔气动力功率谱峰值对应的约化频率随间距减小而变小。值得注意的是由此造成在小于涡激临界风速时(即相应的约化频率大于独塔的Strouhal数),上游塔的风振响应有可能略大于相应的独塔,而在大于涡激临界风速时(即相应的约化频率小于独塔的Strouhal数),下游塔的风振响应有可能大于相应的独塔。但在涡激临界区,双子塔的风振响应都会明显小于相应独塔的涡激共振响应。
针对角对角双子塔,另一个值得关注的风向角是80°。图 11给出80°风向角下的气动力功率谱。上游塔的尾流在下游塔上形成一个能量非常集中的气动力,其卓越频率在0.08~0.09,略小于相应的独塔Strouhal数。但是当双塔间距大于1.5以后,该气动力迅速减弱。

|
图 11 80°风向角下的气动力功率谱 Fig. 11 Spectra of force coefficients in wind direction of 80° |
结构风振响应大小不但取决于气动力的脉动分量,而且与脉动分量的频谱特性密切相关。为了把握角对角双子塔风振响应的普遍规律,采用时域计算方法进行风振响应的无量纲分析,即建立无量纲风振加速度与无量纲约化风速的函数关系。
结构风致响应的运动方程以广义坐标的形式表达为
| $ \left\{\ddot{\eta}_j(t)\right\}+2 \zeta \omega_j\left\{\dot{\eta}_j(t)\right\}+\omega_j^2\left\{\eta_j(t)\right\}=\frac{P_j(t)}{M_j} $ | (3) |
式中:
将风洞试验得到的采样数据按照振型函数进行加权积分得到广义气动力,然后使用时域计算方法四阶Runge-Kutta法求解式(3)的运动方程,求出结构的加速度时程,最后通过统计分析方法得到加速度响应的标准差。计算中依据工程经验假设结构自振周期为8 s,结构阻尼比2%,典型结构层高4 m,楼层质量2 500 t,基本振型近似为(z/H)1.25。
将加速度标准差按广义质量与参考风压等进行无量纲约化,表示为约化加速度标准差:
| $ a^*=\sigma_a\left(\frac{M_j \sqrt{\zeta}}{q_{\mathrm{r}} B H}\right) $ | (4) |
式中σa为楼顶高度的加速度标准差,qr为楼顶高度的参考风压。
由于上述角对角双子塔气动力的频谱特性的复杂性,相应的风振响应也比较复杂,特别是结构的风振加速度随风向角的变化规律在不同风速下呈现极大的差异。图 12给出双塔间距为S/B=1.0时,约化加速度标准差在不同约化风速下随风向角的变化。其中ax1和ay1为T1塔楼沿x和y方向的加速度,ax2和ay2为T2塔楼沿x和y方向的加速度,U/fB表示约化风速,f为结构自振频率。
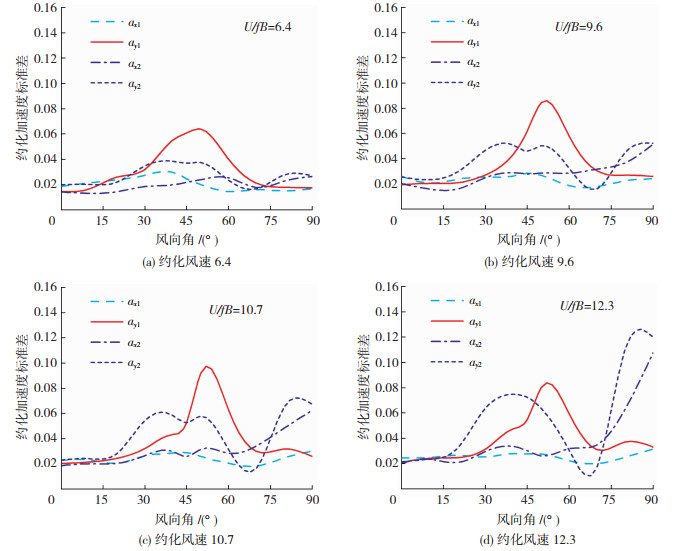
|
图 12 约化加速度随风向角的变化 Fig. 12 Normalized accelerations in different wind directions |
由图 12可得,当约化风速处于低亚临界与临界风速区间时,最大风振加速度发生在45°风向角附近,主要表现为上游塔的横风向振动。随着约化风速的提高,下游塔的横风向振幅逐渐接近上游塔的横风向振幅,但两者的最不利风向角略有差别。下游塔的最不利风向角略小于45°,而上游塔的最不利风向角略大于45°。随着约化风速的进一步提高,下游塔的风致振动快速增大。当约化风速达到12.3时,角对角双子塔的风振响应将受尾流激振控制,而涡激振动则退居其次。在约化风速较高时,最大风振加速度发生在80°风向角附近。
从工程应用角度考虑,最为关心的是在所有风向角下的最大合加速度以及最不利风向角。为此,对0°到90°风向角下的x和y方向的加速度逐时计算合加速度,然后取所有风向角下的最大值作为最大合加速度,该最大值出现时对应的风向角即为最不利风向角。为了对角对角双子塔的风振加速度大小有一个基本评判,图 13给出不同约化风速下的最大合加速度及其对应的风向角。

|
图 13 合加速度及最不利风向角 Fig. 13 Resultant acceleration and most unfavorable wind direction |
从图 13可得角对角双子塔风振响应的一般规律:当约化风速远低于涡激临界风速时,角对角双子塔的最大风振加速度与独塔相似或略高。当约化风速达到涡激临界风速附近时,角对角双子塔的最大风振加速度将大大低于独塔情况。当约化风速超过涡激临界风速后,有可能出现剧烈的尾流激振,由此造成的振动加速度将高于独塔情况。45°与80°风向角是角对角双子塔两个最不利的风向角,前者对应于亚临界与临界风速时的横风向涡激振动,后者对应于超临界风速时出现的尾流激振。
图 14对比了双子塔与独塔在不利风向角下的运动轨迹,从中可以看出尾流激振与涡激振动的形态差异。虽然尾流激振与涡激振动都是横风向的,但尾流激振时下游塔的振幅大大高于上游塔。
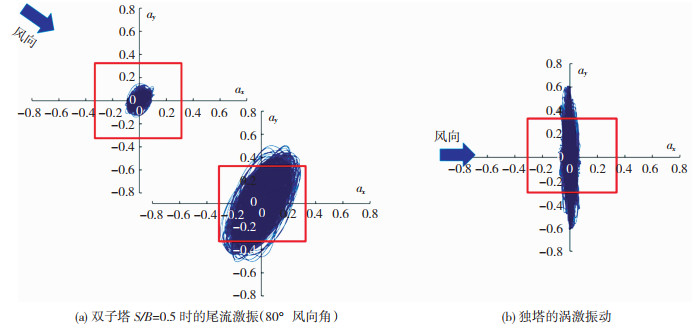
|
图 14 双子塔与独塔的运动轨迹对比 Fig. 14 Comparison of motion trajectories between twin towers and single tower |
为了判断双塔间距变化对风振加速度的影响,取不同间距下两栋塔中的最大合加速度表示成风速比的函数,见图 15。其中纵坐标为约化合加速度的标准差,横坐标为实际风速与相应独塔涡激临界风速之比。在本研究中,独塔的约化临界风速为10.67。
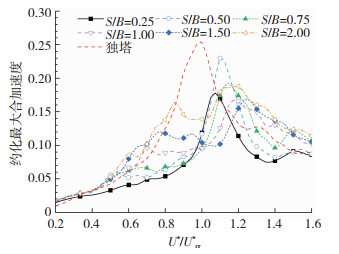
|
图 15 最大合加速度 Fig. 15 Maximum resultant acceleration |
由图 15可知,如果两塔非常靠近(S/B=0.25),则相应的气动干扰作用是最有利的。不但能抑制涡激振动,而且在高风速时的尾流激振也较弱。整个风速范围内的风振加速度都小于独塔的情况。间距比S/B=1.0是另一个较好的间距,对应的尾流激振振幅也较小,同时在亚临界区较少受到气动干扰的不利影响。间距比S/B=0.5左右需要谨慎考虑。在该间距下,剧烈的尾流激振会产生与涡激共振类似甚至更大的振幅,但尾流激振的临界风速会高于涡激临界风速。
大多数矩形超高层建筑的设计风速都小于或接近涡激临界风速。图 15表明在这种情况下,较小间距的双子塔布置对风致响应是有利的。
值得指出,本文所述角对角双子塔的气动特性和风致响应基于刚性模型试验得出,气弹效应不在讨论范围内。气弹效应使得涡脱气流受到结构振动的反馈影响,不但涡脱频率被结构振动频率锁定,而且涡脱的规律性与烈度也会加强。但在实际建筑工程中,气弹效应一般不显著。这一方面是由于大气湍流干扰了涡脱的规律性,另一方面是由于高层建筑的质量与刚度限制了风致振动的振幅。在这种情况下,气弹效应可以用相对简单的气动阻尼来表示,即将建筑的涡激振动问题归结为考虑气动阻尼作用的强迫振动问题。研究结果表明独塔的气动阻尼比一般不大于-0.5%[17],双塔干扰工况下的气动阻尼比大约为-0.2%[18],显著小于结构阻尼比。所以认为气弹效应不会改变角对角双子塔的一般气动特点。
4 结论研究了不同间距的角对角双子塔的气动力和风振加速度随风向角变化的特性,结果表明:
1) 受双塔相互干扰的影响,当风向正对塔楼立面时,左侧上游塔的合平均气动力出现明显向左偏转,而右侧下游塔的合平均气动力则略微向右偏转,从而在横风向上产生相向的平均气动力分量。
2) 与单塔相比,角对角布置时上游塔的横风向脉动气动力大幅减小,并且有利的双塔效应随着间距的减小而进一步增强。而双塔效应对下游塔的脉动气动力降低作用不如上游塔明显。特别是在串联风向角下,下游塔受到尾流影响,会出现较大振幅的尾流激振。
3) 当约化风速处于低亚临界与临界风速区间时,角对角双子塔的最不利风向角在45°附近。而当约化风速超过临界风速后,最不利风向角在80°附近。
4) 考虑到大多数矩形超高层建筑的设计风速都小于或接近涡激临界风速,较小间距的角对角双子塔对抗风设计有利。间距过大的角对角双子塔在低风速时可能出现大于独塔的风致振动。
| [1] |
谢壮宁, 顾明. 任意排列双柱体的风致干扰效应[J]. 土木工程学报, 2005, 38(10): 32. XIE Zhuangning, GU Ming. Wind-induced interference effects between two arbitrarily arranged prisms[J]. China Civil Engineering Journal, 2005, 38(10): 32. DOI:10.3321/j.issn:1000-131X.2005.10.006 |
| [2] |
XIE Zhuangning, GU Ming. Mean interference effects among tall buildings[J]. Engineering Structures, 2004, 26(9): 1173. DOI:10.1016/j.engstruct.2004.03.007 |
| [3] |
XIE Zhuangning, GU Ming. Simplified formulas for evaluation of wind-induced interference effects among three tall buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95(1): 31. DOI:10.1016/j.jweia.2006.05.003 |
| [4] |
谢壮宁, 朱剑波. 并列布置超高层建筑间的风压干扰效应[J]. 土木工程学报, 2012, 45(10): 23. XIE Zhuangning, ZHU Jianbo. Interference effects of wind pressures on tall buildings in side-by-side arrangement[J]. China Civil Engineering Journal, 2012, 45(10): 23. |
| [5] |
杜晓庆, 许汉林, 马文勇, 等. 串列双方柱气动干扰效应试验研究[J]. 建筑结构学报, 2019, 40(11): 27. DU Xiaoqing, XU Hanlin, MA Wenyong, et al. Experimental study on aerodynamic interference effect of two square cylinders in a tandem arrangement[J]. Journal of Building Structures, 2019, 40(11): 27. DOI:10.14006/j.jzjgxb.2018.0282 |
| [6] |
XIE Jiming, IRWIN P A. Wind-induced response of a twin-tower structure[J]. Wind and Structures, 2001, 4(6): 495. DOI:10.12989/was.2015.21.5.505 |
| [7] |
石俊阳, 谢霁明. 双子塔气动力及其相关性对间距的敏感度研究[J]. 振动与冲击, 2020, 39(23): 8. SHI Junyang, XIE Jiming. Sensitivity of twin-tower's aerodynamic forces and their correlation to spacing[J]. Journal of Vibration and Shock, 2020, 39(23): 8. DOI:10.13465/j.cnki.jvs.2020.23.002 |
| [8] |
QIN Weifeng, SHI Junyang, YANG Xiaoyue, et al. Characteristics of wind loads on twin-tower structure in comparison with single tower[J]. Engineering Structures, 2022, 251: 112780. DOI:10.1016/j.engstruct.2021.112780 |
| [9] |
SONG Jie, TSE K T. Dynamic characteristics of wind-excited linked twin buildings based on a 3-dimensional analytical model[J]. Engineering Structures, 2014, 79: 169. DOI:10.1016/j.engstruct.2014.08.015 |
| [10] |
SONG Jie, TSE K T, TAMURA Y, et al. Aerodynamics of closely spaced buildings: with application to linked buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2016, 149: 16. DOI:10.1016/j.jweia.2015.11.007 |
| [11] |
KIM B, TSE K T. POD analysis of aerodynamic correlations and wind-induced responses of two tall linked buildings[J]. Engineering Structures, 2018, 176: 369. DOI:10.1016/j.engstruct.2018.09.013 |
| [12] |
KIM B, TSE K T, YOSHIDA A, et al. Statistical analysis of wind-induced pressure fields and PIV measurements on two buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2019, 188: 161. DOI:10.1016/j.jweia.2019.01.016 |
| [13] |
KHANDURI A C, STATHOPOULOS T, BEDARD C. Generalization of wind-induced interference effects for two buildings[J]. Wind and Structures, 2000, 3(4): 255. DOI:10.12989/was.2000.3.4.255 |
| [14] |
NI Zhenhua, HE C K, XIE Zhuangning, et al. Experimental test on bridge jointed twin-towered buildings to stochastic wind loads[J]. Wind & Structures, 2001, 4(1): 65. DOI:10.12989/was.2001.4.1.063 |
| [15] |
陈强, 陈水福, 史卓然. 等距布局双塔高层建筑风荷载特性研究[J]. 建筑结构, 2019, 49(14): 129. CHEN Qiang, CHEN Shuifu, SHI Zhuoran. Study on wind-load characteristics of twin-tower high-rise buildings in equal distance layout[J]. Building Structure, 2019, 49(14): 129. DOI:10.19701/j.jzjg.2019.14.023 |
| [16] |
DU Xiaoqing, CHEN Ruyi, DONG Haotian, et al. Aerodynamic characteristics of two closely spaced square cylinders in different arrangements[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2021, 208: 104462. DOI:10.1016/j.jweia.2020.104462 |
| [17] |
全涌, 顾明. 方形断面高层建筑的气动阻尼研究[J]. 工程力学, 2004, 21(1): 28. QUAN Yong, GU Ming. Wind tunnel test study of aerodynamic damping of super highrise buildings[J]. Engineering Mechanics, 2004, 21(1): 28. DOI:10.3969/j.issn.1000-4750.2004.01.005 |
| [18] |
黄鹏, 顾明. 高层建筑干扰气动阻尼的试验研究[J]. 同济大学学报(自然科学版), 2003(6): 656. HUANG Peng, GU Ming. Experimental study on aerodynamic damping of tall buildings after being interfered[J]. Journal of Tongji University (Natural Science), 2003(6): 656. DOI:10.3321/j.issn:0253-374X.2003.06.005 |
 2022, Vol. 54
2022, Vol. 54


