2. 风工程及风资源利用重庆市重点实验室(重庆大学),重庆 400045;
3. 山地城镇建设与新技术教育部重点实验室(重庆大学),重庆 400045
2. Chongqing Key Lab of Wind Engineering and Wind Resources Utilization (Chongqing University), Chongqing 400045, China;
3. Key Lab of New Technology for Construction of Cities in Mountain Area (Chongqing University), Ministry of Education, Chongqing 400045, China
直立锁缝屋面系统是将相邻屋面板的卷边通过电动锁边机与支座立板进行咬合,再将支座通过螺栓连接到檩条的屋面系统[1]。该屋面系统被广泛应用于机场航站楼、体育场馆、高铁站房等大跨建筑的屋面围护结构中,但在强风作用下常发生屋面表层被掀起的事件,其风揭损毁问题突出。
为此,国内外学者围绕直立锁缝屋面系统的实验和数值模拟开展了大量研究。Farquhar等[2]与Habte等[3]对直立锁缝屋面系统开展风洞试验研究,分析了该系统在真实风荷载作用下力学性能;Damatty等[4]引入等效弹簧系统模拟屋面板和支座立板锁缝处的相互作用,通过试验对比验证了该简化方法准确性;夏俞超等[1]通过足尺试验和精细化有限元方法,对直立锁缝屋面系统风致破坏全过程进行了研究。为了提高屋面系统的抗风揭性能,近年来,研究者建议使用抗风夹加强锁边处咬合作用[5]。通过试验和数值研究表明[6],带抗风夹直立锁边屋面系统的抗风承载力明显提高。然而,现有研究[6]主要针对带抗风夹直立锁边屋面系统,见图 1(a),而对于带抗风夹直立锁缝屋面系统抗风揭性能却鲜有涉及,见图 1(b)。由于不同屋面板连接形式的抗风揭性能差别较大[7],对带抗风夹直立锁缝屋面系统的抗风揭性能的研究仍需进一步开展。

|
图 1 屋面连接形式 Fig. 1 Connection forms of roof |
此外,由于材料、荷载等存在不可避免的随机性[8-9],对带抗风夹直立锁缝屋面系统进行可靠度分析亦是抗风揭设计的重要环节之一。类似于传统直立锁缝屋面系统[10],带抗风夹直立锁缝屋面系统亦可能存在多种失效模式,故而带抗风夹直立锁缝屋面可靠度属于多失效模式可靠度问题,也即体系可靠度问题。对于此类可靠度问题,虽然大致存在失效模式识别法[11]、Monte Carlo模拟法[12]和等价描述法[13-14]3种思路,但失效模式识别法实现较为繁琐且存在相关信息和组合爆炸等问题[15],而Monte Carlo模拟法需耗费的成本巨大难以应用于屋面系统的可靠度分析。相对而言,等价描述法基于等价极值事件原理,通过一个等价功能函数描述各个失效模式,将结构体系可靠度转化为简单可靠度问题求解,有效解决了组合爆炸和相关失效问题,是一个执行简单且实用的思路[13-14]。屋面系统对应的失效模式经等价描述后,其功能函数形式变得较为复杂,由于基于验算点的方法处理函数形式复杂的功能函数会存在多验算点问题而使其计算精度不理想[16],采用验算点无关的可靠度方法不失为一种可行的思路[17]。特别地,文献[18-20]基于共轭无迹变换方法,通过引入正态和非正态变换提出了扩展型共轭无迹变换法,该方法不依赖验算点且兼顾计算效率和精度,能够精确地进行随机系统不确定性传播分析和结构构件及体系可靠度评估。然而,无论是等价极值事件原理还是扩展型共轭无迹变换法,当前主要应用于简单数值算例和框架结构[13-14, 18-21]。由于带抗风夹的直立锁缝屋面系统结构复杂且具有较高的几何非线性,因此,此类方法在多失效模式下屋面系统抗风揭可靠度分析的适用性尚待进一步研究与探讨。
因此,本文以某特高压换流站阀厅带抗风夹直立锁缝屋面系统为研究对象,首先基于有限元软件ANSYS/LS-DYNA建立该屋面系统精细化非线性力学模型,分析及推导其可能存在的失效模式和对应的功能函数;进而引入等价极值事件和扩展型共轭无迹变换法建立了多失效模式下带抗风夹直立锁缝屋面系统抗风揭可靠度分析框架;最后结合工程算例进行抗风揭可靠度分析,以期为多失效模式下带抗风夹直立锁缝屋面系统可靠度计算提供依据。
1 带抗风夹直立锁缝屋面系统的力学模型及失效准则 1.1 带抗风夹直立锁缝屋面系统抗风揭受力机理带抗风夹直立锁缝屋面系统由屋面板、直立支座、檩条和抗风夹共同组成,见图 2。风荷载在迎风面前缘产生流动分离,将在屋面板表面形成负压;此时,相邻屋面板通过和支座立板咬合以抵抗风荷载,然后支座通过自攻螺钉将反力传给檩条;而抗风夹作用在屋面板卷边和支座立板咬合处,在屋面板大耳边产生变形的过程中,抗风夹通过约束大耳边的径向位移来提高锁缝处的咬合作用,从而保证直立锁缝屋面系统的抗风揭性能。

|
图 2 带抗风夹直立锁缝屋面系统示意 Fig. 2 Schematic of SSRS-AWC |
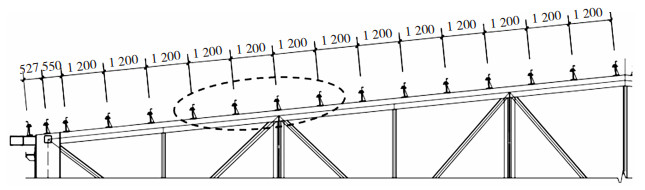
本文以某特高压换流站高端阀厅为对象,采用ANSYS/LS-DYNA建立带抗风夹直立锁缝屋面系统有限元模型。该阀厅屋面形式为双坡屋面,坡度为7°,其左半部分尺寸见图 3。为了节约计算时间,利用结构的对称性建立局部模型,纵向选取中间四跨,每跨跨度为1 200 mm,横向沿屋面板中部断开,分别沿横向和纵向设置对称边界条件。屋面板采用YX75-473外层彩色镀铝锌压型钢板,支座采用360°咬口锁边支座,檩条为Z180×2.5 mm冷弯镀锌附檩条,抗风夹选取矮立边双片夹具。
|
图 3 阀厅檩条布置(mm) Fig. 3 Purlin arrangement of valve hall (mm) |
采用SHELL163单元模拟屋面板、支座和檩条,以SOLID164单元模拟抗风夹,两类单元均适用于大变形分析。屋面板材料选用Q355钢材,本构关系采用双线性随动强化模型。通过映射方法划分网格,对屋面板和支座锁缝处进行局部加密,同时为了兼顾网格质量,屋面板和支座锁缝处圆弧边采用直角边简化,最终单元最小尺寸为2 mm,最大尺寸为15 mm,单元总数为35 232,有限元模型见图 4。

|
图 4 带抗风夹直立锁缝屋面系统有限元模型 Fig. 4 Finite element model of SSRS-AWC |
支座和檩条采用螺栓连接,工程中不易产生破坏,因此将支座和檩条节点进行耦合;抗风夹左右夹具顶部通常由螺栓连接,通过约束抗风夹侧向位移以模拟螺栓对两侧的顶紧作用;带抗风夹直立锁缝屋面系统在变形过程中,屋面板和支座立板锁缝处、屋面板和抗风夹以及相邻屋面板的大耳边和小耳边之间均存在复杂的接触关系,采用自动通用接触(CONTACT_AUTOMATIC_GENERAL)模拟各组件之间的接触效应,该接触形式可有效考虑各个部件的接触关系以及部件的自接触,适用于复杂大变形问题[1];由于屋面局部模型尺寸较小,研究者通常将该范围内的风荷载等效为均匀布置进行加载[6-7],本文亦沿用该加载方式对屋面板施加竖直向上的均布力。此外,文中有限元模型尺寸、约束以及边界条件等均按实际结构考虑,最终破坏模式、抗风承载力等符合工程实际,可用于后续分析。
1.3 带抗风夹直立锁缝屋面系统失效准则根据带抗风夹的直立锁缝屋面系统的组成和变形规律,其可能存在的失效模式为[22]:屋面板和支座锁缝分离(脱扣破坏)、屋面板撕裂破坏、支座破坏和抗风夹破坏。
1.3.1 脱扣破坏在风荷载作用下,由于抗风夹约束了大耳边的径向位移,观察到大耳边径向变形不易开展,见图 5(a),但随着变形的加大,小耳边将逐渐脱离支座的束缚,沿着约束路径逐渐脱开,见图 5(b),此时屋面板和支座发生脱扣破坏。根据小耳边前后变形的状态,得出变形简图见图 5(c)。

|
图 5 脱扣破坏示意 Fig. 5 Schematic of clip separation from seam |
根据图 5(c),小耳边在抗风夹弯折处初始为A点,破坏后A点变形到A′,位置恰好与抗风夹右边缘点重合,用L表示A点到抗风夹右侧边缘点距离,当AA′等于L时,屋面板和支座将发生脱扣破坏。
设A和A′点坐标分别为(xA, yA, zA)和(xA′, yA′, zA′),则有
| $ \begin{array}{l} \overrightarrow {A{A^\prime }} = \left( {{x_{{{\rm{A}}^\prime }}} - {x_{\rm{A}}}, {y_{{{\rm{A}}^\prime }}} - {y_{\rm{A}}}, {z_{{{\rm{A}}^\prime }}} - {z_{\rm{A}}}} \right) = \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left( {\overrightarrow {\Delta {x_{\rm{A}}}} , \overrightarrow {\Delta {y_{\rm{A}}}} , \overrightarrow {\Delta {z_{\rm{A}}}} } \right) \end{array} $ | (1) |
式中
根据式(1)并结合带抗风夹直立锁缝屋面系统脱扣破坏准则有
| $ \left|A A^{\prime}\right|=\sqrt{{\overrightarrow{\Delta x_{\mathrm{A}}}}^2+{\overrightarrow{\Delta y_{\mathrm{A}}}}^2+{\overrightarrow{\Delta z_{\mathrm{A}}}}^2} \geqslant L $ | (2) |
脱扣破坏的功能函数可相应给出
| $ {G_1}(\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}) = L - \sqrt {{{\overrightarrow {\Delta {x_{\rm{A}}}} }^2} + {{\overrightarrow {\Delta {y_{\rm{A}}}} }^2} + \overrightarrow {\Delta {z_{\rm{A}}}} } $ | (3) |
式中Θ为随机向量。
1.3.2 屋面板撕裂破坏在屋面板锁缝处,屋面板在风荷载作用下产生竖向变形,当变形过大时,抗风夹和屋面板将产生相互挤压,从而造成抗风夹附近的屋面板应力较大,当应力超过其极限强度,屋面板将发生撕裂破坏[22],应力云图见图 6。设屋面板最大应力为σmax, 板,极限强度为fu, 板,则屋面板撕裂破坏功能函数为
| $ G_2(\mathit{\boldsymbol{ \boldsymbol{\varTheta} }})=f_{\mathrm{u}, \text { 板 }}-\sigma_{\max , 板} $ | (4) |

|
图 6 屋面板锁缝处应力云图(MPa) Fig. 6 Stress cloud diagram of roof panel at seam (MPa) |
在风荷载作用下,支座卷边处应力较大,当应力超过其极限强度时,支座可能发生断裂破坏,其应力云图见图 7(a),对应的功能函数为
| $ G_3(\mathit{\boldsymbol{ \boldsymbol{\varTheta} }})=f_{\mathrm{u}, \text { 支 }}-\sigma_{\max \text {, 支 }} $ | (5) |

|
图 7 支座和抗风夹应力云图(MPa) Fig. 7 Stress cloud diagram of support and anti-wind clip (MPa) |
式中fu, 支为支座极限强度,σmax, 支为支座最大应力。
1.3.4 抗风夹失效破坏屋面板向上变形的过程中,抗风夹两端和凹槽处与屋面板由于存在相互挤压,应力较大点主要在抗风夹尾端及其凹槽处,观察到该区域的应力始终保持在材料可承受范围内,因此不考虑抗风夹的失效破坏,抗风夹应力云图见图 7(b)。
综上所述,本文带抗风夹直立锁缝屋面系统可靠度分析主要考虑屋面板和支座锁缝脱扣破坏、屋面板撕裂破坏以及支座破坏3种失效模式。
2 多失效模式下带抗风夹直立锁缝屋面系统可靠度分析 2.1 等价功能函数的建立对于带抗风夹直立锁缝屋面系统的3种失效模式,只要存在1种模式发生失效,则整个结构系统发生破坏。因此,此3种失效模式对应的是串联体系可靠度问题。对于此类问题,基于等价极值事件[13-14],可建立等价功能函数为
| $ Z = {G_{\min }}(\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}) = \min \left\{ {{G_1}(\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}), {G_2}(\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}), {G_3}(\mathit{\boldsymbol{ \boldsymbol{\varTheta} }})} \right\} $ | (6) |
获取等价功能函数Z后,可结合扩展型共轭无迹变化法和最大熵原理分别进行带抗风夹直立锁缝屋面系统统计矩估计和体系可靠度分析。
2.2 基于扩展型共轭无迹变换法的等价功能函数统计矩估计由于带抗风夹直立锁缝屋面系统结构复杂且非线性较高,本文采用精度较高的8阶扩展型共轭无迹变换法[18-20]进行等价功能函数统计矩估计。通过变量变换,等效功能函数Z=Gmin(Θ) 可改写为
| $ Z = {G_{{\rm{min }}}}(\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}) = {G_{{\rm{min }}}}\left( {{R^{ - 1}}(\mathit{\boldsymbol{U}})} \right) \buildrel \Delta \over = h(\mathit{\boldsymbol{U}}) $ | (7) |
式中: R-1为等概率变换(对于独立变量)或Nataf变换(对于相关变量)[23],U={U1, …, UN}表示相互独立的标准正态向量,h(·)为变换后的功能函数。
相应地,等价功能函数Z的k阶原点矩MZ, k可表示为
| $ \begin{aligned} {M_{Z, k}} &= \int\limits_{\Omega U} {{h^k}} (\mathit{\boldsymbol{u}})\prod\limits_{i = 1}^N \phi \left( {{u_i}} \right){\rm{d}}\mathit{\boldsymbol{u}} \approx \\ & \sum\limits_{i = 0}^{{N_{\rm{p}}} - 1} {{\alpha _i}} {\left[ {h\left( {{u_{1, i}}, {u_{2, i}}, \cdots , {u_{N, i}}} \right)} \right]^k} \end{aligned} $ | (8) |
式中: ϕ(·)为标准正态分布的概率密度函数,N为随机变量数目,Np表示样本点数量,ui和αi是共轭无迹变换法求积节点向量和权系数,取值见表 1,表中N1=4N(N-1)(N-2)/3,σi、ciN和siN分别表示主轴、共轭轴和缩放共轭轴,具体解释参考文献[18]。
| 表 1 积分节点ui和权系数αi Tab. 1 Integral nodes ui and weights αi |
表 1中ri和wi分别表示尺度变量和权系数,目前常用的计算方法是通过Isserlis定理[21]建立矩约束方程并求解得到,该方程可表示为
| $ \left\{\begin{array}{l} E\left[\prod_{j=1}^N U_j^{\kappa_j}\right]=\sum\limits_{i=1}^N w_i \prod_{j=1}^N u_{j, i}^{\kappa_j} \\ \sum\limits_{i=0}^n w_i=1, r_i=\sqrt{\sum_{j=1}^N u_{j, i}^2} \end{array}\right. $ | (9) |
式中: n为除零点外求积节点的数量,uj, iκj为求积节点的坐标,κj为非负的整数且1≤κ1+κ2 +…+κν≤9,通过求解式(9),可获得尺度变量ri和权系数wi。
需要说明的是,由于本文重点关注直立锁缝屋面系统抗风揭可靠度分析的应用研究,限于文章篇幅,对于扩展型共轭无迹变换法的详细推导及介绍可参考文献[20]。
2.3 基于最大熵原理的带抗风夹直立锁缝屋面系统可靠度分析获取等价功能函数Z的统计矩之后,可通过最大熵原理进行结构体系可靠性评估[24]。以等价功能函数Z熵的最大值为目标函数,前4阶原点矩MZ, k(k=0, 1, …, 4)为约束条件,建立优化模型为
| $ \begin{aligned} &\max H=\int_{-\infty}^{\infty} f_Z(z) \ln f_z(z) \mathrm{d} z \\ &\text { s.t. }\left\{\begin{array}{l} \int_{-\infty}^{\infty} z^k f_z(z) \mathrm{d} z=M_{Z, k} \\ \int_{-\infty}^{\infty} f_z(z) \mathrm{d} z=1 \end{array}\right. \end{aligned} $ | (10) |
通过Lagrange乘子法可将上式的约束优化问题转换为无约束优化问题,进而可通过牛顿法求解。最终,等价功能函数Z的概率密度函数可表示为
| $ f_z(z)=\exp \left(\lambda_0-\sum\limits_{k=1}^4 \lambda_k z^k\right) $ | (11) |
式中λ0,λ1,…,λ4为Lagrange系数。
对此,带抗风夹直立锁缝屋面系统的失效概率Pf与可靠指标β为
| $ \left\{ {\begin{array}{*{20}{l}} {{P_{\rm{f}}} = P(Z \le 0) = \int_{ - \infty }^0 {\exp } \left( {{\lambda _0} - \sum\limits_{k = 1}^4 {{\lambda _k}} {z^k}} \right){\rm{d}}z}\\ {\beta = - {\mathit{\Phi }^{ - 1}}\left( {{P_{\rm{f}}}} \right)} \end{array}} \right. $ | (12) |
结合带抗风夹直立锁缝屋面系统非线性力学模型、等价极值事件原理、扩展型共轭无迹变换法以及最大熵原理,可计算带抗风夹直立锁缝屋面系统抗风揭失效概率pf和可靠指标β,具体流程见图 8,计算步骤如下:

|
图 8 带抗风夹直立锁缝屋面系统抗风揭可靠度分析流程 Fig. 8 Process of anti-wind reliability analysis of SSRS-AWC |
步骤1:建立带抗风夹的直立锁缝屋面系统非线性力学模型,结合有限元计算结果、已有屋面研究以及灾害调查总结带抗风夹的直立锁缝屋面系统常见失效模式并给出对应的功能函数Gi(Θ)。
步骤2:根据等价极值事件原理和各失效模式功能函数Gi(Θ),即式(3)~(6)建立带抗风夹直立锁缝屋面系统等价功能函数Z。
步骤3:确定带抗风夹直立锁缝屋面系统随机变量参数及其分布类型,基于共轭无迹变换法,即式(9)和表 1获取样本点,形成样本点集合X。
步骤4:调用有限元模型,计算各个样本点对应的带抗风夹直立锁缝屋面系统等价功能函数值, 得到响应集合Y。
步骤5:根据扩展型共轭无迹变换法和响应集合Y,即式(8)计算等价功能函数Z前4阶原点矩MZ, k。
步骤6:基于最大熵原理和前4阶原点矩MZ, k,即式(10)~(12)计算带抗风夹直立锁缝屋面系统的失效概率pf和可靠指标β。
3 算例分析为验证本文方法可行性,以某特高压换流站阀厅带抗风夹直立锁缝屋面系统为例进行可靠度分析。该阀厅建筑高度为32.6 m,地貌类型为A类,基本风压为0.9 kN/m2(100 a一遇),示意见图 9。

|
图 9 阀厅示意 Fig. 9 Schematic of valve hall |
结构自身参数的随机性以及荷载作用的随机性是影响工程结构的抗风性能的主要因素[25]。对于本文带抗风夹直立锁缝屋面系统而言,结构的随机性主要体现在弹性模量、屈服强度、极限强度和摩擦系数,其均值和变异系数按文献[26-28]选取;荷载随机性方面,根据文献[29-30],风荷载服从极值I型分布,变量参数包括均值μw和变异系数αw,其中均值μw=0.999×wk,变异系数αw取0.193。式中wk表示风荷载标准值,可通过GB 50009—2012《建筑结构荷载规范》围护结构的风荷载计算得到。
| $ w_{\mathrm{k}}=\beta_{\mathrm{g} z} \mu_{\mathrm{s} 1} \mu_{\mathrm{z}} \omega_0 $ | (13) |
式中: βgz为z高度处的阵风系数,μsl为局部体型系数,μz为风压高度变化系数,w0为基本风压,所有系数均按该规范相应取值。
根据式(13)以及文献[27-30],得到带抗风夹直立锁缝屋面系统随机变量参数及分布类型见表 2。
| 表 2 随机变量参数及其分布类型 Tab. 2 Random variable parameters and their distribution types |
根据工程实际参数,结合式(3)~(6),得到带抗风夹直立锁缝屋面系统等价功能函数为
| $ Z = {G_{\min }}(\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}) = \min \left\{ {\begin{array}{*{20}{c}} {20 - \sqrt {{{\overrightarrow {\Delta x_{\rm{A}}^2} }^2} + {{\overrightarrow {\Delta {y_{\rm{A}}}} }^2} + {{\overrightarrow {\Delta {z_{\rm{A}}}} }^2}} }\\ {{f_{{\rm{u, 板}}}} - {\sigma _{\max , 板}}}\\ {{f_{{\rm{u}}, 支{\rm{ }}}} - {\sigma _{\max {\rm{, 支 }}}}} \end{array}} \right. $ | (14) |
式中位移和应力参数可通过调用ANSYS/LS-DYNA进行有限元计算得出。
通过矩约束方程(式(9)),结合本文五维系统求解方程,得到尺度变量ri和权系数wi见表 3。
| 表 3 五维系统下ri和wi参数值 Tab. 3 Parameter values of ri and wi in five dimensional system |
根据表 1、3,生成355个样本点, 结合式(8),计算出多失效模式下带抗风夹直立锁缝屋面系统等价功能函数Z统计矩和可靠指标分别见表 4、5。
| 表 4 等价功能函数前四阶统计矩结果 Tab. 4 Results of first four-order moments of equivalent limit state function |
| 表 5 多失效可靠度计算结果 Tab. 5 Calculation results of multiple failure reliability |
此外,为验证本文方法的精度和效率,采用Monte Carlo法[12]结果作为标准解进行校核。该方法主要通过若干次随机模拟获得随机事件的统计特征,其抽样次数按50/pf ~100/pf确定[31]。由于带抗风夹的直立锁缝屋面系统风揭破坏为小概率事件,失效概率pf预估为10-4量级[26],因此本文选取106个样本点保证计算精度,相关计算结果亦列于表 4、5。
3.3 结果分析由表 4可知,本文方法对多失效模式下带抗风夹直立锁缝屋面系统估计的前4阶矩具有较高的精度,与MCS法相比,本文方法能精确的估计其均值和标准差,而偏度和峰度相对误差也仅为1.76%和0.44%。就可靠指标的精度与效率而言,由表 5可知,本文方法计算得出的可靠指标为2.901,相比MCS法计算的2.895,相对误差为0.54%;计算效率方面,MCS法需要106次计算,而本文方法有限元计算次数为355次,仅为MCS的0.04%,计算效率得到了极大的提高。因此,本文方法极大地兼顾了精度和计算效率,能准确且高效地应用于多失效模式下带抗风夹直立锁缝屋面系统抗风揭可靠度分析。
结合各失效模式的功能函数Gi(Θ)(i=1、2、3) 得到单失效模式下的可靠度计算结果见表 6(表中INF表示无穷大)。由表 6可知,本文方法计算的单一失效模式下的可靠指标相比MCS法的最大相对误差仅为0.63%,进一步验证了本文方法的准确性。此外,对比表 6中各失效模式的可靠指标,其中屋面板撕裂破坏的可靠指标最小,即相比其他失效模式,屋面板发生撕裂破坏的概率最大。这主要由于屋面板在风荷载作用下将和抗风夹产生相互挤压,导致抗风夹附近的屋面板处更易破坏;而脱扣破坏的可靠指标为无穷大,说明添加抗风夹后能有效防止直立锁缝屋面系统发生脱扣破坏。
| 表 6 单失效可靠度计算结果 Tab. 6 Calculation results of single failure reliability |
对比表 5、6,3种单失效模式中带抗风夹直立锁缝屋面系统的失效概率分别为0、6.58×10-4和7.11×10-5,相比考虑多失效模式计算的失效概率1.90×10-3偏低,即单失效模式低估了结构的失效概率。为了保证结构的安全性,建议考虑多重失效模式评估带抗风夹直立锁缝屋面系统抗风揭安全水平。
需要说明的是,虽然本节算例得出带抗风夹的直立锁缝屋面系统脱扣破坏的失效概率为0,但该结果仅适用于本节工程实例。对于不同工程的带抗风夹的直立锁缝屋面体系,仍有发生脱扣破坏的可能性,需根据其工程实际参数,进而结合本文方法进行具体分析。
4 结论本文发展了多失效模式下带抗风夹直立锁缝屋面系统抗风揭可靠度分析方法,并结合工程算例进行了可靠度分析,得出主要结论:
1) 通过带抗风夹直立锁缝屋面系统非线性全过程研究,得出该系统主要存在屋面板撕裂破坏、支座断裂破坏和脱扣破坏3种失效模式并推导了对应的功能函数。
2) 对比3种单失效模式下的可靠度计算结果,按失效概率从大到小依次为:屋面板撕裂破坏、支座破坏和脱扣破坏。屋面板由于变形过程中和抗风夹存在相互挤压,发生撕裂破坏的概率最大,而脱扣破坏失效概率为0,说明添加抗风夹后能有效防止直立锁缝屋面系统发生脱扣破坏。
3) 对比单失效和多失效的可靠度计算结果,单失效模式计算得出的失效概率相比多失效模式结果偏小,即单失效模式低估了结构的失效概率。出于结构的安全性考虑,建议采用多失效模式来反映带抗风夹直立锁缝屋面系统的可靠指标。
4) 本文所引入的扩展型共轭无迹变换法,不依赖验算点且兼顾计算效率和精度,可准确且高效地进行多失效模式下带抗风夹直立锁缝屋面系统抗风揭可靠度分析。
| [1] |
夏俞超, 陈水福. 直立锁缝屋面系统风致破坏全过程研究[J]. 哈尔滨工业大学学报, 2021, 53(4): 136. XIA Yuchao, CHEN Shuifu. Wind-induced damage processes of standing seam metal roof systems[J]. Journal of Harbin Institute of Technology, 2021, 53(4): 136. DOI:10.11918/202008089 |
| [2] |
FARQUHAR S, KOPP G A, SURRY D. Wind tunnel and uniform pressure tests of a standing seam metal roof model[J]. Journal of Structural Engineering, 2005, 131(4): 650. DOI:10.1061/(ASCE)0733-9445(2005)131:4(650) |
| [3] |
HABTE F, MOONEGHI M A, CHOWDHURY A G, et al. Full-scale testing to evaluate the performance of standing seam metal roofs under simulated wind loading[J]. Engineering Structures, 2015, 105(15): 231. DOI:10.1016/j.engstruct.2015.10.006 |
| [4] |
DAMATTY A A E, RAHMAN M, RAGHEB O. Component testing and finite element modeling of standing seam roofs[J]. Thin-Walled Structures, 2003, 41(11): 1053. DOI:10.1016/S0263-8231(03)00048-X |
| [5] |
许秋华, 万恬, 刘凯. 直立锁缝金属屋面加强抗风揭能力的优化设计[J]. 工程力学, 2020, 37(7): 25. XU Qiuhua, WAN Tian, LIU Kai. Optimal design of strengthening wind exposure resistance of vertical whipstitch mental roofing board[J]. Mechanics Engineering, 2020, 37(7): 25. DOI:10.6052/j.issn.1000-4750.2020.02.ST13 |
| [6] |
孙瑛, 武涛, 武岳. 带抗风夹的直立锁边屋面系统抗风性能的参数研究[J]. 工程力学, 2020, 37(2): 185. SUN Ying, WU Tao, WU Yue. Parameter study on wind resistant performance of standing seam roof system with anti-wind clip[J]. Engineering Mechanics, 2020, 37(2): 185. DOI:10.6052/j.issn.1000-4750.2019.05.0136 |
| [7] |
宣颖, 谢壮宁. 大跨度金属屋面风荷载特性和抗风承载力研究进展[J]. 建筑结构学报, 2019, 40(3): 42. XUAN Ying, XIE Zhuangning. Research progress on wind loads and wind resistance bearing capacity of large span metal roof structures[J]. Journal of Building Structures, 2019, 40(3): 42. DOI:10.14006/j.jzjgxb.2019.03.004 |
| [8] |
吕大刚, 宋鹏彦, 王光远. 考虑模型不确定性的结构可靠度分析方法[J]. 哈尔滨工业大学学报, 2011, 43(10): 1. LV Dagang, SONG Pengyan, WANG Guangyuan. Reliability analysis methods of structures considering modeling uncertainty[J]. Journal of Harbin Institute of Technology, 2011, 43(10): 1. DOI:10.11918/j.issn.0367-6234.2011.10.001 |
| [9] |
吕大刚, 宋鹏彦, 王光远. 考虑统计不确定性的结构可靠度分析方法[J]. 哈尔滨工业大学学报, 2011, 43(8): 11. LV Dagang, SONG Pengyan, WANG Guangyuan. Reliability analysis methods of structures considering statistical uncertainty[J]. Journal of Harbin Institute of Technology, 2011, 43(8): 11. DOI:10.11918/j.issn.0367-6234.2011.08.003 |
| [10] |
孙成疆. 直立锁缝金属屋面系统在模拟极端暴风工况下抗风揭能力测试和分析[J]. 建筑结构, 2011, 41(增刊1): 1438. SUN Chengjiang. Simulated wind uplift pressure analysis and tests of the standing seam metal roof system[J]. Building Structure, 2011, 41(S1): 1438. DOI:10.19701/j.jzjg.2011.s1.342 |
| [11] |
THOFT-CHRISTENSEN P, MUROTSU Y. Application of structural systems reliability theory[M]. Berlin: Springer, 1986.
|
| [12] |
SHINOZUKA M. Monte Carlo solution of structural dynamics[J]. Computers & Structures, 1972, 2(5): 855. DOI:10.1016/0045-7949(72)90043-0 |
| [13] |
LI J, CHEN J, FAN W. The equivalent extreme-value event and evaluation of the structural system reliability[J]. Structural Safety, 2007, 29(2): 112. DOI:10.1016/j.strusafe.2006.03.002 |
| [14] |
范文亮, 李杰. 考虑多重失效机制的结构体系可靠度分析[J]. 土木工程学报, 2011, 44(11): 9. FAN Wenliang, LI Jie. Structural system reliability under multiple failure mechanisms[J]. China Civil Engineering Journal, 2011, 44(11): 9. DOI:10.15951/j.tmgcxb.2011.11.015 |
| [15] |
李杰. 工程结构整体可靠性分析研究进展[J]. 土木工程学报, 2018, 51(8): 1. LI Jie. Advances in global reliability analysis of engineering structures[J]. China Civil Engineering Journal, 2018, 51(8): 1. DOI:10.15951/j.tmgcxb.2018.08.001 |
| [16] |
KIUREGHIAN A D, DAKESSIAN T. Multiple design points in first and second-order reliability[J]. Structural Safety, 1998, 20(1): 37. DOI:10.1016/S0167-4730(97)00026-X |
| [17] |
吕大刚, 宋鹏彦, 于晓辉, 等. 基于矩法的结构非线性整体抗震可靠性分析[J]. 建筑结构学报, 2010, 31(增刊2): 119. LV Dagang, SONG Pengyan, YU Xiaohui, et al. Nonlinear global seismic reliability analysis of structures based on moment methods[J]. Journal of Building Structures, 2010, 31(S2): 119. DOI:10.14006/j.jzjgxb.2010.s2.002 |
| [18] |
王涛, 李正良, 范文亮. 基于扩展型共轭无迹变换的随机不确定性传播分析方法[J]. 工程力学, 2021, 38(8): 16. WANG Tao, LI Zhengliang, FAN Wenliang. An uncertainty propagation analysis method for stochastic system based on extended conjugate unscented transform[J]. Engineering Mechanics, 2021, 38(8): 16. DOI:10.6052/j.issn.1000-4750.2020.08.0569 |
| [19] |
王涛, 李正良, 范文亮. 基于改进统计矩点估计法和最大熵原理的结构整体可靠度分析[J]. 工程力学, 2022, 39(3): 193. WANG Tao, LI Zhengliang, FAN Wenliang. Global reliability analysis of structures based on improved statistical moments point estimation method and maximum entropy principle[J]. Engineering Mechanics, 2022, 39(3): 193. DOI:10.6052/j.issn.1000-4750.2021.01.0092 |
| [20] |
WANG T, LI Z L, FAN W L, et al. Structural reliability assessment based on enhanced conjugate unscented transformation and improved maximum entropy method[J]. Journal of Structural Engineering, 2021, 147(12): 04021213. DOI:10.1061/(ASCE)ST.1943-541X.0003194 |
| [21] |
MICHALOWICZ J V, NICHOLS J M, BUCHOLTZ F, et al. A general Isserlis theorem for mixed-Gaussian random variables[J]. Statistics & Probability Letters, 2011, 81(8): 1233. DOI:10.1016/j.spl.2011.03.022 |
| [22] |
刘威. 带抗风夹的直立锁边金属屋面系统抗风性能研究[D]. 哈尔滨: 哈尔滨工业大学, 2018 LIU Wei. Wind resistant performance of standing seam mental roof system with anti-wind clip[D]. Harbin: Harbin Institute of Technology, 2018 |
| [23] |
DER KIUREGHIAN A, LIU P L. Structural reliability under incomplete probability information[J]. Journal of Engineering Mechanics, 1986, 112(1): 85. DOI:10.1061/(ASCE)0733-9399(1986)112:1(85) |
| [24] |
LI G, ZHANG K. A combined reliability analysis approach with dimension reduction method and maximum entropy method[J]. Structural and Multidisciplinary Optimization, 2011, 43(1): 121. DOI:10.1007/s00158-010-0546-2 |
| [25] |
雷旭, 付兴, 肖凯, 等. 强风作用下输电塔结构不确定性倒塌分析[J]. 中国电机工程学报, 2018, 38(增刊1): 268. LEI Xu, FU Xing, XIAO Kai, et al. Failure analysis of a transmission tower subjected to wind load using uncertainty method[J]. Proceedings of the CSEE, 2018, 38(S1): 268. DOI:10.13334/j.0258-8013.pcsee.180665 |
| [26] |
李正良, 王成, 王涛, 等. 基于主动学习Kriging模型的直立锁缝屋面系统抗风揭可靠度分析[J/OL]. 工程力学. [2022-02-28]. http://dx.doi.org/10.6052/j.issn.1000-4750.2021.06.0430 LI Zhengliang, WANG Cheng, WANG Tao, et al. Reliability analysis of wind-resistance of standing seam roof system based on active learning kriging model[J/OL]. Engineering Mechanics. [2022-02-28]. http://dx.doi.org/10.6052/j.issn.1000-4750.2021.06.0430 |
| [27] |
吕虹波. 直立锁边金属屋面系统风灾易损性研究[D]. 哈尔滨: 哈尔滨工业大学, 2019 LV Hongbo. Wind disaster vulnerability study of the standing seam mental roof system[D]. Harbin: Harbin Institute of Technology, 2019 |
| [28] |
SUN Y, WU T, CAO Z G. Wind vulnerability analysis of standing seam roof system with consideration of multistage performance levels[J]. Thin-Walled Structures, 2021, 165: 107942. DOI:10.1016/j.tws.2021.107942 |
| [29] |
戴国欣, 夏正中. 建筑钢结构适用性分析[J]. 建筑结构学报, 2000, 21(3): 39. DAI Guoxin, XIA Zhengzhong. Applicability analysis of building steel structure[J]. Journal of Building Structures, 2000, 21(3): 39. DOI:10.3321/j.issn:1000-6869.2000.03.006 |
| [30] |
李继华, 林忠民, 李明顺, 等. 建筑结构概率极限状态设计[M]. 北京: 中国建筑工业出版社, 1990. LI Jihua, LIN Zhongmin, LI Mingshun, et al. Probabilistic limit state design of building structures[M]. Beijing: China Building Industry Press, 1990. |
| [31] |
ANG H S, TANG W H. Probability concepts in engineering[M]. 2nd ed. New York: John Wiley & Sons, 2007.
|
 2022, Vol. 54
2022, Vol. 54


