近年来输电线路覆冰灾害频发,易导致大面积停电、断线、倒塔等事故的发生,给电网的安全可靠运行带来了极大威胁。各国学者和研究机构开展了大量输电线路覆冰研究,主要的研究方法包括:现场观冰实测[1-3]、人工覆冰试验[4]和数值仿真[5-6]。相比现场实测和人工试验,基于流体动力学和覆冰增长机理的数值仿真为输电线路导线覆冰厚度和性状等预测提供了更加便捷的途径,对指导电网的冰灾防治具有重要工程意义。
目前已有的输电导线覆冰模型可归纳为3类:统计经验模型、机器学习模型和机理模型。统计经验模型是通过分析运行和试验获得的覆冰数据建立覆冰影响因素与导线质量的经验统计学解析模型,如Goodwin模型[1]、Jones模型[2]、湖南覆冰估算模型[3]等。但该类模型受制于有限的样本数据,往往仅适用于某些特定的环境条件,通用性较差。机器学习模型是在数据统计分析的基础上通过机器学习智能算法构建的覆冰预测模型,该类模型采用的智能算法具有良好的非线性拟合能力。但该类模型尚处于研究的初期阶段,无法反映导线覆冰的动力学与热力学特性,模型泛化能力较差[4-6]。机理模型则是通过分析过冷却水滴的碰撞和冻结这两个导线覆冰的主要物理过程而构建的物理模型,在此基础上结合数值仿真技术发展出了覆冰过程动态数值仿真模型。文献[7]首次提出了导线覆冰增长的动态模型,该模型简单地假设导线保持圆柱形均匀覆冰且其直径随时间不断增大。文献[8]综合分析了湿增长过程中导线表面的水膜流动状态,建立了基于边界单元法的二维导线覆冰仿真计算模型。文献[9]同样采用边界单元法建立了导线覆冰时变数值模型,并考虑了水滴所受电场力和电流产生的焦耳热影响。文献[10]基于UDF和动网格技术实现对导线覆冰过程的动态仿真。文献[11]研究了分裂导线中子导线遮蔽效应对流场的影响,提出了分裂导线覆冰增长的数值模型。文献[12-13]研究了导线覆冰数值计算中最优时间步长模型,并分析了导线覆冰过程中的扭转特性,提高了模型预测精度。然而,现有覆冰数值仿真研究大多着眼于单一固定覆冰的气象条件[14],未考虑实时变化的微气象条件对导线覆冰所产生的影响,因此仅对短期覆冰预测具有较好的效果,而难以适用于工程实际中冰冻严重的复杂情况。
鉴于此,本文基于欧拉气液两相流计算方法和水滴冻结热力学模型,建立了考虑时变气象参数情况下的输电导线覆冰数值仿真模型,提出了基于FLUENT和FENSAP-ICE软件的导线覆冰动态仿真框架,在此基础上分析了温度、风速、液态水含量、水滴中值体积直径等覆冰参数对导线覆冰过程的影响规律,最终通过输电线路现场覆冰实测结果验证了本文数值仿真方法的有效性。
1 输电线路导线的覆冰仿真模型 1.1 覆冰数值模型1) 导线建模及网格划分
本文采用了一个长宽为40D×20D(D为导线直径)大型计算域,以满足尾流及涡脱的充分发展,算例中D=34.9 mm。网格质量是影响流场计算精度和计算效率的重要因素。相较于非结构化网格,本文采用了质量更高、边界条件清晰的四边形结构化网格。将计算域划分为9个区域,中间的zone5为核心加密区,远离导线表面的网格以1.05的系数逐渐扩散。对于近壁面网格,采用附面层网格,第一层网格高度为0.003D,该情况下壁面y+接近1。由于导线覆冰的复杂性以及FENSAP-ICE软件的需求,本文通过二维网格拉伸生成三维结构化网格,充分考虑流场湍流的三维效应[15]。以3D的展向长度共划分30层,每层网格尺度为0.1D,总节点数为2 193 064个,共2 104 470个六面体网格单元,三维模型的x-y平面网格划分见图 1。

|
图 1 计算域与网格划分 Fig. 1 Computational domain and meshing |
2) 空气流场计算
基于计算流体力学原理,将含有过冷却水滴的空气流动视为气液两相流动,由于水滴粒径较小,一般忽略过冷却水滴运动对流场的影响,将水滴视为离散相。故先求解导线周围的空气流场,再分析过冷却水滴的运动轨迹和碰撞特性。根据粘性不可压缩流体动量守恒的运动方程,即Navier-Stokes方程(N-S方程),以及连续性方程可求得空气流场的速度分布,方程具体形式如下[18]:
| $ \frac{\partial u_{i}}{\partial t}+u_{j} \frac{\partial u_{i}}{\partial x_{j}}=F_{i}-\frac{1}{\rho} \frac{\partial p}{\partial x_{i}}+\nu \frac{\partial^{2} u_{i}}{\partial x_{j} \partial x_{j}} $ | (1) |
| $ \sum \frac{\partial u_{i}}{\partial x_{i}}=0 $ | (2) |
式中:ui(i=1, 2, 3)、uj (j=1, 2, 3)为流场在3个方向上的速度分量,Fi(i=1, 2, 3)为单位流体上所受质量力在3个方向上的分量,ρ为空气密度,p为空气压强,ν为空气运动粘度。
N-S方程是一个复杂的二阶线性偏微分方程,直接求解较为困难,一般需要对方程组进行离散。本文通过FLUENT软件进行导线周围空气流场的计算,采用有限体积法离散控制方程,离散格式采用二阶迎风格式,并对控制方程进行Reynolds平均,可得非定常不可压缩流动的RANS方程[16]:
| $ \frac{\partial}{\partial t}\left(\rho u_{i}\right)+\frac{\partial}{\partial x_{j}}\left(\rho u_{i} u_{j}\right)=\frac{\partial}{\partial x_{j}}\left[\mu\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right)-\rho \overline{u_{i}^{\prime} u_j^{\prime}}\right]-\frac{\partial \rho}{\partial x_{i}} $ | (3) |
| $ \frac{\partial \rho}{\partial t}+\frac{\partial}{\partial x_{i}}\left(\rho u_{i}\right)=0 $ | (4) |
式中:μ为空气动力粘度,
由于雷诺应力的出现,上述方程组不封闭,需要引入新的湍流模型才能求解。本文采用k-ω SST两方程湍流模型,该模型考虑了湍流中剪切应力对湍流粘度的影响,具有较高的计算精度。
3) 冷却水滴碰撞轨迹计算
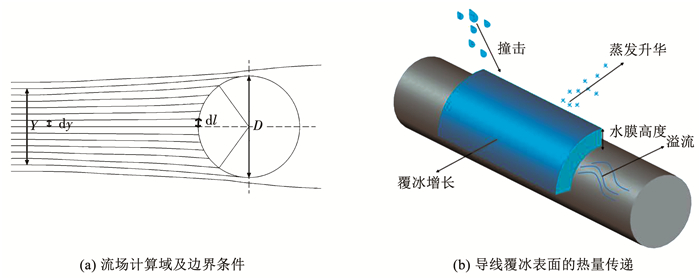
基覆冰导线周围过冷却水滴的运动轨迹见图 2(a)。过冷却水滴的局部碰撞系数反映了各个微元的实际水滴碰撞率与最大可能的水滴碰撞率之比,是后续导线覆冰形状及覆冰质量预测重要参数,其定义式为
| $ \beta=\frac{\mathrm{d} y}{\mathrm{~d} l} $ | (5) |
|
图 2 过冷却水滴的碰撞与冻结过程 Fig. 2 Freezing and colliding of supercooled water droplets |
式中:β为局部碰撞系数,dy为相邻入射点的初始竖向坐标之差,dl为相邻碰撞点之间的导线表面圆弧的距离。
本文采用FENSAP-ICE有限元软件分析过冷却水滴的碰撞过程,该软件采用欧拉法分析气液两相流,引入了相体积分数的概念,表示某一相的体积占总体积的比例,定义为
| $\alpha_{i}=\frac{V_{i}}{V} $ | (6) |
碰撞系数的计算取决于过冷却水滴的运动轨迹。本文基于欧拉法得到欧拉气液两相粘性流模型的由ANSYS FENSAP-ICE用户手册可知N-S方程和连续性方程为
| $ \begin{gathered} \frac{\partial\left(\alpha \vec{V}_{\mathrm{d}}\right)}{\partial t}+\vec{\nabla} \cdot\left[\alpha \vec{V}_{\mathrm{d}} \otimes \vec{V}_{\mathrm{d}}\right]= \\ \frac{C_{\mathrm{D}} R e_{\mathrm{d}}}{24 K} \alpha\left(\vec{V}_{\mathrm{a}}-\vec{V}_{\mathrm{d}}\right)+\alpha\left(1-\frac{\rho_{\mathrm{a}}}{\rho_{\mathrm{d}}}\right) \frac{1}{F r^{2}} \end{gathered} $ | (7) |
| $ \frac{\partial \alpha}{\partial t}+\vec{\nabla} \cdot\left(\alpha \vec{V}_{\mathrm{d}}\right)=0 $ | (8) |
式中:α为水滴相体积分数,表示水滴体积占总体积的比例,
| $K=\frac{\rho_{\mathrm{d}} d^{2} V_{\mathrm{a}, \infty}}{18 L_{\infty} \mu} $ | (9) |
式中:Va, ∞为自由来流空气速度;d为导线直径;L∞为特征长度,取导线半径。由上述方程组可求解导线周围各点水的相体积分数和速度,进而计算水滴的碰撞区域和局部碰撞系数。
4) 水滴冻结过程计算
导线表面水滴冻结过程本质上是热交换过程,是一个热力学平衡过程,主要表现为对流、传导、蒸发、升华等形式,见图 2(b)。在覆冰湿增长过程中,水滴碰撞后只有部分立即冻结,会在导线表面形成液态水膜,基于覆冰表面热质传递的热力学模型,可建立导线覆冰表面微元的质量守恒方程和能量守恒方程:
| $\rho_{\mathrm{f}}\left[\frac{\partial h_{\mathrm{f}}}{\partial t}+\vec{\nabla} \cdot\left(\bar{V}_{\mathrm{f}} h_{\mathrm{f}}\right)\right]=V_{\infty} \omega_{\mathrm{LWC}} \beta-\dot{m}_{\mathrm{evap}}-\dot{m}_{\mathrm{ice}} $ | (10) |
| $ \begin{gathered} \rho_{\mathrm{f}}\left[\frac{\partial h_{\mathrm{f}} c_{\mathrm{f}} \widetilde{T}_{\mathrm{f}}}{\partial t}+\vec{\nabla} \cdot\left(\bar{V}_{\mathrm{f}} h_{\mathrm{f}} c_{\mathrm{f}} \widetilde{T}_{\mathrm{f}}\right)\right]= \\ {\left[c_{\mathrm{f}}\left(\widetilde{T}_{\infty}-\widetilde{T}_{\mathrm{f}}\right)+\frac{\left\|\vec{V}_{\mathrm{d}}\right\|^{2}}{2}\right] V_{\infty} \omega_{\mathrm{LWC}} \beta-} \\ L_{\text {evap }} \dot{m}_{\text {evap }}+\left(L_{\text {fusion }}-c_{\mathrm{s}} \widetilde{T}\right) \dot{m}_{\text {ice }}+ \\ \sigma \varepsilon A\left(T_{\infty}^{4}-T_{\mathrm{f}}^{4}\right)-h_{\mathrm{c}} A\left(\widetilde{T}_{\mathrm{f}}-\widetilde{T}_{\text {ice, rec }}\right)+Q_{\text {anti - icing }} \end{gathered} $ | (11) |
式中: hf、Vf、ρf分别为水膜的高度、速度和密度;V∞为自由来流空气速度;ωLWC为空气液态水含量;β为局部碰撞系数;
为使上述方程组封闭,补充一组物理方程,其物理意义是当覆冰界面平衡温度低于冰点(0 ℃)时,模型中不会存在液态水,且高于冰点(0 ℃)时模型不会形成覆冰:
| $ h_{\mathrm{f}} \geqslant 0 ; \dot{m}_{\text {ice }} \geqslant 0 ; h_{\mathrm{f}} \widetilde{T}_{\mathrm{f}} \geqslant 0 ; \dot{m}_{\text {ice }} \widetilde{T}_{\mathrm{f}} \leqslant 0 $ | (12) |
覆冰密度是导线覆冰预测中的重要参数,本文采用Makkonen-Stallabrass密度公式[7],该公式考虑了较全面的覆冰影响参数,表达为
| $ \rho=378+425 \lg R_{\mathrm{M}}-82.3\left(\lg R_{\mathrm{M}}\right)^{2} $ | (13) |
| $ R_{\mathrm{M}}=\frac{d \cdot\left\|\bar{V}_{\mathrm{d}}\right\|}{2 \widetilde{T}_{\text {wall }}} $ | (14) |
式中:RM为导线覆冰密度计算参数;d为过冷却水滴直径;Vd为过冷却水滴的碰撞速度;
获得导线微元体在某时间步长下的覆冰质量和覆冰密度后,可基于微元体体积计算该时间步长下的覆冰厚度。假定每个微元体的覆冰增长沿覆冰表面法线方向,综合所有微元体的覆冰增长情况,可以得到该时间步长后导线覆冰形状。
1.2 导线覆冰仿真框架基于导线覆冰机理和上述导线覆冰数值模型,本文提出了更为精细地考虑气象参数时变情况下的输电线路导线覆冰数值仿真框架,见图 3。首先,根据所获取的输电线路附近的风速、风向、温度和相对湿度等气象数据得到仿真计算所需的条件参数;其次,建立覆冰导线的三维仿真模型并进行网格划分;然后,假定每小时内气象参数保持其均值不变,并基于导线覆冰速率及气象条件选择合适的时间步长,在此基础上采用FENSAP-ICE软件进行多时间步的导线覆冰增长仿真计算。在每个时间步内先后依次开展FLUENT流场计算、FENSAP-ICE水滴碰撞及冻结仿真和基于网格置换的覆冰边界自动更新;最后,分析多个时间步后的网格大小及横纵比,当网格质量降低而无法满足计算精度时,输出覆冰导线形状重新划分网格,然后继续计算直至达到预计的覆冰时间。

|
图 3 导线覆冰过程数值仿真流程图 Fig. 3 Flow chart of numerical simulation of conductor icing process |
为考察本文导线覆冰数值仿真方法的有效性,选取了文献中的两组导线人工覆冰试验数据[8]作为验证。人工试验导线覆冰参数如表 1中工况1和2所示。
| 表 1 不同工况下的导线覆冰参数 Tab. 1 Conductor icing parameters under different working conditions |
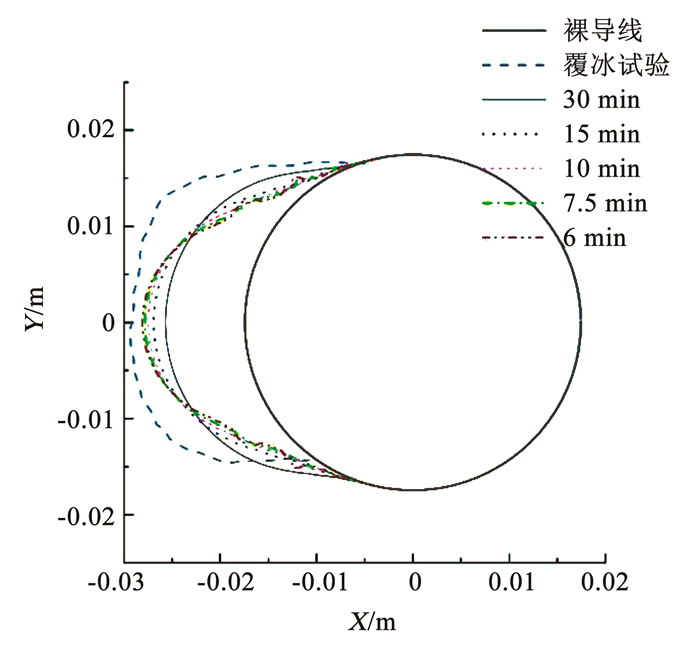
图 4给出了工况1下多时间步导线覆冰仿真计算结果。总覆冰时间为30 min,计算时间步分别取2、3、4、5步,对应时间步长15、10、7.5、6 min,经迭代计算后获得导线覆冰预测结果。
|
图 4 不同时间步长下导线覆冰仿真计算结果 Fig. 4 Simulation results of conductor icing under different time steps |
由图 4可知,不同时间步长下仿真计算获得的导线覆冰形状存在差异,多时间步长下覆冰形状仿真效果较单时间步好。随着时间步长的减小,导线最大覆冰厚度逐步增加,两侧覆冰宽度也略有减小,这是由于迭代更新导线覆冰外形后,过冷却水滴的碰撞范围会逐渐减小,覆冰往中心处生长,这也较符合实际覆冰情况。对比分析可知,10 min时间步长已可较好地模拟实际覆冰情况,再增加时间步对覆冰模拟效果改善不大但却大大增加了计算资源的消耗。因此,应合理选择时间步长进行多时间步计算,建议取10 min。
对工况1和2的试验导线和环境参数工况进行覆冰仿真分析,计算中采用Langmuir D水滴多尺寸分布和多时间步,时间步长取10 min,总覆冰时间为30 min,启用砂粒粗糙度模型,仿真计算结果见图 5。由图 5可知,仿真计算所得的覆冰极限位置和覆冰形状与试验结果整体吻合较好,仅在覆冰的上下边缘处与实际情况存在一定差异,这是由导线形成了不规则的锯齿状覆冰造成的,由于自动置换网格后节点数不变而覆冰面积增加,导线覆冰边界网格质量会降低,网格横纵比过大,需人工更新覆冰导线外形。将计算好的覆冰外形边界数据导出,在ICEM里面重新划分网格。由此可见,本文提出的导线覆冰仿真方法能较好地反演人工覆冰试验结果,具有良好的预测能力。

|
图 5 导线覆冰数值仿真与人工覆冰试验结果对比 Fig. 5 Comparison of conductor icing numerical simulation and artificial icing test results |
导线覆冰是一个非线性、多因素综合影响的时序变化过程,其覆冰形状和覆冰质量与微气象和自身结构等有关,是多种覆冰参数共同作用的结果。本节通过仿真计算研究风速、温度、水滴中值体积直径、液态水含量和导线直径等因素对导线覆冰质量及形状的影响。采用控制变量法进行研究,即当研究某一影响因素时保持其他参数为基准值。导线覆冰参数基准值如表 1中的工况3所示。总覆冰时长为30 min,具体各参数变化范围及覆冰计算结果详见图 6~7。需要说明的是,计算中假设风向与导线长度方向垂直。图中19.98、26.82、33.6、38.4 mm的导线直径分别对应于LGJ-210/25、LGJ-400/35、LGJ-630/45、LGJ-800/55的实际导线型号。

|
图 6 不同覆冰参数对导线覆冰形状的影响 Fig. 6 Influence of different icing parameters on icing shape of conductor |

|
图 7 不同覆冰参数对导线覆冰质量的影响 Fig. 7 Influence of different icing parameters on conductor icing mass |
由图 6(a)可知,导线径向覆冰厚度和环向覆冰宽度均随风速的增加而增大。当风速较低时,导线覆冰呈较规则的新月形,随着风速增大导线覆冰逐渐向上下两侧发展。这是因为随着风速的增加,单位时间内撞击到导线表面上的水滴增多,导线覆冰由干增长逐渐变为湿增长,碰撞后未立即冻结的水滴形成液态水膜向两侧流动导致上下覆冰极限增加。由于驻点处过冷却水滴受气流影响最小,故该处局部碰撞系数和覆冰厚度最大。图 6(b)表明,当温度较低时导线覆冰形态受温度影响较小,而当温度较高(如-3 ℃)时,导线上下两侧覆冰增加呈湿增长状态,这是由于温度主要影响导线覆冰密度和干湿增长过程,对覆冰形状影响较小。由图 6(c)可知,导线覆冰形状受水滴中值体积直径(DMVD)影响较大,随着DMVD的增大,过冷却水滴的碰撞极限和局部碰撞系数逐渐增大,导线覆冰横截面积也越来越大,导线覆冰逐渐变为湿增长。这是因为水滴直径越大,其惯性越大,受气流影响较小,且更容易被导线捕获。图 6(d)说明,当液态水含量(ωLWC)从0.5 g/m3增加到1.5 g/m3时,导线覆冰厚度明显增大,而继续增加ωLWC(如1.5~3.5)则覆冰厚度变化有限,覆冰沿导线表面上下两侧发展,由干增长转变为湿增长。对液态水含量为3.5 g/m3和2.5 g/m3这两种工况,导线覆冰形状几乎一致,因为此时水滴冻结系数随ωLWC量的增加而降低,冻结能力受到限制。图 6(e)~(h)则表明相同环境条件下导线直径不同将导致覆冰形状有较大差异。随着导线直径的增加,导线径向覆冰厚度略有减小,水滴上下碰撞极限及导线侧向覆冰饱满度变小,单位面积覆冰量逐渐降低。这是因为导线直径越大,其对周围空气流场的干扰越强,则水滴在流场中的运动轨迹偏移程度更高,使得局部碰撞系数降低。
图 7给出了不同覆冰参数对导线覆冰质量的影响。由图 7(a)和(b)可知,导线覆冰质量增长速度随风速的增大而增大,但随温度的升高而呈减少趋势。当气温较高(-3 ℃)时,降低温度有助于增加导线覆冰质量,这是由于温度降低而冻结系数增加,冻结的过冷却水滴质量也有所增加,但当环境温度较低(-5 ℃以下)时,继续降低温度对导线覆冰质量影响不大。图 7(c)和(d)则说明,导线覆冰质量增长速度随DMVD和ωLWC的增大而增大。当ωLWC较高(2.5 g/m3)时,继续增加ωLWC使得导线覆冰质量增加有限,这是由于导线覆冰已逐渐趋于饱和状态,这与图 7(d)的观测结果一致。由图 7(e)可以发现,导线覆冰质量增长速度随着导线直径的增大而增大。这可能受两个方面的因素综合影响,一方面导线直径的增加导致水滴局部碰撞系数的降低,但是另一方面随着导线直径的增加, 水滴的碰撞接触面增大。从计算结果来看,在计算微气象条件下后者占主导地位,导线碰撞面积的增大作用对覆冰量的影响大于碰撞率的降低作用。
3 覆冰影响因素分析 3.1 覆冰仿真模型验证导线覆冰是一个受多种微气象因素影响、随时间推移而发展变化的连续性过程,在导线覆冰预测中有必要考虑气象因素时间累积效应,是一个长周期过程。脉动风周期短,对覆冰过程的影响较小,因此验证时所用的数据为气象站现场观测得到的平均风速。为进一步检验导线覆冰预测模型的有效性,在浙江省嵊州市某山上试验基地开展输电线路覆冰监测试验。以该基地内一条已退役的500 kV线路作为监测对象,在试验线路的2#和3#塔上设置输电线路在线监测系统,并在该线路下方设置气象站监测系统,见图 8。气象站监测系统采用中尺度六要素自动气象站,能监测风速、风向、温度、相对湿度、气压、降水量等气象六要素,主要用于实时监测线路周围的气象参数。输电线路在线监测系统主要用于获取2#~4#塔档距内的实时等值覆冰厚度,该系统由绝缘子串拉力传感器、绝缘子串倾角传感器以及导线倾角传感器组成,可由覆冰荷载改变引起的应力应变变化求解出输电线路的等值覆冰厚度[14]。

|
图 8 输电线路监测系统示意 Fig. 8 Schematic diagram of transmission line monitoring system |
本文选取输电线路覆冰情况较为严重的2018年观测结果作为研究对象。选择该冰期内输电线路覆冰初始的增长阶段即2018年1月24日0时作为仿真计算的起始点,对当时的历史气象数据进行处理。由于天气恶劣导致仪器故障,因而该时段的现场风速风向数据缺失。故根据嵊州市风速数据与试验基地已有数据的线性关系,将该时段嵊州市市区的风速数据折算为试验基地风速,再根据线路走向计算出投影到垂直于导线方向的投影风速。根据线路走向计算出垂直导线风速。通过实测的空气相对湿度和环境温度计算出液态水含量,然后计算各气象参数的逐时平均值。导线覆冰时段的逐时气象参数及等值覆冰厚度见表 2。
| 表 2 导线覆冰逐时气象参数及等值覆冰厚度 Tab. 2 Hourly weather conditions and equivalent icing thickness |
该试验线路所用导线型号为LGJ-630/45,导线外径为33.6 mm。首先需确定气象条件未给出的水滴中值体积直径参数,对实测0~4时进行不同DMVD下的导线覆冰仿真计算,结果见图 9(a)。通过对比仿真计算与实测得到的等值覆冰厚度,综合考虑导线覆冰形状及覆冰速率来推得符合条件的DMVD值。根据覆冰质量不变原则,等效为圆形均匀覆冰导线的等值覆冰厚度计算公式为
| $ b=\frac{\sqrt{\frac{4 \rho S}{0.9 {\rm{ \mathsf{ π}}}}+D^{2}}-D}{2} $ | (15) |

|
图 9 导线覆冰形态仿真计算结果 Fig. 9 Simulation results of conductor icing shape |
式中:b为导线等值覆冰厚度,ρ为导线覆冰密度,S为导线覆冰面积。
由图 9(a)可知,不同DMVD下导线轴向覆冰厚度相近,而侧向覆冰宽度存在一定差异。由式(12)可计算DMVD为15、18、22、25 μm时导线等值覆冰厚度分别为1.602、2.412、2.691、2.731 mm。与实测4时的等值覆冰厚度2.665 mm相比,15 μm和25 μm条件下导线等值覆冰厚度与实际差异较大,而22 μm条件下导线覆冰增长速率较实测偏大,容易导致后续仿真中因为覆冰速度过快而产生冰形和质量失真。因此,综合考虑导线覆冰速率、覆冰形状以及等值覆冰厚度等因素后,仿真计算采用18 μm水滴中值体积直径。
3.4 气象参数逐时变化对导线覆冰的影响针对实测的0~6时,分别进行考虑气象参数时变和保持气象参数恒定情况下的导线覆冰仿真,相应的计算结果绘于图 9(b)和(c)中。其中气象参数恒定情况是指气象参数始终与初始第1小时相同。由图 9(b)和(c)比较可知,两种气象条件情况下导线覆冰形状和覆冰厚度均差异较大。对于气象参数恒定的情况,导线覆冰厚度随时间均匀增长。这是因为气象参数保持不变,导线覆冰增长速度仅受导线覆冰边界改变的影响,且该恒定气象条件下覆冰增长较缓,导线局部碰撞系数和覆冰增长速度变化不大。对于气象参数时变的情况,导线覆冰厚度增长逐渐变快,两侧覆冰宽度逐渐变小,覆冰向冰形的中心线处聚集。这是由于时变气象条件下,环境温度随着时间逐渐降低,导线覆冰增长速度逐渐变快,导线覆冰形状因气象条件每小时变化而各不相同。两种计算工况下0~6时的导线等值覆冰厚度见图 10。

|
图 10 0~6时不同气象条件下的导线等值覆冰厚度 Fig. 10 Equivalent icing thickness of conductor under different weather conditions during 0:00-6:00 |
由图 10可知,考虑时变气象条件下的仿真结果更加接近现场观测结果,而采用恒定的气象条件的仿真结果则会产生较大误差。因此在导线覆冰仿真计算中应考虑气象参数实时变化。
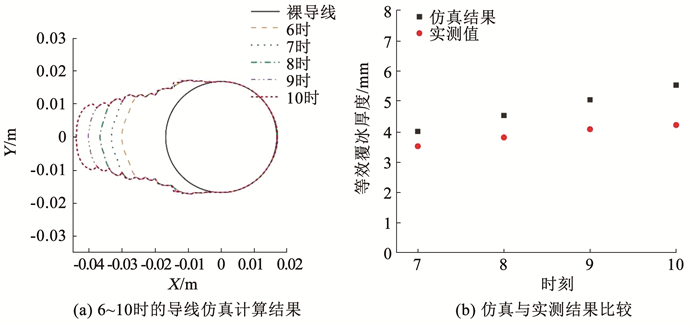
3.5 数值仿真方法验证图 11(a)给出了实测6~10时考虑气象参数时变情况下的导线覆冰计算结果。由图 11(a)可知,随着环境温度和液态含水量的继续降低,6~10时内导线覆冰厚度较均匀增长,覆冰宽度进一步收缩变小。计算得7~10时的导线等值覆冰厚度绘于图 11(b)。仿真结果的覆冰增长规律与实测结果具有较好的一致性,预测覆冰厚度稍稍偏大,但整体平均绝对误差仅约为14.6%,证明了本文提出的仿真方法在覆冰质量的预测上具有良好的精度。
|
图 11 预测和试验获得的导线覆冰形态 Fig. 11 Predicted and experimental conductor icing morphologies |
图 12为本次输电线路覆冰监测观测得到的导线覆冰形状,可以看出其冰形与本文仿真结果较为类似,验证了本文模型对导线覆冰形状预测的有效性。综上所述,本文预测模型在导线覆冰质量与冰形上均有较好的预测精确度。

|
图 12 覆冰监测试验中脱落的冰块 Fig. 12 Ice cube falling off during icing monitoring test |
在覆冰的初始和结束阶段,导线的等值覆冰厚度仿真结果与实测值误差较大,其主要原因可能包含以下两个方面:1)在初始计算时刻前,即23日下午已有一段缓慢覆冰过程,到23日晚上时导线覆冰处于维持阶段,直到24日凌晨覆冰才开始较快增长。覆冰仿真难以模拟计算时刻之前的覆冰情况,而实际初始观测点的导线等值覆冰厚度包含了前一阶段的覆冰从而与预测结果产生较大误差。2)本文通过0~4时的导线覆冰结果确定恒定的水滴中值体积直径参数,但由于初始阶段的误差可能过高地估计了导线覆冰增长速度,从而导致最终阶段仿真预测的结果偏大。此外,受输电线路所处山区微地形与微气象条件的影响,计算时采用恒定的水滴中值体积直径与实际情况可能存在差异也将造成预测结果的偏差。因此,建议后续研究中进一步对水滴中值体积直径的取值方法进行探索,以提高模型的预测精度。
4 结论本文基于导线覆冰机理和欧拉气液两相流模型,提出了考虑气象参数时变影响下的输电线路导线覆冰数值仿真方法,在此基础上建立了基于FLUENT和FENSAP-ICE软件的导线覆冰增长数值模拟框架,研究了温度、风速、液态水含量、水滴中值体积直径和导线直径等因素对导线覆冰质量及覆冰性状的影响,最终利用输电线路现场覆冰监测数据对仿真计算方法的有效性进行了验证,预测结果与输电线路覆冰监测结果吻合度较好,该方法能有效地预测导线实时覆冰形状和质量,表明本文提出的导线覆冰仿真方法具有较好的精度。主要结论如下:
1) 覆冰过程中,环境参数以及导线直径会影响局部碰撞系数与覆冰的干湿增长过程,进而影响导线覆冰形状。干增长条件下导线覆冰形状呈钝体或流线体,通常倾向于遵循导线的原始轮廓,而湿增长条件下由于导线表面液态水膜的存在,覆冰极限和覆冰宽度更大,导线覆冰形态可能超越导线的原始轮廓。导线覆冰形状受风速、过冷却水滴中值体积直径、液态含水量和导线直径影响较大,受温度影响较小。
2) 本文算例表明,导线覆冰质量增长速度随风速、过冷却水滴中值体积直径、液态含水量、导线直径的增大而增大,但随环境温度的升高而减小。相较于其他环境参数,温度对导线覆冰质量较不敏感。
3) 采用恒定的气象计算参数会造成较大的导线覆冰预测误差,本文提出了考虑气象参数时变的输电线路导线覆冰数值仿真方法,预测结果与输电线路覆冰监测结果吻合度较好。该方法能有效地预测导线实时覆冰形状和质量,可为输电线路冰灾风险分析和预警提供参考。
| [1] |
GOODWIN E J, MOZER J D, DIGIOIA A M, et al. Predicting ice and snow loads for transmission line design[C]//Proceedings of the First IWAIS. Hanover: [s. n.], 1983
|
| [2] |
JONES K F. A simple model for freezing rain ice loads[J]. Atmospheric Research, 1998, 46(1/2): 87. DOI:10.1016/S0169-8095(97)00053-7 |
| [3] |
廖玉芳, 段丽洁. 湖南电线覆冰厚度估算模型研究[J]. 大气科学学报, 2010, 33(4): 395. LIAO Yufang, DUAN Lijie. Study on estimation model of wire icing thickness in human province[J]. Transactions of Atmospheric Sciences, 2010, 33(4): 395. DOI:10.13878/j.cnki.dqkxxb.2010.04.016 |
| [4] |
XIONG Wei, YUAN Hejin, YOU Lang. Prediction method of icing thickness of transmission line based on MEAO[J]. Cluster Computing, 2018, 21(1): 845. DOI:10.1007/s10586-017-0923-3 |
| [5] |
黄新波, 李弘博, 朱永灿, 等. 基于时间序列分析与卡尔曼滤波的输电线路覆冰短期预测[J]. 高电压技术, 2017, 43(6): 1943. HUANG Xinbo, LI Hongbo, ZHU Yongcan, et al. Short-term forecast for transmission line icing by time series analysis and Kalman filtering[J]. High Voltage Engineering, 2017, 43(6): 1943. DOI:10.13336/j.1003-6520.hve.20170527027 |
| [6] |
戴栋, 黄筱婷, 代洲, 等. 基于支持向量机的输电线路覆冰回归模型[J]. 高电压技术, 2013, 39(11): 2822. DAI Dong, HUANG Xiaoting, DAI Zhou, et al. Regression model for transmission lines icing based on support vector machine[J]. High Voltage Engineering, 2013, 39(11): 2822. DOI:10.3969/j.issn.1003-6520.2013.11.034 |
| [7] |
MAKKONEN L. Modeling of ice accretion on wires[J]. Journal of Applied Meteorology and Climatology, 1984, 23(6): 929. DOI:10.1175/1520-0450(1984)023<0929:MOIAOW>2.0.CO;2 |
| [8] |
FU Ping, FARZANEH M, BOUCHARD G. Two-dimensional modelling of the ice accretion process on transmission line wires and conductors[J]. Cold Regions Science and Technology, 2006, 46(2): 132. DOI:10.1016/j.coldregions.2006.06.004 |
| [9] |
梁曦东, 李雨佳, 张轶博, 等. 输电导线的覆冰时变仿真模型[J]. 高电压技术, 2014, 40(2): 336. LIANG Xidong, LI Yujia, ZHANG Yibo, et al. Time-dependent simulation model of ice accretion on transmission line[J]. High Voltage Engineering, 2014, 40(2): 336. DOI:10.13336/j.1003-6520.hve.2014.02.002 |
| [10] |
刘胜春, 司佳钧, 郭昊, 等. 输电线路导线覆冰模拟计算与试验研究[J]. 中国电机工程学报, 2014, 34(增刊1): 246. LIU Shengchun, SI Jiajun, GUO Hao, et al. Numerical and experimental study on accreted ice on conductor of transmission lines[J]. Proceedings of the CSEE, 2014, 34(S1): 246. DOI:10.13334/j.0258-8013.pcsee.2014.S.036 |
| [11] |
胡琴, 于洪杰, 李毅, 等. 分裂导线覆冰增长模拟计算及试验验证[J]. 高电压技术, 2017, 43(3): 900. HU Qin, YU Hongjie, LI Yi, et al. Numerical and experimental study of accreted ice on bundle conductor[J]. High Voltage Engineering, 2017, 43(3): 900. DOI:10.13336/j.1003-6520.hve.20170303029 |
| [12] |
蒋兴良, 姜方义, 汪泉霖, 等. 基于最优时间步长模型的输电导线雾凇覆冰预测[J]. 电工技术学报, 2018, 33(18): 4408. JIANG Xingliang, JIANG Fangyi, WANG Quanlin, et al. Prediction of rime accretion on transmission line based on optimal time step model[J]. Transactions of China Electrotechnical Society, 2018, 33(18): 4408. DOI:10.19595/j.cnki.1000-6753.tces.170941 |
| [13] |
蒋兴良, 侯乐东, 韩兴波, 等. 输电线路导线覆冰扭转特性的数值模拟[J]. 电工技术学报, 2020, 35(8): 1818 JIANG Xingliang, HOU Ledong, HAN Xingbo, et al. Numerical simulation of torsion characteristics of transmission line conductor[J]. 2020, 35(8): 1818. DOI: 10.19595/j.cnki.1000-6753.tces.190181 |
| [14] |
林巍. 覆冰输电导线气动力特性风洞试验及数值模拟研究[D]. 杭州: 浙江大学, 2012 LIN Wei. Wind tunnel and numerical study on aerodynamic characteristics of ice accreted transmission lines[D]. Hangzhou: Zhejiang University, 2012 |
| [15] |
YANG Fengli, YANG Jingbo, HAN Junke, et al. Dynamic responses of transmission tower-line system under ice shedding[J]. International Journal of Structural Stability and Dynamics, 2012, 10(3): 461. DOI:10.1142/S0219455410003579 |
| [16] |
OKA S, ISHIHARA T. Numerical study of aerodynamic characteristics of a square prism in a uniform flow[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2009, 97(11/12): 548. DOI:10.1016/j.jweia.2009.08.006 |
| [17] |
王福军. 计算流体动力学分析—CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004. WANG Fujun. Computational fluid dynamics analysis—CFD software principle and application[M]. Beijing: Tsinghua University Press, 2004. |
| [18] |
MAKKONEN L. Modeling power line icing in freezing precipitation[J]. Atmospheric Research, 1998, 46(1/2): 131. DOI:10.1016/S0169-8095(97)00056-2 |
| [19] |
李大鸣, 范玉. 计算流体力学[M]. 天津: 天津大学出版社, 2014. LI Daming, FAN Yu. Computational fluid dynamics[M]. Tianjin: Tianjin University Press, 2014. |
 2022, Vol. 54
2022, Vol. 54


