2. 对海监测与信息处理工业和信息化部重点实验室(哈尔滨工业大学),哈尔滨 150001
2. Key Laboratory of Marine Environmental Monitoring and Information Processing (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150001, China
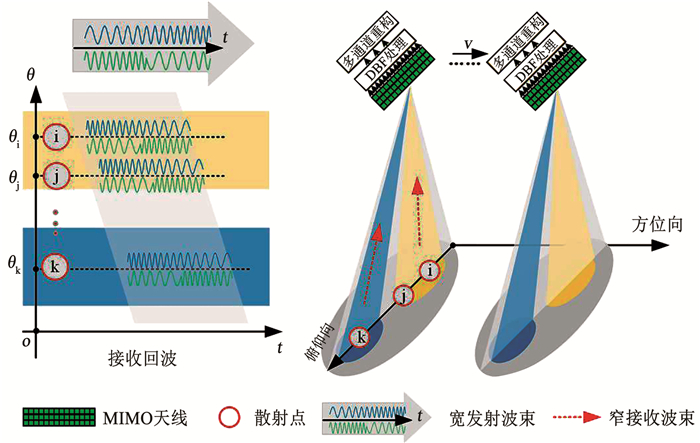
合成孔径雷达(synthetic aperture radar, SAR)在很多领域都发挥了重要的作用,但是传统单天线SAR成像在实现高分宽幅成像存在着不可调和的矛盾。高分宽幅SAR成为未来新体制雷达发展的方向,多发多收(multiple input multiple output, MIMO)SAR是其中一种[1]。MIMO SAR通过发射多个波形、同时接收多个回波,实现了自由度、等效相位中心的增加及多任务协同的目标探测。
MIMO SAR的系统设计有两个问题亟需解决:如何有效分离回波和发射波形的设计[2]。依据发射波形的特征,MIMO SAR可进一步分为分时同频、同时分频和同时同频三大类[3]。其中同时同频应用最广,自由度最高,但也对波形设计提出了更高的要求,如何分离雷达回波、抑制干扰是提升系统性能的关键。文献[4]指出,将正负线调频信号应用在MIMO SAR中,失配的信号能量会散布在图像中,导致图像中噪声干扰严重。文献[5]提出多维波形编码的概念,多相位中心个数和基线长度增加,结合二维阵列天线和俯仰向数字波束合成(digital beam forming, DBF)技术区分波形,提高了成像能力。文献[6]提出短时移正交(short term shift orthogonal, STSO)波形,在MIMO SAR中具有良好的性能,改善聚焦性。
正交频分复用(orthogonal frequency division modulation, OFDM)技术也可与空时编码技术结合,对线调频信号进行调制。文献[7]提出在MIMO SAR中应用OFDM chirp信号,保证信号之间零互相关,模糊函数具有良好的特性,但存在对多普勒频率敏感的问题。文献[8]致力于解决因MIMO SAR发射信号非理想正交而成像模糊的问题,提出将OFDM与chirp结合的体制,但存在脉冲间频移影响正交性的问题。基于与空时编码结合的思路,文献[9]提出一种具有多个正交发射波形的调频连续波,信号之间具有较低的互相关性和较高的自相关。文献[10]提出一种结合空时编码的ODFM-LFM信号,分离效果良好。基于此思想,文献[11]通过循环移位获得多路短时正交信号,降低了信号间的串扰。实际应用方面,文献[12]进行了机载同时同频MIMO SAR试飞试验,效果良好。MIMO SAR的波形设计与系统技术实现得到了快速发展,逐步向工程应用发展。
MIMO SAR实现的基础是使回波能够得到良好分离的发射波形,而目前研究较多的码分正交波形有良好的自相关和互相关性能,但不同天线的干扰能量被分散而不是消除。利用OFDM调制可以确保信号零互相关,但如何减轻多普勒偏移是一个难点。利用空时编码可以有效分离回波,但是在实现稳定的通道响应存在问题。在MIMO SAR中不同发射信号的回波在时域和频域相互叠加,只有将这些回波进行良好的分离,才能够获取独立低耦合的信号通道,这对分离回波的方法提出更高的要求。本文提出的MIMO SAR体制对于较近的散射体回波利用信号性质分离,对于较远的散射体回波利用DBF技术分离,后进行成像拼接,从而减缓了俯仰维成像带宽变小的缺陷,回波分离效果良好。
基于上述研究,本文开展基于多维波形编码技术的STSO波形设计,并与正负线调频信号、OFDM chirp信号进行对比分析。进一步给出了MIMO SAR信号处理流程,分析波形信号调制解调及处理过程,验证这3种信号在MIMO SAR系统中的性能,STSO点目标的性能与传统单通道SAR近似。首先,本文对3种信号数学模型模型及性能进行分析,开展MIMO SAR体制下的成像仿真,并通过峰值旁瓣比、积分旁瓣比和分辨率进行性能对比; 其次,采用两发多收的系统进行验证,基于多维波形编码理论,在俯仰维采取DBF技术分离不同距离的回波,在方位维采取多通道重构法将多个欠采样的回波数据重构,进而采用Chirp Scaling成像算法(简称CS算法)进行点目标成像,验证了STSO信号在MIMO SAR体制下的有效性和可靠性。
1 MIMO SAR信号数学模型 1.1 正负线调频信号模型及原理线调频信号是SAR系统最常用的波形,正负线调频信号具有良好的正交性,是现有雷达较常用的信号。假设子孔径1发射的信号为s1(t),子孔径2发射的信号为s2(t),则发射信号为
| $ s_{1}(t)=\operatorname{rect}\left(t / T_{\mathrm{p}}\right) \exp \left(\mathrm{j} {\rm{ \mathsf{ π} }} K_{\mathrm{r}} t^{2}\right) $ | (1) |
| $ s_{2}(t)=\operatorname{rect}\left(t / T_{\mathrm{p}}\right) \exp \left(-\mathrm{j} {\rm{ \mathsf{ π} }} K_{\mathrm{r}} t^{2}\right) $ | (2) |
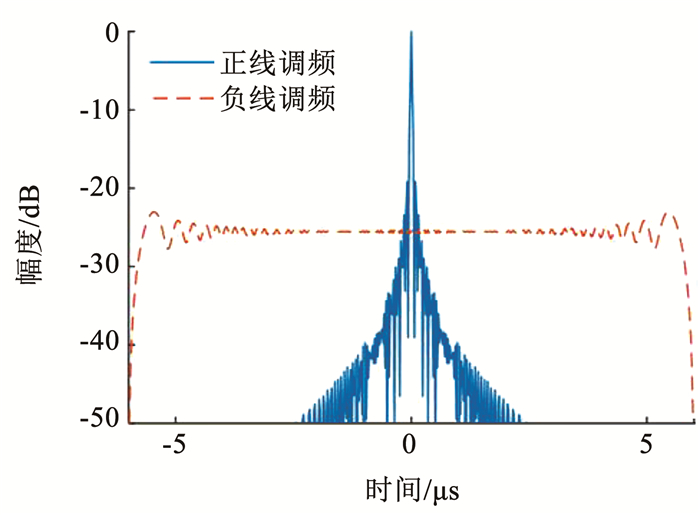
式中:Tp为脉冲宽度,Kr为调频率。回波信号经正线调频信号匹配滤波器处理,结果见图 1。
|
图 1 线调频信号匹配滤波结果 Fig. 1 Filtering results of linear frequency modulation signal matching |
线调频信号的自相关函数为
| $ A(t)=T_{\mathrm{p}} \operatorname{rect}\left(t / 2 T_{\mathrm{p}}\right) \operatorname{sinc}\left(K_{\mathrm{r}} T_{\mathrm{p}} t\right) $ | (3) |
正负线调频信号的互相关函数为
| $ C_{1, 2}(t)=\frac{1}{\sqrt{2\left|K_{\mathrm{r}}\right|}} \operatorname{rect}\left(t / 2 T_{\mathrm{p}}\right) \exp \left(-\mathrm{j} {\rm{ \mathsf{ π} }} K_{\mathrm{r}} t^{2} / 2\right) $ | (4) |
自相关计算与匹配滤波等价,见图 1。正负线调频信号本质问题为信号间不正交,两者相关实质是将互相关能量分散在成像区域中,降低成像质量,从而影响真实目标的判断。
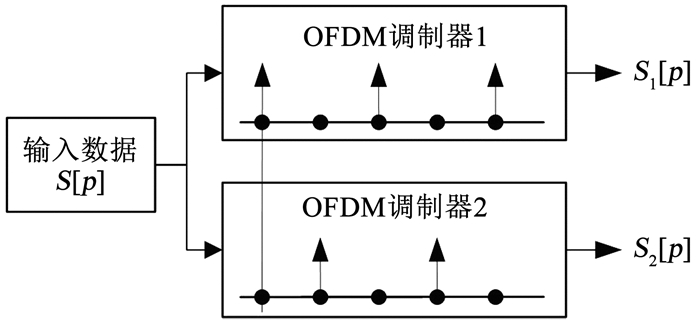
1.2 OFDM chirp信号模型及原理多通道OFDM chirp波形利用了频分复用技术,本节OFDM调制的方法使得各通道所占的频带重复,但是子载频间不重叠,调制框图见图 2。以两路正交波形产生为例,每路有N个子载频,由于接收信号是两路信号的叠加,共有2N个子载频,即需要使用2N点DFT进行OFDM的解调。假设S[p]为输入数据,由N个子载频分量构成,且相邻频率间隔为2Δf,Δf=1/NTs,Ts为采样间隔。在输入序列S[p]每个子载波之间插入一个零载波,得到S1[p],进行频移Δf得到S2[p]。在图 2中,使用箭头表示非零载波,使用实心圆点表示零载波。
|
图 2 两路正交波形产生框架图 Fig. 2 Frame diagram of two orthogonal waveforms |
频域chirp信号用于实现恒包络,S[p]为输入数据,是chirp信号N点FFT的结果。根据图 2,当输入数据为S[p]时,用2N点IFFT进行调制,经过数模转换,得到发射信号的时域形式为:
| $ \begin{gathered} s_{1}(t)=\operatorname{rect}\left(t / T_{\mathrm{p}}\right) \exp \left(\mathrm{j} {\rm{ \mathsf{ π} }} K_{\mathrm{r}} t^{2}\right)+ \\ \operatorname{rect}\left(\left(t-T_{\mathrm{p}}\right) / T_{\mathrm{p}}\right) \exp \left(\mathrm{j} {\rm{ \mathsf{ π} }} K_{\mathrm{r}}\left(t-T_{\mathrm{p}}\right)^{2}\right) \end{gathered} $ | (5) |
| $ s_{2}(t)=s_{1}(t) \exp (\mathrm{j} 2 {\rm{ \mathsf{ π} }} \Delta f t) $ | (6) |
由式(5)和式(6)可得波形1是由chirp信号与时移Tp后相加得到,波形2比波形1附加了线性相位。
由于OFDM调制的限制,解调与调制的长度需相等,即要求待解调信号的时延不能超过chirp信号的长度Tp,需要结合DBF技术将测绘带划分为多个子测绘带,保证该区域回波时延小于Tp,减少干扰。由于接收到的回波有时延,并不与调制的信号等长,需进行圆周循环移位[7]后才能进行成像处理。
1.3 STSO信号模型及原理MIMO SAR的波形设计需考虑相邻的散射点回波互相关能量的影响。若不同发射通道的信号是时移正交的,则互相关能量可消除,由此提出短时移正交波形[6],它要求不同发射通道的信号在成像区域对应的时间延迟范围内是正交的,见下式:
| $ \int h(\tau) s_{\mathrm{p}}(t) s_{\mathrm{q}}^{*}(t-\tau) \mathrm{d} t=0 $ | (7) |
式中: h(τ)是与成像区域相对应的窗函数,选择为h(τ)=rect(τ/T0),T0为一个波束主瓣内雷达回波时延的范围。
STSO设计使互相关能量在小时间偏移量情况下消失。而对于大时间偏移量,回波通过窄接收波束后被分离。短时移正交波形是由经过平移的线性调频信号组成,波形信号模型表达式如下:
| $ s_{1}(t)=\operatorname{rect}\left(t / T_{\mathrm{p}}\right) \exp \left(\mathrm{j} {\rm{ \mathsf{ π} }} K_{\mathrm{r}} t^{2}\right) $ | (8) |
| $ \begin{aligned} s_{2}(t)=& \operatorname{rect}\left(\frac{t+T_{\mathrm{p}} / 4}{T_{\mathrm{p}} / 2}\right) \exp \left(\mathrm{j} {\rm{ \mathsf{ π} }} K_{\mathrm{r}}\left(t+T_{\mathrm{p}} / 2\right)^{2}\right)+\\ & \operatorname{rect}\left(\frac{t-T_{\mathrm{p}} / 4}{T_{\mathrm{p}} / 2}\right) \exp \left(\mathrm{j} {\rm{ \mathsf{ π} }} K_{\mathrm{r}}\left(t-T_{\mathrm{p}} / 2\right)^{2}\right) \end{aligned} $ | (9) |
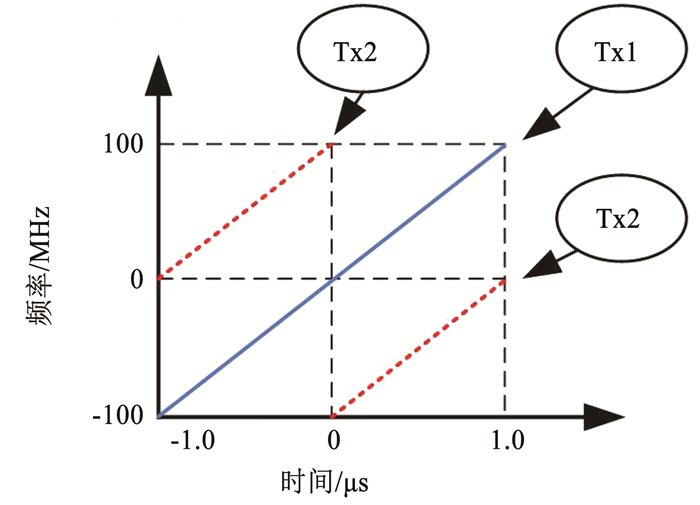
根据波形时频关系可知,如图 3所示,两个STSO波形的时域和频域占的区域相同,有利于降低雷达发射机系统设计中的复杂程度。STSO信号具体发射过程见图 4。
|
图 3 STSO时频关系 Fig. 3 Time-frequency diagram of STSO |
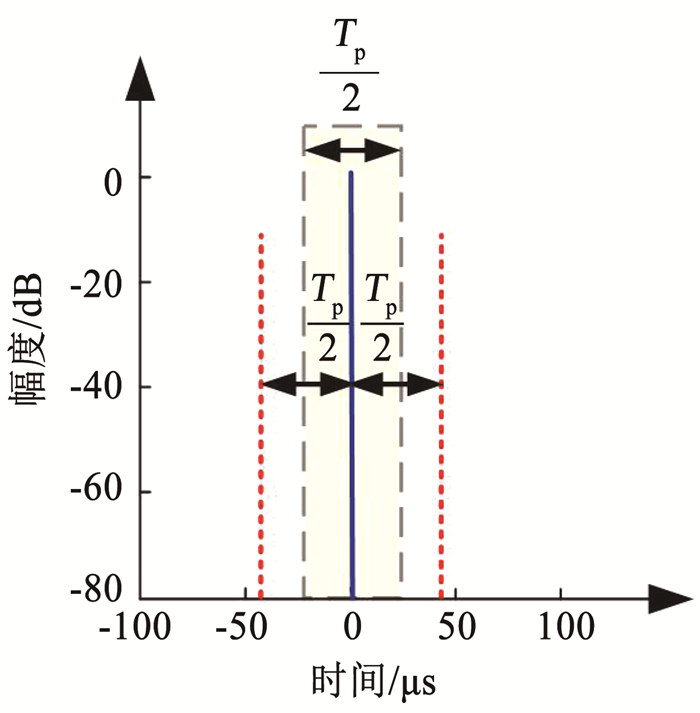
图 5是对STSO信号脉冲压缩后的结果,由图可知,两波形的脉压结果峰值相距Tp/2。即当STSO信号应用到MIMO SAR中时,对于场景中双程回波时延差超过Tp/2的两个目标回波,匹配滤波的结果将互相影响,成像出现模糊。但若回波时延差小于此值,经过匹配滤波后能量出现在不同区域。
|
图 5 STSO波形压缩结果 Fig. 5 Compression results of STSO waveform |
实际中,SAR的测绘带场景远大于对应的回波宽度,故处理时应用俯仰向DBF技术同时产生多个窄波束,将回波在角度域分离成多个子测绘带,使每个子测绘带对应的角度范围在Tp/2内[13],这样不会产生因回波之间的相互干扰而造成的模糊。
DBF加权可提取不同测绘带的回波,匹配滤波将波形1和波形2分离,主要以时间窗的形式对波形能量提取。波形1匹配滤波公式为
| $ \bar{r}_{1}(t)=F^{-1}\left\{F\{r(t)\} S_{\mathrm{MF}}(f)\right\} \cdot \operatorname{rect}\left(\frac{t-t_{\mathrm{m}}}{T_{\mathrm{m}}}\right) $ | (10) |
波形2需要在波形1基础上进行平移,即乘以exp(-jπfTp)+exp(jπfTp),将两个波形的峰值对齐,如下式
| $ \begin{aligned} \bar{r}_{2}(t)=& F^{-1}\left\{F \{ r ( t ) \} S _ { \mathrm { MF } } ( f ) \cdot \left(\exp \left(-\mathrm{j} {\rm{ \mathsf{ π} }} f T_{\mathrm{p}}\right)+\right.\right.\\ &\left.\left.\exp \left(\mathrm{j} {\rm{ \mathsf{ π} }} f T_{\mathrm{p}}\right)\right)\right\} \cdot \operatorname{rect}\left(\frac{t-t_{\mathrm{m}}}{T_{\mathrm{m}}}\right) \end{aligned} $ | (11) |
式中:F-1{ · }、F{ · }分别为傅里叶逆变换和傅里叶变换,SMF(f)为波形1匹配滤波器的频域形式,Tm为子测绘带需要提取的回波时延间隔,即Tp/2,tm为子测绘带中心的双程时延。
2 MIMO SAR模型构建与成像 2.1 MIMO SAR系统成像模型构建本文采取两发多收的形式,为了增加等效相位中心,在方位维两个通道发射信号3个通道接收,从而在不提高脉冲重复频率(pulse repetition frequency, PRF)的情况下增加方位维采样频率,保证高分宽幅成像。
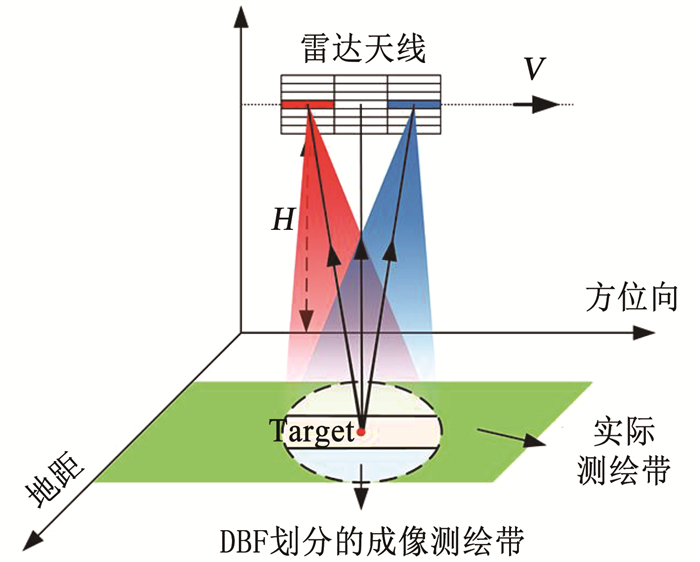
图 6为MIMO SAR两个通道发射信号时的系统几何模型。接收天线在距离维有Ne个子孔径,在方位维有Na个子孔径,发射天线为Tx1和Tx2,分别发射波形1和波形2,实际上为两发Ne·Na收。两个发射天线波束覆盖区域与接收波束覆盖区域相同,由于波形应用条件的限制,应用DBF技术划分成多个子测绘带进行成像。
|
图 6 MIMO SAR几何模型 Fig. 6 Geometric model of MIMO SAR |
如图 6所示,接收天线在距离维有Ne个子孔径,第n个子孔径接收到的回波信号为
| $ \begin{aligned} &r_{n}(t)=\int_{x_{\text {near }}}^{x_{\text {far }}} A \sigma\left[s_{1}\left(t-T_{\mathrm{m}}(x)\right)+s_{2}\left(t-T_{\mathrm{m}}(x)\right)\right]· \\ &\exp \left(-\mathrm{j} 2 {\rm{ \mathsf{ π} }} f_{\mathrm{c}} T_{\mathrm{m}}(x)\right) \cdot \exp \left(\frac{\mathrm{j} 2 {\rm{ \mathsf{ π} }} f_{\mathrm{c}} h_{n} \sin \left(\theta(x)-\theta_{\mathrm{c}}\right)}{c}\right) \mathrm{d} x \end{aligned} $ | (12) |
式中:A为距离维天线方向图,θ(x)为下视角,θc为场景中心的下视角,σ为目标的后向散射系数,x为目标到雷达的距离,Tm(x)为目标的双程回波的延迟,hn=(n-(Ne+1)/2)hr表示距离向第n个子孔径到中间子孔径的距离[13],hr为天线距离向子孔径的宽度,fc为载频。距离维所有孔径的回波可写成
| $ R=\left[r_{1}, r_{2}, \cdots, r_{N_{\mathrm{e}}}\right]^{\mathrm{T}} $ | (13) |
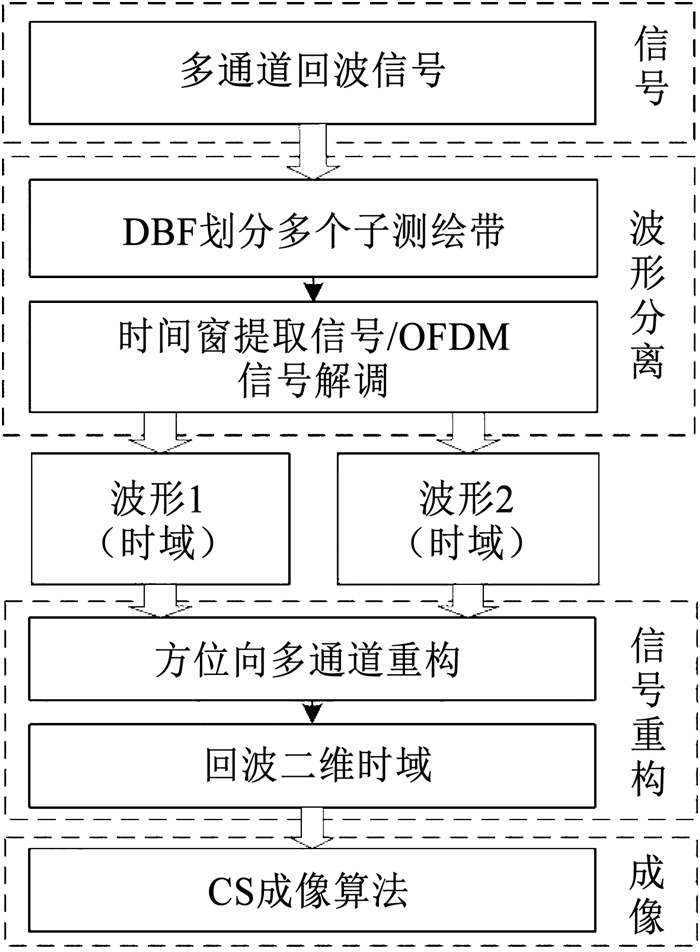
利用MIMO SAR发射信号进行成像流程见图 7,具体步骤如下:
|
图 7 MIMO SAR成像仿真流程图 Fig. 7 MIMO SAR imaging simulation process |
步骤1:获取MIMO SAR多孔径回波,记作R=[r1, r2, …, rNe]T。
步骤2:将距离向回波进行DBF处理。利用加权,得到单个子测绘带回波,即X=WHS。
步骤3:对回波进行分离处理。不同波形处理不同,对于LFM、STSO波形进行匹配滤波并使用时间窗截取,对于OFDM chirp波形进行解调。分别得到波形1和波形2的回波数据。
步骤4:产生重构滤波器组。对方位维不同相位中心的信号进行多通道重构处理,得到重构后的单波束信号。
步骤5:成像算法处理。使用CS算法对回波信号进行成像。
步骤6:对下一个子测绘带进行处理。改变DBF加权系数,加权窄波束的角度发生变化,从而子测绘带中心移动,回到步骤2,直至覆盖整个成像场景。
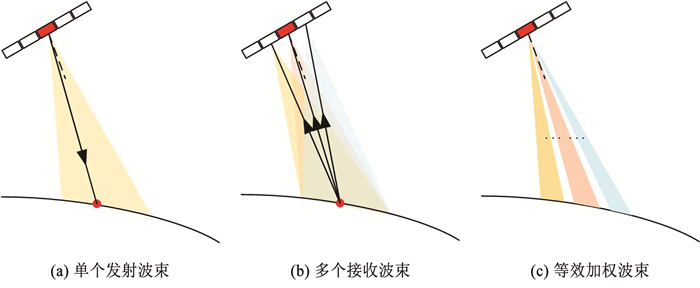
2.2 成像流程分析本文选取为非自适应DBF加权,采用“宽发窄收”模式,图 8(a)为发射波束,发射区域大,图 8(b)为接收波束,扫描区域大,图 8(c)通过DBF加权等效形成多个窄波束进行接收。
|
图 8 DBF等效过程 Fig. 8 Equivalent process of DBF |
DBF加权产生的多个窄波束在地面上形成了多个子测绘带,通过改变DBF系数来改变接收回波的主瓣宽度和角度,子测绘带中心位置和宽度也相应改变。该DBF处理过程是在接收回波后进行处理,优点在于可改变测绘带中心的位置,减少成像区域盲区。
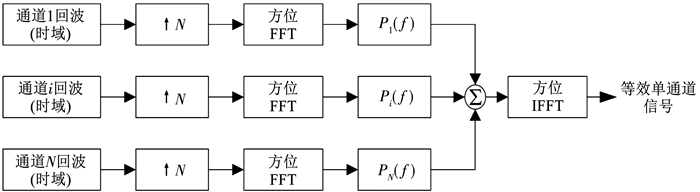
经过DBF加权后,对回波进行分离处理,利用匹配滤波和时间窗进行能量提取,将波形恢复到时域,根据等效相位中心的不同将回波按照顺序排列。此时,对于单个通道的信号,不满足采样定理,会出现方位模糊现象,故需要通过多通道重构法将周期非均匀采样信号恢复成均匀采样的信号,见图 9。在时域回波的基础上进行N维升采样,通过FFT到多普勒域,按照顺序与重构滤波器[14]相乘再相加,通过IFFT得到等效的单通道信号,进行成像处理。
|
图 9 多通道重构法仿真框图 Fig. 9 Block diagram of multichannel reconstruction algorithm |
根据多维波形编码理论在MIMO SAR体制下对正负线调频信号、OFDM chirp与STSO信号进行仿真,在俯仰维利用DBF技术实现“宽发窄收”,实现俯仰维多个子测绘带的划分,在方位维利用多通道重构算法将数据由周期性非均匀采样恢复成均匀采样,利用传统成像算法进行成像,最后将多个子测绘带成像进行拼接,并对不同的波形成像效果进行对比。本实验采取星载MIMO SAR系统来验证波形有效性,仿真参数见表 1[13]。
| 表 1 仿真参数 Tab. 1 Simulation parameters |
根据MIMO SAR几何模型,在方位维有2个发射通道,3个接收通道,故沿航迹向有5个等效相位中心。仿真时脉冲重复频率选取890 Hz,即方位维采样频率,而多普勒带宽为3 806 Hz,经过计算,该参数选取满足采样定理的要求。
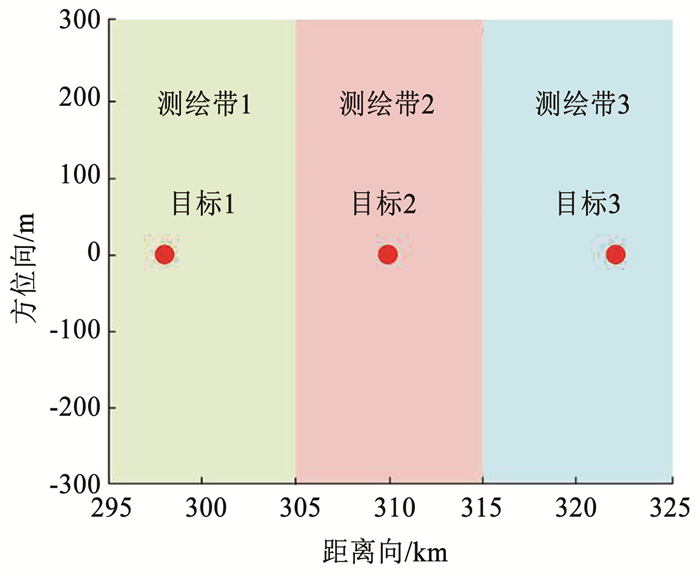
3.1 单个点目标仿真实验在测绘带中设置点目标,图 10为点目标分布示意,为了对比不同波形成像效果,在这里选取点目标2的参数进行对比。
|
图 10 点目标分布 Fig. 10 Distribution of point targets |
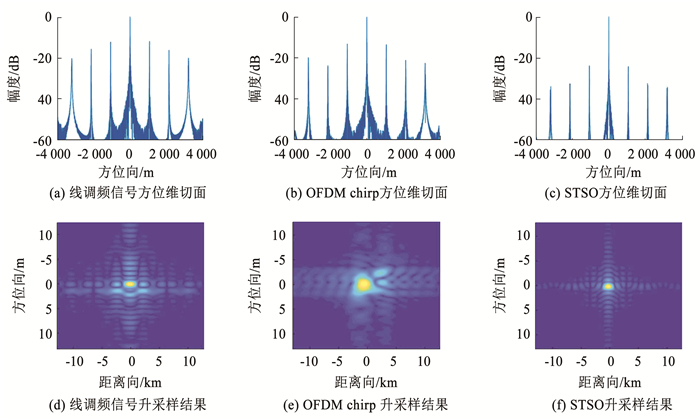
分别进行MIMO SAR利用正负线调频信号、OFDM chirp信号以及STSO信号的成像仿真,为了便于对比,获取点目标2的方位维剖面和升采样。图 11为不同发射波形下的目标2的仿真结果,包括方位维切面和升采样后的结果,图 11(a)、(d)对应正负线调频信号的结果,图 11(b)、(e)对应OFDM chirp信号的结果,图 11(c)、(f)对应STSO信号的结果。
|
图 11 点目标2仿真结果 Fig. 11 Simulation results of point target 2 |
对比不同发射波形下MIMO SAR的点目标方位维切面结果,真实目标的两侧会出现伪目标,此峰值大小会对沿航迹向真实目标的判断产生影响。伪目标的出现是因为模糊能量未被完全消除,虽然多通道重构法将回波恢复成均匀采样,但是经验证,此算法在非均匀性强的情况下,不能完全消除回波的模糊能量[15]。表 2为不同波形下点目标的成像指标。
| 表 2 点目标成像指标 Tab. 2 Imaging indexes of point target |
在相同仿真环境中,不同发射波形成像时的伪目标的幅度大小也是评判波形好坏的指标。对比不同发射波形下点目标的升采样结果,可得STSO信号下点目标的成像质量最好。对比不同信号的主瓣宽度,OFDM chirp信号的主瓣较宽,与点目标成像图分析结论相同。主瓣展宽是由于信号周期性非均匀采样引起的,正负线调频信号和STSO信号对主瓣展宽都有一定的抑制,OFDM chirp信号在抑制主瓣展宽方面性能较差。
如表 2,STSO与传统单通道SAR在距离向和方位向的ISLR和PSLR性能接近,这对于MIMO SAR的波形设计结果优异。SAR的测绘带宽最大为c/2PRF,MIMO SAR降低PRF,使测绘带宽扩展为原来的5倍,同时单个点目标性能优越。
与单通道SAR对比,MIMO SAR实现了高分宽幅成像和等相位中心的大幅度提升,与之伴随的是系统复杂度的提升和模糊能量对成像的影响。由图 7可得,OFDM chirp较之其他两种信号需增加调制与解调模块,一定程度增加系统复杂度。由于波形的性质会使测绘带宽降低,利用俯仰维的DBF技术可将不同子测绘带进行拼接,从而实现俯仰维大测绘带宽成像。除此之外,由于MIMO SAR等效相位中心增加,由欠采样信号恢复为均匀采样的信号时抑制模糊能量不彻底,会有主瓣展宽的现象,进而影响分辨率,需调整系统参数满足分辨要求。
就分辨率而言,3个发射波形在方位向和距离向均为1.6 m左右。综合对比距离向和方位向的峰值旁瓣比(PSLR)、积分旁瓣比(ISLR),可得STSO波形模糊能量抑制效果最好,聚焦效果良好。伪目标幅度对航迹向真实目标的辨别有一定的影响,在3种波形中,STSO作为发射信号时伪目标幅度最低,目标模糊能量被抑制得最彻底。
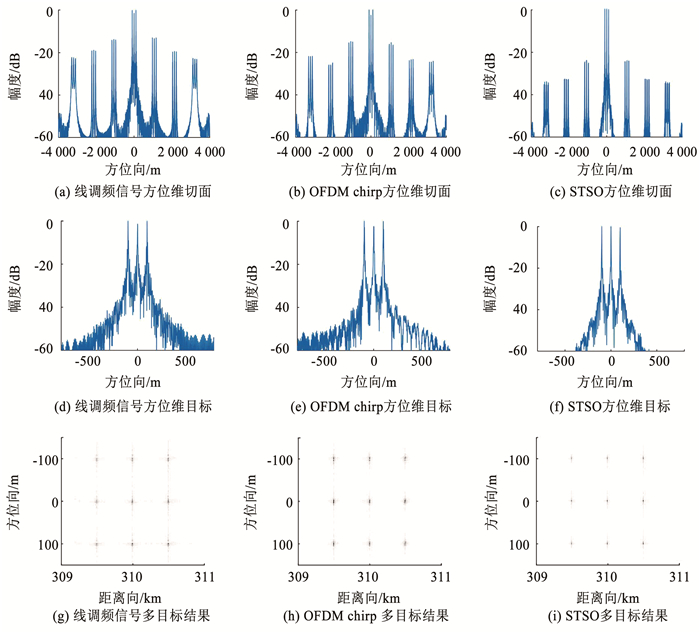
3.2 多点目标仿真实验本节在测绘带2中设置9个点目标,观察在MIMO SAR体制下应用不同波形时多点目标的成像结果及边缘点目标的成像效果。图 12为不同发射波形下的多点目标的仿真结果,包括方位维切面、方位维切面目标的主瓣细节以及成像结果,图 12(a)、(d)、(g)对应正负线调频信号的结果,图 12(b)、(e)、(h)对应OFDM chirp信号的结果,图 12(c)、(f)、(i)对应STSO信号的结果。
|
图 12 多目标仿真结果 Fig. 12 Simulation results of point targets |
对比波形的方位维切面,3个目标均清晰可见。STSO的伪目标幅度明显低于正负线调频信号和OFDM chirp信号,且STSO信号的旁瓣能量较之前者更低,与单个点目标实验结论相同。观察多点目标成像结果,可得chirp信号成像结果目标点有虚影,而OFDM chirp与STSO的成像中此现象并不明显,这是线调频信号的能量分散导致。STSO成像结果分辨率高,聚焦效果好。
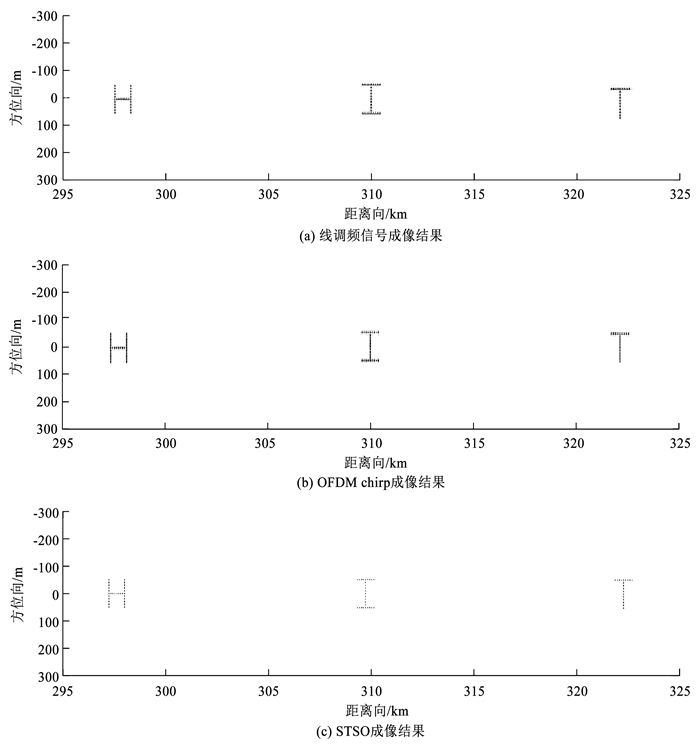
3.3 分布目标仿真实验在成像场景中设置3个字母“HIT”,分布在3个子测绘带中,利用3个波形进行成像仿真。图 13(a)是发射信号为正负线调频信号时成像结果,图 13(b)是发射信号为OFDM chirp时成像结果,图 13(c)是发射信号为STSO信号时成像结果。线调频信号成像场景中有模糊能量,影响分布目标的成像质量。OFDM chirp成像结果较STSO信号的结果聚焦效果略差,STSO信号的分辨率更好。
|
图 13 分布目标成像结果 Fig. 13 Multi-target imaging results |
针对多发多收SAR体制中多通道之间回波信号互相干扰等问题影响成像质量,本文提出一种多维波形编码设计,可以有效抑制通道间模糊。本文对比正负线调频信号、OFDM chirp与STSO信号的性能,通过俯仰维的DBF加权划分子测绘带,多通道重构技术恢复单通道回波,对点目标成像质量进行对比,验证了STSO信号具有明显的成像性能优势,进一步提出使用最大伪目标幅度的指标对波形进行评价,从PSLR、ISLR以及分辨率等方面对成像质量进行评价,STSO信号具有明显的优势。
| [1] |
庞礴, 邢世其, 代大海, 等. MIMO-SAR成像技术发展与展望[J]. 系统工程与电子技术, 2020, 42(6): 1248. PANG Bo, XING Shiqi, DAI Dahai, et al. Development and perspective of MIMO-SAR imaging technology[J]. Systems Engineering and Electronics, 2020, 42(6): 1248. DOI:10.3969/j.issn.1001-506X.2020.06.07 |
| [2] |
ZHANG Jiajia, ZHOU Fang, SUN Long, et al. MIMO-SAR solution based on azimuth phase coding waveforms and digital beamforming[C]//Proceedings of the 2016 CIE International Conference on Radar (RADAR). Guangzhou: IEEE, 2016: 1. DOI: 10.1109/RADAR.2016.8059308
|
| [3] |
邓云凯, 禹卫东, 张衡, 等. 未来星载SAR技术发展趋势[J]. 雷达学报, 2020, 9(1): 1. DENG Yunkai, YU Weidong, ZHANG Heng, et al. Forthcoming spaceborne SAR development[J]. Journal of Radars, 2020, 9(1): 1. DOI:10.12000/JR20008 |
| [4] |
MITTERMAYER J, MARTINEZ J M. Analysis of range ambiguity suppression in SAR by up and down chirp modulation for point and distributed targets[C]//Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium. Toulouse: IEEE, 2003: 4077. DOI: 10.1109/IGARSS.2003.1295367
|
| [5] |
KRIEGER G, GEBERT N, MOREIRA A. Multidimensional waveform encoding: a new digital beam-forming technique for synthetic aperture radar remote sensing[J]. IEEE Transactions on Geoscience & Remote Sensing, 2007, 46(1): 31. DOI:10.1109/TGRS.2007.905974 |
| [6] |
KRIEGER G. MIMO-SAR: opportunities and pitfalls[J]. IEEE Transactions on Geoscience & Remote Sensing, 2014, 52(5): 2628. DOI:10.1109/TGRS.2013.2263934 |
| [7] |
KIM J H, YOUNIS M, MOREIRA A, et al. A novel OFDM chirp waveform scheme for use of multiple transmitters in SAR[J]. IEEE Geoscience & Remote Sensing Letters, 2013, 10(3): 568. DOI:10.1109/LGRS.2012.2213577 |
| [8] |
WANG Jie, LIANG Xingdong, CHEN Longyong. MIMO SAR system using digital implemented OFDM waveforms[C]//Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium. Munich: IEEE, 2013: 7428. DOI: 10.1109/IGARSS.2012.6351944
|
| [9] |
CHENG Pu, WANG Zhan, XIN Qin, et al. Imaging of FMCW MIMO radar with interleaved OFDM waveform[C]//Proceedings of the 12th International Conference on Signal Processing. Hangzhou: IEEE, 2014: 1944. DOI: 10.1109/ICOSP.2014.7015332
|
| [10] |
WANG Wenqin. Mitigating range ambiguities in High-PRF SAR with OFDM waveform diversity[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(1): 101. DOI:10.1109/LGRS.2012.2193870 |
| [11] |
LIU Shangwen, ZHANG Zenghui, YU Wenxian. A space-time coding scheme with time and frequency comb-like chirp waveforms for MIMO-SAR[J]. IEEE Journal of Selected Topics in Signal Processing, 2017, 11(2): 391. DOI:10.1109/JSTSP.2016.2631945 |
| [12] |
王杰, 丁赤飚, 梁兴东. 机载同时同频MIMO-SAR系统研究概述[J]. 雷达学报, 2018, 7(2): 220. WANG Jie, DING Chibiao, LIANG Xingdong, et al. Research outline of airborne MIMO-SAR system with same time-frequency Coverage[J]. Journal of Radars, 2018, 7(2): 220. DOI:10.12000/JR17046 |
| [13] |
叶恺, 禹卫东, 王伟. 一种基于短偏移正交波形的MIMO SAR处理方案研究[J]. 雷达学报, 2017, 6(4): 376. YE Kai, YU Weidong, WANG Wei. Investigation on processing scheme for MIMO SAR with STSO chirp waveforms[J]. Journal of Radars, 2017, 6(4): 376. DOI:10.12000/JR17048 |
| [14] |
徐伟, 魏正彬, 黄平平, 等. 星载SAR斜视模式运动目标方位多通道信号重建方法[J]. 电子与信息学报, 2021, 43(8): 2276. XU Wei, WEI Zhengbin, HUANG Pingping, et al. Azimuth multichannel reconstruction for moving targets in spaceborne squinted multichannel synthetic aperture radar[J]. Journal of Electronics & Information Technology, 2021, 43(8): 2276. DOI:10.11999/JEIT200785 |
| [15] |
谭岳峰, 刘军鹰, 朱学勇, 等. 基于多通道重构的DPCA SAR方位向信号处理[J]. 信息与电子工程, 2012, 10(2): 201. TAN Yuefeng, LIU Junying, ZHU Xueyong, et al. Nonuniform azimuth signal processing of airborne DPCA SAR based on multichannel reconstruction[J]. Information and Electronic Engineering, 2012, 10(2): 201. |
 2022, Vol. 54
2022, Vol. 54