2. 中国科学院大学,北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
小行星作为太阳系形成之初遗留的原始物质,保存着太阳系形成与早期演化信息,对研究太阳系起源与早期演化、地球生命和水的来源等重大科学问题具有重要意义。对小行星的探索在一定程度上还能牵引深空探测技术的发展。
最早的小行星探测是由美国的Galileo木星探测器完成的,探测器借力飞行序列为金星-地球-地球,第一次地球借力后于1991年12月顺访了小行星Gaspre,在第二次地球借力后于1993年8月顺访了小行星Ida[1]。此后,美国的Dawn探测器是第一个探测小行星带的探测器,采用电推进和一次火星借力,分别于2012年2月、2015年9月抵达Vesta、Ceres进行探测[2];OSIRIS-Rex探测器采用深空机动和一次地球借力,于2018年11月抵达小行星Bennu,计划完成采样并返回[3]。日本Hayabusa探测器利用地球借力与小推力转移,于2005年9月13日飞抵Itokawa进行观测[4];Hayabusa 2探测器采用小推力与地球借力的方式实现轨道转移,完成了对小行星1999 JU3采样返回[5]。
对于深空探测,通过月球借力(lunar gravity assist,LGA)逃逸来转移,可以减小发射能量,提升送入深空的有效载荷质量[6]。月球借力最早可以追溯到美国宇航局的ISEE-3任务,1982年完成任务后飞行器利用月球借力从日地L1点转移至L2附近探测地球磁尾,并于1983年12月22日再次利用月球借力逃逸前往与彗星交会[7]。日本航天局1990年的Hiten任务中,飞行器完成10次月球借力[8];之后的Planet-A与Planet-B计划中,均利用月球引力,前者用于研究考虑太阳引力影响下月球借力的效果,后者两次月球借力后前往火星[9]。Gil-Fernandez等[10]以美欧探测器ExoMars为背景,研究了单次、二次、三次月球借力发射探测器的情况,并且增加脉冲辅助,发现ExoMars探测器在脉冲辅助的作用下,入轨质量比单次借力和两次借力分别提升150 kg和270 kg。Casalino等[11]以探测近地小行星为背景,研究了两次月球借力的情形。对于多次借力,一般有Backflip借力、Coplanar借力以及共振借力。Backflip借力指航天器在一次借力后转过180°的地心角,然后进行第二次借力。Coplanar借力指第一次借力后的轨道平面与月球轨道共面[11]。共振借力指一次借力后的轨道周期与借力天体轨道周期比为p∶q(p、q均为正整数)。He等[12]研究了小推力情况下多次月球共振借力的小行星采样返回轨道设计,推导了p∶q共振借力计算方法;杨洪伟等[13]解析推导了n∶1(n为正整数)共振借力轨道的充要条件。
本文考虑化学推进,采用圆锥曲线拼接法[14]。任务轨道分为两段,第一段为探测器从地球停泊轨道出发,经月球借力转移至地球影响球边界;第二段为日心段,从影响球边界至小行星。单次月球借力深空逃逸轨道设计方法有两种:正向法,设计顺序与航天器运行顺序相同[15], 缺点是由于优化变量较多,使用全局优化算法优化耗时长;反向法,首先求解最优日心转移轨道,然后根据飞行器在地球影响球边界处的状态求解地心段轨道[16], 缺点是依赖于日心段解,设计时没有考虑月球借力窗口约束,并不一定是全局最优,并且由于模型采取了较多假设,解的精度较差。
本文结合正向法精度高与反向法收敛速度快的优点,提出了混合优化方法。并以交会近地小行星为例开展数值仿真,验证了本文方法的有效性。
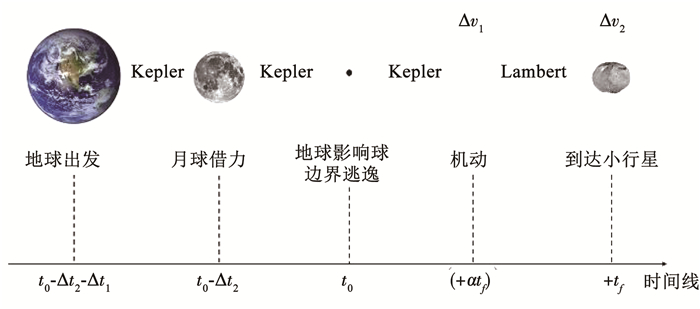
1 模型介绍 1.1 正向法模型正向法的月球借力转移轨道各时刻如下:t0时刻从地球停泊轨道出发;t0+Δt1到达月球附近,借力;t0+Δt1+Δt2时刻到达地球影响球边界,逃逸;t0+Δt1+Δt2+αtf时刻深空机动;t0+Δt1+Δt2+tf时刻到达小行星[17]。任务时序见图 1。

|
图 1 正向法月球借力逃逸转移示意 Fig. 1 Lunar gravity assist transfer trajectory in forward patched method |
飞行器以双曲线轨道逃逸,轨道方程为
| $ R=|a|(e \cosh F-1) $ | (1) |
式中:R为探测器到地心的距离,a为轨道半长轴,F为偏近点角。偏心率e为
| $e=\frac{R_{\mathrm{p}} V_{0}^{2}}{\mu_{\mathrm{E}}}-1 $ | (2) |
式中:Rp为逃逸时地心距;V0为逃逸速度。F与真近点角f的关系为
| $\tan \frac{f}{2}=\sqrt{\frac{e+1}{e-1}} \tanh \frac{F}{2} $ | (3) |
从近地点到偏近点角为F的位置用时为Δt1=(-F+esinh F)/n,式中
在计算中,取R为t0时刻地月距离,由式(1)~(3)可以求得F、f,进而求得近地点到月球的转移时间Δt。
借力时月球的赤经λm和赤纬Bm,需满足ω0=U-f,Ω0=λm-ΔΩ0, 见图 2。

|
图 2 航天器轨道根数与月球交会点关系 Fig. 2 Relationship between orbital elements and Moon intersection |
根据球面三角关系,便得到借力前的其余轨道根数。给出一组借力高度hm和角度参数ψm,即可求出借力后探测器的位置和速度,借力后至地球影响球边界的飞行时间为Δt2。再进行日心段的递推,采取先滑行、后机动的策略,转移总时间tf,滑行时长占转移时间的占比为α。求解以施加机动处为起点、到达时刻小行星位置为终点的Lambert问题,即可求出两处所需速度脉冲Δv1、Δv2。以上过程形成如下优化问题:
优化变量X=(t0, V0, hm, ψm, tf, α);目标函数J=Δv1+Δv2。
1.2 反向法模型反向法先利用Lambert转移优化日心段的深空转移轨道,用优化出的地球影响球边界处的
|
图 3 反向法月球借力逃逸转移示意 Fig. 3 Lunar gravity assist transfer trajectory in backward patched method |
日心段转移模型与正向法相同。优化变量X=(t0, v∞, A, δ, tf, α),v∞、A、δ分别为双曲超速的模长、赤经、赤纬。t0为飞行器在地球影响球边界处逃逸时刻,此时飞行器位置速度视作[rE, vE+v∞],rE、vE为地球的位置和速度。求解对应的Lambert问题,可得到机动处与到达小行星时所需速度脉冲Δv1、Δv2。目标函数J=Δv1+Δv2。
1) 月球至逃逸的轨道设计
为了求解这一段的轨道,定义新坐标系——月球轨道面坐标系,并且将各量无量纲化,详细过程参见文献[16]。
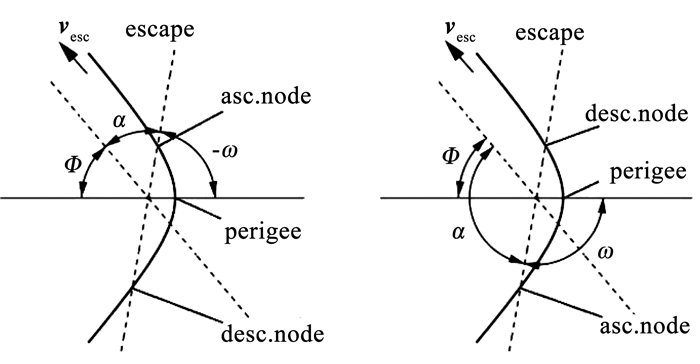
日心段优化后可得逃逸地球时的双曲超速v∞。将v∞坐标变换后到月球轨道面坐标系,记为vesc。对于正负vesc, z,逃逸和升交点赤经在同侧、异侧记作iz=±1,见图 4。
|
图 4 逃逸双曲超速地心示意 Fig. 4 Geometry of escape hyperbola |
轨道的半长轴由vesc的大小确定。指向升交点的单位矢量un=(cos Ω2, sin Ω2, 0),可求出vesc与un间的夹角α。
由图 4可得到如下的角度关系
| $ \left\{\begin{array}{l} \alpha+\varPhi-\omega_{2}={\rm{ \mathsf{ π} }}, \boldsymbol{v}_{\mathrm{esc}, \mathrm{z}} \geqslant 0 \\ \alpha-\varPhi+\omega_{2}={\rm{ \mathsf{ π} }}, \boldsymbol{v}_{\mathrm{esc}, \mathrm{z}} \leqslant 0 \end{array}\right. $ | (4) |
式中Φ=arccos(1/e2)。使用ia=±1分别标记在升交点处借力与降交点处,真近点角对应ν2=-ω2与ν2=-ω2+π。整理(4)式可得关于e2的方程
| $ i_{\mathrm{a}} i_{\mathrm{z}} \sin \alpha \sqrt{e_{2}^{2}-1}=i_{\mathrm{a}} \cos \alpha-\frac{a_{2}\left(e_{2}^{2}-1\right)}{r_{\mathrm{M}}}-1 $ | (5) |
这是关于
至此,给定初始猜测值Ω2,可依次得到轨道根数、转移时间Δt2、月球真实位置,根据位置可求出下一步迭代Ω2的初值。经过若干次迭代后,可快速收敛到真实的Ω2,得到月球至地球影响球边界的转移轨道。
2) 地月转移轨道设计
这段轨道的升交点赤经Ω1与前一段的升交点赤经Ω2关系为Ω1=Ω2或Ω1=Ω2+π。假设月球沿圆轨道运行,u, v, w分别是航天器与月球相遇时的径向、切向和法向速度,VM是月球的速度,则满足
| $V_{\infty-}^{2}=u^{2}+\left(v-V_{\mathrm{M}}\right)^{2}+w^{2}=V_{\infty+}^{2} $ | (6) |
式中u、v、w可以用下式表示:
| $ u=\frac{e_{1} \sin \nu_{1}}{\sqrt{r_{\mathrm{p}}\left(1+e_{1}\right)}} $ | (7) |
| $ v=\frac{\left(1+e_{1} \cos \nu_{1}\right) \cos i_{1}}{\sqrt{r_{\mathrm{p}}\left(1+e_{1}\right)}} $ | (8) |
| $ w=i_{\mathrm{a}} \frac{\left(1+e_{1} \cos \nu_{1}\right) \sin i_{1}}{\sqrt{r_{\mathrm{p}}\left(1+e_{1}\right)}} $ | (9) |
式中ν1是和月球相遇时转移轨道的真近点角, rp为逃逸时地心距, 整理方程(6)~(9)可得
| $ \left(V_{\infty+}^{2}-\frac{3}{r_{\mathrm{M}}}\right)+\frac{1-e_{1}}{r_{\mathrm{p}}}=-2 \sqrt{\frac{r_{\mathrm{p}}\left(1+e_{1}\right)}{r_{\mathrm{M}}^{3}}} \cos i_{1} $ | (10) |
式(10)为关于e1的一元二次方程,可直接解出e1。进而解出地月转移轨道根数,可求得借力前的速度矢量和相对月球的双曲超速。借力前后的双曲超速已知,便可求出转角,进而解出借力半径。为了尽量充分利用月球引力并保证飞越时飞行器的安全,本文设置最低借力高度为100 km。
2 混合法模型首先利用反向法计算效率高的特点,采用多目标优化算法,快速求解出N组分布在不同参数空间的参考轨道;然后将参考轨道参数代入反向法的优化模型,使用局部优化算法在参考轨道附近搜索;最后选取速度增量较小的M组解(M < N),代入正向法使用全局搜索进行优化,获得满足正向法精度要求的月球借力逃逸转移最优轨道解。程序流程见图 5。

|
图 5 混合法计算流程图 Fig. 5 Algorithm of hybrid method |
本文多目标优化算法采用NSGA-Ⅱ算法[18],该算法主要使用Pareto前沿(Pareto front)机制:对于一个决策变量,如果不存在其他决策变量可以支配它,则称该决策变量为非支配解。非支配解意味着无法在改进任何目标函数的同时不削弱至少一个其他的目标函数。所以每一个非支配解都是多目标优化问题的一个最优解,这些解在目标空间可视作在一个超曲面上,即Pareto前沿。并且算法中引入拥挤度的概念,使得到的解尽量均匀地分布在目标空间内。
通过多目标优化,可以得到分散的若干个解。这样可以为下一步序列二次优化提供较好的初值。
序列二次优化将非线性问题转化为一系列二次规划子问题来求解[19]。利用多目标优化得到的初值在初值附近优化,优化速度快,并可以确保优化出的解都达到各自的局部最优(即从图 6所示三角形代表的解优化至五角星解)。

|
图 6 模型差异示意 Fig. 6 Illustration of difference between two models |
最后将上一步中得到的解带入正向法模型。由于正向法的模型比反向法的更精确,两种模型下的解空间可能有所差异,见图 6。因局部优化受初值影响较大,全局搜索算法[20]会在反向法给出的初始解附近生成若干起始点,然后基于正向法模型进行局部优化(即从图 6中五角星代表的解优化至星号解)。在保证解满足正向法精度的同时,也提高了收敛到全局最优解的概率。
混合优化方法的好处是:充分利用多目标优化解的多样性、局部优化算法快速收敛性和全局搜索算法对初值的鲁棒性,可以加强解的稳定性,并提升计算速度。
3 仿真结果 3.1 算例1以探测1989 ML小行星为例,开展月球借力逃逸转移轨道优化设计。1989 ML的轨道根数见表 1。
| 表 1 1989 ML历元及轨道根数(日心黄道坐标系) Tab. 1 Epoch and orbital elements of 1989 ML (referenced in the heliocentric ecliptic coordinate frame) |
正向法设置发射窗口为2024~2027年,转移时间100~600 d;反向法设置发射窗口为2025年5月~ 2025年11月,转移时间200~600 d。
设置遗传算法种群数1 000,最大代数500。仿真计算机CPU为i7-7700,主频3.60 GHz,四核并行。正向法、反向法、混合法的仿真结果见表 2。
| 表 2 1989 ML各方法仿真结果 Tab. 2 Results of 1989 ML obtained by different methods |
从表 2可以看出:直接利用遗传算法开展正向法优化,解的稳定性较差,10次仿真只有2次收敛到最优解;并且单次优化用时688 s,效率在几种方法中最低。直接利用遗传算法开展反向法优化,虽然单次优化用时只有100 s,但从1.480 km·s-1的速度增量和其他量的值,可以看出并没有优化至最优解;并且10次优化只有3次收敛到该解,稳定性较差。混合法中,多目标优化两个优化目标分别是速度增量与发射C3;设置保留6组多目标优化个体(N=6)。反向法多目标优化时Pareto前沿见图 7,当前前沿包含的解对应的轨道速度增量分布在1.5~5.5 km·s-1,C3分布在0~4.5 km2·s-2,可见,通过多目标优化能够获得具备多样性的解。局部优化后选择速度增量小的前3组解(M=3),再使用全局搜索算法优化。仿真结果显示,混合法对局部优化后的3组解进行了有效优化,10次仿真中有8次收敛到最优解,混合优化法解的稳定性相比正向法提升4倍。单次优化用时相比正向法节省355 s,用时缩短50%以上。

|
图 7 1989 ML速度增量-C3 Pareto Fig. 7 1989 ML Pareto front of Δv and C3 |
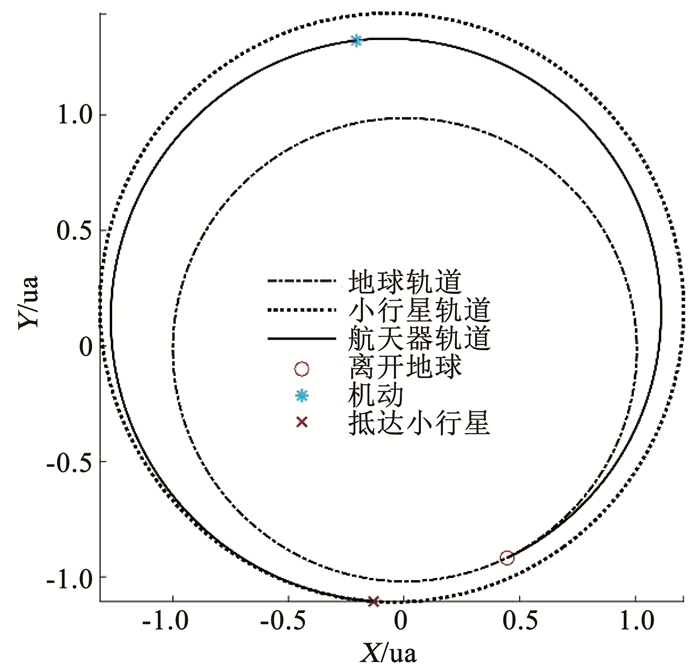
交会小行星1989 ML混合法优化结果对应的轨道见图 8、9。

|
图 8 1989 ML月球借力转移示意 Fig. 8 Illustration of LGA transfer to 1989 ML |
|
图 9 1989 ML日心转移轨道示意 Fig. 9 Illustration of heliocentric transfer to 1989 ML |
以探测2003 SM84小行星为例,开展月球借力逃逸转移轨道优化设计。2003 SM84的轨道根数见表 3。
| 表 3 2003 SM84历元及轨道根数(日心黄道坐标系) Tab. 3 Epoch and orbital elements of 2003 SM84 (referenced in the heliocentric ecliptic coordinate frame) |
正向法设置发射窗口为2027~2030年, 转移时间100~600 d; 反向法设置发射窗口为2027年5月~ 2027年11月,转移时间200~600 d。
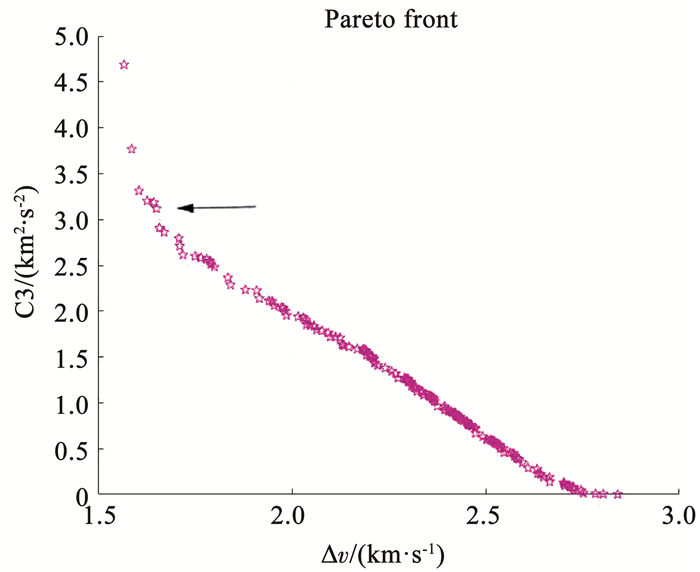
仿真结果见表 4。从表 4可以看出:利用遗传算法开展正向法优化,10次仿真只有2次收敛到最优解,解的稳定性较差;平均单次优化用时623 s,效率在几种方法中最低。利用遗传算法开展反向法优化,10次仿真有4次收敛到最优解,虽然单次优化用时少,但由于反向法的模型简单,得出的轨道并不是最优解。混合法中,多目标优化时Pareto前沿见图 10。当前前沿包含的解对应的轨道速度增量分布在1.5~3 km·s-1,C3分布在0~5 km2·s-2,可见,通过多目标优化获得了具备多样性的解。仿真结果显示,10次仿真中有6次能收敛到最优解,稳定性相比正向法提升3倍。单次优化用时相比正向法节省312 s,用时缩短约50%。有效地提升了解的稳定性和计算效率。
| 表 4 2003 SM84各方法仿真结果 Tab. 4 Results of 2003 SM84 obtained by different methods |
|
图 10 2003 SM84速度增量-C3 Pareto Fig. 10 2003 SM84 Pareto front of Δv and C3 |
交会小行星2003 SM84混合法优化结果对应的轨道见图 11、12。

|
图 11 2003 SM84月球借力转移示意 Fig. 11 Illustration of LGA transfer to 2003 SM84 |

|
图 12 2003 SM84日心转移轨道示意 Fig. 12 Illustration of heliocentric transfer to 2003 SM84 |
针对正向法全局优化效率低、收敛稳定性差、反向法模型精度不高的缺点,为进一步提升算法收敛稳定性和收敛速度,本文提出了结合两种方法优点的混合优化方法:以多目标优化反向法快速求解出的Pareto解集为初始参考轨道,局部优化后再利用正向法精确模型下在参考轨道附近开展全局搜索,获得最优转移轨道。最后以1989 ML和2003 SM84小行星为探测目标进行仿真,结果显示解的收敛稳定性相比正向法提升3倍以上,计算用时缩短50%以上。验证了该方法的有效性。
| [1] |
JOHNSON T V, YEATES C M, YOUNG R. Space science reviews volume on Galileo Mission overview[J]. Space Science Review, 1992, 60: 3. DOI:10.1007/BF00216848 |
| [2] |
RUSSELL C T, CAPACCIONI F, CORADINI A, et al. Dawn Mission to Vesta and Ceres[J]. Earth, Moon, and Planets, 2007, 101: 65. DOI:10.1007/s11038-007-9151-9 |
| [3] |
LAURETTA D S, BALRAM-KNUTSON S S, BESHORE E, et al. OSIRIS-REx: sample return from asteroid (101955) Bennu[J]. Space Science Review, 2017, 212: 925. DOI:10.1007/s11214-017-0405-1 |
| [4] |
KAWAGUCHI J. The Hayabusa mission—its seven years flight[C]//Proceedings of 2011 Symposium on VLSI Circuits-Digest of Technical Papers. Kyoto: IEEE, 2011: 2
|
| [5] |
WATANABE S I, TSUDA Y, YOSHIKAWA M, et al. Hayabusa2 mission overview[J]. Space Science Review, 2017, 208: 3. DOI:10.1007/s11214-017-0377-1 |
| [6] |
CAMPAGNOLA S, JEHN R, VAN DAMME C C, et al. Design of lunar gravity assist for the bepicolombo mission to mercury[J]. Advances in the Astronautical Sciences, 2005, 119: 427. |
| [7] |
FARQUHAR R, MUHONEN D, CHURCH L. Trajectories and orbital maneuvers for the ISEE-3/ICE comet mission[C]// Astrodynamics Conference. Seattle: AIAA, 1984. DOI: 10.2514/6.1984-1976
|
| [8] |
UESUGI K, MATSUO H, KAWAGUCHI J, et al. Japanese first double lunar swing-by mission "Hiten"[J]. Acta Astronautica, 1991, 25(7): 347. DOI:10.1016/0094-5765(91)90014-V |
| [9] |
KAWAGUCHI J, YAMAKAWA H, UESUGI T, et al. On making use of lunar and solar gravity assists in LUNAR-A, PLANET-B missions[J]. Acta Astronautica, 1995, 35(9/10/11): 633. DOI:10.1016/0094-5765(95)00013-p |
| [10] |
GIL-FERNÁNDEZ J, VAN DAMME C C, GRAZIANO M, et al. ExoMars alternative escape trajectories with Soyuz/Fregat[J]. Annals of the New York Academy of Sciences, 2005, 1065: 15. DOI:10.1196/annals.1370.011 |
| [11] |
CASALINO L, LANTOINE G. Design of lunar-gravity-assisted escape trajectories[J]. Journal of the Astronautical Sciences, 2020, 427: 21. DOI:10.1007/s40295-020-00229-w |
| [12] |
HE Shengmao, ZHU Zhengfan, PENG Chao, et al. Optimal design of near-Earth asteroid sample-return trajectories in the Sun-Earth-Moon system[J]. Acta Mechanica Sinica, 2016, 32(4): 753. DOI:10.1007/s10409-015-0527-1 |
| [13] |
杨洪伟, 陈杨, 宝音贺西, 等. 共振引力辅助轨道的设计方法及应用[C]//中国宇航学会深空探测技术专业委员会第九届学术年会论文集(上册). 北京: 中国宇航学会, 2012: 194 YANG Hongwei, CHEN Yang, BAOYIN Hexi, et al. Design method and application of resonant gravity assist orbit[C]// Proceedings of the 9th Annual Conference of Deep Space Exploration Technology Professional Committee of Chinese Astronautical Society (Volume 1). Beijing: Chinese Society of Astronautics, 2012: 194 |
| [14] |
BREAKWELL J V, PERKO L M. Matched asymptotic expansions, patched conics, and the computation of interplanetary trajectories[J]. Progress in Astronautics and Rocketry, 1966, 17: 159. DOI:10.1016/b978-1-4832-2729-0.50015-6 |
| [15] |
何巍, 茹家欣, 陈风雨. 月球借力发射火星探测器方法研究[J]. 中国科学: 技术科学, 2009, 39(3): 516. HE Wei, RU Jiaxin, CHEN Fengyu. Research on the method of launching mars probe by lunar gravity assist[J]. Science China Technical Science, 2009, 39(3): 516. |
| [16] |
CASALINO L, FILIZOLA. Design of high-energy escape trjactories with lunar gravity assist[C]//Proceedings of the 26th International Symposium on Space Flight Dynamics. Matsuyama: [s. n.], 2017
|
| [17] |
刘靖怡. 近地小行星取样返回任务转移轨道优化设计[D]. 北京: 中国科学院大学, 2020 LIU Jingyi. Transfer trajectory optimization of near-Earth asteroid sample return mission[D]. Beijing: University of Chinese Academy of Sciences, 2020 |
| [18] |
DEB K, AGRAWAL S, PRATAP A, et al. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-Ⅱ[C]//Proceedings of International Conference on Parallel Problem Solving from Nature. [S. l.]: Springer, 2000: 849. DOI: 10.1007/3-540-45356-3_83
|
| [19] |
刘红英, 夏勇, 周永生. 数学规划基础[M]. 北京: 北京航空航天大学出版, 2012. LIU Hongying, XIA Yong, ZHOU Yongsheng. Fundamentals of mathematical programming[M]. Beijing: Beihang University Press, 2012. |
| [20] |
UGRAY Z, LASDON L, PLUMMER J, et al. Scatter search and local NLP solvers: a multistart framework for global optimization[J]. INFORMS Journal on Computing, 2007, 19(3): 328. DOI:10.1287/ijoc.1060.0175 |
 2022, Vol. 54
2022, Vol. 54


