2. 东南大学 土木工程学院,南京 211189;
3. 长安大学 建筑工程学院,西安 710061;
4. 西安建筑科技大学 土木工程学院,西安 710055
2. School of Civil Engineering, Southeast University, Nanjing 211189, China;
3. School of Civil Engineering, Chang'an University, Xi'an 710061, China;
4. School of Civil Engineering, Xi'an University of Architecture and Technology, Xi'an 710055, China
高强混凝土(high-strength concrete,HSC)具有较高的抗压强度、良好的混凝土工作性能以及长期性能和耐久性,其抗压强度值大于60 MPa[1]。由于其在力学性能和长期工作性能等方面所呈现的显著优势,使得HSC在建筑结构中得到广泛应用,在结构中使用HSC可以提高建筑材料的利用率,有效减少材料用量和降低构件截面尺寸[2-3]。
钢筋混凝土(reinforced concrete,RC)梁受剪破坏的影响因素众多,传力机理复杂,特别是在混凝土出现裂缝后,裂缝在主拉应力影响下逐渐沿着斜向发展,使得钢筋与混凝土之间的相互作用以及裂缝发展情况愈加复杂。通过理论分析和试验研究等方法,研究学者对剪切破坏问题进行不断深入的研究,但问题迄今为止尚未得到合理解决[4-5]。现阶段的RC梁抗剪设计计算方法可以分为两种:通过分析梁构件斜截面受剪力学特性所建立的“受剪理论模型”和对大量剪切试验结果的非线性回归拟合分析所建立的经验计算公式,研究学者先后提出了各种受剪理论模型,如修正压力场理论、压力路径理论、塑性理论、劈裂破坏理论等,但不同学者对受剪分析模型中的骨料咬合力及纵筋销栓作用的抗剪贡献的认识存在较大偏差[6]。而通过对试验结果的非线性回归拟合分析所建立的经验计算公式,虽然形式简单、计算方便,但缺乏相应的理论模型,而且问题本身的随机特征也在一定程度上掩盖了剪切破坏的物理属性[7]。上述两种适用于普通强度混凝土(normal-strength concrete,NSC)构件的受剪承载力计算方法,对于HSC的适用性需要进一步深入探究。
鉴于HSC构件剪切破坏机理的复杂性和剪切破坏模式的多样性以及高强材料所特有的力学性能,特别是伴随混凝土强度增加所出现的更为显著的脆性特征,目前国内外学者对HSC构件剪切计算理论尚未形成明确统一的认识,各国规范仍沿用普通强度钢筋混凝土构件剪切设计原理,通过引入较普通强度钢筋混凝土构件更高的可靠指标或设定材料的上限强度值来对高强混凝土构件进行受剪设计计算,这对于强度等级更高的混凝土材料以及采用高强混凝土和高强钢筋的双高强材料混凝土梁存在一定的局限性[8-9]。
为此,本文基于梁作用和拱作用来考虑高强混凝土对梁构件受剪承载力的贡献,而箍筋项则采用简化修正压力场理论(modified compression field theory, MCFT)进行计算,同时考虑尺寸效应影响,建立了集中荷载作用下高强混凝土梁受剪承载力计算模型。
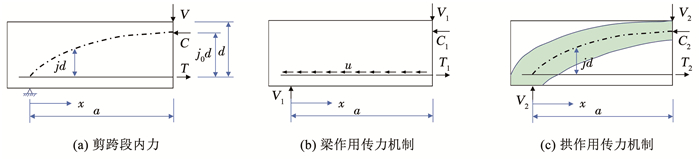
1 HSC受弯构件斜截面受剪计算 1.1 剪力传递途径分析图 1(a)为RC简支梁剪跨段内力图,图 1(b)~(c)为集中荷载作用下RC梁构件剪力在剪跨段内的梁作用和拱作用传力机制,混凝土梁构件的抗剪可分为以下两种形式:
|
图 1 剪力传递的“梁作用”和“拱作用” Fig. 1 "Beam action" and "arch action" in shear transfer |
1) 梁作用,即作用于恒定内力臂j0d(混凝土纵向压应力的合力作用点至受拉钢筋重心的距离)上的纵向钢筋拉力T的变化来平衡外弯矩;2)拱作用,即在拉力T保持不变的情况下,通过剪跨段内各截面内力臂jd的改变来平衡外弯矩作用。而RC梁受剪承载力采用梁作用和拱作用的两项贡献相叠加形式来考虑。
1.2 受剪承载力计算图 1中,离支座任意位置处的弯矩M可表示为
| $ M=T \cdot j d $ | (1) |
式中:T=T(x)为纵向钢筋的拉力;jd=jd(x)为内力臂长。
同时,距离支座点x位置处的弯矩M与剪力V满足如下关系
| $ M=V x $ | (2) |
联立式(1)和式(2),并对x取微分,可得梁剪跨段内距支座点x位置截面上的剪力V
| $ V=\frac{{\mathrm{d}} M}{{\mathrm{d}} x}=j_{0} d \frac{{\mathrm{d}} T}{{\mathrm{d}} x}+T \frac{{\mathrm{d}}(j d)}{{\mathrm{d}} x} $ | (3) |
根据式(3),两项分别为梁作用和拱作用的贡献,将梁作用和拱作用贡献项分别定义为V1和V2,则有
| $ V=V_{1}+V_{2} $ | (4) |
梁作用主要依靠钢筋与混凝土之间的黏结作用来传递应力,见图 1(b)。混凝土较低的抗拉强度导致其较早地发生开裂,由于混凝土的开裂以及开裂后出现的黏结滑移现象,梁作用所需的全部黏结力无法完全达到,此时分量V2通过内部倾斜压应力来提供所需的剪切分量,即拱作用参与传力,见图 1(c)。在混凝土梁构件中,上述两种机制复合受力,协同工作提供受剪承载力,见式(4)。
首先考虑梁作用的贡献V1
| $ V_{1}=j_{0} d \frac{{\mathrm{d}} T(x)}{{\mathrm{d}} x} $ | (5) |
文献[10]研究指出,在梁剪跨段实际内力臂jd沿跨度方向逐渐递减,即jd沿梁跨方向呈现出指数形式的变化趋势,基于此现象,通过合理简化提出了内力臂系数j的计算表达式[10]如下:
| $ j=\left(\frac{x}{a}\right)^{r} j_{0} $ | (6) |
| $ r=\left(\frac{d}{a}\right)^{0.6} \rho^{-0.1} \leqslant 1 $ | (7) |
式中x为受力点与支座之间的距离。
研究表明[11],在适筋梁的受拉区出现弯曲裂缝后,初始弯曲裂缝将快速延伸至受压区下缘,此时,梁构件上部范围内会形成一定高度的剪压区,裂缝的分布区域也随着外荷载的增加而逐渐变广,但受压区的高度变化趋于稳定。文献[12]忽略混凝土拉应力,采用线性弯曲理论并基于应变平截面假定提出了j0与受压区高度系数c/d之间的解析关系式:
| $ j_{0}=1-\frac{1}{3} \frac{c}{d} $ | (8) |
| $ \frac{c}{d}=\sqrt{n^{2} \rho^{2}+2 n \rho}-n \rho $ | (9) |
式中: n为纵筋弹性模量与混凝土弹性模量的比值,n=Es/Ec;ρ为纵筋配筋率。
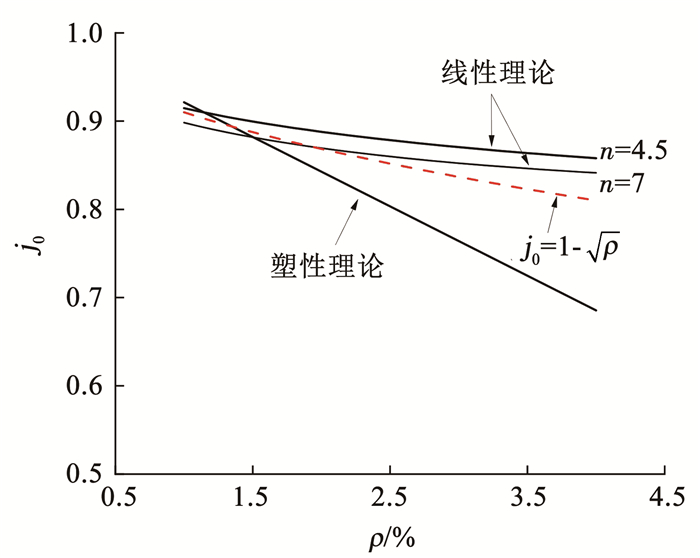
同时,j0也可以通过塑性理论进行求解,两种方法在配筋率ρ较大时j0结果差异较大,见图 2,塑性理论对剪跨段较长的梁能给出了较为准确的j0值,而对于短梁,线性理论将提供更准确的结果,因为出现剪切斜裂缝时的荷载值远小于构件的受弯承载力。而j0的准确值位于塑性理论和线性理论计算结果之间,为此,本文针对HSC提出j0的简化形式计算式。
| $ j_{0}=1-\sqrt{\rho} $ | (10) |
|
图 2 j0随配筋率变化关系 Fig. 2 Relationship between j0 and ratio of longitudinal reinforcement |
式(5)中,梁作用贡献项V1与dT/dx非线性相关,通过引入钢筋与混凝土之间黏结应力τbond来计算dT/dx[13]。
| $ \frac{{\mathrm{d}} T}{{\mathrm{d}} x}=\pi \sum\limits_{i=1}^{n} \tau_{{\mathrm{bond}} i} D_{i} $ | (11) |
式中Di为梁构件横截面上第i根纵筋直径。将式(10)、式(11)代入式(5),可得
| $ V_{1}=(1-\sqrt{\rho}) d \frac{{\mathrm{d}} T}{{\mathrm{~d}} x}=(1-\sqrt{\rho}) d \pi \sum\limits_{i=1}^{n} \tau_{{\mathrm{bond}} i} D_{i} $ | (12) |
则梁作用贡献项应力v1为
| $ v_{1}=\frac{V_{1}}{b d}=\frac{(1-\sqrt{\rho}) \pi \sum\limits_{i=1}^{n} \tau_{{\mathrm{bond }} i} D_{i}}{b} $ | (13) |
钢筋与混凝土之间的咬合作用与混凝土抗拉强度ft密切相关,抗拉强度ft越高,则在混凝土材料内的钢筋与混凝土界面之间的咬合作用所产生的黏结应力越大。文献[14]考虑HSC材料较低的拉压比以及特有的脆性特征,假定HSC梁发生破坏后黏结应力不再变化,建议纵筋与HSC之间的黏结应力τbond取为
| $ \tau_{{\mathrm{bond}} i}=0.25 \sqrt{f_{{\mathrm{c}}}^{\prime}} $ | (14) |
式中f′c为混凝土圆柱体抗压强度。
引入纵筋的等效直径Deq
| $ D_{{\mathrm{eq}}}=\sum D_{i} $ | (15) |
则有
| $ D_{{\mathrm{eq}}}=2 \sqrt{\frac{b d \rho}{\pi}} $ | (16) |
式中:b为截面宽度;d为截面有效高度。
联立式(13)、式(14)、式(16),可得
| $ v_{1}=0.44(\sqrt{\rho}-\rho) \sqrt{\frac{d}{b}} \sqrt{f_{c}^{\prime}} $ | (17) |
作用于梁构件的部分剪应力可以直接通过拱作用传递到支座处,对于拱作用贡献项V2的计算取值
| $ V_{2}=T d \frac{{\mathrm{d}} j}{{\mathrm{~d}} x} $ | (18) |
根据文献[10]给出的j与x计算关系式(6),式(6)对x取微分,则有
| $ \frac{{\mathrm{d}} j(x)}{{\mathrm{d}} x}=j_{0} \frac{r}{a}\left(\frac{x}{a}\right)^{r-1} $ | (19) |
剪跨段内力臂jd的计算在斜截面受剪破坏内力分析中,起着至关重要的作用,其直接同内力分布及传递相关。根据文献[15]的研究成果,将j与x两者简化考虑为线性关系,即r取1,则式(19)改写为
| $ \frac{{\mathrm{d}} j(x)}{{\mathrm{d}} x}=\frac{j_{0}}{a} $ | (20) |
而HSC梁中纵筋内力Ts满足
| $ T_{{\mathrm{s}}}=\sigma_{{\mathrm{s}}} \rho b d $ | (21) |
式中σs为纵筋应力。
联立式(18)、式(20)、式(21),则HSC梁中拱作用贡献项应力v2满足
| $ v_{2}=\frac{V_{2}}{b d}=\frac{j_{0}}{b d} \frac{d}{a} \sigma_{{\mathrm{s}}} \rho b d $ | (22) |
考虑剪切裂缝间距内的内力平衡关系,钢筋应力σs与黏结应力τbond之间满足如下关系:
| $ \pi S_{{\mathrm{rm}}} \sum \tau_{{\mathrm{bond }} i} D_{i}=\frac{\pi}{4} \sigma_{{\mathrm{s}}} \sum D_{i}^{2} $ | (23) |
式中Srm为裂缝间距,则纵筋应力σs为
| $ \sigma_{{\mathrm{s}}}=\frac{4 S_{{\mathrm{rm}}} \tau_{{\mathrm{bond}} i}}{\sum D_{i}} $ | (24) |
裂缝间距Srm的计算参考规范EN 1992-1-1:2004[16]中的计算公式为
| $ S_{{\mathrm{rm}}}=50+0.1 \frac{D}{\rho_{{\mathrm{eff}}}} $ | (25) |
| $ \rho_{{\mathrm{eff }}}=\frac{\pi \sum D_{i}^{2}}{4} \frac{1}{b\left(h-x_{{\mathrm{c}}}\right)} $ | (26) |
式中xc为混凝土中性轴高度。
联立式(15)、式(16)及式(22),代入式(24),得到应力v2
| $ v_{2}=\frac{3.54(\sqrt{\rho}-\rho) S_{{\mathrm{rm}}} \tau_{{\mathrm{bond}} i}}{\sqrt{b d}} \frac{d}{a} $ | (27) |
将式(14)代入式(27),可得
| $ v_{2}=\frac{0.89(\sqrt{\rho}-\rho) S_{{\mathrm{rm}}}}{\sqrt{b d}} \frac{d}{a} \sqrt{f_{{\mathrm{c}}}^{\prime}} $ | (28) |
大量试验结果揭示RC梁的抗剪强度具有显著的尺寸效应,同时HSC梁受高强混凝土材料本身脆性特性的影响更加需要合理准确地考虑尺寸效应引起的强度折减。文献[17]进行了梁高h范围为170~1 000 mm的无腹筋HSC梁剪切破坏试验,其中剪跨比a/d=1.5~6.0,纵筋配筋率ρ=1.0%~4.7%,试验表明HSC梁抗剪强度尺寸效应规律与NSC类似,且尺寸效应影响规律不随配筋率发生变化。GB 50010—2010《混凝土结构设计规范》引入截面高度修正系数βh以考虑尺寸效应,但试验结果表明该系数不能合理反映尺寸效应的影响,而尺寸效应在ACI 318规范数次修订中均未纳入考虑,因此本文考虑尺寸效应对抗剪强度的影响。
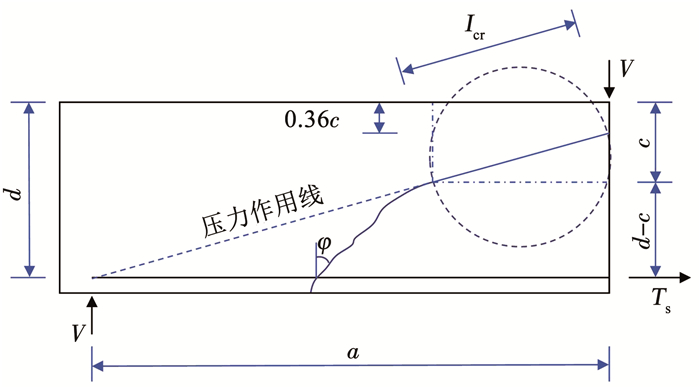
文献[11]假定RC梁在发生斜拉剪切破坏极限状态下的临界斜裂缝可细分为两段分支:第一分支为剪切斜裂缝,在靠近支座附近的弯曲裂缝端点或弯曲裂缝之间的区域内形成,裂缝高度与弯曲裂缝相一致,走向近乎直线;第二分支裂缝由第一分支顶点沿着压力作用线穿过构件受压区向加载点延伸发展,见图 3,混凝土沿第二分支发生劈裂破坏最终导致梁构件剪切破坏的发生。同时他们认为梁构件的受剪尺寸效应本质上源于混凝土圆柱体所发生的劈裂破坏,并给出了劈裂直径D的近似取值(D=0.16a),即图 3中Icr长度,引用文献[18]通过试验提出的试件名义强度σn与直径D的关系σn=(1.20-1.30D)ft,则使用该修正系数即(1.20-0.20a)来考虑尺寸效应影响。
则HSC梁抗剪强度vc为梁作用和拱作用抗剪贡献相叠加,并考虑尺寸效应,可得
| $ \begin{array}{c} v_{{\mathrm{c}}}=(1.20-0.20 a)\left(0.44+0.89 \frac{S_{{\mathrm{rm}}}}{a}\right)(\sqrt{\rho}-\rho) \\ \sqrt{\frac{d}{b}} \sqrt{f_{{\mathrm{c}}}^{\prime}} \end{array} $ | (29) |
参考桁架模型,混凝土斜压杆发生压碎破坏时,斜压杆轴力极限值为[19]
| $ N_{{\mathrm{u}}}=v f_{{\mathrm{c}}}^{\prime} b c \cos \theta $ | (30) |
式中: υ为开裂混凝土抗压强度软化系数,这里考虑高强混凝土脆性的影响,按照文献[20]方法进行计算;θ为斜压杆倾角(其中θ≤45°)。
| $ v=0.6\left(\frac{30}{f_{{\mathrm{c}}}^{\prime}}\right)^{0.33} $ | (31) |
根据支座处平衡关系
| $ V_{{\mathrm{u}}}=N_{{\mathrm{u}}} \sin \theta $ | (32) |
由平截面受弯分析[21]可知
| $ \frac{c}{d}=\rho \frac{1}{\alpha \beta} \frac{f_{{\mathrm{y}}}}{f_{{\mathrm{c}}}^{\prime}} $ | (33) |
式中α、β为混凝土等效矩形应力图系数。
为保证混凝土梁构件安全不发生破坏,依据平截面假定和应变协调条件,式(33)应满足下列关系
| $ \frac{c}{d} \leqslant \frac{c_{\max }}{d}=\frac{\varepsilon_{{\mathrm{u}}}}{\varepsilon_{{\mathrm{y}}}+\varepsilon_{{\mathrm{u}}}} $ | (34) |
参照文献[22]定义的相对剪压区高度ζ=ρwfy/f′c,联立式(33)和式(34),可得
| $ \zeta=\rho \frac{f_{{\mathrm{y}}}}{f_{{\mathrm{c}}}^{\prime}} \leqslant \alpha \beta \frac{\varepsilon_{{\mathrm{u}}}}{\varepsilon_{{\mathrm{y}}}+\varepsilon_{{\mathrm{u}}}} $ | (35) |
式中εu、εy分别为混凝土压应变和纵向受拉钢筋屈服应变。
因此,当斜压杆混凝土被压碎时,HSC梁构件抗剪强度为
| $ v_{{\mathrm{uc}}}=0.3\left(\frac{30}{f_{{\mathrm{c}}}^{\prime}}\right)^{0.33} \rho \frac{f_{{\mathrm{y}}}}{\alpha \beta} \sin 2 \theta $ | (36) |
则集中荷载作用下混凝土对HSC梁的抗剪强度贡献取式(29)和式(36)两者中的较小值。
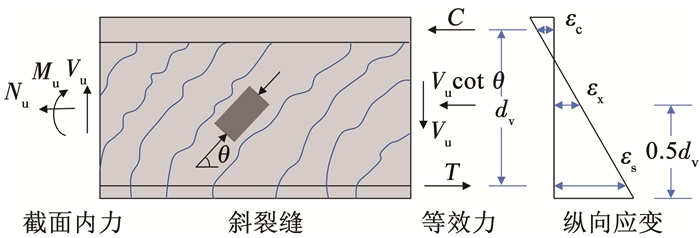
在梁构件中配置箍筋能有效限制斜裂缝的发展,并改善混凝土的传力,两者在极限状态下相互影响并协同工作。为了便于研究,有腹筋HSC梁受剪承载力考虑为在无腹筋HSC梁受剪承载力Vc的基础上叠加箍筋剪切贡献Vs,本文采用文献[23]提出的修正压力场理论(MCFT)简化公式来计算HSC梁中箍筋的剪切分量vs,图 4为简化修正压力场理论模型。
| $ v_{{\mathrm{s}}}=\frac{1}{b d} \frac{A_{{\mathrm{st}}} f_{{\mathrm{yw}}}}{s} d_{{\mathrm{v}}} \cot \theta=\frac{d_{{\mathrm{v}}}}{d} \rho_{{\mathrm{sw}}} f_{{\mathrm{yw}}} \cot \theta $ | (37) |
式中:Ast为同一截面内所配置的各肢箍筋总截面积;fyw为箍筋屈服强度;s为箍筋间距;ρsw为箍筋配筋率。
文献[24]研究指出当ρswfyw>0.06(f′c)0.5时,钢筋混凝土梁构件裂缝间距Srm可得到有效控制,依据文献[24]的研究成果,箍筋配置应满足:
| $ \rho_{{\mathrm{sw}}} f_{{\mathrm{yw}}}>0.06 \sqrt{f_{{\mathrm{c}}}^{\prime}} $ | (38) |
| $ \theta=29^{\circ}+7\;000 \varepsilon_{{\mathrm{x}}} $ | (39) |
| $ \varepsilon_{{\mathrm{x}}}=\frac{\left|M_{{\mathrm{u}}} / d_{{\mathrm{v}}}\right|+\left|V_{{\mathrm{u}}}\right|}{2 E_{{\mathrm{s}}} A_{{\mathrm{s}}}} $ | (40) |
| $ d_{{\mathrm{v}}}=\max \{0.9 d, 0.72 h\} $ | (41) |
式中:εx为梁截面一半高度处的纵向应变值;Mu、Vu分别为计算截面上的弯矩值和剪力值;dv为有效剪切高度;Es为纵向受力钢筋的弹性模量,取Es=2.0×105 MPa。
则集中荷载作用下HSC梁构件抗剪强度vu为
| $ v_{{\mathrm{u}}}=v_{{\mathrm{c}}}+v_{{\mathrm{s}}} $ | (42) |
选取中国规范GB 50010—2010[25]、美国规范ACI 318-19[26]、欧洲规范EN 1992-1-1:2004[16]、Zararis公式[27]和Zsutty公式[28]对比分析不同受剪计算模型在预测HSC梁构件受剪承载力时的预测精度,上述受剪计算模型概述见表 1。
| 表 1 钢筋混凝土梁受剪承载力计算模型 Tab. 1 Calculation models for shear capacity of reinforced concrete beams |
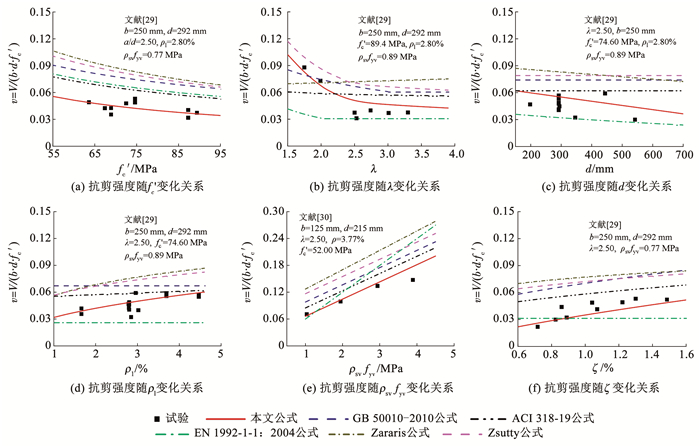
由于剪切破坏影响因素较多,各影响因素相互关联、相互作用,因此将各影响因素剥离出来分别反映各因素对梁构件的抗剪强度影响。为了评估上述计算模型中设计参数的合理性,选取文献[29]、文献[30]的试验结果比较上述模型中受剪参数对抗剪强度的影响程度以及抗剪强度随各参数的变化规律,结果见图 5。
|
图 5 不同计算模型中设计参数对抗剪强度影响分析 Fig. 5 Influence of design parameters for shear strength in different calculation models |
图 5表明上述计算模型总体上可以体现承载力随各受剪参数的变化关系,但不同模型在各受剪参数对抗剪强度的影响规律上没有取得统一认识:GB 50010—2010、ACI 318-19、EN 1992-1-1: 2004、Zararis、Zsutty公式在预测抗剪强度随混凝土强度增长时预测值均偏大;Zararis公式无法反映抗剪强度与剪跨比之间逐渐降低的变化规律,而EN 1992-1-1:2004公式在av=0.5d~2.0d时乘以系数av/(2d)来考虑剪跨比的影响;ACI 318-19和Zsutty公式未明显考虑尺寸效应,而当截面有效高度h0>800 mm时,GB 50010—2010公式通过引入截面高度影响作用系数βh来考虑尺寸效应;GB 50010—2010、EN 1992-1-1:2004公式无法显现抗剪强度随纵筋配筋率的非比例增长关系,其中GB 50010—2010规范在修订过程中,拟提出系数βρ=0.7+20ρ来量化纵筋配筋率ρ对抗剪强度vc的影响,但考虑到ρ>1.5%影响作用才较为明显,故在公式中未纳入系数βρ;EN 1992-1-1: 2004规范无法反映抗剪强度随相对剪压区高度ζ的变化关系,这是由于其在计算有腹筋RC梁受剪承载力时采用的是变角桁架模型,忽略了混凝土对受剪承载力的贡献。
对比表明,本文所提理论模型对不同受剪参数具有较好的适应性,受剪承载力预测结果表现出良好的稳定性,预测精度较上述其他计算模型公式有较大提高。
2.3 HSC梁构件抗剪试验数据整理为验证本文基于梁-拱作用所提理论模型的适用性,收集整理了207根集中荷载作用下发生受剪破坏的有腹筋HSC矩形梁试验梁数据,数据主要参数范围为:51.48 MPa≤f′c≤128.28 MPa,126 mm≤d≤762 mm,0.98≤λ≤4,0.01≤ρl≤0.07,0.33 MPa≤ ρsvfyv≤8.05 MPa,试验数据参数见表 2。
| 表 2 有腹筋高强混凝土梁受剪试验数据汇总表 Tab. 2 Summary of shear test data for high-strength concrete beams with web reinforcement |
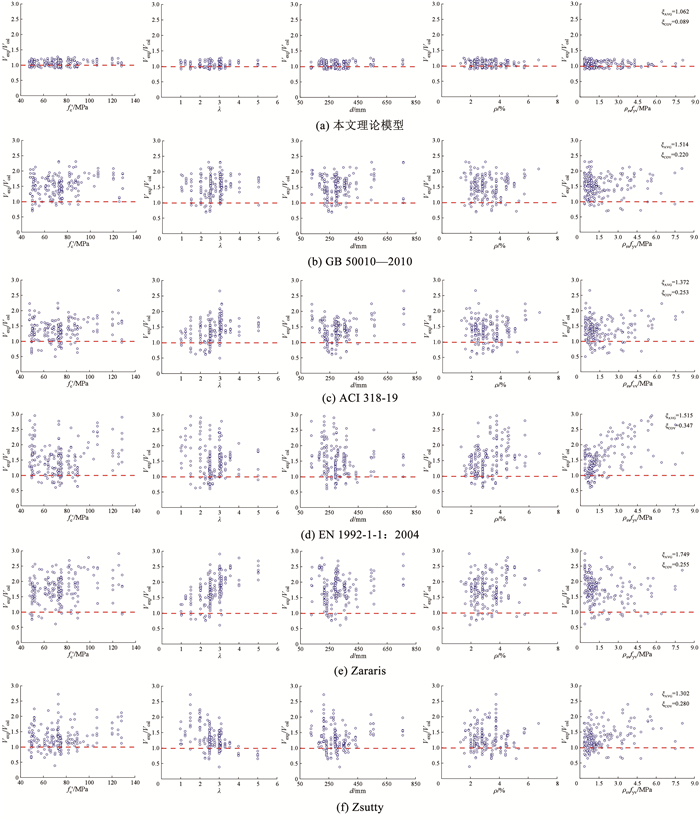
为了明确本文理论模型、GB 50010—2010、ACI 318-19、EN 1992-1-1:2004、Zararis公式、Zsutty公式对HSC梁受剪承载力计算的适用性和预测效果,基于所收集的207根HSC试验梁数据,采用表 1中的计算模型进行分析,结果见图 6和表 3。
|
图 6 不同计算模型公式试验结果与预测结果比较 Fig. 6 Comparison of test results and prediction results of different calculation models |
| 表 3 不同计算模型公式预测结果的统计指标 Tab. 3 Statistics indictors of prediction results for different calculation models |
分析图 6和表 3的结果表明:1)试验值与所提模型的受剪承载力预测结果比值的均值ξAVG为1.062,预测结果与试验值较好吻合,标准差ξSTD和变异系数ξCOV分别为0.095、0.089,预测结果的分布较其他模型更为合理,表明文中所提模型能够准确地预测HSC梁的受剪承载力,同时具有更为显著的预测稳定性;2)试验值与GB 50010—2010、ACI 318-19、EN 1992-1-1:2004、Zararis公式和Zsutty公式计算值比值的均值ξAVG分别为1.514、1.372、1.515、1.749、1.302,变异系数ξCOV分别为0.220、0.253、0.347、0.255、0.280,其中,Zsutty公式的受剪承载力预测结果相对于中美欧规范及Zararis公式的预测结果更为接近试验值,预测效果更好,但总体来说,现有计算模型的预测结果具有离散性较大和偏于保守的特点。
此外,由图 6还可以发现,受剪承载力的主要影响因素(f′c、λ、d、ρ、ρsvfyv)的大范围变化对本文所提理论模型结果的影响很小,表明本文所提模型对较大范围受剪参数的剪切破坏试验梁受剪承载力预测结果较为稳定。同时,不同计算模型在反映各受剪参数时体现出差异性的预测精度,说明不同模型对剪切破坏机理和影响因素的认识存在着一定差异。
3 结论1) 通过分析HSC梁发生剪切破坏时剪跨段内剪力传递路径,基于梁作用和拱作用考虑高强混凝土对梁构件受剪承载力的贡献,箍筋项采用简化的修正压力场理论计算,同时考虑尺寸效应影响,建立了集中荷载作用下HSC梁受剪承载力计算模型,模型物理意义清晰明确,可以真实反映梁构件斜截面受剪破坏机理;
2) 基于梁-拱复合受力机制和简化修正压力场理论所建立的集中荷载作用下HSC梁受剪分析模型能较好地反映混凝土强度、剪跨比、相对剪压区高度、纵筋配筋率、配箍率以及尺寸效应的影响,且预测精度随受剪参数的大范围变化无明显相关性,具有较好的预测稳定性;
3) 本文模型公式与207根梁试验结果较好吻合,试验值与模型计算值比值的均值为1.062,变异系数为0.089,离散程度较低,而试验值与规范GB 50010—2010、ACI 318-19、EN 1992-1-1: 2004、Zararis公式、Zsutty公式的计算值比值的均值最小为1.302,变异系数最小为0.220,预测精度较低且过于保守。通过上述比较表明,本文所提模型在预测精度和稳定性方面都有一定程度的提高。
| [1] |
高强混凝土应用技术规程: JGJ/T 281—2012[S]. 北京: 中国建筑工业出版社, 2012 Technical specification for application of high strength concrete: JGJ/T 281—2012[S]. Beijing: China Architecture & Building Press, 2012 |
| [2] |
祖坤, 熊二刚, 宋良英, 等. 高强混凝土构件力学性能研究综述[J]. 硅酸盐通报, 2019, 38(10): 3178. ZU Kun, XIONG Ergang, SONG Liangying, et al. Review on mechanical properties of high-strength concrete members[J]. Bulletin of the Chinese Ceramic Society, 2019, 38(10): 3178. DOI:10.16552/j.cnki.issn1001-1625.2019.10.021 |
| [3] |
BEUSHAUSEN H, DITTMER T. The influence of aggregate type on the strength and elastic modulus of high strength concrete[J]. Construction and Building Materials, 2015, 74: 132. DOI:10.1016/j.conbuildmat.2014.08.055 |
| [4] |
WU Weikuo, HSU T T C, HWANG S J. Shear strength of reinforced concrete beams[J]. ACI Structural Journal, 2014, 111(4): 812. DOI:10.14359/51686733 |
| [5] |
祖坤. 基于力学分析的无腹筋RC梁受剪承载力研究[D]. 西安: 长安大学, 2020 ZU Kun. Study on the shear capacity of RC beams without web reinforcement based on mechanical analysis[D]. Xi'an: Chang'an University, 2020 |
| [6] |
ZHANG Tao, VISINTIN P, OEHLERS D J. Shear strength of RC beams with steel stirrups[J]. Journal of Structural Engineering, 2016, 142(2): 04015135. DOI:10.1061/(ASCE)ST.1943-541X.0001404 |
| [7] |
AHMAD S, BHARGAVA P. Shear strength models for reinforced concrete slender beams: a comparative study[J]. Structures, 2018, 16: 119. DOI:10.1016/j.istruc.2018.09.004 |
| [8] |
PERERA S V T, MUTSUYOSHI H. Shear behavior of reinforced high-strength concrete beams[J]. ACI Structural Journal, 2013, 110(1): 48. DOI:10.14359/51684328 |
| [9] |
BUKHARI I A, AHMAD S. Evaluation of shear strength of high-strength concrete beams without stirrups[J]. Arabian Journal for Science and Engineering, 2008, 33(2): 331. |
| [10] |
KIM D, KIM W, WHITE R N. Arch action in reinforced concrete beams—A rational prediction of shear strength[J]. ACI Structural Journal, 1999, 96(4): 588. DOI:10.14359/695 |
| [11] |
ZARARIS P D, PAPADAKIS G C. Diagonal shear failure and size effect in RC beams without web reinforcement[J]. Journal of Structural Engineering, 2001, 127(7): 736. DOI:10.1061/(ASCE)0733-9445(2001)127:7(733) |
| [12] |
BAŽANT Z P, KIM J K. Size effect in shear failure of longitudinally reinforced beams[J]. ACI Structural Journal, 1984, 81(5): 460. DOI:10.14359/10696 |
| [13] |
CAMPIONE G, CANNELLA F, CAVALERI L. Shear and flexural strength prediction of corroded RC beams[J]. Construction and Building Materials, 2017, 149: 400. DOI:10.1016/j.conbuildmat.2017.05.125 |
| [14] |
ELIGEHAUSEN R, POPOV E P, BERTERO V V. Local bond stress-slip relationships of deformed bars under generalized excitations: experimental results and analytical model: UCB/ERC-83/23[R]. Berkeley: Earthquake Engineering Research Center, 1983
|
| [15] |
SWAMY R N, JONES R, CHIAM A T P. Influence of steel fibers on the shear resistance of lightweight concrete Ⅰ-beams[J]. ACI Structural Journal, 1993, 90(1): 108. DOI:10.14359/4201 |
| [16] |
Design of concrete structures-Part 1-1: general rules and rules for buildings: EN 1992-1-1: 2004[S]. Brussels: European Committee for Standardization, 2004
|
| [17] |
KIM J K, PARK Y D. Shear strength of reinforced high strength concrete beams without web reinforcement[J]. Magazine of Concrete Research, 1994, 46(166): 10. DOI:10.1680/macr.1994.46.166.7 |
| [18] |
HASEGAWA T, SHIOYA T, OKADA T. Size effect on splitting tensile strength of concrete[C]//Proceedings Japan Concrete Institute 7th Conference. Alexandroupolis: [s. n. ], 1985: 310
|
| [19] |
贺志启, 刘钊, 张宇峰. 基于桁-拱叠加模型的体外预应力混凝土梁抗剪承载力计算方法[J]. 土木工程学报, 2010, 43(1): 59. HE Zhiqi, LIU Zhao, ZHANG Yufeng. A method based on truss-arch model for calculating the shear strength of externally prestressed concrete beams[J]. China Civil Engineering Journal, 2010, 43(1): 59. DOI:10.15951/j.tmgcxb.2010.01.017 |
| [20] |
Code 262 for concrete structures: SIA 262: 2003[S]. Zürich: Swiss Society of Engineers and Architects, 2003
|
| [21] |
CAMPIONE G, MONACO A, MINAFÒ G. Shear strength of high-strength concrete beams: modeling and design recommendations[J]. Engineering Structures, 2014, 69: 119. DOI:10.1016/j.engstruct.2014.02.029 |
| [22] |
郑文忠, 李健, 王刚, 等. 剪压区和剪跨比对混凝土板受剪承载力的影响[J]. 哈尔滨工业大学学报, 2022, 54(4): 7. ZHENG Wenzhong, LI Jian, WANG Gang, et al. Effects of shear compression zone and shear span ratio on shear capacity of concrete slabs[J]. Journal of Harbin Institute of Technology, 2022, 54(4): 7. DOI:10.11918/202106059 |
| [23] |
COLLINS M P, MITCHELL D, ADEBAR P, et al. A general shear design method[J]. ACI Structural Journal, 1996, 93(1): 40. DOI:10.14359/9838 |
| [24] |
BLANKSVÄRD T. Strengthening of concrete structures by the use of mineral based composites[D]. Luleå: Luleå Tekniska Universitet, 2007
|
| [25] |
混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2015 Code for the design of concrete structures: GB 50010—2010[S]. Beijing: China Architecture & Building Press, 2015 |
| [26] |
Building code requirements for structural concrete and commentary: ACI 318-19[S]. Farmington Hills: American Concrete Institute, 2019
|
| [27] |
ZARARIS P D. Shear strength and minimum shear reinforcement of reinforced concrete slender beams[J]. ACI Structural Journal, 2003, 100(2): 208. DOI:10.14359/12484 |
| [28] |
ZSUTTY T C. Beam shear strength prediction by analysis of existing data[J]. ACI Structural Journal, 1968, 65(11): 949. DOI:10.14359/7526 |
| [29] |
KONGP Y L, RANGAN B V. Shear strength of high-performance concrete beams[J]. ACI Structural Journal, 1998, 95(6): 682. DOI:10.14359/581 |
| [30] |
SHIN S W, LEE K S, MOON J I, et al. Shear strength of reinforced high-strength concrete beams with shear span-to-depth ratios between 1.5 and 2.5[J]. ACI Structural Journal, 1999, 96(4): 550. DOI:10.14359/691 |
| [31] |
JOHNSON M K, RAMIREZ J A. Minimum shear reinforcement in beams with higher strength concrete[J]. ACI Structural Journal, 1989, 86(4): 373. DOI:10.14359/2896 |
| [32] |
ROLLER J J, RUSSEL H G. Shear strength of high-strength concrete beams with web reinforcement[J]. ACI Structural Journal, 1990, 87(2): 194. DOI:10.14359/2682 |
| [33] |
SARSAM K F, AL-MUSAWI J M S. Shear design of high and normal strength concrete beams with web reinforcement[J]. ACI Structural Journal, 1992, 89(6): 662. DOI:10.14359/9644 |
| [34] |
XIE Yuliang, AHMAD S H, YU Tiejun, et al. Shear ductility of reinforced concrete beams of normal and high-strength concrete[J]. ACI Structural Journal, 1994, 91(2): 145. DOI:10.14359/4592 |
| [35] |
OZCEBE G, ERSOY U, TANKUT T. Evaluation of minimum shear reinforcement requirements for higher strength concrete[J]. ACI Structural Journal, 1999, 96(3): 361. DOI:10.14359/669 |
| [36] |
康明. 集中荷载作用下超高强混凝土有腹筋简支梁抗剪强度的试验研究[D]. 重庆: 重庆大学, 1999 KANG Ming. Shear strength of reinforcement high-strength concrete beams with web reinforcement subject to the point load[D]. Chongqing: Chongqing University, 1999 |
| [37] |
李立仁, 支运芳, 陈永庆, 等. 集中荷载下超高强混凝土有腹筋约束梁抗剪强度的试验研究[J]. 建筑结构学报, 2001, 22(5): 35. LI Liren, ZHI Yunfang, CHEN Yongqing, et al. Experimental research on shear capacity of high strength of super strength concrete beam constrained with web bars[J]. Journal of Building Structures, 2001, 22(5): 35. DOI:10.14006/j.jzjgxb.2001.05.007 |
| [38] |
CLADERA A, MARI A R. Experimental study on high-strength concrete beams failing in shear[J]. Engineering Structures, 2005, 27(10): 1523. DOI:10.1016/j.engstruct.2005.04.010 |
| [39] |
SATO R, KAWAKANE H, KAWAMOTO T, et al. Shrinkage effect on shear strength of reinforced, high strength concrete beams[J]. ACI Special Publication, 2007, 246: 265. |
| [40] |
吕艳梅. 高强箍筋高强混凝土梁抗剪性能试验研究与理论分析[D]. 长沙: 湖南大学, 2008 LV Yanmei. Theoretical and experimental research on shear capacity of high strength concrete beams with high strength stirrups[D]. Changsha: Hunan University, 2008 |
| [41] |
白家荣. 高强箍筋高强混凝土梁受剪性能试验研究及有限元分析[D]. 西安: 西安建筑科技大学, 2009 BAI Jiarong. Experiments and finite element analysis of shear behavior for high strength concrete beams with high strength stirrups[D]. Xi'an: Xi'an University of Architecture and Technology, 2009 |
| [42] |
潘柏荣. 高强混凝土梁抗剪性能试验研究[D]. 长沙: 湖南大学, 2009 PAN Bairong. Research on shear capacity of high strength concrete beams[D]. Changsha: Hunan University, 2009 |
| [43] |
史庆轩, 侯炜, 姜维山, 等. 高强箍筋高强混凝土梁受剪承载力研究[J]. 建筑结构学报, 2009, 30(增刊2): 99. SHI Qingxuan, HOU Wei, JIANG Weishan, et al. Shear capacity of high-strength concrete beams with high-strength stirrups[J]. Journal of Building Structures, 2009, 30(S2): 99. DOI:10.14006/j.jzjgxb.2009.s2.018 |
| [44] |
LEE J Y, CHOI I J, KIM S W. Shear behavior of reinforced concrete beams with high-strength stirrups[J]. ACI Structural Journal, 2011, 108(5): 624. DOI:10.14359/51683219 |
| [45] |
叶献国, 王程成, 种迅, 等. HRBF500钢筋C100混凝土梁抗剪性能试验研究[J]. 工业建筑, 2012, 42(7): 87. YE Xianguo, WANG Chengcheng, CHONG Xun, et al. Experimental study on shear behavior of beam with C100 concrete and HRBF500 grade rebar[J]. Industrial Construction, 2012, 42(7): 87. DOI:10.13204/j.gyjz2012.07.022 |
| [46] |
叶献国, 张煜, 种迅, 等. 高强钢筋高强混凝土简支梁抗剪试验研究[J]. 建筑结构, 2013, 43(8): 49. YE Xianguo, ZHANG Yu, CHONG Xun, et al. Experimental study on shear behavior of simple supported high-strength concrete beams with high-strength steel[J]. Building Structure, 2013, 43(8): 49. DOI:10.19701/j.jzjg.2013.08.012 |
| [47] |
钟亚丽. 高强箍筋高强混凝土梁受剪性能研究[D]. 马鞍山: 安徽工业大学, 2015 ZHONG Yali. Analysis on the shear behavior of high-strength concrete beams with high-strength stirrups[D]. Ma'anshan: Anhui University of Technology, 2015 |
| [48] |
张杰强, 石启印, 杨帆, 等. 高强混凝土梁抗剪性能试验研究[J]. 建筑科学, 2016, 32(9): 82. ZHANG Jieqiang, SHI Qiyin, YANG Fan, et al. Experimental study on shear resistance of high strength concrete beams[J]. Building Science, 2016, 32(9): 82. DOI:10.13614/j.cnki.11-1962/tu.2016.09.014 |
 2022, Vol. 54
2022, Vol. 54