1962年Gallager[1]提出了低密度奇偶校验码(low density parity check, LDPC),但是因为其译码效果不理想而被“休眠”。直到30 a后,又一次将目光聚焦在LDPC码上。文献[2]证明了LDPC码的误码性能能够接近理论香农限。目前,LDPC码已被应用到深空通信、无人机数据链等场景下,并作为一种中长码的编码方式,应用在5G数据信道中。
置信度传播(belief propagation, BP)算法是LDPC码的基础译码算法,LDPC码的译码算法大多是在BP译码算法的基础上改进而来。将BP译码算法中的软信息取对数进行计算,得到了对数似然比(log likelihood ratio, LLR)BP译码算法。为了使LLR BP译码算法的计算更加简便,文献[3]在校验节点的更新过程中取近似运算,提出了最小和(minimum sum, MS) 译码算法,以误码性能下降为代价换取了复杂度的降低;在MS算法基础上,文献[4-5] 提出了偏移最小和(offset minimum sum, OMS)译码算法和归一化最小和(normalized minimum sum, NMS)译码算法,分别通过减法和乘法运算使结果更加准确;文献[6]根据置信传播算法与最小和译码算法的校验节点信息,推导出一种新的近似因子用来修正MS算法;文献[7-9]分别将最小和译码算法中的取一个最小值的方法,改进为综合分析多个最小值进行计算;文献[10-12]在迭代更新的过程中对不可靠信息做出处理;文献[13]中用不同的偏移因子去修正最小值和次小值,并用次序统计量进行分析;文献[14]通过在最小和译码算法的最小值上增加一个可变因子,来达到近似修正的目的,这些算法都对MS算法中存在的性能损失做出了弥补,提升了误码性能;文献[15-16]介绍了一种基于分层的LDPC码译码算法,改变了算法的调度方式,提升了译码效果。
在一定程度上,这些算法都对MS算法中存在的性能损失做了补偿,提升了误码性能。OMS算法和NMS算法中,虽然算法本身的复杂度增加不多,但是偏移系数以及归一化系数的计算势必会带来工作量的增加,且固定的系数必然无法准确的对MS算法中存在的误差进行修正,以及改进MS算法由于取值的个数增加导致复杂度提升等问题。
基于此,本文提出一种类拟合修正最小和(class fitting modified minimum sum, CFMMS)译码算法,该算法首先根据校验节点更新中的非线性函数构造了一个类拟合函数,来根据变量节点信息最小值所在阈值的不同而做出不同的处理,因此能够更加准确的对MS算法中存在的误差进行修正;在此基础上,将类拟合修正最小和译码算法与分层译码的思想相结合,提出一种分层类拟合修正最小和(layered class fitting modified minimum sum, LCFMMS)译码算法,改变了传统译码算法的调度方式,将更新顺序由整体更新变成了分层进行更新,加快了译码收敛速度,提升了误码性能。同时,不再需要储存所有的校验节点信息,压缩了算法所需的储存空间。
1 LDPC译码算法LDPC码有基于硬判决和基于软判决的两类译码方式[7],前者虽然较为简单,但是译码效果差;后者虽误码性能较好,但复杂度较大。因此,对于BP译码算法的研究,不仅要关注译码效果,也要关注对复杂度的影响。
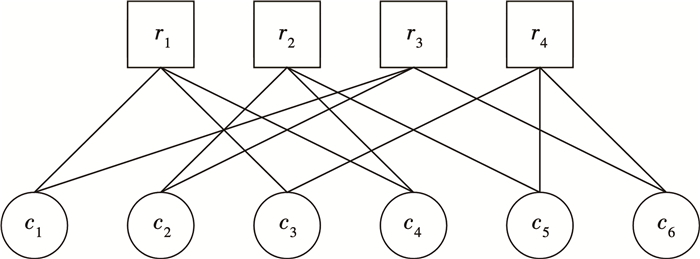
1.1 LLR BP译码算法LDPC码的译码算法是在Tanner图的基础上进行的[12],以(6,2)LDPC码为例,其校验矩阵及校验方程见式(1),Tanner图见图 1。
| $ {\boldsymbol{H}}=\left[\begin{array}{llllll} 1 & 0 & 1 & 1 & 0 & 0 \\ 0 & 1 & 0 & 1 & 1 & 0 \\ 1 & 1 & 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 & 1 & 1 \end{array}\right] \begin{array}{l} c_{1}+c_{3}+c_{4}=0 \\ c_{2}+c_{4}+c_{5}=0 \\ c_{1}+c_{2}+c_{6}=0 \\ c_{3}+c_{5}+c_{6}=0 \end{array} $ | (1) |
|
图 1 校验矩阵对应的Tanner图 Fig. 1 Tanner diagram corresponding to check matrix |
假设发送端预传输的信息序列经LDPC编码器后得到的编码序列为c=(c1, c2, …, cn),编码序列经BPSK调制后得到的传输序列为x=(x1, x2, …, xn),传输序列经高斯白噪声信道传输后,接收端的接收序列为r=(r1, r2, …, rn),最后经过LDPC译码器后得到的译码序列为y=(y1, y2, …, yn)。
在LLR BP[17]译码算法中,首先接收端接收到来自信道的概率信息,并计算初始对数似然比为
| $ V_{i j}^{0}=\ln \frac{P(0)}{P(1)}=\ln \frac{P\left(x_{i}=0 \mid r_{i}\right)}{P\left(x_{i}=1 \mid r_{i}\right)}=2 r_{i} / \sigma^{2} $ | (2) |
式中σ2为噪声方差。
随后更新校验节点信息及变量节点信息分别为
| $ C_{i j}^{l}=2 \tanh ^{-1}\left[\prod\limits_{j_{1} \in J(i) \backslash j} \tanh \left(V_{i j_{1}}^{l-1} / 2\right)\right] $ | (3) |
| $ V_{i j}^{l}=V_{i j}^{0}+\sum\limits_{i_{1} \in I(j) \backslash i} C_{i_{1} j}^{l} $ | (4) |
式中:J(i)为第i行对应的变量节点的集合,J(i)\j为第i行对应的变量节点的集合(不包含第j个变量节点),I(j)为第j列对应的校验节点的集合,I(j)\i为第j列对应的校验节点的集合(不包含第i个校验节点)。
最后根据得到的信息进行判决。与概率域BP译码算法相比,LLR BP译码算法完成了运算方式由乘法到加法的转化,复杂度有所降低。
1.2 最小和译码算法及其改进算法虽然,将概率域BP译码算法放在对数域运算会降低一定程度的复杂度,但是算法内却存在非线性函数,复杂度依然较高。因此,出现了MS算法,MS算法是在LLR BP译码算法中采取了近似运算,将乘法运算转化为比较运算[17]。
由于双曲正切函数和反双曲正切函数都是奇函数,式(3)可继续推导为
| $ C_{i j}^{l}=2\left[\prod\limits_{j_{1} \in J(i) \backslash j} {\rm{sign}}\left(V_{i j_{1}}^{l-1}\right)\right] \tanh ^{-1}\left[\prod\limits_{j_{1} \in J(i) \backslash j} \tanh \left(\left|V_{i j_{1}}^{l-1} / 2\right|\right)\right] $ | (5) |
对于任意的实数x,都有tanh(|x|)∈(0, 1),式(5)取近似运算可转换为
| $ C_{i j}^{l}=2\left[\prod\limits_{j_{1} \in J(i) \backslash j} {\rm{sign}}\left(V_{i j_{1}}^{l-1}\right)\right] \tanh ^{-1}\left[\tanh \left(\frac{1}{2} \min\limits _{j_{1} \in J(i) \backslash j}\left|V_{i j_{1}}^{l-1}\right|\right)\right] $ | (6) |
由此,MS算法中校验节点的更新公式可简化为
| $ C_{i j}^{l}=\prod\limits_{j_{1} \in J(i) \backslash j} {\rm{sign}}\left(V_{i j_{1}}^{l-1}\right) \min\limits _{j_{1} \in J(i) \backslash j}\left|V_{i j_{1}}^{l-1}\right| $ | (7) |
MS算法的大致思想是将ωc-1个xi相乘近似为xi中的最小值(其中ωc为列重,xi∈(0, 1),i=1, 2, …, ωc-1),这样得到的结果要比实际值偏大。因此,对MS算法的改进过程便是使得到的结果更接近于置信传播算法的过程。
对于MS算法以部分误码性能换取低复杂度的问题,出现了各种各样的改进算法,两种比较经典的改进算法,分别为NMS算法和OMS算法[4],在式(7)的基础上,得到两种改进算法的校验节点更新过程:
| $ C_{i j}^{l}=\alpha \prod\limits_{j_{1} \in J(i) \backslash j} {\rm{sign}}\left(V_{i j_{1}}^{l-1}\right) \min\limits _{j_{1} \in J(i) \backslash j}\left|V_{i j_{1}}^{l-1}\right| $ | (8) |
| $ C_{i j}^{l}=\prod\limits_{j_{1} \in J(i) \backslash j} {\rm{sign}}\left(V_{i j_{1}}^{l-1}\right) \max \left(\min\limits _{j_{1} \in J(i) \backslash j}\left|V_{i j_{1}}^{l-1}\right|-\beta, 0\right) $ | (9) |
式中:α∈(0, 1),β>0。
显然,这两种算法都在一定程度上减小了得到的校验节点信息数值,对MS算法中存在的误差起到了一定的补偿作用,使得到的结果更加接近置信传播算法。
2 改进的LDPC译码算法 2.1 类拟合修正最小和译码算法NMS算法和OMS算法的性能都在一定程度上优于MS算法,但是算法中系数α和β的值是需要根据仿真得到的[10],对于系数的计算,在一定程度上增加了算法的工作量。因此本节给出了另外一种修正方案,提出了类拟合修正最小和(CFMMS)译码算法,对MS算法再一次做近似处理。MS算法对LLR BP算法的近似是向上取近似,本文提出的算法,是在MS算法的基础上向下取近似,达到减小误差的目的。
根据MS算法可得校验节点的更新过程为
| $ C_{i j}^{l}=2\left[\prod\limits_{j_{1} \in J(i) \backslash j} {\rm{sign}}\left(V_{i j_{1}}^{l-1}\right)\right] \tanh ^{-1}\left[\tanh \left(\min\limits _{j_{1} \in J(i) \backslash j}\left|V_{i j_{1}}^{l-1} / 2\right|\right)\right] $ | (10) |
首先,定义式(10)中的后半部分为类拟合函数,即为
| $ {\rm{CFF}}(v)=\tanh ^{-1}[\tanh (v)] $ | (11) |
式中v为任意实数。
由式(10)可知,本文中v≥0,因此在函数y=tanh(x)和y=tanh-1(x)中只考虑x≥0(下文关于分段函数的段数问题均在该范围内讨论)的部分即可。将两个函数分别近似为一个含有3段的分段函数,对y=tanh(x)函数均匀的选择的4个点分别为(0,0)、(1,0.76)、(2,0.96)、(3,1),在y=artanh(x)中,考虑斜率的变化选择的4个点分别为(0,0)、(0.4,0.42)、(0.8,1.1)、(1,2.5),得到两个非线性函数与其近似函数图像见图 2。

|
图 2 近似线性函数 Fig. 2 Approximate linear function |
将两个分段函数分别代入类拟合函数中,为保证类拟合函数拥有较低的复杂度,同时考虑变量节点最小值的变化范围,得到类拟合函数为
| $ {\rm{CFF}}\left(\min\limits _{j_{1} \in J(i) \backslash j}\left|V_{i j_{1}}^{l-1} / 2\right|\right)=\left\{\begin{array}{l} 0.8 \cdot \min\limits _{j_{1} \in J(i) \backslash j}\left|V_{i j_{1}}^{l-1} / 2\right|, 0 \leqslant \min\limits _{j_{1} \in J(i) \backslash j}\left|V_{i j_{1}}^{l-1} / 2\right|<0.53 \\ 1.29 \cdot \min\limits _{j_{1} \in J(i) \backslash j}\left|V_{i j_{1}}^{l-1} / 2\right|-0.26, 0.53 \leqslant \min\limits _{j_{1} \in J(i) \backslash j}\left|V_{i j_{1}}^{i-1} / 2\right|<1 \\ \min\limits _{j_{1} \in J(i) \backslash j}\left|V_{i j_{1}}^{l-1} / 2\right|, \min\limits _{j_{1} \in J(i) \backslash j}\left|V_{i j_{1}}^{l-1} / 2\right| \geqslant 1 \end{array}\right. $ | (12) |
由类拟合函数可以看出,该函数会根据变量节点最小值所在阈值的不同,做出不同的处理,每一部分的计算都是为了得到与置信传播算法更接近的结果。
综上分析,CFMMS算法的校验节点更新公式为
| $ C_{i j}^{l}=2\left[\prod\limits_{j_{1} \in J(i) \backslash j} {\rm{sign}}\left(V_{i j_{1}}^{l-1}\right)\right] \cdot {\rm{CFF}}\left(\min\limits _{j_{1} \in J(i) \backslash j}\left|V_{i j_{1}}^{l-1} / 2\right|\right) $ | (13) |
如果在MS算法中引入类拟合函数的概念,MS算法中类拟合函数的表达式应为
| $ {\mathrm{CFF}}_{\rm {MS }}\left(\min\limits _{j_{1} \in J(i) \backslash j}\left|V_{i j_{1}}^{l-1} / 2\right|\right)=\min\limits _{j_{1} \in J(i) \backslash j}\left|V_{i j_{1}}^{l-1} / 2\right| $ | (14) |
很明显,MS算法中存在的类拟合函数只是一个简单的线性函数,且不会受变量节点信息的影响。而在式(12)中,类拟合函数会根据最小值的不同而采取不同的处理方式,得到的校验节点信息会更加准确。
此外,分段函数的段数也会影响其与原函数的近似程度。因此,对于分段函数段数的选取并不是随意的,如果分段函数的段数过多,就会出现近似函数与原函数拟合程度过高,进而达不到修正的目的;反之,分段函数的段数过少,则会导致近似函数与原函数偏离程度过大,进而出现修正过度的现象。
2.2 基于分层的类拟合修正最小和译码算法针对CFMMS算法增加了少量复杂度且译码收敛速度较慢的问题,将CFMMS算法与分层译码的思想相结合,提出了一种基于分层的类拟合修正最小和(LCFMMS)译码算法。
分层译码与普通译码的区别就在于调度方式不同,普通的LDPC译码算法对于校验节点和变量节点的更新都是成片的,这种调度方式对算法所需的储存空间容量需求较高;而基于分层思想的LDPC译码算法,采用的是分层式调度,这种调度方式需要将校验矩阵以行为单位进行分层,并以层为单位进行更新(具体流程见图 3,假设校验矩阵分为D层,当前层数为l)。在前提条件相同的情况下,分层式调度所需的储存空间仅为前者的1/D,节省了存储空间。而且,每一层变量节点的更新用到的都是上一层刚刚更新的校验节点信息,提升了信息的可靠度。

|
图 3 分层迭代译码算法处理流程图 Fig. 3 Processing flow of layered iterative decoding algorithm |
LCFMMS算法的迭代更新具体过程如下:
1) 首先将校验矩阵HM×N以行为单位分成D层(0 < D≤M);
2) 初始化信息
| $ V_{i j}^{0}=\ln \frac{P(0)}{P(1)}=\ln \frac{P\left(x_{i}=0 \mid r_{i}\right)}{P\left(x_{i}=1 \mid r_{i}\right)}=2 r_{i} / \sigma^{2} $ | (15) |
3) 层内变量节点更新
| $ V_{i j}^{l}=V_{i j}^{0}+\sum\limits_{i_{1} \in I(j) \backslash i} C_{i_{1} j}^{l-1} $ | (16) |
4) 层内校验节点更新
| $ C_{i j}^{l}=2\left[\prod\limits_{j_{1} \in J(i) \backslash j} {\rm{sign}}\left(V_{i j_{1}}^{l}\right)\right] \cdot {\rm{CFF}}\left(\min\limits _{j_{1} \in J(i) \backslash j}\left|V_{i j_{1}}^{l} / 2\right|\right) $ | (17) |
5) 后验概率更新
| $ V_{i}=V_{i j}^{l}+\sum\limits_{i_{1} \in I(j)} C_{i_{1 }j}^{l} $ | (18) |
6) 判断是否已到达最大层数,如果未到达最大层数,则返回步骤3继续进行更新;如果已到达最大层数,则进入步骤7。
7) 判决:如果Vi>0,则判yi=0;否则判yi=1。
8) 最后,检验信息序列y是否满足校验方程H·yT=0,如果满足校验方程,则译码完成;否则,信息序列y将被作为初始对数似然比信息重新回到步骤3进行更新,直到满足译码完成的条件,即可停止译码。
3 算法仿真及分析 3.1 算法复杂度分析表 1给出了MS算法、CFMMS算法、LCFMMS算法3种算法在一次迭代中节点更新所需要的各类运算(“+”、“×”、“ < ”)的次数,其中m为校验矩阵H的行数,n为校验矩阵H的列数,ωr为校验矩阵H的行重,ωc为检验矩阵H的列重,D取值为m。
| 表 1 算法复杂度 Tab. 1 Algorithm complexity |
CFMMS算法相比较于MS算法来说,3种运算的次数均稍有增加;而LCFMMS算法在复杂度方面有了明显的下降,不论行重大小如何,乘法运算、加法运算和比较运算次数都在一定程度上有所减少。由表 1可以看出,不论何种译码算法,在码率以及行重、列重固定的条件下,完成译码所需各种运算的次数与LDPC码的码长是成正比关系的,即各算法的运算复杂度会随着码长的增加而增加。
3.2 算法仿真结果为验证本文提出的CFMMS算法和LCFMMS算法的性能,在AWGN信道下,调制方式采用BPSK调制,最大迭代次数设为10次,码率为1/2,码长分别选取较短码长128、中等码长1 024和较长码长2 048,根据以上条件对LDPC码进行仿真分析。在文献[4-5, 18]中,关于改进的LDPC译码算法的性能分析,都以误码率作为指标。因此,在本文中也分析其误码率曲线,其仿真结果及分析如下。
在图 4中,分别为在码长2 048和码长128下,MS算法、CFMMS算法和LCFMMS算法3种译码算法的误码率曲线。可以看出,不论码长如何,在前提条件相同的情况下,这3种译码算法的误码性能都是MS算法最差,CFMMS算法次之,LCFMMS算法最好。在码长为2 048,误码率接近10-4时,CFMMS算法较MS算法、LCFMMS算法较CFMMS算法来说,误码性能分别提升了约0.4 dB;在码长为128,误码率为10-5时,CFMMS算法较MS算法来说,误码性能提升了约0.5 dB,LCFMMS算法相比较于CFMMS算法来说,亦具有0.3 dB的性能增益。

|
图 4 各译码算法在不同码长下误码性能对比 Fig. 4 Comparison of BER performance of decoding algorithms under different code lengths |
图 5展示了在采用LCFMMS算法进行译码的前提下,码长对于译码算法误码性能的影响。从图中可以看出,随着码长的增加,译码算法的误码性能是越来越好的,即译码算法对于长码长LDPC码的误码性能要优于短码长LDPC码的误码性能,这也是LDPC码更适用于长码的原因。但是,由分析可知,译码算法的算法复杂度与LDPC码的码长成正比关系。因此,在实际应用中并不可一味的追求长码长的优异性能,还要综合考虑复杂度的问题,这样才能选出合适的码长。

|
图 5 不同码长下的误码性能对比 Fig. 5 Comparison of BER performance under different code lengths |
图 6为在码长分别为2 048和128,最大迭代次数为10次的情况下,3种不同的译码算法完成译码所需要的迭代次数。从图中可以看出,不论码长如何,CFMMS译码算法所需要的迭代次数要比MS算法稍少一些,但是差别不大;而LCFMMS算法由于应用了分层调度的调度方式,提高了信息的可靠度,使得译码能够快速收敛,因此所需要的迭代次数会在一定程度上有所下降。

|
图 6 不同算法所需迭代次数 Fig. 6 Number of iterations required by different algorithms |
图 7为不同最大迭代次数下的误码率曲线,采用的译码算法为LCFMMS译码算法。由图可知,在一定范围内,误码性能与最大迭代次数是呈正比关系的,尤其在最大迭代次数小于10次的情况下,误码性能的提升最为明显;但是,当最大迭代次数超过10次后,误码率曲线的变化趋势会减小;且最大迭代次数超过20次后,误码率曲线不会再随着迭代次数的增加而发生明显的变化。在实际应用中最大迭代次数的选取要经过充分的考虑。如果数值选取过小会影响误码性能,选取过大会浪费资源。

|
图 7 不同最大迭代次数下的误码率曲线 Fig. 7 BER curves under different maximum iterations |
本文首先基于MS算法提出了一种CFMMS算法,对MS算法中近似运算带来校验节点信息数值偏大的问题进行了修正,虽然计算复杂度较MS算法稍有增加,但是得到的校验节点信息值更为准确。在此基础上,改变了CFMMS算法的调度方式,将原来的洪水式调度变为分层式调度,对算法所需的储存空间进行了压缩,而且每层变量节点更新用到的都是上一层刚刚更新的节点信息,因此得到的信息更加具有实时性和可靠性。仿真结果与复杂度分析表明,本文所提出的CFMMS和LCFMMS算法,在误码性能方面都有所提升。而且,LCFMMS算法不仅提升了误码性能,还降低了算法的实现复杂度,加快了译码的收敛速度,带来了更低的译码延时。
| [1] |
GALLAGER R. Low-density parity-check code[J]. IRE Transactions on Information Theory, 1962, 8(1): 21. DOI:10.1109/TIT.1962.1057683 |
| [2] |
RICHARDSON T J, SHOKROLLAHI M A, URBANKE R L. Design of capacity-approaching irregular low-density parity-check codes[J]. IEEE Transactions on Information Theory, 2001, 47(2): 619. DOI:10.1109/18.910578 |
| [3] |
FOSSORIER M P C, MIHALJEVIC M, IMAI H. Reduced complexity iterative decoding of low-density parity check codes based on belief propagation[J]. IEEE Transactions on Communications, 1999, 47(5): 673. DOI:10.1109/26.768759 |
| [4] |
CHEN Jinghu, FOSSORIER M P C. Density evolution for two improved BP-based decoding algorithms of LDPC codes[J]. IEEE Communications Letters, 2002, 6(5): 208. DOI:10.1109/4234.1001666 |
| [5] |
CHEN Jinghu, FOSSORIER M P C. Near optimum universal belief propagation based decoding of low-density parity check codes[J]. IEEE Transactions on Communications, 2002, 50(3): 406. DOI:10.1109/26.990903 |
| [6] |
CAO Yue. An improved LDPC decoding algorithm based on min-sum algorithm[C]//Proceedings of 2011 11th International Symposium on Communications & Information Technologies (ISCIT). Hangzhou: IEEE, 2011: 26. DOI: 10.1109/ISCIT.2011.6089747
|
| [7] |
许欣. 5G URLLC数据信道中LDPC编译码方法研究[D]. 北京: 北京交通大学, 2020 XU Xin. Research on LDPC coding and decoding method in 5G URLLC data channel[D]. Beijing: Beijing Jiaotong University, 2020 |
| [8] |
KIM N I, LEE S Q, KIM J U. A modified min sum decoding algorithm based on approximation enhancement for LDPC codes[C]//Proceedings of 2020 International Conference on Information and Communication Technology Convergence (ICTC). Jeju: IEEE, 2020: 1407. DOI: 10.1109/ICTC49870.2020.9289334
|
| [9] |
VITYAZEV V V, LIKHOBABIN E A, USTINOVA E A. Min-sum algorithm-structure based decoding algorithms for LDPC codes[C]//Proceedings of 2014 3rd Mediterranean Conference on Embedded Computing (MECO). Budva: IEEE, 2014: 256. DOI: 10.1109/MECO.2014.6862710
|
| [10] |
韩少聪, 高飞飞, 李云洲, 等. 一种改进的自纠正最小和LDPC码的译码算法[J]. 电信科学, 2013, 29(6): 89. HAN Shaocong, GAO Feifei, LI Yunzhou, et al. An improved self-correct min-sum decoding algorithm for low-density parity-check code[J]. Journal of Telecommunications Science, 2013, 29(6): 89. DOI:10.3969/j.issn.1000-0801.2013.06.014 |
| [11] |
陈容, 陈岚. 一种动态自纠正最小和LDPC码的译码算法[J]. 北京邮电大学学报, 2020, 43(4): 15. CHEN Rong, CHEN Lan. A dynamic self-corrected minimum sum decoding algorithm for LDPC codes[J]. Journal of Beijing University of Posts and Telecommunications, 2020, 43(4): 15. DOI:10.13190/j.jbupt.2019-222 |
| [12] |
周志伟, 孙发鱼, 白瑞青. 偏置自纠错最小和译码算法[J]. 探测与控制学报, 2021, 43(2): 76. ZHOU Zhiwei, SUN Fayu, BAI Ruiqing. Bias self-correcting minimum sum algorithm[J]. Journal of Detection and Control, 2021, 43(2): 76. |
| [13] |
陈发堂, 李贺宾, 李平安. 基于偏移最小和LDPC译码改进算法[J/OL]. 系统工程与电子技术[2022-04-14]. http://kns.cnki.net/kcms/detail/11.2422.TN.20210817.1336.010.html CHEN Fatang, LI Hebin, LI Ping'an. Improved algorithm based on offset min-sum decoding for LDPC codes[J/OL]. Systems Engineering and Electronics[2022-04-14]. http://kns.cnki.net/kcms/detail/11.2422.TN.20210817.1336.010.html |
| [14] |
WU Ruizhen, WANG Lin, YUAN Tao, et al. A check nodes correction approximate min-sum decoding algorithm for LDPC[C]//Proceedings of 2019 7th International Conference on Information and Communication Technology (ICoICT). Kuala: IEEE, 2019: 1. DOI: 10.1109/ICoICT.2019.8835237
|
| [15] |
HOCEVAR D E. A reduced complexity decoder architecture via layered decoding of LDPC codes[C]//Proceedings of IEEE Workshop on Signal Processing Systems. Austin: IEEE, 2004: 107. DOI: 10.1109/SIPS.2004.1363033
|
| [16] |
ZHANG Xinmiao, TAI Ying. High-speed multi-block-row layered decoding for quasi-cyclic LDPC codes[C]//Proceedings of the 2014 IEEE Global Conference on Signal and Information Processing. Atlanta: IEEE, 2014: 11. DOI: 10.1109/GlobalSIP.2014.7032068
|
| [17] |
贺鹤云. LDPC码基础与应用[M]. 北京: 人民邮电出版社, 2009: 122. HE Heyun. LDPC code foundation and application[M]. Beijing: Posts and Telecommunications Press, 2009: 122. |
| [18] |
LIU Xingcheng, ZHOU Zhenzhu, CUI Ru, et al. Informed decoding algorithms of LDPC codes based on dynamic selection strategy[J]. IEEE Transactions on Communications, 2016, 64(4): 1357. DOI:10.1109/TCOMM.2016.2527642 |
 2022, Vol. 54
2022, Vol. 54


