2. 郑州大学 机械与动力工程学院, 郑州 450066;
3. 复旦大学 计算机科学技术学院, 上海 201203;
4. 云南省教育厅 教育科学研究院, 昆明 650021
2. School of Mechanical and Power Engineering, Zhengzhou University, Zhengzhou 450066, China;
3. School of Computer Science, Fudan University, Shanghai 201203, China;
4. Educational and Scientific Institute, Education Department of Yunnan Province, Kunming 650021, China
樽海鞘群算法(salp swarm algorithm, SSA)[1]是2017年提出的一种新型群体智能优化算法, 它源于对海洋生物樽海鞘导航和群体觅食行为的模拟, 通过领导、跟随等过程, 构建一种高效的寻优方案。SSA算法具有寻优机制简单、参数设置少、全局搜索能力强等特点。文献[1]的研究表明, SSA算法的寻优能力优于遗传算法(genetic algorithm, GA)[2]、粒子群优化(particle swarm optimization, PSO)[3]、人工蜂群(artificial bee colony, ABC)算法[4]等传统智能优化算法, 与灰狼优化(grey wolf optimizer, GWO)[5]、鲸鱼优化算法(whale optimization algorithm, WOA)[6]、萤火虫算法(firefly algorithm, FA)[7]等新型群体智能算法相比, SSA也有较强的竞争力[1]。自提出以来, SSA算法已被成功应用于目标分类[8]、特征选择[9]、图像处理[10]、混合动力系统[11]等领域中。
然而, 与其他元启发式算法相似, SSA算法也存在开发与勘探能力不平衡、寻优精度低、易陷入局部最优等缺点。针对这些问题, 研究学者开发出了许多性能较好的SSA变体。文献[12]在领导者位置更新公式中引入一种控制搜索范围的非线性衰减因子, 提高算法的局部搜索能力, 同时在跟随者位置更新公式中引入动态学习策略, 增强精英个体对领导者的协助作用, 以此提高算法的寻优能力。文献[13]提出追随者共生概念, 可以优化樽海鞘追随者的跟随方式, 从而增强算法的全局开采能力, 并通过引入非均匀高斯变异提高种群多样性。文献[14]通过引入疯狂算子对食物源进行扰动, 以此提高种群多样性, 同时提出自适应惯性权重, 能够平衡算法的开采与勘探能力。文献[15]提出动态惯性权重, 以此优化领导者的位置更新方式, 从而提高算法的全局搜素能力, 并随算法迭代自适应地调整樽海鞘领导者和追随者的数量, 加快收敛速度的同时提高收敛精度。文献[16]在领导者位置更新公式中引入指数系数, 并在跟随者位置更新公式中引入随机参数, 加快算法收敛速度的同时改善了算法的求解精度。文献[17]引入一种突变机制帮助算法跳出局部最优, 改善了算法求解精度不足的问题。文献[18]将SSA算法与PSO算法进行混合, 提高算法勘探阶段的灵活性, 获得了更高的寻优效率, 并成功应用于特征提取问题。
上述SSA变体均在一定程度上增强了SSA算法的优化性能, 但早熟收敛、全局开发与局部探索能力不平衡等问题仍然存在。此外, “没有免费午餐”(no-free-lunch, NFL)定理[19]指出, 不存在一种适用于所有优化问题的优化算法。因此, 提出一种性能较好的SSA变体是非常有价值的。基于上述分析, 本文提出一种基于正交设计的折射反向学习樽海鞘群算法(orthogonal opposition-based salp swarm algorithm, OOSSA)。
1 研究背景 1.1 樽海鞘群算法樽海鞘是一种外形类似水母的胶状海洋生物, 通过吸入和排出海水完成移动。研究人员将樽海鞘群体的链式结构数学化, 提出SSA。在基本SSA中, 位于樽海鞘链最前端的个体为领导者, 其余个体为跟随者。领导者根据食物源信息更新自身位置, 数学模型为[1]
| $ X_{j}^{1}=\left\{\begin{array}{l} F_{j}+c_{1}\left(\left(u_{j}-l_{j}\right) c_{2}+l_{j}\right), c_{3} \geqslant 0.5 \\ F_{j}-c_{1}\left(\left(u_{j}-l_{j}\right) c_{2}+l_{j}\right), c_{3}<0.5 \end{array}\right. $ | (1) |
式中: Xj1为领导者在第j维上的位置, Fj为食物源在第j维上的位置, uj和lj分别为搜索空间第j维的上下限, c2、c3为区间[0, 1]内的随机数, 分别决定领导者的移动步长和移动方向。
c1为距离控制因子, 其值随算法迭代非线性减小到趋于零, 计算公式如下:
| $ c_{1}=2 \mathrm{e}^{-\left(\frac{4 t}{T}\right)^{2}} $ | (2) |
式中: t为当前迭代次数, T为最大迭代次数。
跟随者位置更新的数学模型为[1]
| $ X_{j}^{i}=\frac{1}{2}\left(X_{j}^{i}+X_{j}^{i-1}\right) $ | (3) |
式中: Xji为第i个跟随者在第j维上的位置, 且i≥2。
SSA算法包括全局勘探和局部开采两个阶段。初始化时期, 樽海鞘链群在搜索空间中勘探, 并锁定最优解区域。随后, 算法进入开采阶段, 搜索代理在最优解区域内精确搜索, 以提高求解精度。其中, 距离控制因子c1对算法的寻优过程有重要影响。迭代前期, 较大的c1帮助种群勘探整个解空间; 迭代后期, 较小的c1帮助种群在特定的区域内精确开采。由于缺乏关于食物源位置(全局最优解)信息的先验知识, 将每轮迭代中的全局最优个体更新为当前食物源的位置。
1.2 反向学习反向学习(opposition-based learning, OBL)最初由Tizhoosh[20]提出, 已成功应用于多种智能优化算法, 其主要思想是同时评估当前可行解和其反向解, 并选择较优解进入下一代的迭代计算。Rahnamayan等[21]证明: 相比于当前解, 反向解有更大概率接近全局最优。因此, 反向学习策略能够有效提高算法性能。根据樽海鞘群算法分析可知, 基本SSA中, 领导者负责带领群体向全局最优解所在的区域移动。因此, 领导者的位置一定程度上决定了群体的移动方向。如果领导者陷入局部最优, 则群体将跟随至局部极值区域, 导致算法早熟收敛。将反向学习策略应用于领导者个体上避免其陷入局部最优, 则该个体能够更好的带领群体移动至更有前景的搜索区域。
定义1 反向数(opposite number)[22]。假设x∈[a, b]为一个实数, 则x的反向数
| $ \tilde{x}=a+b-x $ | (4) |
将反向数的概念推广到多维空间, 给出反向点的定义。
定义2 反向点(opposite point)[22]。假设X=(x1, x2, …, xD)为D维空间中的一点, x1, x2, …, xD∈R且xj∈[aj, bj](j=1, 2, …, D), 则反向点
| $ \tilde{x}_{j}=a_{j}+b_{j}-x_{j} $ | (5) |
基于透镜成像原理的折射反向学习策略(lens opposition-based learning, LOBL)是一种新型智能技术, 其本质是在OBL的基础上, 结合光学透镜成像原理所设计的一种动态反向学习策略, 以帮助算法寻找更优的候选解, 已成功与粒子群算法[23]、灰狼优化算法[24]等结合, 并大幅提高了算法性能。
定义3 基点(cardinal point)[23]: 若D维空间中存在若干点o1, o2, …, om, 任意点X=(x1, x2, …, xD)和其反向点
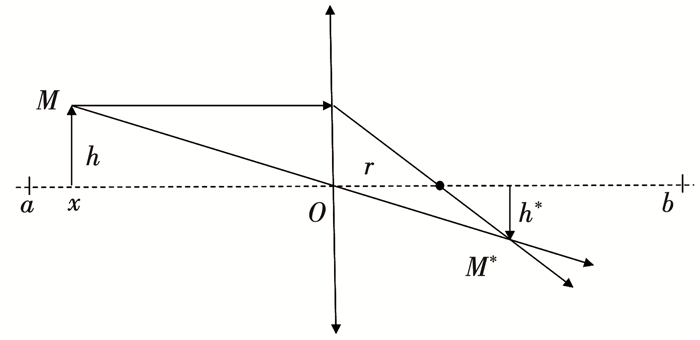
以一维空间为例, 假设坐标轴上x处有高度为h的物体M, 且x∈[a, b], 基点位置o(本文取[a, b]中点作为基点)上放置焦距为r的透镜, 基于透镜成像可得到高度为h*的像M*, 透镜成像原理见图 1。
|
图 1 透镜成像原理示意 Fig. 1 Optical lens imaging principle |
图 1中, x以o为基点得到对应的反向点
| $ \frac{(a+b) / 2-x}{\tilde{x}-(a+b) / 2}=\frac{h}{h^{*}} $ | (6) |
令h/h*=k, k为缩放因子。变换式(6)即可得到反向点的计算公式为
| $ \tilde{x}=(a+b) / 2+(a+b) / 2 k-x / k $ | (7) |
当k=1时, 式(7)即为中心位置在坐标点[-(a+b)/2, (a+b)/2] 的OBL[22]。根据OBL策略得到的反向个体是固定的, 而根据k值不同, 通过LOBL得到的反向个体是动态的。
将式(7)推广到D维空间, 一般化透镜折射反向学习策略得到
| $ \tilde{x}_{j}=\left(a_{j}+b_{j}\right) / 2+\left(a_{j}+b_{j}\right) / 2 k-x_{j} / k $ | (8) |
式中: xj和
正交试验设计(orthogonal experimental design, OED)能够通过少量试验次数找到多因素、多水平实验的最优试验组合[25]。例如, 对于2水平7因素的试验, 若采用测试的方法找出最优组合, 需27=128次试验。若采用正交试验设计, 根据正交表L8(27), 如式(9), 仅通过8次试验即可找出最优或较优组合, 大幅提高了试验效率。但根据正交试验特性, 并不能保证正交表中的试验解包含该试验的最优解[25]。因此在使用正交表时, 通常需要进行因素分析来找到试验的理论最优组合, 并结合正交表中的所有组合一起确定试验的最优解。因此, 对于2水平7因素的试验, 需首先根据正交表L8(27)得到8组候选最优试验解, 其次进行因素分析, 找到一组理论最优组合, 最后对9种组合进行评估, 找出该实验的最优组合。
| $ L_{8}\left(2^{7}\right)=\left[\begin{array}{lllllll} 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 2 & 2 & 2 & 2 \\ 1 & 2 & 2 & 1 & 1 & 2 & 2 \\ 1 & 2 & 2 & 2 & 2 & 1 & 1 \\ 2 & 1 & 2 & 1 & 2 & 1 & 2 \\ 2 & 1 & 2 & 2 & 1 & 2 & 1 \\ 2 & 2 & 1 & 1 & 2 & 2 & 1 \\ 2 & 2 & 1 & 2 & 1 & 1 & 2 \end{array}\right] $ | (9) |
由式(1)可知, 领导者仅在食物源的引导下更新自身位置, 由于缺乏先验知识, 难以确定当前食物源是否处于全局最优。如果食物源处于局部最优, 则整个樽海鞘链群都将聚集在局部最优区域, 种群多样性缺失, 导致算法收敛至局部最优。为增强SSA算法跳出局部最优的能力, 提出一种正交反向学习策略(orthogonal lens opposition-based learning, OLOBL), 并将其应用到领导者个体上产生新的候选个体。
OLOBL是结合OED与LOBL技术所设计的一种策略。领导者执行OLOBL策略, 跳跃到更有前景的搜索区域, 从而提高种群多样性, 降低算法陷入局部最优的概率。但文献[26]的研究表明: 对于一个个体, 其反向个体仅在部分维度上的值优于当前个体。因此, 对个体的所有维度均取基于OLOBL的折射反向值会造成维度退化现象, 即部分维度反而远离全局最优解。针对这一问题, 结合OED和LOBL技术, 设计一种正交折射反向学习策略, 充分挖掘当前个体与反向个体的每一维分量, 并对二者的优势维度进行组合, 产生部分折射反向解。
将OLOBL策略嵌入SSA算法, 优化问题的维度D对应正交试验设计中的因素, 个体与折射反向个体即为正交试验设计中的两个水平。构建部分反向解的具体描述过程为: 对当前个体和其折射反向个体设计一个2水平D因素的正交试验, 产生M个部分折射反向解, M按照式(10)进行计算。其中, 根据正交试验表产生部分反向解时, 若正交表的元素为1, 试验解对应维上取当前个体的值; 若正交表的元素为2, 试验解对应维上取折射反向个体的值。
| $ M=2^{\left\lceil\log _{2}(D+1)\right\rceil} $ | (10) |
根据正交试验特性, 正交表中第一行的元素全为1, 这就代表第一组试验解即为个体本身, 不需要评估。另外M-1组试验解是当前个体与其反向个体优势维度的组合, 即部分折射反向解, 需要评估。在使用正交试验设计时, 需进行因素分析, 找出一组不存在于正交表中的理论最优组合, 需要评估。因此, 执行一次OLOBL策略需要的函数评估次数为M次。在进化迭代过程中, 仅对领导者执行OLOBL策略, 并从领导者和其正交折射反向个体中选择较优个体进入下一代, 这样可以有效增强算法的全局勘探能力, 同时减少函数的评价次数, 从而改善算法的整体性能。
2.2 惯性权重策略由追随者位置更新模型可知, 基本SSA中追随者在保留自身特征的同时学习前一个个体, 完成位置更新。其位置更新机制较为单一, 一旦领导者陷入局部最优, 追随者必然跟随至该局部极值区域。为增强跟随者位置更新机制的灵活性, 本文引入一种非线性递减惯性权重来评价前一个个体对当前追随者的影响程度。新的追随者位置更新公式为
| $ X_{j}^{i}=\frac{1}{2}\left(X_{j}^{i}+\omega X_{j}^{i-1}\right) $ | (11) |
| $ \omega=\omega_{\max }-\left(\omega_{\max }-\omega_{\min }\right) \frac{2}{2+\mathrm{e}^{10-0.04 t}} $ | (12) |
式中: ω为本文设计的惯性权重, ωmax和ωmin分别为初始惯性权重和最终惯性权重。
2.3 OOSSA算法所提OOSSA算法的实现流程如下:
Step1 设置算法参数: 种群规模N, 最大函数评估次数Fmax, 搜索维度D, 搜索区域上下边界u、l; 在搜索空间中随机生成N个樽海鞘个体构成初始种群;
Step2 计算初始种群的适应值并排序, 首个个体定义为领导者, 其余个体为跟随者, 并将适应值最优个体的位置作为当前食物源;
Step3 判断樽海鞘个体角色: 若为领导者则进入Step4;若为跟随者则进入Step5;
Step4 根据式(1)更新领导者位置, 产生候选解1, 同时执行OLOBL策略, 产生候选解2, 根据适应值保留候选解1和候选解2中的较优个体;
Step5 根据式(11)更新跟随者位置;
Step6 比较食物源和当前最优个体的适应值, 取较优者作为新的食物源;
Step7 若函数评估次数达到最大函数评估次数Fmax, 则输出食物源位置, 即为最优解; 否则, 返回Step3继续迭代。
OOSSA在保持SSA算法基本框架和整体流程不变的情况下, 在领导者位置更新的同时执行OLOBL策略, 同时修改了跟随者的位置更新公式。设函数维度为D, 种群规模为N, 最大迭代次数为T。樽海鞘群体移位操作的时间复杂度为O(TND), 领导者执行OLOBL操作的时间复杂度为O(TD2), 因此, OOSSA算法总的时间复杂度为O(TN2), 与原SSA算法时间复杂度一致, 这表明在改进算法的同时并没有增加计算开销。
3 仿真实验及结果分析 3.1 测试函数为了验证OOSSA算法的有效性, 实验选取12个CEC2017测试函数进行, 见表 1。其中, 函数维度设置为100维。表 1中, f1~f6为单峰函数, 此类函数没有局部极值点, 只有一个全局最优解, 用于测试算法的局部开采能力; f7~f12为复杂多峰函数, 此类函数有一个全局最优解的同时包含多个局部极值点, 用于测试算法平衡全局勘探和局部开采的能力。
| 表 1 CEC2017测试函数 Tab. 1 CEC2017 benchmark functions |
实验环境为: Windows 10操作系统, Intel(R) Core(TM) i7-7700处理器, 主频3.60 GHz, 8 GB内存, 算法基于Matlab R2014b用M语言编写。
3.2 与基本SSA和改进SSA算法的比较利用OOSSA算法求解表 1中的12个经典测试函数, 并与基本SSA算法(SSA, 2017)[1]、多子群的共生非均匀高斯变异SSA算法(MSNSSA, 2020)[13]、生命周期启发的SSA算法(LSSA, 2020)[27]、自适应SSA算法(ASSA, 2021)[28]、高斯SSA算法(GSSA, 2021)[29]、改进反向学习的SSA算法(OBSSA, 2021)[30]、具有惯性权重的自适应SSA算法(ASSO, 2021)[31]、随机取代的双惯性权重SSA算法(RDSSA, 2021)[32]、混合鲸鱼优化的SSA算法(IWOSSA, 2021)[33]进行比较。为保证比较的公平性, 所有算法均使用相同的种群规模N=30, 最大函数评价次数15 000。对比算法的其他参数设置与各自原文献保持一致。在OOSSA算法中, 缩放因子k=10 000。每种算法对每个测试函数独立运行30次实验, 分别记录它们的平均值和标准差, 并采用Friedman检验[34]对算法进行排名, 见表 2。
| 表 2 OOSSA与多种SSA变体对12个100维测试函数的结果比较 Tab. 2 Comparison of OOSSA and SSA variants on twelve 100-dimensional test functions |
由表 2可知, 除了函数f5、f7、f9、f11, OOSSA算法在其他8个测试函数上均一致收敛到全局最优。与SSA、LSSA、ASSA、GSSA和IWOSSA算法相比, OOSSA在所有基准函数上取得了较好的结果, 且收敛精度与求解稳定性远优于对比算法。与MSNSSA算法相比, OOSSA分别在9个和2个函数上取得了较好和相似的结果。OOSSA分别在7个和4个测试函数上获得了比OBSSA算法较好和相似的结果; 然而, 对于f4, OBSSA得到了较好的结果。与ASSO算法相比, OOSSA分别在9个和3个测试函数上获得了较好和相似的结果。与RDSSA算法相比, OOSSA分别在9个和2个测试函数上取得了较好和相似的结果; 然而, RDSSA在f7上获得了稍优的结果。根据表 2中Friedman排名检验结果, OOSSA算法排名第一, RDSSA排名第二, 其次为OBSSA、ASSO、MSNSSA、GSSA、ASSA、LSSA、IWOSSA和SSA。证明不同SSA变体的改进策略均有一定效果, 求解性能优于基本SSA算法, 但不如OOSSA算法。
此外, 本文采用Wilcoxon秩和检验[34](显著性水平设为0.05)从统计意义上对10种算法的寻优结果进行评价。在表 3中给出所有基准函数的OOSSA和其他对比算法的Wilcoxon秩和检验中计算的p值。例如, 如果最优算法为OOSSA, 则在OOSSA versus SSA, OOSSA versus LSSA等之间进行成对比较。其中, N/A表示不适用, 意味着相应算法在该函数上表现最优, 没有统计数据与自身进行比较。符号“-”“+”“=”分别表示OOSSA劣于、优于、相当于各算法的结果。当p < 0.05时, 拒绝零假设, 即认为两种对比算法有显著差异[34]。
| 表 3 100维基准函数Wilcoxon秩和检验的p值 Tab. 3 p-value for Wilcoxon's rank-sum test on 100-dimensional benchmark functions |
由表 3可以看出, 除了f5的OOSSA versus OBSSA和OOSSA versus ASSO这两种情形下p>0.05, 其他对比算法的p < 0.05, 根据Wilcoxon秩和检验, 这说明OOSSA算法的整体性能明显优于基本SSA算法和其他8种改进SSA算法, 且OOSSA算法的优越性在统计上是显著的。总体来说, 相比于基本SSA算法和其他最新的SSA变体, OOSSA算法能够提供竞争性的性能。
3.3 两种改进策略的有效性分析本文对基本SSA算法做了两个方面的改进, 分别为OLOBL策略和惯性权重策略(inertia weight, IW), 为了验证两种改进策略的有效性, 分别将它们嵌入到基本SSA算法中, 得到OLOBL-SSA和IW-SSA算法。此外, 将结合OBL的正交反向学习(orthogonal opposition-based learning, OOBL)嵌入SSA中, 得到OOBL-SSA, 并与OLOBL-SSA进行对比, 以验证LOBL和OBL策略的有效性。本节选取表 1中的12个测试函数进行仿真实验来比较OOSSA、OLOBL-SSA、IW-SSA、OOBL-SSA和基本SSA算法。设置所有算法的种群规模均为30, 最大函数评价次数均为15 000, 函数维度设置为100维, 每种算法在每个函数上独立运行30次, 分别记录它们的平均值、标准差和Friedman排名检验结果, 见表 4。
| 表 4 采用不同改进策略的SSA算法在CEC2017上的实验结果 Tab. 4 Comparison of SSA with different improvement strategies for CEC2017 |
从表 4可知, OLOBL-SSA、IW-SSA和OOBL-SSA算法在所有函数上的求解精度和求解稳定性均优于原SSA算法, 这证明了改进策略的有效性。与IW-SSA和OOBL-SSA算法相比, OOSSA在除f8和f10之外的10个函数上均取得了较优的结果; 对于f8和f10, 3种算法均达到了理论最优值。OLOBL-SSA算法则和OOSSA算法一样, 在多个测试函数上均能达到理论最优值, 但对于函数f5、f7和f11, OOSSA的寻优精度和寻优稳定性明显优于OLOBL-SSA, 尤其在函数f11上, OOSSA算法获得了显著的优势。基于上述分析, 两种改进策略均具备一定效果, 且两种改进策略同时作用能够进一步提高算法的寻优性能。此外, 从表 4可以看出, 相比于OOBL-SSA算法, OLOBL-SSA在除f8和f10之外的10个基准函数上均获得了显著的优势; 对于f8和f10, 两种算法均达到了理论最优值。这表明正交反向学习中采用LOBL策略能够更加有效地帮助算法跳出局部最优。此外, 由表 4中Friedman排名检验结果可知, OOSSA排名第一, OLOBL-SSA排名第二, 依次是IW-SSA、OOBL-SSA和SSA, 这进一步验证了改进策略的有效性以及OOSSA算法比单策略改进算法具备明显优势。
3.4 OOSSA算法求解大规模优化问题的可行性分析为验证OOSSA算法应用于求解大规模优化问题的可行性, 本节选取表 1中12个测试函数进行仿真实验, 并将函数维度设置为10 000维。设置所有算法的种群规模均为30, 最大函数评价次数均为15 000。表 5给出了OOSSA算法对12个大规模测试函数30次独立实验获得的最优解、最差解、平均值和标准差结果。此外, 在实验结果中加入求解成功率指标, 用于评价OOSSA算法处理大规模优化问题的效率。判断一次求解是否成功的标准为
| $ \left\{\begin{array}{l} \left|f_{\mathrm{A}}-f_{\mathrm{T}}\right| / f_{\mathrm{T}}<10^{-5}, f_{\mathrm{T}} \neq 0 \\ \left|f_{\mathrm{A}}-f_{\mathrm{T}}\right|<10^{-5}, f_{\mathrm{T}}=0 \end{array}\right. $ | (13) |
| 表 5 OOSSA算法求解10 000维测试函数的实验结果 Tab. 5 Experimental results of OOSSA for solving 10 000-dimensional test functions |
式中: fA为算法在测试函数上取得的结果, fT为测试函数的理论最优值。
由表 5可以看出, 除了f5、f7、f9、f11, OOSSA算法在其他8个测试函数上均能收敛到理论最优值, 且根据标准差能够看出, OOSSA在保持高求解精度的同时具备同样优越的求解稳定性; 对于函数f5、f7、f9和f11, OOSSA虽未能找到理论最优解, 但仍获得了令人满意的结果。这充分说明OOSSA算法在处理大规模优化问题时具备较强的鲁棒性。在求解成功率方面, OOSSA在除f5和f7之外的10个测试函数上均能达到100%的成功率, 这也充分说明OOSSA算法能够有效应用于求解大规模优化问题。
3.5 与其他群体智能算法的比较为了进一步验证OOSSA算法的有效性, 将其与9种最新的群体智能优化算法进行对比, 它们分别是海洋捕食者算法(MPA, 2020)[35]、平衡优化器(EO, 2020)[36]、基于选择对立的灰狼优化器(SOGWO, 2020)[37]、改进的灰狼优化器(IGWO, 2021)[38]、算数优化算法(ArOA, 2021)[39]、阿基米德优化算法(AOA, 2020)[40]、基于多样性和突变机制的飞蛾扑火优化(DMMFO, 2021)[41]、双重自适应权重的飞蛾扑火优化(WEMFO, 2021)[42]、基于反向学习的灰狼优化器(OGWO, 2021)[43]。本节选取表 1中的12个测试函数进行仿真实验, 并将函数维度设置为D=100。设置所有算法的种群规模均为30, 最大函数评价次数均为15 000。对比算法的其他参数设置与原文献保持一致。表 6给出了10种算法对12个测试函数30次独立实验获得的平均值和标准差, 并采用Friedman检验对算法进行排名。
| 表 6 OOSSA与多种前沿算法对12个测试函数的结果比较 Tab. 6 Comparison of OOSSA and nine cutting-edge algorithms for 12 test functions |
比较表 6中结果可知, 与SOGWO、WEMFO、DMMFO和OGWO算法相比, OOSSA在所有测试函数上均获得了较好的结果。与MPA和EO算法相比, OOSSA在9个函数上获得了较好的性能和2个函数上得到了相似的性能; 然而, 对于f7, OOSSA获得稍差的结果。与ArOA和IGWO算法相比, OOSSA分别在11个和1个测试函数上取得了较好和相似的性能。OOSSA在10个测试函数上获得了比AOA算法较好的结果; 对于函数f8和f10, 两种算法均收敛至全局最优。此外, 从Friedman排名检验结果可以看出, OOSSA排名第一, AOA和EO排名并列第二, 其余依次是MPA、WEMFO、ArOA、OGWO、IGWO、SOGWO和DMMFO。这进一步验证了OOSSA算法的优越性。
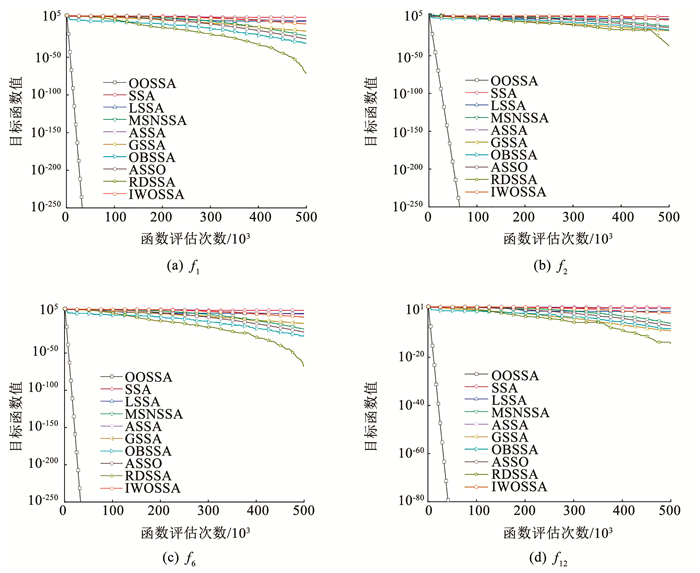
3.6 收敛性分析为进一步验证OOSSA算法的收敛性能, 图 2给出了OOSSA、SSA、和各SSA变体对表 1中部分代表性基准函数的收敛曲线。图 3给出了OOSSA和各前沿算法对表 1中部分代表性测试函数的收敛曲线。设置所有算法的种群规模均为30, 最大函数评价次数均为15 000, 函数维度设置为D=100。
|
图 2 多种SSA变体对4个代表性测试函数的收敛曲线 Fig. 2 Convergence curves of different SSA variants for four representative test functions |
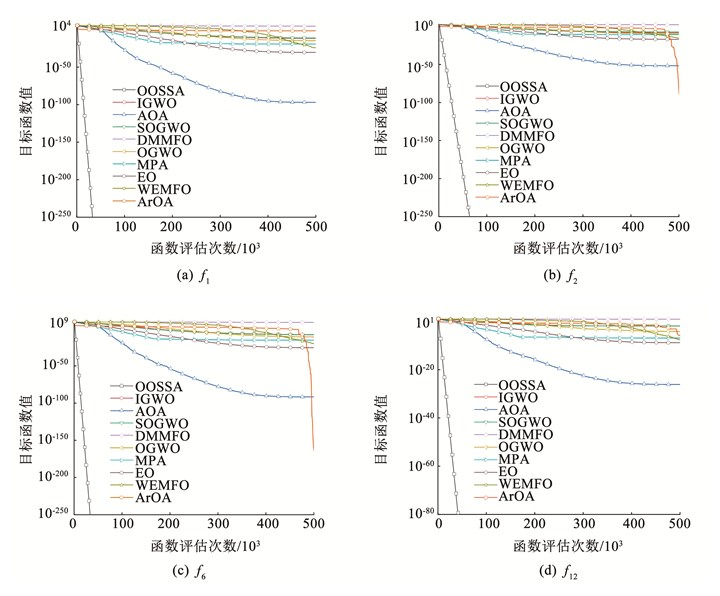
|
图 3 多种前沿算法对4个代表性测试函数的收敛曲线 Fig. 3 Convergence curves of different cutting-edge algorithms for four representative test functions |
从图 2和图 3可以看出, 与基本SSA和8种SSA变体相比, OOSSA算法在所有函数上均获得了较高的解精度和收敛速度。与其他9种最新的群体智能算法相比, OOSSA在求解精度和收敛速度方面同样表现出较大优势。
4 OOSSA的工程优化应用案例 4.1 压力容器设计问题从文献[44]中选取圆柱形压力容器设计优化问题来测试OOSSA算法解决实际工程设计问题的能力。压力容器设计问题的目标为最小化制作成本。其中制作成本包括焊接、材料和成型3部分。为解决该问题, 需要确定管壁厚度Ts, 顶盖壁厚Th, 内壁直径R和容器管身长度L这4个设计变量的最佳值。首先, 将设计变量编号, 得到
| $ \begin{gathered} f(\boldsymbol{x})=0.6224 x_{1} x_{2} x_{3}+1.7781 x_{2} x_{3}^{2}+ \\ 3.1661 x_{1}^{2} x_{4}+19.84 x_{1}^{2} x_{3} \end{gathered} $ |
| $ \left\{\begin{array}{l} g_{1}(\boldsymbol{x})=-x_{1}+0.0193 x_{3} \leqslant 0 \\ g_{2}(\boldsymbol{x})=-x_{3}+0.00954 x_{3} \leqslant 0 \\ g_{3}(\boldsymbol{x})=-\pi x_{3}^{2} x_{4}-\frac{4}{3} \pi x_{3}^{3}+1296000 \leqslant 0 \\ g_{4}(\boldsymbol{x})=x_{4}-240 \leqslant 0 \end{array}\right. $ |
式中: x1≤0, x2≤99, x3≤10, x4≤200。
利用OOSSA算法求解压力容器设计问题, 并与文献[44]中的几种先进算法进行比较。根据文献[44], 将OOSSA的种群规模设置为30, 最大函数评价次数设置为15 000, 独立运行30次后取最优解。将所得结果以及文献[44]中已有的实验结果列于表 7。从表中可以看出, OOSSA获得了最低的设计成本5 933.766 65, 明显优于其他10种对比算法, 进一步证明OOSSA算法能够有效应用于工程优化问题。
| 表 7 各算法的压力容器设计结果对比 Tab. 7 Comparison of optimization results of different algorithms for press vessel design |
随着智能化时代的到来, 自主移动机器人被广泛应用到越来越多的领域中, 如智能送餐、智能仓储、军事战争等。在机器人学中, 路径规划是一项关键技术。传统的路径规划算法在面对复杂地形时难以生成理想的轨迹。因此, 研究人员试图使用群体智能优化算法解决机器人路径规划问题。智能优化算法在搜索过程中表现出较强的随机性, 因此在规划路径时表现出的性能有较大差距。提出一种收敛速度快、鲁棒性强、环境适应能力好的算法是非常有意义的。基于上述分析, 本节提出一种基于OOSSA的自主移动机器人路径规划算法。
5.1 编码在设计路径规划算法时, 采用导航点模型构建机器人的工作环境设置, 并采用三次样条插值对路径进行平滑。其中, 导航点能够反映所规划路径的转向次数, 因此将路径上所有导航点编码为一个樽海鞘个体。
5.2 构建适应度函数为机器人规划路径时, 需要考虑两个因素: 1)路径长度最短; 2)避开所有障碍物。基于这两个因素, 本文设计了一种高效的适应度函数, 以评价路径的质量, 见式(14)。
| $ f=L \cdot(1+\rho \cdot \tau) $ | (14) |
式中ρ为路径非法度放大系数, 用于排除有碰撞的路径, 取值为1 000。L为当前路径的长度, 按照下式进行计算
| $ L=\sum\limits_{i=1}^{n} \sqrt{\left(x_{i+1}-x_{i}\right)^{2}+\left(y_{i+1}-x_{i}\right)^{2}} $ | (15) |
式中(xi, yi)为插值点i的坐标。
τ为路径非法度, 按照下式进行计算
| $ \tau=\sum\limits_{k=1}^{s} \sum\limits_{j=1}^{m} \max \left(1-\frac{d_{j, k}}{r_{k}}, 0\right) $ | (16) |
式中: s为障碍物的数量, m为路径中插值点的数量, dj, k为第j个插值点到第k个障碍物的距离, rk为第k个障碍物的半径。根据式(16)可知, 如果路径过障碍, 则τ>0, 反之, τ=0。
5.3 实验设置本节对所提算法进行仿真实验, 并与基本SSA算法、人工蜂群算法(ABC)、粒子群算法(PSO)、灰狼优化器(GWO)和萤火虫算法(FA)进行对比。设置所有算法的种群规模均为30, 最大函数评价次数均为15 000, 对比算法的参数与原始文献保持一致。为使实验结果更加可靠, 选取文献[45]中的两种测试环境进行仿真, 每种算法为每个地形独立规划30次路径, 并记录最优路径长度和平均寻优耗时。比较结果见表 8。各算法获得的路径见图 4。
| 表 8 不同环境下6种算法所求路径长度与平均寻优耗时比较 Tab. 8 Comparison of path lengths and average search time of six algorithms in different environments |
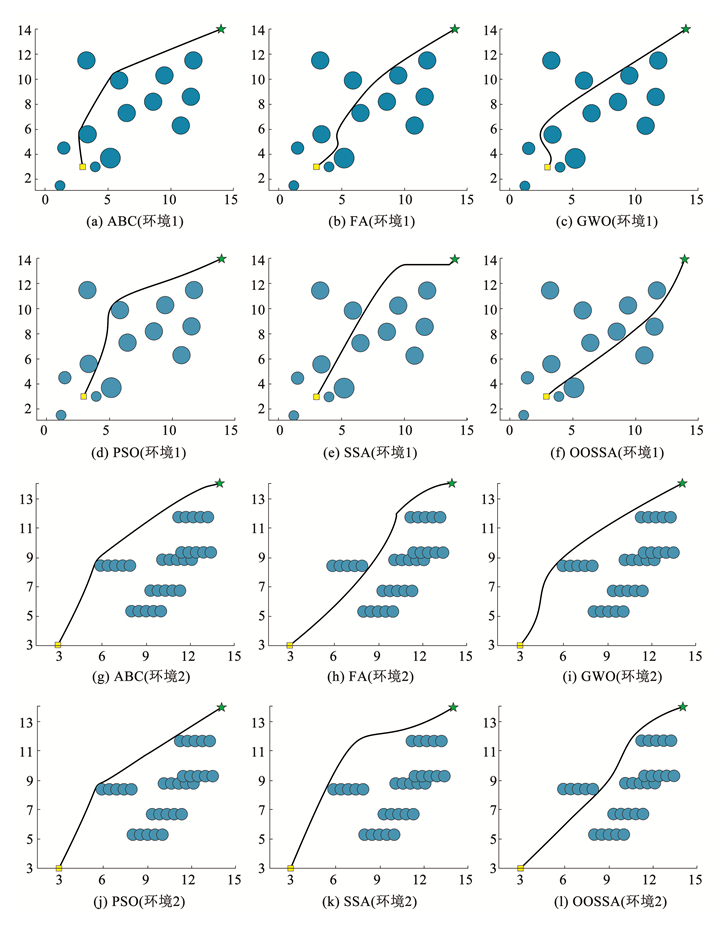
|
图 4 不同算法的规划路径对比 Fig. 4 Comparison of paths planned by different algorithms |
根据表 8可知, 在两种不同的地形设置中, 所提算法得到的最优路径长度均优于对比算法。在平均寻优耗时方面, OOSSA算法与PSO、ABC、GWO和SSA算法耗时相近, FA算法则消耗了较长的时间。从图 4可以看出, 6种算法在两种环境设置中所规划的路径均能避开所有障碍物。而OOSSA均可生成最合理的轨迹以帮助机器人从起点移动到终点, 这是因为OLOBL策略能够降低算法陷入局部最优的概率, 使算法在迭代前期能够规划出较为合理的轨迹。在迭代后期, 引入非线性惯性权重的跟随者位置更新模式能够帮助算法不断调整该路径, 进一步降低了路径长度。
6 结论本文提出一种基于正交设计的折射学习樽海鞘群算法。首先利用透镜折射反向学习和正交试验设计构造了一种正交折射学习策略OLOBL, 并应用到SSA中, 提高算法勘探能力的同时解决了反向学习存在的维度退化问题。其次, 在跟随者位置更新阶段引入自适应惯性权重因子, 以平衡算法的全局勘探和局部开采能力。对12个CEC2017基准测试函数、1个工程优化问题和移动机器人路径规划问题进行仿真实验研究, 并通过多种方式详细分析了所提算法的全局勘探、局部开采和跳出局部最优的能力。研究结果表明: OOSSA算法能够有效提升基本SSA算法的性能, 其在整体性能上要明显优于多种当前最先进的SSA变体和多种最新开发的群体智能优化算法。OOSSA在解决工程设计优化问题和机器人路径规划问题时, 同样获得了满意的结果。在未来的研究中, OOSSA算法将与光伏电池模块参数识别等问题相结合, 以期解决更多实际工程设计优化问题。
| [1] |
MIRJALILI S, GANDOMI A H, MIRJALILI S Z, et al. Salp swarm algorithm: a bio-inspired optimizer for engineering design problems[J]. Advances in Engineering Software, 2017, 114: 163. DOI:10.1016/j.advengsoft.2017.07.002 |
| [2] |
LIANG Haibo, ZOU Jialing, ZUO Kai, et al. An improved genetic algorithm optimization fuzzy controller applied to the wellhead back pressure control system[J]. Mechanical Systems and Signal Processing, 2020, 142: 106708. DOI:10.1016/j.ymssp.2020.106708 |
| [3] |
张艺瀛, 金志刚. 一种高维多模态优化的量子粒子群优化算法[J]. 哈尔滨工业大学学报, 2018, 50(11): 50. ZHANG Yiying, JIN Zhigang. Quantum particle swarmoptimization algorithm for high-dimensional multi-model optimization[J]. Journal of Harbin Institute of Technology, 2018, 50(11): 50. DOI:10.11918/j.issn.0367-6234.201806065 |
| [4] |
WANG Zongshan, DING Hongwei, LI Bo, et al. An energy efficient routing protocol based on improved artificial bee colony algorithm for wireless sensor networks[J]. IEEE Access, 2020, 8: 133577. DOI:10.1109/ACCESS.2020.3010313 |
| [5] |
李长安, 谢宗奎, 吴忠强, 等. 改进灰狼算法及其在港口泊位调度中的应用[J]. 哈尔滨工业大学学报, 2021, 53(1): 101. LI Chang'an, XIE Zongkui, WU Zhongqiang, et al. Improved grey wolf algorithm and its application in port berth scheduling[J]. Journal of Harbin Institute of Technology, 2021, 53(1): 101. DOI:10.11918/201911117 |
| [6] |
MIRJALILI S, LEWIS A. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51. DOI:10.1016/j.advengsoft.2016.01.008 |
| [7] |
WANG Zongshan, DING Hongwei, LI Bo, et al. Energy efficient cluster based routing protocol for WSN using firefly algorithm and ant colony optimization[J]. Wireless Personal Communications, 2022, 1. DOI:10.1007/s11277-022-09651-9 |
| [8] |
KHISHE M, MOHAMMADI H. Passive sonar target classification using multi-layer perceptron trained by salp swarm algorithm[J]. Ocean Engineering, 2019, 181: 98. DOI:10.1016/j.oceaneng.2019.04.013 |
| [9] |
TUBISHAT M, JA'AFAR S, ALSWAITTI M, et al. Dynamic salp swarm algorithm for feature selection[J]. Expert Systems with Applications, 2020, 164: 113873. DOI:10.1016/j.eswa.2020.113873 |
| [10] |
刘森, 贾志成, 陈雷, 等. 基于樽海鞘群体优化非负矩阵分解的高光谱图像解混算法[J]. 计算机辅助设计与图形学学报, 2019, 31(2): 315. LIU Sen, JIA Zhicheng, CHEN Lei, et al. Hyperspectral images unmixing based on nonnegative matrix factorization optimized by salp swarm algorithm[J]. Journal of Computer-Aided Design & Computer Graphics, 2019, 31(2): 315. DOI:10.3724/SP.J.1089.2019.17189 |
| [11] |
FATHY A, REZK H, NASSEF A M. Robust hydrogen-consumption-minimization strategy based salp swarm algorithm for energy management of fuel cell/supercapacitor/batteries in highly fluctuated load condition[J]. Renewable Energy, 2019, 139: 147. DOI:10.1016/j.renene.2019.02.076 |
| [12] |
陈雷, 蔺悦, 康志龙. 基于衰减因子和动态学习的改进樽海鞘群算法[J]. 控制理论与应用, 2020, 37(8): 1766. CHEN Lei, LIN Yue, KANG Zhilong. Improved salp swarm algorithm based on reduction factor and dynamic learning[J]. Control Theory & Applications, 2020, 37(8): 1766. DOI:10.7641/CTA.2020.90766 |
| [13] |
陈忠云, 张达敏, 辛梓芸. 多子群的共生非均匀高斯变异樽海鞘群算法[J/OL]. 自动化学报[2021-10-20] CHEN Zhongyun, ZHANG Damin, XIN Ziyun. Multi-subpopulation based symbiosis and non-uniform Gaussian mutation salp swarm algorithm[J/OL]. Acta Automatica Sinica[2021-10-20]. DOI: 10.16383/j.aas.c190684 |
| [14] |
张达敏, 陈忠云, 辛梓芸, 等. 基于疯狂自适应的樽海鞘群算法[J]. 控制与决策, 2020, 35(9): 2112. ZHANG Damin, CHEN Zhongyun, XIN Ziyun, et al. Salp swarm algorithm based on craziness and adaptive[J]. Control and Decision, 2020, 35(9): 2112. DOI:10.13195/j.kzyjc.2019.0012 |
| [15] |
刘景森, 袁蒙蒙, 左方. 面向全局搜索的自适应领导者樽海鞘群算法[J]. 控制与决策, 2021, 36(9): 2152. LIU Jingsen, YUAN Mengmeng, ZUO Fang. Global search-oriented adaptive leader salp swarm algorithm[J]. Control and Decision, 2021, 36(9): 2152. DOI:10.13195/j.kzyjc.2020.0090 |
| [16] |
QAIS M H, HASANIEN H M, ALGHUWAINEM S. Enhanced salp swarm algorithm: application to variable speed wind generators[J]. Engineering Applications of Artificial Intelligence, 2019, 80: 82. DOI:10.1016/j.engappai.2019.01.011 |
| [17] |
GHOLAMI K, PARVANEH M H. A mutated salp swarm algorithm for optimum allocation of active and reactive power sources in radial distribution systems[J]. Applied Soft Computing, 2019, 85: 105833. DOI:10.1016/j.asoc.2019.105833 |
| [18] |
IBRAHIM R A, EWEES A A, OLIVA D, et al. Improved salp swarm algorithm based on particle swarm optimization for feature selection[J]. Journal of Ambient Intelligence and Humanized Computing, 2019, 10(8): 3155. DOI:10.1007/s12652-018-1031-9 |
| [19] |
WOLPERT D H, MACREADY W G. No free lunch theorems for optimization[J]. IEEE Transactions on Evolutionary Computation, 1997, 1(1): 67. DOI:10.1109/4235.585893 |
| [20] |
TIZHOOSH H R. Opposition-based learning: a new scheme for machine intelligence[C]//Proceedings of International Conference on Computational Intelligence for Modelling Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce. Vienna: IEEE, 2005: 695. DOI: 10.1109/CIMCA.2005.1631345
|
| [21] |
RAHNAMAYAN S, TIZHOOSH H R, SALAMA M M A. Opposition versus randomness in soft computing techniques[J]. Applied Soft Computing, 2008, 8(2): 906. DOI:10.1016/j.asoc.2007.07.010 |
| [22] |
RAHNAMAYAN S, TIZHOOSH H R, SALAMA M M A. Opposition-based differential evolution[J]. IEEE Transactions on Evolutionary Computation, 2008, 12(1): 64. DOI:10.1109/TEVC.2007.894200 |
| [23] |
喻飞, 李元香, 魏波, 等. 透镜成像反学习策略在粒子群算法中的应用[J]. 电子学报, 2014, 42(2): 230. YU Fei, LI Yuanxiang, WEI Bo, et al. The application of a novel OBL based on lens imaging principle in PSO[J]. Acta Electronica Sinica, 2014, 42(2): 230. DOI:10.3969/j.issn.0372-2112.2014.02.004 |
| [24] |
龙文, 伍铁斌, 唐明珠, 等. 基于透镜成像学习策略的灰狼优化算法[J]. 自动化学报, 2020, 46(10): 2148. LONG Wen, WU Tiebin, TANG Mingzhu, et al. Grey wolf optimizer algorithm based on lens imaging learning strategy[J]. Acta Automatica Sinica, 2020, 46(10): 2148. DOI:10.3969/j.issn.0372-2112.2014.02.004 |
| [25] |
ZHANG Hongliang, HEIDARI A A, WANG Mingjing, et al. Orthogonal Nelder-Mead moth flame method for parameters identification of photovoltaic modules[J]. Energy Conversion and Management, 2020, 211: 112764. DOI:10.1016/j.enconman.2020.112764 |
| [26] |
PARK S Y, LEE J J. Stochastic opposition-based learning using a beta distribution in differential evolution[J]. IEEE Transactions on Cybernetics, 2016, 46(10): 2184. DOI:10.1109/TCYB.2015.2469722 |
| [27] |
BRAIK M, SHETA A, TURABIEH H, et al. A novel lifetime scheme for enhancing the convergence performance of salp swarm algorithm[J]. Soft Computing, 2021, 25(1): 181. DOI:10.1007/s00500-020-05130-0 |
| [28] |
SALGOTRA R, SINGH U, SINGH S, et al. Self-adaptive salp swarm algorithm for engineering optimization problems[J]. Applied Mathematical Modelling, 2020, 89: 188. DOI:10.1016/j.apm.2020.08.014 |
| [29] |
NAUTIYAL B, PRAKASH R, VIMAL V, et al. Improved salp swarm algorithm with mutation schemes for solving global optimization and engineering problems[J]. Engineering with Computers, 2021, 1. DOI:10.1007/s00366-020-01252-z |
| [30] |
HUSSIEN A G. An enhanced opposition-based salp swarm algorithm for global optimization and engineering problems[J]. Journal of Ambient Intelligence and Humanized Computing, 2021, 13(1): 1. DOI:10.1007/s12652-021-02892-9 |
| [31] |
OZBAY F A, ALATAS B. Adaptive salp swarm optimization algorithms with inertia weights for novel fake news detection model in online social media[J]. Multimedia Tools and Applications, 2021, 80(26): 1. DOI:10.1007/s11042-021-11006-8 |
| [32] |
REN Hao, LI Jun, CHEN Huiling, et al. Stability of salp swarm algorithm with random replacement and double adaptive weighting[J]. Applied Mathematical Modelling, 2021, 95: 503. DOI:10.1016/j.apm.2021.02.002 |
| [33] |
SAAFAN M M, EL-GENDY E M. IWOSSA: an improved whale optimization salp swarm algorithm for solving optimization problems[J]. Expert Systems with Applications, 2021, 176: 114901. DOI:10.1016/j.eswa.2021.114901 |
| [34] |
DERRAC J, CARCIA S, MOLINA D, et al. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms[J]. Swarm and Evolutionary Computation, 2011, 1(1): 3. DOI:10.1016/j.swevo.2011.02.002 |
| [35] |
FARAMARZI A, HEIDARINEHAD M, MIRJALILI S, et al. Marine predators algorithm: a nature-inspired metaheuristic[J]. Expert Systems with Applications, 2020, 152: 113377. DOI:10.1016/j.eswa.2020.113377 |
| [36] |
FARAMARZI A, HEIDARINEJAD M, STEPHENS B, et al. Equilibrium optimizer: a novel optimization algorithm[J]. Knowledge-Based Systems, 2020, 191: 105190. DOI:10.1016/j.knosys.2019.105190 |
| [37] |
DHARGUPTA S, GHOSH M, MIRJALILI S, et al. Selective opposition based grey wolf optimization[J]. Expert Systems with Applications, 2020, 151: 113389. DOI:10.1016/j.eswa.2020.113389 |
| [38] |
NADIMI-SHAHRAKI M H, TAGHIAN S, MIRJALILI S. An improved grey wolf optimizer for solving engineering problems[J]. Expert Systems with Applications, 2021, 166: 113917. DOI:10.1016/j.eswa.2020.113917 |
| [39] |
ABUALIGAH L, DIABAT A, MIRJALILI S, et al. The arithmetic optimization algorithm[J]. Computer Methods in Applied Mechanics and Engineering, 2021, 376: 113609. DOI:10.1016/j.cma.2020.113609 |
| [40] |
HASHIM F A, HUSSAIN K, HOUSSEIN E H, et al. Archimedes optimization algorithm: a new metaheuristic algorithm for solving optimization problems[J]. Applied Intelligence, 2021, 51(3): 1531. DOI:10.1007/s10489-020-01893-z |
| [41] |
MA Lei, WANG Chao, XIE Nenggang, et al. Moth-flame optimization algorithm based on diversity and mutation strategy[J]. Applied Intelligence, 2021, 51(8): 5836. DOI:10.1007/s10489-020-02081-9 |
| [42] |
SHAN Weifeng, QIAO Zenglin, HEIDARI A A, et al. Double adaptive weights for stabilization of moth flame optimizer: balance analysis, engineering cases, and medical diagnosis[J]. Knowledge-Based Systems, 2021, 214: 106728. DOI:10.1016/j.knosys.2020.106728 |
| [43] |
YU Xiaobing, XU Wangying, LI Chenliang. Opposition-based learning grey wolf optimizer for global optimization[J]. Knowledge-Based Systems, 2021, 226: 107139. DOI:10.1016/j.knosys.2021.107139 |
| [44] |
HEIDARI A A, MIRJALILI S, FARIS H, et al. Harris hawks optimization: algorithm and applications[J]. Future Generation Computer Systems, 2019, 97: 849. DOI:10.1016/j.future.2019.02.028 |
| [45] |
AGARWAL D, BHARTI P S. Implementing modified swarm intelligence algorithm based on Slime moulds for path planning and obstacle avoidance problem in mobile robots[J]. Applied Soft Computing, 2021, 107: 107372. DOI:10.1016/j.asoc.2021.107372 |
 2022, Vol. 54
2022, Vol. 54


