近年来,大量基于元启发的仿生优化算法用来解决科学领域的各种优化难题并有较好的优化效果,如工程难题、商业最优问题、经济学和复杂多目标优化问题。元启发算法因其灵活、结构简单、无梯度机制等优点受到研究者的关注[1]。近年来出现各种基于仿生优化算法和基于物理模型的算法,如基于模仿自然界中的鸟群和鱼群的觅食行为提出了粒子群算法(particle swarm optimization, PSO)[2]、受麻雀的觅食行为和反捕食行为的启发提出麻雀搜索算法(sparrow search algorithm, SSA)[3]、受狼群的等级领导行为和守猎过程的启发提出了灰狼算法(grey wolf optimization, GWO)[4]、基于裸鼹鼠和繁育者的繁殖行为,培育精英后代提出裸鼹鼠算法(naked mole-rat algorithm, NMRA)[5]、模拟自然界中成虫发光萤火虫聚集行为提出萤火虫算法(firefly algorithm, FA)[6]、模拟生物在自然环境的遗传和进化过程提出遗传算法(genetic algorithm, GA)、受领导者引导和跟随者跟进共同在海洋中和寻食启发提出樽海鞘群算法(salp swarm algorithm, SSA)[1]以及2021年根据变色龙群体在搜索食物、360°眼睛转动和捕猎行为提出变色龙群算法(chameleon swarm algorithm,CSA)[7]等。
2020年,文献[8]根据雌雄蜉蝣群体的聚集、婚配行为和交配繁殖行为提出一种基于群体仿生优化算法——蜉蝣算法(mayflies algorithm,MA)[8], 其灵感来自蜉蝣群体的社会行为,尤其是它们的交配过程,雄雌性蜉蝣成熟后婚配及求偶和繁殖而启发。从MA的结构表达形式上看,是由PSO、GA和FA算法的结合改进,由此MA也符合优胜劣汰规律的种群进化算法,具有较好的局部搜索性能和良好的种群多样性。遗憾的是,MA虽具备上述良好的性能和优势,但前期的全局搜索能力不理想导致后期即使具备较好的开发能力也达不到理想求解精度和算法稳定性,且易陷入局部最优[8]。但提出至今,在工程优化设计、车间调度和动力系统中的应用已有相关报道,说明MA在实际应用和求解上具备不同优越性能。MA和其他群体智能算法一样,依然存在局部最优、搜索和开发之间得不到平衡和寻优精度低下,在实际求解问题时导致精度低下,求解结果不稳定等缺点。
近年,针对其他形式的群体智能算法的缺点,有不少研究者提出不同策略进行优化改进,改善其全局寻优性能和求解的稳定性; 文献[9]利用Circle映射初始化鲸鱼优化算法的种群,使种群初始化过程中有更好的遍历性和降低群体的盲目性,且引入反向学习策略对鲸鱼的位置求出反向解,提高了鲸鱼优化算法的搜索能力和求解的稳定性; 文献[10]将樽海鞘链按照不同的适应度划分成3个子群,引入敏感性分析、共生策略和非均匀高斯变异对樽海鞘链的3个子群针对性改进,结果表明改进的樽海鞘群体有更好的引导作用和较强的多样性,提升了算法的性能; 文献[11]引入黄金正弦机制和自适应惯性权重,改善蝴蝶优化算法的全局搜索能力和搜索的自适应能力; 文献[12]将速度边界和能量边界的方法引入粒子群算法,证明出粒子群的惯性部分和社会部分间建立了良好的平衡,结果表明它能跳出局部最优,具有更好的搜索能力。
为改善MA的全局寻优能力、算法的稳定性能和探索搜索的自适应性,提出增强全局搜索和自适应的蜉蝣算法(MIWMA),补偿算法的劣势保留已有优势结合,提高搜索能力和稳定性能,更好建立MA存在的搜索和开发之间得不到平衡的问题。为增强蜉蝣种群的多样性,引入非均匀变异和全局最优位置更新策略,同时不放弃适应度差的个体,并指引其向全局最优位置靠近,增强了蜉蝣群体搜索的多样性,提升算法跳出局部最优的能力;引入不完全伽马函数和Beta累加分布惯性权重,使其在已提出的惯性权重基础上能自适应动态调节惯性系数,增强全局搜索和开发之间的平衡,同时其自适应动态搜索能力得到提升,进一步提高了算法的搜索精度;引入局部停滞策略调节原有的搜索特性,在惯性部分和社会部分间进行调节,使蜉蝣群体间进行信息交流共享和合作,增强算法搜索能力。
1 蜉蝣算法蜉蝣算法受雄性蜉蝣与雌性蜉蝣婚配的社会吸引行为启发的优化算法。其寻优过程为:雄性蜉蝣个体的寻优、雌性蜉蝣个体的寻优和优异个体的雄雌交配。设蜉蝣在d维空间的位置表示为X=(x1, x2, …, xd), 其d维空间的速度表示为V=(v1, v2, …, vd)。
1.1 雄性蜉蝣的运动当雄性蜉蝣投放在一个固定的区域内会容易发生聚集行为,向着群体中心位置靠近。蜉蝣个体的位置是按照自身经验或邻近个体的行为调节。用xijt表示个体i在j维空间的第t次迭代的位置,vijt则表示个体i在j维空间的第t次迭代的速度。蜉蝣会向中心聚集不断地移动和在水面上舞蹈训练,蜉蝣的速度更新如下:
| $ v_{i j}^{t+1}=\left\{\begin{array}{l} v_{i j}^{t}+a_{1} \mathrm{e}^{-\beta r_{\mathrm{P}}^{2}}\left(p_{j}-x_{i j}^{t}\right)+ \\ \;\;\;\;\;\;\;a_{2} \mathrm{e}^{-\beta r_{\mathrm{g}}^{2}}\left(g_{j}-x_{i j}^{t}\right), f\left(y_{i}\right)>f\left(x_{i}\right) \\ v_{i j}^{t}+d \cdot r, f\left(y_{i}\right) \leqslant f\left(x_{i}\right) \end{array}\right. $ | (1) |
式中: vijt+1是雄性蜉蝣i在j维空间上t+1次迭代的速度,a1和a2为雄性蜉蝣移动行为的吸引系数,p为先前迭代的最好位置,g是全局最优位置,β为能见度系数,其目的是控制蜉蝣的能见范围。d代表舞蹈系数,不断吸引异性靠近它。r是一个随机系数,取值为[-1, 1]。rp和rg分别为当前位置与p的距离和当前位置与g的距离。
由上,rp和rg是最优位置与当前位置的距离,其距离的计算用欧氏距离表示,欧氏距离计算公式如下:
| $ \left\|x_{i}-X_{i}\right\|=\sqrt{\sum\limits_{j=1}^{n}\left(x_{i j}-X_{i j}\right)^{2}} $ | (2) |
式中: xij为蜉蝣i的j维,Xi为pi或gi的位置。
雄性蜉蝣的位置更新为
| $ x_{i}^{t+1}=x_{i}^{t}+v_{i}^{t+1} $ | (3) |
式中: vit+1是雄性蜉蝣i的第t+1次迭代的速度,yit为蜉蝣i的第t次迭代的位置。
1.2 雌性蜉蝣的运动雌性蜉蝣与雄性蜉蝣相比的显著特点是雄性蜉蝣投放在固定区域内会发现聚集行为而雌性蜉蝣则不会,雌性蜉蝣会与雄性蜉蝣靠近完成繁殖。雌性蜉蝣的位置更新如下:
| $ y_{i}^{t+1}=y_{i}^{t}+v_{i}^{t+1} $ | (4) |
雌性蜉蝣的速度更新表达如下:
| $ v_{i j}^{t+1}=\left\{\begin{array}{l} v_{i j}^{t}+a_{2} \mathrm{e}^{-\beta r_{\mathrm{m}}^{2}}\left(x_{i j}^{t}-y_{i j}^{t}\right), f\left(y_{i}\right)>f\left(x_{i}\right) \\ v_{i j}^{t}+l_{\mathrm{f}} \cdot r, f\left(y_{i}\right) \leqslant f\left(x_{i}\right) \end{array}\right. $ | (5) |
式中: vijt为蜉蝣i在j维空间上的速度,yijt为蜉蝣i在j维空间上的位置。a2为雄雌蜉蝣吸引系数,β为能见度系数, rm为雄性蜉蝣和雄性蜉蝣的距离。lfl是随机游走系数,r为随机数,取值为[-1, 1]。
1.3 雌雌蜉蝣的交配蜉蝣的交配过程可用交叉算子表示,从雄性蜉蝣中选择一个父本,雌性蜉蝣选取母本。父本选择的方式与雄雌吸引的方式一致。优胜劣汰机制,将最优个体的雄性和雌性蜉蝣进行繁殖得到最优个体,依次类推,得到的两个子代表达式为
| $ S_{\text {offspring1 }}=L \cdot S_{\text {male }}+(1-L) \cdot S_{\text {female }} $ | (6) |
| $ S_{\text {offspring2 }}=(1-L) \cdot S_{\text {male }}+L \cdot S_{\text {female }} $ | (7) |
式中: L为服从高斯分布的随机数,取值范围为L∈[0, 1];Smale是父本,Sfemale是母本。
2 增强全局搜索和自适应权重的蜉蝣算法 2.1 非均匀变异下的位置更新策略 2.1.1 引入上一次位置更新指引策略蜉蝣群体每经一次迭代更新,都会保留历史的最好位置。历史最优位置可为后续搜索提供新方向,新位置既受历史最优位置的指引又受上一次迭代位置的影响,可有效避免算法易陷入局部最优的缺陷,提高算法的搜索能力。引入历史位置和上一次指引的位置更新表达式为
| $ x_{i}^{t}=x_{i}^{t-1}+c \cdot\left(g-x_{i}^{t-1}\right) $ | (8) |
式中: t为当前迭代次数,xit为当前迭代的位置,xit-1为上一次迭代位置,g为历史迭代的全局最优位置。c为取值[0, 1]之间随机数。
2.1.2 非均匀的高斯变异由式(8)可看出,历史迭代的最优位置有可能不是目标优化中的最优位置,完全按照历史最优位置去搜索,将会导致陷入局部最优达不到搜索效果,多样性得不到保证。针对这一缺陷,对全局最优位置g变异,增强搜索多样性,使全局搜索能力得到进一步增强,利用一种非均匀随机高斯变异策略。非均匀随机高斯变异策略的表达式如下:
| $ \Delta(t, N)=N\left(1-r^{\left(1-\frac{t}{T_{\max }}\right)^{2}}\right) $ | (9) |
| $ N \sim N\left(\left(g-x_{i}^{i-1}\right), \sigma\right) $ | (10) |
| $ {\sigma}={\sigma}_{0}^{2} e^{-\frac{t}{T_{\max }}} $ | (11) |
式中: Tmax为最大迭代次数,Δ为非均匀高斯变异的步长,N服从参数的高斯分布, σ为高斯分布的标准差。σ02初始迭代方差,用来控制变异范围,r为随机数。结合式(9)~(11)对雄性群体和雌性群体的位置变异更新,新的位置更新表达式为
| $ x_{i}^{t}=x_{i}^{t-1}+c\left(\mathit{\Delta} \cdot g_{x}-x_{i}^{t-1}\right) $ | (12) |
| $ y_{i}^{t}=y_{i}^{t-1}+c\left(\mathit{\Delta} \cdot g_{y}-y_{i}^{t-1}\right) $ | (13) |
引入非均匀高斯变异下的位置更新策略有以下特点:在迭代前期,Δ相较于后期较大,引入位置更新后,前期g有较强的变异效果,使其向上一次迭代的位置引导向g靠近,能增强种群的多样性和前期具有较强的全局寻优能力;前期具备较强的全局寻优能力,其g与xit-1位置距离较大,同时保持前期较大的方差,生成的高斯分布随机数增强变异步长和策略的寻优性能; 后期,g与xit-1位置距离缩小,同时保持方差逐渐变小,搜索趋于稳定,蜉蝣向局部最优位置精细搜索增强开发能力。
2.2 不完全伽马函数和Beta累加分布权重 2.2.1 非线性惯性权重指引策略惯性权重因子对算法的搜索能力和开发能力具有一定的指导作用,体现出雄性蜉蝣和雌性蜉蝣能够借鉴一定先验行为的能力。文献[13]指出,较大的惯性权重具有良好的全局搜索能力;较小的惯性权重具有较好的开发能力,使其能得到更好局部搜索能力。引入一种非线性递减的自适应惯性权重,惯性权重因子的表达式如下:
| $ \omega(t)=\left(1-\frac{t}{T_{\max }}\right)^{\sqrt[\alpha]{\frac{t}{T_{\max }}}} $ | (14) |
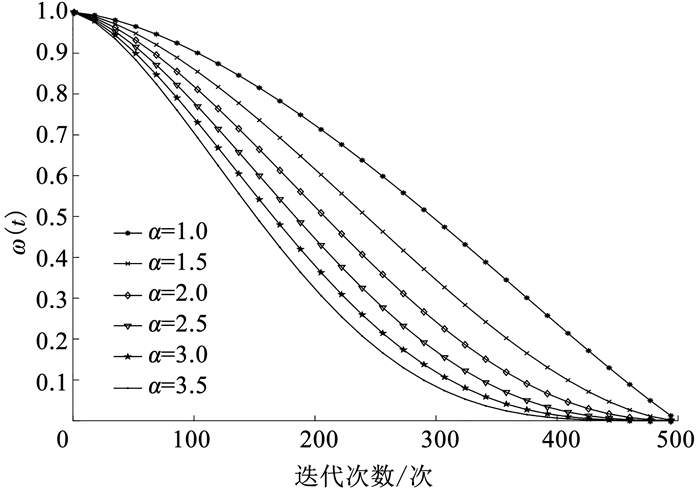
式中: t为当前的迭代次数,Tmax为最大迭代次数,α为惯性权重的控制参数。即不同的α值对MA的搜索具有一定的影响,图 1为α=1.0、1.5、2.0、2.5、3.0、3.5,迭代500次的ω权重变化。
|
图 1 不同参数的惯性权重 Fig. 1 Inertial weights of different parameters |
上述ω(t)具有确定性的数学表达,即整个搜索和开发过程会按照ω(t)的关系执行,容易按照一定规律搜索,算法同样会进行局部最优的可能,做不到真正的自适应机制。为使ω能进行自适应动态调整,引入不完全伽马函数[14]和Beta分布累加函数[15],其新的数学表达式如下:
| $ \omega^{\prime}(t)=\frac{1}{\lambda} \omega(t) \cdot \Gamma\left(\lambda, 1-\frac{t}{T_{\max }}\right)+\nu \mathrm{B}\left(\sigma ; b_{1}, b_{2}\right) $ | (15) |
| $ \Gamma(\lambda, u)=\int_{0}^{\lambda} \mathrm{e}^{-t} t^{u-1} \mathrm{~d} t $ | (16) |
| $ \mathrm{B}\left(\sigma ; b_{1}, b_{2}\right)=\frac{1}{\mathrm{~B}\left(b_{1}, b_{2}\right)} \int_{0}^{\sigma} t^{b_{1}-1}(1-t)^{b_{2}-1} \mathrm{~d} t $ | (17) |
式中:Γ(λ,u)为不完全的伽马函数,λ>0的随机变量,取值为λ=0.1;ν为偏移调整因子,调整ω的偏移程度,取ν=0.1;B(σ; b1, b2)为服从Beta分布的累加分布函数的逆函数, 经大量实验结果取b1=1, b2=2,σ取值与式(11)一致。
引入不完全伽马函数和Beta累加分布函数的自适应惯性权重,雄性蜉蝣与雌性的位置更新表达式为
| $ x_{i}^{t+1}=\omega^{\prime}(t) \cdot x_{i}^{t}+v_{i}^{t+1} $ | (18) |
| $ y_{i}^{t+1}=\omega^{\prime}(t) \cdot y_{i}^{t}+v_{i}^{t+1} $ | (19) |
为了选取一个合适的α值并探究引入不完全伽马函数和Beta累加分布的惯性权重优势,利用经典测试函数f1对不同参数和不同权重独立运行30次,实验迭代500次,维度为30, 运行的结果见表 1。
| 表 1 不同α值和适应权重的搜索结果 Tab. 1 Search results with different α values and adaptive weights |
由表 1结果可知,参数α的选取直接影响算法寻优能力。当α=1时,MA具有较好的搜索能力,因此本文取α=1。同样,表 1是ω和ω′在不同参数和同一参数下的对比结果,在同样的α的取值下,ω′具有更好的收敛精度,目标求解的性能更好。说明引入的不完全伽马函数和Beta累加分布的惯性权重优势较ω更明显,与ω相比具有更好的自适应动态调整能力。
2.3 局部停滞对抗策略在基本MA表达式中,社会部分中雄性蜉蝣和雌性蜉蝣的速度更新总会满足以下关系:
| $ v_{i}=a_{i} \mathrm{e}^{-\beta r^{2}}\left(p_{j}-p_{i}\right) $ | (20) |
式中若pj和pi相邻很近,其欧氏距离r就很小, 由于式(20)中含有指数关系式, 呈现指数衰减慢,但后面的距离非常小;同理,pj和pi相邻较远,指数衰减严重,因此社会部分难以达到平衡。针对这一缺陷,对蜉蝣的速度更新机制进行改进。
首先,引入监测搜索停滞系数[12],用于控制是否出现局部迭代收敛的情况,停滞系数为
| $ C_{t}=\min \left\{1, \max \left\{\frac{t-\psi_{t}}{\widetilde{T}}-1, 0\right\}\right\} $ | (21) |
式中:
| $ \eta=\eta_{-} C_{t}+\eta_{+}\left(1-C_{t}\right) $ | (22) |
式中:η为平衡调节算子,调节蜉蝣的速度更新,根据Ct选择出合适的调节值调整惯性部分和社会认知部分,加强群体间的信息交流协作。取η+=1和η-=0.1。引入调节算子,雄性蜉蝣的速度表达式为
| $ v_{i j}^{t+1}=\left\{\begin{array}{l} \left(1-\omega^{\prime} \eta\right) v_{i j}^{t}+\eta a_{2} \mathrm{e}^{-\beta r_{\mathrm{m}}^{2}}\left(x_{i j}^{t}-y_{i j}^{t}\right), f\left(y_{i}\right)>f\left(x_{i}\right) \\ \left(1-\omega^{\prime} \eta\right) v_{i j}^{t}+\eta \cdot l_{\mathrm{f}} \cdot r, f\left(y_{i}\right) \leqslant f\left(x_{i}\right) \end{array}\right. $ | (23) |
雄性蜉蝣的速度表达式为
| $ v_{i j}^{t+1}=\left\{\begin{array}{c} \left(1-\omega^{\prime} \eta\right) v_{i j}^{t}+\eta a_{1} \mathrm{e}^{-\beta r_{\mathrm{P}}^{2}}\left(p_{j}-x_{i j}^{t}\right)+ \\ \eta a_{2} \mathrm{e}^{-\beta r_{\mathrm{B}}^{2}}\left(g_{j}-x_{i j}^{t}\right), f\left(y_{i}\right)>f\left(x_{i}\right) \\ \left(1-\omega^{\prime} \eta\right) v_{i j}^{t}+\eta \cdot d \cdot r, f\left(y_{i}\right) \leqslant f\left(x_{i}\right) \end{array}\right. $ | (24) |
式中ω′为式(15)自适应惯性权重。在式(20)的监测搜索停滞系数,判断是否存在搜索停滞,利用式(21)得出停滞的步长值。由式(22)和式(23)知,蜉蝣的速度更新具有惯性部分和社会部分。惯性部分用于调节蜉蝣自身的状态,遵循前期较强的全局搜索能力及后期的开发能力,使其随迭代的增加保持平衡;社会部分则是蜉蝣群体的信息交流和吸引。当蜉蝣搜索状态陷入局部最优时,按照调节算子平衡惯性部分和社会部分,使其调节自身状态和吸引、信息交流间合作,快速跳出局部最优,增强算法的搜索能力。
2.4 MIWMA算法流程图及复杂度分析 2.4.1 MIWMA算法流程图综合上述引入的3种策略,文中提出的MIWMA算法的流程图和步骤见图 2。

|
图 2 MIWMA算法执行流程图 Fig. 2 MIWMA algorithm execution flow chart |
根据运算规则,设MA算法的目标运行计算量为T(n), 维度为D,雌性蜉蝣种群大小为N1,雄性蜉蝣种群大小为N2,蜉蝣的交配数量为n, 因此交配过程的复杂度记为
对MA引进策略中,引入了非均匀变异的位置更新策略,对每一维位置都变异更新,其此过程的复杂度为O(DN1+DN2), 引入不完全伽马函数和Beta累加分布的权重策略的复杂度为O(1),引入的停滞策略的复杂度为O(1)。两种策略都嵌入在速度和位置更新中,因此MIWMA的时间复杂度依然为
为证实MIWMA的有效性和优异性,对不同策略进行实验测试,文中引入两个实验测试。其中,引入非均匀变异下的位置更新记为MMA;引入不完全伽马函数和Beta累加分布权重记为WMA;引入停滞对抗措施策略记为IMA; 组合优化策略记为MIWMA。另外,引入最近的其他优异的改进的智能算法对比, 如自适应惯性权重的樽海鞘群算法(AIWSSA)[16]、共生非均匀高斯变异的樽海鞘群算法(MSNSSA)[10]以及稳定边界和收敛增强的改进粒子群算法(IPSO)[12]进行复现比较。
3.1 参数设置实验选取种群规模为40(雄性20,雌性20),种群交叉个数为20。为了公平比较,设置MSNSSA、AIWSSA以及IPSO的种群大小均为40,实验结果均独立运行50次,各算法具体参数设置见表 2。
| 表 2 不同算法的参数设置 Tab. 2 Parameter setting of different algorithms |
实验1:为验证改进的算法与其他算法的数据有效性比较,实验1利用12个经典基准测试函数测试,包括5个单峰(unimodal)函数,4个多峰(multi-modal)函数及3个维度固定(fix-dimension)的测试函数。函数类型有可分(separable)和不可分(non-separable)。测试函数的具体信息见表 3。
| 表 3 基准测试函数 Tab. 3 Benchmark function |
实验1记录算法的最优值、平均值、标准差、每次独立运行的平均耗时(T/s),见表 4。表 4中,从最优值上看,除函数f8以外,整体而言MIWMA与MA相比具有显著性优势。对于函数f8,整体而言, 引入非均匀变异的位置更新策略和不完全函数与Beta累加分布惯性权重最能凸显出算法的优化性能。另外,不同策略(MMA、WMA、IMA)与MA对比,都优于原始MA, 且函数f7和f9在多峰函数测试下能够达到理论值0,f7的维度取值为100维,同样具有显著性优势。另外,由表中可看出, 对MSNSSA和AIWSSA以及IPSO复现算法而言,性能介于MA与MIWMA之间,即对复现的算法较原始MA有效,但不及MIWMA。对于函数(f10~f12)而言,由于维度是固定的,维度的大小不高,虽然测试函数中含有参数,但求解相对容易,所以引入的策略和原始MA和其他复现算法能够达到较好最优值。通过表 7的秩和检验效果看,引入的策略与其他算法也有更好的效果。由此,MIWMA的优势较为明显。
| 表 4 经典测试函数下的优化结果对比 Tab. 4 Comparison of optimization results under classic test functions |
平均值能够呈现独立运行50次后的平均效果。从单峰和多峰测试看,平均值整体都要比MA、MSNSSA、AIWSSA以及IPSO的效果更好。对于函数f8,其效果不及MMA策略的MIWMA,体现出非均匀变异的位置更新对优化的敏感度非常高,比混合策略还要好。标准差可以反映出独立运行结果的偏离程度,独立运行次数越多,标准差就显得更加精确。对单峰函数和多峰函数,其融合策略的标准差最小,即平均值的偏离程度较小,进一步体现了MIWMA的稳定性较好。从维度固定的函数可看出,最优值上与其他算法相比性能相当,平均值直接折射出MIWMA的优势。由此f10~f12的平均值效果最好,且达到理论值,其次是MMA和AIWSSA。标准差衡量它们的偏离程度,虽然f10和f11的标准差没有其他好,均值不在最优范围,整体而言没有实现最优。
从耗时分析上看,MA、WMA、IMA、MMA和MIWMA的耗时基本持平。因为MA引入的几个策略从复杂度上看并没有增加过多的复杂度开销,MIWMA和MA处于同一量级,只是增加了少量语句的执行。与其他算法比较而言,MA时间复杂度略高于IPSO、MSNSSA和AIWSSA,因为运行MA涉及到雄性和雌性蜉蝣的更新和交配,且后续的变异等增加了运算时间,耗时多数都在0.5~2.5 s之间,单次运行时间也不会太长。但从表 4中看出,部分函数下MA的时间比改进策略还长,主要原因就是受到运行环境的影响,但都不会相差太多,耗时差处于可接受范围内。
算法在整个搜索的平均情况,可以从图形上直观看出各算法搜索的优劣,绘制部分函数收敛曲线见图 3,直观看出迭代500次的平均收敛特性。由图 3可看出,MIWMA的精度最高,且与其他算法相比整个过程具备较好的搜索性能。从曲线上看,MIWMA算法在前期具备很好的搜索效果,说明引入的自适应惯性权重策略发挥着较好的搜索指引作用,动态调整能力较好;另外,算法在后期的搜索中也具备较好的寻优能力,迭代曲线持续降低,则引入非均匀的高斯变异和局部停滞发挥了较好的搜索能力。由此,从收敛曲线分析,3种改进策略的有效性得到进一步验证。

|
图 3 部分测试函数平均收敛曲线 Fig. 3 Average convergence curves of some test functions |
实验2:为了进一步显现改进的MIWMA的优势,对比其有效性和稳定性等性能,实验2利用IEEE CEC2021函数集中基本、转换和旋转组合集进行性能测试。选取CEC2021中单峰、多峰、混合(hybrid)和复合(composition)类别的函数进行测试。函数集的具体信息见表 5,函数定义见文献[17]。
| 表 5 CEC2021函数具体信息 Tab. 5 Detailed information of CEC2021 functions |
实验2验证每种策略的性能对比,设置最大迭代次数为20 000次,维度为20。同样引入改进MSNSSA、AIWSSA和IPSO对比,对比结果见表 6。
| 表 6 CEC2021优化对比 Tab. 6 Optimization comparison of CEC2021 functions |
由表 6,分别记录CEC01~CEC10在不同算法运行下的平均值和标准差。由于IEEE CEC函数具有复杂的函数特征,难以找到目标函数值。由表中可看出,MIWMA中只有少部分目标值劣于其他算法,总体上看依然具有较好的性能,靠近目标最优值的函数个数最多。可判断引入策略是有效的,且从标准差来看也具备良好的稳定性。因此,本文从两个实验证实了MIWMA的有效性和算法的性能。
3.3 与其他智能算法对比为更清晰突出算法的先进性,引入近年其他研究者的成果进行对比, 包括:麻雀搜索算法(SSA)[2]、差分进化的裸鼹鼠算法(DE-NMRA)[5]、正弦差分进化算法(SinDE)[18]、协方差矩阵适应进化算法(CMA-ES)[18]、记忆指导的正弦余弦算法(MG-CSA)[18]、迭代映射和单纯形法的灰狼算法(SMIGWO)[14]、嵌入Circle映射和小孔成像反向学习的鲸鱼优化算法(MGWO)[9]以及自适应正态云模型的引力樽海鞘群算法(CGSSA)[19]。对比结果见表 7。
| 表 7 与其他智能算法的均值对比 Tab. 7 Comparison of mean value with other intelligent algorithms |
根据表 7与其他智能算法的对比,虽然其部分函数与其他算法相比不是最优效果,从总体上看,依然具有较好的寻优优势。
3.4 统计分析实验中对各算法独立运行50次,8个算法以及12个测试函数进行对比测试,数据量达到统计分析要求。可以从统计学的角度分析MIWMA的优越性,判断是否存在统计学的显著差异。首先,利用非参数检验的Wilcoxon秩和检验[20]方法计算出相应的P值,对经典测试函数进行分析; 然后,利用Friedman’s统计检验[21]得出经典测试函数与CEC集测试函数的算法排名和综合性评估。表 8为Wilcoxon秩和检验在α=5%的显著性水平下的P值。若P < 0.05,则拒绝原假设接受备择假设,即拒绝两组数据没有显著性的差异, 得出两组数据存在差异的结论。表 8中,+/-/=分别表示MIWMA算法与其他算法对比的性能为优于/劣于/性能相当的个数,其中NaN标记性能相当。
| 表 8 经典测试函数下MIWMA与其他算法对比的秩和检验P值 Tab. 8 P values of rank sum test of MIWMA compared with other algoritlms under classic test functions |
由表 8可知,大部分的秩和检验P值小于0.05,从而说明融合策略算法的性能较其他算法的差异是显著的,即可认定该算法有优异的收敛性能。
上述是不同测试函数下评估不同算法的性能,但还需要进一步验证整个算法在统计学上是否有差异。因此,利用Friedman’s的统计检验,利用卡方检验(χ2)[22]来评估所得临界值的差异,判断拒绝或接受原假设得出结论。设显著水平α=0.05, 对8个算法进行性能检验,见表 9。排名计算公式如下:
| $ R_{j}=\frac{1}{N} \sum\limits_{i=1}^{N} r_{i}^{j} $ | (25) |
| 表 9 经典函数Friedman’s测试下算法的统计排名 Tab. 9 Statistical ranking of algorithms under Friedman's test of classic functions |
式中: N为测试函数个数,rij为测试函数i的算法j的排名, Rj越小,性能越好,反之则性能越劣。由表 9,MIWMA的排名最小,说明其性能是最优越的,其次是MMA、AIWSSA、WMA, 最后是IMA和MA,说明提出的MIWMA较其他算法和原始算法都有效,排名也在其之前。
根据表 4中的结果,算法个数为8,其自由度为7,测试函数为12个,卡方值为31.534 4。查表得自由度为7,显著水平α=0.05下, 卡方值为14.067 14,由此计算的卡方值远大于查表临界的卡方值,说明所给的数据存在显著性差异。根据自由度、卡方值与P值的换算,得出P值为4.953 47×10-5。因此,计算P值明显小于0.05,由此可判定这些算法在精度上存在显著性差异,所以总体MIWMA存在统计学差异,性能表现最好。
上述只是说明总体的MIWMA存在统计学差异,但具体的组间差异还需进一步比对。因此,需要进行两两比较调整α值,根据P值从小到大进行排序,将最小的P值和α/i进行比较,i代表算法个数。引入Holm-Bonferroni进行后续校正[23]。MIWMA的排名和各方面效果都很好,设MIWMA为控制算法。进行后续检验来进一步区分算法。表 10为控制算法与其他算法的校正结果。
| 表 10 经典函数Holm's后续检验下的结果 Tab. 10 Results of Holm's subsequent test of classic function |
根据表 10中的结果,有MIWMA vs.MMA和MIWMA vs.AIWSSA的判定决策是接受,即0.180 942 1> 0.05和0.050 926 3>0.025,即MIWMA与MMA、AIWSSA的组间差异不明显,与其他性能比较差异明显,MA的统计分析结果最差。表中虽不能拒绝AIWSSA的假设,但从均值、平均排名等信息也能充分说明与MIWMA存在差异的。从表中可看出,MIWMA与MMA判决结果为接受,这与MIWMA的统计分析不显著,说明非均匀变异的位置更新策略最有效,较于其他两个改进策略而言更具有显著性。统计分析证明该统计方法进行整体算法性能的比较是科学、可靠的。结果反映MIWMA算法的优越性和可靠性。
表 11是CEC2021测试函数的统计检验对比。由表 11,MIWMA的平均排名最低,说明它的性能在比较的几个算法中是最优的。同样,根据上述方法,设置MIWMA为后续检验的控制算法进一步分析它们之间的差异。
| 表 11 CEC2021的Friedman’s测试下的统计排名 Tab. 11 Statistical ranking under Friedman's test of CEC2021 |
利用CEC2021的算法个数为8,自由度为7,卡方值为22.933,大于临界卡方值14.067 14,计算出P=0.001 751,小于0.05,由此存在显著的统计学差异。表 12可看出,MIWMA vs. WMA和MIWMA vs. AIWSSA的判决是接受,其他均拒绝。这说明,WMA和AIWSSA在CEC2021性能测试具有较好的性能,从表 12中的数据看, 相对劣于MIWMA。与其他函数相比,具有统计学上的统计差异,表现最差的为MA。结合经典测试函数与CEC2021测试函数而言,MIWMA在两种测试函数的基础上都能够表现较好的性能,从统计学上分析MIWMA的性能的可靠性。
| 表 12 CEC2021的Holm’s后续检验下的结果 Tab. 12 Results of Holm's follow-up test for CEC2021 |
为证实提出的融合策略在实际工程案例中的可行性,引入两种工程优化案例为测试背景,用于解决工程中的NP难题和目标约束问题.选用三杆桁架设计问题和拉/压弹簧设计问题进行各算法的优化对比,利用静态罚函数法[24]对约束条件进行处理,使各种对比方法达到公平的比较。其罚函数定义为
| $ \begin{gathered} \zeta(z)=f(z) \mp \\ {\left[\sum\limits_{i=1}^{m} l_{i} \cdot \max \left(0, t_{i}(z)\right)^{\alpha}+\sum\limits_{j=1}^{n} o_{j}\left|U_{j}(z)\right|^{\varphi}\right]} \end{gathered} $ | (26) |
式中:ζ(z)为目标函数,oj和li为惩罚系数,ti(z)和Uj(z)为约束条件。为了与其他算法对比,取值与文献[25]和文献[16]设置的参数值保持一致,取α和φ的值分别为2和1,惩罚因子取1 000。每个算法分别对具体工程优化50次。
4.1 拉/压弹簧设计问题拉/压弹簧设计问题是一种经典的约束优化问题,其目标是减轻拉/压弹簧设计的重量,见图 4。其主要约束条件有4个,还包括剪应力、踹振频率和最小扰度。参数主要有导线直径(d),平均线圈直径(D)和有效线圈数(N)等。为方便, 将其表示为X=(x1, x2, x3), 其中向量X的元素分别对应(d, D, N)。因此,其数学模型为
| $ \operatorname{Minimize} f(\boldsymbol{X})=\left(x_{3}+2\right) x_{2} x_{1}^{2} $ | (27) |
| $ \begin{gathered} \text { s. t. } g_{1}(\boldsymbol{X})=1-\frac{x_{2}^{3} x_{3}}{71785 x_{1}^{4}} \leqslant 0 \\ \mathrm{~g}_{2}(\boldsymbol{X})=\frac{4 x_{2}^{2}-x_{1} x_{2}}{12566\left(x_{2} x_{1}^{3}-x_{1}^{4}\right)}+\frac{1}{5108 x_{1}^{2}}-1 \leqslant 0 \\ g_{3}(\boldsymbol{X})=1-\frac{140.45 x_{1}}{x_{2}^{2} x_{3}} \leqslant 0 \\ g_{4}(\boldsymbol{X})=\frac{x_{1}+x_{2}}{1.5}-1 \leqslant 0 \end{gathered} $ | (28) |

|
图 4 拉/压弹簧设计示意 Fig. 4 Schematic diagram of tension/pressure spring design |
式中:0.05≤x1≤2, 0.25≤x2≤1.3, 2≤x3≤15。对拉/压弹簧问题,用7种不同算法进行对比。为比较明显的优势,引入SSA[1]、PSO[2]、MFO[26]、CSA[7]、SCA分别优化, 结果见表 13。
| 表 13 不同算法优化拉/压弹簧设计问题对比 Tab. 13 Comparison of design problems of tension/pressure springs optimized by different algorithms |
由表 13,MIWMA算法在拉/压弹簧问题具有良好的搜索能力;且独立运行50次后,均值与最优值之间也较为稳定,且优于其他对比算法。不难从表 13中看出,f(X)通过MIWMA的算法优化后,最优值也仅在0.000 01的精度上出现差别。算法的搜索都达到最优取值范围的附近,通过优化也只能进一步得出在更小搜索空间中也有好的搜索能力。
4.2 三杆桁架设计问题三杆桁架设计是满足压力条件下使得结构的重量最小为目标优化问题。三杆桁架的示意见图 5。其中包括3个决策变量,分别为A1、A2和A3。由于A1、A3对称,因此A1=A3。同理,为方便表示,将变量表示为X=(x1, x2)。其数学模型如下:
| $ \text { Minimize } f(\boldsymbol{X})=\left(2 \sqrt{2} x_{1}+x_{2}\right) l $ | (29) |
| $ \begin{aligned} \text { s.t. } g_{1}(\boldsymbol{X}) &=\frac{\sqrt{2} x_{1}+x_{2}}{\sqrt{2} x_{1}^{2}+2 x_{1} x_{2}} P-\sigma \leqslant 0 \\ g_{2}(\boldsymbol{X}) &=\frac{x_{2}}{\sqrt{2} x_{1}^{2}+2 x_{1} x_{2}} P-\sigma \leqslant 0 \\ g_{3}(\boldsymbol{X}) &=\frac{1}{x_{1}+\sqrt{2} x_{2}} P-\sigma \leqslant 0 \\ 0 & \leqslant x_{i} \leqslant 1, i=1, 2 \end{aligned} $ | (30) |

|
图 5 三杆桁架示意 Fig. 5 Schematic diagram of three-bar truss |
式中,取l=100 cm, P=2 kN/cm2, σ=2 kN/cm2。不同优化算法的结果见表 14。该问题在MIWMA和MA的基础上,还引入SSA、SMA[27]、MFO以及其他通过改进的算法ATMDE和AIWSSA在相应文献进行比较,保证对比公平。
| 表 14 不同算法的三杆桁架设计求解对比 Tab. 14 Comparison of three-bar truss design solutions of different algorithms |
由表 14,MIWMA对三杆桁架设计的工程问题同样能保持良好的性能,工程优化问题的局部搜索有更好寻优效果,并优于后面通过改进的算法,适用于解决工程优化中需求精度高的问题。通过引入的工程优化案例可看出,表 13和表 14体现出在工程应用中也有更好的局部搜索能力。
5 结论针对MA算法搜索和开发的不平衡和易陷入局部最优的缺点进行改进,提出一种增强全局搜索和自适应的蜉蝣算法——MIWMA。引入非均匀变异和上一次的位置更新策略指引其向精英位置移动,提高其多样性和搜索能力; 引入不完全伽马函数与Beta累加函数的分布数克服非线性自适应惯性权重的缺陷,动态调整算法搜索的自适应能力,进一步提高算法的收敛精度;引入停滞策略使其跳出局优,调节群体间信息交流合作,从而增强搜索性能。为证实MIWMA的性能和先进性,分别引入经典测试函数集验证算法的有效性和可靠性,引入CEC2021函数验证算法的性能。最后验证在工程难题中的应用潜能,在工程问题具有一定适用能力。对于大规模复杂问题、通信网络的资源分配和多约束调度下的最优问题,是下一步的研究重点。
| [1] |
MIRJALILI S, GANDOMI A H, MIRJALILI S Z, et al. Salp swarm algorithm: a bio-inspired optimizer for engineering design problems[J]. Advances in Engineering Software, 2017, 114: 118. DOI:10.1016/j.advengsoft.2017.07.002 |
| [2] |
RICCI F, ROKACH L, SHAPIRA B, et al. Recommender systems handbook[M]. Berlin: Springer, 2011: 1. DOI:10.1007/978-0-387-85820-3
|
| [3] |
XUE Jiankai, SHEN Bo. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems Science & Control Engineering, 2020, 8(1): 22. DOI:10.1080/21642583.2019.1708830 |
| [4] |
PANDA M, DAS B, PATI B B. Grey wolf optimization for global path planning of autonomous underwater vehicle[C]//Proceedings of the Third International Conference on Advanced Informatics for Computing Research. New York: Association for Computing Machinery, 2019: 177. DOI: 10.1145/3339311.3339314
|
| [5] |
SALGOTRA R, SINGH U, SINGH G, et al. A self-adaptive hybridized differential evolution naked mole-rat algorithm for engineering optimization problems[J]. Computer Methods in Applied Mechanics and Engineering, 2021, 383: 113916. DOI:10.1016/J.CMA.2021.113916 |
| [6] |
YANG Xinshe. Firefly algorithms for multimodal optimization[C]//Proceedings of International Symposium on Stochastic Algorithms. Heidelberg: Springer, 2009: 169. DOI: 10.1007/978-3-642-04944-6_14
|
| [7] |
MALIK S B. Chameleon swarm algorithm: a bio-inspired optimizer for solving engineering design problems[J]. Expert Systems with Applications, 2021, 174: 114685. DOI:10.1016/J.ESWA.2021.114685 |
| [8] |
ZERVOUDAKIS K, TSAFARAKIS S. A mayfly optimization algorithm[J]. Computers & Industrial Engineering, 2020, 145: 106559. DOI:10.1016/j.cie.2020.106559 |
| [9] |
张达敏, 徐航, 王依柔, 等. 嵌入Circle映射和逐维小孔成像反向学习的鲸鱼优化算法[J]. 控制与决策, 2021, 36(5): 1173. ZHANG Damin, XU Hang, WANG Yirou, et al. Whale optimization algorithm for embedded circle mapping and one-dimensional oppositional learning based small hole imaging[J]. Control and Decision, 2021, 36(5): 1173. DOI:10.13195/j.kzyjc.2019.1362 |
| [10] |
陈忠云, 张达敏, 辛梓芸. 多子群的共生非均匀高斯变异樽海鞘群算法[J/OL]. 自动化学报[2022-04-14] CHEN Zhongyun, ZHANG Damin, XIN Ziyun. Multi-subpopulation based symbiosis and non-uniform Gaussian mutation salp swarm algorithm[J/OL]. Acta Automatica Sinica[2022-04-14]. DOI: 10.16383/j.aas.c190684 |
| [11] |
高文欣, 刘升, 肖子雅, 等. 收敛因子和黄金正弦指引机制的蝴蝶优化算法[J]. 计算机工程与设计, 2020, 41(12): 3384. GAO Wenxin, LIU Sheng, XIAO Ziya, et al. Butterfly optimization algorithm based on convergence factor and gold sinusoidal guidance mechanism[J]. Computer Engineering and Design, 2020, 41(12): 3384. DOI:10.16208/j.issn1000-7024.2020.12.013 |
| [12] |
TONG X T, CHOI K P, LAI T L, et al. Stability bounds and almost sure convergence of improved particle swarm optimization methods[J]. Research in the Mathematical Sciences, 2021, 8(2): 18. DOI:10.1007/S40687-020-00241-4 |
| [13] |
SHI Yuhui, EBERHART R C. A modified particle swarm optimizer[C]//Proceedings of 1998 IEEE International Conference on Evolutionary Computation. Piscataway: IEEE, 1998: 69. DOI: 10.1109/ICEC.1998.699146
|
| [14] |
王梦娜, 王秋萍, 王晓峰. 基于Iterative映射和单纯形法的改进灰狼优化算法[J]. 计算机应用, 2018, 38. WANG Mengna, WANG Qiuping, WANG Xiaofeng. Improved grey wolf optimization algorithm based on iterative mapping and simplex method[J]. Journal of Computer Applications, 2018, 38(S2): 16. |
| [15] |
黄洋, 鲁海燕, 许凯波, 等. 一种动态调整惯性权重的简化均值粒子群优化算法[J]. 小型微型计算机系统, 2018, 39(12): 2590. HUANG Yang, LU Haiyan, XU Kaibo, et al. Simplified mean particle swarm optimization algorithm with dynamic adjustment of inertia weight[J]. Journal of Chinese Computer Systems, 2018, 39(12): 2590. |
| [16] |
白钰, 彭珍瑞. 基于自适应惯性权重的樽海鞘群算法[J]. 控制与决策, 2022, 37(1): 237. BAI Yu, PENG Zhenrui. Salp swarm algorithm based on adaptive inertia weight[J]. Control and Decision, 2022, 37(1): 237. DOI:10.13195/j.kzyjc.2020.0454 |
| [17] |
MOHAMED A W, HADI A, MOHAMED A K, et al. Problem definitions and evaluation criteria for the CEC 2021 special session and competition on single objection bound constrained numerical optimization[C]//Proceedings of 2021 IEEE Congress On Evolutionary Computation. [S. l. ]: IEEE, 2020
|
| [18] |
GUPTA S, DEEP K, ENGELBRECHT A P. A memory guided sine cosine algorithm for global optimization[J]. Engineering Applications of Artificial Intelligence, 2020, 93: 103718. DOI:10.1016/j.engappai.2020.103718 |
| [19] |
张铸, 张仕杰, 饶盛华, 等. 基于自适应正态云模型的引力樽海鞘群算法[J]. 控制与决策, 2022, 37(2): 344. ZHANG Zhu, ZHANG Shijie, RAO Shenghua, et al. Gravity salp swarm algorithm based on adaptive normal cloud model[J]. Control and Decision, 2022, 37(2): 344. DOI:10.13195/j.kzyjc.2020.1292 |
| [20] |
WILCOXON F. Individual comparisons by ranking methods[J]. Biometrics Bulletin, 1945, 1(6): 80. DOI:10.2307/3001968 |
| [21] |
CARABANTE K M, CHOKUMNOYPORN N, SRIWATTANA S, et al. Comparing Friedman versus Mack-Skillings data analyses on duplicated rank data: a case of visual color intensity[J]. Journal of the Science of Food and Agriculture, 2019, 99(13): 5696. DOI:10.1002/jsfa.9832 |
| [22] |
WOSNIOK W, HAECKEL R. A new indirect estimation of reference intervals: truncated minimum chi-square (TMC) approach[J]. Clinical Chemistry and Laboratory Medicine, 2019, 57(12): 1933. DOI:10.1515/cclm-2018-1341 |
| [23] |
LIU S H, MERNIK M, HRNC ˇ IC ˇ D, et al. A parameter control method of evolutionary algorithms using exploration and exploitation measures with a practical application for fitting Sova's mass transfer model[J]. Applied Soft Computing, 2013, 13(9): 3792. DOI:10.1016/j.asoc.2013.05.010 |
| [24] |
JAYSWAL A, PREETI. An exact l1 penalty function method for multi-dimensional first-order PDE constrained control optimization problem[J]. European Journal of Control, 2020, 52: 34. DOI:10.1016/j.ejcon.2019.07.004 |
| [25] |
FU Chunming, XU Yadong, JIANG Chao, et al. Improved differential evolution with shrinking space technique for constrained optimization[J]. Chinese Journal of Mechanical Engineering, 2017, 30(3): 553. DOI:10.1007/s10033-017-0130-4 |
| [26] |
MIRJALILI S. Moth-flame optimization algorithm: a novel nature-inspired heuristic paradigm[J]. Knowledge-Based Systems, 2015, 89: 228. DOI:10.1016/j.knosys.2015.07.006 |
| [27] |
KUMAR C, RAJ T D, PREMKUMAR M, et al. A new stochastic slime mould optimization algorithm for the estimation of solar photovoltaic cell parameters[J]. Optik, 2020, 223: 165277. DOI:10.1016/j.ijleo.2020.165277 |
 2022, Vol. 54
2022, Vol. 54



