2. 中国电力科学研究院有限公司,北京 102401
2. China Electric Power Research Institute, Beijing 102401, China
避雷器是变电站中的重要电气设备之一。由于结构特征和材料属性,避雷器在地震中很容易受损, 所以提高避雷器的抗震性能是提高变电站整体抗震性能的一个关键。中国电力科学研究院[1-5]使用一种铅合金减震装置来提高避雷器的抗震性能。在设备的抗震性能分析时,主要采用振动台试验和有限元仿真分析。已有研究显示了该减震装置的优秀减震效率,但目前还面临着对减震装置的优化设计问题。由于有限元仿真模型自由度高,在处理结构的非线性动力学分析、参数优化以及大变形等问题时,计算工作量大,效率不高。建立设备的低自由度简化模型对于减震装置的优化设计具有一定实用意义。
上世纪80年代末期,中国地震局的研究人员杨亚弟等[6-7]针对瓷立柱式电气设备提出质量—弹簧动力学模型,并得到一个关键的结论:对瓷套管之间的法兰连接处采用弹性处理,引入法兰连接弯曲刚度,得到的分析结果比以往采用刚性处理时更接近试验结果。该结论也被引进到GB 50260—2013《电力设施抗震设计规范》[8]中,该规范指定了计算瓷套管与法兰连接处弯曲刚度的公式。近期在立柱式电气设备的低自由度模型建立方面,有学者[9-10]针对支架—设备耦合体系,建立了2单元4自由度(2E-4D)的简化模型。该模型形式简单,计算方便,有利于进行地震响应分析和参数优化分析。但是,该方法把设备的主体看作一个单元,忽略了法兰连接处的弯曲特性。针对瓷立柱式电气设备,杜永峰等[11-12]提出了一种求解系统地震响应的半解析方法:把电气设备中的每节瓷瓶用具有分布参数的梁模拟,瓷瓶与瓷瓶的法兰连接作为柔性节点,设备顶部金属夹具等装置作为集中质量,得到具有集中分布参数和柔性节点的多节梁模型。但是得到的系统运动方程表达式比较复杂,推导过程也比较繁琐。
近年来,多体系统动力学在结构工程领域取得了很大的发展,并展示了广阔的应用前景[13-15]。与有限元模型相比,多体模型的单元之间不必满足变形连续性条件,对结构单元的变形和运动没有限制,因此在处理大变形等问题时具有一定的优势。
为建立易于理论分析且满足一定工程精度要求的数值模型,本文将利用多体动力学理论,提出一种新的建立避雷器模型的方法:把每节瓷瓶看作刚体单元,法兰连接用铰链模拟,系统的弹性用铰接点处的回转弹簧刻画,建立避雷器的多体模型。本文首先定量分析瓷套管与法兰连接处的弯曲特性,以此作为建立多刚体模型合理性的依据。其次,建立特高压瓷套管避雷器的多刚体—铰链—回转弹簧模型,并利用铰接点坐标法给出系统在地震动激励下的运动方程。最后,以1 000 kV某型号避雷器为算例进行实例分析,对比理论结果与试验结果来显示该方法的合理性和应用意义。本文所提出的建模方法形式简单,相比GB 50260—2013《电力设施抗震设计规范》[8]推荐的质量—弹簧模型,多体模型自由度更小,每节瓷瓶只需一个自由度。系统的运动方程的构建高度程式化,易于推导。
1 多刚体—铰链—回转弹簧模型 1.1 法兰连接处抗弯刚度特性特高压瓷套管避雷器主体一般由多节瓷瓶通过法兰连接组成,结构示意图如图 1(a)所示,每节瓷瓶由上、下法兰、瓷套管和内部器件构成。按照现行GB 50260—2013《电力设施抗震设计规范》[8]推荐,建立设备的有限元模型时,需要对瓷套管与法兰连接处进行等效梁处理。按此方法,瓷套管的抗弯刚度采用下列等环形截面梁的抗弯刚度计算:

|
图 1 特高压避雷器结构及其有限元模型示意 Fig. 1 Structural diagram of an UHV porcelain-housed surge arrester and its finite element model |
| $ E I=\frac{\pi}{64} E\left(D^4-d^4\right) $ | (1) |
式中:E为瓷套管弹性模量,D为瓷套管外径,d为瓷套管内径。
GB 50260—2013《电力设施抗震设计规范》[8]中给出了法兰连接处等效梁单元的二次截面矩的计算公式:
| $ I_{\mathrm{c}}=K_{\mathrm{c}} \frac{L_{\mathrm{c}}}{E_{\mathrm{c}}} $ | (2) |
式中:Ic为等效梁的二次截面矩; Lc为等效梁单元的长度,取为瓷套管长度的1/20;Ec为等效梁的弹性模量; 取与瓷套管相同的弹性模量;Kc为瓷套管与法兰连接处的弯曲刚度。这样,瓷套管的抗弯刚度与等效梁单元的抗弯刚度之比可用下式表示:
| $ \frac{E I}{E_{\mathrm{c}} I_{\mathrm{c}}}=\frac{5 \pi E\left(D^4-d^4\right)}{16 K_{\mathrm{c}} L} $ | (3) |
根据9种不同规格瓷瓶的数据,具体见表 1,取陶瓷弹性模量E=110 GPa,根据式(1)~(3)计算瓷套管抗弯刚度、瓷套管与法兰连接处的等效梁的抗弯刚度以及二者之比,结果列于表 2。由此可以看出,瓷套管抗弯刚度约为法兰连接处等效梁抗弯刚度的7~11倍,这定量地反映了抗弯刚度沿着避雷器的轴向分布很不均匀。按GB 50260—2013《电力设施抗震设计规范》[8]推荐得到的有限元模型如图 1(b)所示,由此可知,考虑了法兰连接处弯曲刚度的避雷器有限元模型是一个变截面连续梁模型。
| 表 1 瓷瓶试件的参数 Tab. 1 Parameters of porcelain unit specimens |
| 表 2 E=110 GPa时抗弯刚度对比 Tab. 2 Comparison of flexural rigidity when E=110 GPa |
在法兰连接处抗弯刚度特性中,瓷套管与法兰连接处的弯曲刚度Kc的取值由实验测得,它还可以由GB 50260—2013《电力设施抗震设计规范》[8]中给出的经验公式计算得到。该经验公式如下:
| $ K_{\mathrm{c}}=\beta \frac{d_{\mathrm{c}} h_{\mathrm{c}}^2}{t_{\mathrm{e}}} $ | (4) |
式中:β为弯曲刚度计算系数,dc为胶装部位瓷套管的外径,hc为胶装高度,te为胶装间隙。
对于弯曲刚度计算系数,在dc、hc和te的单位均取为m,Kc的单位取为N · m · rad-1的情况下,GB 50260—2013《电力设施抗震设计规范》[8]给定β=6.54×107。但是,该系数是早期基于低电压等级瓷套管类电气设备分析得到,对现阶段高电压等级的、瓷套管外径很大的电气设备,该系数取值不再适用。中国电力科学研究院[16-18]针对特高压电气设备的瓷套管与法兰连接处的弯曲刚度进行了试验研究,提出了新的弯曲刚度计算系数计算公式。新的弯曲刚度计算系数β根据胶装部位瓷套管外径尺寸dc(单位为m)取不同的数值,表达式如下[17]:
| $ \beta= \begin{cases}6.54 \times 10^7, & d_{\mathrm{c}} \leqslant 0.275 \\ \left(-15.4 d_{\mathrm{c}}+10.775\right) \times 10^7, & 0.275<d_{\mathrm{c}}<0.375 \\ 5.00 \times 10^7, & d_{\mathrm{c}} \geqslant 0.375\end{cases} $ | (5) |
在后续分析中,将采用系数公式(5)和式(4)计算瓷套管与法兰胶装连接处的弯曲刚度。
1.3 多刚体—铰链—回转弹簧模型描述上述分析表明,抗弯刚度的分布在法兰连接处会降低一个数量级左右,这可以启发本文对避雷器的分布弹性进行离散,把每节瓷瓶看作一个刚体,而将弹性集中到容易变形的法兰与瓷套管连接处。本文以如图 1(a)所示的主体由4节瓷瓶组成的特高压避雷器为例建立设备的模型。
由于设备的对称性,可以用平面系统模拟设备。把每节瓷瓶看作一个质量分布均匀的平面刚性杆件,用回转弹簧模拟瓷套管与法兰胶装连接处的弹性,构成如图 2(a)所示的上、下两端分别连接回转弹簧的刚体单元;瓷瓶与瓷瓶的连接法兰用光滑铰链模拟,并把相连端的两个回转弹簧串联形成铰接点处的一个等效回转弹簧。当考虑阻尼效应时,可以在铰接点处增加阻尼元件。把避雷器顶部均压环、金属夹具等部件看作集中质量,固接在最上节瓷瓶的顶端。整体动力学模型如图 2(b)所示。

|
图 2 避雷器瓷瓶的刚体单元模型及避雷器的多体模型 Fig. 2 Rigid body model of a porcelain unit and multibody model of an UHV arrester |
这样,本文对避雷器建立的力学模型是一个由多个刚体,并且相邻刚体之间由光滑铰链和回转弹簧连接构成的多体系统,更具体地说,是一个无杈树型开链多体系统。
1.4 动力学方程的建立本文主要利用铰接点坐标法[19]建立该多体系统的动力学方程。主要步骤如下:
1) 对系统中的刚体单元进行编号;
2) 构建全局静止直角坐标参考系;
3) 选取铰接点坐标θ,个数与系统自由度相等;
4) 用铰接点坐标θ表示系统构型坐标向量c;
5) 计算速度变换矩阵B,即c关于θ的Jacobian矩阵;
6) 构建系统的质量矩阵
在得到的速度变换矩阵B、质量矩阵
| $ \boldsymbol{B}^{\mathrm{T}}(\tilde{\boldsymbol{M}} \ddot{\boldsymbol{c}}-\boldsymbol{h})=\bf{0} $ | (6) |
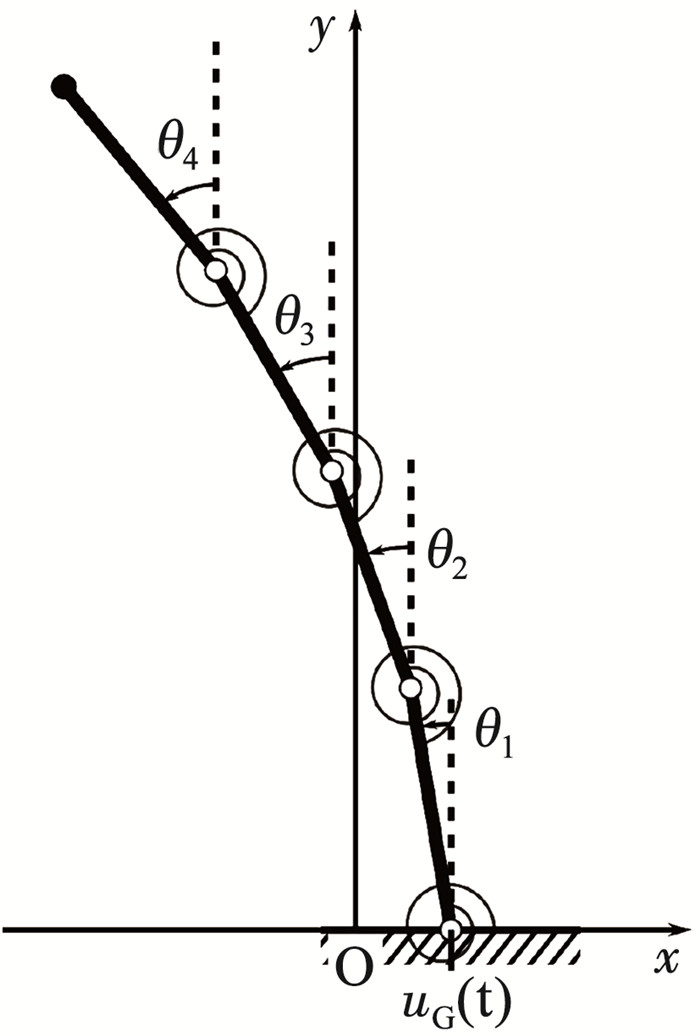
以图 1(a)所示的避雷器为例,动力学方程的具体推导过程描述如下。建立如图 3所示全局静坐标系,坐标原点位于初始时刻设备底部。4节瓷瓶从下往上分别编号1、2、3、4,顶部均压环对应的集中质量编号“top”。
|
图 3 多体系统模型变形示意 Fig. 3 Diagram of deformation of the multibody system |
易知该系统具有4个自由度,选择瓷瓶单元在铰接点处的绝对偏转角θi作为铰接点坐标,记θ=(θ1, θ2, θ3, θ4)T。记单元i的质心在全局静参考系中的坐标为ci=(xi, yi, φi)T,因为质量分布均匀,刚体单元的质心与几何中心重合,设地面运动时程为uG(t),则刚体单元的全局坐标可表达为如下:
| $ \left\{\begin{array}{l} x_1=u_{\mathrm{G}}(t)-\frac{l_1}{2} \sin \theta_1 \\ y_1=\frac{l_1}{2} \cos \theta_1 \\ \varphi_1=\theta_1 \end{array}\right. $ | (7) |
| $ \left\{\begin{array}{l} x_i=u_{\mathrm{G}}(t)-l_1 \sin \theta_1-\cdots-l_{i-1} \sin \theta_{i-1}-\frac{l_i}{2} \sin \theta_i \\ y_i=l_1 \cos \theta_1+\cdots+l_{i-1} \cos \theta_{i-1}+\frac{l_i}{2} \cos \theta_i \\ \varphi_i=\theta_i \end{array}\right. $ | (8) |
| $ \left\{\begin{array}{l} x_{\text {top }}=u_{\mathrm{G}}(t)-l_1 \sin \theta_1-\cdots-l_4 \sin \theta_4 \\ y_{\text {top }}=l_1 \cos \theta_1+\cdots+l_4 \cos \theta_4 \\ \varphi_{\text {top }}=\theta_4 \end{array}\right. $ | (9) |
利用式(7)~式(9),很容易求得系统的位形坐标c=(c1T, …, cnT, ctopT)T和速度变换矩阵B。
令mi和li分别表示瓷瓶单元i(i=1, 2, 3, 4) 的质量和长度,则刚体单元i关于穿过质心且垂直纸面的轴线的转动惯量为Ji=mili2/12. 令mtop表示顶部集中质量,忽略转动惯量,记Jtop=0。则系统的质量阵
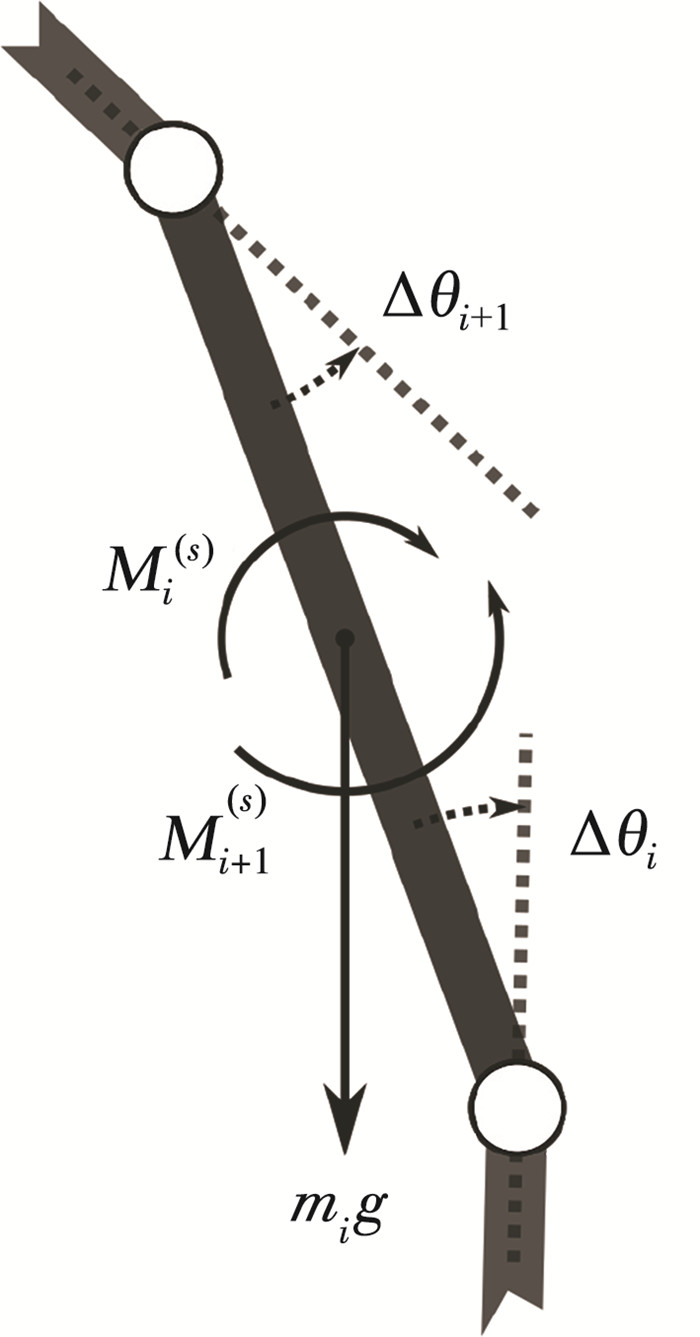
记单元i(i=1, …, 4, top)与ci相对应的受力向量为hi=(fi(x), fi(y), ηi)T,其中分量分别表示单元i水平方向受力、竖直方向受力和所受力矩。则系统所受作用力向量可表示为h=(h1T, …, hnT, htopT)T。因为每个刚体单元水平方向不受外力,记为fi(x)=0,竖直方向只受重力,考虑方向,记fi(y)=-mig。对每个刚体单元,因为所受重力过质心,不会对单元产生力矩,只有与其相连的回转弹簧会对该单元产生力矩。记刚体i受回转弹簧i和i+1作用的力矩的大小分别为Mi(s)和Mi+1(s), 方向如受力分析图 4中所示。假设回转弹簧是线弹性的,记si为回转弹簧i的转动刚度,令Δθi=θi-θi-1(其中θ0=0)表示相对偏转角,则Mi(s)=siΔθi和Mi+1(s)=si+1Δθi+1。
|
图 4 刚体单元i的受力分析图 Fig. 4 Diagram of applied force on body unit i |
若考虑阻尼效应,刚体单元还受到阻尼力矩。假设阻尼是线性粘滞阻尼,铰接点i处的阻尼系数为di。设阻尼器i和i+1作用的阻尼力矩大小分别为Mi(d)和Mi+1(d). 令
把所得B、
| $ \boldsymbol{M}(\boldsymbol{\theta}) \ddot{\boldsymbol{\theta}}+\boldsymbol{D} \dot{\boldsymbol{\theta}}+\boldsymbol{S} \boldsymbol{\theta}+\boldsymbol{F}(\boldsymbol{\theta}, \dot{\boldsymbol{\theta}})=\ddot{u}_{\mathrm{G}}(t) \boldsymbol{m}_t(\boldsymbol{\theta}) $ | (10) |
式中:广义质量阵M(θ)不是常值矩阵,F(θ,
在得到系统的运动方程(10)后,从实际应用的角度,可以利用小角度假设,sin θi≈θi, cosθi≈1, 略去方程中的高阶项得到如下线性化近似系统:
| $ \boldsymbol{M} \ddot{\boldsymbol{\theta}}+\dot{\boldsymbol{D} \boldsymbol{\theta}}+(\boldsymbol{S}-\boldsymbol{G}) \boldsymbol{\theta}=\ddot{u}_{\mathrm{G}}(t) \boldsymbol{m}_t $ | (11) |
其中:
| $ M=\left[\begin{array}{cccc} \left(\frac{m_1}{3}+\hat{m}_1\right) l_1^2 & \left(\frac{m_2}{2}+\hat{m}_2\right) l_1 l_2 & \left(\frac{m_3}{2}+\hat{m}_3\right) l_1 l_3 & \left(\frac{m_4}{2}+\hat{m}_4\right) l_1 l_4 \\ \left(\frac{m_2}{2}+\hat{m}_2\right) l_2 l_1 & \left(\frac{m_2}{3}+\hat{m}_2\right) l_2^2 & \left(\frac{m_3}{2}+\hat{m}_3\right) l_2 l_3 & \left(\frac{m_4}{2}+\hat{m}_4\right) l_2 l_4 \\ \left(\frac{m_3}{2}+\hat{m}_3\right) l_3 l_1 & \left(\frac{m_3}{2}+\hat{m}_3\right) l_3 l_2 & \left(\frac{m_3}{3}+\hat{m}_3\right) l_3^2 & \left(\frac{m_4}{2}+\hat{m}_4\right) l_3 l_4 \\ \left(\frac{m_4}{2}+\hat{m}_4\right) l_4 l_1 & \left(\frac{m_4}{2}+\hat{m}_4\right) l_4 l_2 & \left(\frac{m_4}{2}+\hat{m}_4\right) l_4 l_3 & \left(\frac{m_4}{3}+\hat{m}_4\right) l_4^2 \end{array}\right] $ |
| $ \boldsymbol{D}=\left[\begin{array}{cccc} d_1+d_2 & -d_2 & 0 & 0 \\ -d_2 & d_2+d_3 & -d_3 & 0 \\ 0 & -d_3 & d_3+d_4 & -d_4 \\ 0 & 0 & -d_4 & d_4 \end{array}\right] $ |
| $ \boldsymbol{S}=\left[\begin{array}{cccc} s_1+s_2 & -s_2 & 0 & 0 \\ -s_2 & s_2+s_3 & -s_3 & 0 \\ 0 & -s_3 & s_3+s_4 & -s_4 \\ 0 & 0 & -s_4 & s_4 \end{array}\right] $ |
| $ \boldsymbol{G}=\left[\begin{array}{cccc} g\left(\frac{m_1}{2}+\hat{m}_1\right)l_1 & 0 & 0 & 0 \\ 0 & g\left(\frac{m_2}{2}+\hat{m}_2\right)l_2 & 0 & 0 \\ 0 & 0 & g\left(\frac{m_3}{2}+\hat{m}_3\right)l_3 & 0 \\ 0 & 0 & 0 & g\left(\frac{m_4}{2}+\hat{m}_4\right)l_4 \end{array}\right] $ |
| $ \boldsymbol{m}_t=\left[\begin{array}{l} \left(\frac{m_1}{2}+\hat{m}_1\right) l_1 \\ \left(\frac{m_2}{2}+\hat{m}_2\right) l_2 \\ \left(\frac{m_3}{2}+\hat{m}_3\right) l_3 \\ \left(\frac{m_4}{2}+\hat{m}_4\right) l_4 \end{array}\right] $ |
式中:M为广义质量阵,D为广义阻尼矩阵,(S - G)为广义刚度矩阵,
利用线性化系统(11)可以计算系统的基础频率和振型,即求解矩阵M和(S - G)的广义特征值问题。此时需要给定系统的参数包括:质量参数mi,长度参数li和刚度参数si。质量参数和长度参数可以直接通过设备的出厂参数给定,而系统的刚度参数可根据设备的胶装参数和经验公式(4)计算得到。把图 2(a)中刚体单元i的上、下两端连接的回转弹簧的刚度分别记为si+和si-,则铰接点i处串联回转弹簧的刚度si可用
在得到系统的线性近似运动方程(11)后,可以进行地震响应时程分析,常用的数值积分方法包括中心差分法和Newmark法[20]。在进行数值求解时,除了质量参数mi,长度参数li和刚度参数si,还需要给定阻尼参数di。工程上,对阻尼分布均匀的弱阻尼结构,通常假设系统具有比例阻尼,因为本文系统在铰接点处的阻尼机理相似,分布均匀,可以采用Rayleigh阻尼假设。
通过数值积分得到每个单元的绝对偏转角θi的响应时程后,则可以利用小角度假设,按下式计算顶部相对水平位移响应时程:
| $ \tilde{x}_{\mathrm{top}}=-\sum\limits_{i=1}^n l_i \theta_i $ | (12) |
用下式计算顶部绝对加速度响应时程:
| $ \ddot{x}_{\mathrm{top}}=\ddot{u}_{\mathrm{G}}-\sum\limits_{i=1}^n l_i \ddot{\theta}_i $ | (13) |
用下式计算各个回转弹簧的内力矩响应时程:
| $ M_i^{(s)}=-s_i \Delta \theta_i $ | (14) |
在动力学方程的构建过程中进行受力分析时,在向量h相应位置加上外部载荷,去掉阻尼力作用的力矩,去掉动力平衡方程(6)中的广义速度和广义加速度项,可以得到系统的静力平衡方程:
| $ \boldsymbol{B}^{\mathrm{T}} \boldsymbol{h}=0 $ | (15) |
该方程的展开式是关于铰接点坐标θ的非线性代数方程组。可以利用Newton法进行数值求解,进行结构静力分析。例如,分析避雷器顶端水平方向的加载与水平位移的关系。
2 地震响应分析本文以1 000 kV某型号避雷器为算例,计算其力学特性和进行地震响应分析,并与文献[1, 21]中的试验结果作对比。
该型号避雷器主体由5节相同规格的瓷瓶构成,每节瓷瓶长2 115 mm,质量为912 kg;每节瓷瓶的上、下法兰胶装参数相同:胶装高度200 mm,胶装间隙10 mm,胶装部位瓷套管外径510 mm。在试验时,基础端安装了底座瓷瓶,长623 mm,质量为300 kg,胶装高度200 mm,胶装间隙10 mm,胶装部位瓷套外径495 mm。该设备均压环及金属夹具质量为380 kg。用本文提出的方法,建立了一个6自由度平面多刚体—铰链—回转弹簧系统。
文献[21]对避雷器进行了两种工况下的抗弯试验研究:工况1最大加载力22.99 kN, 工况2最大加载力43.10 kN. 取重力加速度g=9.8 m · s-2,本文理论计算结果与试验结果对比如图 5所示。

|
图 5 试样避雷器顶部水平力与位移关系 Fig. 5 Horizontal force-displacement relationship at top end of arrester specimen |
在加载力不超过35.00 kN时,理论值与试验值误差很小。在工况1最大加载力下,理论值167.33 mm与测量值169.02 mm仅有1%相对误差。加载力超过35.00 kN后,理论值与测量值误差逐渐增大,在工况2最大加载力下理论值267.15 mm与测量值376.39 mm相对误差达到29.02%. 误差增大的原因可归结为如下:工况2进行的是破坏试验,在最大加载下,某些套管与法兰胶装连接处的变形超出了初始线弹性变形阶段,刚度有所退化;而理论计算是在假设一直处于线弹性变形阶段情况下进行的。
本文计算得到设备的基础频率为1.57 Hz,与试验值1.56 Hz对比,相对误差0.64%. 可以说理论计算结果和试验结果吻合地很好。
为了进行地震响应分析,本文利用前两阶自然频率和振型阻尼比来给定系统的Rayleigh阻尼阵。在未知电瓷设备实际阻尼比的情况下,GB 50260—2013《电力设施抗震设计规范》[8]建议阻尼比取值不超过2%. 而文献[20]指出,从小幅强迫振动试验中确定的阻尼比不应该直接应用于产生结构较大运动的地震反应分析中;在结构较小运动时确定的阻尼比并不代表结构运动的较大幅值时的阻尼。鉴于试验时,结构响应幅值较大,假设系统前两阶振型阻尼比均为3.5%。
本文计算所选择的地震动激励是0.2 g等级下中国电力科学研究院[1]试验用标准时程波。如图 6所示,标准时程波地面加速度峰值1.0 g。数值计算时,该波形乘以0.2表示抗震等级, 并乘以1.4代表支架放大系数。

|
图 6 标准地震动地面加速度激励 Fig. 6 Normalized input of seismic ground acceleration |
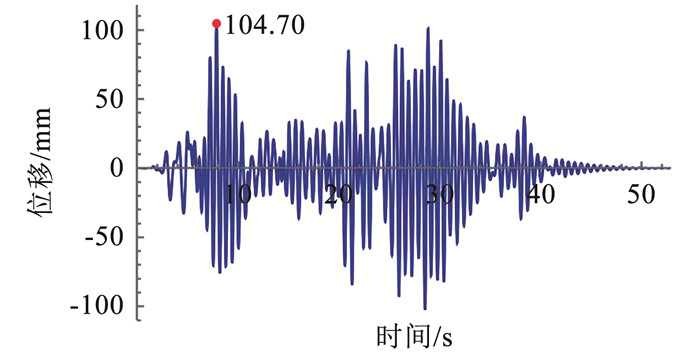
在数值求解系统各刚体单元转动角度θi的响应后,按式(12)计算顶端水平相对位移响应,结果图 7所示,最大位移为104.70 mm。按式(13)计算顶端绝对加速度响应,结果如图 8所示,加速度峰值为-1.08 g,与文献[1]中试验结果1.04 g误差为3.8%。
|
图 7 顶端水平相对位移响应时程 Fig. 7 Response history of relative horizontal displacement at top end of arrester |

|
图 8 顶端绝对加速度响应时程 Fig. 8 Response history of absolute acceleration at top end of arrester |
1) 特高压避雷器瓷套管抗弯刚度是法兰连接处等效梁单元抗弯刚度的7~11倍,表明抗弯刚度沿避雷器轴向分布很不均匀。
2) 特高压避雷器的多刚体—铰链—回转弹簧模型自由度数与避雷器瓷瓶个数相等,通常不大于6,与有限元模型相比自由度数低,计算量小。多体模型的动力学方程推导过程程式化,有利于编程实现。
3) 1 000 kV某型号避雷器算例的基础频率理论计算值与试验结果误差很小,仅有0.64%;顶端水平力加载与位移关系的理论结果与试验结果符合很好;地震响应时程分析加速度峰值与试验结果误差为3.8%。
4) 本文所提出的建模方法形式简单,有利于进一步对加装减震装置的设备进行抗震分析和减震装置参数优化分析工作。本文虽然以避雷器为具体研究对象,但该建模方法能够方便地推广到特高压变电站中其他瓷立柱式电气设备的抗震分析中。
| [1] |
李圣, 卢智成, 邱宁, 等. 加装金属减震装置的1000kV避雷器振动台试验研究[J]. 高电压技术, 2015, 41(5): 1740. LI Sheng, LU Zhicheng, QIU Ning, et al. Study on shaking table test of 1 000 kV surge arrester with metal damper device[J]. High Voltage Engineering, 2015, 41(5): 1740. DOI:10.13336/j.1003-6520.hve.2015.05.044 |
| [2] |
刘振林, 卢智成, 孟宪政, 等. 用于高压电气设备的剪切型铅减震器性能影响研究[J]. 地震工程学报, 2016, 38(4): 564. LIU Zhenlin, LU Zhicheng, MENG Xianzheng, et al. Performance of a shear lead damper applied to high-voltage electrical equipment[J]. China Earthquake Engineering Journal, 2016, 38(4): 564. DOI:10.3969/j.issn.1000-0844.2016.04.0564 |
| [3] |
林森, 程永锋, 卢智成, 等. ±1100 kV换流站内避雷器抗震及减震研究[J]. 高电压技术, 2017, 43(10): 3198. LIN Sen, CHENG Yongfeng, LU Zhicheng, et al. Investigation on seismic performance and shock absorption of arrester in ±1 100 kV converter station[J]. High Voltage Engineering, 2017, 43(10): 3198. DOI:10.13336/j.1003-6520.hve.20170925008 |
| [4] |
刘振林, 程永锋, 卢智成, 等. 安装剪切型铅减震器的特高压标准化避雷器地震模拟振动台试验[J]. 高电压技术, 2018, 44(8): 2595. LIU Zhenlin, CHENG Yongfeng, LU Zhicheng, et al. Shake table test on UHV standardization lightning arrester installed with shear-type lead dampers[J]. High Voltage Engineering, 2018, 44(8): 2595. DOI:10.13336/j.1003-6520.hve.20180731018 |
| [5] |
CHENG Yongfeng, LI Sheng, LU Zhicheng, et al. Seismic risk mitigation of cylindrical electrical equipment with a novel isolation device[J]. Soil Dynamics and Earthquake Engineering, 2018, 111: 41. DOI:10.1016/j.soildyn.2018.04.001 |
| [6] |
杨亚弟, 张其浩, 苏文藻, 等. FZ-110J型避雷器体系抗震分析[J]. 地震工程与工程振动, 1988, 8(2): 55. YANG Yadi, ZHANG Qihao, SU Wenzao, et al. Aseismic analysis of the FZ-110J lighting arrestor[J]. Earthquake Engineering and Engineering Vibration, 1988, 8(2): 55. DOI:10.13197/j.eeev.1988.02.007 |
| [7] |
杨亚弟, 张其浩. 具有柔性结点的有限元法及其应用[J]. 工程力学, 1988, 5(3): 83. YANG Yadi, ZHANG Qihao. The FEM with flexible nodal point and its application[J]. Engineering Mechanics, 1988, 5(3): 83. |
| [8] |
中华人民共和国住房和城乡建设部. 电力设施抗震设计规范: GB 50260—2013[S]. 北京: 中国计划出版社, 2013 Ministry of Housing and Urban-Rural Development of the People's Republic of China. Code for seismic design of electrical installations: GB 50260—2013[S]. Beijing: China Planning Press, 2013 |
| [9] |
MOHAMMADI R K, AKRAMI V, NIKFAR F. Dynamic properties of substation support structures[J]. Journal of Constructional Steel Research, 2012, 78: 173. DOI:10.1016/j.jcsr.2012.06.016 |
| [10] |
李黎, 汪国良, 胡亮, 等. 特高压支架-设备体系动力响应简化分析及参数研究[J]. 工程力学, 2015, 32(3): 82. LI Li, WANG Guoliang, HU Liang, et al. Simplified analysis and parametric study of dynamic response for UHV electrical support-equipment system[J]. Engineering Mechanics, 2015, 32(3): 82. DOI:10.6052/j.issn.1000-4750.2013.08.0797 |
| [11] |
杜永峰, 刘彦辉, 李慧. 串联电气设备支架隔震体系地震响应半解析法[J]. 力学学报, 2009, 41(3): 440. DU Yongfeng, LIU Yanhui, LI Hui. Semi-analytical solution of seismic response of serially isolated equipment and supporter[J]. Chinese Journal of Theoretical and Applied Mechanics, 2009, 41(3): 440. DOI:10.3321/j.issn:0459-1879.2009.03.020 |
| [12] |
杜永峰, 刘彦辉, 李慧. 带分布参数高压电气设备地震响应半解析法[J]. 工程力学, 2009, 26(3): 182. DU Yongfeng, LIU Yanhui, LI Hui. Seismic response of high- voltage equipment based on semi-analytical method[J]. Engineering Mechanics, 2009, 26(3): 182. |
| [13] |
袁勇, 申中原, 禹海涛. 沉管隧道纵向地震响应分析的多体动力学方法[J]. 工程力学, 2015, 32(5): 76. YUAN Yong, SHEN Zhongyuan, YU Haitao. Multibody dynamics method for longitudinal seismic response analysis of immersed tunnels[J]. Engineering Mechanics, 2015, 32(5): 76. DOI:10.6052/j.issn.1000-4750.2013.11.1041 |
| [14] |
ZAHARIEV E V. Earthquake dynamic response of large flexible multibody systems[J]. Mechanical Sciences, 2013, 4(1): 131. DOI:10.5194/ms-4-131-2013 |
| [15] |
蔡建国, 韩志宏, 冯健, 等. 多刚体动力学在结构地震响应分析中的应用[J]. 工程力学, 2010, 27(11): 250. CAI Jianguo, HAN Zhihong, FENG Jian, et al. Application of dynamics of multi-rigid body to seismic response analysis of structures[J]. Engineering Mechanics, 2010, 27(11): 250. |
| [16] |
张雪松, 代泽兵, 卢智成, 等. 特高压电气设备瓷套与法兰连接弯曲刚度的计算系数[J]. 武汉大学学报(工学版), 2014, 47(6): 794. ZHANG Xuesong, DAI Zebing, LU Zhicheng, et al. Coefficient of bending stiffness of interconnected parts between ultra-high voltage porcelain bushings and flanges[J]. Engineering Journal of Wuhan University, 2014, 47(6): 794. |
| [17] |
朱祝兵, 代泽兵, 卢智成, 等. 特高压电气设备法兰连接处的弯曲刚度试验研究[J]. 中国电力, 2014, 47(6): 6. ZHU Zhubing, DAI Zebing, LU Zhicheng, et al. Experimental study of the bending rigidity at flange connection of UHV electrical equipment[J]. Electric Power, 2014, 47(6): 6. |
| [18] |
WANG Haibo, CHENG Yongfeng, LU Zhicheng, et al. Research on bending rigidity at flange connections of UHV composite electrical equipment[J]. Shock and Vibration, 2020, 2020: e2031357. DOI:10.1155/2020/2031357 |
| [19] |
NIKRAVESH P E. Planar multibody dynamics: Formulation, programming with MATLAB, and applications[M]. Boca Raton, FL: CRC Press, 2007.
|
| [20] |
CHOPRA A K. Dynamics of structures: theory and applications to earthquake engineering[M]. 4th ed. Upper Saddle River, N.J: Prentice Hall, 2012: 174.
|
| [21] |
朱祝兵, 代泽兵, 刘振林, 等. 1 000 kV特高压避雷器抗弯性能试验与仿真研究[J]. 电瓷避雷器, 2014(1): 32. ZHU Zhubing, DAI Zebing, LIU Zhenlin, et al. Experimental and simulation study on flexural performance of 1 000 kV UHV arrester[J]. Insulators and Surge Arresters, 2014(1): 32. DOI:10.16188/j.isa.1003-8337.2014.01.012 |
 2022, Vol. 54
2022, Vol. 54


