2. 无人水下运载技术工业和信息化部重点实验室(西北工业大学), 西安 710072
2. Key Laboratory of Unmanned Underwater Vehicle Technology (Northwestern Polytechnical University), Ministry of Industry and Information Technology, Xi'an 710072, China
泵喷推进器(Pumpjet, 简称泵喷)是包含定子、转子和导管的一种组合式推进器, 一般以定子相对转子前后顺序分为前置定子式和后置定子式[1]。其中前置泵喷虽然相对后置虽然效率低, 但由于定子工作在相对压力波动较低的区域, 避免了转子高速尾流的冲击, 可极大减小推进器噪声[2], 因此目前被广泛应用于核潜艇, 如以英国、法国、美国、俄罗斯分别为代表的最新研制的“无畏级”、“哥伦比亚级”、“梭鱼级”和“北风之神级”核潜艇均采用前置泵喷。
目前前置泵喷水动力性能获取主要途径为数值模拟和实验方法, 由于数值方法成本相对低, 并能最大程度保留流场信息, 是泵喷设计阶段和校核阶段普遍采用的方法。已有文献如Huyer等[3]将定子安装角度沿周向按照正弦函数排列, 由于单个转子进流条件不同, 最终产生了侧向力, 可作为新型矢量推进器。Park等[4]采用低雷诺数k-ε方程研究了带前置定子的导管桨, 主要分析了桨叶表面流线和不同半径处的压力系数。Ahn等[5]以单方程S-A模型分析了转子叶梢加叶冠后的水动力性能, 结果表明虽然叶冠可有效控制叶梢泄露涡, 但却造成推力损失, 而效率保持不变。赵威等[6]研究了前置定子弯曲对桨叶前三阶非定常推力的性能, 结果表明前弯和后弯均可有效降低推力脉动, 并分析了不同轴向位置处定子尾流沿周向分布, 文中指出可能是由于定子尾迹相位差引起。Wang等[7]针对叶梢涡模型, 并结合面元法分析了水动力性能。彭云龙等[8]从敞水特性、空化特性和脉动特性3方面比较了前置和后置泵喷的性能, 结果表明前置泵喷效率较低, 空化性能较差, 但导管进出口压力脉动远低于后置泵喷。Qin等[9]同样分析了前置和后置泵喷区别, 除非定常脉动性能外, 重点分析了泵喷尾涡动力特性。结果表明前置泵喷毂涡相对稳定, 梢涡同样受导管和叶梢相互作用而增强。由于前置泵喷特殊应用, 公开实验研究较少, 如Yu等[10]通过空泡水筒的实验验证了前置泵喷计算方法的准确性。
虽然前置泵喷在民用方面已有普及, 如美国通用电气公司(General electric Company, GE)和ABB分别研发的吊舱推进器[11], 但目前仍以潜艇应用居多, 故噪声指标极为重要。泵喷噪声与流场低频脉动息息相关, 改善泵喷噪声的重点在于如何调整推进器的结构, 以促使流场向更有利于声隐性的方向发展。而前置定子结构是泵喷水动力性能和流场特性的决定性因素之一, 如饶志强等[12]采用RNG k-ε模型研究了定子叶片数、翼型厚度及安装角对泵喷定常性能的影响, 表明安装角对推力、扭矩和效率影响最大。Yu等[13]采用SSTk-ω分析了定子弦长、安装角、转定距离对泵喷的非定常性能的影响, 结果同样表明安装角对桨叶表面脉动特性和推力脉动影响最大。基于上述研究, 本文将以某泵喷为原型, 采用Ansys/Fluent重点研究前置定子角度对包括桨叶在内的各部件及转定之间流场点的低频脉动性能影响。不同于其他学者, 本文将定子角度分为进流角、出流角和安装角, 并对其分别进行调整研究。
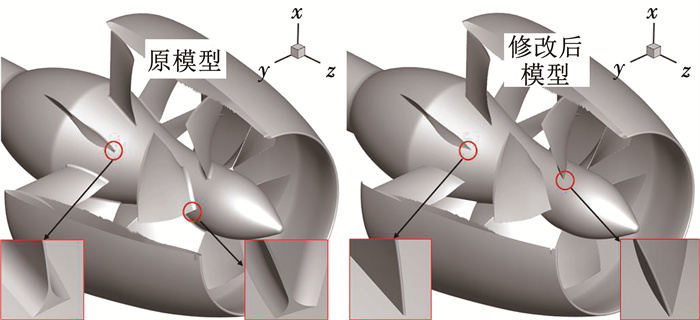
1 泵喷模型 1.1 几何参数本文采用的泵喷, 其原始几何模型(origin model)如图 1所示, 定子和转子叶片随边为钝边, 叶根部分别有2.0, 2.5 mm半径的倒圆, 为后续几何模型处理及离散网格的方便, 本文研究的模型取消了叶根倒圆, 并且将叶片随边处理为圆角。改型后的泵喷(modified model)如图 1所示, 其中定子和转子叶片数目分别为8和6, 转子的直径(Dr)为166.4 mm, 间隙为1 mm, 大约为0.6%Dr, 毂径比为0.3, 投影盘面比Ap/A0=0.8。转子各半径处螺距比(P/D)见表 1。图 2为定子和导管的主要几何参数示意图, 具体参数见表 2。由于泵喷进流段与潜艇尾端相匹配, 故定子桨毂为圆锥面, 导致前后定子直径不同。图 2中Ds1和Ds2分别为定子进口和出口直径, H为定子叶高, 表示叶片轴向长度。Dd1、Dd2分别为导管进口和出口直径, Ld为导管轴向总长, 坐标原点位于转子中间正对下方r=0的位置。
|
图 1 前置泵喷外观 Fig. 1 Pre-whirl PJP model |
| 表 1 转子各半径处螺距比 Tab. 1 Pitch ratio of rotor at different radii |

|
图 2 泵喷模型几何参数 Fig. 2 Geometry parameters of PJP model |
| 表 2 定子和导管参数 Tab. 2 Parameters of stator and duct |
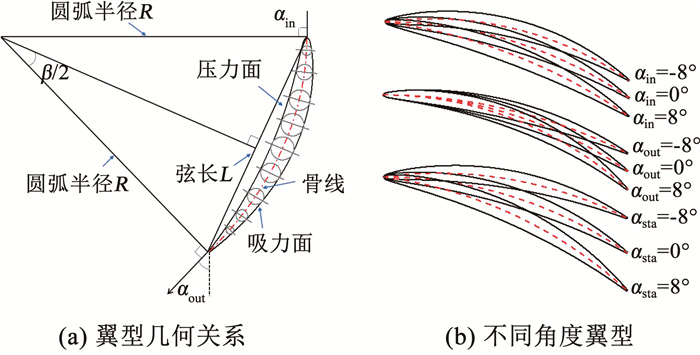
本文泵喷定子采用圆弧设计法, 即骨线(中弧线)为圆弧段, 通过控制沿进流和出流方向切线角度以确定圆弧形状, 再将其根据翼型沿弦长的厚度分布进行加厚。图 3(a)所示为定子在径向为0.7展面时剖面翼型示意图。其中进流角和出流角的几何关系为αin+αout=90°+β。
|
图 3 定子剖面翼型几何示意 Fig. 3 Geometric diagram of cross-section airfoil of stator |
在调节定子出流角和进流角时, 控制另一个角度不变, 通过几何关系先求得圆弧半径R, 得到骨线。再根据原始翼型厚度分布沿半径方向加厚, 加厚方法为:以骨线某一点为圆心, 以对应位置厚度为直径作圆, 与半径方向相交的点即为压力面和吸力面的坐标点, 由此得到新调整的翼型。在调节安装角αsta时, 则直接将翼型绕前缘点旋转对应的角度。定子角度调节为
| $ \alpha_{\varphi}^{\prime}=\alpha_{\varphi 0}+\alpha_{\varphi} $ | (1) |
式中:α′φ、αφ0和αφ分别对应调整后的角度、原角度、调整角度。下标φ对应3种角度, 即αin、αout和αsta。为保证泵喷水动力性能不受严重损失, αφ调整范围为-8°~8°。正角度表示沿桨叶进流方向, 负角度表示与桨叶进流方向相反。
此外角度的调整将引起定子投影面轴向长度不一致, 为消除定子尾缘到转子距离对压力脉动的影响, 将定子不同剖面处翼型等比例扩展到与原模型轴向长度一致。图 3(b)为采用不同预旋角调整方式后的翼型示意图。
2 数值分析方法与验证 2.1 控制方程采用基于雷诺平均的N-S控制方程:
| $ \frac{\partial \rho}{\partial t}+\frac{\partial\left(\rho u_i\right)}{\partial x_i}=0 $ | (2) |
| $ \begin{aligned} & \frac{\partial\left(\rho u_i\right)}{\partial t}+\frac{\partial\left(\rho u_i u_j\right)}{\partial x_j}=-\frac{\partial p}{\partial x_i}+\frac{\partial}{\partial x_j} \cdot\left[\mu \frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_j}-\frac{2}{3} \delta_{i j} \frac{\partial u_l}{\partial x_l}\right]+ \\ & \frac{\partial}{\partial x_j}\left(-\rho \overline{u_i^{\prime} u_j^{\prime}}\right) \\ & \end{aligned} $ | (3) |
式中:式(2)为连续性方程, 式(3)为动量方程。ui为x方向的绝对速度, p为静压, μ为流体的黏性系数, δij为克罗内克函数,
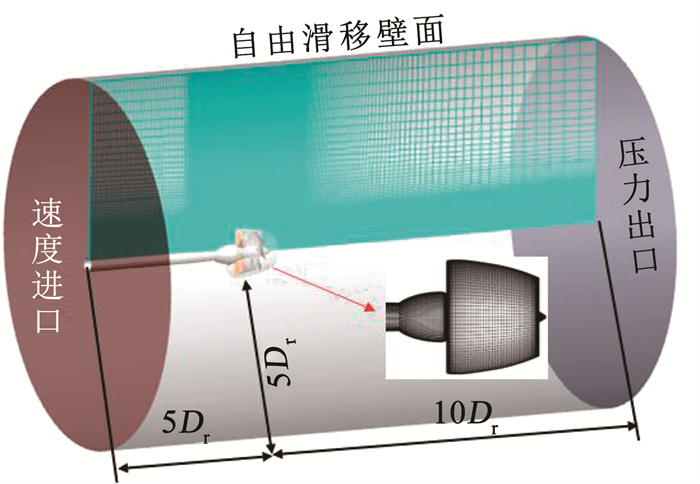
将求解区域划分为内流域和外流域, 其中内流域又可分为定子域和转子域, 考虑到计算成本及后处理时高保真度, 计算域全部采用结构化网格。如图 4、5分别展示了外流场和内流程的网格, 为避免进口及出口区域对流场的干扰, 外流域的前后距离分别为5Dr和10Dr, 在径向处距离同样设为5Dr, 使流场充分延伸, 具体边界条件如图 4所示。在网格划分过程中充分考虑到近壁面影响, 通过布拉休斯公式, 即
| $ y=6\left(\frac{V_{\mathrm{ref}}}{\nu}\right)^{-\frac{7}{8}}\left(\frac{L_{\mathrm{ref}}}{2}\right)^{\frac{1}{8}} y^{+} $ | (4) |
|
图 4 计算域及边界条件 Fig. 4 Computational domain and boundary condition |
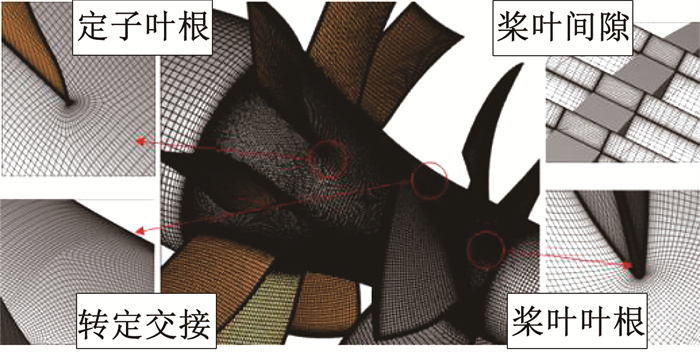
|
图 5 内流域结构化网格 Fig. 5 Structure mesh of internal domain |
计算得到y+为1时, 壁面第1层网格y应为2.6×10-6 m, 其中Vref为特征速度, 取桨叶在0.75半径处剖面翼型的进流速度, ν为流体运动黏性系数, 即μ/ρ。Lref为特征长度, 取转子0.75半径处翼型弦长, 即128 mm。为得到精确的结果, 本文采用y=2.0×10-6 m, 保证壁面处有足够密的附面层网格。对于定常工况, 基于多重参考系(MRF)模型迭代不小于1 000步, 保证结果收敛, 并提取最后一步作为泵喷敞水特性结果; 而非定常工况则基于Sliding Mesh技术在定常流场的基础上求解, 并以桨叶转过1°的时间为时间步长, 共计算6个周期, 以第4个周期以后结果作为有效数据。
2.3 网格验证泵喷完全沉入深水中, 且不受自由液面的影响, 在边界条件设置中出口处相对压力设为0, 在分析流场形态时可加上水压头。固定螺旋桨转速n=20 r/s, 改变进速VA来模拟在水槽中的实验状态。进速与z轴正方向同向, 转速根据右手定则为z轴负方向。分析泵喷的性能时, 其各部件包括转子、定子和导管的推力系数和扭矩系数及敞水效率可分别为
| $ \begin{aligned} & K_{T_r}=\frac{T_r}{\rho n^2 D_r^4} \\ & K_{T_s}=\frac{T_s}{\rho n^2 D_r^4} \\ & K_{T_d}=\frac{T_d}{\rho n^2 D_r^4} \\ & K_T=\frac{T_r+T_s+T_d}{\rho n^2 D_r^4}=K_{T_r}+K_{T_s}+K_{T_d} \\ & K_{Q_r}=\frac{Q_r}{\rho n^2 D_r^5} \\ & K_{Q_s}=\frac{Q_s}{\rho n^2 D_r^5} \\ & \eta_0=\frac{T V_A}{2 \pi n Q}=\frac{\left(T_r+T_s+T_d\right) V_A}{2 \pi n Q}=\frac{J K_T}{2 \pi K_Q} \end{aligned} $ | (5) |
式中:Tr、Ts、Td、Qs、Qs分别为桨叶推力、定子推力、导管推力、桨叶扭矩、定子扭矩, 总推力为T, η0为敞水效率, n为螺旋桨转速, ρ为水在常温25°时的密度, 取997 kg/m3。
为保证计算结果的准确度, 对比了不同数目网格的计算结果, 表 3所示为3种不同内流场网格单个计算通道数目的对比。而外域网格一般只进行微调, 除保证导管近壁面足够多的网格外, 针对与之相匹配的转子域和定子域的网格大小, 网格要保证较好地连续过渡。最终外域网格数目约为259万。
| 表 3 不同数目网格 Tab. 3 Grid number of different meshes |
图 6所示为泵喷在n=20 r/s水动力性能曲线, 图 6(a)为不同网格数目的桨叶推力系数和扭矩系数同实验数据[14]的对比, 可以看出, 网格的细化对结果并不会造成太大的影响, 对比中等网格与实验结果, 发现在进速系数J=0.1~0.8时, 推力系数误差为5%~7%, 扭矩系数为2%~4%, 而误差值随着进速系数的提高逐步呈非线性增加, 在进速系数为1.2时误差最大, 推力系数和扭矩系数的误差分别达到10%和8%。由于是非设计工况, 故不予考虑。考虑到计算成本, 本文后续将采用中等网格做进一步研究。图 6(b)所示为泵喷各部件及总体性能, 注意其中定子推力系数为负, 其扭矩系数方向与桨叶相反, 为方便后续分析, 取其绝对值。导管在不同进速下对泵喷总推力所体现的作用不同, 可以看到在进速系数约为0.7时导管推力由正转负, 并随进速的增加逐步增加。对比不同进速系数下由总推力系数和桨叶扭矩系数计算得到的敞水效率η0, 可以看出相比传统螺旋桨, η0在较广的进速系数范围内变化并不大, 这也是泵喷优于传统螺旋桨的原因之一。本文泵喷最高效率大约为J=0.9, 考虑到一般舰艇设计工况低于最高效率点, 故本文后续将以J=0.8为主要分析工况。

|
图 6 泵喷水动力系数曲线 Fig. 6 Hydrodynamic coefficient curves of PJP |
图 7所示为泵喷在J为0.8时近壁面y+分布云图, 其中桨叶和定子从左向右分别为压力面和吸力面, 可以看到桨叶导边靠近叶梢处y+值最大, 但不超过1, 而其他部位都在0.5左右, 对于定子和导管, 由于其特征速度较低, 采用与桨叶相同的第一层附面层网格导致y+值远小于1。总体来看, 满足后续分析的精度要求。

|
图 7 壁面y+分布云图 Fig. 7 Wall plus y+ contour |
图 8所示为泵喷在不同定子角度时敞水特性曲线, 可以看出, 随着泵喷的推力、扭矩和最高效率都随着定子角度的增大而增大。其中αsta的影响最大, 且最高效率点随αsta的增大而向较高进速系数偏移, αout影响次之, αin影响最小。综合分析认为:定子角度的增大将使流体预旋更强烈, 即增加了桨叶进流位置周向速度, 使桨叶各半径翼型剖面攻角增大, 与螺旋桨中增大桨叶螺距角作用相同。由于αout改变的是出流位置, 更接近于桨叶进流位置, 而调整αin虽然增大了定子首部预旋角, 但流体却在流过定子狭长的通道后导致出流位置的预旋损失, 因此αout影响比αin更显著; 由于调整αsta是同时改变αin和αout, αsta每增大1.0°, αin和αout都要增大0.5°, 因此αsta的效果更明显。此外, 虽然角度的增大会导致定子阻力增大, 但由于定子负载相对转子小的多, 其绝对增大值远小于转子, 故使得总推力、扭矩和效率均呈现增大趋势。

|
图 8 不同定子角度泵喷敞水曲线 Fig. 8 Open-water coefficient curves with different pre-whirl angles |
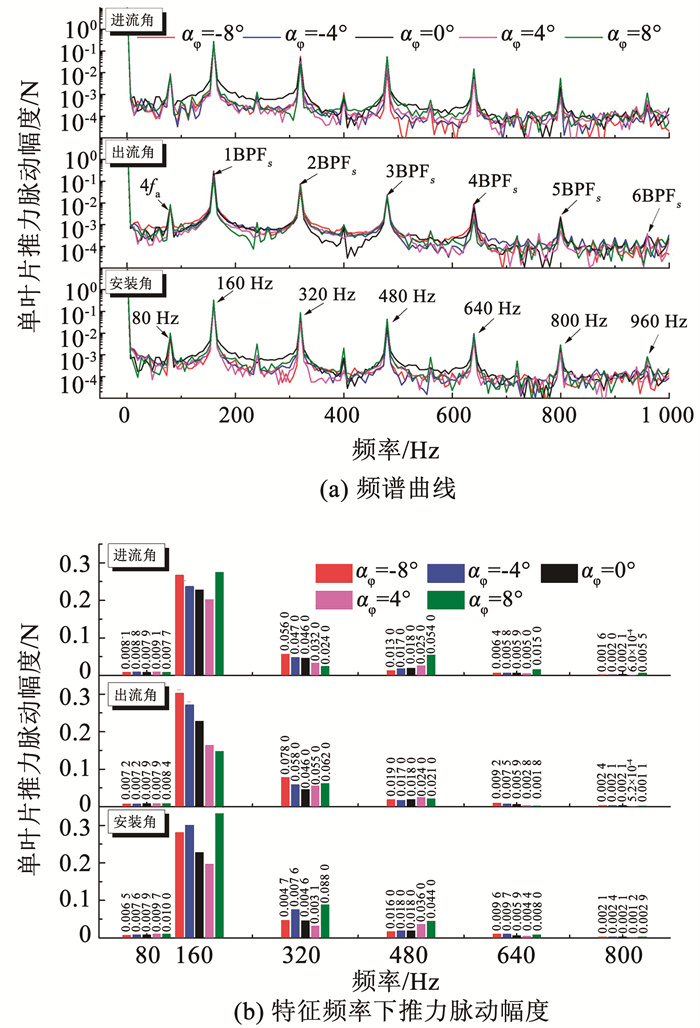
桨叶非定常力可以从一定程度上反应叶片表面压力脉动, 并常用来分析叶片激振力是否满足设计要求。图 9所示为J=0.8时, 不同定子角度下转子单叶片非定常推力在频域的结果, 图 9(a)为推力的频谱曲线, 纵坐标表示推力在对应频率下的脉动幅度。可以发现, 受定子干扰, 转子单叶片的推力脉动峰值对应频率主要为BPFs(定子数和转速的乘积)的倍频程。此外还存在大量离散低幅轴频fa(即转速)的倍频程信息, 并在4fa时有相对较大的脉动力。图 9(b)为进一步对比包括4fa和1BPFs~6BPFs特征频率处推力脉动具体幅值大小, 结果表明:1BPFs脉动幅度相对其他频率最大, 以αφ=0°为例, 2BPFs下降了80%, 其他频率下降超过90%。在1BPFs处, 推力脉动幅度最低值在αin和αsta为4°时分别达到最小; 而至于αout, 脉动幅度与之呈单调性减小趋势, 并且该趋势随αout的增大逐渐变缓; 对比同一αφ下不同αφ调整方式的脉动幅度, 可以发现当αφ为正时, αsta影响最大, αin次之, αout最小; 当αφ为负时, 影响规律不是特别明显。在2BPFs处, 脉动幅度分别在αin=8°、αout=0°和αsta=4°达到最小。在3BPFs处, 最小值分别为αin=-8°、αout=-4°和αsta=-8°。其他频率处脉动幅度最小值对应的角度也均存在差异。
|
图 9 不同角度时单叶片推力频域结果 Fig. 9 Thrust of single rotor in frequency domain with different angles |
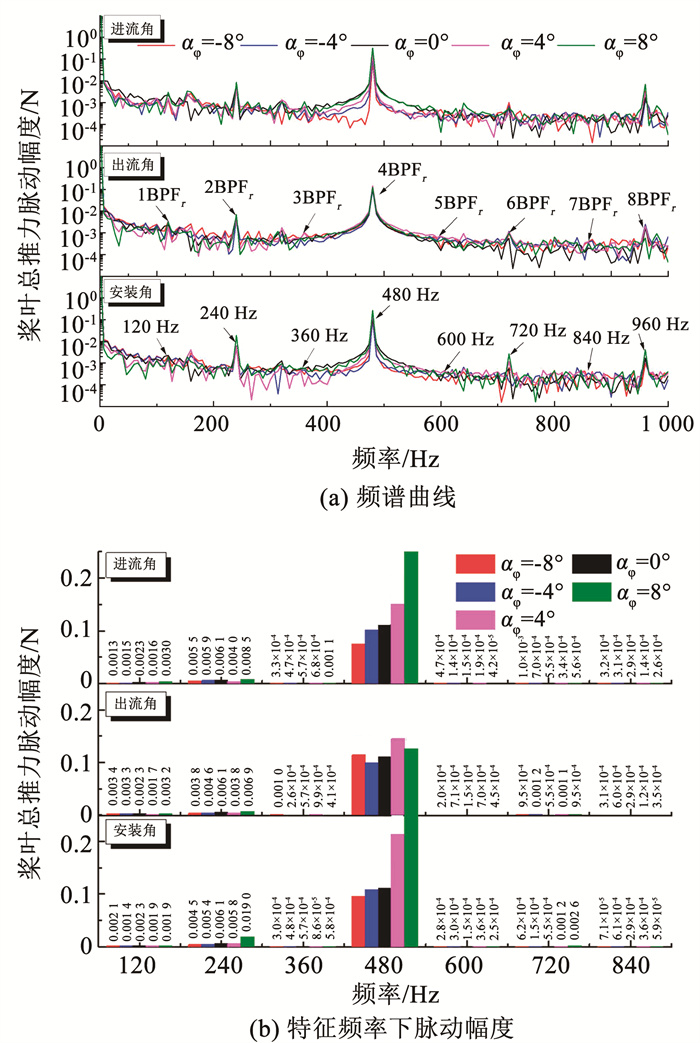
图 10所示为J=0.8时, 不同定子角度下桨叶总推力的非定常脉动幅度在频域的结果, 图 10(a)为对应的频谱曲线, 可以发现, 受转定子数目干扰, 最大脉动幅度对应频率为4BPFr(转子数目与转速的乘积), 同时也是3BPFs。根据文献[15]的推导, 在对转螺旋桨中, 一般非定常推力和扭矩的变化频率为:
|
图 10 不同角度时桨叶总推力频域结果 Fig. 10 Thrust of total rotor in frequency domain with different angles |
叶片表面的压力脉动是推进器重要的物理量之一, 不仅反映水动力噪声强度, 而且是非定常激振力的成因之一。本文主要分析定子和转子叶片表面的压力脉动, 并以式(5)中的压力标准差来衡量。
| $ \begin{aligned} \bar{p}(\vec{r}) & =\frac{1}{N_t} \sum\limits_{i=1}^{N_t} p(\vec{r}, i \cdot \Delta t) \\ \dot{p}(\vec{r}, t) & =p(\vec{r}, t)-\bar{p}(\vec{r}) \\ \sigma(\vec{r}) & =\sqrt{\frac{1}{N_t} \sum\limits_{i=1}^{N_t}(p(\vec{r}, i \cdot \Delta t)-\bar{p}(\vec{r}))^2}= \\ & \sqrt{\frac{1}{N_t} \sum\limits_{i=1}^{N_t} \hat{p}^2(\vec{r}, i \cdot \Delta t)} \end{aligned} $ | (6) |
式中:
图 11为J=0.8时桨叶表面压力标准差云图, 其中图 11(a)为桨叶压力面, 图 11(b)为桨叶吸力面, 从左到右分别对应αφ为-8°, -4°, 0°, 4°和8°的云图, 从上到下分别为不同αin、αout、αsta的影响, 流向从左向右。

|
图 11 不同角度时桨叶压力标准差 Fig. 11 Standard deviation of rotor pressure with different angles |
可以看到, 桨叶压力面和吸力面均存在较强的压力脉动。叶片前缘因与流体首先相接触而受到冲击, 其压力脉动最强, 并且最大值超过1 000 Pa, 随着角度增大, 前缘局部较大的压力标准差范围逐渐增大。叶梢附近由于受叶梢泄露涡(Tip leakage vortex,TLV)、叶梢泄露流(Tip leakage flow,TLF)[16]影响, 在压力面和吸力面均存在较大脉动压力, 定子角度的增大均使得叶梢压力脉动增强; 然而3种角度的调整方式对叶梢脉动影响规律在αφ为正、负时不同, 在同一角度下, 当αφ为负时, 脉动强度规律为:αin>αout>αsta, 而当αφ为正时, αin < αout < αsta。此外, 在经过叶片前缘较高的脉动强度区域后, 靠近前缘部分范围内及叶根处均存在局部较高的脉动幅值; 而叶片径向中部存在一定压力波动平稳区域。整体来看, 随着定子角度增大, 该区域范围逐渐减小, 尤其当αsta增大到8°时, 脉动较平稳区域大幅减小, 并且在αφ=8°时, 该区域范围大小规律为αsta>αin>αout, 同时也印证了桨叶推力脉动中定子角度调整方式对单桨叶推力脉动幅度的影响规律。而对于其他αφ, 3种角度调整方式对该区域范围大小的影响规律并不完全一致。
图 12所示为J=0.8时不同定子叶片表面的压力标准差云图, 该图从左到右及从上到下布置对应的角度大小及调整方式同图 11不同的是, 每个角度对应两个云图, 左右分别为定子压力面和吸力面。流向从左向右。

|
图 12 不同角度时定子压力标准差 Fig. 12 Standard deviation of stator pressure with different angles |
由于定子围流场变化不是特别剧烈, 其负载相对转子小得多, 故脉动幅度也较低。而定子叶片在较高径向位置及后缘区域存在较大分层显示的压力标准差, 并且越靠近后缘, 其脉动幅度越大; 但压力面高脉动区范围小于吸力面。分析原因可能为叶片吸力面边界层出现分离, 导致定子尾缘存在周期性脱落涡, 进而使定子随边压力脉动较大。
此外, 当αφ为正时, 随着角度增大, 吸力面前缘位置压力波动幅度及范围均剧烈增加, 所不同的是, 调整αsta和αin均比αout影响大, 尤其当αsta=8°时, 吸力面高压力波动范围区域大幅增加。而对于同一角度下, 3种角度调整方式对叶表脉动强度的影响规律有所不同, 如在压力面, 当αφ为负时, 叶片尾缘局部脉动强度规律为αin>αout>αsta, 当αφ为正时, αin < αout < αsta; 而吸力面规律在αφ为负时并不明显。
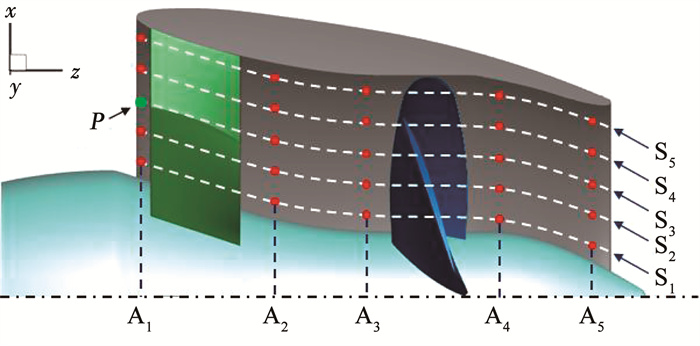
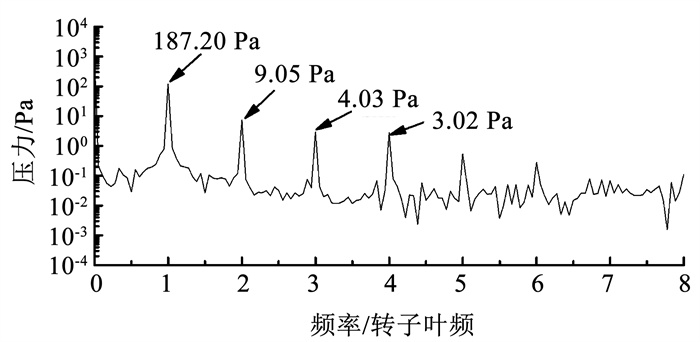
3.4 泵喷内部流场点压力脉动为进一步分析定子角度对泵喷流场压力脉动的影响, 在非定常计算中引入多个监控点, 监测位置如图 13所示, 在包括定子前缘、转定子之间及喷尾部不同轴向位置(A1~A5)和桨毂到桨罩之间的径向位置(S1~S5)分别布置压力监控点。其中轴向坐标分别为z=-0.09, -0.06, -0.03, 0.03, 0.06;径向截面位置分别为Span=0.1, 0.2, 0.3, 0.4, 0.5。监测点以轴向和径向位置命名, 如图 13中的P点为:A1S3, 其压力频谱曲线如图 14所示。可以看出, 压力脉动最大幅值位于1BPFr处, 2BPFr~4BPFr对应的脉动幅值已经下降了95%~98%。因此本文将主要分析各监测点在1BPFr处的脉动幅值。
|
图 13 压力监控点布置 Fig. 13 Probes arrangements |
|
图 14 监测点P(A1S3)的频谱曲线 Fig. 14 Pressure spectrum at probe P(A1S3) |
图 15所示为原模型, 即αφ=0°时各监测点经傅里叶变换后在120 Hz的压力信息, 图 15(a)为所有监测点的压力幅度云图, 可以看出, 在径向方向, 压力幅度由桨毂到桨罩呈先增大后减小的规律, 这是由于桨叶在位于中间及较高半径处的叶元体为主要做功位置所致; 在轴向方向, 呈现从上游到下游逐步增大的趋势, 并且最大位置出现在泵喷尾部, 这是由于泵喷尾涡结构不稳定作用所引起。图 15(b)为不同轴向位置处, 展向S2~S5截面监测点相对于S1处的相位差。由于叶表及附近压力脉动与非定常流动直接相关, 而各展向截面处的流动表达式为
| $ m(r, t)=m(r)+m^{\prime}\left[r, \omega t+\varphi_m(r)\right] $ | (7) |

|
图 15 各监控点在1BPFr处压力信息 Fig. 15 Pressure fluctuation information of different probes with 1BPFr |
式中m为流场中物理量, 可表示为流量、速度、压力等, 其中m为平均值, m′为脉动量, 并且在不同半径r处以同频角速度ω, 不同角速度φm呈正弦脉动。因此各监测点相位信息也是泵喷低频脉动的关键信息。可以看出在包含0.5及以下的径向位置处, 各点相较于S1处相位均均为延迟; 而大于0.5展向后均有延迟或超前, 尤其轴向A2和A5位置, 在0.9展向处相位变化剧烈, 这是由于在叶顶端壁黏性涡漩及泵喷尾流复杂的涡流所致。
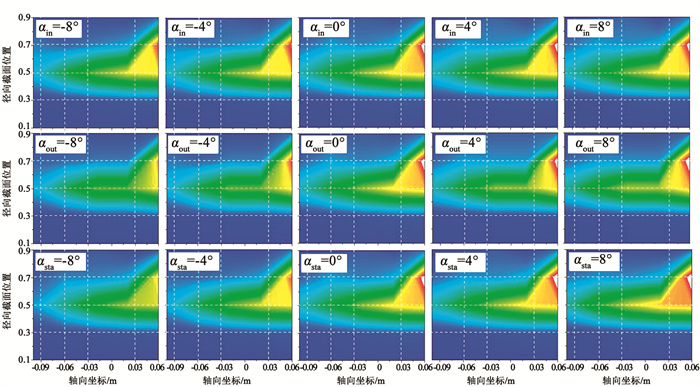
图 16所示为J=0.8时, 所有监测点在120 Hz的压力幅度云图, 云图色阶及范围同图 15(a)。比较不同定子角度调整方式对最大位置及附近压力脉动幅度的影响, 可以发现其与定子角度呈正相关; 当角度为负时, 角度调整方式对其影响规律为:αin>αout>αsta; 而角度为正时, 该处的压力脉动幅度影响规律为:αin < αout < αsta。
|
图 16 监测点在1BPFr压力幅值云图 Fig. 16 Pressure fluctuation amplitude at different probes with 1BPFr |
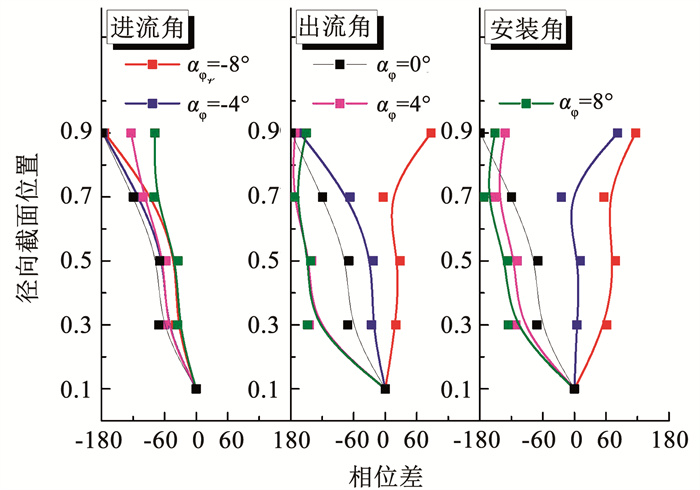
桨叶入流条件是决定叶片表面非定常脉动特性的因素之一, 因此需重点分析桨叶前缘的流动。图 17给出了A3位置不同径向处120 Hz的相位关系, 其中相位差计算时以0.1展向截面处即S1位置为基准。可以看出, 不同定子角度相位差在调整αin时变化相对较小, 并且相位与原模型一致, 均落后于基准点。而αout和αsta均以αφ的正、负为区别表现出两极化的趋势, 其中αsta表现更为明显, 即当αφ为正时, 相位均落后基准点; 当αφ为负时, 相位提前于基准点; 并且角度绝对值越大, 其相位绝对值也越大。由于较高半径处(S5位置)监测点靠近导管黏性壁面, 而该区域以壁面黏涡和桨叶附近复杂二次流动主导, 其相位关系与其他监测点相比差异较大。
|
图 17 A3位置监测点相位差 Fig. 17 Phase difference at probe A3 |
1) 数值分析了3种定子角度调整方式对泵喷性能影响, 发现增大进流角, 出流角和安装角均能增大泵喷推力、扭矩及最高效率, 但安装角影响最大, 出流角次之, 进流角最小。
2) 分析J为0.8时, 不同定子角度下推力、叶片表面、各监测点脉动幅度。发现: ①单桨叶受定子叶片数影响, 在1倍定子叶频处达到最大, 并且在调整角度为正时, 对幅度影响规律为:安装角>进流角>出流角, 影响规律不明显。而总推力脉动幅度受定子和转子叶片数影响, 在4倍转子叶频达到最大, 其受定子角度调整方式影响规律与单桨叶相同。②桨叶前缘和叶梢附近脉动强度最大, 而定子则在尾缘最强, 并且两者都随定子角度增大而增强, 但角度调整方式对其影响规律在调整角分别为正、负时相反。③泵喷较强压力脉动分布在径向中部及定子尾部, 最大位置在尾部中高半径处, 并随角度增加而增加; 角度调整方式对其影响规律同样在角度为正和负时相反。桨叶入流位置不同监测点相位关系在调整进流角时差异较小, 但出流角和安装角的调整使其按定子角度正、负呈两极化分布。
| [1] |
伍赛特. 泵喷推进器技术研究现状及未来发展趋势展望[J]. 自动化应用, 2019(11): 49. WU Saite. Research status and future development trend of pump-jet propulsion technology[J]. Automation Application, 2019(11): 49. DOI:10.19769/j.zdhy.2019.11.019 |
| [2] |
王永生. 喷水推进和泵喷推进的概念: 共性, 特性及区别[J]. 中国舰船研究, 2019, 14(5): 1. WANG Yongsheng. Concepts of waterjet propulsion and pumpjet propulsion: Their common characteristics, special characteristics and differences[J]. Chinese Journal of Ship Research, 2019, 14(5): 1. DOI:10.19693/j.issn.1673-3185.01605 |
| [3] |
HUYER S A, DROPKIN A, BEAL D N, et al. Preswirl maneuvering propulsor[J]. IEEE Journal of Oceanic Engineering, 2011, 37(1): 122. DOI:10.1109/JOE.2011.2175509 |
| [4] |
PARK W G, JUNG Y R, KIM C K. Numerical flow analysis of single-stage ducted marine propulsor[J]. Ocean Engineering, 2005, 32(10): 1260. DOI:10.1016/j.oceaneng.2004.10.022 |
| [5] |
AHN S J, KWON O J. Numerical investigation of a pump-jet with ring rotor using an unstructured mesh technique[J]. Journal of Mechanical Science and Technology, 2015, 29(7): 2897. DOI:10.1007/s12206-015-0619-7 |
| [6] |
赵威, 刘敏, 彭旭, 等. 前置定子叶片周向弯曲对导管桨非定常特性的影响[J]. 中国造船, 2018, 59(2): 24. ZHAO Wei, LIU Min, PENG Xu, et al. Influence of skewed angle of pre-swirl stator blades on unsteady characteristics of ducted propeller[J]. Shipbuilding of China, 2018, 59(2): 24. DOI:10.3969/j.issn.1000-4882.2018.02.003 |
| [7] |
WANG Chao, WENG Kaiqiang, GUO Chunyu, et al. Prediction of hydrodynamic performance of pump propeller considering the effect of tip vortex[J]. Ocean Engineering, 2019, 171: 259. DOI:10.1016/j.oceaneng.2018.10.039 |
| [8] |
彭云龙, 王永生, 刘承江, 等. 前置与后置定子泵喷推进器的水动力性能对比[J]. 哈尔滨工程大学学报, 2019, 40(1): 132. PENG Yunlong, WANG Yongsheng, LIU Chengjiang, et al. Comparative analysis of the hydrodynamic performance of front-stator and rear-stator pump-jets[J]. Journal of Harbin Engineering University, 2019, 40(1): 132. DOI:10.11990/jheu.201707018 |
| [9] |
QIN Denghui, HUANG Qiaogao, SHI Yuejun, et al. Comparison of hydrodynamic performance and wake vortices of two typical types of pumpjet propulsor[J]. Ocean Engineering, 2021, 224: 108700. DOI:10.1016/j.oceaneng.2021.108700 |
| [10] |
YU Haiting, ZHANG Zhenguo, HUA Hongxing. Numerical investigation of tip clearance effects on propulsion performance and pressure fluctuation of a pump-jet propulsor[J]. Ocean Engineering, 2019, 192: 106500. DOI:10.1016/j.oceaneng.2019.106500 |
| [11] |
VEIKONHEIMO T, MIETTINEN P, HUISMAN J. On the advanced extrapolation method for a new type of podded propulsor via CFD simulations and model measurements[C]//Proceedings of the 5th International Symposium on Marine Propulsors. Espoo, Finland: [s. n. ], 2017
|
| [12] |
饶志强, 李巍, 杨晨俊. 定子参数变化对前置定子导管桨性能的影响[J]. 上海交通大学学报, 2013, 47(2): 269. RAO Zhiqiang, LI Wei, YANG Chenjun. The effect of stator parameters on performance of ducted propeller withpre-swirl stators[J]. Journal of Shanghai Jiao Tong University, 2013, 47(2): 269. DOI:10.16183/j.cnki.jsjtu.2013.02.019 |
| [13] |
YU Haiting, DUAN Ningyuan, HUA Hongxing, et al. Propulsion performance and unsteady forces of a pump-jet propulsor with different pre-swirl stator parameters[J]. Applied Ocean Research, 2020, 100: 102184. DOI:10.1016/j.apor.2020.102184 |
| [14] |
GUO Jun, ZHANG Yan, CHEN Zuogang, et al. CFD-based multi-objective optimization of a waterjet-propelled trimaran[J]. Ocean Engineering, 2020, 195: 106755. DOI:10.1016/j.oceaneng.2019.106755 |
| [15] |
饶志强. 泵喷推进器水动力性能数值模拟[D]. 上海: 上海交通大学, 2012 RAO Zhiqiang. Numerical simulation of hydrodynamical performance of pump jet propulsor[D]. Shanghai: Shanghai Jiao Tong University, 2012 |
| [16] |
周军伟, 王大政. 导管螺旋桨不同桨叶的叶梢泄露涡分析[J]. 哈尔滨工业大学学报, 2014, 46(7): 14. ZHOU Junwei, WANG Dazheng. Analysis of tip leakage vortex of different blade in ducted propeller[J]. Journal of Harbin Institute of Technology, 2014, 46(7): 14. DOI:10.11918/j.issn.0367-6234.2014.07.003 |
 2022, Vol. 54
2022, Vol. 54


