2. 陕西省飞行控制与仿真技术重点实验室(西北工业大学), 西安 710072
2. Shaanxi Province Key Laboratory of Flight Control and Simulation Technology (Northwestern Polytechnical University), Xi'an 710072, China
系统辨识技术基于飞行试验中飞行运动和控制变量的测量值,建立输入输出量间的关系。飞机系统辨识是飞机研发过程中的一个重要环节,对控制律的设计、飞行模拟器的设计和飞行包线的扩展都有重要的意义[1]。飞机系统辨识技术分为频域辨识和时域辨识,频域辨识方法建立系统的线性模型,时域识别方法可用于提取线性模型和非线性模型[2]。目前最常用的时域飞机系统辨识方法是方程误差法以及输出误差法。方程误差法是一种直接方法,受自变量中的测量噪声影响,其估计结果是有偏差的。输出误差法基于极大似然原理,通过最小化测量值和模型输出的均方差来估计参数,其估计结果是渐近无偏的。针对稳定飞机,输出误差法是最常用的参数辨识方法之一[3]。
不稳定飞机的主要特点为:1)飞行试验过程中需要引入控制器;2)求解不稳定飞机的模型输出时,若参数选取稍有不适,求解过程将发散。如图 1所示,针对不稳定飞机,系统辨识有两种可能的方法,即闭环辨识和开环辨识[4]。经典的闭环辨识方法建模飞行员输入δp与测量值z之间的动力学关系,不会产生任何数值问题,因为整个系统是稳定的。此方法的局限是只能得到闭环系统的等价模型,若要从中推导出开环动力学模型,还需要精确的控制器回路动力学模型,而这通常是不容易得到的。

|
图 1 不稳定飞机的闭环与开环辨识 Fig. 1 Closed-loop and open-loop identification of unstable aircraft |
开环辨识方法直接建模飞机舵面输入δe与测量值z之间的动力学关系。然而,输出误差法不能直接应用于不稳定飞机。输出误差法需要求解待辨识系统的运动方程,应用于不稳定的飞机时,会产生数值发散问题,导致参数估计过程失败[4]。
近年来,随着神经网络学科的发展,神经网络方法逐渐应用于飞机系统辨识领域[5-7]。Hess[8]通过神经网络直接建模飞机的气动系数。Ghosh等[9]基于前向神经网络,使用Delta法和Zero法提取飞机的气动导数。Peyada等[10]提出了一种新的思想——将神经网络与输出误差法相结合,以神经网络代替飞机动力学模型,并采用高斯-牛顿法最小化网络输出与试验测量值间的均方差,从而进行参数估计。随后多位学者[11-13]遵循类似的思路,应用不同的网络或者对不同的对象进行辨识。但是,这些文献都是基于高斯-牛顿法来最小化代价函数的。高斯-牛顿法具有固有的缺陷,即容易陷入局部最小值[2]。本文基于粒子群优化对LM (levenberg-marquardt)方法进行了改进,以改进的LM算法代替高斯-牛顿法,并与神经网络方法相结合,形成一种改进的输出误差法,用于不稳定飞机的参数辨识。
1 神经网络建模神经网络由于其强大的非线性映射能力,可以直接应用于对非线性动力学特性建模。网络输入向量选取为动力学系统第k时刻的输入量以及状态量,网络输出向量选取为第(k+1)时刻的输出量,经过大量样本训练后,神经网络可以依据第k时刻(当前时刻)的状态和输入,对第k+1时刻(下一时刻)的状态量进行预测。换句话说,神经网络用于近似系统的动力学特性,其作用相当于线性或者非线性动力学系统的运动方程。
本文选择了常用的BP神经网络[4],其网络结构如图 2所示。

|
图 2 BP神经网络结构 Fig. 2 Structure of BP neural network |
BP神经网络分为输入层、隐含层和输出层。W1、W2分别为输入层到隐含层和隐含层到输出层的权重以及偏差矩阵,网络的传播遵循式(1)~(4),其中f(x)为非线性S形激活函数。xr为网络输入向量,x1、x2分别为隐含层和输出层的输入向量,xh、xo分别为隐含层和输出层的输出向量。
| $ \boldsymbol{x}_1=\boldsymbol{W}_1 \boldsymbol{x}_{\mathrm{r}}+\boldsymbol{W}_{1 \mathrm{~b}} $ | (1) |
| $ \boldsymbol{x}_{\mathrm{h}}=f\left(\boldsymbol{x}_1\right) $ | (2) |
| $ \boldsymbol{x}_2=\boldsymbol{W}_2 \boldsymbol{x}_{\mathrm{h}}+\boldsymbol{W}_{2 \mathrm{~b}} $ | (3) |
| $ \boldsymbol{x}_{\mathrm{o}}=f\left(\boldsymbol{x}_2\right) $ | (4) |
S形激活函数选择双曲正切函数:
| $ f(\boldsymbol{x})=\tanh \left(\frac{\gamma}{2} \boldsymbol{x}\right) $ | (5) |
如上所述,网络输入向量U选取为动力学系统k时刻的输入以及状态量,网络输出Z选取为k+1时刻的状态向量。即
| $ \left\{\begin{array}{l} \boldsymbol{U}(k)=[\boldsymbol{u}(k), \boldsymbol{x}(k)] \\ \boldsymbol{Z}(k+1)=[\boldsymbol{z}(k+1)] \end{array}\right.$ | (6) |
由于不同的试验测量数据的数量级不同,要对网络输入输出数据进行归一化,见式(7),其中x为原始的输入或者输出测量数据,x为归一化之后的数据;原始数据的范围为(xmin, xmax);其归一化范围为(xmin, xmax), 本文取为(-1, 1)。
| $ \bar{x}=\bar{x}_{\min }+\frac{\left(\bar{x}_{\max }-\bar{x}_{\min }\right)}{\left(x_{\max }-x_{\min }\right)}\left(x-x_{\min }\right) $ | (7) |
通过连续调整网络参数W1和W2,可以最大程度地减小网络输出和测量值之间的误差。在第k个离散数据点上,将成本函数选择为第k步的局部输出误差, 即
| $ E(k)=\frac{1}{2}\left[\boldsymbol{Z}(k)-\boldsymbol{x}_{\mathrm{o}}(k)\right]^{\mathrm{T}}\left[\boldsymbol{Z}(k)-\boldsymbol{x}_{\mathrm{o}}(k)\right] $ | (8) |
基于最速下降法,网络参数W1, W2通过式(9)、(10)进行调整:
| $ \begin{aligned} \boldsymbol{W}_2(k+1)= & \boldsymbol{W}_2(k)-\mu \frac{\partial E(k)}{\partial \boldsymbol{W}_2}= \\ & \boldsymbol{W}_2(k)+\lambda f^{\prime}\left(\boldsymbol{x}_2\right)\left[\boldsymbol{z}(k)-\boldsymbol{x}_{\mathrm{o}}(k)\right] \boldsymbol{x}_{\mathrm{h}}^{\mathrm{T}}(k) \end{aligned} $ | (9) |
| $ \begin{aligned} \boldsymbol{W}_1(k+1)= & \boldsymbol{W}_1(k)-\mu \frac{\partial E(k)}{\partial \boldsymbol{W}_1}= \\ & \boldsymbol{W}_1(k)+\lambda f^{\prime}\left(\boldsymbol{x}_1\right) \boldsymbol{W}_2^{\mathrm{T}} f^{\prime}\left(\boldsymbol{x}_2\right)\left[\boldsymbol{z}(k)-\boldsymbol{x}_{\mathrm{0}}(k)\right] \boldsymbol{x}_{\mathrm{r}}^{\mathrm{T}} \end{aligned} $ | (10) |
激活函数的导数为
| $ f^{\prime}(\boldsymbol{x})=\frac{\gamma}{2}\left[1-\tanh ^2\left(\frac{\gamma}{2} \boldsymbol{x}\right)\right] $ | (11) |
网络参数W1, W2通过迭代更新之后,网络将具有满意的拟合性能,网络的最终拟合性能通过均方差(MSE)进行衡量,即
| $ \operatorname{MSE}=\frac{1}{N} \sum\limits_{k=1}^N \sum\limits_{j=1}^{n_y}\left[\boldsymbol{z}_j(k)-\boldsymbol{x}_{\mathrm{oj}}(k)\right]^2 $ | (12) |
本文详细陈述基于粒子群优化改进的输出误差法,以及应用神经网络和改进的输出误差法进行参数辨识的算法流程。
2.1 粒子群优化粒子群优化算法(Particle swarm optimization, PSO)最初是由Eberhant等[14]于1995年提出的一种基于直接搜索的优化算法。此算法基于个体粒子之间的协作与竞争,经过数次迭代后实现复杂空间中最优解的搜索。PSO算法是一种有记忆能力的算法, 对于低维优化问题十分有效[15]。粒子群中的每个粒子,都是所求优化问题的一个潜在的解。而粒子的品质由事先设定好的适应度函数来评价。假设在n维搜索空间中,有m个粒子, 第h个粒子的位置表示为
| $ \begin{aligned} \boldsymbol{v}_{h d}(t+1)= & \omega r_1 \boldsymbol{v}_{h d}(t)+\xi_1 r_2\left(\boldsymbol{p}_{h d}(t)-\boldsymbol{x}_{h d}(t)\right)+ \\ & \xi_2 r_3\left(\boldsymbol{p}_{g d}(t)-\boldsymbol{x}_{h d}(t)\right) \end{aligned} $ | (13) |
| $ \boldsymbol{x}_{h d}(t+1)=\boldsymbol{x}_{h d}(t)+\boldsymbol{v}_{h d}(t+1) $ | (14) |
神经网络训练完成后,基于LM算法对代价函数进行优化,使得网络输出和测量输出的均方差最小,从而对未知参数进行辨识。LM算法是对高斯-牛顿法的改进,为解释LM算法,首先简要介绍基于高斯-牛顿法的传统输出误差算法[3]。
当神经网络训练完成后,网络可以用来代替系统的运动方程预测系统响应。基于待辨识系统的状态方程以及输出方程,将网络输入
| $ \widehat {\bf{Y}}(k + 1) = g\left( {\widehat {\bf{U}}(k, \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}), {{\bf{W}}_1}, {{\bf{W}}_2}} \right) $ | (15) |
| $ J(\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}, \mathit{\boldsymbol{R}}) = \frac{1}{2}\sum\limits_{i = 1}^N {\mathit{\boldsymbol{v}}_k^{\rm{T}}} {\mathit{\boldsymbol{R}}^{ - 1}}{\mathit{\boldsymbol{v}}_k} + \frac{N}{2}\ln \det (\mathit{\boldsymbol{R}}) + \frac{{{n_y}N}}{2}\ln 2{\rm{ \mathit{ π} }} $ | (16) |
式中R为协方差矩阵,R的极大似然估计如式(17)所示。高斯-牛顿法通过式(18)、(19)求解未知参数。
| $ \boldsymbol{R}=\frac{1}{N} \sum\limits_{k=1}^N \boldsymbol{v}_k \boldsymbol{v}_k^{\mathrm{T}} $ | (17) |
| $ \begin{array}{l} \mathit{\boldsymbol{M}}\left( {{\mathit{\boldsymbol{Z}}_i}} \right) = \left\{ {{\mathit{\boldsymbol{Z}}_j}\mid {a_{ij}} \ne 0} \right\}\\ {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{i + 1}} = {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_i} + \Delta \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} \end{array} $ | (18) |
| $ \mathit{\boldsymbol{F}}\Delta \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} = - \mathit{\boldsymbol{G}} $ | (19) |
其中F、G分别为Hessian矩阵和梯度向量,即:
| $ \mathit{\boldsymbol{F}} = \sum\limits_{k = 1}^N {{{\left[ {\frac{{\partial \mathit{\boldsymbol{Y}}(k)}}{{\partial \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}}}} \right]}^{\rm{T}}}} {\mathit{\boldsymbol{R}}^{ - 1}}\left[ {\frac{{\partial \mathit{\boldsymbol{Y}}(k)}}{{\partial \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}}}} \right] $ | (20) |
| $ \mathit{\boldsymbol{G}} = - \sum\limits_{k = 1}^N {{{\left[ {\frac{{\partial \mathit{\boldsymbol{Y}}(k)}}{{\partial \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}}}} \right]}^{\rm{T}}}} {\mathit{\boldsymbol{R}}^{ - 1}}[\mathit{\boldsymbol{Z}}(k) - \mathit{\boldsymbol{Y}}(k)] $ | (21) |
式中:
| $ \begin{aligned} & \left(\frac{\partial \boldsymbol{Y}(k)}{\partial \boldsymbol{\varTheta}}\right)_{h j}=\frac{\boldsymbol{Y}\left(k, \boldsymbol{\varTheta}+\delta \boldsymbol{\varTheta}_j\right)_h-\boldsymbol{Y}(k, \boldsymbol{\varTheta})_h}{\delta \boldsymbol{\varTheta}_j}= \\ & \frac{g\left(\hat{\boldsymbol{U}}(k-1, \boldsymbol{\varTheta}+\delta \boldsymbol{\varTheta}), \boldsymbol{W}_1, \boldsymbol{W}_2\right)_h-g\left(\hat{\boldsymbol{U}}(k-1, \boldsymbol{\varTheta}), \boldsymbol{W}_1, \boldsymbol{W}_2\right)_h}{\delta \boldsymbol{\varTheta}_j} \end{aligned} $ | (22) |
传统输出误差法中,输出向量
LM算法由Levenberg[16]和Marquardt[17]提出,其结合了高斯-牛顿法和最速下降法,LM算法在两个梯度方向上优化代价函数,因此包含更宽的收敛范围[4]。与高斯-牛顿法相比,LM算法中添加了一个非负阻尼因子λ,其参数迭代计算如式(23)、(24)所示,其中,Hessian矩阵F和梯度向量G按照式(20)、(21)计算,与高斯-牛顿法一致。当阻尼因子接近于0时,LM算法的性能与高斯-牛顿法一致;而当阻尼因子充分大时,LM算法的性能接近于最速下降法。
| $ {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{i + 1}} = {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_i} + \Delta \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} $ | (23) |
| $ (\boldsymbol{F}+\lambda \boldsymbol{I}) \Delta \boldsymbol{\varTheta}=-\boldsymbol{G} $ | (24) |
传统的LM算法根据代价函数的增减对阻尼因子进行某种调整,例如通过对阻尼因子乘以10或除以10以保证代价函数的下降[4]。然而这种调整得到的阻尼因子并不是最佳的,从而限制了算法性能提升的效果。在本文中,LM算法的每次迭代时采用粒子群算法来求解最佳阻尼因子,即,基于粒子群算法最小化代价函数(25),以确保求解的阻尼因子是局部最优的,或者说是次最优的。需要指出的是,增加粒子群算法的粒子数以及搜索次数后,还可以找到最优的阻尼因子,但是这样会增加计算代价,这是非必要的。本文设置了20个粒子,最多搜索5次。结果表明这样的设置对于改善LM算法的性能是足够的。
| $ J\left( {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{i + 1}}} \right) = J\left( {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_i} + \Delta \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} \right) = {J_1}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_i}, {\lambda _i}, \mathit{\boldsymbol{F}}, \mathit{\boldsymbol{G}}} \right) = {J_2}\left( {{\lambda _i}} \right) $ | (25) |
最终的神经网络LM(NN-LM)参数辨识算法包含了两部分:神经网络训练以及参数估计。整个算法的流程如图 3所示。

|
图 3 神经网络LM(NNLM)算法流程图 Fig. 3 Flow chart of neural network LM(NNLM) algorithm |
算法的求解步骤如下:
1) 从飞行试验数据中提取状态量和输入量,构成神经网络的输入向量U(k);从飞行试验数据中提取输出量,构成神经网络的输出向量Z(k+1),例如本文的应用算例中,U(k),Z(k+1)分别为式(31)、(32);并按照式(9)~(11)进行网络训练。
2) 将网络输入U(k)替换为包含飞行试验数据中状态量、输入量以及待辨识参数Θi的新的输入向量Û(k, Θi),如下文应用算例中的式(33)。并根据神经网络前向传递式(1)~(4)(或者是式(15))进行网络预测,计算网络输出向量Ŷ(k+1)。
3) 基于传统输出误差法,分别根据式(22)计算灵敏度矩阵
4) 将粒子群中每个粒子的适应度函数取为代价函数(25),基于粒子群优化过程,即式(13)、(14)求解局部最优阻尼因子λ。
5) 基于LM算法,根据式(23)、(24)更新待辨识参数Θi。
重复步骤2)~5),直至算法收敛。
3 不稳定飞机模型与仿真试验数据本文应用了De Havilland DHC-2 “BEAVER“测试机[4, 18]的不稳定短周期模型。“BEAVER“飞机的短周期状态方程为:
| $ \begin{gathered} \dot{w}=Z_w w+\left(U_0+Z_q\right) q+Z_{\delta_e} \delta_e \\ \dot{q}=M_w w+M_q q+M_{\delta_e} \delta_e \end{gathered} $ | (26) |
式中:w为纵向速度,q为俯仰角速率,az为纵向加速度,δe为升降舵偏转量。
模型的观测方程为:
| $ \begin{gathered} w=w \\ q=q \\ \dot{w}=Z_w w+\left(U_0+Z_q\right) q+Z_{\delta_e} \delta_e \\ \dot{q}=M_w w+M_q q+M_{\delta_e} \delta_e \\ a_z=Z_w w+Z_q q+Z_{\delta_e} \delta_e \end{gathered} $ | (27) |
式中:q, w为模型的状态变量, δe为输入变量, q, w,
在本文的研究中,这些模型参数构成了待辨识的未知参数向量,即
| $ \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} = {\left[ {{Z_w}, {Z_q}, {Z_{{\delta _e}}}, {M_w}, {M_q}, {M_{{\delta _e}}}} \right]^{\rm{T}}} $ | (28) |
式中Zw, Zq, Zδe, Mw, Mq, Mδe为模型参数,其标称值见表 1。
| 表 1 模型参数的标称值以及基于3种方法的估计结果 Tab. 1 Nominal values of model parameters and estimated results based on three methods |
系统矩阵A如式(29)所示,将U0和表 1中模型参数的标称值Θ代入系统矩阵A,可计算出其两个特征值分别为0.693 4和-5.825 0,其中正的特征值对应着不稳定模态。这种不稳定飞机的仿真飞行试验只能在引入控制器后(闭环条件下)进行。文献中对此模型引入了垂直速度比例反馈控制器(30),并进行了闭环机动试验,其中δp为飞行员输入[4]。
| $ \boldsymbol{A}=\left[\begin{array}{cc} Z_w & U_0+Z_q \\ M_w & M_q \end{array}\right] $ | (29) |
| $ \delta_e=\delta_p+K w $ | (30) |
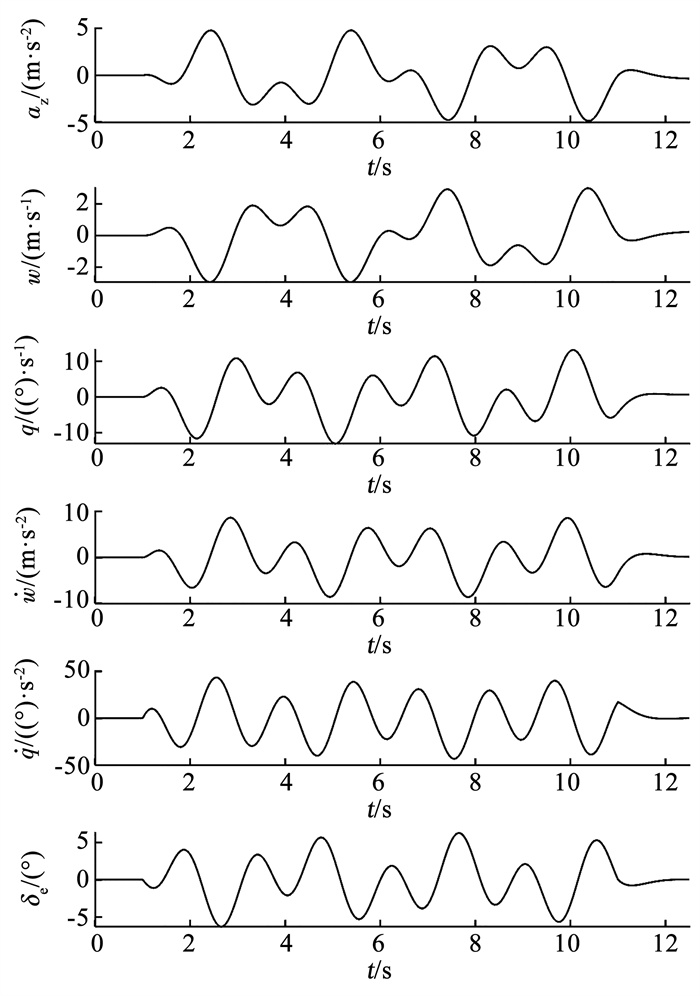
尽管仿真飞行试验是在闭环条件下进行的,本文对模型参数的估计在开环条件下进行,将升降舵偏转量δe视为模型输入,进行开环辨识,在辨识过程中并未使用飞行员输入δp的信息。使用JATEGAONKAR[4]设计的输入信号激励仿真模型,模型的试验数据如图 4所示。
|
图 4 “BEAVER“飞机短周期模型的仿真试验数据 Fig. 4 Simulation test data of short-period model of "BEAVER" aircraft |
本文基于NN-LM方法,从仿真数据中提取模型参数。首先,选取神经网络输入向量为仿真模型第k时刻的状态及输入为
| $ \boldsymbol{U}(k)=\left[w(k), q(k), \dot{w}(k), \dot{q}(k), \delta_e(k)\right]^{\mathrm{T}} $ | (31) |
式中w(k)为k时刻的纵向速度采样值。
选取网络输出向量为仿真模型第k+1时刻的输出Z(k+1)为
| $ \begin{aligned} \boldsymbol{Z}(k+1)= & {[w(k+1), q(k+1), \dot{w}(k+1)} \\ & \left.\dot{q}(k+1), a_z(k+1)\right]^{\mathrm{T}} \end{aligned} $ | (32) |
以最速下降法调整网络参数。在神经网络训练完成后,用于替换“BEAVER“模型的运动方程(26),预测k+1时刻的模型输出Ŷ(k+1)。
接下来,在参数估计的过程中,将神经网络输入向量U(k)中的
| $ \begin{aligned} & \dot{\dot{w}}(k)=Z_w w(k)+\left(U_0+Z_q\right) q(k)+Z_{\delta_e} \delta_e(k) \\ & \dot{\dot{q}}(k)=M_w w(k)+M_q q(k)+M_{\delta_e} \delta_e(k) \\ & \hat{\boldsymbol{U}}(k, \boldsymbol{\varTheta})=\left[w(k), q(k), \dot{w}(k), \dot{\dot{w}}(k), \delta_e(k)\right]^{\mathrm{T}} \end{aligned} $ | (33) |
网络输入U(k)替换为Û(k, Θ)后,网络输出演变成了参数向量Θ的非线性函数,见式(15)。使用粒子群改进的LM算法优化代价函数(16),求解模型参数向量Θ,求解结果见表 1。对于本文研究的不稳定飞机模型,传统的输出误差法无法用于参数估计,JATEGAONKAR[4]应用最小二乘法以及输出误差法的几种变体对其参数进行了估计,表 1列出了其中两种方法,分别为最小二乘法(LS)和人工稳定的输出误差法(SOEM),与本文的估计结果用作对比。其中括号内的数值表示参数估计的标准差,SOME方法中,Zq的估计值有“*”标注,表示在参数估计过程中,Zq需要设置为已知参数。由表 1可知,NN-LM方法的求解结果更接近参数标称值,并且此方法不需要设置任何的已知参数。
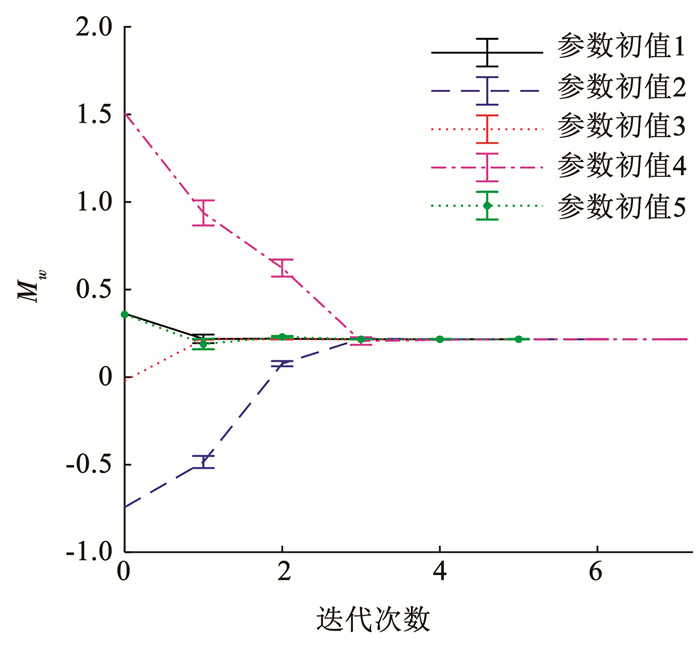
综上所述,传统的输出误差法需要参数的先验信息,将参数初值设置在标称值附近,否则算法将发散或者收敛至局部极小值点。而改进的LM算法具有更宽的收敛范围,即不需要参数的先验信息。本文参数估计过程中,所有的未知参数向量Θ均以[-2, 2]范围内的随机数初始化,从不同的初始值开始迭代时算法均可以收敛。图 5、6为选取不同随机初始值时,参数Zδe和Mw的收敛过程。可以看出,参数初值选取不同时,算法均可在7步内收敛,参数初始值离标称值较远时,算法收敛较慢,参数初始值离标称值较近时,算法收敛较快。

|
图 5 参数Zδe收敛过程以及对应的标准差 Fig. 5 Convergence process of Zδe and corresponding standard deviation |
|
图 6 参数Mw收敛过程以及对应的标准差 Fig. 6 Convergence process of Mw and corresponding standard deviation |
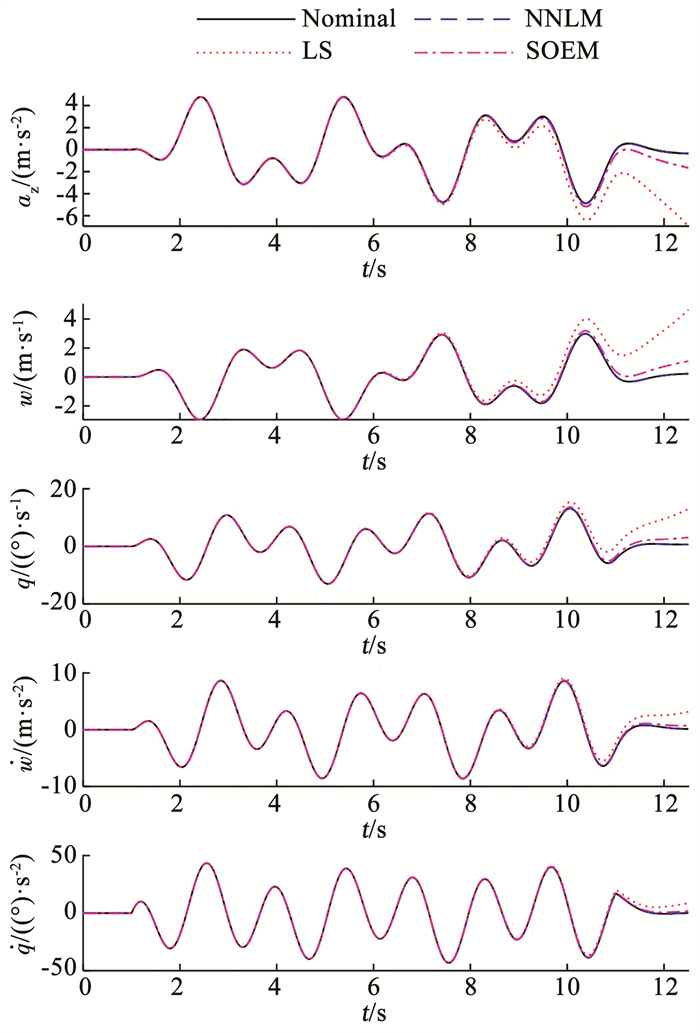
将3种方法估计的参数代入运动方程(26),得到3种估计模型,并且由仿真试验中的升降舵偏转驱动3种模型,模型的输出如图 7所示。并结合Theil不等系数(Theil’s inequality coefficient,TIC)[19]来评价3种模型的输出量对试验值的拟合效果。输出量的TIC定义如式(34),其中zi为仿真试验测量值,yi为模型的输出值,N为离散测量数据点的个数。TIC值越低表示模型输出与试验测量值符合度越高,TIC值低于0.25~0.30代表了较好的拟合效果[4]。3种模型的各个输出量的TIC值见表 2。
| $ \begin{array}{*{20}{c}} {{{{\mathop{\rm TIC}\nolimits} }_i} = \frac{{\sqrt {\frac{1}{N}\sum\limits_{k = 1}^N {{{\left[ {{z_i}\left( {{t_k}} \right) - {y_i}\left( {{t_k}} \right)} \right]}^2}} } }}{{\sqrt {\frac{1}{N}\sum\limits_{k = 1}^N {{{\left[ {{z_i}\left( {{t_k}} \right)} \right]}^2}} } + \sqrt {\frac{1}{N}\sum\limits_{k = 1}^N {{{\left[ {{y_i}\left( {{t_k}} \right)} \right]}^2}} } }}, }\\ {i = 1, 2, \cdots , {n_y}} \end{array} $ | (34) |
|
图 7 3种估计模型的升降舵驱动结果 Fig. 7 Elevator driving results of three estimation models |
| 表 2 3种模型各个输出量的TIC值 Tab. 2 TIC values of each output of three models |
由图 6可以看出,基于NN-LM方法辨识的模型可以很好地拟合仿真试验数据,效果优于传统的最小二乘法(LS)和人工稳定的输出误差方法(SOEM)。由表 2中的TIC值可以看出,对于NN-LM辨识出的模型,其各个输出量的TIC值均低于LS方法和SOME方法,且远小于0.25,说明了此模型的输出对试验测量值的拟合效果更好。
5 结论1) 基于飞行试验数据训练前向神经网络,以神经网络代替飞机的运动方程来预测飞机响应,从而避免了输出误差法中求解运动方程的要求。因而可以应用于不稳定飞机以及大迎角飞行条件下的飞机参数辨识。同时,相比于求解运动方程,计算网络输出的运算成本更小,因此NN-LM算法对于稳定飞机的参数辨识也具有一定的优势。
2) NN-LM算法基于粒子群优化,求解LM算法的最佳阻尼因子,放宽了高斯-牛顿法对参数初值的依赖,待辨识参数的初值可随机选取。本文的算例中,未知参数向量均以随机数初始化,从不同的初始值开始迭代时算法均可以收敛。
3) NN-LM算法保留了输出误差法的精确性。仿真结果表明,改进后的算法可以成功辨识出不稳定飞机的参数。与传统算法相比,NN-LM算法得到的TIC值更低,说明NN-LM算法辨识出的模型可以更好地拟合试验测量值,估计效果有明显改善。
4) NN-LM算法本质上是对高斯-牛顿法的改进,因此还适用于其他的非线性方程求解问题。接下来将进一步围绕稳定以及不稳定飞机的气动系数建模来开展研究。基于NN-LM算法,从真实以及仿真的飞行试验数据中提取气动导数,与风洞试验结果进行对比和补充。
| [1] |
SIMMONS B M, MCCLELLAND H G, WOOLSEY C A. Nonlinear model identification methodology for small, fixed-wing, unmanned aircraft[J]. Journal of Aircraft, 2019, 56(3): 1056. DOI:10.2514/1.C035160 |
| [2] |
郑宇昕. 最优输入设计方法及其在飞行器参数辨识中的应用[D]. 长沙: 国防科技大学, 2018 ZHENG Yuxin. Optimal input design method and aircraft parameter identification[D]. Changsha: National University of Defense Technology, 2018 |
| [3] |
MORELLI E A, KLEIN V. Aircraft system identification: Theory and practice[M]. Williamsburg, VA: Sunflyte Enterprises, 2016. DOI:10.2514/4.861505
|
| [4] |
JATEGAONKAR R V. Flight vehicle system identification: A time-domain methodology[M]. 2nd ed. Reston, VA: American Institute of Aeronautics and Astronautics, Inc., 2015. DOI:10.2514/4.102790
|
| [5] |
郑羽彤. 面向固定翼飞行器的智能辨识算法研究[D]. 长沙: 国防科技大学, 2018 ZHENG Yutong. Research on intelligent identification algorithms based on fixed-wing aircraft[D]. Changsha: National University of Defense Technology, 2018 |
| [6] |
SINGH S, GHOSH A K. Estimation of lateral-directional parameters using neural networks based modified delta method[J]. The Aeronautical Journal, 2007, 111(1124): 659. DOI:10.1017/S0001924000004838 |
| [7] |
黄睿. 基于神经网络的飞行器系统辨识方法研究[D]. 西安: 西北工业大学, 2002 HUANG Rui. Study of aircraft system identification based on neural networks[D]. Xi'an: Northwestern Polytechnical University, 2002 |
| [8] |
HESS R. On the use of back propagation with feed-forward neural networks for the aerodynamic estimation problem[J]. Flight Simulation and Technologies, 1993, 233. DOI:10.2514/6.1993-3638 |
| [9] |
GHOSH A K, RAISINGHANI S C. Parameter estimation from flight data of an unstable aircraft using neural networks[J]. Journal of Aircraft, 2002, 39(5): 892. DOI:10.2514/2.3012 |
| [10] |
PEYADA N K, GHOSH A K. Aircraft parameter estimation using a new filtering technique based upon a neural network and Gauss-Newton method[J]. The Aeronautical Journal, 2009, 113(1142): 243. DOI:10.1017/S0001924000002918 |
| [11] |
王瑜. 基于神经网络的飞机系统辨识研究[D]. 西安: 西北工业大学, 2012 WANG Yu. Aircraft system identification based on neural network[D]. Xi'an: Northwestern Polytechnical University, 2012 |
| [12] |
VERMA H O, PEYADA N K. Parameter estimation of unstable aircraft using extreme learning machine[J]. Defence Science Journal, 2017, 67(6): 603. DOI:10.14429/dsj.67.11401 |
| [13] |
VERMA H O, PEYADA N K. Estimation of aerodynamic parameters near stall using maximum likelihood and extreme learning machine-based methods[J]. The Aeronautical Journal, 2021, 125(1285): 489. DOI:10.1017/aer.2020.95 |
| [14] |
EBERHART R, KENNEDY J. A new optimizer using particle swarm theory[C]//Proceedings of the Sixth International Symposium on Micro Machine and Human Science. Nagoya, Japan: IEEE, 1995: 39. DOI: 10.1109/MHS.1995.494215
|
| [15] |
高卫峰, 罗宇婷, 原杨飞. 求解非线性方程组的智能优化算法综述[J]. 控制与决策, 2021, 36(4): 769. GAO Weifeng, LUO Yuting, YUAN Yangfei. Overview of intelligent optimization algorithms for solving nonlinear equation systems[J]. Control and Decision, 2021, 36(4): 769. DOI:10.13195/j.kzyjc.2020.0379 |
| [16] |
LEVENBERG K. A method for the solution of certain non-linear problems in least squares[J]. Quarterly of Applied Mathematics, 1944, 2(2): 164. DOI:10.1090/qam/10666 |
| [17] |
MARQUARDT D W. An algorithm for least-squares estimation of nonlinear parameters[J]. Journal of the Society for Industrial and Applied Mathematics, 1963, 11(2): 431. DOI:10.1137/0111030 |
| [18] |
JATEGAONKAR R V, THIELECKE F. Evaluation of parameter estimation methods for unstable aircraft[J]. Journal of Aircraft, 1994, 31(3): 510. DOI:10.2514/3.46523 |
| [19] |
RUIST E, THEIL H. Applied economic forecasting[J]. The Swedish Journal of Economics, 1967, 69(1): 83. DOI:10.2307/3439127 |
 2022, Vol. 54
2022, Vol. 54


